Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych
Nr 60
Politechniki Wrocławskiej
Nr 60
Studia i Materiały
Nr 27
2007
maszyny synchroniczne, turbogeneratory,
modelowanie polowo-obwodowe, zwarcie,
współpraca z systemem, stabilność
Piotr KISIELEWSKI
*
, Ludwik ANTAL
∗
ZAKŁÓCENIA PRACY TURBOGENERATORA
SPOWODOWANE ZWARCIAMI W SYSTEMIE
ELEKTROENERGETYCZNYM
W
pracy
przedstawiono
sposób modelowania zakłóceń zwarciowych w systemie
elektroenergetycznym. Symulowano występowanie zakłóceń w postaci zwarć, a następnie zachowanie
się układu po odłączeniu uszkodzonej części systemu. Po odłączeniu zakłócenia kontynuowano
obliczenia aż do zaniknięcia stanu przejściowego w układzie. Przedstawiono przebiegi czasowe
wybranych wielkości elektromechanicznych określających pracę turbogeneratora w stanach
dynamicznych. Obliczenia symulacyjne wykonano za pomocą dwuwymiarowego, polowo-
obwodowego modelu turbogeneratora, umożliwiającego wyznaczenie statycznych oraz dynamicznych
charakterystyk maszyny.
1. WSTĘP
Aktualnie stosowane obwodowe metody analityczne nie uwzględniają w pełni
zjawisk zachodzących w stanach dynamicznych maszyn największych mocy, jakimi są
turbogeneratory. Nieliniowości charakterystyk magnesowania oraz obecność prądów
wirowych w uzwojeniach i elementach masywnych maszyny utrudniają analizę pracy
maszyny w stanach przejściowych. Konieczne w metodach obwodowych uproszczenia
powodują, że stany te analizowane są niezbyt precyzyjnie. Nowe możliwości w tym
względzie, niesie modelowanie polowo-obwodowe. Modele łączące numeryczne
obliczenia pola w domenie elementów skończonych z jednoczesnym rozwiązywaniem
układu równań napięciowych i równania ruchu pozwalają na uwzględnienie w
__________
∗
Politechnika Wrocławska, Instytut Maszyn, Napędów i Pomiarów Elektrycznych, 50-372 Wrocław
ul. Smoluchowskiego 19, piotr.kisielewski@pwr.wroc.pl, ludwik.antal@pwr.wroc.pl,
obliczeniach rzeczywistych własności materiałów konstrukcyjnych oraz parametrów
obwodów zewnętrznych i regulacyjnych. Możliwe jest również obliczanie pól
sprzężonych np. elektromagnetycznych i cieplnych. Stwarza to szansę na dokładniejszą
analizę zjawisk fizycznych w najtrudniejszych dla maszyny stanach pracy. Modele
polowo-obwodowe mają również duże znaczenie dla projektowania optymalnych
konstrukcji maszyn. Parametryzacja modelu pozwala na analizę wpływu dowolnych
czynników, nie wyłączając kształtów, na jej własności eksploatacyjne. Polowo-
obwodowy, dwuwymiarowy model turbogeneratora opisany w [2] opracowano dla
realizacji wymienionych wcześniej celów. Model został zweryfikowany poprzez
wyznaczenie parametrów elektromagnetycznych, podstawowych charakterystyk i
przebiegów prądów oraz momentu w [3, 4, 5]. W niniejszej pracy pokazano wyniki
modelowania
stanów
przejściowych
pracy
turbogeneratora
w
systemie
elektroenergetycznym.
2. MODELOWANIE ZWARĆ
Model i obliczenia turbogeneratora o mocy 500 MVA wykonano za pomocą pakietu
obliczeniowego Flux 9.2.2 [1]. Opis maszyny, jej dane znamionowe oraz geometrię
przedstawiono w [2].
Wykorzystując
opracowany,
dwuwymiarowy,
polowo-obwodowy
model
turbogeneratora wykonano obliczenia zwarć symetrycznych oraz niesymetrycznych.
Uwzględniono nieliniowości materiałów magnetycznych, efekt wypierania prądu oraz
indukowanie się prądów wirowych w elementach litych. Obliczenia wykonano dla
prędkości synchronicznej maszyny w początkowej chwili zwarcia.
Przebiegi prądowe w uzwojeniach stojana zależne są od chwili w której wystąpi
zwarcie udarowe. W przypadku zwarcia maszyny ze stanu jałowego, biorąc pod uwagę
siłę elektromotoryczną, można wyróżnić dwa charakterystyczne przypadki: siła ta
przechodzi przez zero lub jest maksymalna. Jeżeli w chwili zwarcia siła
elektromotoryczna przechodzi przez zero, wówczas składowa aperiodyczna osiąga
wartość maksymalną. W przypadku, gdy siła elektromotoryczna przechodzi przez
maksimum, składowa aperiodyczna prądu zwarciowego nie występuje. Podczas pracy
maszyny w systemie wartości poszczególnych składowych zależą nie tylko od chwili
wystąpienia zwarcia, ale również od obciążenia generatora. W obliczeniach rozważono
różne czasy trwania zwarć dla P
n
oraz 0,5 P
n
.
Przedstawiony w [2] polowo - obwodowy model turbogeneratora został
rozbudowany
aby
umożliwić
symulacje
pracy
maszyny
w
systemie
elektroenergetycznym. W modelu polowym uwzględniono przykładowe parametry
dwutorowej linii przesyłowej oraz transformatora blokowego. Model obwodowy
przedstawiono na rysunku 1.
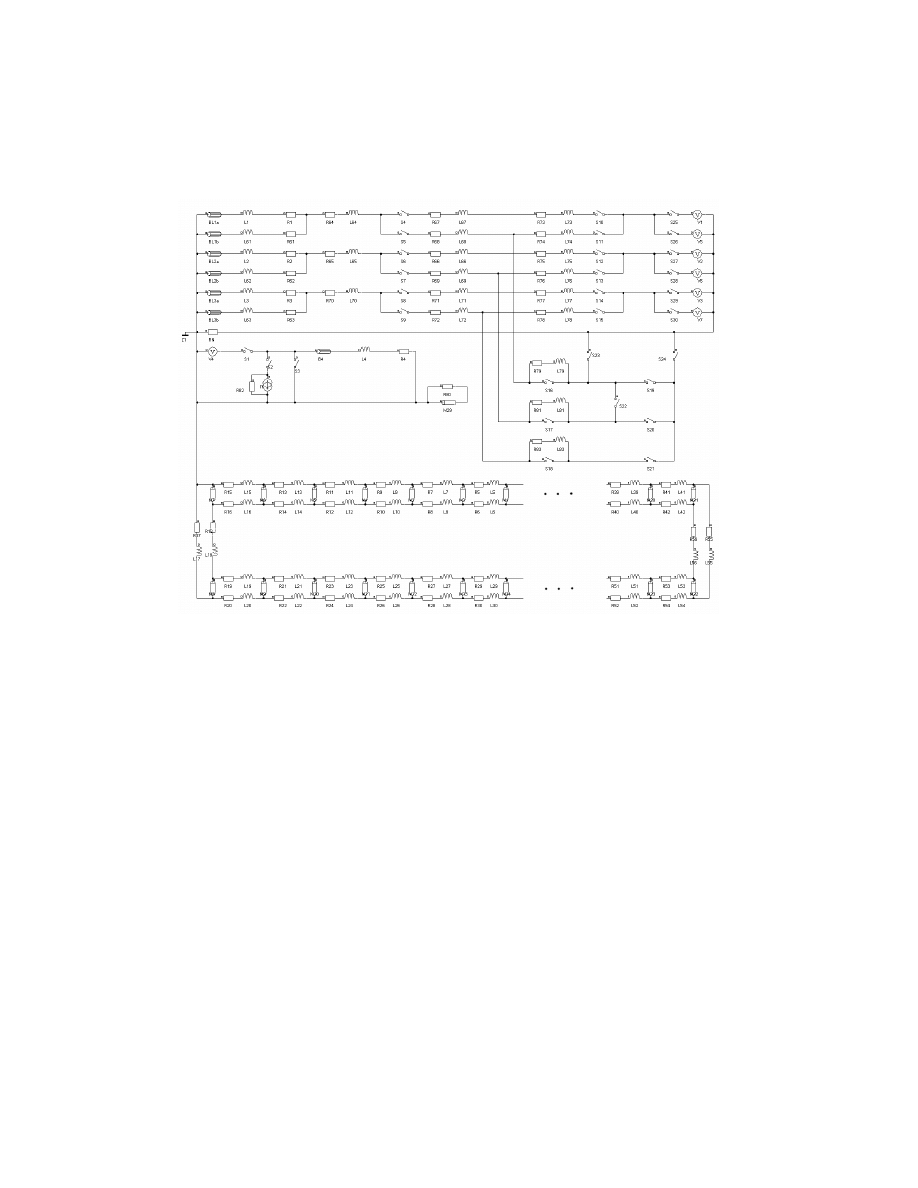
Rys. 1. Część obwodowa modelu maszyny
Fig. 1. Circuit part of the machine model
3. WYNIKI OBLICZEŃ
Dla różnych obciążeń turbogeneratora w wybranych chwilach czasowych zwierano
dwie lub trzy fazy linii przesyłowej. W wyniku symulacji obliczone zostały przebiegi
prądów w uzwojeniach twornika, prędkość oraz moment elektromagnetyczny na wale.
Modelowanie zwarć realizowano poprzez zwieranie jednego z torów linii
przesyłowej, a następnie odłączeniu tego toru po określonym czasie. W obliczeniach
uwzględniono rzeczywisty moment bezwładności turbozespołu. Uzyskane wyniki
obliczeń przedstawiono na rys. 2-16.
-80
-60
-40
-20
0
20
40
60
80
100
0
1
2
3
4
5
6
t [s]
I [kA]
-80
-60
-40
-20
0
20
40
60
80
100
0,00
0,05
0,10
0,15
0,20
t [s]
I [kA]
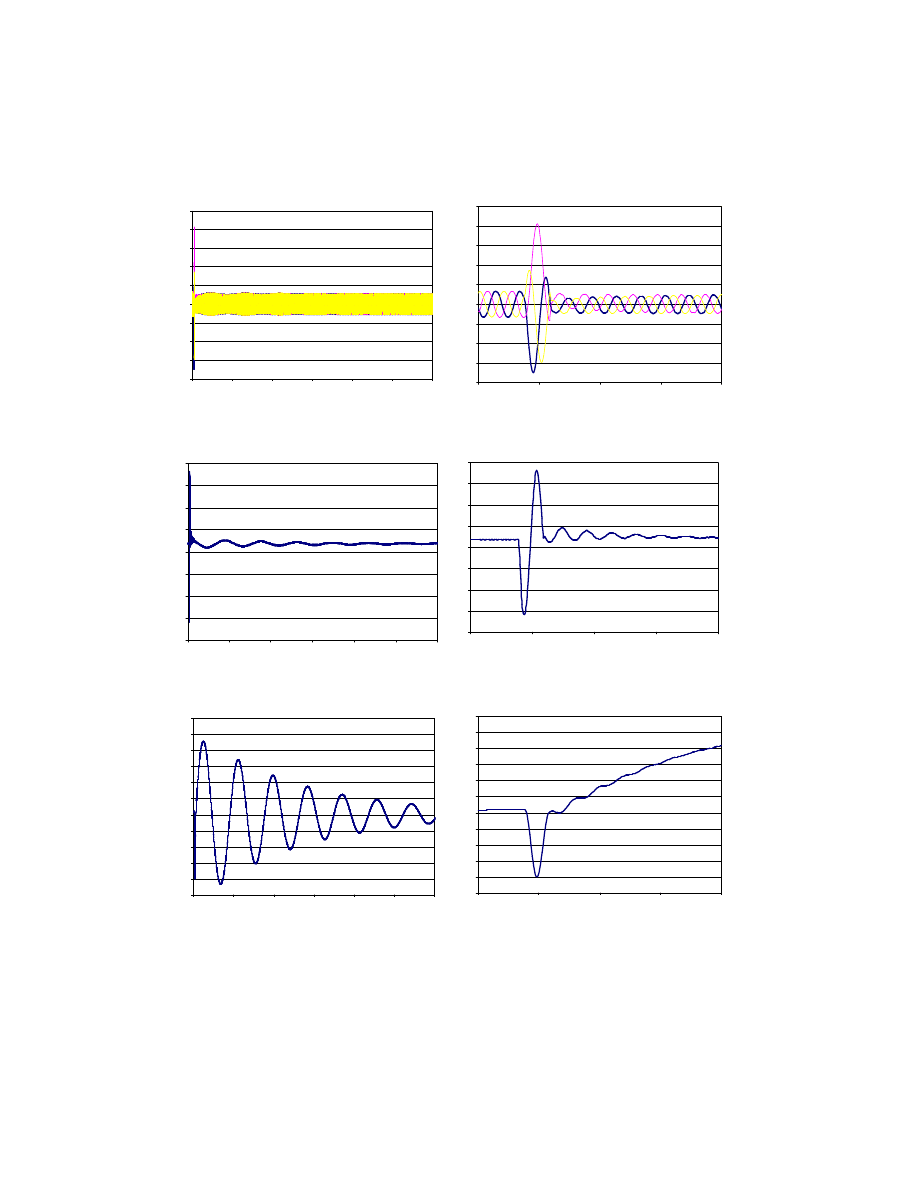
Rys. 2. Prąd stojana dla zwarcia 3-fazowego, t
z
= 20 ms, P = 0,5P
n
Fig. 2. Stator current for 3-phase short circuit, t
z
= 20 ms, P = 0.5P
n
-5
-4
-3
-2
-1
0
1
2
3
0
1
2
3
4
5
6
t [s]
T [MNm ]
-5
-4
-3
-2
-1
0
1
2
3
0,00
0,05
0,10
0,15
0,20
t [s]
T [MNm ]
Rys. 3. Moment elektromagnetyczny dla zwarcia 3-fazowego, t
z
= 20 ms, P = 0,5P
n
Fig. 3. Electromagnetic torque for 3-phase short circuit, t
z
= 20 ms, P = 0.5P
n
2995
2996
2997
2998
2999
3000
3001
3002
3003
3004
3005
3006
0
1
2
3
4
5
6
t [s]
n [obr/m in]
2995
2996
2997
2998
2999
3000
3001
3002
3003
3004
3005
3006
0,00
0,05
0,10
0,15
0,20
t [s]
n [obr/m in]
Rys. 4. Prędkość obrotowa dla zwarcia 3-fazowego, t
z
= 20 ms, P = 0,5P
n
Fig. 4. Rotating speed for 3-phase short circuit, t
z
= 20 ms, P = 0.5P
n
-80
-60
-40
-20
0
20
40
60
80
100
0
1
2
3
4
5
6
t [s]
I [kA]
-80
-60
-40
-20
0
20
40
60
80
100
0,00
0,10
0,20
0,30
0,40
0,50
0,60
t [s]
I [kA]
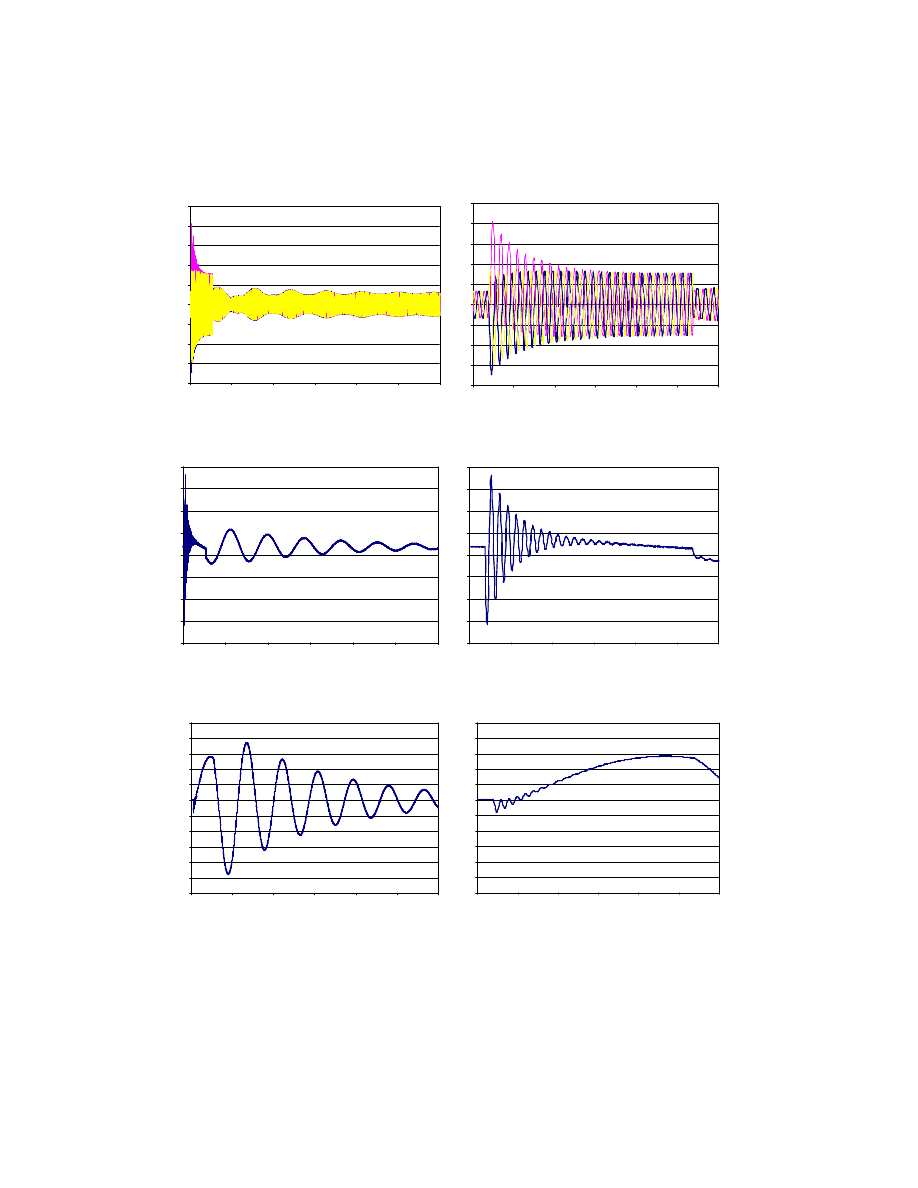
Rys. 5. Prąd stojana dla zwarcia 3-fazowego, t
z
= 500 ms, P = 0,5P
n
Fig. 5. Stator current for 3-phase short circuit, t
z
= 500 ms, P = 0.5P
n
-5
-4
-3
-2
-1
0
1
2
3
0
1
2
3
4
5
6
t [s]
T [MNm ]
-5
-4
-3
-2
-1
0
1
2
3
0,00
0,10
0,20
0,30
0,40
0,50
0,60
t [s]
T [MNm]
Rys. 6. Moment elektromagnetyczny dla zwarcia 3-fazowego, t
z
= 500 ms, P = 0,5P
n
Fig. 6. Electromagnetic torque for 3-phase short circuit, t
z
= 500 ms, P = 0.5P
n
2970
2975
2980
2985
2990
2995
3000
3005
3010
3015
3020
3025
0
1
2
3
4
5
6
t [s]
n [obr/m in]
2970
2975
2980
2985
2990
2995
3000
3005
3010
3015
3020
3025
0,00
0,10
0,20
0,30
0,40
0,50
0,60
t [s]
n [obr/m in]
Rys. 7. Prędkość obrotowa dla zwarcia 3-fazowego, t
z
= 500 ms, P = 0,5P
n
Fig. 7. Rotating speed for 3-phase short circuit, t
z
= 500 ms, P = 0.5P
n
-80
-60
-40
-20
0
20
40
60
80
100
0
1
2
3
4
5
6
t [s]
I [kA]
-80
-60
-40
-20
0
20
40
60
80
100
0,00
0,05
0,10
0,15
0,20
t [s]
I [kA]
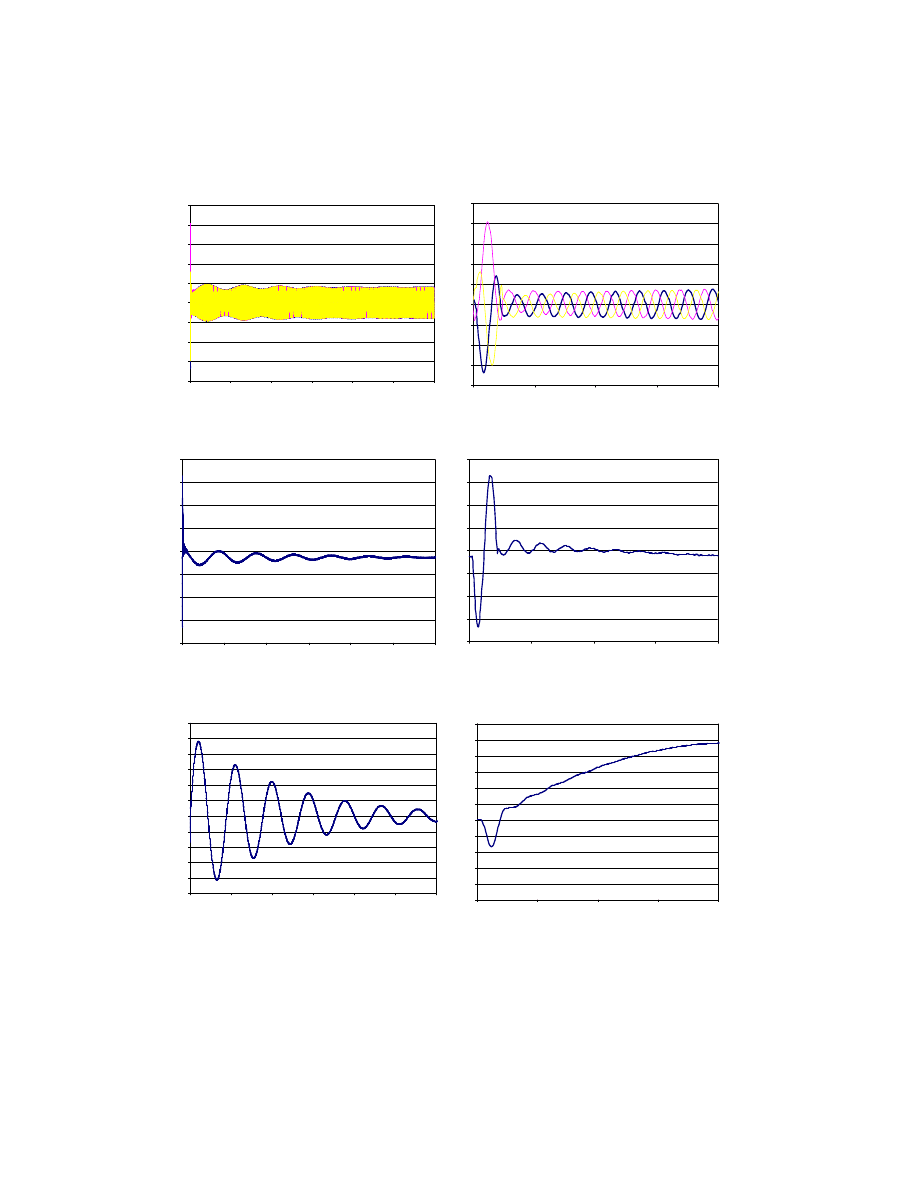
Rys. 8. Prąd stojana dla zwarcia 3-fazowego, t
z
= 20 ms, P = P
n
Fig. 8. Stator current for 3-phase short circuit, t
z
= 20 ms, P = P
n
-5
-4
-3
-2
-1
0
1
2
3
0
1
2
3
4
5
6
t [s]
T [MNm]
-5
-4
-3
-2
-1
0
1
2
3
0,00
0,05
0,10
0,15
0,20
t [s]
T [MNm]
Rys. 9. Moment elektromagnetyczny dla zwarcia 3-fazowego, t
z
= 20 ms, P = P
n
Fig. 9. Electromagnetic torque for 3-phase short circuit, t
z
= 20 ms, P = P
n
2990
2992
2994
2996
2998
3000
3002
3004
3006
3008
3010
3012
0
1
2
3
4
5
6
t [s]
n [obr/m in]
2990
2992
2994
2996
2998
3000
3002
3004
3006
3008
3010
3012
0,00
0,05
0,10
0,15
0,20
t [s]
n [obr/m in]
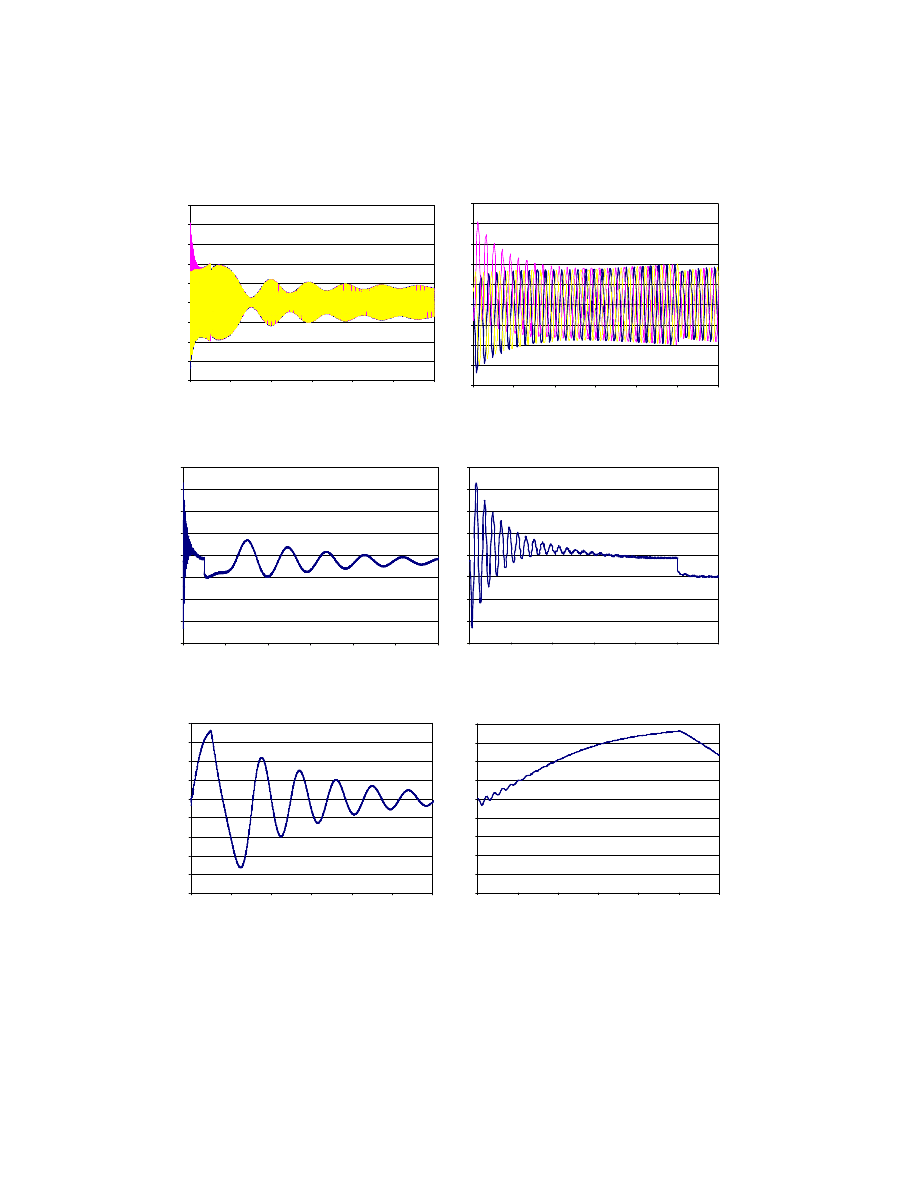
Rys. 10. Prędkość obrotowa dla zwarcia 3-fazowego, t
z
= 20 ms, P = P
n
Fig. 10. Rotating speed for 3-phase short circuit, t
z
= 20 ms, P = P
n
-80
-60
-40
-20
0
20
40
60
80
100
0
1
2
3
4
5
6
t [s]
I [kA]
-80
-60
-40
-20
0
20
40
60
80
100
0,00
0,10
0,20
0,30
0,40
0,50
0,60
t [s]
I [kA]
Rys. 11. Prąd stojana dla zwarcia 3-fazowego, t
z
= 500 ms, P = P
n
Fig. 11. Stator current for 3-phase short circuit, t
z
= 500 ms, P = P
n
-5
-4
-3
-2
-1
0
1
2
3
0
1
2
3
4
5
6
t [s]
T [MNm ]
-5
-4
-3
-2
-1
0
1
2
3
0,00
0,10
0,20
0,30
0,40
0,50
0,60
t [s]
T [MNm ]
Rys. 12. Moment elektromagnetyczny dla zwarcia 3-fazowego, t
z
= 500 ms, P = P
n
Fig. 12. Electromagnetic torque for 3-phase short circuit, t
z
= 500 ms, P = P
n
2950
2960
2970
2980
2990
3000
3010
3020
3030
3040
0
1
2
3
4
5
6
t [s]
n [obr/m in]
2950
2960
2970
2980
2990
3000
3010
3020
3030
3040
0,00
0,10
0,20
0,30
0,40
0,50
0,60
t [s]
n [obr/m in]
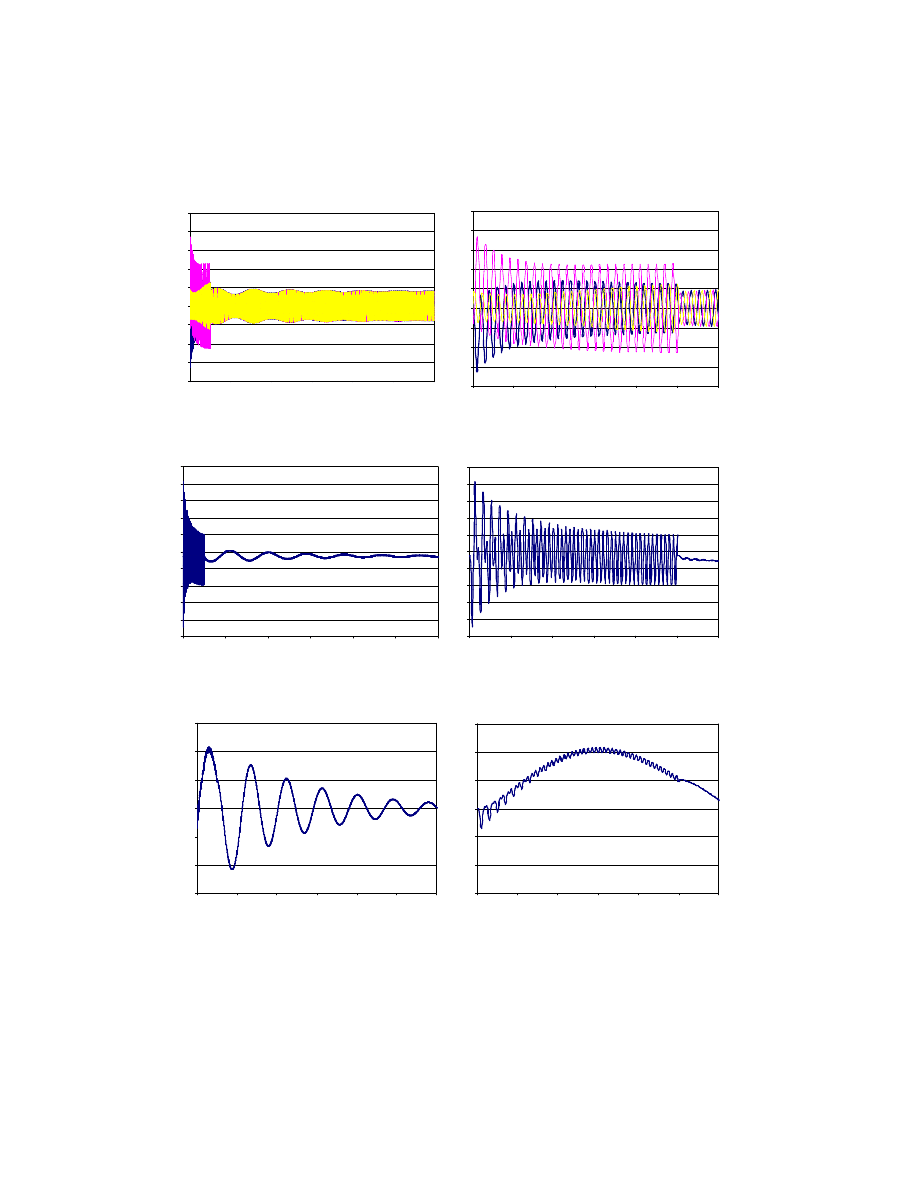
Rys. 13. Prędkość obrotowa dla zwarcia 3-fazowego, t
z
= 500 ms, P = P
n
Fig. 13. Rotating speed for 3-phase short circuit, t
z
= 500 ms, P = P
n
-80
-60
-40
-20
0
20
40
60
80
100
0
1
2
3
4
5
6
t [s]
I [kA]
-80
-60
-40
-20
0
20
40
60
80
100
0,00
0,10
0,20
0,30
0,40
0,50
0,60
t [s]
I [kA]
Rys. 14. Prąd stojana dla zwarcia 2-fazowego, t
z
= 500 ms, P = P
n
Fig. 14. Stator current for 2-phase short circuit, t
z
= 500 ms, P = P
n
-6
-5
-4
-3
-2
-1
0
1
2
3
4
0
1
2
3
4
5
6
t [s]
T [MNm ]
-6
-5
-4
-3
-2
-1
0
1
2
3
4
0,00
0,10
0,20
0,30
0,40
0,50
0,60
t [s]
T [M Nm ]
Rys. 15. Moment elektromagnetyczny dla zwarcia 2-fazowego, t
z
= 500 ms, P = P
n
Fig. 15. Electromagnetic torque for 2-phase short circuit, t
z
= 500 ms, P = P
n
2985
2990
2995
3000
3005
3010
3015
0
1
2
3
4
5
6
t [s]
n [obr/min]
2985
2990
2995
3000
3005
3010
3015
0,00
0,10
0,20
0,30
0,40
0,50
0,60
t [s]
n [obr/m in]
Rys. 16. Prędkość obrotowa dla zwarcia 2-fazowego, t
z
= 500 ms, P = P
n
Fig. 16. Rotating speed for 2-phase short circuit, t
z
= 500 ms, P = P
n
4. PODSUMOWANIE
Uzyskane wyniki obliczeń pokazują, iż pojedyncze zwarcia w systemie, nawet
długotrwałe nie powodują istotnego zaburzenia stabilnej pracy turbogeneratora. Na-
wet zwarcia trwające 500 ms nie spowodują utraty stabilności pojedynczej maszyny.
W rzeczywistości czas zadziałania zabezpieczeń zwarciowych jest znacznie mniejszy.
Bardzo duża bezwładność układu turbogeneratora i turbiny parowej uniemożliwiają,
pomimo dużych zmian momentu elektromagnetycznego, powstanie gwałtownych
zmian prędkości, co sprzyja utrzymaniu maszyny w synchronizmie po odłączeniu
zakłócenia. Zakłócenia takie powodują powstanie udarów prądów i momentu oraz
kołysań maszyny w systemie elektroenergetycznym. Jeżeli pozostałe generatory
w systemie poddane są kołysaniom, zwarcia na linii zasilającej badanego generatora
mogą przyczynić się do utraty stabilności systemu.
LITERATURA
[1] CEDRAT, FLUX® 9.20 User’s guide, November 2005.
[2] KISIELEWSKI P., ANTAL L.:
Polowo-obwodowy model turbogeneratora, Prace Nauk. IMNiPE
PWr. nr 59, SiM nr 26, 2006, s. 53 – 60.
[3] KISIELEWSKI P., ANTAL L.: Weryfikacja pomiarowa obliczonych charakterystyk statycznych
turbogeneratora,
Zeszyty Problemowe BOBRME "Komel nr 77, 2007. s. 167 – 170.
[4] KISIELEWSKI P., ANTAL L.: Przebiegi prądów w obwodach zwartych wirnika turbogeneratora
w czasie zwarcia udarowego
, XLIII Międzynarodowe Sympozjum Maszyn Elektrycznych, Poznań
2007, s. 273 – 276.
[5] KISIELEWSKI P., ANTAL L.:
Zjawiska w turbogeneratorze przy udarowym zwarciu symetrycznym,
Prace Nauk. IMNiPE PWr. nr 59, SiM nr 26, 2006, s. 61 – 68.
[6] RAMIREZ C., TU XUAN M., SIMOND J., SCHAFER D., STEPHAN C.: Synchronous machines
parameters determination using finite element method
, International Conference on Electrical Ma-
chines. ICEM 2000, 28-30 August 2000, Espoo, Finland, ref. 1130,
PERTURBATIONS IN THE TURBOGENERATOR WORK CAUSED BY SHORT-
CIRCUITS IN POWER SYSTEM
The paper presents procedure of modeling perturbations in the turbogenerator work in power system.
The examples transients of currents, torques and rotating speeds during the 2-phase and 3-phase short
circuits were showed. Different powers of machine during the short circuits were considered.
Praca naukowa finansowana ze środków na naukę w latach 2007-2009 jako projekt badawczy Nr
N511 021 32/4169.