Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych

Nr 58

Politechniki Wrocławskiej

Nr 58

Studia i Materiały Nr

25

2005

__________

nadprzewodnictwo, maszyny elektryczne, synchroniczne,

turbogeneratory, projektowanie

Ludwik ANTAL

F

*

GENERATORY NADPRZEWODNIKOWE

Omówiono niektóre wyniki prac badawczych nad konstrukcją generatorów nadprzewodnikowych

realizowanych w Instytucie Maszyn, Napędów i Pomiarów Elektrycznych. Generatory nadprzewod-
nikowe to bezżłobkowe maszyny synchroniczne z nadprzewodzącym uzwojeniem wzbudzenia. Ma-
szyny takie umożliwiają przekroczenie obecnych granic mocy znamionowych. Specyficzna kon-
strukcja tych ma-szyn wymusza konieczność opracowania nowych metod projektowania.
Opracowanie takiej metody wymagało wykonania obliczeń pól elektromagnetycznych uzwojeń i
ekranów maszyny. Wykonano obliczenia analityczne i numeryczne pól oraz parametrów maszyny i
porównano ich wyniki z wynikami pomiarów na modelu bezżłobkowego uzwojenia twornika z cy-
lindrycznymi ekranami elektromagnetycznymi. Opracowana w Instytucie metodyka obliczeń elek-
tromagnetycznych, stanowiąca zasadniczą część metody projektowania generatorów nadprzewodni-
kowych, została pomyślnie zweryfikowana wynikami eksperymentów wykonanych na modelach
maszyn nadprzewodnikowych wykonanych przez innych uczestników programu międzynarodowego
„INTERKRIOLEP”. Jej podstawowe elementy omówiono w niniejszej pracy.

1. WSTĘP

W latach siedemdziesiątych przodujące w budowie turbogeneratorów firmy

(„Brown Boveri”, „General Electric”, „Kraftwerk Union”, „Alsthom-Atlantique”,
„Westinghouse”, „Elektrosila”) osiągnęły graniczne dla wówczas stosowanych mate-
riałów moce znamionowe turbogeneratorów (

∼1200 MVA dla maszyn dwubieguno-

wych i

∼1600 MVA dla maszyn czterobiegunowych) [19], [26] Wzrost mocy znamio-

nowej turbogeneratorów, towarzyszący wzrostowi zapotrzebowania na energię
elektryczną, miał do tej pory charakter wykładniczy [18][37], a rozwój technologiczny
przejawiał się w zmniejszaniu masy względnej materiałów elektromagnetycznie czyn-
nych. Wykorzystanie materiałów czynnych wzrastało głównie poprzez wprowadzanie
bardziej efektywnych systemów chłodzenia. Wzrostowi mocy znamionowych od 30

*

Politechnika Wrocławska, Instytut Maszyn, Napędów i Pomiarów Elektrycznych, 50-372 Wrocław,

ul. Smoluchowskiego 19, [e-mail]

do 660 MVA towarzyszyło zmniejszenie masy względnej z 2,2 do 0,4 kg/kVA [48],
przy zmianie systemu chłodzenia z pośredniego powietrznego, poprzez bezpośredni
wodorowy do bezpośredniego wodnego. W efekcie zmian systemów chłodzenia okład
prądowy zwiększył się z 60 do 250kA/m [42]. Postęp w technologii materiałów ma-
gnetycznych pozwolił na ograniczenie strat mocy w rdzeniach ale indukcja w szczeli-
nie maszyny wzrosła zaledwie do 1T. Zwiększanie wymiarów maszyn doprowadziło
do osiągnięcia granic wyznaczonych przez wytrzymałość mechaniczną materiałów
konstrukcyjnych wirnika i prędkości krytyczne. Wzrost długości wirnika zwiększył
stosunek długości do średnicy do wartości 7:1, co zbliżyło prędkości krytyczne do
prędkości znamionowej stwarzając ryzyko niebezpiecznych drgań [43]. Naprężenia
wirnika będące wynikiem działania sił odśrodkowych, sił elektrodynamicznych, sił
ciężkości i przemieszczeń cieplnych, w powiązaniu z wytrzymałością mechaniczną
ograniczyły średnicę wirnika maszyn dwubiegunowych do 1,3 m [15]. Graniczne war-
tości obciążeń elektromagnetycznych, cieplnych i mechanicznych pozwalały przy-
puszczać, że z uwzględnieniem dalszego rozwoju technologicznego graniczne warto-
ści mocy znamionowych wyniosą, dla maszyn dwubiegunowych 1600-2000 MVA i
2500-3000 MVA dla maszyn czterobiegunowych [34]. Wzrost mocy reaktorów ją-
drowych, a także perspektywy budowy reaktorów termojądrowych wskazywały na
potrzebę budowy turbogeneratorów o mocach 2000-3000 MVA. Również wzrost
wielkości systemów energetycznych, mierzony mocą zainstalowaną (8...40 GW), uza-
sadniał takie moce znamionowe generatorów. Zakładając, że optymalna moc znamio-
nowa jednostki stanowi 4...10% mocy systemu energetycznego [13], uzyskano prze-
dział pożądanych mocy znamionowych 0,8...3,2 GW. Budowa turbogeneratorów o
takich mocach i wysokich współczynnikach techniczno-ekonomicznych byłaby moż-
liwa tylko poprzez istotne zwiększenie wydajności systemów chłodzenia i usunięcie
ograniczenia wzrostu indukcji w szczelinie maszyny. Najbardziej radykalną propozy-

cją spełniającą te postulaty było wykorzystanie nadprzewodników do budowy uzwo-
jenia wzbudzenia i usunięcie zębów z obszaru uzwojenia twornika. W 1965 roku zbu-
dowano i przebadano pierwszy model takiej maszyny o niewielkiej mocy (8 kW) i
odwróconej budowie tzn. z nieruchomym uzwojeniem wzbudzenia wykonanym z
nadprzewodnika i wirującym uzwojeniem twornika [44]. Była to maszyna z piono-
wym wałem. Maszyny z wałem poziomym o mocach 1,5; 2 i 5 MVA zbudowano w
roku 1973 w USA i ZSRR [14], [27], [32]. Do roku 1980 zbudowano w wielu krajach
(Japonia, Francja, Chiny, Niemcy, Czechosłowacja) modele maszyn o mocach
0,3-6,25 MVA. Na początku lat 80-tych przedstawiono wyniki badań maszyn o mo-
cach 20 MVA [17],[24], [36] i 30 MVA [21] , oraz wirników z uzwojeniem nadprze-
wodnikowym dla maszyn o dużych mocach. Opanowanie technologii uzwojeń nad-
przewodnikowych wirujących oraz doświadczalne sprawdzenie konstrukcji maszyn
bezżłobkowych wywołało zainteresowanie przemysłu. Do badań włączyły się naj-
większe koncerny i organizacje rządowe. Firmy „Westinghouse” [20] i „Elektrosiła”
[25] rozpoczęły budowę generatorów o mocach 300 MVA, „Alsthom” - 250 MVA

[40], „Kraftwerk Union” – 400 MVA [29] i „Hitachi” - 50 MVA [49]. Perspektywy
osiągnięcia sukcesu wydawały się być pomyślne. Sformułowane zostały programy
badawcze przewidujące budowę jednostek przemysłowych o mocach przekraczają-
cych 2000 MVA około roku 1990. Prognozowany na lata 90 rozwój energetyki, a
także rozwój turbogeneratorów (w tym maszyn nadprzewodnikowych) nie nastąpił.
Kryzys energetyczny lat 80-tych i przemiany polityczno-ekonomiczne przełomu 89/90
przyniosły rewizję programów badawczych. Niektóre z nich zostały przerwane, inne
utraciły źródła finansowania i swą pierwotną dynamikę. Badania dużych modeli ma-
szyn nadprzewodnikowych kontynuowane są w Niemczech [30], Rosji [35] i Japonii
[28]. Najbardziej dynamicznie prowadzone są prace w ramach zainicjowanego w 1987
roku japońskiego programu Super–GM. W programie tym zrzeszającym organizacje
rządowe, przemysłowe i naukowe, między innymi realizowane są projekty trzech ge-
neratorów o mocy 70 MW różniących się prędkością reakcji wzbudzenia, rodzajem
nadprzewodnika, strukturą ekranów i mechanizmem absorpcji naprężeń termicznych
w wirniku. Ograniczenie badań dużych maszyn nie oznacza jednak rezygnacji z idei
maszyn nadprzewodnikowych. Do roku 1994 zbudowano ponad 30 modeli maszyn
synchronicznych, z czego 14 w przedziale mocy 1-50 MW. Ponadto w latach 90-tych
pojawiły się modele maszyn synchronicznych (5-20 kVA) w pełni nadprzewodniko-
wych ( uzwojenia wzbudzenia i twornika wykonane z nadprzewodników) np. [45],
oraz modele małych maszyn (1,5-3,7 kW) z uzwojeniem wzbudzenia wykonanym
z wysokotemperaturowego nadprzewodnika (HTS) tzn. z nadprzewodnika pracujące-
go w temperaturze ciekłego azotu (77 K) lub ciekłego wodoru (20 K) np. [33]. Rozwój
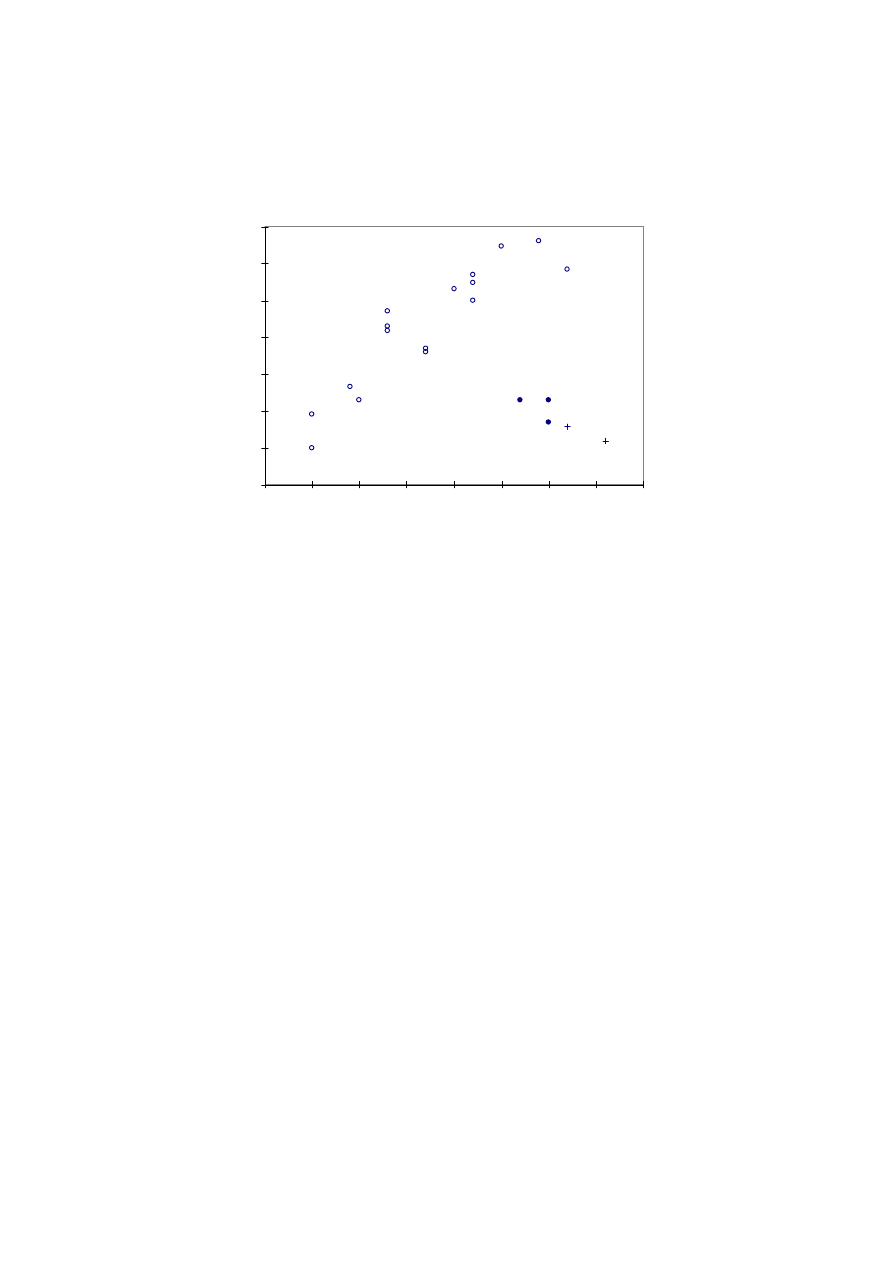
badań synchronicznych maszyn nadprzewodnikowych ilustruje rys. 1.

W ciągu 15 lat badań nad maszynami nadprzewodnikowymi, do 1980 r. zbudowa-

no wiele modeli maszyn. Nie były to jednak konstrukcje optymalne, gdyż nie opraco-
wano właściwych metod projektowania. Ponadto prace nad niektórymi węzłami kon-
strukcyjnymi (a szczególnie nad bezżłobkowym twornikiem) były zaniedbywane
i wyraźnie widoczna była niechęć zespołów badawczych do testowania maszyn przy
pełnym obciążeniu i w warunkach zakłóceń. Najtrudniejszy element maszyny nad-
przewodnikowej, wirujące uzwojenie wzbudzenia, jako element całkowicie nowy w
konstrukcji maszyn elektrycznych skupiał na sobie zainteresowanie niemal wszystkich
zespołów badawczych. Dążąc do szybkiego uzyskania sukcesu budowano obiekty
badawcze,. posługując się nieco zmodyfikowanymi metodami obliczeniowymi ma-
szyn konwencjonalnych. W efekcie uzyskiwane charakterystyki maszyn były odległe
od oczekiwanych. Uzwojenie i rdzeń twornika w wielu modelach niewiele odbiegały
od rozwiązań konwencjonalnych, co nie pozwalało na uzyskanie większej gęstości
mocy w maszynie, czyli podstawowego celu zastosowania nadprzewodnika. Brak
metody projektowania, prowadzący do nieoptymalnych konstrukcji maszyn modelo-
wych, był również przyczyną braku testów obciążeniowych. Możliwość uszkodzenia
kosztownych modeli maszyn skłaniała do ostrożności w trakcie ich badania.

0,00825

30

300

400

0,02

70

0,001

2

10

0,0015

0,4

20

1,5

0,02

0,045

0,02

0,005

0,0037

0,5

50

5

0,0001

0,001

0,01

0,1

1

10

100

1000

1960

1965

1970

1975

1980

1985

1990

1995

2000

lata

mo

c [

M

V

A

]

3x

3x

Rys. 1. Trendy rozwojowe generatorów nadprzewodnikowych;

ο - maszyny z nadprzewodnikowym uzwojeniem wzbudzenia (MARS); • - maszyny w pełni nadprze-

wodnikowe; + - maszyny z nadprzewodnikiem wysokotemperaturowym (HTSC)

Fig. 1. Trends in development of superconducting generators;

ο - machines with superconducting excitation winding (MARS), • - entirely superconducting machines;

+ - machines with high temperature superconductor (HTSC);

Niezależnie od tej krytycznej oceny maszyn modelowych, zaawansowanie prac

teoretycznych było już bardzo duże. Szczególnie rozwinięte obszary badań to:

− trójwymiarowa analiza pola magnetycznego stojana i twornika
− symulacja stanów przejściowych maszyny nadprzewodnikowej
− analiza dyfuzji pola i rozkładu prądów wirowych w ekranach wirnika
− analiza naprężeń wirnika
− dynamika ruchu wieloekranowego wirnika
− ocena strat mocy w nadprzewodniku
− analiza stabilności termicznej nadprzewodnika
− symulacje stanów przejściowych helowego systemu chłodzenia.

Dotychczasowa strategia, szczególnie w kontekście rozpoczętych prac nad maszy-

nami o mocach rzędu 300 MVA, została oceniona jako wysoce ryzykowna. Pojawiły
się więc propozycje [41] intensyfikacji prac badawczych w następujących, kierun-
kach:

− opracowanie podstaw obliczania maszyn nadprzewodnikowych i rozwój synte-

tycznej metody projektowania,

− rozwój technologii wytwarzania materiałów i maszyn,
− budowa węzłów konstrukcyjnych i prototypów maszyn.

Odzew w literaturze, na temat pierwszego z wymienionych kierunków badań, był

niewielki. Badania węzłów konstrukcyjnych były prowadzone w wielu ośrodkach
naukowych nie mających technicznych możliwości budowy i badania kompletnych
modeli maszyn nadprzewodnikowych. Najczęściej badane były rozwiązania konstruk-
cyjne wirującego, nadprzewodnikowego uzwojenia wzbudzenia lub systemu dostar-
czania („sprzęgło helowe”) i rozprowadzania w uzwojeniu ciekłego helu. Podobnie
badane były systemy ekranujące, przy czym modele takich układów, pracujące w
temperaturach normalnych, najczęściej służyły do weryfikacji metod obliczeniowych.
Układ takiego typu, składający się z bezżłobkowego uzwojenia twornika i zestawu
ekranów, był badany również w Instytucie Maszyn i Napędów Elektrycznych Poli-
techniki Wrocławskiej. Zespół badawczy Instytutu od 1972 r uczestniczył w realizacji
problemu węzłowego „Krioelektrotechnika” i programu międzynarodowego
„INTERKRIOLEP” [1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 46]. W ramach tego ostatniego
programu członkowie zespołu uczestniczyli we wspólnych pracach badawczych [5],
demonstracjach i szkołach [39]. Prace badawcze dotyczyły krioturbogeneratora
KTG-5 [50] i obejmowały:

− badania kriogeniczne,
− pomiar drgań w czasie schładzania,
− badanie hydraulicznych oporów wodnego chłodzenia bezżłobkowego uzwoje-

nia twornika,

− pomiar charakterystyk biegu jałowego i zwarcia,
− wyznaczenie reaktancji maszyny.

Demonstracje turbogeneratorów KTG-20 [23] i 2 MW [47] obejmowały szczegó-

łowy opis konstrukcji i prezentacje stanowisk badawczych maszyn i ich węzłów kon-
strukcyjnych.

Opracowana w Instytucie metodyka obliczeń elektromagnetycznych [6] stanowią-

ca zasadniczą część metody projektowania generatorów nadprzewodnikowych została
zweryfikowana wynikami eksperymentów wykonanych na wspomnianym stanowisku
badawczym i modelach maszyn zrealizowanych w programie „INTERKRIOLEP”. Jej
podstawowe elementy, a mianowicie równania konstrukcyjne i obliczanie sprawności,
omówiono w niniejszej pracy.

2. OBLICZENIA ELEKTROMAGNETYCZNE

Podstawowe dane do projektowania maszyny dwubiegunowej to moc znamionowa

S

n

, napięcie znamionowe U

n

, współczynnik mocy cos

ϕ

n

. W celu obliczenia wymiarów

maszyny należy dane znamionowe uzupełnić wielkościami charakteryzującymi obcią-
żalność używanych materiałów, stosowane systemy chłodzenia i rozwiązania kon-
strukcyjne. Wielkościami o takim charakterze są okład lub gęstość prądu, ale również

współczynnik wypełnienia uzwojenia miedzią czy materiałem nadprzewodnikowym.
Od wyboru tych założonych na wstępie wielkości zależy forma równania konstruk-
cyjnego maszyny, które zawsze jest równaniem mocy maszyny, ale może być wyrażo-
ne różnymi wielkościami fizycznymi i konstrukcyjnymi. Równanie konstrukcyjne
pozwala obliczyć główne wymiary maszyny, a te z kolei prowadzą poprzez różnego
rodzaju kryteria elektromagnetyczne, mechaniczne i cieplne do określenia pozostałych
wymiarów elementów maszyny. Sprawdzenie poprawności zaprojektowanej konstruk-
cji, poprzez obliczenie jej charakterystyk i parametrów eksploatacyjnych, kończy cykl
obliczeniowy.

2.1. RÓWNANIE KONSTRUKCYJNE

Równanie mocy w swej klasycznej postaci uzależnia główne wymiary maszyny D,

l od okładu prądowego stojana A

s

i indukcji w szczelinie maszyny B

δ

:

.

S

k B A lD

n

a

s

=

π

δ

2

2

2

n

(1)

W przypadku maszyn bezżłobkowych indukcję w szczelinie należy zastąpić in-

dukcją średnią w obszarze uzwojenia twornika, średnicę stojana - średnią średnicą
twornika, długość - długością obliczeniową twornika. Okład prądowy stojana powi-
nien być większy niż w maszynie konwencjonalnej o takim samym systemie chłodze-
nia, bo ilość miedzi w uzwojeniu bezżłobkowym jest większa. W początkowej fazie
projektowania nie jest możliwe określenie tego powiększenia okładu, chociaż pewną
wskazówkę daje współczynnik wypełnienia uzwojenia twornika miedzią, który zależy
od wartości napięcia znamionowego i systemu chłodzenia. Dla chłodzenia wodnego
i normalnego szeregu napięć znamionowych współczynnik ten przyjmuje wartości z
przedziału 0,20-0,25. Wygodniejszą postać (1) można uzyskać wykorzystując związek
względnej reaktancji synchronicznej z okładem prądowym i indukcją

mo

oa

ci

a

s

a

d

l

l

R

R

B

A

k

x

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

2

0

1

2

2

δ

μ

(2)

i zastępując A

s

w równaniu (1) wyrażeniem

mo

oa

ci

a

a

d

s

l

l

R

R

k

B

x

A

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

2

0

1

2

μ

δ

(3)

Przyjmując dodatkowo, że l

mo

= l

ao

= l

aśr

otrzymuje się

2

2

2

0

1

2

a

aúr

ci

a

d

n

R

l

R

R

B

x

S

π

μ

ω

δ

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

(4)

Zależność (4) pozwala obliczyć główne wymiary twornika maszyny o zadanej

wartości reaktancji synchronicznej, a ponadto pokazuje, że wzrost gęstości mocy s

V

w

maszynie, przy stałej wartości indukcji może odbywać się tylko przez zwiększanie
względnej wartości reaktancji synchronicznej

s

S

V

x B

R

R

V

n

a

d

a

ci

=

=

+

⎛
⎝

⎜

⎞
⎠

⎟

⎡

⎣

⎢

⎢

⎤

⎦

⎥

⎥

2

1

0

2

2

ω

μ

δ

(5)

przy czym
V

a

=

π

R

a

2

l

aśr

- objętość walca o średnich wymiarach uzwojenia twornika.

Wymagana wartość względna reaktancji synchronicznej wynika z kompromisu

między gęstością mocy a stabilnością maszyny i zazwyczaj nie przekracza wartości
0,5. Wymagana wartość indukcji w uzwojeniu twornika zależy z jednej strony od
maksymalnej dopuszczalnej wartości indukcji w uzwojeniu wzbudzenia, a z drugiej
jest ograniczona nasyceniem rdzenia stojana.

Obie wielkości określające obciążenie elektromagnetyczne maszyny, czyli A

s

i B

δ

:

mogą być zastąpione gęstością prądów wzbudzenia i twornika. Wówczas w odróżnie-
niu od równań (1) i (3) będą uwzględnione wymiary przekroju poprzecznego uzwojeń.
Punktem wyjścia jest równanie mocy pozornej

S

I U

n

an

an

= 3

(6)

Możliwe są dwa rozwiązania. Pierwsze korzysta z fazowego napięcia znamiono-

wego:

(

)

U

E

I X

I X

an

fn

an

d

an

d

=

−

−

2

2

cos

sin

ϕ

ϕ

,

(7)

drugie z fazowego napięcia znamionowego przy biegu jałowym:

.

U

E

M I

an

f n

af

f n

=

=

0

0

2

2

ω

(8)

Równanie mocy dla przypadku pierwszego jest funkcją znamionowych wartości

gęstości prądów twornika i wzbudzenia

(

)

S

r

k j R l

k j
k j

l

l

r
r

r

n

a

d wa an

ao ao

wf

fn

wa an

af

d

mo

ao

f

a

fa

n

n

=

−

−
−

⎛
⎝

⎜⎜

⎞
⎠

⎟⎟ −

−

⎛

⎝

⎜

⎜

⎞

⎠

⎟

⎟

π

ωμ

λ

π

λ

λ

ϕ

ϕ

2

0

2 2

2

2

4

3

2

2

3

2

2

12

1

12 6

1
1

cos

sin

(9)

W drugim przypadku w równaniu występuje gęstość znamionowego prądu wzbu-

dzenia przy biegu jałowym j

f0n

( )

(

)

S

r

r

r

r

r

k k j j

R

n

fa

f

a

ac

a

wf

wa an

f n

ao mo

=

−

− +

−

⎛

⎝⎜

⎞

⎠⎟

6

1

1

1

3

1

0

3

3

2

3

0

4

π

ωμ

l

.

(10)

Względna wartość znamionowego prądu wzbudzenia

(

)

i

x

x

fn

d

d

=

+

+

1

2

2

sin arccos

ϕ

(11)

pozwala przeliczyć znamionową gęstość prądu przy biegu jałowym na gęstość zna-
mionową

.

j

j

i

f n

fn

fn

0

=

(12)

Wówczas równania (9) i (10) stają się równoważne, z tym że to drugie wymaga za-

łożenia względnej wartości reaktancji synchronicznej. Podobny charakter mają rów-
nania wyprowadzone z podstawowych zależności

S

I Z

U

Z

Z

X

x

n

an

n

an

n

n

d

d

=

=

=

3

3

2

2

(13)

Wyrażając znamionowy prąd twornika znamionową gęstością prądu otrzymuje się:

(

) (

)

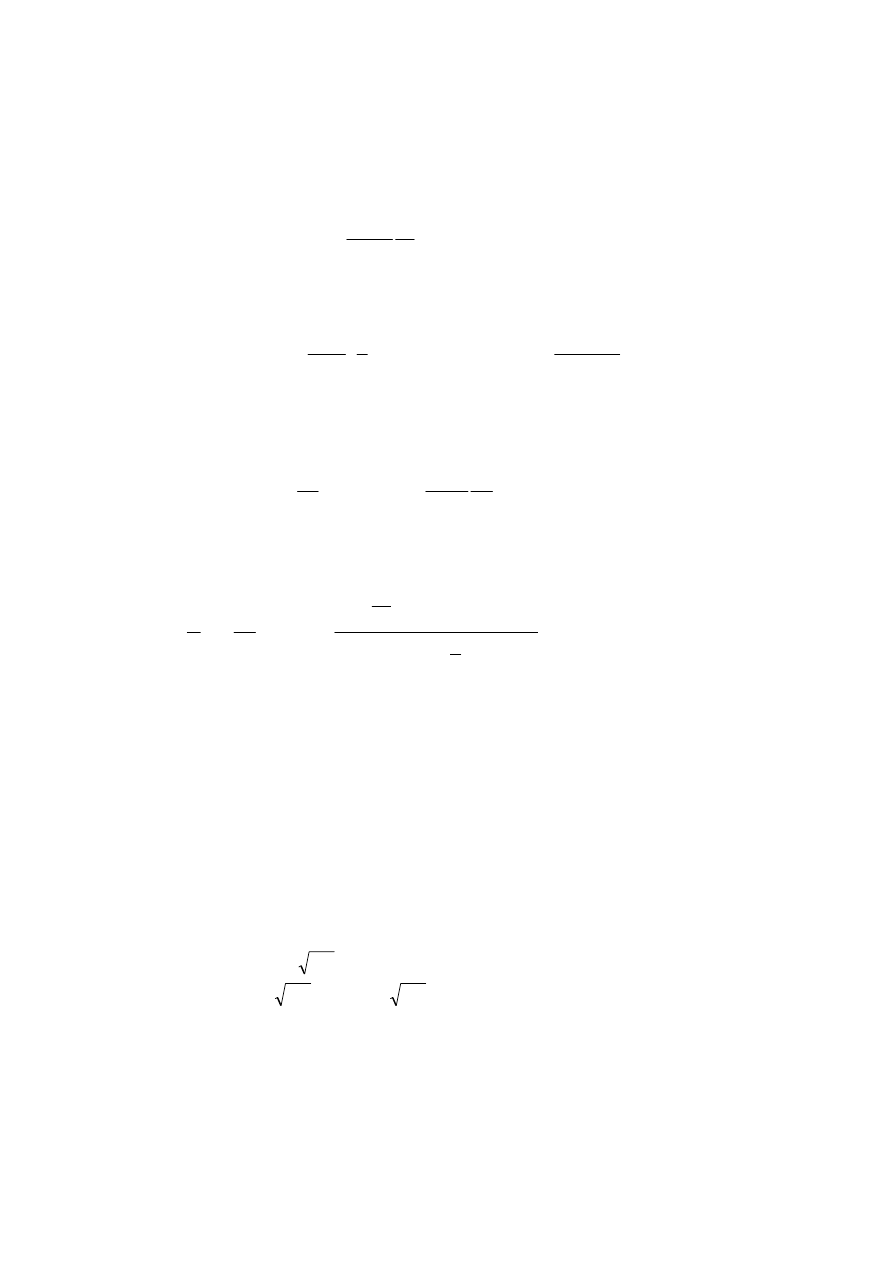
S

x

r

k j

l R

n

d

d

a

wa an

oa

=

−

π ωμ λ

2

0

2 2

2

4

12

1

ao

.

(14)

Po uwzględnieniu zależności dla

λ

d

[6]

(

)

(

)

S

r

r

r

r

k j

x

l R

n

ac

a

a

a

wa an

d

oa

ao

=

−

+ −

+

⎛

⎝⎜

⎞

⎠⎟

3

2

2
3

1

1 4

3

0

2

3 2

3

4

2

4

ωμ

π

(15)

Korzystając ze znamionowej gęstości prądu wzbudzenia przy biegu jałowym, uzy-

skuje się

(

) ( )

(

)

S

r

r

l

l

x k j

l R

n

f

fa

af

d

mo

ao

d

wf

f n

mo

ao

=

−

π

ωμ

λ

λ

2

0

2

2

4

2

0

2

4

6

1

(16)

co po uwzględnieniu zależności dla

λ

af

i

λ

d

[41]prowadzi do wzoru

( )

(

)

(

) (

)

(

)

S

l

l

r

r

r

r

r

r

r

r

r

x k j

l R

n

mo

ao

f

fa

ac

a

a

a

a

a

ac

d

wf

f n

mo

ao

=

−

−

+ −

⎛
⎝

⎜

⎞
⎠

⎟

−

+

+

−

4

1

3

1

1

1 4

3

2
3

1

0

3

2

6

2

3

2

3

4

3 2 2

0

2

4

π

ωμ

(17)

Porównując poszczególne równania można zauważyć, że równanie (14) zawiera

najmniejszą liczbę współczynników wymagających wstępnego określenia i dlatego to
właśnie równanie zostało wybrane do dalszych rozważań. W równaniu tym wartością
poszukiwaną jest iloczyn długości obliczeniowej twornika l

ao

i czwartej potęgi pro-

mienia zewnętrznej powierzchni miedzi twornika R

ao

. Wyznaczenie z tego iloczynu

promienia twornika R

ao

i długości obliczeniowej l

ao

umożliwia analiza prędkości kry-

tycznych. Pełne obliczenia częstotliwości własnych, prędkości krytycznych i form
kołysań należą do grupy obliczeń sprawdzających i wykraczają poza zakres pracy.
Uproszczone obliczenia wykonane dla prostego modelu wirnika po przyjęciu przewi-
dywanych proporcji wymiarowych i cech materiałowych [6] pozwalają sformułować
związki całkowitej długości wirnika l

c

z jego promieniem zewnętrznym R

ao

dla dwóch

przedziałów prędkości obrotowej. I tak

2

1

1

625

,

0

3

,

1

aby

2

,

12

1

,

10

5

,

1

aby

1

,

7

k

n

k

so

c

so

n

k

so

c

n

n

n

R

l

R

n

n

R

l

≤

≤

≤

≤

≥

≤

(18)

Warunki (18) uwzględnione w równaniu (14) prowadzą do zależności dla mniej-

szych mocy

(

)

(

)

S

x

r

r

r

k j

l R

n

d

d

a

sc

ac

wa an

oa

ao

=

⋅

−

−

1 9 10

1

3

2 2

2

4 5

,

,

λ

(19)

i dla mocy większych

(

)

(

)

S

x

r

r

r

k j

l R

n

d

d

a

sc

ac

wa an

oa

ao

=

⋅

−

−

2 7 10

1

3

2 2

2

4 5

,

,

λ

.

(20)

Równanie (19) stosuje się dopóty, dopóki nie zostanie przekroczona średnica ze-

wnętrzna wirnika R

so

≈ 0,6 m, dopuszczalna ze względu na naprężenia. Dalszy wzrost

mocy znamionowej wymaga znacznego wydłużenia maszyny. Stosuje się wówczas
równanie (20). Skoro kryterium stosowalności (19) i (20) dotyczy promienia R

so

, to

słuszne jest przekształcenie równań do postaci [11]

(

)

(

)

( )

R

S x

k

j

K

g r

so

n

d

wa

an

R

a

=

+

⎡

⎣

⎢

⎢

⎤

⎦

⎥

⎥

2

4

2
9

1

δ

(21)

gdzie

δ

- względna wartość „elektromagnetycznej” szczeliny maszyny, zawierającej w sobie

szczelinę mechaniczną i wewnętrzną warstwę izolacji uzwojenia twornika

δ

=

−

R

R

R

ai

so

so

(22)

K

R

- współczynnik liczbowy uwzględniający zakres prędkości krytycznych (tab. 1),

g(r

a

) - funkcja określająca proporcje wymiarowe uzwojenia twornika i jego odległość

od rdzenia stojana

( )

(

)

(

) (

)

4

2

2

3

4

3

3

4

2

2

1

3

2

3

4

1

18

1

a

ac

a

a

a

a

a

d

a

r

r

r

r

r

r

r

r

g

−

+

+

−

=

−

=

π

λ

(23)

Stała K

R

związana jest ze stałą K

L

(tab. 1) pozwalającą obliczyć długość maszyny l

c

so

L

c

R

K

l

216

,

1

=

(24)

Tabela 1. Współczynniki określające wymiary maszyny ze względu na prędkości krytyczne

Table 1. The coefficients the defining dimensions of machine with respect on critical speeds

n n<n

k1

n

k1

<n<n

k2

n>n

k2

n = 0,67 n

k1

n

=

1,36 n

k1

n

=

0,63 n

k2

n

=

1,3 n

k2

K

R

527,5 369,7 305,9

212,1

K

L

5,84 8,33

10,06

14,51

Funkcja g(r

a

) opisująca wpływ grubości twornika na wymiary maszyny zależy nie

tylko od r

a

będącego stosunkiem promieni zewnętrznych uzwojenia twornika ale rów-

nież od względnej odległości miedzi uzwojenia twornika od rdzenia stojana mierzonej
stosunkiem r

ac

= R

ao

/R

ci

. Ten ostatni współczynnik zależy głównie od grubości izolacji

uzwojenia twornika i zmienia się w bardzo małym zakresie. Jego wpływ na wartość
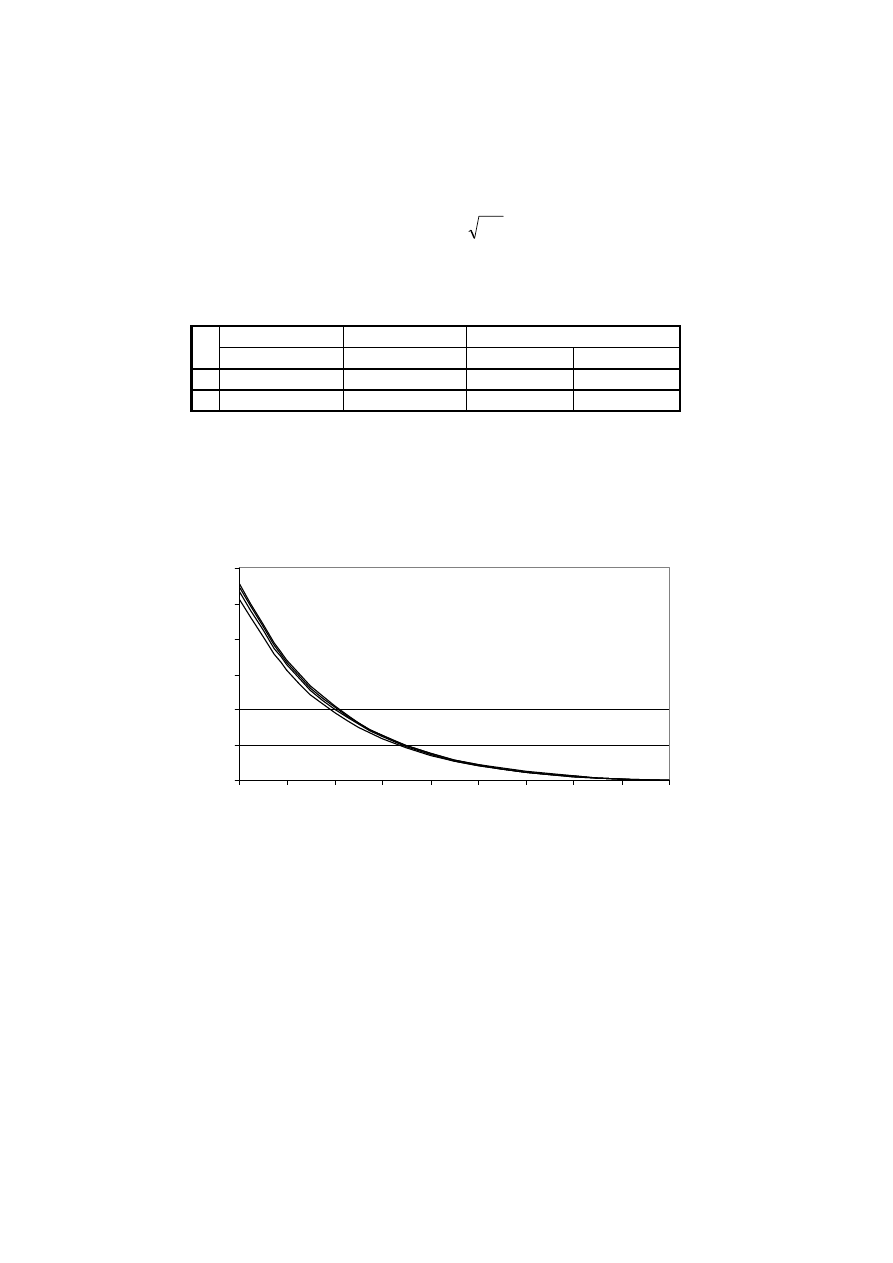
funkcji g(r

a

) jest minimalny (rys. 2).

0

2

4

6

8

10

12

0,50

0,55

0,60

0,65

0,70

0,75

0,80

0,85

0,90

0,95

g (r

a

)

r

ac

= 0,95...1,0

r

a

Rys. 2. Funkcja g(r

a

) w zależności od grubości uzwojenia twornika

Fig. 2. g (r

a

) as a function of the thickness of armature winding

2.2. OBLICZANIE PODSTAWOWYCH WYMIARÓW

Obliczając ze wzoru (21) zewnętrzny promień wirnika należy przyjąć wartości x

d

,

j

an

, k

wa

, r

a

, r

ac

i

δ

. Gęstość prądu twornika przyjmuje się uwzględniając przewidywany

system chłodzenia. Dla bezpośredniego chłodzenia wodą można przyjmować wartości
z przedziału (10-12) 10

6

A/m

2

. Współczynnik wypełnienia uzwojenia twornika mie-

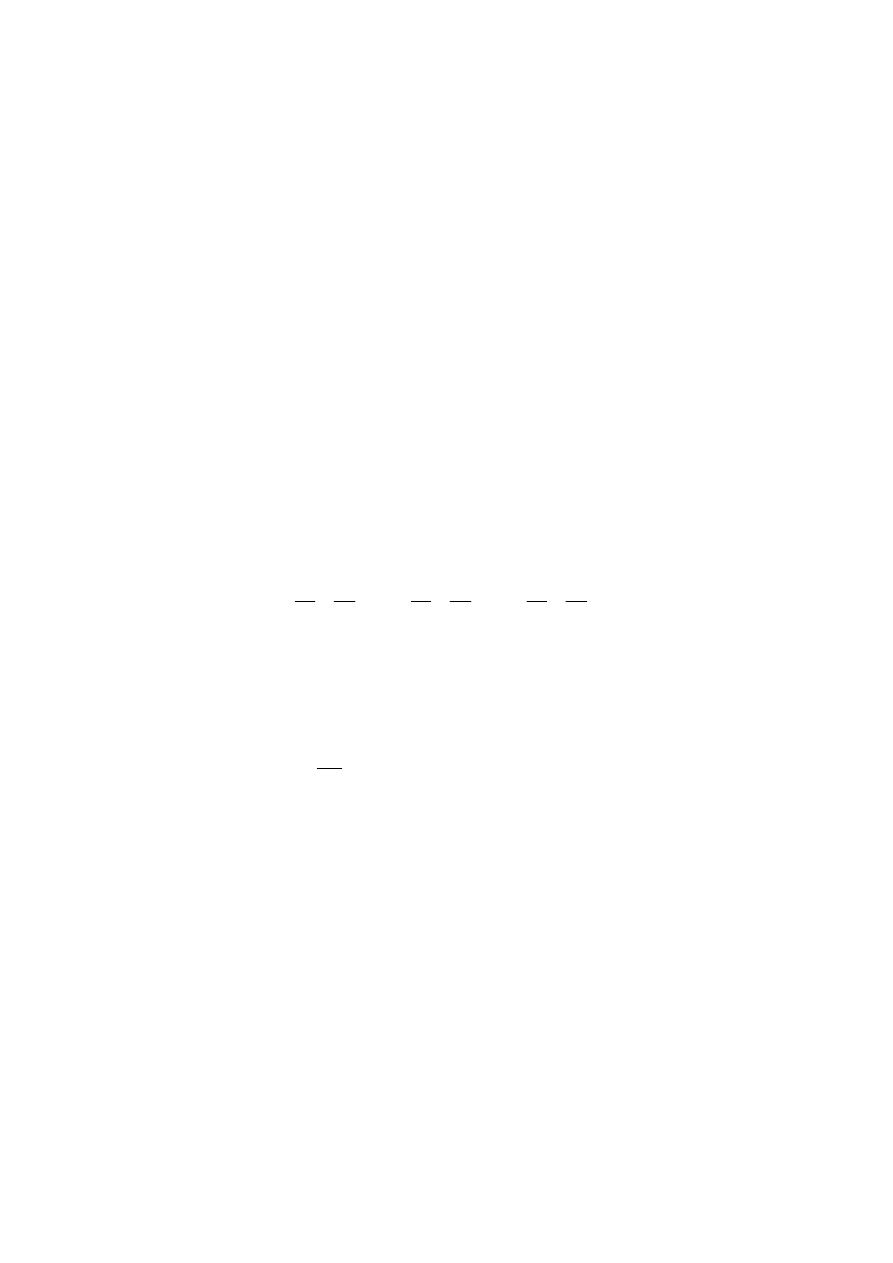
dzią k

wa

jest funkcją napięcia znamionowego i przy zmianie napięcia od 10,5 kV do

35 kV maleje z 0,25 do 0,20. Iloczyn j

an

k

wa

jest gęstością średnią, odnoszącą się do

całej powierzchni przekroju twornika ograniczonej promieniami R

ao

i R

ai

. W różnych

projektach gęstość średnia była przyjmowana z przedziału (1,5-3,0) 10

6

A/m

2

. Współ-

czynnik wymiarowy r

a

zawiera się w przedziale 0,6-0,9, jednakże niezależnie od tego

jaka wartość zostanie wstępnie przyjęta, jest ona w dalszych obliczeniach korygowa-
na. Współczynnik r

ac

jest praktycznie niezależny od mocy znamionowej, gdyż ze

wzrostem mocy rośnie napięcie (a z nim grubość izolacji) oraz promień zewnętrzny
wirnika. Jednoczesna zmiana obu tych czynników powoduje, że r

ac

jest stałe i przyj-

muje wartości z przedziału 0,95-0,97. Reaktancję x

d

wybiera się z przedziału 0,3-0,6.

Jej wartość skutkuje zarówno w parametrach konstrukcyjnych jak i eksploatacyjnych
oraz determinuje wartości reaktancji przejściowych. Względna szczelina

δ

związana

jest z wartością reaktancji x

d

″′. Przyjęcie wartości x

d

i x

d

″′ jednoznacznie wyznacza

wartość

δ

i odwrotnie, przyjęcie x

d

i

δ

przesądza wartość x

d

″′. Wynika to stąd, że przy-

jęte r

a

i r

ac

określają przewodność magnetyczną

λ

d

oraz wspólnie z

δ

, współczynnik

r

sc

. Ten ostatni zaś, wraz z r

a

i r

ac

wyznacza

λ

d

′″. Określenie

λ

d

i

λ

d

′″ przy założonym

x

d

jednoznacznie wyznacza x

d

″′. Wynika to z zależności dla przewodności magnetycz-

nych

λ

d

[6] na podstawie których można zapisać

′

=

′

′′

=

′′

′′′

=

′′′

x
x

x
x

x
x

d

d

d

d

d

d

d

d

d

d

d

d

λ
λ

λ
λ

λ
λ

(25)

Można więc zamiast

δ

założyć x

d

″′ wybierając jej wartość stosownie do przyjętej

wartości x

d

, z przedziału 0,1-0,25, i obliczyć

δ

i r

sc

. Teraz można już obliczyć R

so

z (22) i l

c

z (24). Wymiary innych elementów oblicza się ze współczynników wymia-

rowych:

R

R

r

R

R r

R

R r

ci

sc

sc

ao

ci ac

ai

ao a

=

=

=

(26)

Jeżeli warunek R

so

< 0,6 m jest spełniony, to oblicza się wymiary osiowe zaczyna-

jąc od l

ao

ze wzoru [6]

l

l

ao

c

= 1 216

,

(27)

i następnie wymiary osiowe uzwojeń.

Zewnętrzne promienie ekranu radiacyjnego i uzwojenia wzbudzenia oblicza się

przy użyciu reaktancji x

d

’ i x

d

”. Po przyjęciu x

d

i x

d

″′ przedziały możliwych zmian

pozostałych reaktancji określa nierówność

.

d

d

d

d

x

x

x

x

<

′

<

′′

<

′′′

(27)

Przyjmując wartości x

d

’ i x

d

” spełniające warunek (27) oblicza się z (25) odpo-

wiednie przewodności magnetyczne

λ

i następnie współczynniki r

fa

i r

sc

. Stąd

rc

ci

ro

fa

ao

fo

r

R

R

r

R

R

=

=

(28)

Grubość uzwojenia wzbudzenia wyznacza się biorąc pod uwagę konieczność

wzbudzenia w uzwojeniu twornika napięcia znamionowego oraz nie przekroczenia
krytycznej wartości pola magnetycznego materiału nadprzewodnikowego. Warunek
pierwszy jest spełniony, jeżeli

(

)

r

U

x

x

w

r

r
r

r

r l R k j

f

an

d

d

a

ac

a

a

a

fa mo

ao wf

fn

=

−

+

+

⋅

−

−

+

+

⎛
⎝

⎜

⎞
⎠

⎟

⎛

⎝

⎜

⎜

⎜

⎜⎜

⎞

⎠

⎟

⎟

⎟

⎟⎟

1

1

2

2 6

3

1

1

1

1

2

2

0

2

3

2

3

2

1
3

π

ϕ

ωμ

sin arccos

. (29)

gdzie

(

)

w

R

r U

S

k j

a

ao

a

an

n

wa an

=

−

π

2

2

1

2

(30)

r

fa

= R

fo

/R

ao

.

Współczynnik wypełnienia uzwojenia wzbudzenia nadprzewodnikiem osiąga war-

tości znacznie większe niż taki sam współczynnik dla uzwojenia twornika. Zwykle
przyjmuje się wartości 0,6-0,65. Gęstość prądu wzbudzenia j

fn

zależy od warunków

pracy uzwojenia (B, T) i materiału uzwojenia. Przykładowo dla drutu Nb-Ti pracują-
cego w temperaturze ~

4,3

K w polu o indukcji 6

T można przyjmować

(200-400)·10

6

A/m

2

. Przyjęta wartość indukcji stanowi około połowy wartości kry-

tycznej w temperaturze 4,2 K. Po obliczeniu wymiarów uzwojenia wzbudzenia należy
sprawdzić wartość indukcji w najbardziej narażonym punkcie uzwojenia czyli dla
r = R

fi

i

ϕ

=

θ

f

/2. Chcąc uzyskać założoną wartość indukcji w uzwojeniu wzbudzenia

należy współczynnik r

f

obliczyć z zależności opisującej rozkład pola wzbudzenia [6].

W efekcie obliczona wartość będzie zwykle różnić się od obliczonej z (29), zajdzie
więc potrzeba korekty r

a

i powtarzanie cyklu obliczeń aż do osiągnięcia tych samych

wartości r

f

.

Grubości ekranów wyznacza się z zależności:

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

2

2

2

0

1

1

1

ci

fo

ci

s

s

fo

s

sd

R

R

R

R

R

R

T

T

(31)

przyjmując wymagane wartości stałych czasowych . Dla zewnętrznego ekranu tłumią-
cego należy przyjąć T

s

= (0,1-0,2) s, a dla wewnętrznego ekranu radiacyjnego T

p

= 2 s.

Grubość ekranu magnetycznego stojana oblicza się z dopuszczalnego nagrzania

pakietu blach stalowych lub z częstotliwości drgań własnych rdzenia stojana.

Przyjmując dopuszczalny przyrost temperatury w rdzeniu i współczynnik wnikania

ciepła wyznacza się dopuszczalny poziom strat mocy w rdzeniu i porównuje ze stra-
tami mocy wywołanymi polem magnetycznym obliczanymi jak dla maszyny klasycz-
nej. W wyniku tego porównania uzyskuje się wyrażenie opisujące stosunek promieni
rdzenia, co przy znanym już promieniu wewnętrznym pozwala obliczyć jego grubość
[6].

Na tym etapie obliczeń możliwe już jest określenie struktury uzwojenia twornika

i jego danych, a więc liczby żłobków (podziałek prętowych), szerokości podziałki
prętowej, powierzchni miedzi w pręcie, wymiarów pręta i liczby drutów elementar-
nych. Obliczenia te niewiele różnią się od obliczeń dla maszyny normalnej budowy
i zostały szczegółowo przedstawione w [6].

Obliczenia uzwojenia wzbudzenia należy rozpocząć od wyboru katalogowego

przewodu nadprzewodnikowego, a prąd wzbudzenia dobrać tak by nie przekraczał 2/3
wartości krytycznej. Z drugiej strony przekrój przewodu należy dobierać uwzględnia-
jąc możliwości zestyku ślizgowego czyli nie należy przekraczać prądu 5 kA. Oblicze-
nia związane z rozładowaniem energii zmagazynowanej w uzwojeniu i obliczenia
rezystancji doprowadzeń prądowych, która określa stałą czasową uzwojenia wzbudze-
nia są obliczeniami specyficznymi dla uzwojenia nadprzewodnikowego.

2.3. STRATY MOCY I SPRAWNOŚĆ

Istotne dla obliczenia sprawności maszyny nadprzewodnikowej straty mocy to:

− straty podstawowe i wiroprądowe w uzwojeniu twornika,
− straty w blachowanym rdzeniu stojana,
− straty mechaniczne,
− straty w doprowadzeniach uzwojenia wzbudzenia,
− straty (moc) systemu chłodzenia helowego.
Straty podstawowe w uzwojeniu twornika:

(

)

Δ

P

k

R

r l j

Cup

wa a

ao

a

pr an

=

−

3

1

2

2

2

θ

γ

(32)

gdzie:
l

pr

- całkowita długość pręta uzwojenia twornika.

Straty wiroprądowe w maszynie bezżłobkowej w odróżnieniu od maszyny kon-

wencjonalnej powstają w wyniku działania na pręt uzwojenia pola wypadkowego o
dużej wartości. Wymusza to specyficzną konstrukcję pręta [6], w której stosuje się
przeplot podwójny. Najczęściej przez skręcenie linki miedzianej z drutów o średnicy
mniejszej od 1 mm, z której uformowane są podpręty, i następnie przeplot Roeble’a
podprętów. Taka konstrukcja pozwala uważać, że pojedynczy drut znajduje się w
zewnętrznym polu pulsującym o stałej amplitudzie wewnątrz drutu.

Wiroprądowe straty mocy przy takim założeniu są opisane zależnością [9]:

(

)

Δ

P

r k

R

r

Cuw

wa a

ao

a

oa

śr

=

−

3

8

1

2

0

2

0

2

2

2

ω μ γ

θ

l H

2

(33)

przy czym

r

0

- średnica drutu elementarnego,

H

śr

2

- wartość średnia kwadratu natężenia pola wypadkowego w przekroju tworni-

ka

H

H rdrd

S

śr

S

a

a

2

0

2

=

∫∫

ϕ

(34)

S

a

- pole powierzchni uzwojenia twornika

.

(

)

S

R

r

a

a

ao

a

=

−

3

1

2

2

θ

(35)

Pole wypadkowe dla warunków znamionowych [6] po podniesieniu do kwadratu,

scałkowaniu po powierzchni S

a

i dalszych przekształceniach przyjmuje postać:

(

)(

)

(

)

2

3

0

2

2

2

2

2

1

2

sin

3

2

5

,

0

sin

1

fa

f

fo

f

wf

n

f

fon

d

d

a

ac

fon

úr

r

r

R

k

j

A

x

x

r

r

A

H

−

=

+

+

+

=

−

θ

π

ϕ

(36)

Zastosowanie długości obliczeniowej l

ao

we wzorze (33) zwiększa straty i jest pró-

bą uwzględnienia strat wiroprądowych w połączeniach czołowych.

Straty w rdzeniu stojana oblicza się jak w jarzmie maszyny konwencjonalnej tzn.

(

)

j

jsr

wt

wm

x

ht

hm

x

Fe

m

B

k

k

b

k

k

a

P

2

+

=

Δ

(37)

gdzie masa jarzma

(

)

m

R

R

j

co

= ⋅

−

8 10

3

2

2

π

l

ci

Fe

(38)

a średnia indukcja w jarzmie

( )

B

k j R r r

r

r

r

jśr

wf

fn

fo fc ac

f

c

c

=

⋅

−

−

−

8 3

3

10

1

1

7

2 2

3

(39)

Współczynnik r

c

to stosunek promieni rdzenia R

ci

/R

co

, a współczynniki we wzorze

(37) to parametry blach elektrotechnicznych.

Straty mechaniczne to straty tarcia wirnika o czynnik chłodzący, straty wentyla-

cyjne, straty tarcia w zestyku ślizgowym i straty tarcia w łożyskach. Mogą być jednak
oszacowane jako straty łączne z wymiarów wirnika [6]

Δ

P

R

m

s

≈

⋅

5 12 10

6

4

,

l

o

r

(40)

Straty mocy w doprowadzeniach prądowych uzwojenia wzbudzenia mają niewiel-

ką wartość, ze względu na konstrukcję tych doprowadzeń. Doprowadzenia są konstru-
owane tak by w miarę ich wchodzenia w obszar niskich temperatur zmniejszał się
dopływ ciepła. Efekt taki uzyskuje się poprzez malejący w sposób ciągły ich przekrój i
wydłużanie drogi. Są to więc bardzo różne konstrukcje dla których nie można podać
wzoru ogólnego do obliczania strat. Można je jednak oszacować ze wzoru empirycz-
nego[6]:

Δ

P

I

f

fn

= 7,33

(41)

Moc systemu chłodzenia helowego, wliczana do strat mocy maszyny wynika z za-

potrzebowania na ciekły hel, czyli inaczej mówiąc zależy od sumy strat mocy wydzie-
lających się w strefie chłodzonej. Zależy więc od jakości konstrukcji kriostatu wirni-
ka. W systemach z obiegiem zamkniętym moc ta może być niewielka. Szacuje się ją
ze wzoru [6]

(42)

P

S

ref

n

=

⋅

−

18655

5 110

10

e

,

Tak więc sprawność maszyny nadprzewodnikowej to

∑

∑

+

Δ

+

Δ

+

Δ

+

Δ

+

Δ

=

Δ

+

=

ref

f

m

Fe

Cuw

Cup

n

n

n

n

P

P

P

P

P

P

P

P

S

S

:

gdzie

cos

cos

ϕ

ϕ

η

(43)

2.4. OBLICZENIA SPRAWDZAJĄCE

Obliczenie wymiarów maszyny i struktury uzwojeń z uwzględnieniem wniosków

wynikających z analizy różnych stanów pracy maszyny, stwarza szansę na jej po-
prawną pracę. Nie zwalnia jednak z wykonania obliczeń sprawdzających. Obecnie
obliczenia te wykonuje się najczęściej numerycznie, zwykle metodą elementów skoń-
czonych. Pola elektromagnetyczne, pola naprężeń i pola termiczne są wzajemnie
związane. Siły elektrodynamiczne są źródłem naprężeń, straty mocy generują pola
termiczne, a te znowu pola naprężeń. Najnowsze tendencje idą w kierunku numerycz-
nego powiązania z polami w maszynie zjawisk przejściowych zachodzących w syste-
mie energetycznym [31]. W wyniku takich obliczeń sprawdza się między innymi,
odporność na prądy kolejności przeciwnej, stabilność statyczną i dynamiczną [6].

3. PODSUMOWANIE

Zaproponowana metoda obliczania maszyny bezżłobkowej różni się od metody

klasycznej, w której dla obliczenia podstawowych wymiarów maszyny przy zadanej
mocy zakłada się obciążenia elektromagnetyczne, reprezentowane przez okład prądo-
wy twornika i indukcję w szczelinie. Projektując konstrukcję o radykalnie zmienionej
budowie, nie mamy wiedzy na temat dopuszczalnych obciążeń elektromagnetycznych.
Obie wielkości określające obciążenia elektromagnetyczne maszyny mogą być zastą-
pione gęstościami prądów wzbudzenia i twornika lub lepiej jedną z tych gęstości i
wartością względną reaktancji synchronicznej. Uwzględniając wynikający z analizy
prędkości krytycznych związek długości i promienia wirnika uzyskuje się zależności
pozwalające obliczyć te podstawowe wymiary.

Z analizy zachowania się maszyny w stanach przejściowych wynikają pożądane

wartość reaktancji synchronicznej, reaktancji przejściowych oraz stałych czasowych

ekranów. Użycie tych wartości do obliczenia wymiarów maszyny gwarantuje uzyska-
nie właściwych parametrów.

Rozwiązania analityczne pola magnetostatycznego maszyny bezżłobkowej [6] po-

zwalają wyznaczyć parametry indukcyjne maszyny. Przyjęcie wartości reaktancji
(synchronicznej i przejściowych), oraz wymaganych ze względu na tłumienie kołysań
i skuteczność ekranowania wartości stałych czasowych ekranów, pozwala obliczyć
wszystkie główne wymiary maszyny dla zadanych mocy i napięcia. Określenie wy-
miarów umożliwia obliczenie (najlepiej metodami numerycznymi) obciążeń elektro-
magnetycznych, mechanicznych i cieplnych elementów maszyny oraz zbadanie wła-
sności eksploatacyjnych.

LITERATURA

[1] Antal L., Analiza pola reakcji twornika bezżłobkowej maszyny synchronicznej, Pr. Nauk. Instytutu

Układów Elektromaszynowych PWr. nr 16, Studia i materiały nr 9, 1974

[2] Antal L., Analiza pola wzbudzenia bezżłobkowej maszyny synchronicznej, Pr. Nauk. Instytutu Ukła-

dów Elektromaszynowych PWr. nr 16, Studia i materiały nr 9, 1974

[3] Antal L., Badanie cylindrycznych ekranów elektromagnetycznych, bezżłobkowej maszyny synchro-

nicznej, Prace Naukowe Instytutu Układów Elektromaszynowych Politechniki Wrocławskiej nr 43,
Studia i Materiały nr 18,1993,

[4] Antal L., Długość obliczeniowa synchronicznej maszyny bezżłobkowej, Archiwum Elektrotechniki,

Tom XXIX, zeszyt 3, 1980,

[5] Antal L., Karwacki W., Badania eksperymentalne krioturbogeneratora KTG-5 „Škoda” Raport

Instytutu Układów Elektromaszynowych PWr seria SPR nr 41/84

[6] Antal L., Obliczenia elektromagnetyczne bezżłobkowych maszyn synchronicznych z nadprzewodzą-

cym uzwojeniem wzbudzenia, Oficyna Wydawnicza Politechniki Wrocławskiej, Wrocław, 1999

[7] Antal L., Parametry indukcyjne bezżłobkowej maszyny synchronicznej, Archiwum Elektrotechniki,

Tom XXIX, zeszyt 3, 1980

[8] Antal L., Rozkład pola magnetycznego nad powierzchnią ekranu elektromagnetycznego, cylindrycz-

nego, Pr. Nauk. Instytutu Układów Elektromaszynowych PWr nr 43, Studia i Materiały nr 18,1993

[9] Antal L., Siwiec G.: Wiroprądowe straty mocy w bezżłobkowym uzwojeniu twornika nad-

przewodnikowej maszyny synchronicznej. Rozpr. Elektrot. t.29 z.1, 1983

[10] Antal L., Uczkiewicz J.: Zarys metody projektowania turbogeneratorów nadprzewodnikowych. Prz.

Elektrot. 1980 r.56 nr 8/9

[11] Antal L.: Podstawowe aspekty projektowania nadprzewodnikowych maszyn synchronicznych. W:

XX Sympozjum Maszyn Elektrycznych., Maszyny synchroniczne, Kazimierz Dolny, 28-29 maja
1984

[12] Antal L.: Straty mocy w bezżłobkowym uzwojeniu twornika maszyny synchronicznej. W: Nadprze-

wodnikowe maszyny elektryczne. Cz. II, Pr. Nauk. Instytutu Układów Elektromaszynowych PWr
1982 nr 36, Konferencje nr 9

[13] Baldwin M. S., Starrett C. C., The potentied impact of superconducting turbine-generators on the

electric utility industry, Proc. American Power Conf., Chicago, 1974

[14] Bejan A., Keim T. A., Kirtley J. L. Jr., Smith J. L. Jr., Thullen P., Wilson G. L., Superconducting

alternator test results, Cryogenic Engineering Conference, Atlanta, 1973,B-2

[15] Bogner G., Kullmann D., Electrical machines with superconductors. Part 3, Turbogenerators,

Simens Forsch. -u. Entwickl., 5, 1976

[16] Bumby J.R., Superconducting rotating electrical machines, Clarendon Press, Oxford, 1983
[17] Bykov V. M., Danilevič J. B., Glebov I. A., 20 MVA superconducting generator and its test results,

A.I.M., CEM, V-61, Liege, 1981

[18] Cunningham J. C. , Development of a single generator lead box for 2000MVA and greater, IEEE

PES Summer Meeting, San Francisco, 1975

[19] Elston C. W., Holley C. H., Perpectives on the future of large steam turbine-generators., World

electrotechnical congress, Report 1.02, 1977

[20] Flick C., Superconductig generator development, IEEE CECON ’79 Proc., New York, 1980
[21] Fujino H., Technical overview of japanese superconducting generator development program, IEEE

Trans. on Magnetics, vol. 19, no. 3, 1983

[22] Furuyama M., Kirtley J., L., Jr., Transient stability of superconducting alternators, IEEE Trans. on

PAS, vol. PAS-94, no. 2, 1975

[23] Glebov I. A , Bykov V. M., Danilevič J. B., Šachtarin V. N., Konstrukcija i rezultaty stendovych

ispytanij sverchprovodnikovogo turbogeneratora moščnosti 20 MBA, Prace Naukowe IUE PWr,
nr 36, seria: Konferencje nr 9, 1982

[24] Glebov I. A , Bykov V. M., Danilevič J. B., Šachtarin V. N., Konstrukcija i rezultaty stendovych

ispytanij sverchprovodnikovogo turbogeneratora moščnosti 20 MVA, Prace Naukowe IUE PWr,

[25] Glebov I. A., Šachtarin V. N., High efficiency and low consumption material electrical generators,

IEEE Trans. on Magnetics, vol. 19, no. 3, 1983

[26] Glebov I. A., Danilevič Ja. B., Mamikonjanc L. G., Problemy generatorostroenia na Vsemirnom

elektrotehničeskom kongresse, Električestvo, No 12, 1977

[27] Glebov I. A., Danilevič Ja. B., Problemy krupnogo generatorostroenija v svjazi s ispolzovaniem

sverchprovodimosti, Izv. AN SSSR. Energetika i Transport, no. 3,1975

[28] Hiroki C. i inni, R&D of superconductors for 70MW Class Generators, IEEE Transactions on

Magnetics Vol: 32 no: 4, 1996

[29] Intichar L., Lambrecht D., Technical overwiev of the german program to develop superconducting

AC generatos, IEEE Trans. on Magnetics, vol. 19, no. 3, 1983

[30] Intichar L.; Kulig T.S., Development of turbogenerators in recent years and in the future,

Proceedings. International Conference on the Evolution and Modern Aspects of Synchronous
Machines, Zurich, 1991

[31] Japanese Generator Project, Vector Field, Electromagnetics Newsletter, Vol. 11, no. 2, Winter,

1995

[32] Jones C. K., Litz D. C., Cryogenic Consideration in the development and operation of a large syn-

chronous generator, Cryogenic Engineering Conference, Atlanta, 1973,B-2

[33] Joshi C.H.; Prum C.B.; Schiferl R.F.; Driscoll D.I., Demonstration of two synchronous motors using

high temperature superconducting field coils, IEEE Transactions on Applied Superconductivity
Vol: 5 no: 2, 1995

[34] Joyce J. S., Engelke W., Lambrecht D., Will large turbine generators of the future require super-

conducting field turbogenerators?, Proc. American Power Conf., 1977

[35] Khutoretsky G.M.; Filippov I.F.; Varschawsky V.D.; Rybin Yu.L.; Stefanovich S.G., 300 MWA

superconducting generator and first experiments of its cooling-down, 11

th

International Conference

on Magnet Technology, Tsukuba, 1989

[36] Laskaris T. E., Schoch K. F., Superconducting rotor development for a 20 MVA generator , IEEE

Trans. on PAS, vol. 99, no. 6, 1980

[37] Pannen E., Granzen im Turbogeneratorenbau, Elektrizitätswirtschaft, Jg. 75, nr 20, 1976
[38] Parker J. H., Towne R. A., Design of large superconducting turbine generators for electric utility

application, IEEE Trans. on PAS, vol. 98, no. 6, 1979

[39] Praca zbiorowa, Doklady školy „Sverchprovodimost v elektroenergetike i elektrotechnike”, Cz. I i

II, Varna, 1982

[40] Sabrié J. L., Goyer J., Technical overwiev of the french program, IEEE Trans. on Magnetics, vol.

19, no. 3, 1983

[41] Smith J. L. Jr., Overview of the development of superconducting synchronous generators, IEEE

Trans. on Magnetics, vol. 19, no. 3, 1983

[42] Spooner E., Fully slotless turbogenerators, Proc. IEE, Vol. 120,1973
[43] Steel J. G., New design of large generators, Engineering, Jan. 1978
[44] Stekly Z. J. J., Woodson H. H., Hatch A. M., Hoppie L. O., Halas E., A study of alternators with

superconducting field windings: II - Experiment, IEEE Trans. on PAS, vol. 85, no. 3, 1966

[45] Tixador P., Brunet Y., Vedrine P., Laumond Y., Sabrié J. L., Electrical test on a fully

superconducting synchronous machine, IEEE Transactions on Magnetics Vol: 27 no: 2, 1991

[46] Uczkiewicz J. Cylindryczne ekrany wielowarstwowe, Archiwum Elektrotechniki, t. XXVIII, z. 4,

1979

[47] Verkin B., I., Pogorelov A., V., Fomin B., I., Chutoreckij G. M., Filippov I., F., Papakin V., F.,

Turbogenerator so sverchprovodjaščej obmotkoj vozbuždenija moščnostju 2 MW, Izvestvija FTINT,
Charkov, 1977

[48] Vickers V. J., Recent trends in turbogenerators. Proc. IEE, Vol. 121, 1974
[49] Yamaguchi K., Maki N., Numata S., Sanematsu T., Manufacture of a 50 MVA superconducting

rotor, 9

th

ICEC, Kobe, 1982

[50] Žižek F., Kurka J., Erforschung der Applikationen der Supraleitfähigkeit im Škoda-Konzern, Skoda

Revue nr 2, 1979

W realizacji tematu w różnym stopniu i w różnych latach uczestniczyli:
Ludwik Antal, Wojciech Baranowski, Władysław Karwacki, Grazyna Siwiec, Zdzisław Teodorowicz,
Jacek Uczkiewicz, Piotr Żudrak

SUPERCONDUCTING GENERATORS

The results of investigation of superconducting generator constructions conducted in the Institute of
Electric Machines, Drives and Measurements are presented. Superconducting generators are slotless
synchronous machines with superconducting field winding. These machines enable us to surpass the
present limits of power rating. Specific construction of such machines constrains the necessity of
elaboration new designing methods. New methods required computations of electromagnetic fields
for windings and machine shields. Analytical and numerical calculations of the fields and parameters
of the machine were made and the results were compared with the results of measurements using the
model of slotless armature equipped with electromagnetic shields. Elaborated in Institute methodol-
ogy of electromagnetic computations was successfully verified by experiment results made on super-
conducting machines models within a framework of international project „INTERKRIOLEP”.