1

Jerzy Czesław Ossowski

Katedra Ekonomii i Zarz dzania Przedsi biorstwem

Wydział Zarz dzania i Ekonomii

Politechnika Gda ska

IX Ogólnoposkie Seminarium Naukowe nt. „Dynamiczne modele ekonometryczne,

Katedra Ekonometrii i Statystyki, Uniwersytet Mikołaja Kopernika w Toruniu ,

Toru , 6-8 wrze nia 2005 r.

DYNAMIKA WZROSTU GOSPODARCZEGO

A STOPY PROCENTOWE

W POLSCE W LATACH 1996-2004

1. Realne stopy procentowe a dynamika produktu potencjalnego

Celem artykułu jest przedstawienie teoretycznej koncepcji opisuj cej zwi zki pomi dzy stop

procentow a dynamik produktu krajowego oraz poddanie tego zwi zku empirycznej weryfikacji.

Za punkt wyj cia w rozwa aniach uznajmy agregatow , długookresow , poda ow funkcj

produkcji, opisuj c zale no ci pomi dzy wielko ci produktu krajowego (Y) a nakładami kapitału

rzeczowego (K) i pracy (L) w kolejnych okresach t. Wst pnie załó my, i w analizowanych okresach t

poda pracy (N) i stopa bezrobocia (u) s stałe. Oznacza to, e nakłady pracy (L) nale y uzna za stałe.

W rezultacie funkcj produkcji, uwzgl dniaj c efekty post pu technicznego, zapiszmy nast puj co:

.

const

L

),

t,

K

(

Y

)

t,

L

,

K

(

Y

Y

t

t

t

t

t

=

=

=

(1)

Je li dodatkowo uznamy, e stopa bezrobocia jest równa naturalnej stopie bezrobocia (u

n

), to funkcja

produkcji (1) wyznacza maksymalne ilo ci produktu w warunkach pełnego wykorzystania czynników.

Na podstawie funkcji (1) definiujemy produktywno kra cow kapitału (MPK). W warunkach prawa

malej cych przychodów oraz post pu technicznego uznajemy, i funkcja MPK(K,t) spełnia

nast puj ce warunki:

,

0

)

t,

K

(

MPK

K

/

Y

MPK

t

t

t

t

>

=

=

∆

∆

(2)

,

0

K

/

MPK

t

t

<

∆

∆

(3)

0

MPK

MPK

MPK

1

t

t

t

>

−

=

−

∆

(4)

Ponadto uznajemy, e stany kapitału rzeczowego na koniec kolejnych okresów s funkcj strumienia

nakładów inwestycyjnych brutto (I) w danym okresie oraz wielko ci amortyzacji (D - deprecjacji)

kapitału rzeczowego, co zapisujemy nast puj co:

t

t

1

t

t

D

I

K

K

−

+

=

−

(5)

Na podstawie (5) definiujemy w nast puj cy sposób strumie inwestycji netto ( K) w okresie t:

t

t

1

t

t

t

D

I

K

K

K

−

=

−

=

−

∆

(6)

Z powy szego wynika, e:

t

t

t

t

D

I

0

K

.

const

K

=

=

=

∆

(7)

e

Powiemy wi c, e stało kapitału rzeczowego oznacza, i deprecjacja maj tku (D) w okresie t jest

równowa ona inwestycjami brutto (I) w tym samym okresie. Oznacza to, e w warunkach stało ci

kapitału nast puje odnowienie maj tku produkcyjnego. Wyrazem odnowienia kapitału jest post p

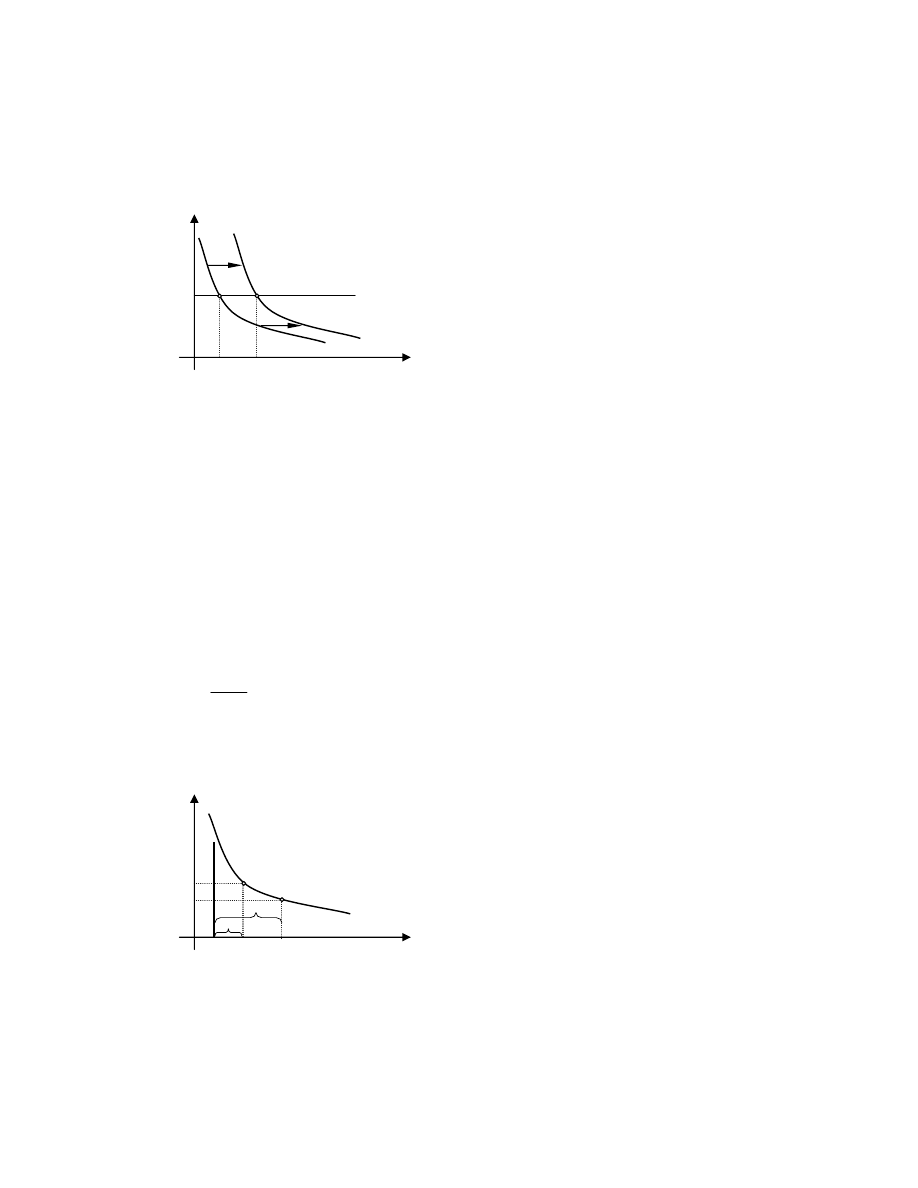
2

techniczny charakteryzuj cy si wzrostem produkcji w warunkach stało ci czynników. W rezultacie

post pu technicznego krzywe MPK(K,t) w kolejnych okresach przesuwaj si w praw stron w

rozpatrywanym na wykrasie 1 układzie współrz dnych. Jest to zgodne z warunkiem zdefiniowanym w

(4).

Dla podmiotów gospodarczych realna centralna stopa procentowa (r), kształtuj ca poziomy

rynkowych stóp procentowych, stanowi alternatyw wzgl dem stopy zwrotu wyznaczonej przez

kra cow produktywno kapitału (MPK). W rezultacie podmioty gospodarcze osi gn maksymalny

zysk ekonomiczny ustalaj c taki poziom kapitału (K) przy którym spełniona b dzie nast puj ca

równo :

)

t,

K

(

MPK

r

t

=

(8)

W warunkach pełnego wykorzystania czynników i ustabilizowanej stopy procentowej (r

c

), na skutek

zmiany poło enia krzywej produktywno ci kra cowej kapitału, co jest wyrazem post pu

technicznego, obserwowa b dziemy zwi kszanie si nakładów kapitałowych, tak jak przedstawiono

to na wykresie 1.

Zauwa my, e w przypadku stopy inflacji ( ) oraz nominalnej stopy procentowej (i), realn stop

procentow (r) dla okresu t definiujemy nast puj co:

t

t

t

t

t

t

i

r

1

i

1

r

1

π

π

−

≅

+

+

=

+

(9)

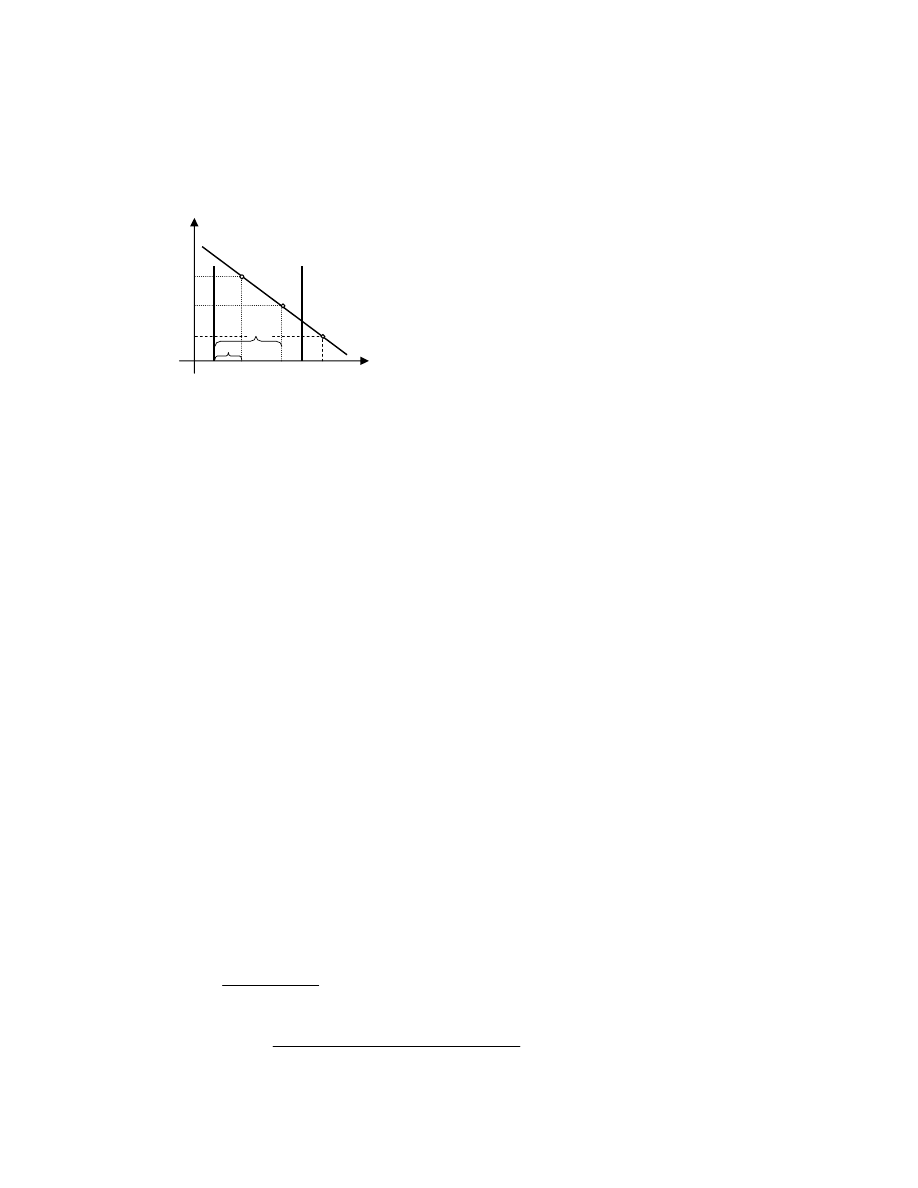
Je li realna stopa procentowa (r) ulegnie zmniejszeniu z poziomu (r

1

) do poziomu (r

2

), wówczas

optymalne nakłady kapitału ulegn zwi kszeniu z poziomu (K

1

) do poziomu (K

2

). W rezultacie

zwi kszy si dynamika nakładów inwestycyjnych netto w relacji do wyst puj cego wcze niej

poziomu kapitału (K

0

), jak przedstawiono to na wykresie 2.

Z powy szego wynika, e w warunkach gospodarki rynkowej tempo wzrostu nakładów

kapitałowych ( K

t

/K

t-1

) jest ujemnie uzale nione od poziomu realnej stopy procentowej z danego

okresu (r

t

), co w wersji liniowej zapiszemy nast puj co:

MPK(K,t) MPK(K,t+1)

MPK

r

K

r

c

K

1

K

2

E

1

E

2

Na skutek post pu technicznego

krzywa produktu kra cowego

kapitału (MPK) przesuwa si w

praw stron . Przy ustalonej

realnej stopie procentowej (r

c

),

przedsi biorstwa

maksymalizuj ce zysk

zwi kszaj nakłady kapitałowe z

poziomu K do K .

Wykres 1. Optymalne nakłady kapitału rzeczowego (K) w warunkach post pu

technicznego i ustalonej realnej stopy procentowej (r

c

).

MPK(K,t=const.)

MPK

r

K

r

1

K

1

K

2

A

1

A

2

Spadek realnej stopy procentowej z r

1

do r

2

wywołuje wzrost przyrostu nakładów

kapitałowych netto z poziomu K

1

do K

2

.

Oznacza to, e:

je eli r

1

> r

2

to K

1

/K

0

< K

2

/K

0

Wykres 2. Zmiana realnej stopy procentowej a tempo wzrostu nakładów

inwestycyjnych

K

1

K

2

K

0

r

2

3

)

0

,

(

,

r

K

/

K

1

0

t

1

0

1

t

t

>

−

=

−

β

β

β

β

∆

(10)

Zało ymy obecnie, e proces produkcji, zdefiniowany przez (1), opisuje funkcja produkcji typu Cobb-

Douglasa:

α

λ

t

t

t

K

e

A

Y

⋅

⋅

=

.

(11)

Z (10) wynika nast puj cy zwi zek pomi dzy tempem wzrostu produktu potencjalnego ( Y

t

/Y

t-1

) a

tempem wzrostu nakładów kapitałowych w warunkach uwzgl dnienia efektów post pu technicznego:

)

K

/

K

(

Y

/

Y

1

t

t

1

t

t

−

−

+

=

∆

α

λ

∆

.

(12)

)

Obecnie wprowadzaj c (10) do (12) ostatecznie otrzymujemy:

)

t

1

0

1

t

t

r

Y

/

Y

γ

γ

∆

−

=

−

,

(13)

.)

gdzie:

0

= +

0

oraz

1

=

1

. Zauwa my, e:

)

1

t

1

t

t

r

/

)

Y

/

Y

(

γ

∆

∆

∆

−

=

−

(14)

Na podstawie (14) powiemy, e wzrost stopy procentowej o jeden punkt procentowy prowadzi do

spadku dynamiki potencjalnego produktu krajowego o

1

punktu procentowego.

2. Nominalne stopy procentowe a dynamika produktu zrównowa onego z popytem

globalnym

Mo liwo ci poda owe, wynikaj ce z funkcji produkcji, ograniczone s przez czynniki kształtuj ce

popyt globalny (AD). Popyt ten jest wyznaczony przez:

1.

poziom popytu konsumpcyjnego (C

d

), kształtowany głównie przez poziom produktu krajowego

(Y), stop podatkow (T) i nominaln stop procentow (i),

2.

poziom popytu inwestycyjnego (I

d

), kształtowany głównie przez nominaln stop procentow (i),

3.

export netto (NX

d

), stanowi cy ró nic pomi dzy exportem i importem krajowym, który jest

kształtowany głównie przez realny kurs wymienny waluty krajowej na walut zagraniczn ( ),

4.

wydatki rz dowe (G) uznawane za wielko autonomiczn .

Uwzgl dniaj c kierunki oddziaływania czynników popytowych na składowe popytu globalnego,

funkcj popytu globalnego zapiszemy nast puj co:

)

(

t

)

(

t

d

)

(

t

d

)

(

t

)

(

t

)

(

t

d

t

G

)

(

NX

)

i

(

I

)

i

,

T

,

Y

(

C

AD

+

+

−

−

−

+

+

+

+

=

ε

(15)

Równowag globaln na rynku towarowym osi gamy przy takim poziomie produktu globalnego (Y

E

),

przy którym popyt globalny (AD) zrówna si z produktem krajowym (Y). W rezultacie funkcj

produktu w stanie równowagi globalnej zapiszemy nast puj co:

)

G

,

,

T

,

i

(

Y

Y

)

(

t

)

(

t

)

(

t

)

(

t

E

Et

+

+

−

−

=

ε

(16)

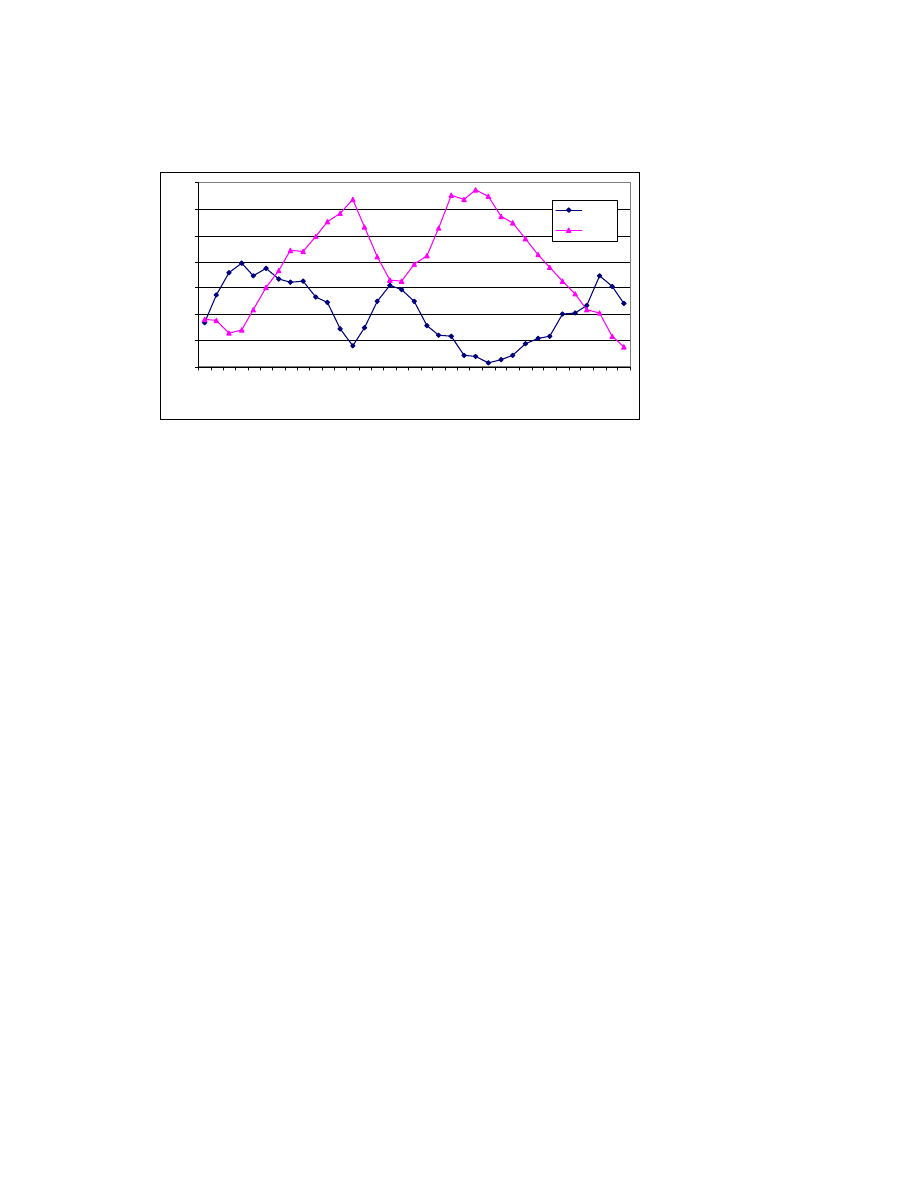
Na podstawie (15) i (16), zakładaj c stało zmiennych T, oraz G, wyprowadza si krzyw IS

przedstawiaj c wszystkie mo liwe kombinacje pomi dzy stop procentow (i) a produktem

krajowym (Y) zrównowa onym z popytem globalnym (AD). Krzywa ta jest opadaj ca w

przedstawionym na wykresie 3 układzie współrz dnych. Jak wynika z wykresu 3, spadkowi

nominalnej stopy procentowej (i) towarzyszy rosn cy produkt krajowy zrównowa ony z popytem

globalnym (Y

E

). Jednocze nie z pogł bionej analizy rysunku wynika, e tempo wzrostu produktu

zrównowa onego ( Y

Et

/Y

E,t-1

) jest ujemnie uzale nione od poziomu nominalnej stopy procentowej z

danego okresu (i

t

). W wersji liniowej zale no t zapiszemy nast puj co:

)

0

,

(

,

i

Y

/

Y

1

0

t

1

0

1

t,

E

Et

>

−

=

−

β

β

β

β

∆

(17)

Zauwa my, e:

0

i

/

)

Y

/

Y

(

1

t

1

t,

E

Et

<

−

=

−

β

∆

∆

∆

(18)

4

Na podstawie (18) powiemy, e wzrost nominalnej stopy procentowej o jeden punkt procentowy

prowadzi do spadku dynamiki zrównowa onego produktu krajowego o

1

punktu procentowego.

Zauwa my, e w analizowanym przypadku popyt inwestycyjny jest traktowany podobnie jak

popyt konsumpcyjny lub rz dowy. Oznacza to, e w tym krótkookresowym uj ciu uznaje si , e

zmiany popytu inwestycyjnego wpływaj jedynie na stopie wykorzystania czynników poda owych.

Nie zakłada si natychmiastowego uruchomienia inwestycji nowo zakupionych. W rezultacie uznaje

si wielko produktu potencjalnego za ustalon . Tym samym je li stopa procentowa wyznaczona

zostanie na zbyt niskim poziomie (i

h

), tak jak przedstawiono to na wykresie 3, wówczas hipotetyczna

wielko produktu zrównowa onego z popytem globalnym (Y

Eh

) przewy szy ustalon wielko

produktu potencjalnego (Y

p

). W konsekwencji wywoła mo e to niekontrolowany przyrost poziomu

cen. Z drugiej strony poziom stóp procentowych decyduje o stanie równowagi na rynku pieni nym.

Zbyt niski jego poziom prowadzi do niedoboru pieni dza transakcyjnego. W sytuacji niedoboru

spadnie popyt na papiery warto ciowe i nast pi jednoczesny wzrost ich poda y. W warunkach

potrzeby finansowania deficytu bud etowego jest to zjawisko niepo dane.

3. Model dynamiki wzrostu PKB – koncepcja, wyniki oszacowa , wnioski ko cowe

Z przeprowadzonych rozwa a wynika, e poziom stóp procentowych rzutuje z jednej strony na

dynamik produktu potencjalnego a z drugiej strony na dynamik produktu zrównowa onego z

popytem globalnym. Ponadto na dynamik produktu zrównowa onego wpływ wywieraj czynniki

zwi zane wydatkami rz dowymi, stop podatkow , kursami waluty krajowej, itp. Jednocze nie nale y

uzna wzajemne adaptowanie si do siebie dynamik produktu potencjalnego i zrównowa onego.

Zauwa my bowiem, e zmniejszenie si dynamiki produktu zrównowa onego, prowadz ce do

gorszego wykorzystania czynników poda owych, wpływa b dzie hamuj co na dynamik

inwestowania, a co za tym idzie na dynamik produktu potencjalnego. Upowa nia nas to do uznania,

e w długich okresach ekonomicznych, w procesach wzajemnego dostosowywania si równowag

krótkookresowych i długookresowych, to nie nominalna ale urealniona stopa procentowa wywiera

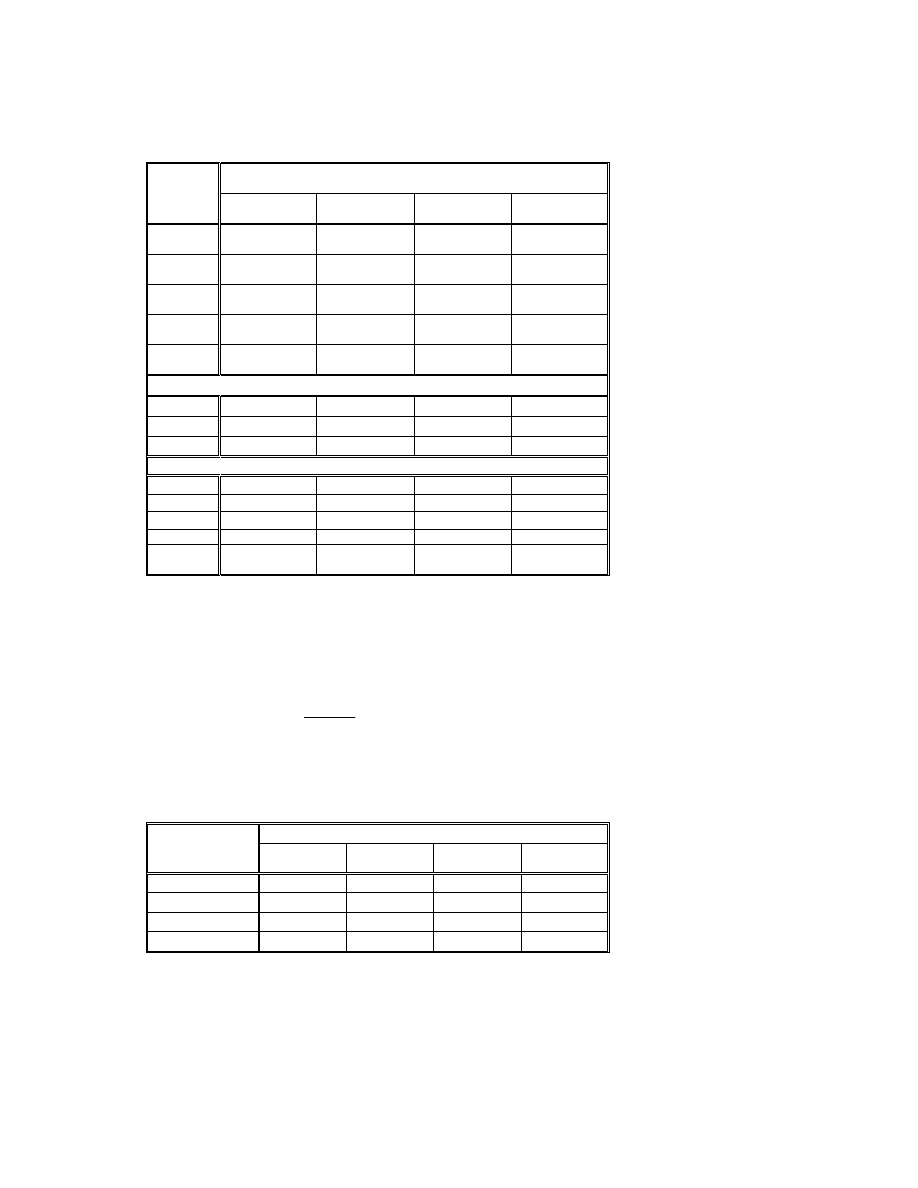
wpływ na dynamik produktu krajowego. O wzajemnych zwi zkach pomi dzy stop wzrostu

produktu krajowego brutto (SPKB) a urealnion redyskontow stop centraln (R) przekona mo emy

si analizuj c wykres 4. Z uwagi na fakt, e analiz roczn prowadzono o dane kwartalne, wielko ci te

wyliczano według nast puj cych formuł:

%

100

PKB

PKB

PKB

SPKB

4

t

4

t

t

t

⋅

−

=

−

−

,

(19)

.)

%

100

1

)]

i

1

)(

i

1

)(

i

1

)(

i

1

[(

%

100

)

R

1

(

t

25

,

0

t

1

t

2

t

3

t

t

⋅

+

+

+

+

+

=

⋅

+

−

−

−

π

(20)

IS

i

Y

E

i

1

Y

E1

Y

E2

E

1

E

2

Spadek nominalnej stopy procentowej z

i

1

do i

2

wywołuje wzrost przyrostu

produktu krajowego zrównowa onego z

popytem globalnym z poziomu Y

E1

do

Y

E2

. Oznacza to, e:

je eli i

1

> i

2

to Y

E1

/Y

0

< Y

E2

/Y

0

W przypadku zbyt niskiej stopy

procentowej (i

h

) produkt w równowadze

(Y

Eh

) przewy sza produkt potencjalny

(Y ).

Wykres 3. Zmiana nominalnej stopy procentowej a tempo wzrostu produktu

krajowego zrównowa onego z popytem globalnym

Y

E1

Y

E2

Y

0

i

2

Y

p

i

h

E

h

Y

Eh

5

Wykres 4. Roczna dynamika wzrostu produktu krajowego brutto (SPKB) i urealnione

roczne stopy redyskontowe (R) w Polsce w latach 1996-2004.

Konstruuj c model analizowanego procesu gospodarczego, mamy podstawy aby zało y , e

urealniona centralna stopa procentowa (R

t

) wraz z pozostałymi czynnikami popytowymi (SX

t

)

wyznaczaj oczekiwan stop wzrostu produktu krajowego (SPKB

E

t

), co zapiszemy nast puj co:

t

t

2

t

1

0

E

t

v

SX

R

SPKB

+

+

+

=

α

α

α

.

(21)

Zakładaj c adaptacyjny charakter dostosowa SPKB do SPKB

E

zapiszemy:

)

).

0

0

(

),

SPKB

SPKB

)(

1

(

SPKB

SPKB

1

t

E

t

1

t

t

<

<

−

−

=

−

−

−

γ

γ

(22)

Wprowadzaj c (20) do (21) i odpowiednio przekształcaj c, ostatecznie otrzymujemy nast puj c

posta modelu dynamicznego:

t

t

2

t

1

1

t

t

u

SX

b

R

b

cSPKB

a

SPKB

+

+

+

+

=

−

,

(23)

)

gdzie: a = (1- )

0

> 0, c = < 1, b

1

= (1- )

1

< 0, b

2

= (1- )

2

, u

t

= (1- )v

t

.

W trakcie procesu estymacji w ród czynników czynników SX zidentyfikowano roczn stop wzrostu

kursu euro (SKE) i zwi zan z ni roczn stop wzrostu kursu dolara w przeliczeniu na euro (SKDE).

W rezultacie proces estymacji, weryfikacji, analizy i symulacji przeprowadzono dla nast puj cego

modelu:

t

t

3

t

2

t

1

1

t

t

u

SKDE

b

SKE

b

R

b

cSPKB

a

SPKB

+

+

+

+

+

=

−

.

(24)

)

Model (24) szacowano wykorzystuj c próby statystyczne obejmuj ce podokresy poprzedzaj ce

przyst pienie Polski do Unii Europejskiej. Wyniki oszacowa przedstawiono w tabeli 1.

0

2

4

6

8

10

12

14

19

96

Q1

19

96

Q3

19

97

Q1

19

97

Q3

19

98

Q1

19

98

Q3

19

99

Q1

19

99

Q3

20

00

Q1

20

00

Q3

20

01

Q1

20

01

Q3

20

02

Q1

20

02

Q3

20

03

Q1

20

03

Q3

20

04

Q1

20

04

Q3

SPKB
R

6

Tabela 1 Wyniki oszacowa MNK modelu (24)

Oszacowane warto ci parametrów strukturalnych

oraz warto ci statystyk t-studenta dla próby z okresów:

Parametr

i

symbol

zmiennej

1996 kw.III

2004 kw.II

1997 kw.I

2004 kw.II

1998 kw.I

2004 kw.II

1999 kw.I

2004 kw.II

a

3,5797

(4,39)

3,2766

(3,59)

3,3245

(3,42)

4,7162

(2,80)

c

SPKB

t-1

0,5331

(5,6)

0,5476

(5,48)

0,5575

(5,28)

0,3938

(2,05)

b

1

R

t

-0,2496

(-4,11)

-0,2241

(-3,23)

-0,2321

(-3,12)

-0,3324

(-2,65)

b

2

SKE

t

0,0806

(3,13)

0,0814

(3,08)

0,0825

(2,77)

0,0683

(2,15)

b

3

SKDE

t

0,0518

(2,62)

0,0492

(2,39)

0,0525

(2,21)

0,0570

(2,07)

Oszacowane efekty długookresowe: SPKB

E

/ X

t

b

1

/(1-c)

-0,53

-0,49

-0,52

-0,55

b

2

/(1-c)

0,17

0,18

0,19

0,11

b

3

/(1-c)

0,11

0,11

0,12

0,09

Charakterystyka próby statystycznej oraz miary jako ci oszacowa modelu

n

32

30

26

22

R

2

0,9172

0,9055

0,8811

0,8824

Se

0,7242

0,7425

0,7694

0,7799

DW

2,0559

1,9959

1,9153

1,9173

D-h

(prob)

-0,1876

(0,851)

0,01354

(0,989)

0,2563

(0,798)

0,4433

(0,658)

ródło: Obliczenia własne na podstawie danych GUS

Na podstawie oszacowanych wersji modelu (24) przeprowadzono symulacj celem wyznaczenia

granicznego tempa wzrostu PKB przy zało onych poziomach realnych stóp procentowych (R

t

) oraz

przyj ciu zało e , i SKE

t

= 0 oraz SKDE

t

= 0. Zgodnie z (21), (22) i (23), przy przyj tych

zało eniach, graniczne tempo wzrostu PKB definiujemy nast puj co:

)

0

SKDE

,

SKE

(

,

cˆ

1

R

bˆ

aˆ

R

ˆ

ˆ

SPKB

t

t

t

1

t

1

0

E

t

=

−

+

=

+

=

∧

α

α

(25)

)

Wyniki przeprowadzonej symulacji przedstawiono w tabeli 2.

Tabela 2 Symulowane graniczne dynamiki wzrostu PKB

Oszacowane graniczne dynamiki wzrostu PKB dla okresów:

Zało ony poziom

realnych stóp

procentowych (R

t

)

1996 kw.III

2004 kw.II

1997 kw.I

2004 kw.II

1998 kw.I

2004 kw.II

1999 kw.I

2004 kw.II

0%

7,67%

7,24%

7,51%

7,78%

5%

4,99%

4,77%

4,89%

5,04%

10%

2,32%

2,29%

2,27%

2,3

15%

-0,35%

-0,19%

-0,35%

-0,44%

ródło: Obliczenia własne

Analizuj c wyniki symulacji zamieszczone w tabeli 2 stwierdzamy, e w warunkach gospodarki

polskiej:

-

utrwalenie tempa wzrostu PKB przekraczaj cego 5% w skali rocznej, wymaga ustabilizowania si

realnych stóp procentowych na poziomie nie przekraczaj cym 5%,

7

-

utrwalony spadek PKB nast pi, je li realne roczne stopy procentowe ustabilizuj si na poziomie

przekraczaj cym 14%.

Literatura

Barro R. (1997), Makroekonomia, PWE, Warszawa

Burda M., Wyplosz Ch. (1995), Makroekonomia, Podr cznik europejski, PWE, Warszawa

Chow G., C. (1995), Ekonometria, Wydawnictwo Naukowe PWN, Warszawa

Dornbusch R., Fischer S., Sparks G. R. (1989), Macroeconomics, Third Canadian Edition, McGraw-Hill

Ryerson Limited, Toronto

Maddala G.,S. (2001), Introduction to Econometrics, John Wiley & Sons LTD, New York

Hall R., E., Taylor J., B. (1995), Makroekonomia, Teoria, funkcjonowanie i polityka, Wydawnictwo Naukowe

PWN, Warszawa

Ossowski J., Cz. (2004), Wybrane zagadnienia z makroekonomii, Poj cia, problemy, przykłady i zadania,

WSFiR, Sopot

Romer D. (2000), Makroekonomia dla zaawansowanych, Wydawnictwo Naukowe PWN, Warszawa