RFID – Radio Frequency Identification
Przekaz energii i informacji za po
średnictwem pola magnetycznego
Wst
ęp.
We wszystkich poni
ższych rozważaniach przyjęto założenie, że źródłem pola
magnetycznego jest toroidalna antena o promieniu uzwojenia R, wykonana z N zwojów drutu
(przewodnika) o promieniu R, przez który płynie pr
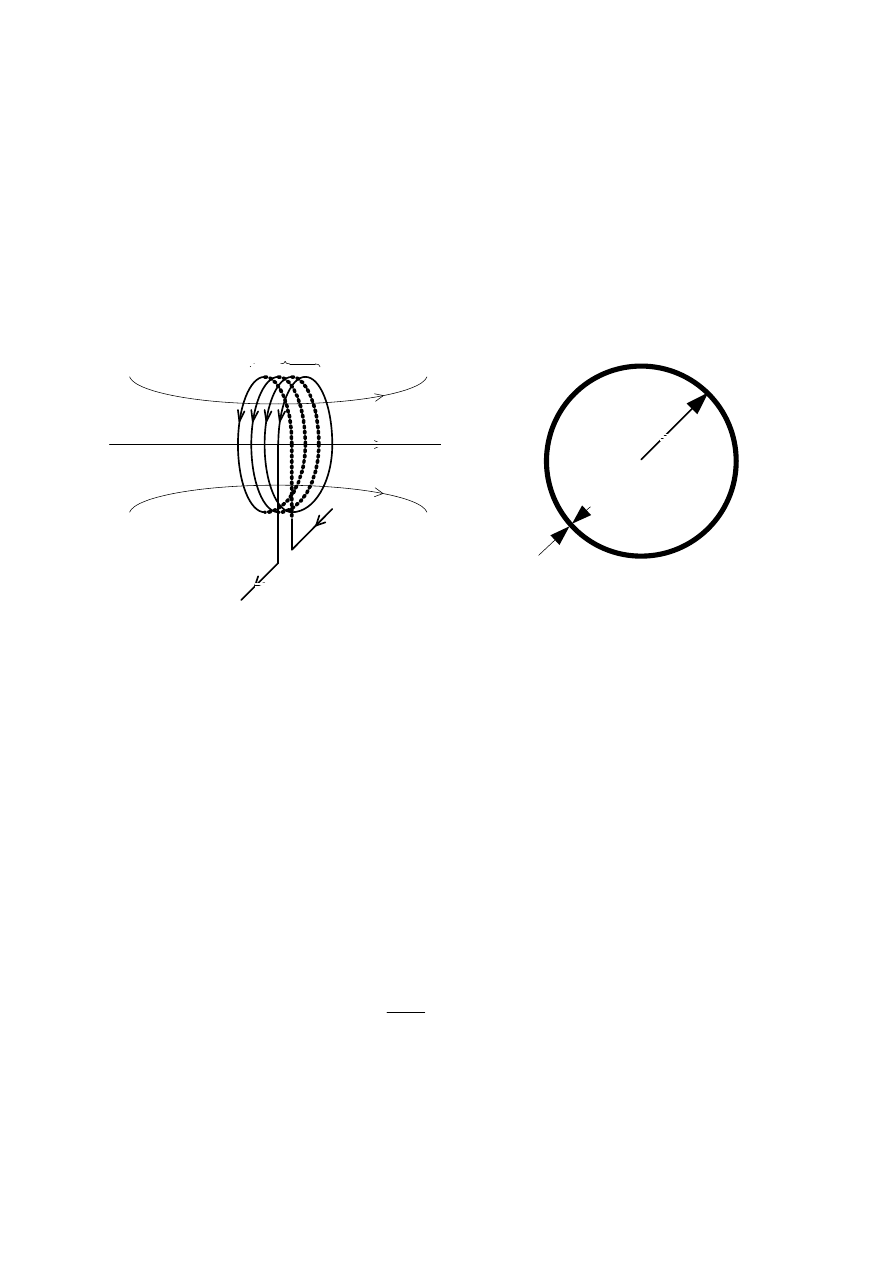
ąd o natężeniu I. Schematyczny wygląd
anteny wraz z podstawowymi parametrami przedstawiono na rys.1.
a)
b)
Rys.1. a) antena z zaznaczonym kierunkiem przepływu pr
ądu I oraz liniami indukowanego pola magnetycznego
(strumie
ń wektora indukcji Φ
B
), b) wymiary pojedynczego zwoju.
Poj
ęcie wektora natężenia pola magnetycznego H
r
i wektora indukcji magnetycznej
B
r
w
obliczeniach pojawiaj
ą się wymiennie i są związane zależnością:
H
H
B
r
r
r
r
µ
µ
µ
=
=
0
gdzie:
0
µ
- bezwzgl
ędny współczynnik przenikalności magnetycznej,
r
µ
- wzgl
ędny
współczynnik przenikalno
ści magnetycznej (zależny od ośrodka).
1. Rozkład pola magnetycznego wzdłu
ż osi anteny.
Wektor indukcji magnetycznej
B
r
wzdłu
ż osi anteny wyznaczono korzystając z prawa
Biota-Savatra:
w którym B
d
r
jest przyczynkiem do wektora indukcji b
ędącym wynikiem przepływu prądu I
przez element długo
ści l
d
r
i wyznaczanym w odległo
ści R
r
od tego elementu. W celu
zwi
ększeni przejrzystości obliczeń wprowadzono następujący zapis wersorowy:
R
l
d
R
I
B
d
r
r
r
×
=
3
4
π
µ
,
(1.1)
N
Φ
B
I
R
2r

w którym
l
u
r
,
B
u
r
,
R
u
r
s
ą wektorami jednostkowymi odpowiednio elementu długości, wektora
indukcji i wektora odległo
ści. W zapisie wersorowym prawo Biota-Savarta przyjmuje
nast
ępującą postać:
Graficzna interpretacja prawa Biota-Savarta dla przypadku ogólnego została przedstawiona na
rys.1.1.
R
l
d
R
I
B
d
r
r
r
×
=
3
4
π
µ
dl
R
u
u
I
u
dB
R
l
B
2
4
r
r
r
×
=
π
µ
Rys.1.1. Prawo Biota-Savarta w przypadku ogólnym.
Na rys.1.2 przedstawiono geometri
ę układu z anteną magnetyczną w postaci jednego zwoju
przewodnika (nale
ży zwrócić uwagę na oznaczenia promienia pętli r, i odległości R). Pole
wyznaczane jest w odległo
ści d mierzonej wzdłuż osi anteny.
l
u
dl
l
d
r
r
=
,
B
u
dB
B
d
r
r
=
,
R
u
R
R
r
r
=
(1.2)
dl
R
u
u
I
u
dB
R
l
B
2
4
r
r
r
×
=
π
µ
,
(1.3)
I
R
r
l
d
r
B
d
r
R
l
B
u
u
u
r
r
r
×
=

Rys.1.2. Układ jednego zwoju anteny magnetycznej.
Wektor indukcji magnetycznej w odległo
ści d od anteny wyznacza się w wyniku całkowania
równania (1.1) lub (1.3)
K
ąt pomiędzy wersorami
l
u
r
i
R
u
r
jest stały i wynosi
2
π
z czego wynika,
że wektor B
r
ma
stał
ą długość, a przy całkowaniu zmienia się jedynie jego orientacja w przestrzeni.
Uwzgl
ędniając dodatkowo, że układ jest symetryczny względem osi anteny, składowa
prostopadła wektora
B
r
wyzeruje si
ę przy obliczaniu całki.
Wektor indukcji magnetycznej b
ędzie miał jedną składową niezerową skierowaną wzdłuż osi
anteny i równ
ą rzutowi wektora B
r
na t
ą oś. Wartość wektora indukcji zastanie wyznaczona w
toku nast
ępujących obliczeń na skalarach:
Z rys.1.2 mo
żna wyznaczyć sinus kąta θ:
∫
×
=
3
4
R
R
l
d
I
B
r
r
r
π
µ
,
∫
×
=
dl
R
u
u
I
u
B
R
l
B
2
4
r
r
r
π
µ
(1.4)
dl
R
I
dB
dB
x
2
)
sin(
4
θ
π
µ
=
=
,
(1.5)
2
2
2
d
r
R
+
=
,
2
2
)
sin(
d
r
r
R
r
+
=
=
θ
(1.6)
θ
θ
B
u
r
R
u
r
l
u
r
θ
r
R
d
O
Ś ANTENY

Podstawiaj
ąc (1.6) do (1.5) otrzymuje się:
Równanie (1.7) nale
ży scałkować po długości przewodnika:
Warto
ść wektora indukcji magnetycznej B w odległości d na osi anteny zbudowanej z N
zwojów przewodnika i maj
ącej promień uzwojenia równy r wynosi:
2. Badanie zale
żności wartości wektora indukcji
)
,
( d
r
B
x
w funkcji odległo
ści d przy
zało
żeniu, że promień uzwojenia jest stały (
)
const
r
=
.
Przebieg zmienno
ści funkcji
)
,
( d
r
B
x
nale
ży zbadać analitycznie tzn. należy znaleźć jej
ekstrema korzystaj
ąc z warunków zerowania się pierwszej i drugiej pochodnej.
Obliczenie pierwszej pochodnej funkcji
)
,
( d
r
B
x
:
Wyznaczenie warunku zerowania si
ę pierwszej pochodnej:
dl
d
r
d
r
r
I
dB
x
2
2
2
2
)
(
4
+
+
=
π
µ
,
dl
d
r
r
I
dB
x
2
3
2
2
)
(
4
+
=
π
µ
(1.7)
2
3
2
2
2
2
3
2
2
2
2
0
2
3
2
2
)
(
2
)
(
2
4
)
(
4
d
r
Ir
d
r
r
I
dl
d
r
r
I
B
r
x
+
=
+
=
+
=
∫
µ
π
π
µ
π
µ
π
,
(1.8)
2
3
2
2
2
)
(
2
)
,
(
d
r
INr
d
r
B
x
+
=
µ
,
(1.9)
2
3
2
2
2
)
(
2
)
,
(
d
r
INr
d
r
B
x
+
=
µ
,
2
5
2
2
2
2
5
2
2
2
2
3
2
2
2
)
(
2
3
2
)
(
2
3
2
)
(
1
2
)
,
(
d
r
d
INr
d
d
r
INr
d
r
d
INr
d
d
r
B
x
+
−
=
+
−
=
+
∂
∂
=
∂
∂
−
µ
µ
µ
(2.1)
∞
→
∨
=
⇔
=
+
−
⇔
=
∂
∂
d
d
d
r
d
INr
d
d
r
B
x
0
0
)
(
2
3
0
)
,
(
2
5
2
2
2
µ
(2.2)
r
IN
d
r
B
x
2
)
0
,
(
µ
=
=
,
0
)
,
(
=
∞
→
d
r
B
x
(2.3)

Obliczenie drugiej pochodnej funkcji
)
,
( d
r
B
x
:
Przypadek w którym
2
r
d
−
=
ma jedynie sens matematyczny i oznacza ujemn
ą współrzędną
na osi anteny.
Zale
żności wartości wektora indukcji
)
,
( d
r
B
x
w funkcji odległo
ści d zostanie przedstawiona
na przykładzie dwóch anten A i B ró
żniących się jedynie promieniami uzwojeń, odpowiednio
A
r
i
B
r
. Warto
ści przyjęte do obliczeń zgromadzono w tabeli 2.1.
Zestawienie warto
ści parametrów anten A i B przyjętych w obliczeniach
Przenikalno
ść magnetyczna próżni:
m
H
7
0
10
4
−
×
=
π
µ
Wzgl
ędna przenikalność ośrodka:
1
=
r
µ
Nat
ężenie prądu w antenach:
A
I
1
=
Liczba zwojów w antenach:
1
=
N
Promie
ń uzwojenia anteny A:
m
r
A
1
=
Promie
ń uzwojenia anteny B:
m
r
B
3
=
Tabela 2.1.
+
∂
∂
−
=
+
−
∂
∂
=
∂
∂
∂
∂
=
∂
∂
2
5
2
2
2
2
5
2
2
2
2
2
)
(
2
3
)
(
2
3
)
,
(
)
,
(
d
r
d
d
INr
d
r
d
INr
d
d
d
r
B
d
d
d
r
B
x
x
µ
µ
(2.4)
(
)
(
)
(
)
(
)
(
)
(
)
(
) (
)
[
]
(
)
(
)
2
7
2
2
2
2
7
2
2
2
2
2
2
7
2
2
7
2
2
2
2
7
2
2
2
9
2
2
5
2
2
2
2
3
2
2
2
5
2
2
2
5
2
2
4
5
2
2
5
2
2
5
)
(
d
r
d
r
d
r
d
d
r
d
r
d
r
d
d
r
d
r
d
r
d
d
r
d
r
d
r
d
d
+
−
=
+
−
+
+
=
+
+
−
+
=
=
+
+
−
+
=
+
∂
∂
(2.5)
2
2
0
4
0
)
,
(
2
2
2
2
r
d
r
d
d
r
d
d
r
B
x
−
=
∨
=
⇔
=
−
⇔
=
∂
∂
(2.6)
398
,
1
)
0
,
(
398
,
1
1
2
4
5
1
2
)
4
(
2
)
2
,
(
2
3
2
3
2
2
2
=
=
≈
=
+
=
=
d
r
B
r
IN
r
IN
r
r
INr
r
d
r
B
x
x
µ
µ
µ
,
(2.7)
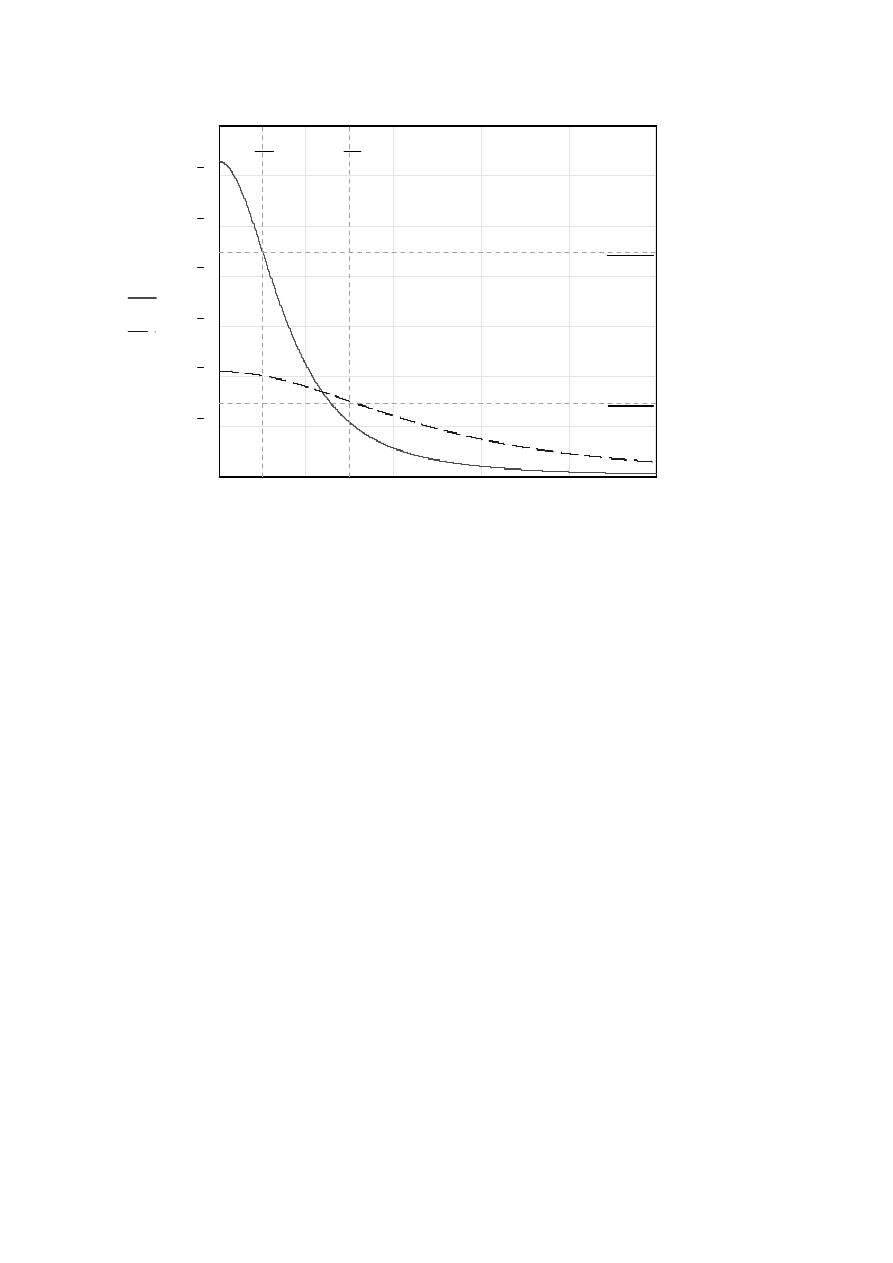
Rys.2.1. Wykres zale
żności wartości wektora indukcji magnetycznej na osiach dwóch anten różniących się
promieniami uzwoje
ń.
Wykresy przedstawione na rys.2.1. stanowi
ą podstawę do określenia fizycznych
parametrów anteny (np. zasi
ęgu) pracującej w systemie RFID. Obecność pola magnetycznego
w danym punkcie przestrzeni jest zwi
ązana z istnieniem w tym punkcie pewnej gęstości
energii zgromadzonej w polu. Odbiornik RFID (tzw. transonder) wykorzystuje cz
ęść tej
energii do zasilania własnych układów elektronicznych (w praktyce jest to niskomocowy
układ ASIC). Krytyczna z punktu widzenia zasilania układu jest minimalna g
ęstość energii
pola, a co za tym idzie minimalna warto
ść natężenia pola. Dlatego znając minimalną wartość
nat
ężenia pola magnetycznego (lub wartości wektora indukcji) można oszacować rozmiary
anteny i jej zasi
ęg. W praktyce rozważa się dwie metody podejścia do problemu w zależności
od wymaga
ń projektowych:
•
zakładamy,
że odbiornik jest umieszczony w stałej odległości d od anteny i w tej
odległo
ści natężenie pola jest większe od minimalnego, wówczas znając
min
x
B
i
zadan
ą odległość d można wyznaczyć promień anteny r.
•
zakładamy,
że odbiornik ma pracować prawidłowo w pewnym przedziale odległości
1
2
d
d
d
−
=
∆
w którym warto
ści wektora
x
B utrzymuj
ą się na zadanym poziomie
1
2
x
x
x
B
B
B
−
=
∆
.
Analiza rys.2.1. pozwala zauwa
żyć, że zmniejszając promień anteny zmniejszeniu ulega
maksymalna warto
ść wektora
x
B , ale jednocze
śnie wzrasta jej zasięg tak, że przy pewnych
odległo
ści d (w przykładzie dla
5
,
1
>≈
d
) warto
ść tego wektora może być większa niż w
przypadku zastosowania anteny dysponuj
ącej większym maksymalnym natężeniem pola.
Jednocze
śnie należy zwrócić uwagę na fakt, że gdy
∞
→
r
to
0
→
x
B
co oznacza,
że istnieje
optymalna długo
ść promienia r, przy której na danej odległości d można uzyskać
maksymalne nat
ężenie pola magnetycznego. Wyznaczenie optymalnej długości promienia
zostało przedstawione w punkcie 3.
0
1
2
3
4
5
0
1
.
10
7
2
.
10
7
3
.
10
7
4
.
10
7
5
.
10
7
6
.
10
7
BxB 0
( )
1.398
BxA 0
( )
1.398
BxA d
( )
BxB d
( )
rA
2
rB
2
d

3. Badanie zale
żności wartości wektora indukcji
)
,
( d
r
B
x
w funkcji promienia r przy
zało
żeniu, że odległość na osi jest stała (
)
const
d
=
.
Przebieg zmienno
ści funkcji
)
,
( d
r
B
x
jest badany analogicznie do punktu 2.
Na podstawie zale
żności (3.4) można stwierdzić, że funkcja
)
,
( d
r
B
x
dla zmiennej r zeruje si
ę
dla skrajnych warto
ści promienia anteny natomiast przyjmuje maksimum dla
2
d
r
±
=
(podobnie jak poprzednio ujemna współrz
ędna położenia na osi anteny ma jedynie
interpretacj
ę matematyczną i wynika z symetrii układu). Wyprowadzenie (3.3) pokazuje, że
funkcja
)
,
( d
r
B
x
wzgl
ędem zmiennej r ma cztery ekstrema. Obliczenia (3.4) uściślają wynik,
na podstawie którego wiadomo,
że funkcja posiada maksimum dla
2
d
r
=
. Wykres funkcji
ilustruj
ący powyższe rozważania przedstawiono na rys.3.1. W obliczeniach przykładowych
przyj
ęto wartości zgromadzone w tabeli 3.1.
2
3
2
2
2
)
(
2
)
,
(
d
r
INr
d
r
B
x
+
=
µ
,
+
∂
∂
=
∂
∂
2
3
2
2
2
)
(
2
)
,
(
d
r
r
r
IN
r
d
r
B
x
µ
(3.1)
(
)
(
)
(
)
(
) (
)
(
)
(
)
(
)
2
5
2
2
2
2
3
2
2
2
1
2
2
3
2
2
3
2
2
3
2
1
2
2
2
3
2
2
2
3
2
2
2
2
2
2
3
2
1
2
2
3
2
)
(
d
r
r
d
r
r
d
r
r
d
r
d
r
d
r
r
d
r
d
r
r
d
r
r
r
+
−
=
−
+
+
+
=
=
+
+
−
+
=
+
∂
∂
(3.2)
(
)
(
)
∞
→
∨
±
=
∨
=
⇔
=
+
−
⇔
=
∂
∂
r
d
r
r
d
r
r
d
r
r
d
r
B
x
2
0
0
2
0
)
,
(
2
5
2
2
2
2
(3.3)
27
)
3
(
)
2
(
2
2
)
,
2
(
2
3
3
2
2
3
2
2
2
d
IN
d
INd
d
d
INd
d
d
r
B
x
µ
µ
µ
=
=
+
=
=
,
0
)
,
0
(
=
=
d
r
B
x
,
0
)
,
(
=
∞
→
d
r
B
x
(3.4)

Zestawienie warto
ści parametrów anteny
Przenikalno
ść magnetyczna próżni:
m
H
7
0
10
4
−
×
=
π
µ
Wzgl
ędna przenikalność ośrodka:
1
=
r
µ
Nat
ężenie prądu w antenach:
A
I
1
=
Liczba zwojów w antenach:
1
=
N
Odległo
ść punktu pomiarowego od anteny
m
d
2
=
Tabela 3.1
Rys.3.1. Wykres zale
żności wartości wektora indukcji magnetycznej na osi anteny od promienia uzwojenia r
przy stałej odległo
ści
2
=
d
.
W przykładzie optymalna długo
ść promienia uzwojenia wynosi:
4. Parametryzacja funkcji
)
,
( d
r
B
x
W celu ułatwienia analizy pola magnetycznego wzdłu
ż osi anteny należy wprowadzić
parametr a b
ędący stosunkiem odległości d i promienia r:
Podstawiaj
ąc (4.1) do wyrażenia funkcji
)
,
( d
r
B
x
(1.9) otrzymuje si
ę:
0
2
4
6
8
10
0
2
.
10
8
4
.
10
8
6
.
10
8
8
.
10
8
1
.
10
7
1.2
.
10
7
Bx d 2
⋅
(
)
Bx r
( )
d
2
⋅
r
83
,
2
2
2
2
≈
=
⇒
=
r
d
r
(3.5)
r
d
a
ar
d
=
⇒
=
(4.1)

Warto
ść wektora indukcji magnetycznej w środku anteny dla
0
=
d
wynosi
Funkcj
ę
)
,
( a
r
B
x
w (4.2) mo
żna uzależnić jedynie od wartości wektora indukcji w środku
anteny (4.3) i parametru a proporcjonalnego do odległo
ści od anteny:
Przedstawienie rozkładu pola magnetycznego w postaci funkcji (4.4) pozwala łatwo bada
ć
jego charakter ogólny niezale
żnie od rozmiarów geometrycznych układu. Ze względu an
warto
ść parametru a można wyróżnić trzy obszary promieniowania występujące w zależności
od odległo
ści od anteny:
Dla
1
<<
a
zagadnienie nale
ży już rozpatrywać w charakterze promieniowania
elektromagnetycznego.
2
3
2
2
2
)
(
2
)
,
(
d
r
INr
d
r
B
x
+
=
µ
,
(1.9)
2
3
2
3
2
2
3
2
2
2
2
)
1
(
2
)
(
2
)
,
(
a
r
INr
r
a
r
INr
a
r
B
x
+
=
+
=
µ
µ
,
(4.2)
r
IN
r
B
x
2
)
0
,
(
µ
=
,
(4.3)
2
3
2
)
1
(
)
0
,
(
)
,
(
a
r
B
a
r
B
x
x
+
=
,
(4.4)
1)
)
0
,
(
)
,
(
1
r
B
a
r
B
r
d
a
x
x
≈
⇒
<<
⇒
<<
(4.5)
2)
8
)
0
,
(
)
,
(
1
r
B
a
r
B
r
d
a
x
x
=
⇒
=
⇒
=
(4.6)
3)
3
)
0
,
(
)
,
(
1
a
r
B
a
r
B
r
d
a
x
x
≈
⇒
>
⇒
>
(4.7)
4)
)
0
,
(
)
,
(
1
r
B
a
r
B
r
d
a
x
x
≈
⇒
<<
⇒
<<
(4.5)
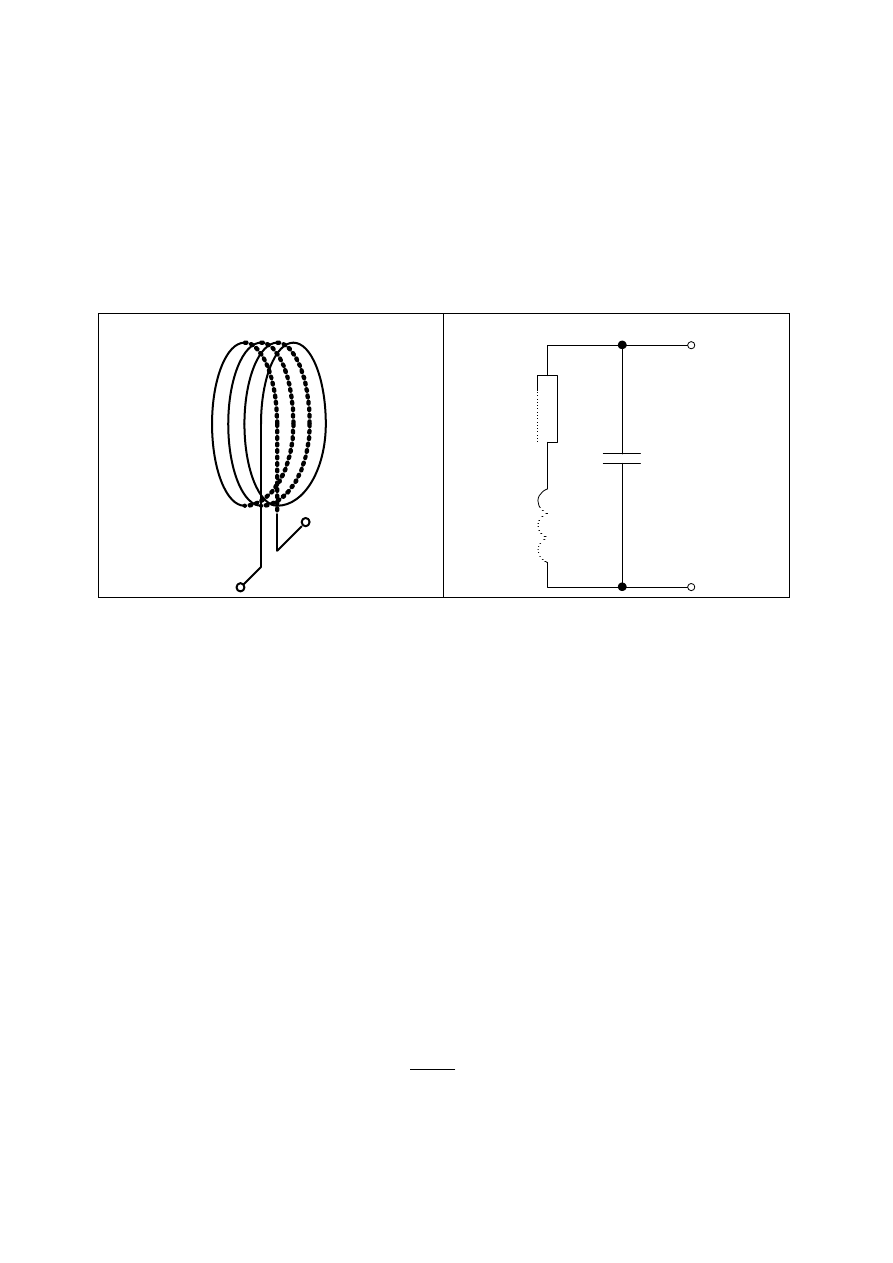
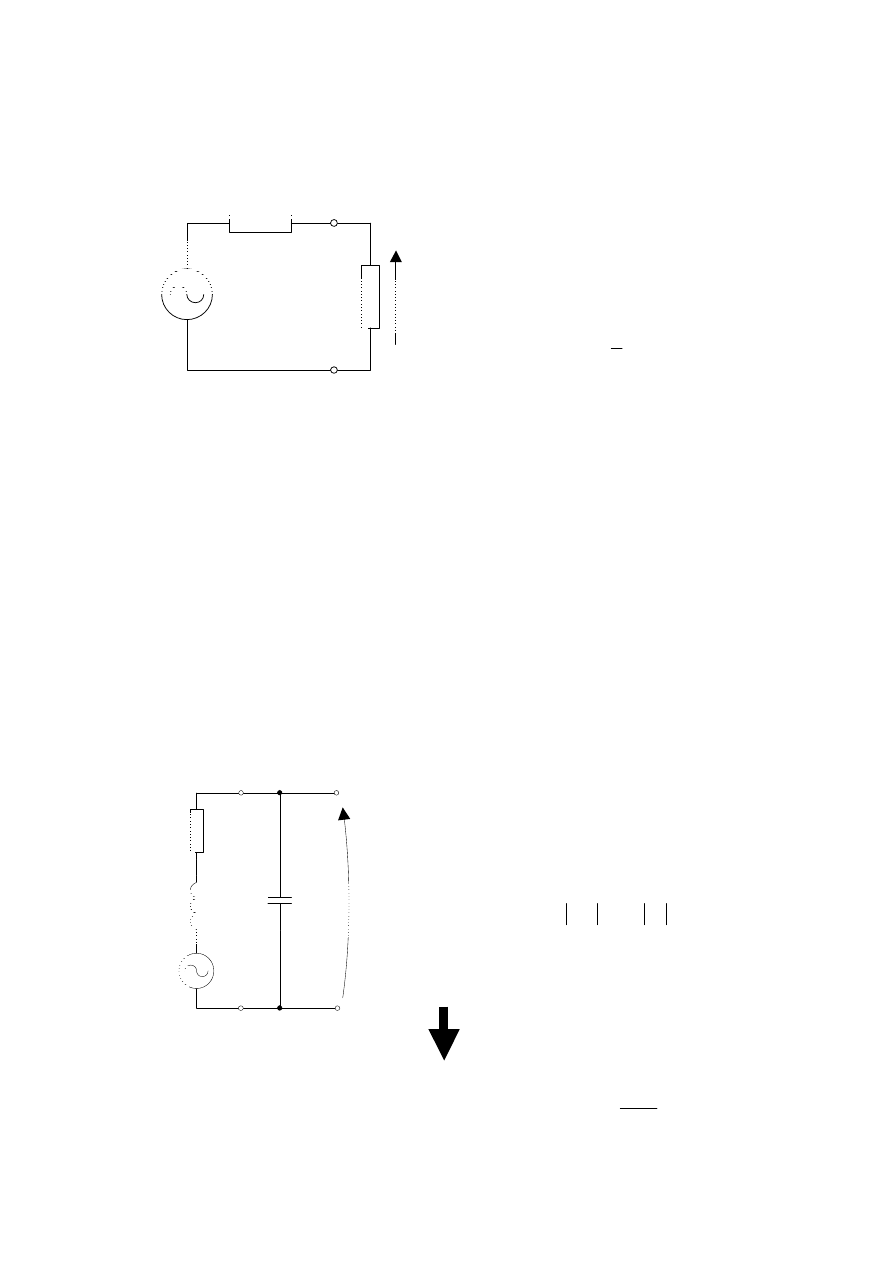
5. Model elektryczny anteny magnetycznej.
Dotychczas anten
ą magnetyczną nazywane było źródło pola magnetycznego. W tym
punkcie zdefiniowana zostanie antena magnetyczna odbiornika, której zadaniem jest zamiana
energii pola na energi
ę elektryczną. Szkic rzeczywistego wyglądu anteny i jej odpowiednika
w postaci obwodu elektrycznego przedstawiono na rys.5.1.
a)
b)
Rys.5.1. a) Szkic przedstawiaj
ący antenę magnetyczną odbiornika, b) pasywny obwód zastępczy anteny (przy
braku obecno
ści pola magnetycznego).
Antena wykonana jest w postaci cewki powietrznej z drutu przewodz
ącego. Analog
elektryczny anteny rzeczywistej przedstawiony na rys. 5.1.b modeluje główne zjawiska
maj
ące miejsce w takim układzie takie jak:
•
indukcyjno
ść uzwojenia L
S
(główny parametr anteny),
•
rezystancj
ę omową drutu nawojowego R
S
(parametr paso
żytniczy),
•
pojemno
ść międzyzwojową C
P
(parametr paso
żytniczy).
Nale
ży zwrócić uwagę na konwencję stosowaną przy indeksowaniu nazw elementów na
schematach elektrycznych. Poniewa
ż często w rozważaniach operuje się wymiennie w
ramach potrzeb postaci
ą szeregową lub równoległą obwodu, dlatego elementy łączone
szeregowo maj
ą w indeksie literę „S” („serial”) natomiast łączone równolegle mają w
indeksie liter
ę „P” („paralel”). Na rys.5.1.b indukcyjność L
S
i rezystancja R
S
tworz
ą
poł
ączenie szeregowa, a pojemność C
P
jest doł
ączona równolegle.
Rzeczywista antena magnetyczna stanowi wi
ęc obwód rezonansowy o dobroci Q
S
,
charakteryzuj
ący się występowaniem pulsacji ω
sr
rezonansu własnego (paso
żytniczego) –
„self resonance”, spełniaj
ącej równanie:
1
=
sr
P
S
C
L
ω
(5.1)
S
sr
S
S
R
L
Q
ω
=
(5.2)
R
S
L
S
C
P

Obwód przedstawiony na rys 5.1.b mo
żna przekształcić obwodu równoległego
przedstawionego na rys 5.2.b.
a)
b)
Rys.5.2 Przekształcenie obwodu szeregowego a) do równoległego b).
Na podstawie dodatku A obwód przedstawiony na rys.5.2.a przekształcamy do postaci
równoległej (rys.5.2.b). Zało
żenie równości dobroci obwodu RL szeregowego i równoległego
(najcz
ęściej występujące w praktyce przekształcenie) pozwala wyprowadzić następujące
zale
żności (dodatek A):
Zakładaj
ąc, że obwód ma dużą dobroć
1
>>
Q
, wówczas równania (5.3) mo
żna uprościć do
postaci:
W praktyce pomija si
ę wpływ pojemności międzyzwojowej anteny a jej schemat zastępczy
sprowadza si
ę do prostego obwodu RL szeregowego bądź równoległego. W systemie RFID
do anteny doł
ączana jest specjalnie dobrana pojemność C
P
w celu wytworzenia rezonansu na
zadanej cz
ęstotliwości, dlatego powyższe przekształcenia nie tracą na wartości.
2
2
1 Q
Q
L
L
P
S
+
=
,
2
1
1
Q
R
R
P
S
+
=
(5.3)
Q
Q
Q
C
R
R
L
Q
L
R
C
R
Q
S
P
S
S
S
S
S
P
P
P
P
P
=
=
=
=
=
=
,
1
,
ω
ω
ω
ω
(5.4)
P
P
S
L
Q
Q
L
L
≈
+
=
2
2
1
,
2
Q
R
R
P
S
≈
(5.5)
R
S
L
S
C
P
C
P
R
P
L
P
Q
S
=Q
P
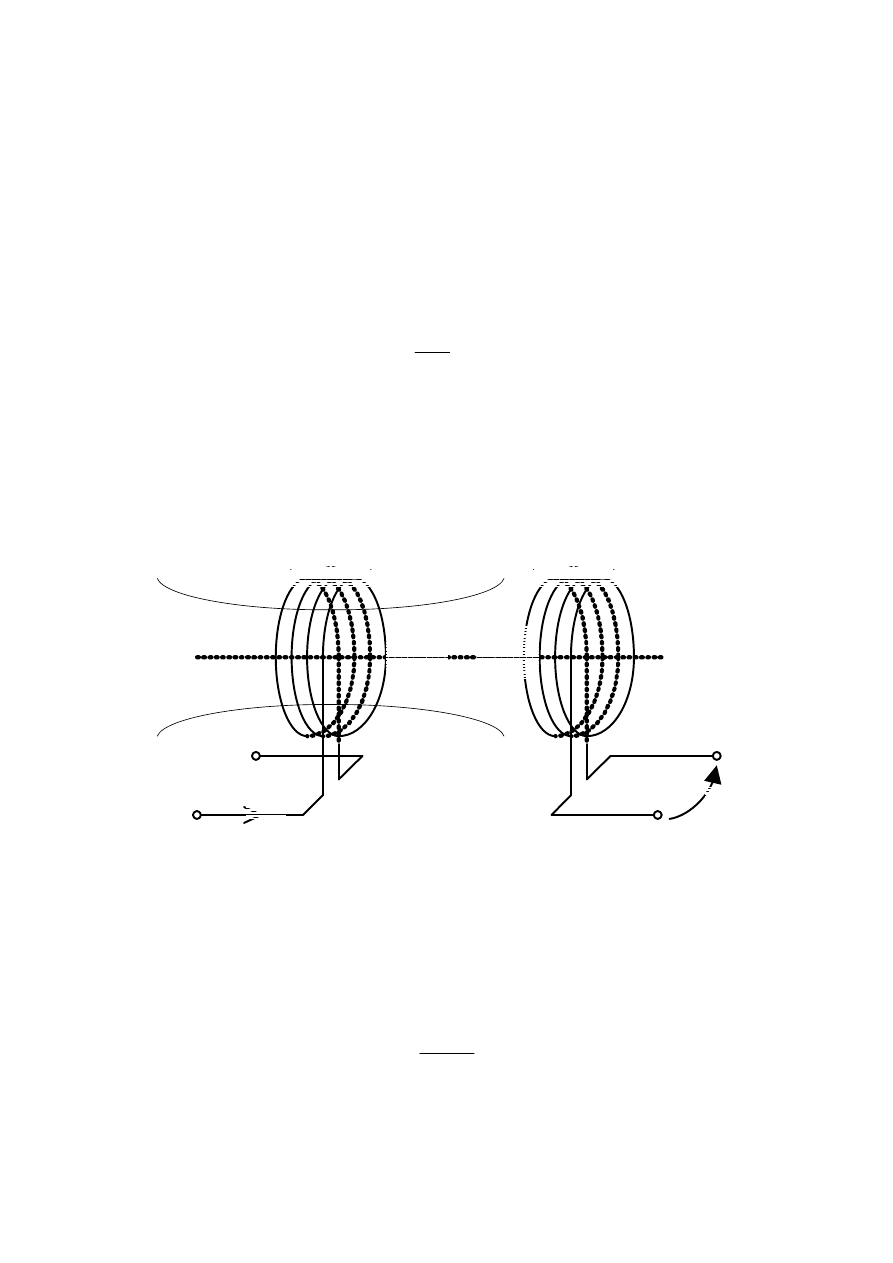
6. Antena w zmiennym polu magnetycznym
Jednym z zada
ń odbiornika systemu RFID jest przetwarzanie energii zgromadzonej w polu
magnetycznym na energi
ę elektryczną. Proces ten wprost wynika z prawa indukcji Faradaya –
na zaciskach anteny (cewki) umieszczonej z zmiennym polu magnetycznym (obserwowana
okresowa zmiana strumienia
Ф
B
) indukuje si
ę okresowo zmienna siła elektromotoryczna ε:
W dalszej cz
ęści tego punktu przeanalizowany zostanie układ cewek sprzężonych z
uwzgl
ędnieniem oddziaływań pomiędzy anteną nadawczą (cewka zasilanej z generatora) i
anten
ą odbiorczą (model obwodowy RL, uproszczony). Szczegóły dotyczące układu
przedstawiono na rys.6.1.
Rys.6.1. Układ nadajnika i odbiornika (układ cewek sprz
ężonych).
Parametry dotycz
ące nadajnika zapisane zostały z indeksem „1”, natomiast parametry
odbiornika maj
ą indeks „2”. Ф
B1
oznacza strumie
ń wektora indukcji magnetycznej
indukowany w cewce nadajnika i liczony przez powierzchni
ę
1
1
s
N
(gdzie s
1
jest powierzchni
ą
jednego zwoju).
Ф
B2
natomiast oznacza strumie
ń przechodzący przez uzwojenia cewki
odbiornika i jest liczony przez powierzchni
ę
2
2
s
N
(gdzie s
2
jest powierzchni
ą jednego
zwoju). Zastosowanie prawa indukcji Faradaya do cewki odbiornika daje:
Zakładaj
ąc, że przez cewkę nadajnika przepływa prąd sinusoidalny postaci:
dt
d
B
Φ
−
=
ε
(6.1)
dt
t
d
t
U
B
)
(
)
(
2
2
φ
−
=
(6.2)
)
sin(
)
(
1
1
t
I
t
I
ω
=
(6.3)
L
1
L
2
N
1
N
2
s
1
s
2
Ф
B1
Ф
B2
I
1
U
2
NADAJNIK
ODBIORNIK

Strumie
ń Ф
B2
na mocy równania (1.9) tak
że jest sinusoidalnie zależny od czasu:
Wówczas równanie (6.2) przyjmuje posta
ć:
Zakładaj
ąc, że pole powierzchni zwoju cewki odbiornika s
2
jest małe, mo
żna przyjąć, że
warto
ść wektora indukcji magnetycznej w dowolnym punkcie obszaru s
2
jest stała i równa
warto
ści na osi anteny. Wówczas strumień Ф
B2
mo
żna obliczyć wprost jako iloczyn
całkowitego pola powierzchni uzwoje
ń cewki odbiornika i wartości wektora indukcji na osi
B
2
:
Podstawienie (6.6) do (6.5) daje:
Dalsze obliczenia zostan
ą przeprowadzone na modułach (amplitudach) analogicznie jak w
metodzie symbolicznej stosowanej w teorii obwodów pr
ądu przemiennego. Amplituda
napi
ęcia indukowanego przyjmuje postać (w odniesieniu do fazy prądu I
1
(t)
):
Tak jak zostało przyj
ęte wartość B
2
jest równa warto
ści wektora indukcji na osi anteny - wzór
(1.9)
- w którym r oznacza promie
ń uzwojenia anteny nadawczej a d odległość pomiędzy antenami.
Na podstawie (6.9) strumie
ń Ф
B2
wynosi:
Strumie
ń Ф
B2
jest zwi
ązany z amplitudą prądu płynącego przez cewkę nadajnika poprzez
współczynnik indukcyjno
ści wzajemnej M:
Z porównania (6.10) z (6.11) mo
żna wyznaczyć współczynnik indukcyjności wzajemnej
zale
żny od wymiarów geometrycznych układu:
)
sin(
)
(
2
2
t
t
B
B
ω
φ
φ
=
(6.4)
)
cos(
)
(
2
2
t
t
U
B
ω
ω
φ
−
=
(6.5)
2
2
2
2
s
N
B
B
=
φ
(6.6)
)
cos(
)
(
2
2
2
2
t
s
N
B
t
U
ω
ω
−
=
(6.7)
2
2
2
2
s
N
B
j
U
ω
−
=
(6.8)
2
3
2
2
2
1
1
2
)
(
2
)
,
(
d
r
r
N
I
d
r
B
B
x
+
=
=
µ
,
(6.9)
2
2
2
3
2
2
2
1
1
2
)
(
2
s
N
d
r
r
N
I
B
+
=
µ
φ
(6.10)
1
2
MI
B
=
φ
(6.11)

Oprócz współczynnika indukcyjno
ści wzajemnej M należy wyprowadzić także
bezwymiarowy współczynnik sprz
ężenia k (wykorzystywany do modelowania obwodów
sprz
ężonych w programach symulacyjnych np. w PSpice). Jest on związany z M następującą
zale
żnością:
W przypadku rozwa
żanego układu, współczynnik k wynosi:
Antena (cewka) umieszczona w polu magnetycznym zaczyna działa
ć jak źródło sygnału. W
odró
żnieniu od cewki izolowanej od pola przedstawionej na rys.5.1.b schemat elektryczny
anteny odbieraj
ącej sygnał należy uzupełnić o źródło sygnału (rys.6.2.b).
a)
b)
Rys.6.2 a) schemat anteny izolowanej, b) schemat anteny, w której indukuje si
ę siła elektromotoryczna.
Napi
ęcie indukowane w cewce odbiornika, na podstawie (6.8) jest równe:
Współczynnik M wyznaczony w (6.13) a tak
że współczynnik k w (6.14) zostały obliczone
wprost z uproszczonej geometrii układu, dlatego maj
ą głównie charakter poglądowy. Na ich
podstawie mo
żna jednak sformułować pewne ogólne wnioski obowiązujące w każdym
układzie rzeczywistym. W układzie istnieje tylko jedno
źródło pola – nadajnik, dlatego
strumienie liczony przez sumaryczn
ą powierzchnię cewki nadajnika Ф
B1
i odbiornika
Ф
B2
s
ą
ró
żne i co do modułów spełniają zależności:
Wiedz
ąc, że
2
3
2
2
2
2
2
1
2
2
2
3
2
2
2
1
1
1
)
(
2
,
)
(
2
d
r
r
s
N
N
M
s
N
d
r
r
N
I
MI
+
=
+
=
µ
µ
(6.12)
2
1
L
L
k
M
=
(6.13)
2
1
2
1
2
3
2
2
2
2
)
(
2
L
L
N
N
d
r
r
s
k
+
=
µ
(6.14)
1
2
2
2
2
2
MI
j
j
s
N
B
j
U
B
ω
ωφ
ω
−
=
−
=
−
=
(6.15)
1
1
1
I
L
B
=
φ
- strumie
ń całkowity
1
2
MI
B
=
φ
- strumie
ń użyteczny
(6.16)
R
2S
R
2S
L
2S
L
2S
U
2

stosunek strumienia u
żytecznego do całkowitego jest równy:
Napi
ęcie zasilające cewkę nadajnika (napięcie na indukcyjności L
1
) w zapisie symbolicznym
jest równe:
Natomiast Napi
ęcie indukowane na indukcyjności odbiornika wynosi:
Stosunek amplitudy napi
ęcia U
2
do U
1
wynosi:
Równanie (6.20) podaje u
żyteczny w sensie praktycznym związek pomiędzy amplitudami
napi
ęć zasilania nadajnika i indukowanego w odbiorniku wyrażony przy pomocy mierzalnych
parametrów obwodu.
7. Antena odbiornika dostrojona i obci
ążona (transmitancja toru).
Schemat elektryczny anteny odbiornika umieszczonej w zmiennym polu magnetycznym
przedstawiono na rys.6.2.b. Amplituda napi
ęcia U
2
indukowanego na zaciskach anteny
nieobci
ążonej jest relatywnie mała w porównaniu z minimalnymi napięciami potrzebnymi do
zasilania układu elektronicznego dlatego równolegle z anten
ą włącza się pojemność C
2P
,
dobran
ą tak aby rezonans powstałego obwodu RLC wypadał w pobliżu częstotliwości pracy
stacji nadawczej. Nale
ży dodatkowo uwzględnić dołączone do anteny obciążenie w postaci
rezystancji R
2L
– odbiornik energii. Opisany układ przedstawiono na rys.7.1.
2
1
L
L
k
M
=
(6.13)
1
2
1
2
1
1
1
2
L
L
k
L
L
L
k
L
M
B
B
=
=
=
φ
φ
(6.17)
1
1
1
I
L
j
U
ω
=
(6.18)
1
2
MI
j
U
ω
−
=
(6.19)
1
2
1
2
L
L
k
U
U
=
(6.20)

Rys.7.1. Schemat elektryczny odbiornika zło
żonego z anteny pracującej jako element indukcyjny dociążonego
obwodu rezonansowego.
Wyznaczenie zale
żności napięcia U
AB
w funkcji U
2
:
Rozpisanie mianownika wyra
żenia w (7.1):
Uwzgl
ędniając (7.2) w (7.1) otrzymuje się:
(
)
(
)
(
)(
)
(
)
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
1
1
||
1
||
U
C
j
R
R
L
j
U
C
R
j
R
L
j
R
R
U
C
R
j
R
R
L
j
C
R
j
R
U
C
j
R
C
j
R
R
L
j
C
j
R
C
j
R
U
C
j
R
R
L
j
C
j
R
U
P
L
S
S
P
L
S
S
L
L
P
L
L
S
S
P
L
L
P
L
P
L
S
S
P
L
P
L
P
L
S
S
P
L
AB
+
+
+
=
=
+
+
+
=
+
+
+
+
=
=
+
+
+
+
=
+
+
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
(7.1)
(
)
+
+
−
+
=
=
−
+
+
+
=
+
+
+
S
P
L
S
P
S
L
S
P
S
S
P
L
S
L
S
P
L
S
S
R
C
R
L
j
C
L
R
R
C
L
R
C
j
R
L
j
R
R
C
j
R
R
L
j
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
1
1
1
ω
ω
ω
ω
ω
ω
ω
ω
(7.2)
R
2S
L
2S
U
2
C
2P
R
2L
U
AB

Uwzgl
ędniając dodatkowo zależność napięcia U
2
od pr
ądu I
1
w (6.15) wyra
żenie na napięcie
indukowane na obci
ążeniu U
AB
wynosi:
Wyra
żenie (7.2) stanowi symboliczny zapis napięcia U
AB
, uwzgl
ędniający jego moduł
(amplitud
ę) i fazę względem fazy prądu I
1
. W badanym systemie RFID istotna jest amplituda
napi
ęcia zasilającego układ, dlatego wyrażenie (7.4) należy obustronnie obłożyć modułem:
Zale
żność (7.5) wiąże amplitudę prądu płynącego przez cewkę nadajnika z amplitudą
napi
ęcia generowaną na obciążeniu dołączonym do rezonansowego układu anteny odbiorczej.
Stanowi ono podstaw
ę analizy systemu RFID.
Wyra
żenie (7.5) stanowi wynik rozważań ogólnych i nie uwzględnia ewentualnych
mo
żliwych uproszczeń wynikających z dostrojenia obwodu i jego dużej dobroci. Zakładając,
że obwód jest dostrojony i pracuje na pulsacji rezonansu własnego
r
ω
mo
żna wprowadzić
nast
ępujące uproszczenia:
Uwzgl
ędniając (7.6) w (7.5) można otrzymać:
Zakładaj
ąc dodatkowo, że obwód rezonansowy ma dużą dobroć (co oznacza, że
0
2
≈
S
R
)
wyra
żenie (7.7) można przedstawić w prostszej postaci:
2
2
2
2
2
2
2
2
2
2
1
1
U
R
C
R
L
j
C
L
R
R
U
S
P
L
S
P
S
L
S
AB
+
+
−
+
=
ω
ω
ω
(7.3)
+
+
−
+
−
=
S
P
L
S
P
S
L
S
AB
R
C
R
L
j
C
L
R
R
MI
j
U
2
2
2
2
2
2
2
2
2
1
1
ω
ω
ω
ω
(7.4)
2
2
2
2
2
2
2
2
2
2
2
1
1
+
+
−
+
=
S
P
L
S
P
S
L
S
AB
R
C
R
L
C
L
R
R
MI
U
ω
ω
ω
ω
(7.5)
0
1
2
2
2
=
−
⇒
=
P
S
r
C
L
ω
ω
ω
(7.6)
2
2
2
2
2
2
2
2
1
+
+
=
S
P
L
S
L
S
AB
R
C
R
L
R
R
MI
U
ω
ω
ω
(7.7)
2
2
2
2
2
1
+
=
S
P
L
S
AB
R
C
R
L
MI
U
ω
ω
ω
(7.8)

Przekształcenie mianownika wyra
żenia (7.8):
Zakładaj
ąc jeszcze, że obwód antenowy jest nieobciążony (
∞
→
L
R
2
) amplituda napi
ęcia U
AB
przyjmuje posta
ć:
gdzie:
S
Q
2
jest dobroci
ą obwodu szeregowego wynikającą z obecności rezystancji szeregowej
S
R
2
i poniewa
ż przyjęte założenie wyeliminowało rezystancję obciążenia
L
R
2
to jest to
zarazem wypadkowa dobro
ć
2
Q całego obwodu. W tym przypadku otrzymuje si
ę:
Nale
ży zwrócić uwagę, że założenie dużej dobroci układu i braku obciążenia są zasadniczo
ró
żnymi założeniami i nie mogą stanowić podstawy do określania wzajemnych relacji
pomi
ędzy rezystancjami
L
R
2
i
S
R
2
.
Innym
podej
ściem do analizy układu odbiorczego jest wyznaczenie jego
Theveninowskiego
źródła zastępczego. Można wtedy łatwo sformułować warunek
energetycznego dopasowania obci
ążenia
L
R
2
do
źródła. Obwód dostrojonej i nieobciążonej
anteny odbiorczej wraz z obwodem
źródła zastępczego przedstawiono na rys.7.2.
a)
b)
Rys.7.2. a) Obwód dostrojonej i nieobci
ążonej anteny odbiorczej, b) źródło zastępcze (odpowiada obwodowi z
punktu a) gdy
r
ω
ω
=
oraz
1
2
>>
S
Q
).
Wyznaczenie impedancji
AB
Z
:
ω
ω
ω
P
S
P
S
C
L
C
L
2
2
2
2
2
1
1
=
⇒
=
2
2
2
2
2
2
2
2
2
2
+
=
+
S
S
L
S
S
P
L
S
L
R
R
L
R
C
R
L
ω
ω
ω
ω
(7.9)
2
2
1
2
2
2
1
2
2
2
2
1
U
Q
MI
Q
L
R
MI
L
R
R
L
MI
U
S
S
S
S
S
S
L
S
AB
=
=
→
+
=
ω
ω
ω
ω
ω
ω
(7.10)
2
2
U
Q
U
S
AB
=
(7.11)
C
2P
U
2
L
2S
R
2S
Z
AB
Z
ABr
Z
ABr
=Q
2S
ω
r
L
2S
U
AB
=U
2
Q
2S

Wyznaczenie impedancji
ABr
Z
dla pulsacji rezonansowej
r
ω
ω
=
Z warunku rezonansu:
wynika
Wyznaczenie impedancji
ABr
Z
przy zało
żeniu dużej dobroci
1
2
>>
S
Q
:
Obliczenie pr
ądu zwarcia dwójnika z rys.7.2.a:
Obliczenie napi
ęcia źródła zastępczego dwójnika z rys.7.2.b:
Zakładaj
ąc, jak poprzednio, dużą dobroć obwodu
1
2
>>
S
Q
napi
ęcie z (7.16) przyjmuje
warto
ść:
Korzystaj
ąc z obwodu zastępczego przedstawionego na rys.7.2.b można wyznaczyć warunek
dopasowania energetycznego odbiornika
L
R
2
do anteny (pełni
ącej rolę generatora) pracującej
(
)
(
)
P
S
P
S
S
S
S
S
P
S
S
P
S
S
P
S
S
AB
C
R
j
C
L
L
j
R
L
j
R
C
j
L
j
R
C
j
L
j
R
C
j
L
j
R
Z
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
1
1
1
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
−
+
=
+
+
+
=
+
+
+
=
(7.12)
P
S
r
P
S
r
S
r
S
ABr
C
R
j
C
L
L
j
R
Z
2
2
2
2
2
2
2
1
ω
ω
ω
+
−
+
=
(7.13)
0
1
2
2
2
=
−
⇒
=
P
S
r
C
L
ω
ω
ω
(7.14)
P
S
r
S
r
S
ABr
C
R
j
L
j
R
Z
2
2
2
2
ω
ω
+
=
(7.15)
S
r
S
P
r
S
P
r
S
P
r
S
S
r
P
S
r
S
r
S
ABr
L
Q
C
Q
C
j
jQ
C
j
R
L
j
C
R
j
L
j
R
Z
2
2
2
2
2
2
2
2
2
2
2
2
2
1
1
ω
ω
ω
ω
ω
ω
ω
=
≈
+
=
+
=
+
=
(7.17)
S
r
S
ZABr
L
j
R
U
I
2
2
2
ω
+
=
(7.18)
S
S
S
S
r
S
S
S
r
S
r
S
S
r
S
ZABr
ABr
AB
Q
Q
U
R
L
Q
R
L
j
U
L
Q
L
j
R
U
I
Z
U
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
1
+
=
+
=
+
=
=
ω
ω
ω
ω
(7.19)
S
S
S
AB
Q
U
Q
Q
U
U
2
2
2
2
2
2
1
≈
+
=
(7.20)
na cz
ęstotliwości rezonansowej. Schemat układu anteny obciążonej i obliczenia
przedstawiono na rys.7.3.
warunek dopasowania energetycznego:
L
ABr
R
Z
2
=
S
r
S
L
L
Q
R
2
2
2
ω
=
S
AB
Q
U
U
2
2
2
1
=
Rys. 7.3. Układ anteny w postaci
źródła zastępczego z obciążeniem.
Obci
ążenie jest energetycznie dopasowane do źródła gdy spełnia zależność:
8. Optymalizacja układu odbiorczego przez zmian
ę dobroci wypadkowej
2
Q .
W pierwszej cz
ęści tego punktu pokazane zostanie wyprowadzenie ogólnego wzoru na
wypadkow
ą dobroć odbiornika. Przedstawione na rys.8.1. przekształcenia są słuszne przy
zało
żeniu, że:
•
dobro
ć wypadkowa każdego z obwodów jest duża,
•
pulsacja
ω
jest równa pulsacji rezonansowej
r
ω
a)
S
S
S
R
L
Q
2
2
2
ω
=
2
2
U
Q
U
S
AB
=
b)
S
P
P
R
Q
R
2
2
2
2
=
S
P
P
L
R
Q
2
2
2
ω
=
S
r
S
L
L
Q
R
2
2
2
ω
=
(7.21)
U
AB
U
2
C
2P
L
2S
R
2S
U
AB
=U
2
Q
2S
U
AB
=U
2
Q
2S
R
2L
Z
ABr
=Q
2S
ω
r
L
2S
Z
ABr
=Q
2S
ω
r
L
2S
Z
ABr
=Q
2S
ω
r
L
2S
Z
ABr
=Q
2S
ω
r
L
2S
U
2
Q
2S
U
AB

2
2
U
Q
U
P
AB
=
S
P
Q
Q
2
2
=
c)
L
P
R
R
R
2
2
2
||
=
S
L
R
Q
2
2
2
ω
=
2
2
U
Q
U
AB
=
Rys.8.1. Kolejne etapy przekształcenia obwodu podstawowego: a) obwód podstawowy – rzeczywista antena
pracuj
ąca w nieobciążonym obwodzie rezonansowym, b) przekształcenie obwodu do postaci równoległej, c)
doł
ączenie obciążenia
.
Rozwini
ęcie wyrażenia na dobroć wypadkową obwodu dociążonego (z rys.8.1.c)
Ogólny wniosek dotycz
ący dobroci wypadkowej obwodu rezonansowego dociążonego:
gdzie:
P
Q
2
jest dobroci
ą jaką miałby układ gdyby istniała tylko rezystancja
P
R
2
,
L
Q
2
jest
obroci
ą jaką miałby układ gdyby istniała tylko rezystancja
L
R
2
, natomiast
2
Q jest dobroci
ą
wypadkow
ą wynikającą z istnienia obu rezystancji w obwodzie.
Wpływ dobroci układu odbiorczego na amplitud
ę napięcia U
AB
:
Wprowadzaj
ąc równanie (6.15) otrzymuje się:
P
L
P
S
L
S
P
L
S
L
P
L
P
S
S
Q
Q
R
L
R
L
R
R
L
R
R
R
R
L
L
R
Q
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
+
=
+
=
+
=
+
=
=
ω
ω
ω
ω
ω
(8.1)
P
L
P
L
Q
Q
Q
Q
Q
Q
2
2
2
2
2
2
1
1
1
1
1
1
+
=
⇒
+
=
(8.2)
AB
AB
U
Q
U
U
Q
U
2
2
2
2
1
=
⇒
=
(8.3)
U
AB
U
AB
U
2
U
2
R
2L
C
2P
C
2P
L
2S
L
2S
R
2P
R
2P
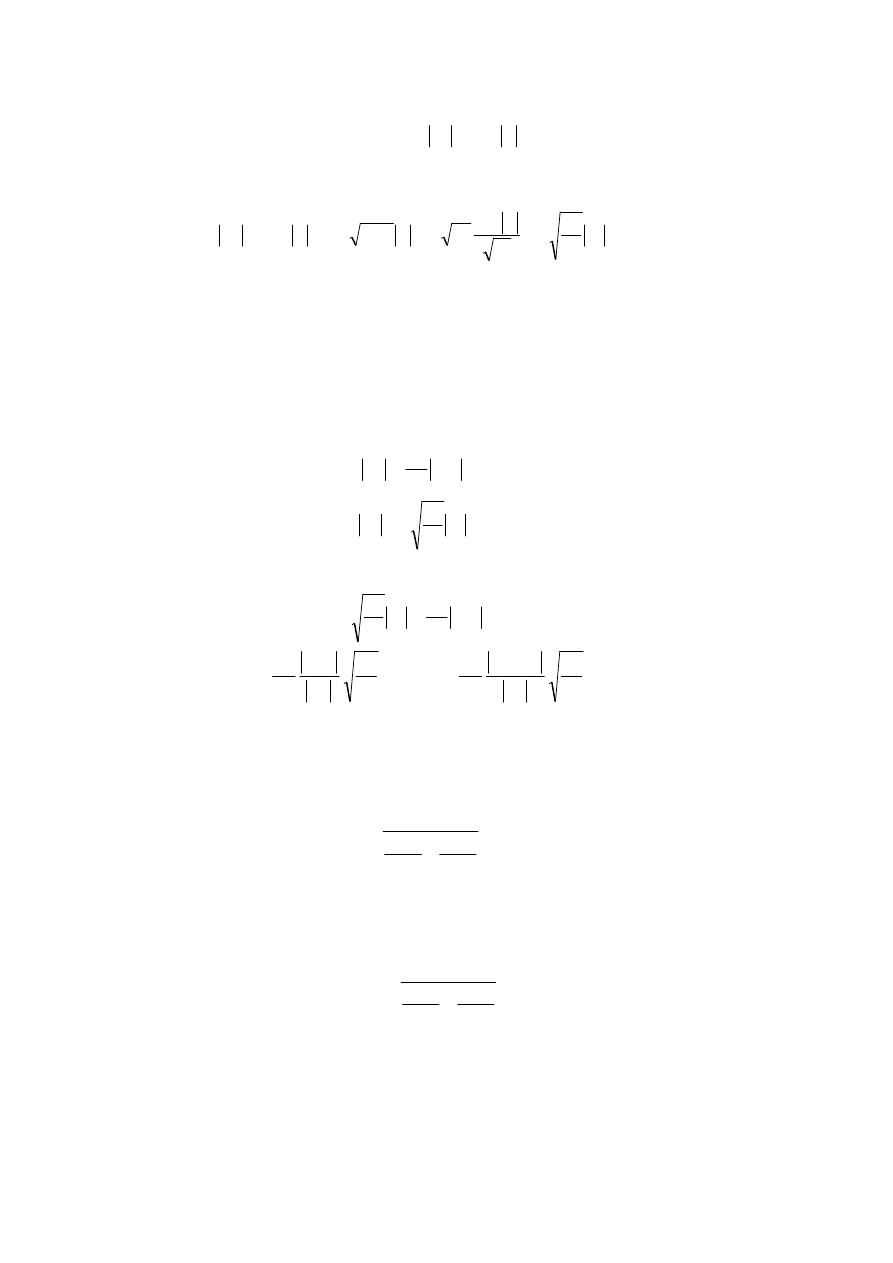
Uwzgl
ędniając zależność pomiędzy M i k:
gdzie: L
1
oraz L
2
s
ą współczynnikami samoindukcji cewek odpowiednio nadajnika i
odbiornika, U
1
– napi
ęcie na zaciskach anteny nadawczej.
Cech
ą charakterystyczną systemu RFID jest to, że odbiornik wraz ze swoimi układami jest
zasilany poprzez pole magnetyczne. Aby zapewni
ć transponderowi odpowiednie warunki
pracy, napi
ęcie zasilające U
AB
nie mo
że być mniejsze od pewnej wartości minimalnej U
ABmin
.
St
ąd z równań (8.1) i (8.3) należy znaleźć warunek minimalnego napięcia zasilania:
Z postaci równania (8.5) wynika,
że minimalna wartość bezwymiarowego współczynnika
sprz
ężenia k
min
jest zale
żna od dobroci wypadkowej układu
2
Q , natomiast korzystaj
ąc z
wyprowadzenia w (8.1) dobro
ć wypadkowa dana jest wzorem:
Zale
żność (8.8) można potraktować jak funkcję, której argumentem jest współczynnik
samoindukcji cewki L
2S
:
Poszukuj
ąc maksimum funkcji (8.9) można rozwiązać problem optymalnego dopasowania
układów odbiornika. W tym celu trzeba jeszcze przekształci
ć wyrażenie (8.9) w następujący
sposób:
1
2
1
2
I
M
U
MI
j
U
ω
ω
=
⇒
−
=
(8.4)
1
1
2
1
1
1
2
1
2
1
1
2
U
L
L
k
L
I
L
L
k
I
L
L
k
I
M
U
=
=
=
=
ω
ω
ω
(8.5)
AB
U
Q
U
2
2
1
=
1
1
2
2
U
L
L
k
U
=
(8.6)
AB
U
Q
U
L
L
k
2
1
1
2
1
=
2
1
1
min
2
min
2
1
1
2
1
1
L
L
U
U
Q
k
L
L
U
U
Q
k
AB
AB
=
⇒
=
(8.7)
P
S
L
S
R
L
R
L
Q
2
2
2
2
2
1
ω
ω
+
=
(8.8)
( )
P
S
L
S
S
R
L
R
L
L
Q
2
2
2
2
2
2
1
ω
ω
+
=
(8.9)

Podstawienie (8.11) do (8.9)
Obliczenie pochodnej funkcji (8.12) wzgl
ędem indukcyjności L
2S
:
Warunek zerowania si
ę pochodnej:
Dla warunku (8.14) funkcja (8.12) przyjmuje maksimum:
Nale
ży zauważyć, że wyrażenie (8.16) nie jest definicją dobroci optymalnej, a jedynie wynika
z zale
żności (8.14) tzn. jeżeli układ jest zaprojektowany optymalnie to jego dobroć
wypadkow
ą można obliczyć z (8.16). Warunek istnienia układu optymalnego jest zapisany w
(8.14) i wynika z niego,
że:
S
S
P
R
Q
R
2
2
2
2
=
(8.10)
S
S
S
S
S
S
S
S
S
p
S
L
R
L
R
R
L
R
Q
L
R
L
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
ω
ω
ω
ω
ω
=
=
=
(8.11)
( )
S
S
L
S
S
L
R
R
L
L
Q
2
2
2
2
2
2
1
ω
ω
+
=
(8.12)
( )
(
)
(
)
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
1
S
L
S
L
S
S
S
L
S
L
S
L
S
L
S
S
L
S
S
L
S
S
S
S
L
S
S
S
S
R
R
L
R
L
L
R
R
L
R
R
R
L
R
L
L
R
L
R
R
L
L
L
R
R
L
L
L
L
Q
+
−
+
=
+
∂
∂
=
=
+
∂
∂
=
+
∂
∂
=
∂
∂
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
(8.13)
( )
(
)
0
2
0
2
2
2
2
2
2
2
2
2
2
2
2
2
=
−
+
⇔
=
∂
∂
L
S
S
S
L
S
L
S
S
R
L
L
R
R
L
R
L
L
Q
ω
ω
ω
ω
,
0
2
2
2
2
2
2
2
2
2
=
−
+
S
S
L
S
L
R
R
L
ω
ω
,
S
L
S
R
R
L
2
2
2
2
2
=
ω
,
ω
S
L
S
R
R
L
2
2
2
=
(8.14)
S
L
S
L
L
S
L
S
L
S
L
S
L
S
L
S
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
L
Q
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
2
1
1
=
=
+
=
=
ω
(8.15)
S
L
opt
R
R
Q
2
2
2
2
1
=
(8.16)

Zwi
ązek (8.17) dla pulsacji rezonansowej
r
ω
jest identyczny z warunkiem dopasowania
energetycznego (7.21).
Z punktu widzenia zasilania transpondera wystarczy konstruowa
ć układ odbiornika tak, by
miał jak najwi
ększą dobroć wypadkową
2
Q . Bior
ąc pod uwagę jednak drugą funkcję jaką ma
spełnia
ć układ, czyli umożliwiać transmisję danych w obu kierunkach, zbyt duża dobroć
obwodu odbiornika wprowadza tłumienie zmian sygnałów indukowanych w antenie. Je
żeli w
systemie stosuje si
ę modulację ASK, dobroć odbiornika nie powinna być zbyt duża. W
kolejnym punkcie przedstawiona zostanie analiza odpowiedzi impulsowej odbiornika, na
podstawie której mo
żna precyzyjnie ustalić dobroć
2
Q tak by zapewni
ć prawidłowe działanie
systemu dla danej przepływno
ści binarnej.
9. Odpowied
ź impulsowa odbiornika.
Antena wraz z doł
ączoną pojemnością C
2P
i obci
ążeniem R
2P
tworzy obwód rezonansowy
obci
ążony przedstawiony na rys.9.1.
Rys.9.1. Układ odbiornika.
Jest to podstawowy układ filtru dolnoprzepustowego LC 2 stopnia,, sterowanego ze
źródła U
2
i obci
ążonego rezystancją R
2P
. Odpowied
ź impulsowa przedstawionego układu zostanie
wyznaczona metod
ą operatorową, w tym celu najpierw należy obliczyć jego transmitancję:
S
L
S
R
R
L
2
2
2
2
2
=
ω
,
L
S
S
S
R
L
R
L
2
2
2
2
=
ω
ω
,
S
S
L
L
Q
R
2
2
2
ω
=
(8.17)
R
2S
L
2S
U
2
C
2P
R
2L
U
AB

Rozpisanie mianownika (9.1):
Transmitancja obwodu po podstawieniu (9.2) do (9.1) wygl
ąda następująco:
Ogólna posta
ć transmitancji rzędu drugiego:
w której:
∆ – logarytmiczny dekrement tłumienia, H
0
– wzmocnienie. Dodatkowo zale
żność
pomi
ędzy ∆ a dobrocią układu jest dana równaniem:
Z to
żsamościowego porównania (9.4) z (9.3) można wyznaczyć:
(
)
(
)
L
P
L
P
S
S
L
P
S
S
L
P
L
P
L
P
L
P
S
S
L
P
L
P
AB
R
sC
R
sC
R
sL
R
sC
R
sL
R
sC
R
sC
R
sC
R
sC
R
sL
R
sC
R
sC
U
U
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
1
+
+
+
=
=
+
+
+
=
+
+
+
+
=
(9.1)
(
)
+
+
+
+
+
+
=
=
+
+
+
+
+
+
=
=
+
+
+
+
=
=
+
+
+
+
=
+
+
+
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
L
S
P
S
L
S
L
S
L
P
S
L
S
L
S
P
S
L
S
L
S
P
S
L
S
P
S
L
S
P
S
L
S
L
P
L
S
P
S
S
S
P
S
L
P
L
P
S
S
R
R
C
R
R
L
s
R
R
R
C
L
s
R
R
R
R
C
R
R
L
s
R
R
C
L
s
R
R
C
sR
R
R
C
L
s
R
L
s
R
sC
R
R
sC
R
R
sL
C
L
R
sC
R
sC
R
sL
(9.2)
+
+
+
+
+
+
=
=
1
1
1
)
(
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
L
S
P
S
L
S
L
S
L
P
S
L
S
AB
R
R
C
R
R
L
s
R
R
R
C
L
s
R
R
U
U
s
H
(9.3)
1
2
2
)
(
2
0
2
0
2
2
0
0
2
0
2
2
0
0
+
∆
+
=
+
∆
+
=
ω
ω
ω
ω
ω
s
s
H
s
s
H
s
H
(9.4)
∆
=
2
1
Q
(9.5)

W praktyce pomiar parametrów odpowiedzi impulsowej układu odbywał by si
ę poprzez jej
obserwacj
ę na oscyloskopie zsynchronizowanym z zewnętrznym generatorem impulsów
Diraca. Konstrukcja takiego generatora nie jest w praktyce mo
żliwa, dlatego znacznie częściej
obserwuje si
ę odpowiedź układu na skok jednostkowy. Znając tzw. odpowiedź skokową
układu mo
żna, obliczając jej pochodną, obliczyć odpowiedź impulsową. W następnym kroku
wyprowadzona zostanie odpowied
ź skokowa układu o transmitancji (9.4).
Bieguny transmitancji funkcji (9.11):
W celu wyznaczenia odpowiedzi skokowej nale
ży obliczyć transformatę odwrotną funkcji
(9.11). Jednym ze sposobów jest wykorzystanie twierdzenia Heaviside’a o residuach, na
mocy którego transformata odwrotna obrazu funkcji maj
ącej postać funkcji wymiernej ma
ogóln
ą postać:
L
P
S
P
S
L
S
L
S
P
S
L
S
L
S
L
P
S
L
S
R
C
L
C
R
R
L
R
R
C
R
R
L
R
R
H
R
C
L
R
R
2
2
2
2
2
2
2
2
2
2
2
2
2
2
0
2
2
0
2
2
2
2
2
2
0
2
2
1
1
+
=
∆
⇒
+
+
=
∆
+
=
+
=
ω
ω
(9.6)
(9.7)
(9.8)
( )
( )
(
)
2
0
2
2
0
0
2
2
,
s
1
)
(
,
s
1
1(t)
)
(
ω
ω
+
∆
+
=
=
↔
=
s
s
s
H
s
U
s
H
s
U
t
U
ABs
ABs
(9.9)
(9.10)
(9.11)
∆
−
−
∆
−
=
∆
−
+
∆
−
=
=
2
2
0
2
2
2
0
1
0
0
ω
ω
j
s
j
s
s
(9.12)
[
]
<
>
=
∑
−
=
=
0
0
0
)
(
Res
)
(
1
0
t
dla
t
dla
e
s
X
t
x
st
K
k
s
s
k
(9.13)
)
(
)
(
s
X
t
x
↔
1
,...,
0
−
=
K
k
(9.14)
gdzie: K – liczba biegunów transmitancji (bieguny wielokrotne s
ą liczone jeden raz), n –
krotno
ść bieguna k.
Poni
żej przedstawiono obliczenia residuów dla kolejnych biegunów.
Na podstawie twierdzenia Heaviside’a (9.13) odpowied
ź skokowa układu jest sumą
wyznaczonych residuów. Najpierw obliczona zostanie suma (9.17) i (9.18), a nast
ępnie
uwzgl
ędniony zostanie składnik (9.16).
[
]
(
)
(
) ( )
[
]
s
F
s
s
ds
d
n
s
F
n
k
n
n
s
s
s
s
k
k
−
−
=
−
−
→
=
1
1
!
1
1
lim
)
(
Res
(9.15)
( )
[
]
(
)( )( )( )
0
2
2
0
2
2
0
2
0
0
2
1
2
0
0
2
1
0
2
0
0
0
0
0
lim
Res
H
j
j
H
s
s
H
e
s
s
s
s
s
s
H
s
s
e
s
U
st
s
s
st
ABs
s
s
=
∆
−
−
∆
−
∆
−
+
∆
−
=
=
=
−
−
−
−
=
→
=
ω
ω
ω
ω
ω
(9.16)
( )
[
]
(
)( )( )( )
(
)
t
j
t
t
s
st
s
s
st
ABs
s
s
e
e
j
j
H
e
s
s
s
H
e
s
s
s
s
s
s
H
s
s
e
s
U
2
2
0
1
1
2
2
0
2
2
0
2
0
0
1
2
1
2
0
0
2
1
0
2
0
0
1
1
2
lim
Res
∆
−
∆
−
→
=
∆
−
+
∆
−
∆
−
=
=
−
=
−
−
−
−
=
ω
ω
ω
ω
ω
ω
(9.17)
( )
[
]
(
)( )( )( )
(
)
t
j
t
t
s
st
s
s
st
ABs
s
s
e
e
j
j
H
e
s
s
s
H
e
s
s
s
s
s
s
H
s
s
e
s
U
2
2
0
2
2
2
2
2
0
2
2
0
2
0
0
2
1
2
2
0
0
2
1
0
2
0
0
2
2
lim
Res
∆
−
−
∆
−
→
=
∆
−
−
∆
−
∆
−
−
=
=
−
=
−
−
−
−
=
ω
ω
ω
ω
ω
ω
(9.18)

Kontynuacj
ę obliczeń dla wnętrza nawiasu głównego w (9.19) przedstawiono osobno, poniżej
(w mianowniku wyci
ągnięto od razu wspólny czynnik przed nawias).
Cz
ęść rzeczywista wyrażenia (9.20) wynosi:
Uwzgl
ędniając wnioski z (9.20) i (9.21) w (9.19), można wyznaczyć sumę (9.17) i (9.18)
(
)
t
t
j
t
t
j
t
j
t
t
j
t
j
t
j
t
t
j
t
e
j
e
H
e
j
j
e
H
j
j
e
H
e
j
j
e
H
j
j
e
H
j
j
e
e
H
j
j
e
e
H
∆
−
∆
−
∆
−
∆
−
∆
−
∆
−
∆
−
−
∆
−
∆
−
−
∆
−
∆
−
∆
−
∆
−
∆
−
∆
−
−
=
=
∆
−
+
∆
−
∆
−
+
∆
−
+
∆
−
∆
−
=
=
∆
−
−
∆
−
∆
−
−
+
∆
−
+
∆
−
∆
−
=
=
∆
−
−
∆
−
∆
−
−
+
∆
−
+
∆
−
∆
−
2
2
0
2
2
0
2
0
0
2
2
0
2
2
0
2
0
0
2
2
0
2
2
0
2
0
0
2
2
0
2
2
0
2
0
0
2
2
0
2
2
0
2
0
0
2
2
0
2
2
0
2
0
0
2
2
0
2
2
0
2
0
0
2
2
Re
2
2
2
2
2
2
2
2
2
0
2
2
0
2
2
0
2
2
0
2
2
0
2
2
0
2
2
0
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
(9.19)
∆
−
+
∆
−
∆
−
−
∆
−
∆
−
−
∆
−
=
=
∆
−
−
∆
−
∆
−
=
=
∆
−
∆
−
∆
−
∆
−
∆
+
∆
−
∆
−
−
∆
−
∆
−
t
j
t
H
j
H
e
j
H
e
j
j
j
H
t
j
t
j
2
2
0
2
2
0
2
0
2
2
0
2
0
0
2
0
2
2
0
2
2
0
2
0
0
2
0
2
2
0
2
2
0
2
0
0
2
2
0
2
2
0
2
2
0
2
2
0
2
0
0
sin
cos
2
2
2
2
2
2
0
2
2
0
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
(9.20)
∆
−
∆
−
∆
−
∆
−
−
=
=
∆
−
∆
−
−
∆
+
∆
−
∆
−
−
∆
−
t
H
t
H
t
H
t
H
2
2
0
2
2
0
0
2
2
0
0
2
2
0
2
0
2
2
0
2
0
0
2
2
0
2
0
2
2
0
2
2
0
2
0
0
sin
2
cos
2
sin
2
cos
2
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
(9.21)

Na podstawie powy
ższych obliczeń można wyznaczyć odpowiedź skokową układu:
Odpowied
ź impulsowa równa jest pochodnej wyrażenia (9.23)
Odpowied
ź impulsowa ma postać końcową (9.24):
Poni
żej przedstawiono związek logarytmicznego dekrementu tłumienia ∆ i pulsacji
charakterystycznej
ω
0
z dobroci
ą wypadkową układu odbiornika
2
Q . Logarytmiczny
dekrement tłumienia wyznaczony w (9.8) ma posta
ć:
Mno
żąc licznik i mianownik przez pulsację rezonansową obwodu odbiornika ω
r
mo
żna
wyznaczy
ć związek ∆ z dobrociami
P
Q
2
i
L
Q
2
(odpowiednio od rezystancji paso
żytniczej
cewki i obci
ążenia dołączonego).
(
)
t
t
t
j
e
t
H
t
H
e
j
e
H
∆
−
∆
−
∆
−
∆
−
∆
−
∆
−
∆
−
−
=
=
∆
−
∆
−
∆
−
−
2
2
0
2
2
0
0
2
2
0
0
2
2
0
2
2
0
2
0
0
sin
2
cos
2
2
2
2
Re
2
2
2
0
ω
ω
ω
ω
ω
ω
ω
(9.22)
( )
t
ABs
e
t
H
t
H
H
t
U
∆
−
∆
−
∆
−
∆
+
∆
−
−
=
2
2
0
2
2
0
0
2
2
0
0
0
sin
cos
ω
ω
ω
(9.23)
( )
t
t
t
t
ABi
e
t
H
e
t
H
e
t
H
e
t
H
t
H
dt
d
t
U
∆
−
∆
−
∆
−
∆
−
∆
−
∆
−
=
=
∆
−
∆
−
∆
−
∆
−
∆
−
−
−
=
=
∆
−
∆
−
∆
+
∆
−
−
=
2
2
0
2
2
0
2
0
0
2
2
0
2
2
0
2
0
2
2
0
2
2
0
0
2
2
0
2
2
0
0
2
2
0
0
sin
sin
sin
sin
cos
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
(9.24)
( )
t
ABi
e
t
H
t
U
∆
−
∆
−
∆
−
=
2
2
0
2
2
0
2
0
0
sin
ω
ω
ω
(9.25)
L
P
S
P
S
L
S
R
C
L
C
R
R
L
2
2
2
2
2
2
2
2
+
=
∆
(9.26)
L
P
S
L
S
L
P
S
r
S
r
P
L
S
r
S
r
L
P
S
r
P
S
L
r
S
R
C
Q
Q
Q
R
C
R
L
C
R
R
L
R
C
L
C
R
R
L
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
+
=
+
=
+
=
∆
ω
ω
ω
ω
ω
ω
(9.27)

Warto przypomnie
ć iż podstawowym założeniem przekształcenia obwodu z szeregowej do
równoległej jest zało
żenie równości dobroci obu układów z czego wynika, że
S
P
Q
Q
2
2
=
,
je
żeli uwzględnić ten warunek w (9.27) wraz z zależnością (8.2) to logarytmiczny dekrement
tłumienia przyjmuje posta
ć:
Na podstawie równania (9.28) mo
żna stwierdzić, że wzrost dobroci wypadkowej obwodu
prowadzi do zmniejszenia
∆, czyli zmniejsza się tłumienie drgań własnych obwodu w
przypadku nagłego zaniku pobudzenia. Je
żeli zanik jest spowodowany modulacją sygnału
steruj
ącego, wówczas układ analizujący sygnał odbierany powinien zarejestrować te zmiany.
Ostateczny warunek doboru
2
Q
narzuca czuło
ść zastosowanego detektora (demodulatora).
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Q
Q
Q
Q
Q
R
C
Q
Q
Q
R
C
Q
Q
Q
r
r
L
P
L
P
r
r
L
P
P
L
P
L
P
S
L
S
ω
ω
ω
ω
=
+
=
+
=
+
=
∆
(9.28)
Wyszukiwarka
Podobne podstrony:
wersja robocza konspekt
Sieci?zprzewodowe (wersja robocza)
Esej - zaliczenie wersja robocza, ZARZĄDZANIE, Zarządzanie przedsiębiorstwem
Praca maturalna wersja robocza prawie got, matura praca matualna szaleństwo
Badanie układów o promieniowym rozkładzie natężenia pola magnetycznego v2, Elektrotechnika semestr 4
Wyznaczenie składowej poziomej indukcji pola magnetycznego Ziemi przy pomocy busoli statycznych, Num
fiz-magnetyzm ściąga, Źródłem pola magnetycznego są: 1 Magnesy naturalne Fe i jego stopy, Ni, Co)
Badanie prędkości łuku przy wydmuchu za pomocą pola magnetycznego , LABORATORIUM TECHNIKI ??CZENIA
Egzamin Klos wszystkie odpowiedzi wersja robocza
PHP (wersja robocza)
SK 1 (wersja robocza)
ginekologia giełda 23.03 15.50 (wersja robocza - nieopracowana do końca)
!!! KOMPENDIUM WIEDZY !!, 26-27, 22.6 Prawo Gaussa dla pola magnetycznego.
Ściągi z fizyki-2003 r, Odziaływanie pola magnetycznego na organizmy żywe
Badanie układów o promieniowym rozkładzie natężenia pola magnetycznego, GRONEK9, Laboratorium Podsta
Wyznaczanie składowej poziomej natężenia pola magnetycznego ziemskiego, 207, fiza207
Ściągi z fizyki-2003 r, Odziaływanie pola magnetycznego na organizmy żywe
Badanie układów o promieniowym rozkładzie natężenia pola magnetycznego, GRONEK9, Laboratorium Podsta
więcej podobnych podstron