edukacja statystyka z programem statistica malgorzata rabiej ebook

Wszelkie prawa zastrzeĪone. Nieautoryzowane rozpowszechnianie caáoĞci lub fragmentu niniejszej
publikacji w jakiejkolwiek postaci jest zabronione. Wykonywanie kopii metodą kserograficzną,
fotograficzną, a takĪe kopiowanie ksiąĪki na noĞniku filmowym, magnetycznym lub innym
powoduje naruszenie praw autorskich niniejszej publikacji.

Wszystkie znaki wystĊpujące w tekĞcie są zastrzeĪonymi znakami firmowymi bądĨ towarowymi
ich wáaĞcicieli.

Autor oraz Wydawnictwo HELION doáoĪyli wszelkich staraĔ, by zawarte w tej ksiąĪce informacje
byáy kompletne i rzetelne. Nie biorą jednak Īadnej odpowiedzialnoĞci ani za ich wykorzystanie, ani
za związane z tym ewentualne naruszenie praw patentowych lub autorskich. Autor oraz
Wydawnictwo HELION nie ponoszą równieĪ Īadnej odpowiedzialnoĞci za ewentualne
szkody wynikáe z wykorzystania informacji zawartych w ksiąĪce.

Redaktor prowadzący: Tomasz Waryszak

Projekt okáadki: Maciej Pasek

Materiaáy graficzne na okáadce zostaáy wykorzystane za zgodą Shutterstock.

Wydawnictwo HELION
ul. KoĞciuszki 1c, 44-100 GLIWICE
tel. 32 231 22 19, 32 230 98 63
e-mail: helion@helion.pl
WWW: http://helion.pl (ksiĊgarnia internetowa, katalog ksiąĪek)

Drogi Czytelniku!
JeĪeli chcesz oceniü tĊ ksiąĪkĊ, zajrzyj pod adres
http://helion.pl/user/opinie?statis
MoĪesz tam wpisaü swoje uwagi, spostrzeĪenia, recenzjĊ.

ISBN: 978-83-246-4110-9

Printed in Poland.

•

Kup książkę

•

Poleć książkę

•

Oceń książkę

•

Księgarnia internetowa

•

Lubię to! » Nasza społeczność

Spis tre"ci

Wprowadzenie .................................................................................. 7

Rozdzia" 1. Organizacja pracy w programie Statistica ........................................ 11

1.1. Interfejs programu. Zmienne i przypadki .............................................................. 11

/wiczenie 1.1.1. Wprowadzanie i zapisywanie danych ........................................ 14
/wiczenie 1.1.2. Edycja danych w arkuszu .......................................................... 18
/wiczenie 1.1.3. Tworzenie wyra8e9 matematycznych ........................................ 24
/wiczenie 1.1.4. Sortowanie danych ..................................................................... 25
/wiczenie 1.1.5. Filtrowanie danych .................................................................... 27
/wiczenie 1.1.6. Wzory matematyczne. Przegl@darka funkcji .............................. 28
/wiczenie 1.1.7. Zarz@dzanie wynikami ............................................................... 29

1.2. Graficzna prezentacja danych w programie Statistica ........................................... 31

/wiczenie 1.2.1. Wykresy rozrzutu ...................................................................... 31
/wiczenie 1.2.2. Wykresy sCupkowe/kolumnowe ................................................. 35
/wiczenie 1.2.3. Wykresy liniowe ........................................................................ 38
/wiczenie 1.2.4. Wykres sCupkowy wielokrotny .................................................. 39
/wiczenie 1.2.5. Wykres 3W sekwencyjny .......................................................... 39
/wiczenie 1.2.6. Wykresy obrazkowe .................................................................. 42
/wiczenie 1.2.7. Wykres liniowy .......................................................................... 45
/wiczenie 1.2.8. Wykres powierzchniowy i warstwicowy ................................... 47

Rozdzia" 2. Statystyka opisowa ........................................................................ 51

/wiczenie 2.1.1. Szereg rozdzielczy. Histogramy ................................................ 52
/wiczenie 2.1.2. Opisowe charakterystyki rozkCadów .......................................... 57
/wiczenie 2.1.3. Wykresy ramka-w@sy ................................................................ 60
/wiczenie 2.1.4. Analiza wielu zmiennych niezale8nych ..................................... 64
/wiczenie 2.1.5. Dane skategoryzowane .............................................................. 66
Zadania .................................................................................................................. 70
Testy wielokrotnego wyboru ................................................................................. 71

Rozdzia" 3. Zmienne losowe. Kalkulator prawdopodobie#stwa ........................... 73

/wiczenie 3.1.1. RozkCad dwumianowy ............................................................... 83
/wiczenie 3.1.2. Standardowy rozkCad normalny ................................................. 85
/wiczenie 3.1.3. RozkCad t-Studenta ..................................................................... 89
/wiczenie 3.1.4. RozkCad chi-kwadrat .................................................................. 93
/wiczenie 3.1.5. RozkCad Nredniej z próby ........................................................... 96
/wiczenie 3.1.6. RozkCad sumy zmiennych losowych .......................................... 97
Zadania .................................................................................................................. 97
Testy wielokrotnego wyboru ................................................................................. 99

Kup ksi

ąĪkĊ

Pole

ü ksiąĪkĊ

Statystyka z programem Statistica

Rozdzia" 4. Estymacja parametryczna ............................................................. 103

/wiczenie 4.1.1. PrzedziaC ufnoNci dla wartoNci oczekiwanej ............................. 105
/wiczenie 4.1.2. PrzedziaC ufnoNci dla odchylenia standardowego ..................... 110
Zadania ................................................................................................................ 111
Testy wielokrotnego wyboru ............................................................................... 112

Rozdzia" 5. Testy statystyczne ....................................................................... 115

5.1. Badanie normalnoNci rozkCadu zmiennych .......................................................... 118

/wiczenie 5.1.1. Testy normalnoNci rozkCadu ..................................................... 120
/wiczenie 5.1.2. Wykresy normalnoNci .............................................................. 125

5.2. Testy jednorodnoNci wariancji ............................................................................. 126

/wiczenie 5.2.1. Test F ....................................................................................... 126
/wiczenie 5.2.2. Test Levene’a .......................................................................... 128
/wiczenie 5.2.3. Test Browna-Forsythe’a .......................................................... 130

5.3. Testy t-Studenta .................................................................................................. 131

/wiczenie 5.3.1. Test t dla pojedynczej próby .................................................... 139
/wiczenie 5.3.2. Test t dla dwóch prób niezale8nych ......................................... 141
/wiczenie 5.3.3. Testy istotnoNci ró8nic dla dwóch prób zale8nych ................... 148
/wiczenie 5.3.4. Inne testy istotnoNci ................................................................. 149

5.4. Testy nieparametryczne dla prób niezale8nych ................................................... 151

/wiczenie 5.4.1. Test U Manna-Whitneya .......................................................... 152
/wiczenie 5.4.2. Test serii Walda-Wolfowitza ................................................... 154

5.5. Testy nieparametryczne dla prób zale8nych ........................................................ 156

/wiczenie 5.5.1. Test znaków ............................................................................. 156
/wiczenie 5.5.2. Test kolejnoNci par Wilcoxona ................................................. 157
Zadania ................................................................................................................ 158
Testy wielokrotnego wyboru ............................................................................... 159

Rozdzia" 6. Porównanie wielu $rednich ........................................................... 165

/wiczenie 6.1.1. ANOVA jednoczynnikowa. Przekroje, prosta ANOVA .......... 166
/wiczenie 6.1.2. ANOVA jednoczynnikowa. ModuC ANOVA .......................... 173
/wiczenie 6.1.3. Wielokrotne porównania .......................................................... 177
/wiczenie 6.1.4. ANOVA efektów gCównych .................................................... 181
/wiczenie 6.1.5. ANOVA dla ukCadów czynnikowych ...................................... 183
/wiczenie 6.1.6. Porównania zaplanowane ........................................................ 186
/wiczenie 6.1.7. Test Kruskala-Wallisa i test mediany ...................................... 195
/wiczenie 6.1.8. UkCady z powtarzanymi pomiarami ......................................... 197
Zadania ................................................................................................................ 205
Testy wielokrotnego wyboru ............................................................................... 206

Rozdzia" 7. Analiza zmiennych jako$ciowych ................................................... 209

/wiczenie 7.1.1. Test McNemary ....................................................................... 209
/wiczenie 7.1.2. Test Q Cochrana ...................................................................... 211
/wiczenie 7.1.3. Tabele wielodzielcze. Test niezale8noNci

............................ 213

Rozdzia" 8. Analiza wspó"zale%no$ci mi&dzy zmiennymi .................................... 217

8.1. Regresja liniowa .................................................................................................. 217

/wiczenie 8.1.1. Badanie korelacji ..................................................................... 219
/wiczenie 8.1.2. Regresja liniowa ...................................................................... 221

8.2. Regresja wieloraka .............................................................................................. 229

/wiczenie 8.2.1. Liniowy model regresji wielorakiej ......................................... 231
/wiczenie 8.2.2. Predykcja zmiennej zale8nej .................................................... 243
/wiczenie 8.2.3. Regresja krokowa .................................................................... 244

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Spis tre$ci

8.3. Linearyzowana regresja nieliniowa ..................................................................... 250

/wiczenie 8.3.1. Logarytmiczna funkcja regresji ............................................... 251
/wiczenie 8.3.2. WykCadnicza funkcja regresji .................................................. 257
/wiczenie 8.3.3. Hiperboliczna funkcja regresji ................................................. 259
/wiczenie 8.3.4. Aproksymacja wielomianem drugiego stopnia ........................ 263

8.4. Estymacja nieliniowa .......................................................................................... 266

/wiczenie 8.4.1. Funkcja u8ytkownika ............................................................... 266
/wiczenie 8.4.2. Regresja logistyczna ................................................................ 271
Zadania ................................................................................................................ 277
Testy wielokrotnego wyboru ............................................................................... 278

Rozdzia" 9. Szeregi czasowe. Metody prognozowania ...................................... 281

/wiczenie 9.1.1. Prognozowanie metod@ Nredniej ruchomej .............................. 284
/wiczenie 9.1.2. WygCadzanie wykCadnicze ....................................................... 295
/wiczenie 9.1.3. Model Holta ............................................................................. 301
/wiczenie 9.1.4. Model trendu liniowego ........................................................... 308
/wiczenie 9.1.5. Metoda wskaaników. Dekompozycja sezonowa (Census 1) .... 312
/wiczenie 9.1.6. Model ARIMA dla pojedynczego szeregu ............................... 326
Zadania ................................................................................................................ 333
Testy wielokrotnego wyboru ............................................................................... 334

Odpowiedzi do testów .................................................................. 337

Bibliografia .................................................................................. 339

Skorowidz .................................................................................... 341

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Statystyka z programem Statistica

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Rozdzia 4.

Estymacja parametryczna

GCównym zadaniem bada9 statystycznych jest wnioskowanie o caCej populacji gene-
ralnej na podstawie wyników uzyskanych w próbie losowej. DziaC statystyki zajmuj@cy
sig tym zagadnieniem jest nazywany wnioskowaniem statystycznym.

Estymacja to dziaC wnioskowania statystycznego, który zajmuje sig szacowaniem warto-
Nci parametrów oraz postaci rozkCadu w populacji generalnej na podstawie obserwacji
uzyskanych w próbie losowej. Metody znajdowania nieznanych wartoNci parametrów
rozkCadu okreNla estymacja parametryczna. Wnioskowaniem o postaci rozkCadu
w populacji generalnej zajmuje sig estymacja nieparametryczna. Punktem wyjNcio-
wym w estymacji jest wylosowanie z populacji n-elementowej próby i wyznaczenie na
jej podstawie wartoNci estymatora nieznanego parametru. Estymatorem parametru

rozkCadu populacji generalnej jest funkcja wyznaczona na podstawie próby losowej,
sCu8@ca do oceny wartoNci tego parametru. Teoria estymacji zajmuje sig konstruowaniem
estymatorów maj@cych okreNlone wCaNciwoNci, takie jak nieobci@8onoNh, zgodnoNh,
efektywnoNh i dostatecznoNh. Wigcej o metodach wyznaczania takich estymatorów
mo8na znaleah w pozycjach [4, 21, 27, 30]. Zgodnym, nieobci@8onym i najefektyw-
niejszym estymatorem wartoNci oczekiwanej populacji jest wartoNh Nrednia x z próby

losowej wyra8ona wzorem

. Zgodnym i nieobci@8onym estymatorem warian-

cji populacji

jest wariancja z próby prostej wyra8ona wzorem

)

(

Estymacja parametryczna mo8e byh punktowa lub przedziaCowa. W estymacji punk-
towej za parametr populacji przyjmuje sig wartoNh estymatora otrzyman@ z danej,
n-elementowej próby losowej. Estymacja punktowa nie daje oszacowania nieznanego
parametru

rozkCadu populacji. Prawdopodobie9stwo, 8e estymator przyjmie wartoNh

równ@ wartoNci szacowanego parametru, jest równe 0. Z tego wynika, 8e przy stosowa-
niu estymacji punktowej prawdopodobie9stwo popeCnienia bCgdu w ocenie parametru
populacji jest równe 1.

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

104

Statystyka z programem Statistica

BC@d oceny parametru populacji

za pomoc@ jego estymatora Q nie powinien prze-

kraczah odpowiednio maCej wartoNci

z przyjgtym du8ym prawdopodobie9stwem 1–

(

czyli musi byh speCnione równanie:

(

)

(

. PrzedziaC liczbowy (Q–

Q+

), który z okreNlonym z góry, du8ym (bliskim jednoNci) prawdopodobie9stwem

bgdzie zawieraC nieznan@ wartoNh parametru zbiorowoNci generalnej, jest nazywany
przedzia&em ufno(ci, a prawdopodobie9stwo 1–

(

— wspó&czynnikiem ufno(ci. Do

wyznaczenia wartoNci

potrzebna jest znajomoNh rozkCadu estymatora Q. Procedura

wyznaczania przedziaCu ufnoNci jest nazywana estymacj) przedzia&ow).

PrzedziaC ufnoNci to losowy przedziaC wyznaczony za pomoc@ rozkCadu estymatora,
maj@cy tg wCasnoNh, 8e z du8ym, z góry zadanym prawdopodobie9stwem pokrywa war-
toNh szacowanego parametru. Zapisujemy go zwykle w postaci: P(a <

< b) = 1–

(

Liczby a i b s@ nazywane doln) i górn) granic) przedziaCu ufnoNci. WspóCczynnik
ufnoNci 1–

(

jest miar@ zaufania do prawidCowego szacunku. NajczgNciej ma on wartoNh

0,99, 0,95 lub 0,90.

PrzedziaC ufnoNci dla wartoNci oczekiwanej E(X) populacji o rozkCadzie normalnym
N(m,

) jest wyznaczany wedCug wzoru:

(

)

gdzie u

(

jest tak@ wartoNci@ w standardowym rozkCadzie, 8e pole pod krzyw@ ggstoNci

w przedziale (–u

(

, u

(

) wynosi 1–

(

, a pole pod krzyw@ ggstoNci na prawo od u

(

i na

lewo od –u

(

wynosi po

(

/2. Z tego wynika, 8e u

(

mo8na wyznaczyh z relacji:

)

(

)

(

1 u

, gdzie 1 jest dystrybuant@ standardowego rozkCadu normalnego.

DCugoNh przedziaCu ufnoNci zale8y od wartoNci Nredniej, obliczonej na podstawie próby,
przyjgtego wspóCczynnika ufnoNci 1–

(

, liczebnoNci próby oraz wariancji

. Aby zatem

oszacowah przedziaC ufnoNci z jak najmniejszym bCgdem, nale8y dokCadnie okreNlih
wartoNh Nredni@.

PrzedziaC ufnoNci dla wartoNci oczekiwanej dla maCych prób oblicza sig wedCug wzoru:

(

)

gdzie t

wartoNh zmiennej losowej t-Studenta dla n–1 stopni swobody wyznaczana

z relacji:

(

)

(

Im wartoNh wspóCczynnika ufnoNci jest wigksza, tym szerszy jest przedziaC ufnoNci,
a wigc mniejsza dokCadnoNh estymacji parametru. DCugoNh przedziaCu ufnoNci jest miar@
precyzji estymacji przedzia&owej. Szeroki przedziaC ufnoNci oznacza mo8liwoNh du8ych
odchyle9 wartoNci z próby od wartoNci rzeczywistych, czyli wartoNci oczekiwanych
z populacji. Im krótszy jest przedziaC ufnoNci, tym dokCadniej obliczony przez nas esty-
mator przybli8a wartoNh oczekiwan@ populacji, czyli tym precyzyjniejsza jest estymacja

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

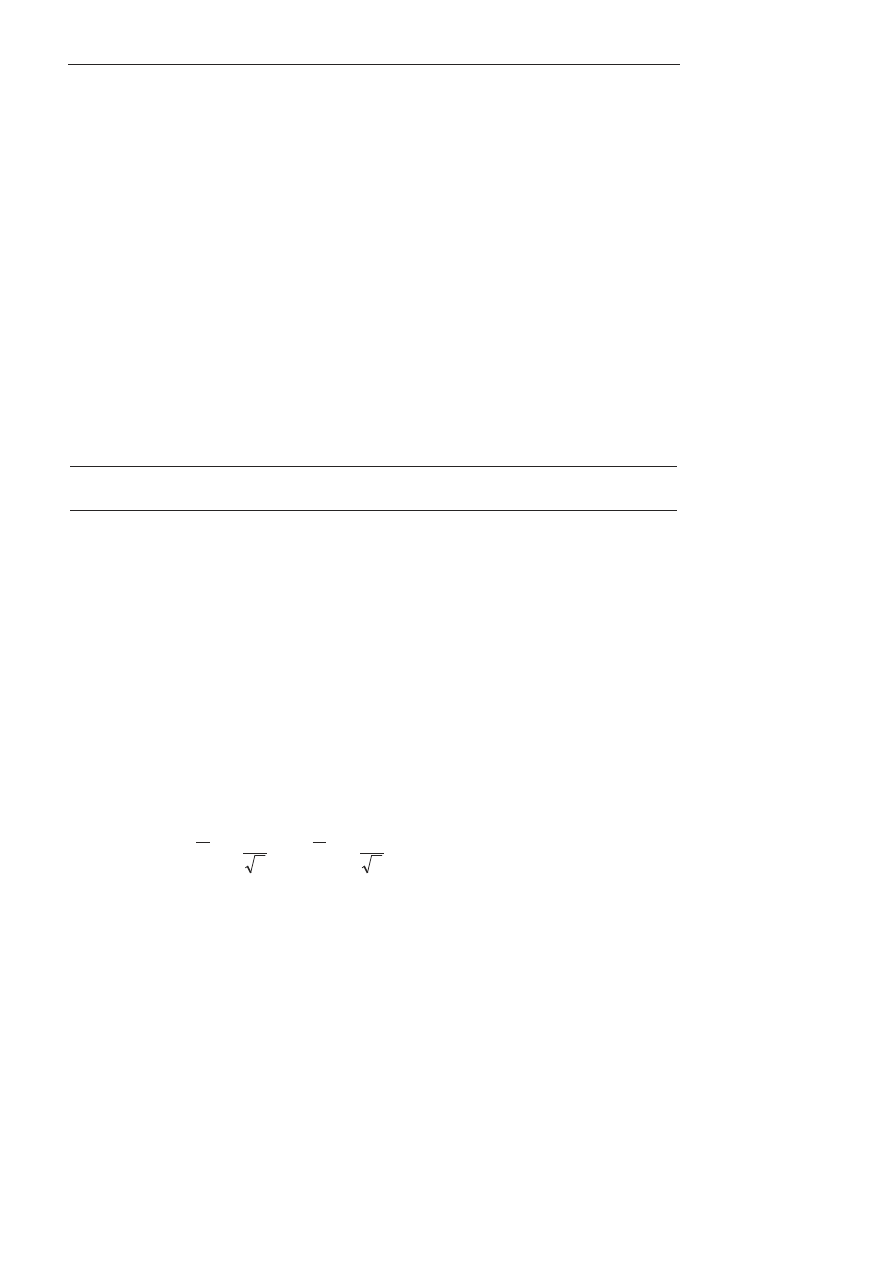
Rozdzia" 4.

2 Estymacja parametryczna

105

przedziaCowa. BCgdy przybli8e9 popeCniane przy szacowaniu Nredniej malej@ wraz ze
zwigkszaniem liczebnoNci próby. Jednym z zada9 estymacji jest wyznaczenie minimal-
nej liczebnoNci próby tak, by oszacowah przedziaC ufnoNci z jak najmniejszym bCgdem.
Zbyt maCa próba mo8e prowadzih do faCszywych wniosków o populacji generalnej.
Aby zwigkszyh dokCadnoNh estymacji, nale8y tak8e poprawih dokCadnoNh pomiarów.

PrzedziaCy ufnoNci s@ wyznaczane dla wartoNci oczekiwanej, wariancji, odchylenia stan-
dardowego i wskaanika struktury. Wyznacza sig je z rozkCadów odpowiednich statystyk
bgd@cych estymatorami tych parametrów.

'wiczenie 4.1.1. Przedzia" ufno$ci
dla warto$ci oczekiwanej

Przyk"ad 34. Przedzia" ufno$ci dla $redniej
(warto$ci oczekiwanej m = E(X)) dla du%ych prób

Dokonano 52 pomiarów zanieczyszczenia gleby oCowiem (w mg/kg suchej masy gleby),
otrzymane wyniki zapisano w tabeli.

59 60 62 58 59 61 65 67 65 65 62 62 65 67 69 64 65 66 67 64 64 66 68 64 63 64
67 69 62 64 67 68 69 61 62 69 66 69 63 65 60 60 65 63 70 68 67 71 61 64 63 66

ZakCadaj@c, 8e rozkCad wyników pomiarów jest rozkCadem normalnym, wyznacz prze-
dziaC ufnoNci ze wspóCczynnikiem ufnoNci 0,95 dla wartoNci Nredniej.

Dane

WspóCczynnik ufnoNci 1–

(

= 0,95. Zmienn@ jest zanieczyszczenie gleby oCowiem.

Rozwi)zanie

Wybierz z menu Plik/Nowy. W oknie Utwórz nowy dokument wprowada:
Liczba zmiennych:

, Liczba przypadków:

Wprowada dane z tabeli.

Zapisz arkusz w pliku o+ów.sta.

Poniewa8 próba jest du8a, mo8na przyj@h, 8e

= s. PrzedziaC ufnoNci dla

du8ych prób obliczany jest wedCug wzoru:

(

)

Dane jest 1–

(

= 0,95, czyli

(

= 0,05. u

(

nale8y wyznaczyh z relacji 1(u

(

) = 1–(

(

/2),

gdzie 1 jest dystrybuant@ standardowego rozkCadu normalnego.

Po podstawieniu 1(u

(

) = 1–(

(

/2) = 0,975.

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

106

Statystyka z programem Statistica

Uruchom kalkulator prawdopodobie9stwa. Wybierz Rozk+ad Z (Normalny).

Wprowada

p = 0,975

(rysunek 4.1). Kliknij przycisk Oblicz. Program oblicza

(

wyNwietlane w polu X, czyli u

(

= 1,96.

Rysunek 4.1.
Okno Kalkulator
prawdopodobie4stwa

Aby wyznaczyh wartoNh Nredni@ i odchylenie standardowe, kliknij lewym
przyciskiem nazwg zmiennej, wybierz Statystyki bloku danych/Kolumny/5rednia,
a nastgpnie Odchylenie standardowe.

Program wyNwietla wyniki

615

Po podstawieniu do wzoru otrzymujemy przedziaC ufnoNci (63,7, 65,5).

Rozwi)zanie z programem Statistica

I sposób

Wybierz z menu: Statystyka/Statystyki podstawowe i tabele/Statystyki opisowe.

Kliknij przycisk Zmienne i jako zmienn@ wprowada

O'ów

Aby wyNwietlih przedziaCy ufnoNci, kliknij zakCadkg Wi7cej i zaznacz parametry:
5rednia, Przedz. ufn. 9redniej. W polu Przedzia+ [%] podany jest wspóCczynnik
ufnoNci równy 95% (rysunek 4.2).

Kliknij przycisk Statystyki lub Podsumowanie. Program wyNwietla arkusz
wynikowy w postaci tabeli (rysunek 4.3).

Odpowied/

PrzedziaC ufnoNci (w programie Statistica: (Ufno9=–95%) = 63,7; (Ufno9=+95%) = 65,5)
ma postah (63,7, 65,5).

II sposób

PrzedziaC ufnoNci jest wyNwietlany na wykresie 5rednia i b+7dy.

Wybierz z menu: Wykresy/Wykresy 9rednia i b+7dy.

Zdefiniuj zmienn@

O'ów

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Rozdzia" 4.

2 Estymacja parametryczna

107

Rysunek 4.2.
Okno wyboru
statystyk opisowych

Rysunek 4.3. Arkusz z wynikami oblicze4 (Ufno9=–95%, Ufno9=+95% to granice przedzia+u ufno9ci
dla wspó+czynnika 1–

(

= 0,95)

WspóCczynnik ufnoNci jest wyNwietlany w polu Prawdopodob. (domyNlna
wartoNh tego wspóCczynnika wynosi 0,95) (rysunek 4.4). Kliknij OK.

Rysunek 4.4. Okno tworzenia wykresów 9redniej i przedzia+ów ufno9ci

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

108

Statystyka z programem Statistica

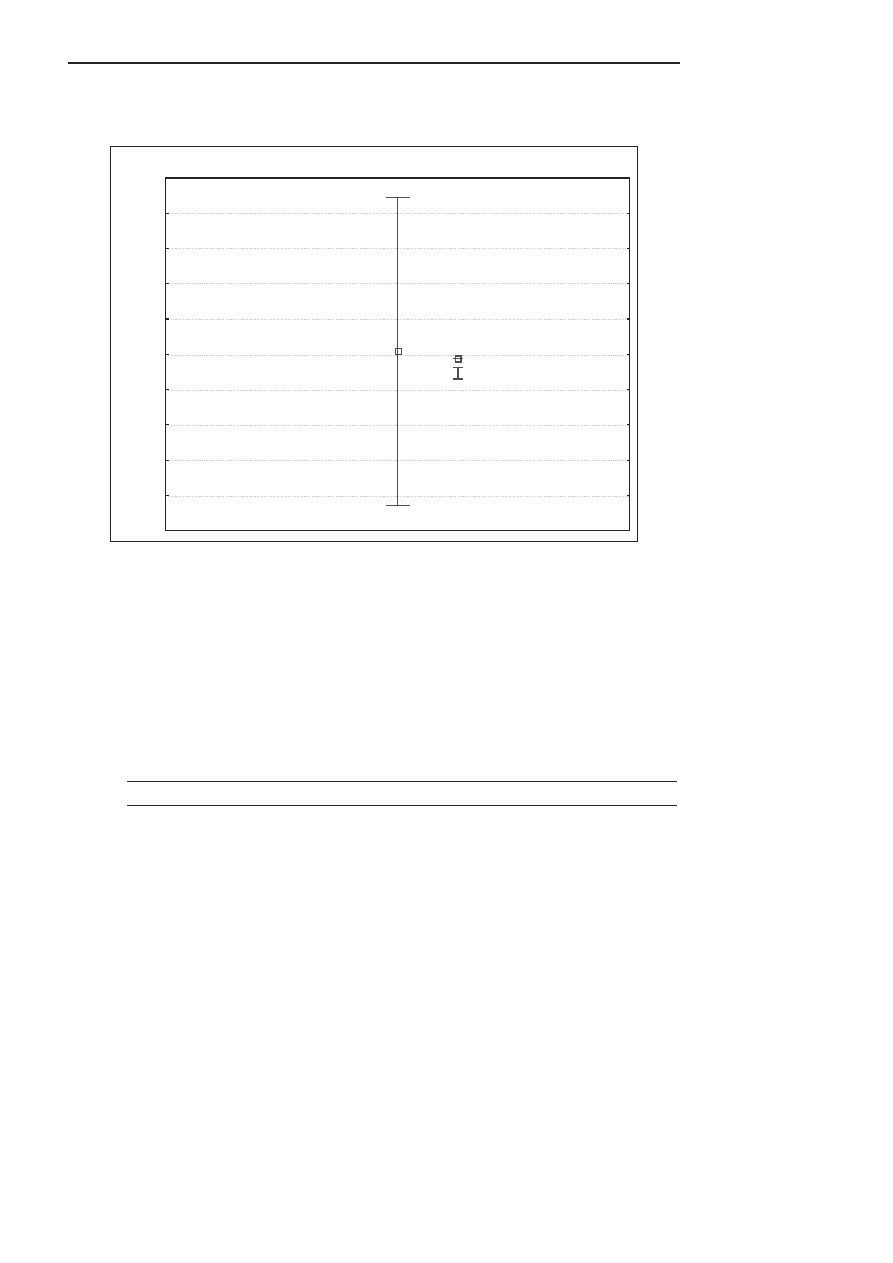
Program tworzy wykres Nredniej i przedziaCów ufnoNci dla tej Nredniej
(rysunek 4.5).

"rednia i przedzia+y ufno0ci

63,6

63,8

64,0

64,2

64,4

64,6

64,8

65,0

65,2

65,4

65,6

+ó

"rednia = 64,6154
"rednia±0,95 Przedz. ufn.

= (63,7434, 65,4874)

Rysunek 4.5. Wykres 9redniej i przedzia+ów ufno9ci dla tej 9redniej

Odpowied/

PrzedziaC ufnoNci jest wyNwietlany na wykresie. Z prawdopodobie9stwem 0,95 mo8na
twierdzih, 8e Nrednie zanieczyszczenie gleby oCowiem zawiera sig w przedziale (63,7,
65,5) mg/kg suchej masy.

Przyk"ad 35. Przedzia" ufno$ci dla $redniej dla ma"ych prób

Dokonano 12 pomiarów zanieczyszczenia gleby oCowiem (w mg/kg suchej masy gleby),
otrzymane wyniki zapisano w tabeli.

ZakCadaj@c, 8e rozkCad zmiennej, czyli zanieczyszczenia gleby oCowiem, jest rozkCa-
dem normalnym, i przyjmuj@c wspóCczynnik ufnoNci 0,95, wyznacz przedziaC ufnoNci
dla Nredniej wartoNci zanieczyszczenia gleby oCowiem.

Dane

1–& $3456753n3$389

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Rozdzia" 4.

2 Estymacja parametryczna

109

Rozwi)zanie

PrzedziaC ufnoNci dla maCych prób oblicza sig wedCug wzoru:

(

)

gdzie t

(

wartoNh zmiennej losowej t-Studenta dla n–1 stopni swobody jest wyznaczana

tak, 8e speCniona jest relacja

(

)

(

Wybierz z menu Plik/Nowy. W oknie Utwórz nowy dokument wprowada:
Liczba zmiennych:

, Liczba przypadków:

Wprowada dane z tabeli i zachowaj w pliku zanieczyszczenie o+owiem.sta.

Wybierz z menu: Statystyka/Statystyki podstawowe i tabele/Statystyki opisowe.

Kliknij przycisk Zmienne i jako zmienn@ wprowada

O'ów

Kliknij zakCadkg Wi7cej i zaznacz pola wyboru: 9rednia, Przedz. ufn. 9redniej.

Pole edycji Przedzia+ zawiera domyNlny wspóCczynnik ufnoNci (0,95) podawany
w procentach.

Program wyNwietla tabelg z przedziaCami ufnoNci (rysunek 4.6).

Rysunek 4.6. Arkusz z wynikami oblicze4

Wybierz z menu: Wykresy/Wykresy 9rednia i b+7dy.

Zdefiniuj zmienn@

O'ów

WspóCczynnik ufnoNci jest wyNwietlany w polu Prawdopodob. (domyNlna wartoNh
tego wspóCczynnika wynosi 0,95). Kliknij OK.

Program tworzy wykres Nredniej i wyNwietla na wykresie przedziaCy ufnoNci
dla tej Nredniej (rysunek 4.7).

Odpowied/

Z prawdopodobie9stwem 0,95 mo8na twierdzih, 8e zanieczyszczenie oCowiem zawiera
sig w przedziale (59,6 mg/kg, 66,1 mg/kg).

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

110

Statystyka z programem Statistica

"rednia i przedzia+y ufno0ci

+ó

"rednia = 62,8333
"rednia±0,95 Przedz. ufn.

= (59,5504, 66,1162)

Rysunek 4.7. Wykres 9redniej i przedzia+ów ufno9ci

'wiczenie 4.1.2. Przedzia" ufno$ci
dla odchylenia standardowego

Przyk"ad 36. Przedzia" ufno$ci dla odchylenia standardowego

Przyjmuj@c wspóCczynnik ufnoNci 0,98, wyznacz przedziaCy ufnoNci dla odchylenia stan-
dardowego dla danych z poprzedniego przykCadu (plik zanieczyszczenie o+owiem.sta).

Sposób wykonania

Otwórz plik zanieczyszczenie o+owiem.sta.

Wybierz z menu: Statystyka/Statystyki podstawowe i tabele/Statystyki opisowe.

Kliknij przycisk Zmienne i jako zmienn@ wprowada

O'ów

Kliknij zakCadkg Wi7cej i zaznacz pola wyboru: Odchylenie standardowe, PU
dla odch. std. (rysunek 4.8).

Pole edycji Przedzia+ zawiera wspóCczynnik ufnoNci podawany w procentach.
Wprowada

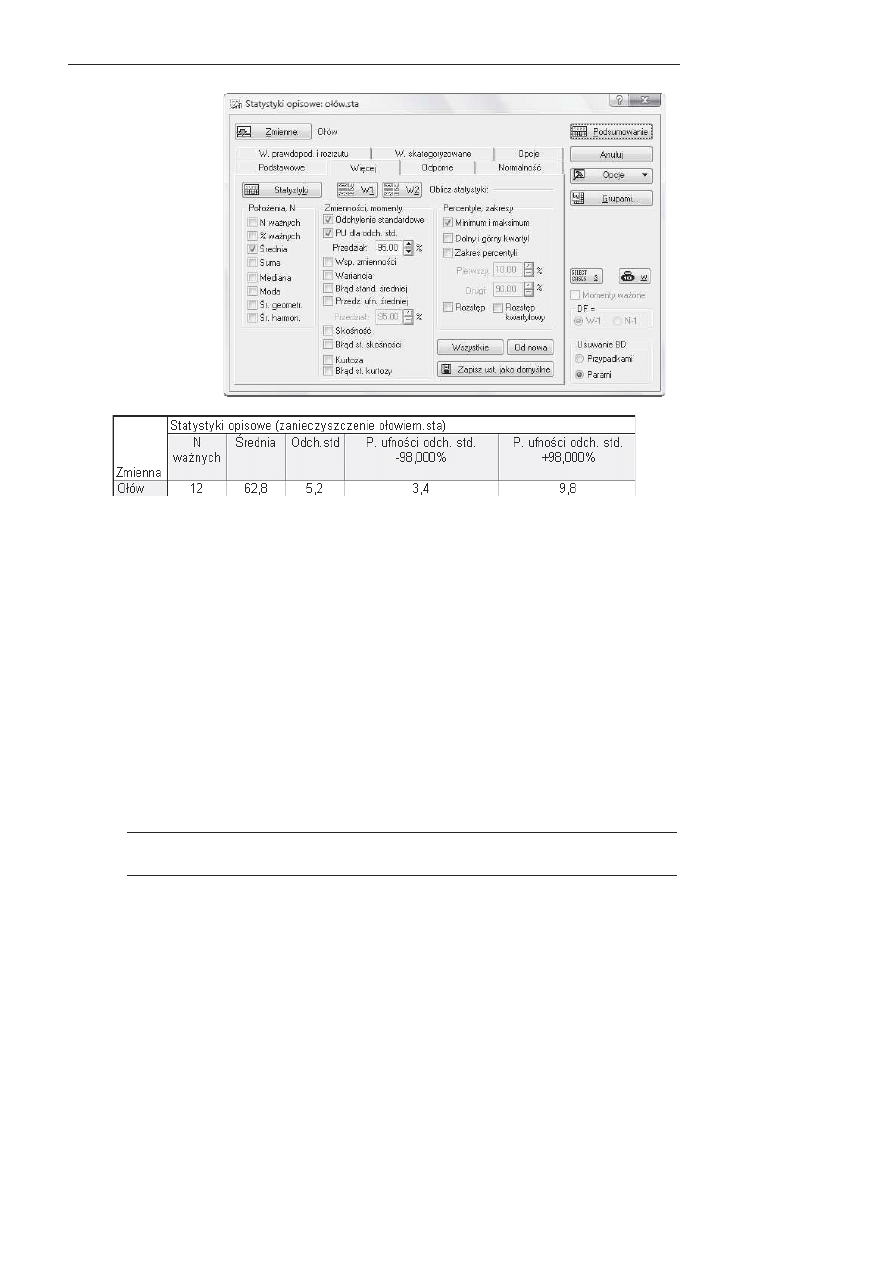
Program tworzy arkusz z wynikami (rysunek 4.9).

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Rozdzia" 4.

2 Estymacja parametryczna

111

Rysunek 4.8.
Okno wyboru
statystyk opisowych

Rysunek 4.9. Arkusz z wynikami statystyk opisowych

Odpowied/

Otrzymany przedziaC (3,4, 9,8) z prawdopodobie9stwem 0,98 pokrywa odchylenie stan-
dardowe zanieczyszczenia gleby oCowiem.

Przy zmniejszaniu wartoNci wspóCczynnika ufnoNci maleje dCugoNh przedziaCu ufnoNci.

Mo8na sprawdzih, 8e przedziaC (3,7, 8,8) z prawdopodobie9stwem 0,95 pokrywa war-
toNh odchylenia standardowego.

Zadania

Zadanie 1.

Przeprowadzono badanie stg8enia azotynów NNO

(mg/l) w wodzie na dwóch odcinkach rzeki.

Wyniki pomiarów zawiera tabela.

Odcinek 1

Odcinek 2

Wyznacz przedziaCy ufnoNci dla Nredniej dla ka8dej grupy. Porównaj wyniki w grupach.

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

112

Statystyka z programem Statistica

Zadanie 2.

W celu ustalenia stopnia krystalicznoNci pewnego polimeru przeprowadzono pomiary tego para-
metru dla 10 próbek i otrzymano wyniki (w %): 61, 57, 63, 62, 59, 60, 58, 62, 59, 61. Zbuduj prze-
dziaCy ufnoNci, które z prawdopodobie9stwem 98% pokryj@ Nredni@ wartoNh tego parametru.

Zadanie 3.

W celu ustalenia temperatury topnienia pewnego polimeru przeprowadzono pomiary tego para-
metru dla oNmiu próbek. Otrzymano (w °C): 220, 225, 223, 226, 224, 225, 223, 221. Przy zadanym
wspóCczynniku ufnoNci 0,99 wyznacz przedziaC ufnoNci dla temperatury topnienia.

Zadanie 4.

W celu ustalenia stg8enia ozonu wystgpuj@cego przy powierzchni Ziemi przeprowadzono pomiary
i otrzymano wyniki (w ppb): 61, 57, 63, 62, 59. Przyjmuj@c wspóCczynnik ufnoNci 0,98:

2 Zbuduj przedziaC ufnoNci, który z prawdopodobie9stwem 98% pokryje Nredni@ wartoNh

tego parametru.

2 Wyznacz przedziaC ufnoNci dla odchylenia standardowego stg8enia ozonu.

Zadanie 5.

DokCadny pomiar odczynu pH dla oznaczenia stanu surowych Ncieków jest wa8ny przy stero-
waniu dozowaniem chemikaliów w procesie neutralizacji. Wykonano 60 pomiarów tego para-

metru i otrzymano:

(°pH) oraz odchylenie standardowe 0,8.

Zbuduj przedziaC, który z prawdopodobie9stwem 0,99 pokryje pH Ncieków.

Zadanie 6.

Biologiczne zapotrzebowanie tlenu Q (mg O

/l) okreNla wskaanik BZT

. Wykonano 12 pomiarów

tego wskaanika i otrzymano wyniki widoczne w tabeli.

BZT

Przyjmuj@c wspóCczynnik ufnoNci 0,95, zbuduj przedziaC ufnoNci dla nieznanej Nredniej wskaa-
nika BZT

Testy wielokrotnego wyboru

1. Estymacja parametryczna

a) dotyczy szacowania warto1ci parametrów rozk adu populacji generalnej.

b) polega na oszacowaniu nieznanego rozk adu zmiennej losowej.

c) polega na szacowaniu warto1ci lub przedzia u pokrywaj8cego z pewnym

prawdopodobie9stwem parametr populacji generalnej.

2. Zmienna losowa X populacji generalnej ma rozk ad normalny o nieznanej warto1ci 1redniej

oraz nieznanym odchyleniu standardowym. Z populacji pobrano ma 8 prób<.

a) Przedzia ufno1ci dla wariancji wyznaczonej na podstawie tej próby jest oparty na rozk adzie

chi-kwadrat.

b) Przedzia ufno1ci dla odchylenia standardowego zmiennej losowej X jest oparty na rozk adzie

F Snedecora.

c) Przedzia ufno1ci dla warto1ci 1redniej wyznaczonej na podstawie tej próby jest oparty

na rozk adzie t-Studenta o n–1 stopniach swobody.

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Rozdzia" 4.

2 Estymacja parametryczna

113

3. Losowy przedzia wyznaczony za pomoc8 rozk adu estymatora, maj8cy t< w asno1F, Ge z duGym,

z góry zadanym prawdopodobie9stwem pokrywa warto1F szacowanego parametru,
jest nazywany

a) przedzia em dopuszczalnym.

b) przedzia em ufno1ci.

c) przedzia em krytycznym.

4. Wspó czynnik ufno1ci to

a) prawdopodobie9stwo odrzucenia prawdziwej hipotezy zerowej.

b) z góry zadane duGe prawdopodobie9stwo równe 1–

(

c) z góry zadane ma e prawdopodobie9stwo równe

(

5. Wyznaczono przedzia ufno1ci dla warto1ci 1redniej, przyjmuj8c warto1F wspó czynnika ufno1ci

0,95. Oznacza to, Ge

(

= 0,95.

b) 1–

(

= 0,95.

c) wyznaczony przedzia z ufno1ci8 0,05 pokrywa nieznan8 warto1F 1redniej.

6. Aby zwi<kszyF precyzj< estymacji przedzia owej, naleGy

a) zwi<kszyF liczebno1F próby.

b) zwi<kszyF wspó czynnik ufno1ci.

c) zmniejszyF wspó czynnik ufno1ci.

7. Wybierz poprawne stwierdzenia.

a) Im wyGsza jest warto1F wspó czynnika ufno1ci, tym szerszy jest przedzia ufno1ci.

b) Im niGsza jest warto1F wspó czynnika ufno1ci, tym szerszy jest przedzia ufno1ci.

c) D ugo1F przedzia u ufno1ci nie zaleGy od wspó czynnika ufno1ci.

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

114

Statystyka z programem Statistica

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Skorowidz

.spf, 14
.sta, 14
.stw, 14

addytywny, model, 284
analiza

kontrastów, 186, 189, 190
log-liniowa, 213
zmiennych jakoNciowych, 209

analiza wariancji, 165

dwuczynnikowa, 181
jednoczynnikowa, 165, 166, 190

ANOVA, 165, 169, 174

dla ukCadów czynnikowych, 165, 183
efektów gCównych, 165, 181
jednoczynnikowa, 165, 166, 167, 168, 173
moduC, 173
zaCo8enia testów, 167

ARIMA, model, 326, 327
arkusz, 13, 14
Arkusz, zakCadka, 14

badanie statystyczne, 51
bC@d drugiego rodzaju, 115
bC@d pierwszego rodzaju, 115
bC@d standardowy, 81

cechy statystyczne, 51
Census 1, 312, 319
centralne twierdzenie graniczne, 80
czynnik pomiarów powtarzanych, 197

dane

edycja, 18
filtrowanie, 27
graficzna prezentacja, 31
skategoryzowane, 66
sortowanie, 25, 26
wprowadzanie, 14, 15
zapisywanie, 14, 17

decyle, 78
dekompozycja sezonowa, 312, 319
dokument, tworzenie, 14, 15
dominanta, 58
Durbina-Watsona, statystyka, 231
dystrybuanta, 77

zmiennej losowej ci@gCej, 77
zmiennej losowej skokowej, 77

estymacja, 103

nieliniowa, 266
nieparametryczna, 103
parametryczna, 103
przedziaCowa, 104
punktowa, 103

estymator, 103
Eta-kwadrat cz@stkowe, 176
ex ante, 282
ex post, 282

formuCy matematyczne, tworzenie, 24
funkcja

ggstoNci rozkCadu prawdopodobie9stwa, 76
prawdopodobie9stwa, 76
rozkCadu prawdopodobie9stwa, 76

funkcje matematyczne, definiowanie, 28

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

342

Statystyka z programem Statistica

heteroscedantycznoNh, 235
hipoteza, 115

alternatywna, 115
zerowa, 115

histogram, 52, 54
Holta, model, 282, 301
homoscedantycznoNh, 235

iloczyn zdarze9, 74
interfejs graficzny, 11

jednostki statystyczne, 51

Kalkulator prawdopodobie9stwa, 82, 86, 89
klucz sortowania, 25
kod braku danych, 24
kolumna

zaznaczanie, 18
zmiana szerokoNci, 18

komórki

formatowanie, 20, 21
kopiowanie zawartoNci, 20
przenoszenie zawartoNci, 19
wypeCnianie seri@ danych, 23, 24
zaznaczanie, 18

kontrast, 186
korelacja, 217

badanie, 219
cz@stkowa, 230
semicz@stkowa, 230

korelogram, 326
kurtoza, 59
kwantyl, 78

rzgdu p, 78

kwartyl, 78

dolny, 58
górny, 58
pierwszy, 58
trzeci, 58

logit, 271, 272

matematyczne formuCy, tworzenie, 24
mediana, 58, 78
metoda

Nredniej ruchomej, 284
wskaaników, 312

miary

asymetrii, 58, 59
koncentracji, 58, 59
poCo8enia, 57, 58
rozproszenia, 58

moc testu, 117
mocne prawo wielkich liczb, 78
moda, 58
model

addytywny, 284
ARIMA, 326, 327
Holta, 282, 301
multiplikatywny, 284
trendu liniowego, 308
Wintersa, 282

multiplikatywny, model, 284

niecentralnoNh, 176

obserwacja statystyczna, 51
obserwacje odstaj@ce, 80
odchylenie hwiartkowe, 58
odchylenie standardowe, 58
okno

ANOVA, 165, 168, 178, 197
edytora wykresu, 34
Inne testy istotnoNci, 149
Kalkulator prawdopodobie9stwa, 82, 84, 86,

90, 91, 151

klasycznej dekompozycji sezonowej, 320
Kryteria autofiltra, 27
podstawowe, 11, 12
Przegl@darka funkcji, 29
raportu, 30
Solver, 296
sortowania, 26
testu t dla pojedynczej próby, 140
tworzenia wykresów, 33
tworzenie nowego dokumentu, 15
wyboru statystyk nieparametrycznych, 152
wyboru statystyk opisowych, 60
wyboru testu, 137
wyboru typu rozkCadu, 119
wykresy sekwencyjne 3W, 41

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Skorowidz

343

populacja generalna, 51
porównywanie zaplanowane, 186
poziom istotnoNci, 115
prawdopodobie9stwo

caCkowite, 75
definicja, 74
warunkowe, 75

prawo wielkich liczb Bernoulliego, 75
precyzja estymacji przedziaCowej, 104
predykatory jakoNciowe, 165
prezentowanie danych, 31
prognoza dopuszczalna, 283
prognoza wygasCa, 282
prognozowanie, 281, 282

bCgdy, 283
metod@ Nredniej ruchomej, 284, 285
model Holta, 282, 301
model trendu liniowego, 308
model Wintersa, 282
wygCadzanie wykCadnicze, 295, 301

próba, 51

liczebnoNh, 51
losowa, 51
losowa prosta, 75
reprezentatywna, 51

próbka, 51
przedziaCy ufnoNci, 104, 105

dla odchylenia standardowego, 110
dla wartoNci oczekiwanej, 105

Przegl@darka funkcji, 28, 29
przestrze9 zdarze9 elementarnych, 73
przypadki

dodawanie, 18, 19
formatowanie nazw, 21, 23
selekcja, 24

punkty

ekstremalne, 62
odstaj@ce, 62, 125

raport, 30

tworzenie, 30
zapisywanie, 30

regresja, 217

cz@stkowe wspóCczynniki, 229
hiperboliczna, 259
krokowa, 244, 245
liniowa, 217, 221
logarytmiczna, 251, 252
logistyczna, 271
nieliniowa, 250
wielokrotna, 229

wieloraka, 229, 231, 238
wykCadnicza, 257

reguCa trzech sigm, 80
reszty, 218

analiza, 237
warunki, 218

rozkCad

asymetryczny, 59
bimodalny, 52
chi-kwadrat, 82, 93
dwumianowy, 78, 83
empiryczny, 52
F Fishera, 82
jednomodalny, 52
normalny, 79, 85
opisowe charakterystyki, 57
Poissona, 79
siodCowy, 52
sumy zmiennych losowych, 97
symetryczny, 59
Nredniej z próby, 96
t-Studenta, 81, 89
zmiennej losowej, 75

rozstgp, 58

kwartylowy, 58

ró8nica zdarze9, 74

sferycznoNh, 198
skoroszyty, 14
sCabe prawo wielkich liczb, 78
standardowy rozkCad normalny, 79, 85
standaryzacja zmiennej, 39, 79
Statistica, 7, 9
statystyka matematyczna, 73
statystyka opisowa, 51, 52, 57, 59, 73
STR, format, 30
suma zdarze9, 73
symetria poC@czona, 198
szereg czasowy, 281, 282
szereg rozdzielczy, 52

dla cechy ci@gCej, 55
dla cechy dyskretnej, 52

Nrednie, porównywanie, 165, 177

tabele

kontyngencji, 213
licznoNci, 52
wielodzielcze, 213

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Czytaj dalej...

344

Statystyka z programem Statistica

tekst, formatowanie, 21
testy istotnoNci, 115
testy statystyczne, 115

, 118, 120

Browna-Forsythe'a, 130, 169
C Cochrana-Coxa, 132
Duncana, 177, 178
Dunnetta, 180
F, 126, 127, 128
jednorodnoNci wariancji, 126
kolejnoNci par Wilcoxona, 157
KoCmogorowa-Smirnowa, 118, 119, 120, 122,

123, 151

Kruskala-Wallisa, 195
Levene'a, 128, 129, 169
Lillieforsa, 119, 122
Mauchleya, 198
McNemary, 209, 210, 211
Newmana i Keulsa, 177, 178
nieparametryczne, 115, 117, 118, 151, 156
niezale8noNci

, 213

NIR, 178
normalnoNci rozkCadu, 120
parametryczne, 115, 117
Q Cochrana, 211, 212, 213
Scheffégo, 177
schemat weryfikacji, 116
test mediany, 195
test znaków, 156
t-Studenta, 118, 131, 132, 137
Tukeya, 177
U Manna-Whitneya, 132, 151, 152
W Shapiro-Wilka, 119, 122
Walda-Wolfowitza, 132, 151, 154
zasady, 116

wariancja, 58
wartoNh

modalna, 58
oczekiwana, 77
Nrednia, 58

widok klasyczny, 11, 12
wielokrotne porównywania, 177
wiersz, zaznaczanie, 18
Wintersa, model, 282
wnioskowanie statystyczne, 103
wspóCczynnik

determinacji, 218
Fi, 215
kontyngencji C-Pearsona, 215
korelacji liniowej, 217
skoNnoNci, 59

ufnoNci, 104
V Craméra, 215
zmiennoNci, 58

wst@8ka, 11, 12
wygCadzanie wykCadnicze, 295, 301
wykresy, 31

3W sekwencyjne, 39, 40, 41
interakcji, 172
liniowe, 38, 45, 46
normalnoNci, 125
obracanie, 41
obrazkowe, 42, 43, 47
powierzchniowe, 47, 48, 49, 50
ramka-w@sy, 60, 61, 62
rozrzutu, 31, 32
skategoryzowane, 66
sCupkowe wielokrotne, 39
sCupkowe/kolumnowe, 35, 37, 40
Twarze Chernoffa, 42, 43, 44, 47
warstwicowe, 47, 48, 49
zmiana ustawie9, 34

wyniki oblicze9, zarz@dzanie, 29, 30
wyra8enia matematyczne, tworzenie, 24
wzory matematyczne, 28

zakresy, zaznaczanie, 20
zbiorowoNh, 51
zdarzenia elementarne, 73
zdarzenia niemo8liwe, 73
zdarzenia niezale8ne, 75
zdarzenia pewne, 73
zdarzenia przeciwne, 73
zdarzenia sprzyjaj@ce, 74
zdarzenie losowe, 73
zmienna losowa, 75

badanie normalnoNci rozkCadu, 118
ci@gCa, 75
rozkCad, 75
skokowa (dyskretna), 75

zmienne, 51

dodawanie, 18, 19
formatowanie nazw, 23
grupuj@ce, 165
niezale8ne, analiza, 64
specyfikacja, 16
specyfikacja za pomoc@ wyra8e9

matematycznych, 25

standaryzacja, 39, 79
zale8ne, 165, 243

Pole

ü ksiąĪkĊ

Kup ksi

ąĪkĊ

Wyszukiwarka

Podobne podstrony:
Statystyka z programem Statistica statis 2
Statystyka z programem Statistica statis
Statystyka z programem Statistica statis
Statystyka z programem Statistica 3
Statystyka z programem Statistica
Statystyka z programem Statistica statis
Edukacja zdrowotna program na zaliczneie
Edukacja zdrowotna program na zaliczneie 2
Rajfura A, Statystyka 2 Program STAT Rol 2012 13
Statystyka w Excelu i Statistice
Edukacja wczesnoszkolna program Nieznany
podstawowe met stat w geologii z programem STATISTICA, Studia, Ekonomia, Wnioskowanie i prognozowani
Statystyka, program
edukacja zdrowia- program, Dokumenty do szkoły, przedszkola; inne, zintegrowana
Metody probabilistyczne i statystyka program
Edukacja matematyczna - program, Matematyka
Edukacja wczesnoszkolna program opinia dyplomowany
Edukacja seksualna program

więcej podobnych podstron