PMN

Scilab — podstawy 1

1

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Podstawowe wiadomości o programie S cilab

1

Ogólne
1.1

Opis tu przedstawiony dotyczy programu Scilab w wersji 4.1.2 (wersja zainstalowana w pracowni
studenckiej). Od pewnego czasu nie jest to już wersja najnowsza (najnowszą wersją jest obecnie 5.1.1), ale na
czas tych zajęć pozostaniemy przy niej. Można ją ściągnąć ze strony domowej programu

http://www.scilab.org

(w dziale „Technical Area” – „Downloads” – „Old Versions”

(

http://www.scilab.org/download/index_download.php?page=old_releases

).

1.2

Opis ten jest przeznaczony dla studentów piątego semestru, którzy będą musieli samodzielnie i od podstaw
napisać programy interpolujące, poszukujące minimów i miejsc zerowych funkcji czy rozwiązujące układy
równań oraz równania różniczkowe zwyczajne — z tego względu nie opisuję tu szczegółowo np. działania
operatora dzielenia macierzowego ani nie podaję opisu procedury

ode

;-).

1.3

Scilab jest programem przeznaczonym do obliczeń numerycznych.

1.4

Scilab jest interpreterem — tzn. pisane w nim programy (skrypty) nie są przed wykonaniem kompilowane —
kolejne wprowadzane z klawiatury (będź odczytywane z pliku) polecenia są interpretowane w trakcie realizacji
programu. Ma to zarówno złe jak i dobre strony: programy interpretowane są wolniejsze od kompilowanych,
z drugiej jednak strony w przypadku interpretacji programu nie musimy z góry znać typów wszystkich
zmiennych czy rozmiarów tablic — mogą się one zmieniać dynamicznie w trakcie wykonywania programu.
Istnieje pewne „odstępstwo” od tej reguły — zdefiniowane przez użytkownika funkcje, zarówno wczytywane
z pliku wcześniej zapisanego na dysku jak i zdefiniowane w treści programu, są podczas odczytywania
„kompilowane”, co przyspiesza wykonywanie ich późniejszych wywołań (jest to domyślne zachowanie
programu — o jego zmianach później).

1.5

Istnieją możliwości dołączania do Scilaba skompilowanych funkcji w C czy Fortranie (tym nie będziemy się
zajmować).

2

Literatura i instrukcje.
2.1

Jak dotąd po polsku, oprócz mojej książki — „Scilab w przykładach”,
wydawnictwo NAKOM 2007, ISBN
13: 978-83-89529-26-8, dostępna jest jeszcze książka Cypriana T. Lachowicza,
„Matlab, Scilab, Maxima. Opis i przykłady zastosowań”, wydawnictwo
Politechniki Opolskiej, 2005, ISBN 83-88492-80-2. Dostępnych jest kilka
polskich pozycji dotyczących Matlaba — trzeba jednak pamiętać, że między
Matlabem i Scilabem istnieją różnice w składni, książki te nie będą więc
przydatne jako instrukcje obsługi Scilaba. Jednak „filozofia” działania obu
programów jest identyczna, w obu też istnieją funkcje mające takie same
działanie (chociaż nie zawsze mają identyczne nazwy i składnię), z tego punktu
widzenia każda książka opisująca sposób działania Matlaba może być przydatna.

2.2

Dla znających jako-tako angielski lub francuski: pliki pomocy Scilaba.

2.3

Warto zapoznać się z programami demonstracyjnymi (uruchamianymi
przyciskiem „Scilab Demos” w menu pomocy — „?” Scilaba) i je przeanalizować (no, ale to dopiero kiedy
coś już się wie o działaniu programu).

2.4

Internet: można znaleźć sporo stron poświęconych pracy ze Scilabem (nie znalazłem jednak stron po polsku,
większość jest po angielsku, niektóre po francusku czy rosyjsku).

2.4.1 Strona domowa Scilaba:

http://www.scilab.org/

2.4.2 Dokumentacja:

http://www.scilab.org/product/

2.4.3 Wiki:

http://wiki.scilab.org/

3

Praca ze Scilabem
3.1

Uruchomienie — bezpośrednio po uruchomieniu Scilab wczytuje swój plik ini, jego zawartość decyduje
np. o foncie używanym w głównym oknie programu, o liście zmiennych systemowych itp. (o możliwości
jego edycji później). W przypadku wcześniejszych wersji równocześnie (a właściwie minimalnie wcześniej) z

PMN

Scilab — podstawy 1

2

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

głównym (a obecnie jedynym) oknem programu pojawiało się jeszcze jedno okno — Scilex — „engine”
Scilaba.

3.2

Wyłączenie — oprócz odpowiedniego przycisku „windowsowego” okna Scilaba można go wyłączyć za
pomocą komendy

exit

(oczywiście użycie jej w skrypcie może „trochę utrudnić” zapoznanie się z wynikami

działania programu, bo wszystkie okna znikną natychmiast nie zadając nawet pytania czy faktycznie o to nam
chodziło).

3.3

Wydawanie poleceń — komendy można wpisywać z klawiatury — są wykonywane natychmiast po
naciśnięciu klawisza „Enter”). Przed wykonaniem komendę można edytować przemieszczając kursor za
pomocą strzałek w prawo i w lewo. Naciśnięcie klawisza „Enter” powoduje wykonanie całego polecenia) –
niezależnie od aktualnej pozycji kursora w linii polecenia.

3.4

Skrypty — za pomocą dowolnego edytora tekstowego można utworzyć plik („czysty” plik tekstowy) o
dowolnej nazwie i rozszerzeniu (tzw. skrypt) zawierający wiele poleceń, które zachowują się jak program —
są interpretowane w miarę wczytywania kolejnych poleceń z pliku przez Scilab. Zwyczajowo plikom
zawierającym skrypty nadaje się rozszerzenie „.sce” jednak tak na prawdę jest to „nazwa zwyczajowa”, która
przydaje się głównie systemowi Windows (do rozpoznania jakim programem należy otworzyć plik z takim
właśnie rozszerzeniem). Podobnie jest z rozszerzeniem „.sci”, które zwyczajowo przypisywane jest plikom
zawierającym funkcje.

3.5

Edytor — poczynając od wersji 2.7 Scilab wyposażony jest w edytor SciPad, który rozpoznaje składnię
poleceń Scilaba i odpowiednio koloruje słowa kluczowe. Można w nim pisać programy i funkcje oraz od razu
przesyłać je do uruchomienia w Scilabie. Uruchamiamy go z menu (pozycja „Editor”). Edytor ten
rozpoznaje wybrany w Scilabie katalog roboczy i domyślnie właśnie w nim szuka plików do otwarcia.

3.6

Ustalenie aktualnego katalogu roboczego — polecenie

chdir('

ś

cie

ż

ka')

. Można też skorzystać z menu

(pozycja „File” i dalej „Change Directory”) — można wówczas przeglądać istniejące katalogi. Po wybraniu
katalogu i zatwierdzeniu wyboru w linii komend pojawi się polecenie

chdir

z odpowiednim argumentem

(ścieżką wybranego katalogu) i od razu zostanie wykonane. Jeżeli w nazwie katalogu występuje znak ' to
wystąpi błąd (Scilab zinterpretuje go jako zakończenie łańcucha definiującego ścieżkę) wystarczy zamienić go
na dwa takie znaki i ponowić komendę.

3.7

Historia — Scilab pamięta pewną liczbę wcześniej wydanych komend. Naciśnięcie strzałki skierowanej w

górę powoduje pojawienie się ostatnio wydanej komendy, kolejne jej naciśnięcia przywołują wcześniejsze
komendy. Strzałka w dół też działa w tym kontekście. Tak więc we wspomnianym wcześniej przykładzie
zmiany katalogu wybór katalogu zawierającego znak ' spowoduje natychmiastowe wystąpienie błędu, można
jednak ponownie wywołać ostatnią komendę i ręcznie dodać jeszcze jeden znak ' .

4

„Dopasowanie” Scilaba do własnych potrzeb
4.1

Plik „scilab.ini” — początkowo nie istnieje, można go jednak stworzyć w aktualnym (w chwili

uruchamiania Scilaba) katalogu. Bezpoednio po zainstalowaniu Scilaba katalogiem tym jest „\Documents
and Settings\nazwa użytkownika”. W pliku tym można umieścić wszelkie komendy jakie chcielibyśmy aby
Scilab wykonywał bezpośredni po uruchomieniu. W szczególności może znaleźć się tam polecenie

chdir('

ś

cie

ż

ka')

wskazujące na katalog, w którym trzymamy pliki Scilaba. Jednak definiowanie w tym

pliku zmiennych, które chcielibyśmy by były zawsze dostępne, mija się z celem bowiem ich „żywotność”
sięga nie dalej niż do najbliższego użycia polecenia

clear

.

4.2

Plik „scilab.star” — znajduje się w domowym katalogu Scilaba. W tym pliku można ewentualnie
zdefiniować zmienne, o których wspomniałem powyżej. Przed eksperymentami warto jednak sporządzić
kopię zapasową tego pliku bo jego błędna zawartość może uniemożliwić uruchomienie programu.

5

Pomoc
5.1

Pozycja w menu „?” — rozwija się lista, na której pierwszą pozycją jest uruchomienie przeglądarki plików
pomocy („Scilab Help”). Równie dobrze możemy posłużyc się standardowym skrótem — klawiszem „F1”.

5.2

W linii komend polecenie

help nazwa

(gdzie nazwa jest nazwą funkcji, polecenia itp.) — otwiera tę samą

przeglądarkę z wybranym już opisem.

5.3

Polecenie

apropos

wyrażenie

(gdzie wyrażenie może być wyrażeniem składającym się z kilku słów) —

także otwiera tę samą przeglądarkę, ale tym razem z listą opisów zawierających wpisane wyrażenie.

PMN

Scilab — podstawy 1

3

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

6

„Notatki” z sesji Scilaba
6.1

Istnieje możliwość dokładnego zapisu przebiegu aktualnej sesji pracy ze Scilabem: polecenie

diary('nazwa_pliku')

powoduje zapis do podanego pliku tekstowego wszystkich wpisywanych przez nas

poleceń oraz wszystkich odpowiedzi Scilaba. Zakończenie:

diary(0)

. Polecenie to „koniecznie” chce założyć

nowy plik tekstowy o podanej nazwie — zatem po przerwaniu zapisu trzeba zacząć zapisywanie do pliku o
innej nazwie (we wcześniejszych wersjach polecenie to zachowywało się na tyle kulturalnie, że nie kasowało
wcześniejszego pliku o podanej nazwie tylko informowało, że taki plik już istnieje, w wersji 3.0 kasuje
utworzony wcześniej plik nie „zawracając głowy” użytkownikowi). W ewentualnie podawanej ścieżce
znakiem oddzielającym katalogi może być zarówno „

/

” jak i „

\

”. Jeżeli nie podamy ścieżki to plik

zostanie utworzony w aktualnym katalogu roboczym (co to za katalog można sprawdzić poleceniem

pwd

(print work directory, a do jego zmiany służy polecenie

chdir

(pkt.3.6).

7

„Konwersacja” ze Scilabem
7.1

Polecenia wpisujemy w linii komend, kończymy je naciskając „Enter” i wtedy Scilab je wykonuje (lub
usiłuje wykonać).

7.2

Jeżeli polecenie jest za długie i wygodniej byłoby nam zapisać je w kilku wierszach to należy wpisać dwie
kropki „

..

” — naciśnięcie klawisza „Enter” spowoduje wówczas przejście do nowej linii, ale Scilab będzie

oczekiwać na dokończenie polecenia w kolejnej linii (albo kolejnych liniach jeśli następne linie też będziemy
kończyć dwiema kropkami). Jak łatwo się domyślić metody tej nie da się zastosować do przeniesienia części
wprowadzanego łańcucha do następnego wiersza.

7.3

Jeśli nie chcemy aby wynik polecenia pojawił się na ekranie (bo np. zdefiniowaliśmy właśnie jakąś ogromną

macierz) to polecenie kończymy średnikiem („

;

”).

7.4

Można wydać kilka poleceń w jednej linii — trzeba je wówczas oddzielić średnikami (wyników nie będzie
widać na ekranie) lub przecinkami (wyniki będą widoczne). Podczas testowania programów wpisywanie
wielu poleceń w jednej linii może być trochę niewygodne — w razie napotkania błędu Scilab poda nam
numer wiersza, w którym wystąpił błąd, nie będzie jednak wiadomo, w którym konkretnie poleceniu. Jeszcze
niewygodniejsze może być skorzystanie z możliwości wprowadzenia jednego polecenia w wielu liniach —
linie „przełamane” za pomocą dwóch kropek są przez Scilaba traktowane jako pojedyncza linia i odpowiednio
do tego zostanie podany numer wiersza z błędem.

7.5

Możliwe jest wkopiowywanie fragmentu tekstu ze schowka do linii komend, w wersji 4.0 można już użyć do
tego skrótu klawiaturowego „Ctrl-v”. Skopiowanie fragmentu polecenia z wiersza poleceń też może odbyć się
z wykorzystaniem skrótu „Ctrl-c” — warunkiem jest jednak aby istniał w tym momencie zaznaczony blok.
Jeśli naciśniemy „Ctrl-C” lub „Ctrl-c” gdy nic nie było zaznacone dotychczasowy znak zachęty (mający
postać

––>

) zmieni się na

–1–>

(liczba może być wyższa jeżeli naciśniemy „Ctrl-C” kilka razy). Naciśnięcie

„Ctrl-C” powoduje przerwanie aktualnie wykonywanych operacji (poleceń wprowadzonych z klawiatury czy
odczytanych ze skryptu) i przekazanie kontroli użytkownikowi (ten sam efekt uzyskamy wykorzystując
pozycję menu „Control” i dalej „Interrupt”). W stanie tym dostępne są wszystkie aktualnie znajdujące się
w pamięci zmienne, można je nie tylko oglądać ale i zmieniać. Po wydaniu polecenia

resume

Scilab powraca

do wykonywania programu (który oczywiście „nie zdając sobie sprawy” z ewentualnych zmian
wprowadzonych przez użytkownika wykorzystuje je „jakby nigdy nic”). Możliwe jest skopiowanie całych
przykładów podawanych w „helpach” i wklejenie ich w edytorze do skryptu — zachęcam do eksperymentów.

8

Zmienne
8.1

Sposób zapisu liczb (dokładność): Do zmiany formatu wyświetlania (i drukowania) liczb służy funkcja

format

. Wywołanie:

format([typ],[długo

ść

])

, gdzie typem może być

'e'

(exponential — postać

wykładnicza) lub

'v'

(variable — format zmienny (domyślny)), a długość domyślnie wynosi 10.

8.2

Macierze — w zasadzie wszystkie zmienne o wartościach liczbowych są przez Scilaba traktowane jak
macierze — nawet skalary są uważane za macierze o wymiarze 1×1. Można odwoływać się do
poszczególnych elementów macierzy albo do ich zakresów (np.

A(2,3)

albo

A(1:3,2:5)

— o operatorze

„ : ” będzie jeszcze później).

8.3

Łańcuchy — ciągi znaków ograniczone znakami ' lub ". Jest między nimi „subtelna” różnica — „podwójne

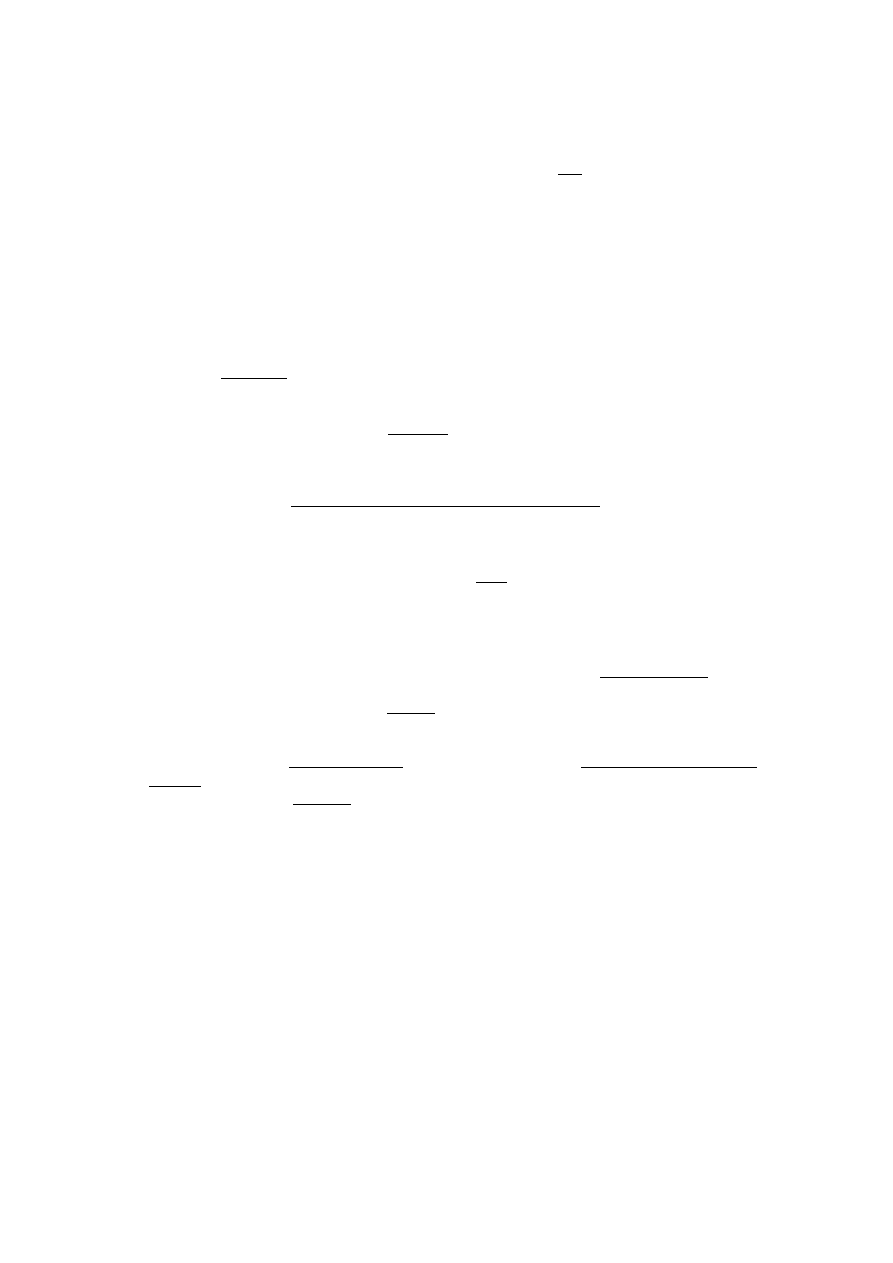
PMN

Scilab — podstawy 1

4

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

uszy” edytor SciPad rozpoznaje jako ogranicznik łańcucha i pokazuje je w innym kolorze. Jeśli chcemy
umieścić w łańcuchu znak cudzysłowu musimy obok siebie zapisać dwa takie znaki.

8.4

Typy zmiennych — każda nowoutworzona zmienna należy do typu „float”, można jednak zmienic jej typ
na całkowity (int8, int16, int32, uint8, uint16, uint32). W tym semestrze jednak nie będziemy się tą kwestią
zajmować.

8.5

„Zarządzanie” zmiennymi

8.5.1 komenda

who

— podaje listę zmiennych i informuje o łącznej zajętości pamięci, stosu itp..

8.5.2 komenda

whos

— podaje bardziej szczegółowe informacje o zmiennych znajdujących się w pamięci (w

szczególności ich wymiary, ile każda z nich zajmuje pamięci itp., pokazywane są również nazwy
zdefiniowanych przez użytkownika funkcji).

8.5.3 komenda

clear

— jeżeli jako parametr podano nazwę konkretnej zmienej (lub kilka nazw) to zostanie

ona (lub one) usunięta z pamięci, jeżeli nie podano parametrów to komenda ta powoduje usunięcie z
pamięci wszystkich zmiennych utworzonych przez użytkownika. Parametry tej komendy podaje się po
spacji (i jeśli jest ich więcej oddziela się je od siebie również spacjami).

8.6

Zmienne o nazwach zaczynających się od znaku „

%

” są zmienymi predefiniowanymi (systemowymi), np.

%eps

,

%t

czy

%pi

. Komenda

clear

ich nie kasuje. Użytkownik może oczywiście utworzyć własne zmienne o

nazwach zaczynających się od „

%

”, jednak taka nazwa nie czyni ich odpornymi na działanie polecenia

clear

.

9

Operatory arytmetyczne

Trzeba pamiętać o tym, że wszystkie operatory domyślnie działają na macierze. Operatory nie muszą być

oddzielane od zmiennych spacjami (chociaż w szczególnych przypadkach spacje pozwalają uniknąć
niejednoznaczności — o tym później).
9.1

Operator przypisania: „

=

”. Wartość wyrażenia po prawej stronie zostaje przypisana zmiennej znajdującej się z

lewej strony. Jeśli w wierszu polecenia wprowadzimy tylko wyrażenie to obliczona wartość zostanie
przypisana domyślnej zmiennej o nazwie

ans

. Długość nazw zmiennych jest nieograniczona, lecz

rozpoznawane są tylko 24 pierwsze znaki. Nazwy muszą zaczynać się od litery lub znaku „

%

”, po których

następują dowolne znaki — litery, cyfry lub inne znaki (poza oczywiście spacją i symbolami operatorów).

9.2

Operatory dodawania i odejmowania („

+

” i „

–

” ). Dodają do siebie lub odejmują od siebie odpowiednie

elementy swoich argumentów. Oczywiście rozmiary dodawanych macierzy muszą się zgadzać (w
szczególności mogą to być i skalary), możliwe jest jednak dodanie (lub odjęcie) skalara do macierzy —
wówczas skalar ten zostanie dodany do każdego elementu macierzy (w tym względzie działanie to jest
analogiczne do mnożenia macierzy przez skalar). Operator dodawania może być stosowany także do łączenia
łańcuchów.

9.3

Mnożenie: „

*

”. Jest to mnożenie macierzy (bądź wektorów, oczywiście muszą one mieć odpowiednie

rozmiary). Dla skalarów działa to całkiem normalnie. Jeśli pomnożymy macierz przez skalar to pomnożone
przez ten skalar zostaną wszystkie elementy macierzy. W szczególności iloczyn skalarny dwóch wektorów
(np. wierszowych) otrzymamy wykonując działanie:

a*b’

(wektor

b

w tym przykładzie jest transponowany

— czyli kolumnowy, o operatorze transpozycji — dalej). Istnieje dodatkowo specjalny operator („

.*

”)

umożliwiający mnożenie macierzy w sposób analogiczny do np. dodawania: element przez odpowiadający
mu element.

-->a = [1,2,3,4]

a =

1. 2. 3. 4.

-->b = a*a

!--error 10

inconsistent multiplication

-->c = a*a'

c =

30.

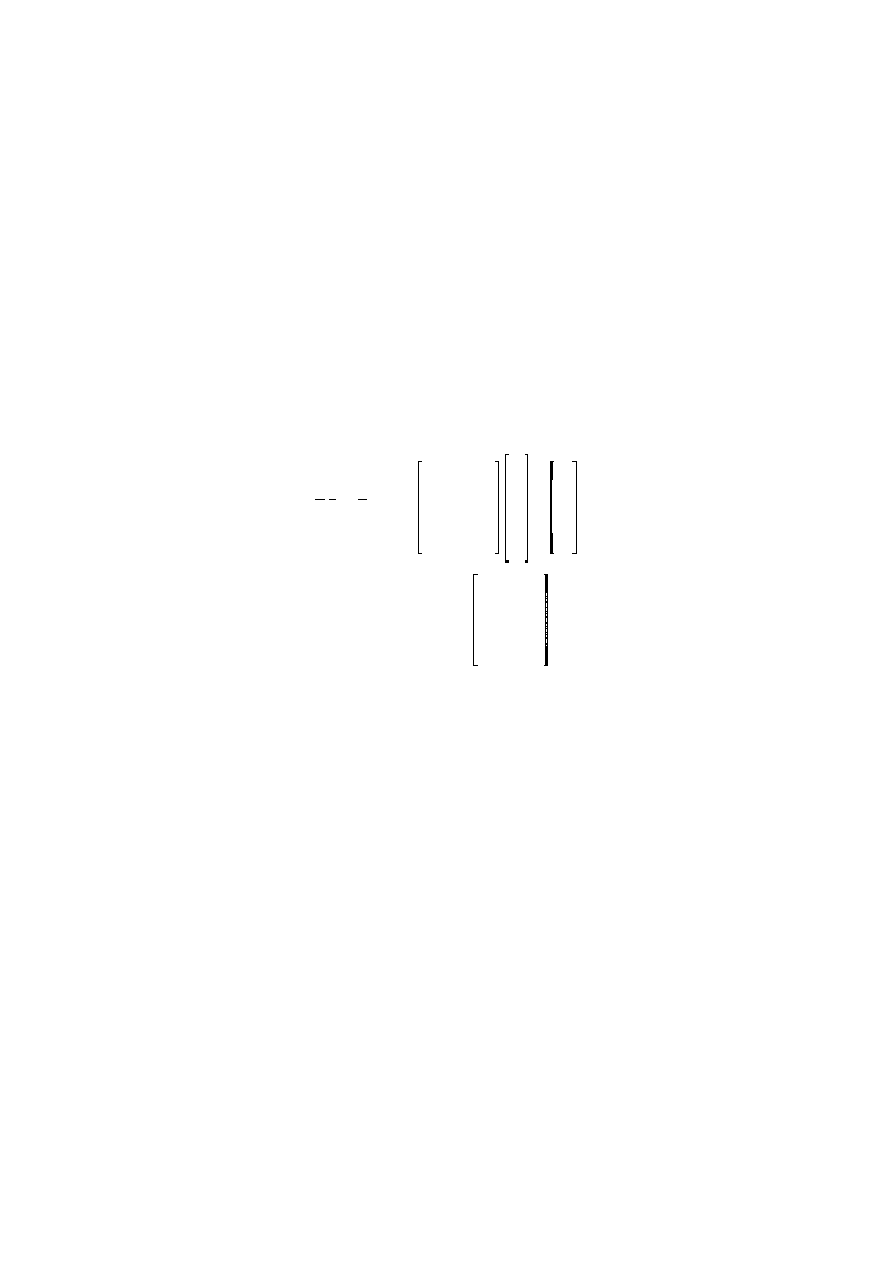
PMN

Scilab — podstawy 1

5

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

-->d = a'*a

d =

1. 2. 3. 4.

2. 4. 6. 8.

3. 6. 9. 12.

4. 8. 12. 16.

-->e = a.*a

e =

1. 4. 9. 16.

9.4

Dzielenie: „

/

”. Dzielenie dwóch skalarów działa całkiem „normalnie”. Podzielenie macierzy przez skalar

powoduje podzielenie wszystkich elementów macierzy przez ten sam skalar. W odniesieniu do macierzy
dzielenie jest zdefiniowane jako mnożenie przez odwrotność macierzy będącej dzielnikiem (funkcja

inv

albo

w zapisie skróconym „

^(-1)

”). Istnieje również operator „

./

” służący do dzielenia przez siebie

odpowiednich elementów macierzy. Poza tym istnieją operatory „

\

” i „

.\

” — mamy więc możliwość

dzielenia lewo- i prawostronnego.

A x

' b

]

1 2 3

4

5 6 7

8

1 7 9 13

2 4 8

5

x

1

x

2

x

3

x

4

'

7

6

&2

8

x

' A\b

Y

x

'

6.1979167

&15.375

4.15625

4.7708333

-->A = [1,2,3,4;5,6,7,8;1,7,9,13;2,4,8,5]

A =

1. 2. 3. 4.

5. 6. 7. 8.

1. 7. 9. 13.

2. 4. 8. 5.

-->b = [7;6;-2;8]

b =

7.

6.

- 2.

8.

-->x = A\b

x =

6.1979167

- 15.375

4.15625

4.7708333

9.5

Potęgowanie: „

^

” lub „

**

”. W przypadku skalarów jest to normane potęgowanie, macierze kwadratowe

mogą być podnoszone do potęgi jako macierze. Do podniesienia do potęgi każdego z elementów macierzy z

PMN

Scilab — podstawy 1

6

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

osobna służy operator „

.^

”.

-->a = [1,2;3,4]

a =

1. 2.

3. 4.

-->b = a^2

b =

7. 10.

15. 22.

-->c = a.^2

c =

1. 4.

9. 16.

9.6

Transpozycja (operator „

.'

”) — zamiana indeksów miejscami, albo „

'

” — transpozycja z zamianą na

wartości sprzężone (oczywiście w przypadku macierzy zawierającej wyłącznie liczby rzeczywiste to
rozróżnienie nie ma znaczenia).

-->a = [1,2,3,4]

a =

1. 2. 3. 4.

-->b = a'

b =

1.

2.

3.

4.

9.7

Uwaga dotycząca specyfiki działania operatorów na macierze i skalary — jeżeli macierz pomnożymy lub
podzielimy przez skalar to oczywiście pomnożony (podzielony) zostanie każdy element macierzy. Jak już
wspomniałem Scilab rozszerza tę zasadę na operatory dodawania, odejmowania i przypisania. Jeśli do
macierzy dodamy skalar (np.

a+2

) to Scilab potraktuje to jako polecenie dodania liczby

2

do każdego

elementu macierzy

a

.

-->a = [1,2,3,4]

a =

1. 2. 3. 4.

-->b = a*2

b =

2. 4. 6. 8.

-->c = a+1

c =

2. 3. 4. 5.

9.8

Gdybyśmy chcieli podzielić lub pomnożyć skalar przez macierz to musimy pamiętać o tym, że polecenie

1/a

będzie dla Scilaba oznaczać obliczenie odwrotności macierzy

a

. Aby uniknąć takiego nieporozumienia

PMN

Scilab — podstawy 1

7

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

moglibyśmy zastosować operator „z kropką”, ale występująca w operatorze kropka mgłaby zostać
zinterpretowana przez Scilaba jako kropka dziesiętna (oczywiście jest to możliwe tylko gdy pierwszym
argumentem będzie liczba całkowita) — np. gdybyśmy chcieli zapisać

1./a

to Scilab zrozumie to jako

1.0/a

(jeśli po kropce dziesiętnej wystąpi zero to nie ma obowiązku zapisywania go — sama kropka

dziesiętna wystarczy). Aby uniknąć takiej pomyłki należałoby wpisać

(1)./a

albo oddzielić operator od

argumentów spacjami (osobiście zalecam ciągłe stosowanie tej ostatniej metody — otrzymujemy wówczas
nieco czytelniejszy kod).

9.9

Reszta z dzielenia —

modulo(x,d)

— gdzie x jest dzielną, a d dzielnikiem (poczynając od wersji 3.0 obie te

liczby nie muszą już być całkowite — jednak wyniki dla liczb niecałkowitych mogą być błędne !!! — w
opisie w plikach pomocy zaznaczono wyraźnie, że funkcja ta jest przeznaczona tylko dla liczb całkowitych).

10 Operatory logiczne:

10.1

Zaprzeczenie: „

~

”. Operator ten może działać na macierze zawierające liczby. Wynikiem będzie macierz

zawierająca wartości logiczne

%F

wszędzie tam gdzie elementy macierzy były różne od zera i

%T

tam gdzie

wartości elementów wynosiły 0. Można oczywiście obliczyć „

~~A

” i dostać

%T

dla wartości niezerowych i

%F

dla zer.

10.2

Koniunkcja:

and

lub „

&

”. Ten operator również może działać na macierze zawierające wartości liczbowe.

Wynikiem będzie

%T

jeśli wszystkie elementy macierzy mają wartości niezerowe i

%F

jeśli choć jedna będzie

zerem. W wywołaniu tej funkcji może wystąpić dodatkowy argument postaci

'c'

lub

'r'

. Jeśli dana będzie

macierz

A = [1,2,0;4,5,6]

, to działanie

and(A,'c')

daje wektor kolumnowy zawierający wynik działania

and

na wiersze macierzy

A

i analogicznie, polecenie

and(A,'r')

daje wektor wierszowy będący wynikiem

działania

and

na kolumny macierzy

A

.

10.3

alternatywa:

or

lub „

|

”. Na macierze działa analogicznie jak

and

.

11 Operatory relacji:

11.1

Nierówność: „

~=

” (inaczej niż w C).

11.2

Równość: „

==

” (tak jak w C).

11.3

Większość, mniejszość itp.: „

<

„, „

>

”, „

<=

”, „

>=

”.

Wynikiem działania operatorów relacji jest wartość logiczna

%T

lub

%F

. Operatory te mogą jednak działać

również na macierze liczbowe. Jeśli np. poleceniem

A = rand(3,4)

wygenerujemy macierz liczb losowych o

3 wierszach i 4 kolumnach, to polecenie

B = A < 0.5

wygeneruje nam macierz o takim samym rozmiarze (3

wiersze na 4 kolumny) zawierającą wartości

%T

tam gdzie relacja jest spełniona i

%F

tam gdzie spełniona nie

jest. Działanie jest analogiczne jeśli oba argumenty relacji będą macierzami liczbowymi (oczywiście muszą
wtedy mieć jednakowe rozmiary). Wartości logiczne

%T

i

%F

na ekranie wyświetlane są jako

T

i

F

(prawdopodobnie dla skrócenia zapisu). Natomiast wprowadzając je z klawiatury równie dobrze możemy
używać zapisu

%T

,

%F

jak i

%t

,

%f

.

12 Zmienne predefiniowane.

Ich nazwy zaczynają się od znaku „

%

” (można jednak tego znaku używać dla nazw zmiennych tworzonych przez

użytkownika). Zmienne predefiniowane nie ulegają usunięciu po wydaniu komendy clear, która wydana bez
dodatkowych parametrów usuwa wszystkie istniejące zmienne.
12.1

Wartość π można uzyskać wpisując

%pi

.

12.2

Podstawa logarytmów naturalnych e:

%e

.

12.3

Jednostka urojona:

%i

— na ekranie pojawia się jako samo

i

.

12.4

Nieskończoność:

%inf

.

12.5

Prawda logiczna:

%t

lub

%T

, fałsz:

%f

lub

%F

.

12.6

Minimana możliwa do zapisania w danym systemie liczba zmiennoprzecinkowa:

%eps

— bardzo pożyteczna

— można ją wykorzystać np. do zatrzymania obliczeń gdy krok zmaleje do praktycznie „niemierzalnej”
wielkości.

12.7

„nie liczba”:

%nan

— not a number.

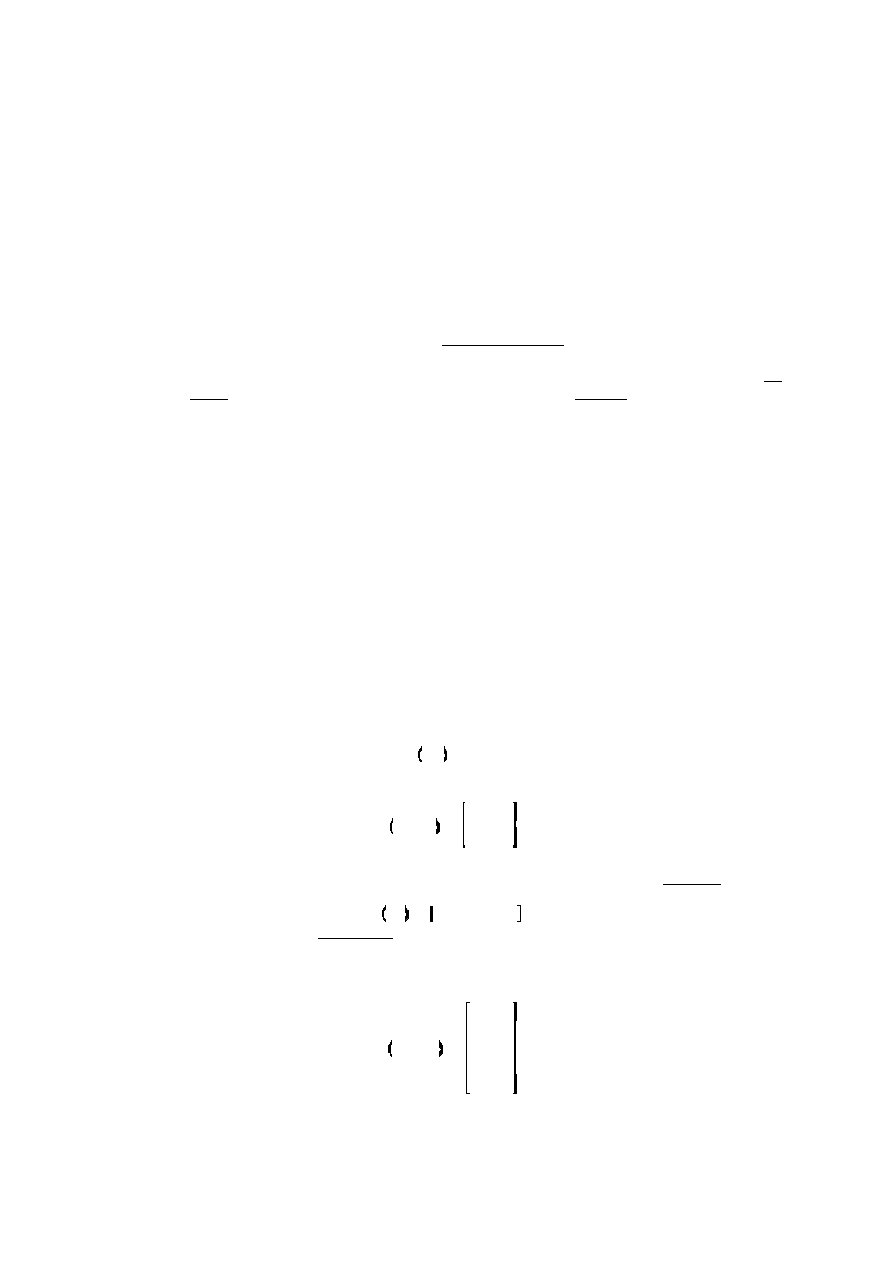
PMN

Scilab — podstawy 1

8

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

12.8

Istnieje jeszcze jedna szczególna zmienna:

ans

. Jest to zmienna, której przypisuje się wynik ostatniego

polecenia, jeśli polecenie to samo tego nie określało. Jeśli np. wprowadzimy polecenie

2+2

, to odpowiedzią

Scilaba będzie:

ans = 4

. Zmienna ta udostępnia obliczoną wartość dopóki nie wydamy kolejnego tego

rodzaju polecenia.

13 Operacje macierzowe.

13.1

Sposoby tworzenia macierzy.

13.1.1

Operator: „ : ”. Operator ten służy do generowania ciągu liczb. Zapis

1:10

oznacza

1,2,3,4,5,6,7,8,9,10. Można też podać krok (umieszczony pomiędzy dwoma dwukropkami):

1:2:10

— to samo co poprzednio tylko z krokiem 2: 1,3,5,7,9 (warto zwrócić uwagę na to, że przy tym
zapisie w wygenerowanym zestawie liczb może nie znaleźć się podana wartość końcowa (w tym
przypadku 10) — dopilnować tego musi sam użytkownik). Krok może być ujemny, wtedy oczywiście
początek musi być większy niż koniec, w przeciwnym razie otrzymamy wektor pusty (a Scilab nie
będzie sygnalizować błędu). No i oczywiście żadna z tych liczb nie musi być całkowita.

13.1.2

Składanie macierzy „z kawałków”. Zdefiniowane wcześniej macierze można łączyć posługując się
nawiasami kwadratowymi oraz przecinkami i średnikami (pod warunkiem zgodności odpowiednich
rozmiarów).

Przykład: Definiujemy macierze:

A=[1,2,3;4,5,6]; B=[7,8;9,0]; C=[11,12,13,14,15;16,17,18,19,20];

Poprawny jest zapis:

-->D = [A,B;C]

i daje macierz:

D =

1. 2. 3. 7. 8.

4. 5. 6. 9. 0.

11. 12. 13. 14. 15.

16. 17. 18. 19. 20.

13.1.3

W tym samym poleceniu można łączyć wszystkie możliwości (wpisywanie z klawiatury, generowanie
i składanie macierzy z kawałków).

13.2

Odwoływanie się do elementów macierzy (jako przykład posłuży nam macierz

D

zdefiniowana powyżej).

13.2.1

Przez podanie indeksów: np.

D(3,4)

— element z 3-go wiersza (pierwszy indeks) i 4-tej kolumny

(drugi indeks).

D 3,4

' 14

13.2.2

Można też wybrać fragment macierzy: np.

D(1:2,1:3)

— wynikiem jest macierz 2×2 z lewego

górnego narożnika macierzy A (wiersze od 1 do 2 i kolumny od 1 do 3).

D 1:2,1:3

'

1 2 3

4 5 6

13.2.3

Symbol „

:

” — gdybyśmy chcieli wybrać np. cały 2-gi wiersz macierzy A należałoby wydać

polecenie:

D(2,:)

— w tym przypadku „osamotniony” symbol „

:

” oznacza wszystkie możliwe

wartości danego indeksu (w tym przykładzie: numeru kolumny).

D 2,:

' 4 5 6 9 0

13.2.4

Symbol „

$

” oznacza maksymalną (końcową) możliwą wartość indeksu/wskaźnika — gdybyśmy np.

chcieli wybrać dwie ostatnie kolumny macierzy A moglibyśmy wydać polecenie

A(:,$-1:$)

— takie

polecenie działa nawet jeśli nie wiemy ile kolumn (czy wierszy) ma macierz

A

w danej chwili (Scilab

jednak to wie).

D :,$

&1:$ '

7

8

9

0

14 15

19 20

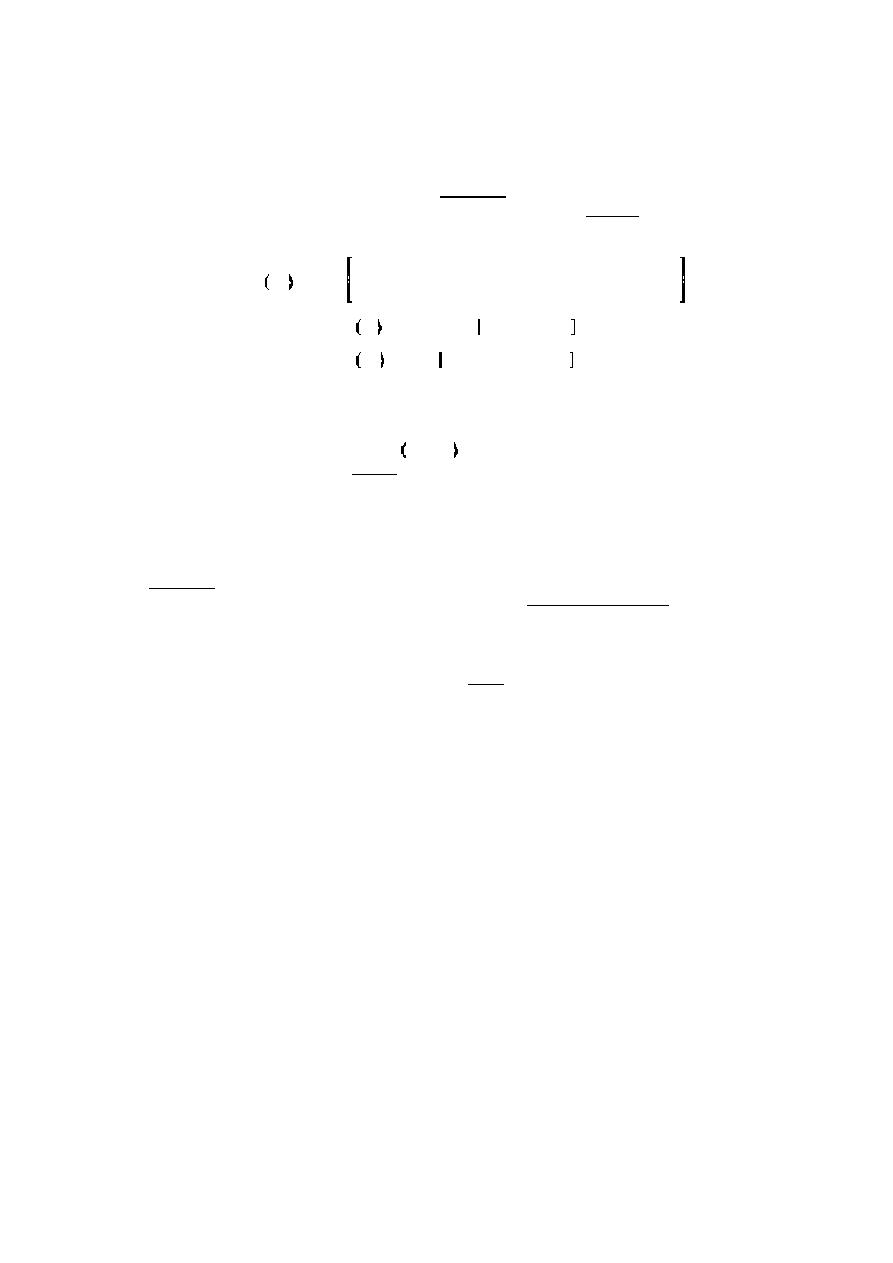
PMN

Scilab — podstawy 1

9

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

13.2.5

Za pomocą macierzy zawierającej wartości logiczne

%T

i

%F

. Najlepiej wytłumaczyć to na przykładzie.

Wygeneruję dwuwierszową macierz liczb losowych:

a = rand(2,5)

. Następnie utworzę macierz

b

zawierającą informację o tym, które wartości pierwszego wiersza macierzy

a

są mniejsze od 0.5:

b = a(1,:)<0.5

. Na koniec utworzę wektor

c

zawierający elementy drugiego wiersza macierzy

a

odpowiadające elementom wiersza pierwszego mniejszym od 0.5 (znajdujące się w tych samych
kolumnach):

c = a(2,b)

.

a

' rand 2,5

Y

.2113249 .0002211 .6653811 .8497452 .8782165

.7560439 .3303271 .6283918 .6857310 .0683740

b

' a 1,: < 0.5

Y

T T F F F

c

' a 2,b

Y

.7560439 .3303271

Innym przykładem wykorzystania tej metody „wybierania” elementów macierzy może być sytuacja gdy

chcemy aby żaden element macierzy nie przekraczał zadanej maksymalnej wartości (macierz może np.
zawierać wartości funkcji dwóch zmiennych, których wykres chcemy sporządzić). Załóżmy, że wartości
funkcji znajdują się w macierzy F, a zadana wartość maksymalna wynosi max:

F F > max

' max

Wyrażenie w nawiasie tworzy macierz wartości logicznych o takim samym rozmiarze jak F, zawierającą

%T

w miejscach, w których elementy macierzy F spełniają podany warunek (są większe niż max). Gdy

macierz zawierająca wartości logiczne zostanie użyta w miejsce indeksów macierzy F spowoduje dokonanie
wyboru tych elementów macierzy F, które znajdują się w miejscach odpowiadających

%T

(wynikiem będzie

oczywiście również macierz). Na koniec operator podstawienia spowoduje podstawienie podanego skalara w
miejsce każdego elementu macierzy. W tym więc przypadku wartość max zostanie podstawiona w miejsce
wszystkich elementów macierzy F, które pierwotnie były większe niż max.

13.3

Sprawdzenie rozmiaru macierzy: funkcja

size

. Wynikiem jest wektor dwuelementowy zawierający liczbę

wierszy i liczbę kolumn. Można odwołać się tylko do jednego elementu tej funkcji:

size(A,1)

daje liczbę

wierszy, a

size(A,2)

daje liczbę kolumn. Nie musimy pamiętać, która składowa jest liczbą kolumn, a która

liczbą wierszy — polecenie może mieć postać

size(A,'r')

(liczba wierszy — rows) lub

size(A,'c')

(liczba kolumn — columns). Gdyby chodziło nam o łączną liczbę elementów

size(A,'*')

— iloczyn obu

poprzednich.

13.4

Znajdowanie elementu o maksymalnej (lub minimalnej) wartości: funkcja

max

(lub

min

). Wynikiem

wywołania polecenia

max

(lub

min

) z jednym argumentem jest maksymalna (minimalna) wartość występująca

w całej macierzy.

-->A = rand(3,4)

A =

! 0.3076091 0.312642 0.5664249 0.5935095 !

! 0.9329616 0.3616361 0.4826472 0.5015342 !

! 0.2146008 0.2922267 0.3321719 0.4368588 !

-->max(A)

ans =

0.9329616

Polecenie to może przyjąć również drugi argument postaci

'r'

lub

'c'

— wówczas wynikiem będzie

odpowiednio wektor wierszowy lub kolumnowy zawierający maksymalne wartości występujące odpowiednio
w wierszach lub w kolumnach macierzy będącej pierwszym argumentem:

-->max(A,'r')

ans =

! 0.9329616 0.3616361 0.5664249 0.5935095 !

-->min(A,'c')

ans =

! 0.3076091 !

! 0.3616361 !

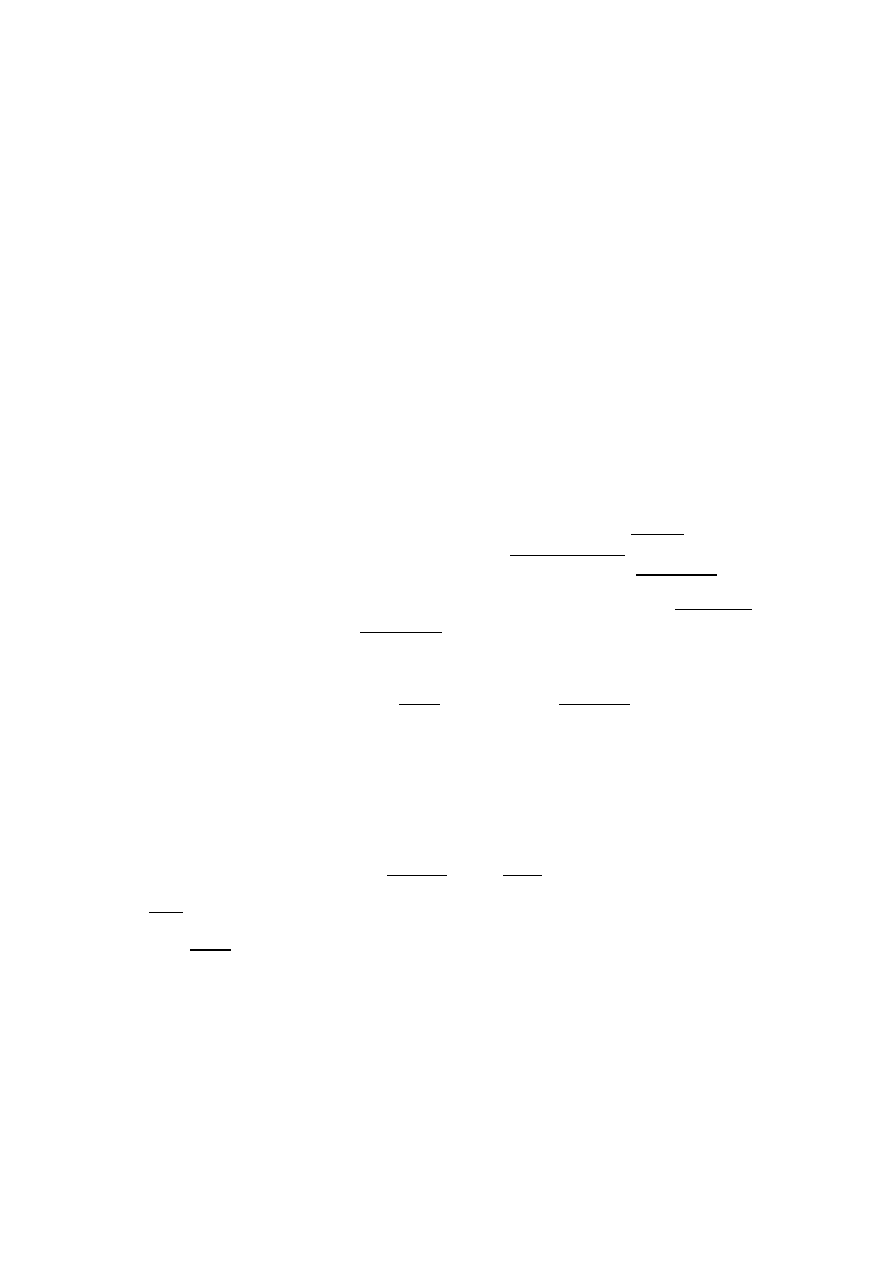
PMN

Scilab — podstawy 1

10

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

! 0.2146008 !

Istnieje też drugi sposób wywołania tego polecenia umożliwiający otrzymanie nie tylko samej wartości
maksymalnej ale i jej współrzędnych:

-->[wart,wsp] = max(A)

wsp =

! 2. 1. !

wart =

0.9329616

albo:

-->[wart,wsp] = min(A,'c')

wsp =

! 1. !

! 2. !

! 1. !

wart =

! 0.3076091 !

! 0.3616361 !

! 0.2146008 !

13.5

Aby zmienić wartość wybranych elementów macierzy dokonujemy przypisania nowej wartości wybranemu
elementowi (albo wybranym elementom — wtedy musimy oczywiście zatroszczyć się o to aby rozmiary
macierzy podstawianej odpowiadały rozmiarom wybranego do zamiany fragmentu macierzy oryginalnej).
Można przypisać im także im macierz pustą —

[]

(oczywiście macierz taka jest skalarem więc dopuszczalne

jest podstawienie postaci

a(:,1:3) = []

— spowoduje to usunięcie w całości pierwszych trzech kolumn

macierzy

a

). Nie uda się podstawienie

a(1,1) = []

— w efekcie dostalibyśmy niekompletną macierz.

13.6

Funkcje służące do generowania macierzy

13.6.1

linspace(x1,x2,N)

i

logspace(x1,x2,N)

. Służą do generowania wektorów wierszowych

zawierających N elementów równomiernie rozłożonych od x1 do x2 (linspace) lub od 10

x1

do 10

x2

(logspace) — będą to np. argumenty, dla których będziemy chcieli potem utworzyć wykres.
Argument N jest opcjonalny, jeżeli go nie ma — przyjmuje się 100 (dla linspace) lub 50 (dla
logspace).

13.6.2

diag

— jako argument przyjmuje wektor zaś zwraca macierz kwadratową, na której głównej

przekątnej znajdują się wartości podane w wektorze a pozostałe wartości sa zerami (np.

diag([1,2,3,4])

).

13.6.3

eye

— macierz jednostkowa (1 na głównej przekątnej, pozostałe 0), jeżeli żądana macierz nie będzie

kwadratowa to jedynki i tak znajdą się na głównej przekątnej — tzn. poczynając od pozycji (1,1) przez
(2,2), (3,3) itd. „jak długo się da” (np.

eye(n1,n2)

).

13.6.4

ones

— same jedynki (np.

ones(n1,n2)

).

13.6.5

zeros

— same zera (np.

zeros(n1,n2)

).

13.6.6

rand

— liczby losowe z zakresu <0,1) (np.

rand(n1,n2)

).

Polecenia z powyższych 4 punktów wymagają podania dwóch argumentów (w przeciwieństwie do

Matlaba) — po podaniu tylko jednego argumentu nie jest generowana macierz kwadratowa ani wektor a
skalar.

13.6.7

diag

— polecenie to ma różne znaczenia w zależności od argumentów. Jeśli argumentem będzie

wektor polecenie utworzy macierz, na której głównej przekątnej znajdą się (kolejno od góry) elementy
podanego wektora, np.:

-->a = [1,2,3];

-->A = diag(a)

A =

! 1. 0. 0. !

! 0. 2. 0. !

! 0. 0. 3. !

Można podać dodatkowy argument — liczbę całkowitą wskazuje ona o którą przekątną powyżej lub

PMN

Scilab — podstawy 1

11

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

poniżej (gdy liczba jest ujemna) głównej nam chodzi. Jeśli na przykład wektor

a

nadal jest określony jak

powyżej to:

-->A = diag(a,-2)

A =

! 0. 0. 0. 0. 0. !

! 0. 0. 0. 0. 0. !

! 1. 0. 0. 0. 0. !

! 0. 2. 0. 0. 0. !

! 0. 0. 3. 0. 0. !

Uzyskujemy w ten sposób możliwość łatwego utworzenia np. macierzy trójdiagonalnej:

-->a = [1,2,3];

-->b = [4,5,6,7];

-->c = [8,9,10];

-->A = diag(a,1) + diag(b) + diag(c,-1)

A =

! 4. 1. 0. 0. !

! 8. 5. 2. 0. !

! 0. 9. 6. 3. !

! 0. 0. 10. 7. !

Drugim zastosowaniem polecenia diag jest „wydobywanie” przekątnej (głównej lub którejś z wyższych

bądź niższych) z już istniejącej macierzy — w takiej sytuacji pierwszym argumentem polecenia nie jest
wektor a macierz. Na przykład:

-->A = rand(4,5)

A =

! 0.2113249 0.6653811 0.8782165 0.7263507 0.2312237 !

! 0.7560439 0.6283918 0.0683740 0.1985144 0.2164633 !

! 0.0002211 0.8497452 0.5608486 0.5442573 0.8833888 !

! 0.3303271 0.6857310 0.6623569 0.2320748 0.6525135 !

-->diag(A)

ans =

! 0.2113249 !

! 0.6283918 !

! 0.5608486 !

! 0.2320748 !

-->diag(A,-1)

ans =

! 0.7560439 !

! 0.8497452 !

! 0.6623569 !

-->diag(A,2)

ans =

! 0.8782165 !

! 0.1985144 !

! 0.8833888 !

13.7

Zapamiętywanie macierzy przez Scilab

13.7.1

full

— macierz „pełna” — zapamiętywane są wszystkie elementy macierzy — w ten sposób

domyślnie jest zapamiętywana każda wprowadzana lub generowana macierz.

13.7.2

sparse

— macierz rzadka — zapamiętywane są tylko elementy niezerowe. Polecenie to tworzy

(nową) macierz jako rzadką, albo „przerabia” istniejącą już macierz na rzadką.

Wywołanie („przerabianie” istniejącej już macierzy):

sp = sparse(X)

lub (tworzenie macierzy od razu jako rzadkiej):

PMN

Scilab — podstawy 1

12

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

sp = sparse(ij,v [,mn])

gdzie:

X — dowolna istniejąca już macierz,
ij — dwukolumnowa macierz liczb integer (współrzędne elementów niezerowych),
v — wektor (niezerowe wartości macierzy),
mn — wektor dwuelementowy (liczba wierszy, liczba kolumn), argument opcjonalny.

Przykład zastosowania („żywcem” z helpów):

sp = sparse([1,2;5,4;3,1],[1,2,3])

sp =

( 5, 4) sparse matrix

( 1, 2) 1.

( 3, 1) 3.

( 5, 4) 2.

A = full(sp)

A =

! 0. 1. 0. 0. !

! 0. 0. 0. 0. !

! 3. 0. 0. 0. !

! 0. 0. 0. 0. !

! 0. 0. 0. 2. !

Jak łatwo się domyślić w powyższym przykładzie celowo nie zakończyłem wydawanych poleceń

ś

rednikami.

Działania na macierzach rzadkich odbywają się w taki sam sposób jak na macierzach pełnych, z tą

jednak różnicą, że w przypadku macierzy pełnej możemy łatwo „dostać się” do dowolnego elementu (za
pomocą polecenia np.: A(1,2)), natomiast takie samo polecenie w przypadku macierzy rzadkiej daje
również macierz rzadką (o wymiarze 1×1):

sp(3,1)

ans =

( 1, 1) sparse matrix

( 1, 1) 3.

Jeżeli chcemy dostać konkretną liczbę musimy wydać polecenie:

full(sp(3,1))

ans =

3.

14 Porady praktyczne

14.1

Na samym początku skryptu warto umieścić polecenie

clear

— dzięki temu w chwili uruchamiania skryptu

dotychczas obecne w pamięci zmienne znikną (mogą one pochodzić np. z poprzednich uruchomień podczas
testowania programu). Po zakończeniu wykonywania poleceń ze skryptu (czy wpisywanych z klawiatury)
wszystkie utworzone zmienne pozostają w pamięci i są dostępne do dalszych operacji, dzięki temu kiedy coś
„nam nie wychodzi” można sprawdzić np. czy utworzone wektory są wierszowe czy kolumnowe i jakie mają
rozmiary (za pomoca polecenia

whos()

). Usunięcie zmiennych na starcie kolejnego uruchomienia ma

znaczenie zwłaszcza podczas testowania nowych skryptów.

14.2

Jeżeli nasz program rysuje jakieś wykresy (może ich być sporo) to umieszczenie na początku polecenia

xdel(winsid())

spowoduje zamknięcie wszystkich otwartych okien graficznych — dzięki temu po

wprowadzeniu poprawek możemy od razu uruchomić skrypt od nowa, a zamykaniem okien zajmie się on
sam.

14.3

Komentowanie skryptu — komentarze zaczynają się od dwóch znaków

//

i rozciągają się do końca wiersza.

Poczynając od wersji 3.0 jest nareszcie możliwość „wykomentowania” większej liczby wierszy. Jednak nie za
pomocą znaków początku i końca komentarza (tak jak ma to miejsce np. w C) — po zaznaczeniu fragmentu
tekstu należy wybrać z menu „Edit” polecenie „Comment selection” (skrót: „Ctrl-m”), co spowoduje

PMN

Scilab — podstawy 1

13

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

wpisanie znaków

//

na początku każdego wiersza. Istnieje oczywiście polecenie „Uncomment selection”

(„Ctrl-M”). Podobnie można zastosować wcięcie dla całego wybranego fragmentu tekstu („Ctrl-d”) lub je
usunąć („Ctrl-D”).