ANALIZA

DYSKRYMINACYJNA

ZARZĄDZANIE INSTYTUCJAMI

FINANSOWYMI

WOJCIECH KACZMARCZYK

MODELE DYSKRYMINACYJNE

• Syntetyczna miara oceny zagrożenia

finansowego przedsiębiorstwa

Budowa:

1. dobór odpowiedniej próby

przedsiębiorstw

2. dobór wskaźników (z około 30 zostaje 5)

3. wyznaczenie punktu granicznego

4. wykonanie testów na innych

przedsiębiorstwach

MODEL ALTMANA

ZARZĄDZANIE INSTYTUCJAMI

FINANSOWYMI

MODEL ALTMANA

• zbudowany na bazie 66 przedsiębiorstw

(33 upadłych i 33 w dobrej kondycji)

• przeznaczony na rynek USA
• skuteczność – 89,73%

*!

MODEL ALTMANA

𝑍 = 1,2𝑋

1

+ 1,4𝑋

2

+ 3,3𝑋

3

+ 0,6𝑋

4

+ 𝑋

5

𝑋

1

=

𝑘𝑎𝑝𝑖𝑡𝑎ł 𝑝𝑟𝑎𝑐𝑢𝑗ą𝑐𝑦∗

𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

𝑋

2

=

𝑧𝑦𝑠𝑘 𝑧𝑎𝑡𝑟𝑧𝑦𝑚𝑎𝑛𝑦∗∗

𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

𝑋

3

=

(𝑧𝑦𝑠𝑘 𝑏𝑟𝑢𝑡𝑡𝑜:𝑘𝑜𝑠𝑧𝑡𝑦 𝑜𝑑𝑠𝑒𝑡𝑒𝑘∗∗∗)

𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

𝑋

4

=

𝑤𝑎𝑟𝑡𝑜ść 𝑟𝑦𝑛𝑘𝑜𝑤𝑎 𝑘𝑎𝑝𝑖𝑡𝑎ł𝑢 𝑤ł𝑎𝑠𝑛𝑒𝑔𝑜∗∗∗∗

𝑤𝑎𝑟𝑡𝑜ść 𝑘𝑠𝑖ę𝑔𝑜𝑤𝑎 𝑘𝑎𝑝𝑖𝑡𝑎łó𝑤 𝑜𝑏𝑐𝑦𝑐𝑕

𝑋

5

=

𝑝𝑟𝑧𝑦𝑐𝑕𝑜𝑑𝑦 𝑧𝑒 𝑠𝑝𝑟𝑧𝑒𝑑𝑎ż𝑦

𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

* aktywa obrotowe – zobowiązania bieżące
** zysk z lat ubiegłych + kapitał rezerwowy
+ kapitał zapasowy
*** koszty finansowe
**** Przyjmujemy, że to kapitał własny

Z < 1,81 – zagrożenie upadłością
Z > 2,99 – dobra kondycja finansowa
1,81 < Z < 2,99 – wynik niejednoznaczny

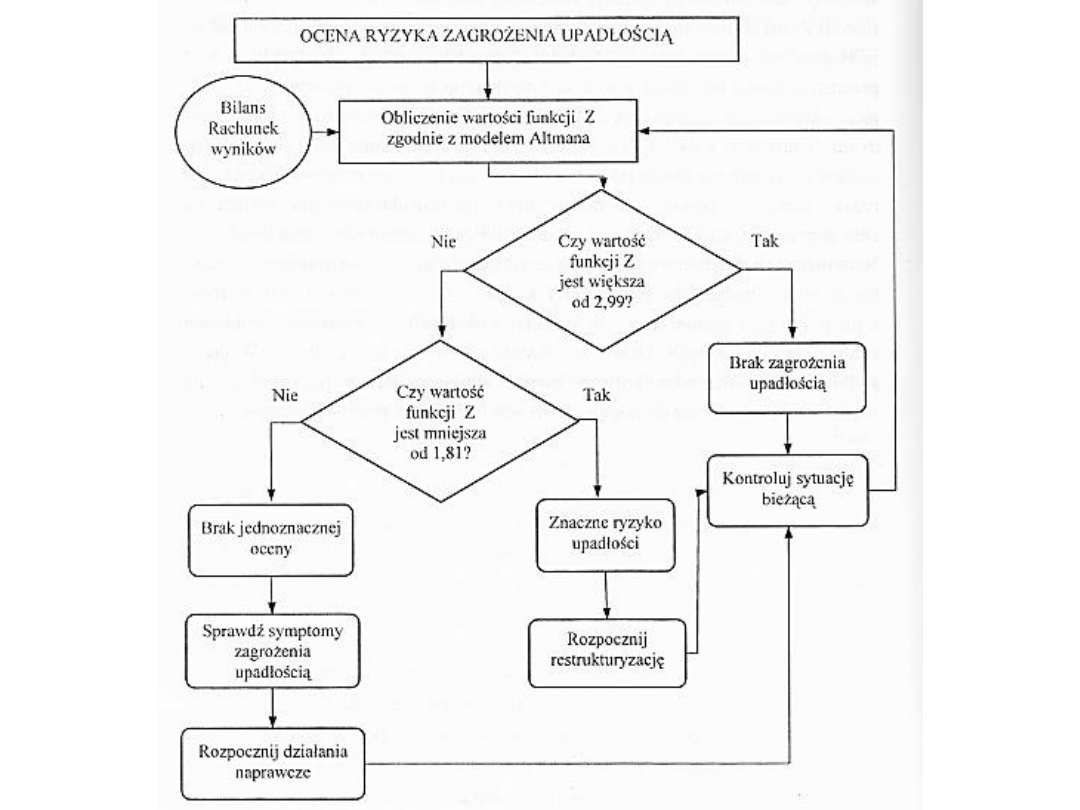
MODEL ALTMANA

MODEL SPRINGATE’A

ZARZĄDZANIE INSTYTUCJAMI

FINANSOWYMI

MODEL SPRINGATE’A

• zbudowany na bazie 40 przedsiębiorstw

(20 upadłych i 20 w dobrej kondycji)

• model kanadyjski
• skuteczność – 92,5%

*!

MODEL SPRINGATE’A

𝑍 = 1,03𝐴 + 3,07𝐵 + 0,66𝐶 + 0,4𝐷

A =

𝑘𝑎𝑝𝑖𝑡𝑎ł 𝑜𝑏𝑟𝑜𝑡𝑜𝑤𝑦 𝑛𝑒𝑡𝑡𝑜∗

𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

𝐵 =

(𝑧𝑦𝑠𝑘 𝑏𝑟𝑢𝑡𝑡𝑜:𝑘𝑜𝑠𝑧𝑡𝑦 𝑜𝑑𝑠𝑒𝑡𝑒𝑘∗∗)

𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

𝐶 =

𝑧𝑦𝑠𝑘 𝑏𝑟𝑢𝑡𝑡𝑜

𝑧𝑜𝑏𝑜𝑤𝑖ą𝑧𝑎𝑛𝑖𝑎 𝑏𝑖𝑒żą𝑐𝑒

𝐷 =

𝑠𝑝𝑟𝑧𝑒𝑑𝑎ż 𝑛𝑒𝑡𝑡𝑜

𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

* aktywa bieżące – zobowiązania bieżące
** koszty finansowe

Wartość graniczna Z = 0,862

MODEL POZNAŃSKI

ZARZĄDZANIE INSTYTUCJAMI

FINANSOWYMI

MODEL POZNAŃSKI

• model polski
• zbudowany na bazie 100

przedsiębiorstw (50 upadłych i 50 w
dobrej kondycji)

• okres badawczy 1993 – 1996
• skuteczność – 96%

*!

MODEL POZNAŃSKI

𝑍 = 3,562𝑋

1

+ 1,588𝑋

2

+ 4,288𝑋

3

+ 6,179𝑋

4

− 2,368

𝑋

1

=

𝑤𝑦𝑛𝑖𝑘 𝑓𝑖𝑛𝑎𝑛𝑠𝑜𝑤𝑦

𝑚𝑎𝑗ą𝑡𝑒𝑘 𝑐𝑎ł𝑘𝑜𝑤𝑖𝑡𝑦∗

𝑋

2

=

𝑚𝑎𝑗ą𝑡𝑒𝑘 𝑜𝑏𝑟𝑜𝑡𝑜𝑤𝑦∗∗ ;𝑧𝑎𝑝𝑎𝑠𝑦

𝑧𝑜𝑏𝑜𝑤𝑖ą𝑧𝑎𝑛𝑖𝑎 𝑘𝑟ó𝑡𝑘𝑜𝑡𝑒𝑟𝑚𝑖𝑛𝑜𝑤𝑒

𝑋

3

=

𝑘𝑎𝑝𝑖𝑡𝑎ł 𝑠𝑡𝑎ł𝑦∗∗∗

𝑚𝑎𝑗ą𝑡𝑒𝑘 𝑐𝑎ł𝑘𝑜𝑤𝑖𝑡𝑦∗

𝑋

4

=

𝑤𝑦𝑛𝑖𝑘 𝑧𝑒 𝑠𝑝𝑟𝑧𝑒𝑑𝑎ż𝑦

𝑝𝑟𝑧𝑦𝑐𝑕𝑜𝑑𝑦 𝑧𝑒 𝑠𝑝𝑟𝑧𝑒𝑑𝑎ż𝑦

Wartość graniczna:
Z = 0

*majątek trwały netto + średni stan
majątku obrotowego
**W skład majątku obrotowego
wchodzą:
1. Środku pieniężne
2. Papiery wartościowe
3. Zapasy (materiały, towary,
produkty pracy)
4. Należności
*** kapitał własny + kapitał obcy
długoterminowy lub
aktywa ogółem – zobowiązania
bieżące

MODEL J. GAJDKI

I D. STOSA

ZARZĄDZANIE INSTYTUCJAMI

FINANSOWYMI

MODEL J. GAJDKI I D. STOSA

• model polski
• zbudowany na bazie 40 przedsiębiorstw

(20 upadłych i 20 w dobrej kondycji)

• okres badawczy 1994 – 1995
• skuteczność – 93%

*!

MODEL J. GAJDKI I D. STOSA

𝑍 = 0,77320590 − 0,0856425𝑋

1

+ 0,000774𝑋

2

+

0,9920985𝑋

3

+ 0,6535995𝑋

4

− 0,594687𝑋

5

𝑋

1

=

𝑝𝑟𝑧𝑦𝑐𝑕𝑜𝑑𝑦 𝑛𝑒𝑡𝑡𝑜 𝑧𝑒 𝑠𝑝𝑟𝑧𝑒𝑑𝑎ż𝑦

ś𝑟𝑒𝑑𝑛𝑖𝑒 𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

𝑋

2

=

ś𝑟𝑒𝑑𝑛𝑖𝑒 𝑧𝑜𝑏𝑜𝑤𝑖ą𝑧𝑎𝑛𝑖𝑎

𝑘𝑜𝑠𝑧𝑡𝑦 𝑝𝑟𝑜𝑑𝑢𝑘𝑐𝑗𝑖 𝑠𝑝𝑟𝑧𝑒𝑑𝑎𝑛𝑒𝑗

𝑋

3

=

𝑧𝑦𝑠𝑘 𝑛𝑒𝑡𝑡𝑜

ś𝑟𝑒𝑑𝑛𝑖𝑒 𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

𝑋

4

=

𝑧𝑦𝑠𝑘 𝑏𝑟𝑢𝑡𝑡𝑜

𝑝𝑟𝑧𝑦𝑐𝑕𝑜𝑑𝑦 𝑛𝑒𝑡𝑡𝑜 𝑧𝑒 𝑠𝑝𝑟𝑧𝑒𝑑𝑎ż𝑦

𝑋

5

=

𝑧𝑜𝑏𝑜𝑤𝑖ą𝑧𝑎𝑛𝑖𝑎 𝑜𝑔ół𝑒𝑚

𝑎𝑘𝑡𝑦𝑤𝑎 𝑜𝑔ół𝑒𝑚

Wartość graniczna:
Z = 0,45

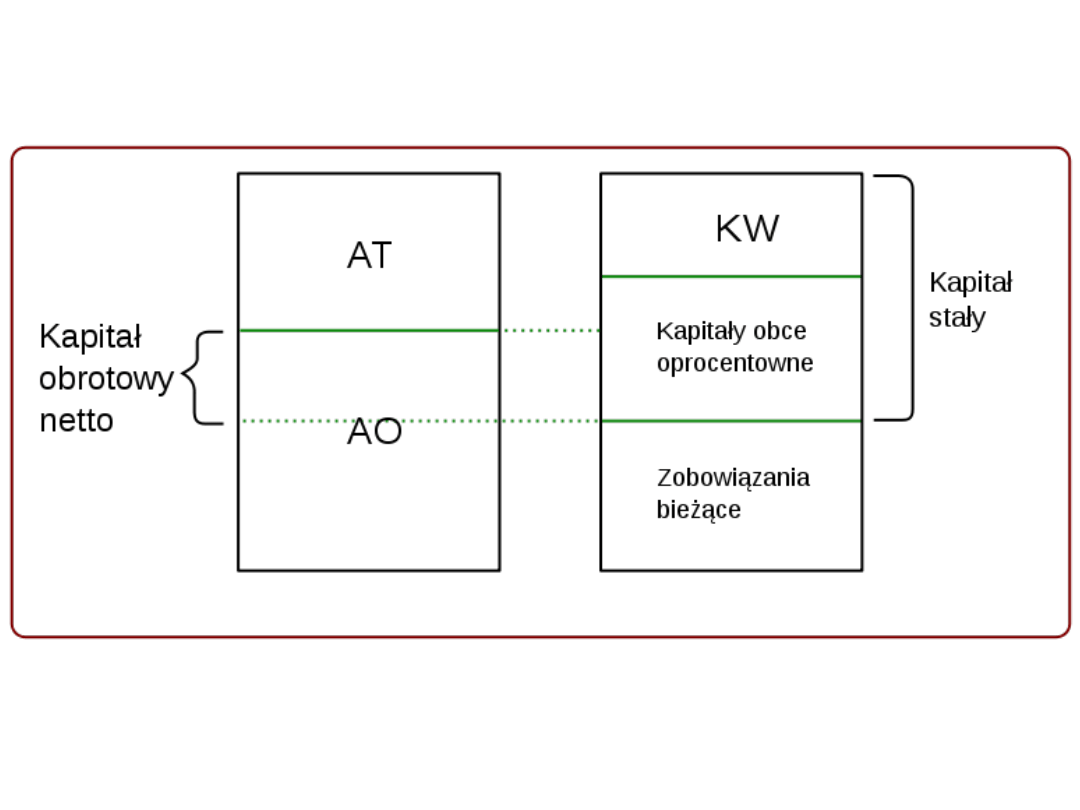
KON I KS

Źródło: Wikipedia

MODEL ALTMANA - KGHM

𝑋

1

=

9 854 ; 4786

33 616

= 0,15076

𝑋

2

=

19 478 ; 51:286

33 616

= 0,58642

𝑋

3

=

6 448 ;146

33 616

= 0,18747

𝑋

4

=

21 710

11 906

= 1,82345

𝑋

5

=

26 705
33 616

= 0,79441

𝑍 = 3,51

MODEL ALTMANA - KGHM

𝑋

1

=

9 854 ; 4786

33 616

= 0,15076

𝑋

2

=

19 478 ; 51:286

33 616

= 0,58642

𝑋

3

=

6 448 ;146

33 616

= 0,18747

𝑋

4

=

21 710

11 906

= 1,82345

𝑋

5

=

26 705
33 616

= 0,79441

𝑍 = 3,51

MODEL ALTMANA - KGHM

𝑋

1

=

9 854 ; 4786

33 616

= 0,15076

𝑋

2

=

19 478 ; 51:286

33 616

= 0,58642

𝑋

3

=

6 448 ;146

33 616

= 0,18747

𝑋

4

=

21 710

11 906

= 1,82345

𝑋

5

=

26 705
33 616

= 0,79441

𝑍 = 3,51

MODEL ALTMANA - KGHM

𝑋

1

=

9 854 ; 4786

33 616

= 0,15076

𝑋

2

=

19 478 ; 51:286

33 616

= 0,58642

𝑋

3

=

6 448 ;146

33 616

= 0,18747

𝑋

4

=

21 710

11 906

= 1,82345

𝑋

5

=

26 705
33 616

= 0,79441

𝑍 = 3,51

MODEL ALTMANA - KGHM

𝑋

1

=

9 854 ; 4786

33 616

= 0,15076

𝑋

2

=

19 478 ; 51:286

33 616

= 0,58642

𝑋

3

=

6 448 ;146

33 616

= 0,18747

𝑋

4

=

21 710

11 906

= 1,82345

𝑋

5

=

26 705
33 616

= 0,79441

𝑍 = 3,51

MODEL ALTMANA - KGHM

𝑋

1

=

9 854 ; 4786

33 616

= 0,15076

𝑋

2

=

19 478 ; 51:286

33 616

= 0,58642

𝑋

3

=

6 448 ;146

33 616

= 0,18747

𝑋

4

=

21 710

11 906

= 1,82345

𝑋

5

=

26 705
33 616

= 0,79441

𝑍 = 3,51

MODEL ALTMANA - KGHM

𝑋

1

=

9 854 ; 4786

33 616

= 0,15076

𝑋

2

=

19 478 ; 51:286

33 616

= 0,58642

𝑋

3

=

6 448 ;146

33 616

= 0,18747

𝑋

4

=

21 710

11 906

= 1,82345

𝑋

5

=

26 705
33 616

= 0,79441

𝑍 = 3,51

LITERATURA

• Analiza finansowa w procesie decyzyjnym współczesnego

przedsiębiorstwa, pr. zbior. pod red. G. Łukasik,
Wydawnictwo Akademii Ekonomicznej im Karola
Adamieckiego, Katowice 2009.

• M. Capiga, W. Gradoń, G. Szustak, Systemy wczesnego

ostrzegania w ocenie działalności instytucji finansowych,
Wydawnictwo CeDeWu, Warszawa 2013.

• B. Kotowska, A. Uziębło, O. Wyszkowska-Kaniewska,

Analiza finansowa w przedsiębiorstwie. Przykłady,
zadania i rozwiązania, Wydawnictwo CeDeWu,
Warszawa 2013.