
Wydawnictwo Helion
ul. Chopina 6
44-100 Gliwice
tel. (32)230-98-63
IDZ DO
IDZ DO
KATALOG KSI¥¯EK
KATALOG KSI¥¯EK
TWÓJ KOSZYK
TWÓJ KOSZYK
CENNIK I INFORMACJE
CENNIK I INFORMACJE
CZYTELNIA
CZYTELNIA
Fizyka z komputerem
dla liceum i technikum
Autor: Maciej Zawacki
ISBN: 83-7361-580-6
Format: B5, stron: 120
Poznaj œwiat fizyki, korzystaj¹c z nowoczesnych metod
• Naucz siê korzystaæ z arkusza kalkulacyjnego
• Opanuj sposoby numerycznego rozwi¹zywania zadañ fizycznych
• PrzeprowadŸ symulacje zjawisk fizycznych
Komputer jest podstawowym narzêdziem stosowanym w laboratoriach, zarówno
badawczych, jak i dydaktycznych. Za jego pomoc¹ mo¿na przeprowadziæ
skomplikowane obliczenia, wykonaæ symulacje zjawisk fizycznych i opracowaæ wyniki
pomiarów. Komputer mo¿na równie¿ wykorzystaæ podczas poznawania mechanizmów
fizycznych rz¹dz¹cych otaczaj¹cym nas œwiatem. Wykorzystuj¹c animacje, wykresy
i szybkie narzêdzia obliczeniowe, mo¿emy przedstawiæ te mechanizmy w czytelny
i ³atwy do zrozumienia sposób.
„Fizyka z komputerem dla liceum i technikum” to ksi¹¿ka opisuj¹ca mo¿liwoœci
zastosowania komputera do wykonywania obliczeñ, do wyznaczania wielkoœci
fizycznych i rozwi¹zywania zadañ z nimi zwi¹zanych. Przedstawia metody u¿ycia
arkusza kalkulacyjnego Excel w roli narzêdzia obliczeniowego i sposoby prezentowania
wyników obliczeñ w postaci graficznej. Dziêki wiadomoœciom w niej zawartych dowiesz
siê, jak modelowaæ zjawiska fizyczne za pomoc¹ komputera. Ka¿de z zagadnieñ jest
opisane zarówno od strony teoretycznej, jak i praktycznej — w postaci gotowego
algorytmu postêpowania.

D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\!Spis tresci.doc
- 3 -
Rozdział 1. Prędkość i przyspieszenie .................................................................................................................. 5
Rozdział 2. Składanie ruchów .................................................................................................................................. 11
Rozdział 3. Modelowanie zjawisk fizycznych ..................................................................................................43
Rozdział 4. Numeryczne całkowanie, czyli obliczanie pracy w polu grawitacyjnym
i natężenia skutecznego prądu ..................................................................................................... 95
Rozdział 5. Zadania różne ....................................................................................................................................... 105
Podsumowanie ...................................................................................................................................... 117
Skorowidz ................................................................................................................................................ 119

D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
- 105 -
W tym rozdziale rozwiążemy kilka zadań związanych z kursem fizyki w szkole ponad-
gimnazjalnej. Żeby rozwiązać tego typu zadania, nie potrzebujemy arkusza kalkulacyj-
nego, gdyż wykorzystujemy metody charakterystyczne dla fizyki. Zastosowanie arkusza
kalkulacyjnego pomoże natomiast wyeksponować ciekawe aspekty rozwiązań, których
bez zastosowania Excela z pewnością nie zauważylibyśmy.
Zadanie 1.
Wyznacz przyspieszenie, z jakim będzie poruszało się ciało o zadanej masie m, pokaza-
ne na rysunku 5.1, jeżeli zadano wartości współczynnika tarcia f masy o podłoże, kąta
a
i siły F.
Rysunek 5.1.
Rysunek pomocniczy
do 1. zadania
Rozwiązanie
Rozwiązanie tego zadania polega na uwzględnieniu wszystkich sił działających na ciało
podczas jego ruchu i zastosowaniu drugiej zasady dynamiki. Siłę F można rozłożyć na
dwie składowe: F
R
— równoległą do podłoża i F
P
— prostopadłą do podłoża, zatem
P
R
F
F
F
r
r
r
+
=
. Ciało porusza się pod działaniem sił F
R
i T (siła tarcia). Zatem z drugiej
zasady dynamiki Newtona otrzymamy:
Nf
F
T
F
ma
R
-
=
-
=
a
cos
106
Fizyka z komputerem dla liceum i technikum
- 106 -
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
gdzie N jest siłą nacisku, którą na podstawie rysunku 5.1 można przedstawić jako:
a
sin
F
mg
N
-
=
.
Podstawiając to ostatnie równanie do równania Newtona, po prostych przekształceniach
otrzymamy wzór określający zależność przyspieszenia od wartości działającej siły, kąta
nachylenia tej siły do podłoża i współczynnika tarcia:
m
fmg
f
F
a
-
+
=
)
sin
(cos
a
a
(5.1)
Ze wzoru (5.1) wynika, że przyspieszenie przy ustalonej wartości siły zależy od kąta
a
nachylenia tej siły do podłoża. Zbadajmy charakter tej zależności. W tym celu łatwo
zbudujmy odpowiedni wykres funkcji a(
a) przy ustalonej wartości współczynnika tar-
cia f. Musimy zarezerwować komórki do przechowywania wartości działającej siły F,
masy m, przyspieszenia ziemskiego g, wartości współczynnika tarcia f i wielkości
Da
określającej krok, z jakim będziemy zmieniać wartość kąta
a. Kąt a zmienia się
w przedziale [0
o
, 90
o
]. Wykres funkcji a(
a) sporządzimy dla następujących wartości pa-
rametrów: F = 20 N, m = 2 kg, g = 9,81 m/s
2
, f = 0,5,
Da
= 1
o
. Sporządzając wykres,
należy pamiętać, żeby funkcje trygonometryczne cos
a i sina wyrazić w stopniach, gdyż
standardowo Excel stosuje miarę łukową kąta, czyli radiany. Wykres określający zależ-
ność a(
a) przedstawiono na rysunku 5.2.
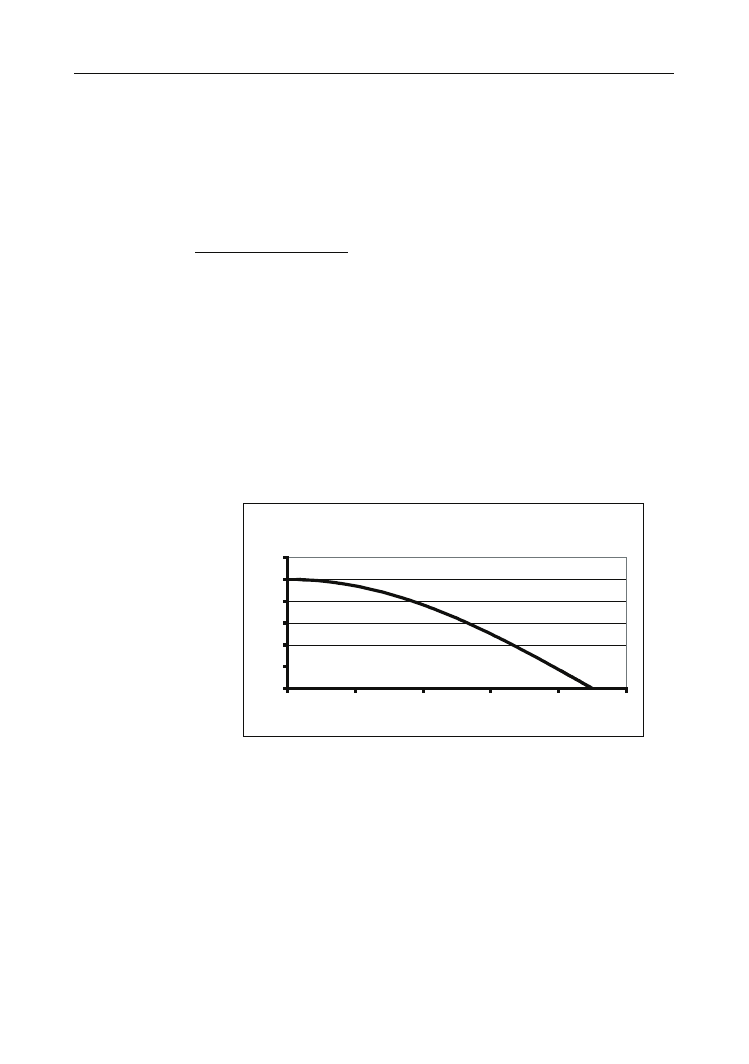
Rysunek 5.2.
Zależność
przyspieszenia od kąta
a dla F = 20 N,
m = 2 kg
,
g = 9,81 m/s
2
,
f = 0
, Da = 1
o
Zależność przyspieszenia od kąta nachylenia
0
2
4
6
8
10
12
0
20
40
60
80
100
kąt nachylenia
przyspieszenie
Z wykresu a(
a) widać, że przy braku tarcia przyspieszenie maleje monotonicznie od
wartości 10 m/s
2
do wartości 0 m/s
2
, co oznacza, że ciało nie porusza się. Jeśli pojawia
się tarcie, to dzięki wykresowi zależności a(
a) widać ciekawą własność przyspieszenia
— patrz rysunek 5.3.
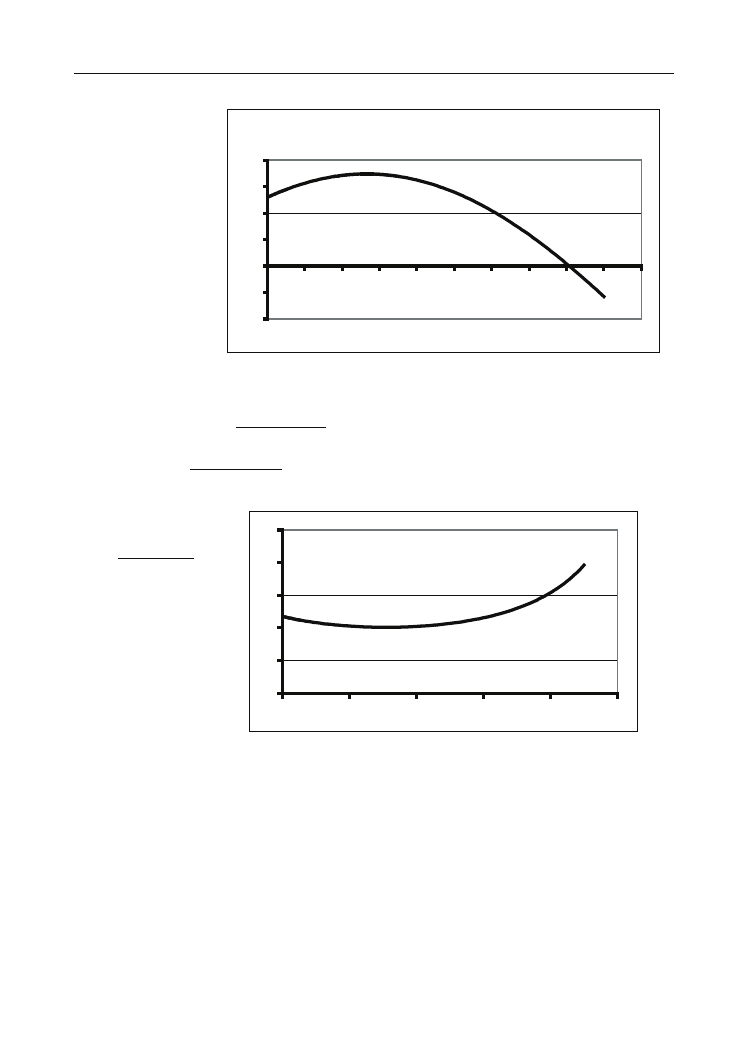
Dla wartości siły F = 15 N pojawia się ujemna wartość przyspieszenia. Przyspiesze-
nie ujemne w tym przypadku nie ma sensu fizycznego. Przyspieszenie ujemne ozna-
cza bowiem ruch w kierunku siły tarcia. Pojawienie się ujemnego przyspieszenia
oznacza, że należy nałożyć dodatkowe warunki na wartość działającej siły F. Ze wzo-
ru (5.1) wynika, że przy ustalonej wartości współczynnika tarcia f i masie poruszanego
Rozdział 5.
v Zadania różne
107
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
- 107 -
Rysunek 5.3.
Zależność
przyspieszenia od kąta
a dla F = 15 N,
m = 2 kg
,
g = 9,81 m/s
2
,
f = 0,6
, Da = 1
o
Zależność przyspieszenia od kąta nachylenia
-2
-1
0
1
2
3
4
0
10
20
30
40
50
60
70
80
90
100
kąt nachylenia
przyspieszenie
obiektu m, aby uzyskać sensowne fizycznie rozwiązania, musi być spełniony waru-
nek:
0
)
sin
(cos
>
-
+
fmg
f
F
a
a
. Oznacza to, że wartość działającej siły musi spełniać
warunek:
a
a
sin
cos
f
fmg
F
+
>
. Na rysunku 5.4 przedstawiono wykres zależności
a
a
a
sin
cos
)
(
f
fmg
f
+
=
dla wartości współczynnika tarcia f = 0,6 i masy m = 2 kg.
Rysunek 5.4.
Wykres zależności
a
a
a
sin
cos
)
(
f
fmg
f
+
=
dla wartości
współczynnika tarcia
f = 0,6 i masy m = 2 kg
0
5
10
15
20
25
0
20
40
60
80
100
Z wykresu widać, że aby rozwiązanie naszego zadania miało sens fizyczny dla wszyst-
kich kątów z przedziału [0
o
,90
o
] przy ustalonych wartościach masy ciała i współczynni-
ka tarcia, należy działać z siłą F większą niż 20 N. Przyjmując zatem wartość działającej
siły jako F = 25 N, otrzymamy dla wartości współczynnika tarcia f = 0,6 i masy m = 2 kg
następujący wykres zależności a(
a) — patrz rysunek 5.5.
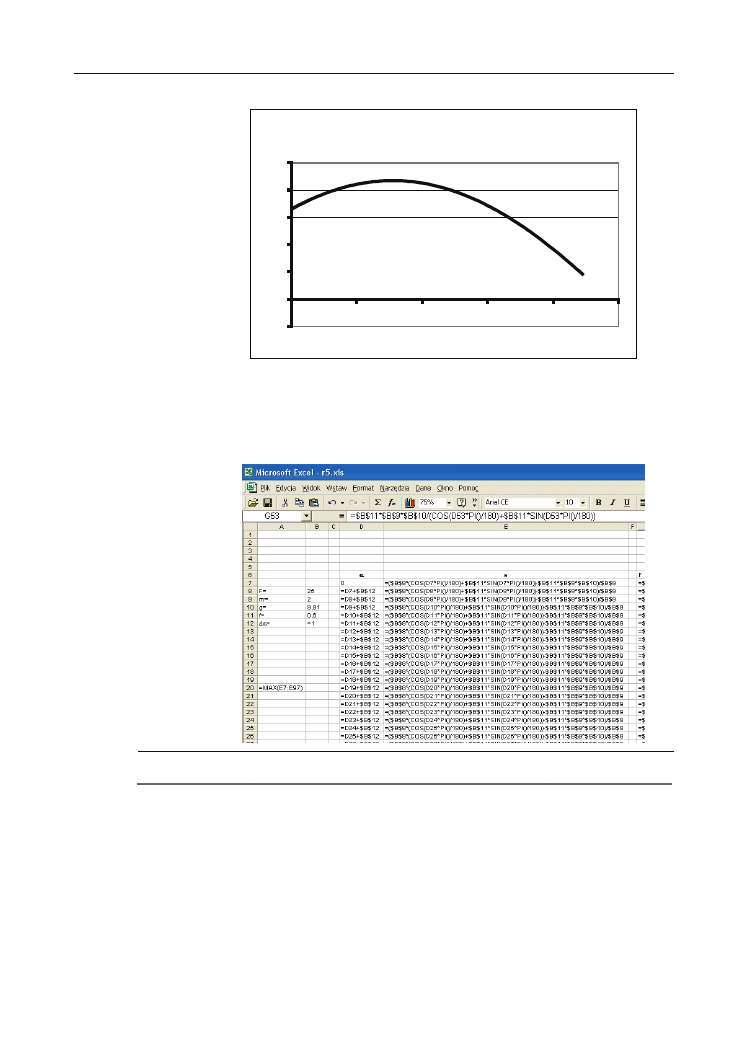
Z wykresu na rysunku 5.5 widać, że dla pewnej wartości kąta
a funkcja a(a) osiąga mak-
simum. Stosując funkcję Excela
max()
do kolumny arkusza zawierającej wartości funkcji
a(
a), otrzymamy wartość tego maksimum. Dla wartości F = 25 N, m = 2 kg, g = 9,81 m/s
2
,
108
Fizyka z komputerem dla liceum i technikum
- 108 -
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
Rysunek 5.5.
Zależność
przyspieszenia od kąta
a
dla
F = 25 N, m = 2 kg,
g = 9,81 m/s
2
, f = 0,6,
Da = 1
o
Zależność przyspieszenia od kąta nachylenia
-2
0
2
4
6
8
10
0
20
40
60
80
100
kąt nachylenia
przyspieszenie
f = 0,6,
Da = 1
o
maksimum to wynosi 8,69 m/s
2
i uzyskuje się je dla kąta
a = 31
o
.
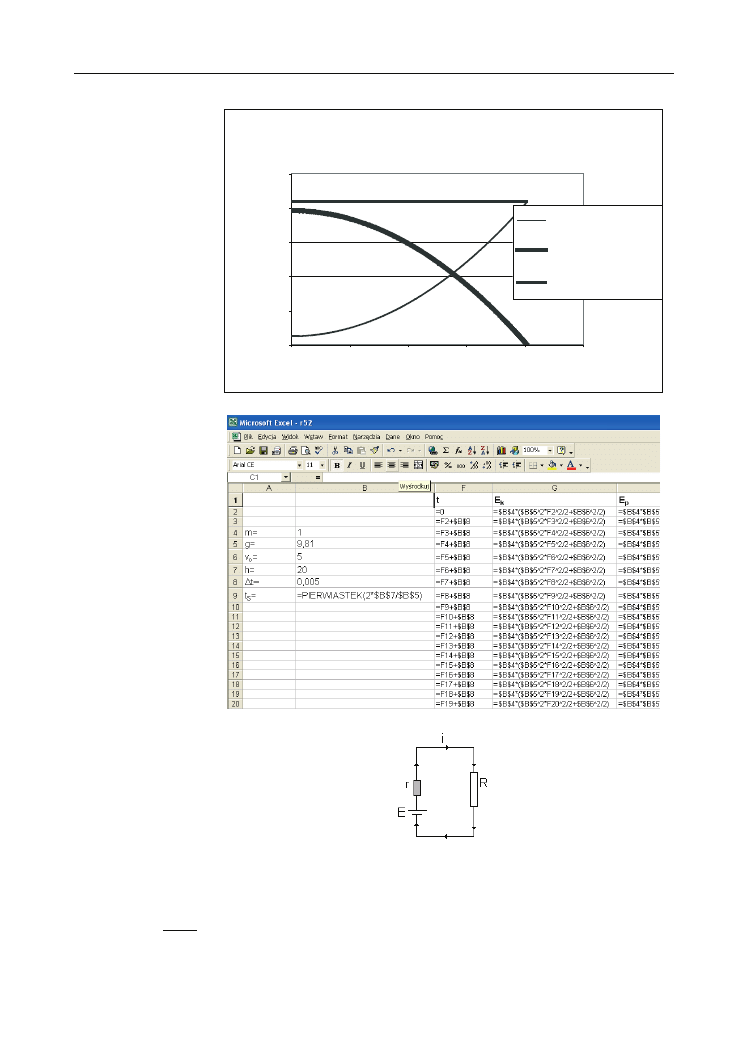
Zmieniając wartości odpowiednich parametrów, można dzięki sporządzonym wykre-
som znakomicie analizować zadanie. Wygląd arkusza w widoku formuł przedstawiono
na rysunku 5.6.
Rysunek 5.6.
Wygląd arkusza
w widoku formuł
Zadanie 2.
Zbadaj przemiany energii mechanicznej w rzucie poziomym.
Rozwiązanie
W tym ruchu całkowita energia mechaniczna jest zawsze sumą energii kinetycznej
i potencjalnej. Zakładamy oczywiście, że ruch zachodzi w warunkach, w których nie
istnieją żadne straty energii, czyli zaniedbujemy opory ruchu związane z tarciem czy oporem

Rozdział 5.
v Zadania różne
109
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
- 109 -
ośrodka. Całkowita energia mechaniczna E
C
jest więc sumą energii kinetycznej E
K
energii potencjalnej E
P
. Nietrudno obliczyć wartość tych energii. Po łatwych rachunkach
dojdziemy do wniosku, że:
)
2
1
(
)
(
2
gt
h
mg
t
E
P
-
=
(5.2)
2
)
(
)
(
2
2
2
t
g
v
m
t
E
o
K
+
=
(5.3)
gdzie m jest masą ciała, v
o
prędkością poziomą, g przyspieszeniem ziemskim, t oznacza
czas ruchu, h jest początkową wysokością ciała. Całkowita energia mechaniczna E
C
(t)
jest sumą energii potencjalnej i energii kinetycznej, czyli:
)
2
(
2
)
(
)
2
1
(
)
(
)
(
)
(
2
0
2
2
2
0
2
v
gh
m
t
g
v
m
gt
h
mg
t
E
t
E
t
E
K
P
C
+
=
+
+
-
=
+
=
(5.4)
Ze wzoru (5.4) wynika, że całkowita energia mechaniczna jest stała w czasie, gdyż za-
leży jedynie od wielkości, które są stałe w czasie. Otrzymujemy zatem zasadę zachowa-
nia energii mechanicznej. Korzystając z Excela, można sporządzić wykresy funkcji
E
P
(t), E
K
(t) i E
C
(t). Wykonanie wykresów nie jest zadaniem trudnym. Należy jedynie
zarezerwować komórki do przechowania wartości: m — masy ciała, v
o
— prędkości po-
ziomej, g — przyspieszenia ziemskiego,
Dt — kroku czasowego i h — początkowej
wysokości ciała. Ponadto trzeba utworzyć kolumny:
t
do przechowywania kolejnych
chwil czasowych zmieniających się z krokiem
Dt, E
P
(t) do przechowywania kolejnych
wartości energii potencjalnej wyznaczonych ze wzoru (5.2), E
K
(t) do przechowywania
kolejnych wartości energii kinetycznej wyznaczonych ze wzoru (5.3) i E
C
(t) do prze-
chowywania kolejnych wartości energii całkowitej wyznaczonych ze wzoru (5.4). Wy-
kresy funkcji E
P
(t), E
K
(t) i E
C
(t) przedstawiono na rysunku 5.7.
Aby uzyskać wykresy, takie jak na rysunku 5.7, trzeba wypełnić dla ustalonych warto-
ści m, g, h, v
0
i
Dt tylko tyle komórek kolumn
t
,
E
P
(t)
,
E
K
(t)
i
E
C
(t)
, aby całkowity czas
spadania nie przekroczył wartości
g
h
t
S
2
=
, czyli czasu swobodnego spadku z wyso-
kości h. Wygląd arkusza w widoku formuł do ilustracji zasady zachowania energii
przedstawiono na rysunku 5.8.
Zadanie 3.
Źródło prądu o sile elektromotorycznej E i oporze wewnętrznym r włączono w obwód
w sposób, taki jak na rysunku 5.9. Oblicz, jaki powinien być opór odbiornika podłączo-
nego do źródła, aby można było uzyskać określoną moc PRO przy możliwie największej
sprawności.
110
Fizyka z komputerem dla liceum i technikum
- 110 -
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
Rysunek 5.7.
Zasada zachowania
energii mechanicznej.
Wykresy otrzymano
dla wartości
: m = 1 kg,
g = 9,81 m/s
2
,
v
0
= 5 m/s
, h = 20 m,
Dt = 0,005 s
Energia kinetyczna i potencjalna w rzucie poziomym
0
50
100
150
200
250
0
0,5
1
1,5
2
2,5
czas[t]
energia w funkcji czasu
Energia kinetyczna
Energia potencjalna
Energia całkowita
Rysunek 5.8.
Wygląd arkusza
w widoku formuł
do ilustracji zasady
zachowania energii
Rysunek 5.9.
Obwód elektryczny
ze źródłem siły
elektromotorycznej E
Rozwiązanie
W obwodzie, na podstawie prawa Ohma dla całego obwodu, płynie prąd o natężeniu
r
R
E
i
+
=
. Moc P
R
uzyskana w odbiorniku o oporze R wynosi
R
i
P
R
2
=
. Korzystając ze
Rozdział 5.
v Zadania różne
111
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
- 111 -
wzoru na natężenie prądu, otrzymamy wzór określający zależność mocy P
R
od wartości
oporu zewnętrznego R:
2
2
)
(
r
R
R
E
P
R
+
=
(5.5)
Korzystając z Excela można sporządzić wykres zależności P
R
(R). Jako jednostkę osi x
przyjmiemy wielokrotności oporu wewnętrznego r. Wykres przedstawiono na rysun-
ku 5.10.
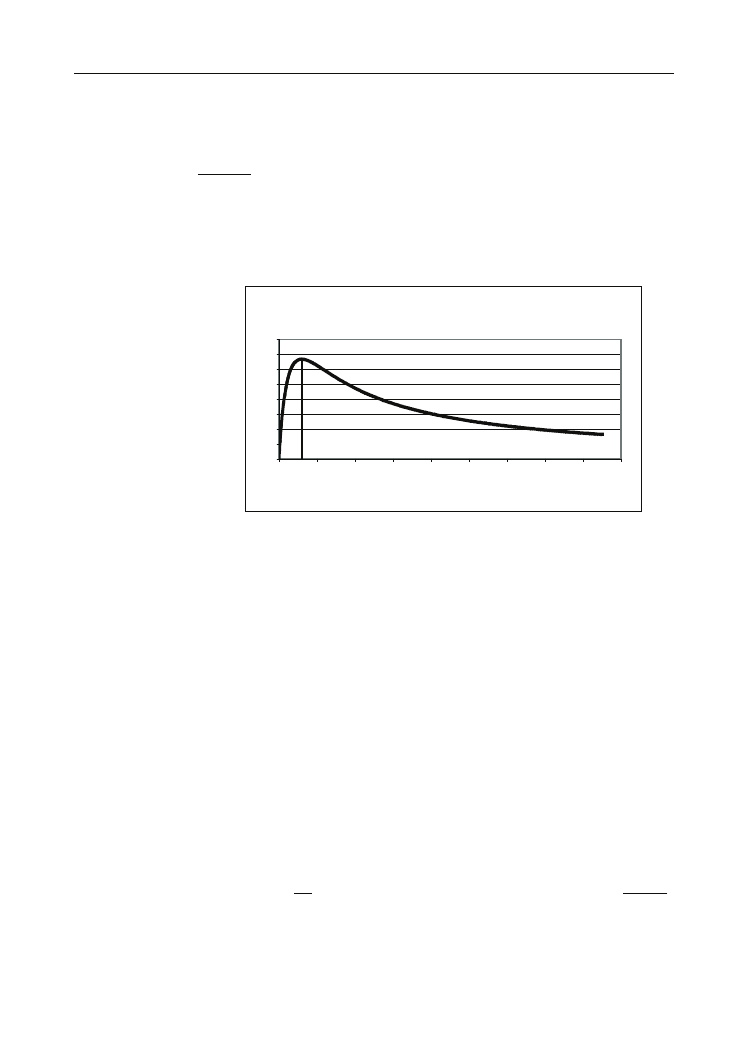
Rysunek 5.10.
Wykres zależności
P
R
(R)
. E=20V, r=100W
Moc w funkcji oporu zewnętrznego
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0
500
1000
1500
2000
2500
3000
3500
4000
4500
opór zewnętrzny
Pionową linię na wykresie poprowadzono w punkcie o współrzędnej R = r. Wykres P
R
(R)
na rysunku 5.10 posiada ciekawe własności. Widać, że dla pewnej wartości oporu ze-
wnętrznego osiąga maksimum. Korzystając z funkcji Excela
max()
zastosowanej do kolum-
ny, w której przechowujemy wartości P
R
(R), można to maksimum wyznaczyć. Dla
wartości siły elektromotorycznej E = 20 V i wartości oporu wewnętrznego r = 100
W funk-
cja P
R
(R) osiąga maksimum 1 dla wartości oporu zewnętrznego R = 100
W. Jest to
ogólna prawidłowość, którą można udowodnić, wyznaczając warunek ekstremum funkcji
P
R
(R) przy użyciu zasad rachunku różniczkowego. Okaże się, że zawsze wartość
)
(
.
max
R
P
R
funkcja P
R
(R) osiąga dla R = r, czyli wtedy, gdy opór zewnętrzny jest równy
oporowi wewnętrznemu. Druga własność funkcji P
R
(R) to taka, że zadaną wartość mocy
P
R0
funkcja osiąga dla dwóch wartości oporu zewnętrznego. Jedna z nich to R
1
<r, a druga
— R
2
>r. Ten sam wniosek można uzyskać, rozwiązując równanie (5.5) jako równanie
kwadratowe względem R. Okaże się, że ma ono dwa pierwiastki spełniające powyższe
zależności. W zadaniu należy wybrać taką wartość oporu zewnętrznego, aby określoną
wartość mocy uzyskać przy największej sprawności. Należy zatem sporządzić wykres
zależności sprawności od wartości oporu zewnętrznego —
)
(R
h
i porównać obie wartości
)
(
1
R
h
i
)
(
2
R
h
. Warunki zadania spełnia większa z nich. Ponieważ moc w obwodzie wy-
dziela się na obu oporach, zewnętrznym i wewnętrznym, więc przez sprawność
h rozumie-
my stosunek mocy uzyskanej w odbiorniku zewnętrznym do całej mocy uzyskanej
w obwodzie, czyli
P
P
R
R
=
)
(
h
. Korzystając ze wzoru (5.5) oraz ze wzoru
)
(
2
r
R
E
iE
P
+
=
=
otrzymamy następującą zależność sprawności od oporu zewnętrznego:
112
Fizyka z komputerem dla liceum i technikum
- 112 -
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
r
R
R
R
+
=
)
(
h
(5.6)
Wykres zależności (5.6) przedstawiono na rysunku 5.11.
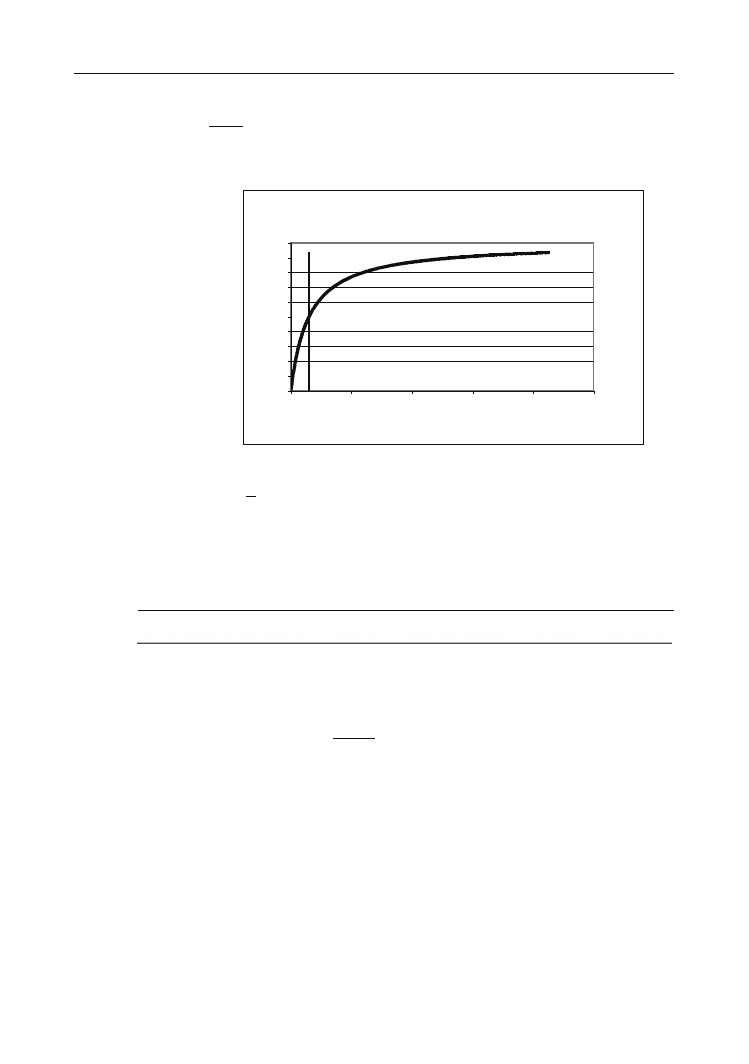
Rysunek 5.11.
Sprawność w funkcji
oporu zewnętrznego
Sprawność w funkcji oporu zewnętrznego
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0
1000
2000
3000
4000
5000
opór zewnętrzny
sprawność
Pionową linię na wykresie poprowadzono w punkcie o współrzędnej R = r. Z wykresu
widać, że
2
1
)
( =
r
h
, a
1
)
( =
¥
®
R
lim
R
h
. Poza tym z wykresu na rysunku 5.11 wynika, że im
wartość oporu zewnętrznego jest większa, tym sprawność rośnie. Zatem wtedy, gdy
mamy podaną wartość P
R0
mocy, jaką chcemy uzyskać na zewnętrznym oporze, tak aby
uzyskać największą sprawność, to należy wybrać zawsze większą wartość oporu. Dla
maksymalnej mocy sprawność wynosi zawsze ½. Wygląd arkusza kalkulacyjnego w wi-
doku formuł do rozwiązania zadania 3. przedstawiono na rysunku 5.12.
Zadanie 4.
Sporządź wykres wartości natężenia i potencjału pola grawitacyjnego w punktach leżą-
cych na symetralnej odcinka łączącego środki dwóch kul o masach m
1
= m
2
i m = 10
10
kg
w funkcji odległości od tego odcinka. Odległość między środkami kul wynosi 2a = 106 m.
Stała grawitacji
2
2
11
10
67
,
6
kg
m
N
G
×
×
=
-
.
Rozwiązanie
Natężenie pola grawitacyjnego wyznaczymy, korzystając z zasady superpozycji. To
znaczy najpierw wyznaczymy natężenie pola, tak jakby źródłem pola była tylko jedna
kula, a następnie oba wektory dodamy — patrz rysunek 5.13.

Rozdział 5.
v Zadania różne
113
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
- 113 -
Rysunek 5.12.
Wygląd arkusza
kalkulacyjnego
w widoku formuł
do rozwiązania 3.
zadania
Rysunek 5.13.
Rysunek pomocniczy
do 4. zadania
Niech x oznacza odległość dowolnego punktu leżącego na symetralnej odcinka łączące-
go środki obu kul od tego odcinka. Wówczas odległość tego punktu od środka kuli wy-
nosi
2
2
x
a
r
+
=
, gdzie a jest połową odcinka łączącego środki obu kul. Natężenie
pola grawitacyjnego
g
r
jest z definicji wektorem o wartości równej
m
F
r
r
=
g
, gdzie
F
r
jest siłą grawitacji działającą w danym punkcie pola, a pochodzącą od jednej i drugiej
kuli, m jest masą próbną umieszczoną w danym punkcie pola. Zatem natężenie wypad-
kowe
w
g
r
jest wektorem
2
1
g
g
g
r
r
r
+
=
w
. Na podstawie rysunku 5.13, wykorzystując od-
powiednie zależności geometryczne i definicję natężenia pola grawitacyjnego, otrzy-
mamy:
2
3
2
2
2
2
2
2
2
1
)
(
2
2
cos
2
cos
2
x
a
x
Gm
x
a
x
x
a
Gm
r
Gm
w
+
×
=
+
×
+
=
=
=
a
a
g
g
(5.7)
114
Fizyka z komputerem dla liceum i technikum
- 114 -
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
Potencjał jest wielkością skalarną, której wartość w polu grawitacyjnym można obli-
czyć jako
m
E
V
p
-
=
, gdzie E
p
jest energią potencjalną w danym punkcie pola, natomiast
m jest masą próbną w danym punkcie pola. Korzystając z definicji energii potencjalnej
w polu grawitacyjnym, potencjał w danym punkcie pola można wyrazić jako:
r
Gm
V -
=
, gdzie teraz m jest masą źródła pola grawitacyjnego, a r jest odległością ma-
sy próbnej od źródła pola. W naszym zadaniu, z uwagi na to, że występują dwa źródła
pola grawitacyjnego, całkowity potencjał jest równy:
2
2
2
1
2
x
a
Gm
V
V
V
+
-
=
+
=
(5.8)
Na podstawie wzorów (5.7) i (5.8) sporządzimy odpowiednie wykresy. Rysunek 5.14
przedstawia zależność
)
(x
g
, natomiast rysunek 5.15 przedstawia zależność
)
(x
V
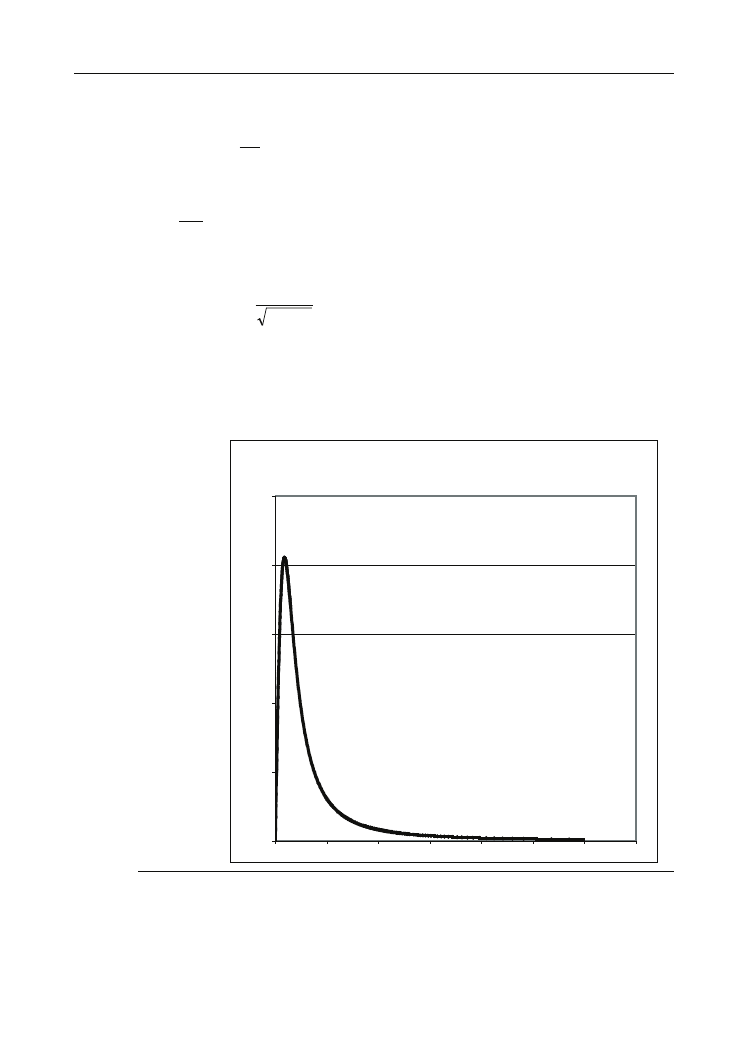
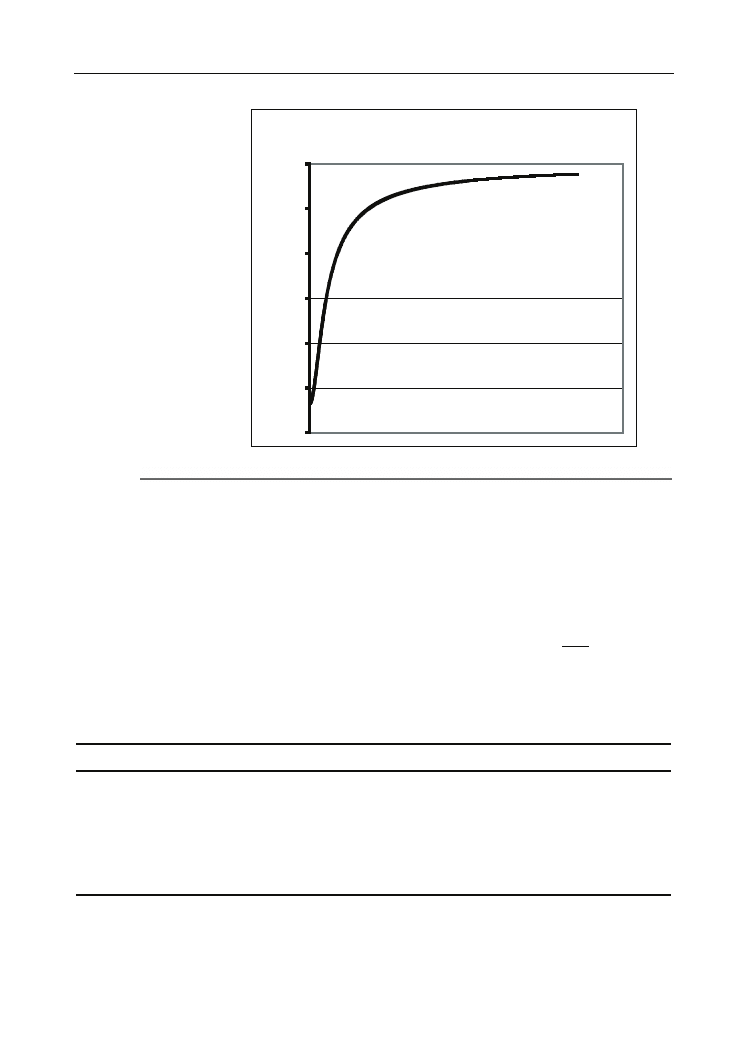
. Z wy-
kresu wynika, że natężenie pola początkowo rośnie liniowo, a następnie maleje. Poten-
cjał natomiast cały czas rośnie, jednak wzrost ten nie jest liniowy.
Rysunek 5.14.
Zależność natężenia
pola grawitacyjnego
od położenia
na symetralnej odcinka
łączącego obie kule
Natężenie pola grawitacyjnego
0
5E-13
1E-12
1,5E-12
2E-12
2,5E-12
0
2000000
4000000
6000000
8000000
10000000 12000000 14000000
Rozdział 5.
v Zadania różne
115
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
- 115 -
Rysunek 5.15.
Zależność potencjału
pola grawitacyjnego
od położenia na
symetralnej odcinka
łączącego obie kule
Potencjał pola grawitacyjnego
-0,000003
-0,0000025
-0,000002
-0,0000015
-0,000001
-0,0000005
0
Zadanie 5.
To zadanie pokaże zalety Excela w zakresie opracowania wyników pomiarów. Załóżmy,
że chcemy wyznaczyć stałą sprężystości sprężyny.
Rozwiązanie
Zadanie to można rozwiązać, wykonując odpowiednie pomiary. Jeśli bowiem wyzna-
czymy zależność
)
(
2
m
T
, gdzie T jest kwadratem okresu drgań sprężyny obciążonej
masą m, to współczynnik sprężystości k wyznaczymy ze wzoru
a
k
2
4p
=
, gdzie a jest
współczynnikiem kierunkowym prostej
)
(
2
m
T
. Załóżmy, że wykonując pomiary,
otrzymaliśmy wyniki przedstawione w tabeli 5.1.
Tabela 5.1. Przykładowe wyniki pomiarów
m (kg)
T (s)
T
2
(s2)
DT (s)
DT
2
(s)
0,05
0,34
0,12
0,02
0,04
0,1
0,46
0,21
0,02
0,04
0,15
0,54
0,29
0,02
0,04
0,20
0,64
0,41
0,02
0,04
0,25
0,72
0,52
0,02
0,04
W tabeli 5.1 kolumna 1. zawiera wyniki pomiarów masy, kolumna 2. — wyniki pomia-
rów okresu drgań, kolumna 3. to kwadrat okresu, kolumny 4. i 5. zawierają wartości
116
Fizyka z komputerem dla liceum i technikum
- 116 -
D:\! AAA DZISIAJ\Fizyka z komputerem dla liceum i technikum\21 druk\r05.doc
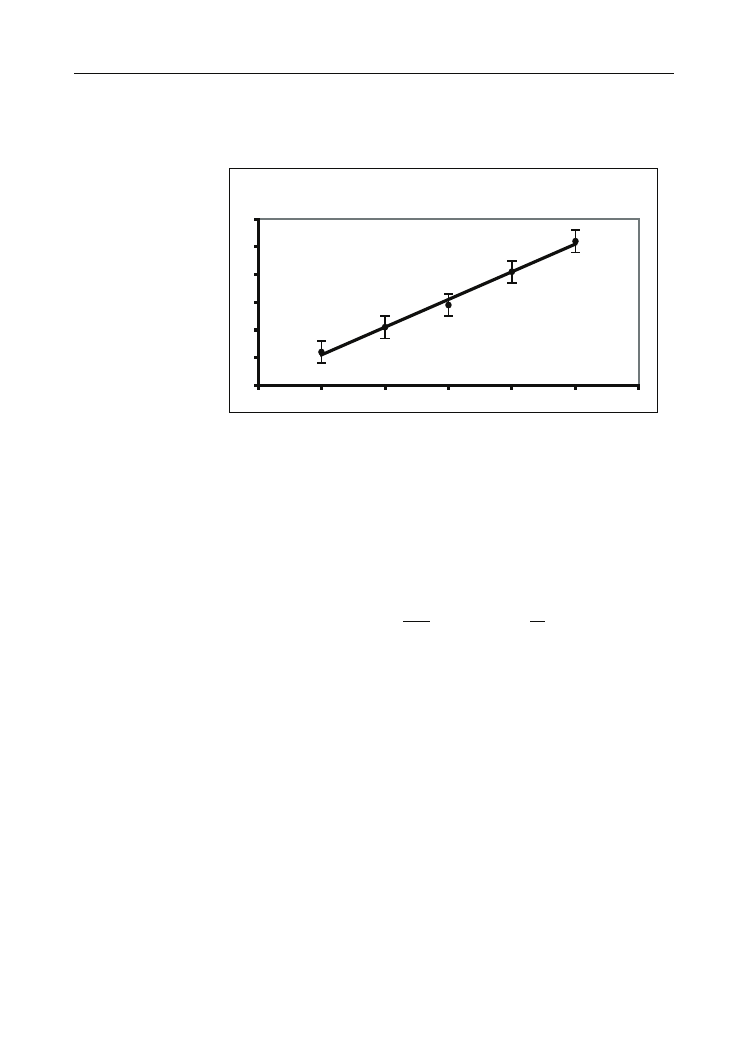
błędu pomiarowego. Wykres
)
(
2
m
T
sporządzony na podstawie wyników pomiarów
wziętych z kolumn 1. i 3. przedstawiono na rysunku 5.16.
Rysunek 5.16.
Zależność
)
(
2
m
T
Zależność kwadratu okresu drgań sprężyny od masy
y = 2x + 0,01
0
0,1
0,2
0,3
0,4
0,5
0,6
0
0,05
0,1
0,15
0,2
0,25
0,3
Wykres na rysunku 5.16 uzyskano, wykorzystując następujące możliwości Excela 2000.
Wykres wykonujemy na podstawie danych uzyskanych z pomiaru. Wybieramy grupę
XY(Punktowy)
. Następnie korzystając z opcji
Formatuj serię danych
, wybieramy opcję
słupki błędów Y
. Nie wybieramy opcji
słupki błędów X
, gdyż dokładność pomiaru ma-
sy jest dużo większa niż dokładność pomiaru czasu. W opcji
słupki błędów Y
ustawia-
my odpowiednie wartości błędu, a następnie wybieramy opcję
Dodaj linię trendu
.
Zostanie wówczas wykreślona prosta, która jest najlepszym dopasowaniem do punktów
pomiarowych naniesionych na wykres. Można jeszcze wyświetlić równanie tej prostej,
uzyskując tym samym wartość współczynnika kierunkowego prostej. W naszym przy-
kładzie współczynnik kierunkowy tej prostej wynosi 2. Stąd doświadczalnie wyznaczo-
na wartość współczynnika k wynosi:
m
N
k
73
,
19
2
2
4
2
2
»
×
=
=
p
p
. Excel ma również
możliwość tworzenia wykresów w skali logarytmicznej. W takiej skali wykresem funk-
cji wykładniczej jest linia prosta. Ułatwia to analizę takich danych doświadczalnych,
które prowadzą do wykładniczej zależności badanych wielkości.
Wyszukiwarka
Podobne podstrony:
Fizyka z komputerem dla liceum i technikum fizkol
Fizyka z komputerem dla liceum i technikum 2
Fizyka z komputerem dla liceum i technikum
Matematyka z komputerem dla liceum i technikum 2
Matematyka z komputerem dla liceum i technikum matlit
Matematyka z komputerem dla liceum i technikum
matematyka 2 podrecznik dla liceum i technikum zakres rozszerzony rozdzial 5 ciagi pdf
Młoda Polska dla liceum i technikum, Pisma
Od XV w do kongresu wiedeńskiego Teksty źródłowe z ćwiczeniami dla liceum i technikum
matematyka 2 podrecznik dla liceum i technikum zakres rozszerzony rozdzial 2 wielomiany pdf
matematyka 2 podrecznik dla liceum i technikum zakres rozszerzony rozdzial 7 statystyka pdf
matematyka 2 podrecznik dla liceum i technikum zakres rozszerzony rozdzial 6 figury podobne pdf
matematyka 2 podrecznik dla liceum i technikum zakres rozszerzony rozdzial 1 potegi pierwiastki i lo
Od XV w do kongresu wiedeńskiego Teksty źródłowe z ćwiczeniami dla liceum i technikum(1)
więcej podobnych podstron