Matlab – środowisko obliczeń numerycznych
• Nazwa Matlab pochodzi od matrix laboratory.
• Jest to język wysokiego poziomu, w którym polecenia są sekwencyjnie interpretowane.
• Kolejne instrukcje wpisywane są w wierszu poleceń specjalnego edytora (command window).
Wykonanie prostych instrukcji następuje po wpisaniu w edytorze nazwy instrukcji i naciśnięciu
klawisza Enter. Wykonanie pętli bądź instrukcji warunkowych (for, while, if, switch)
następuje po zamknięciu bloku instrukcji słowem end i wciśnięciu klawisza Enter.
• Ciągi instrukcji można umieszczać w funkcjach lub skryptach, będących plikami o nazwach
[nazwa].m, po czym wykonywać zawarte w nich instrukcje wpisując w edytorze poleceń
[nazwa] i wciskając Enter.
• Podstawowym typem danych jest macierz, tzn. domyślnym argumentem wejściowym funkcji
(poleceń) jest macierz o nieustalonych z góry rozmiarach i wymiarze.
• Zmienne są inicjalizowane przez przypisanie im wartości (ogólnie macierzy liczbowej), zaś
usuwane są z pamięci poleceniem clear [nazwa_zmiennej].
• Rozmiary zmiennych są dynamicznie skalowane w trakcie wykonywania programu.
Przypisanie wartości elementowi macierzy o indeksie, którego dana zmienna nie obejmowała,
powoduje zwiększenie rozmiaru macierzy.
• Nie operuje się na adresach zmiennych, zaś argumenty są przekazywane do funkcji poprzez
wartość (por. z C, gdzie tablice przekazywane były poprzez referencję). Aby uniknąć
kopiowania zmiennych przy przekazywaniu ich do funkcji, można użyć zmiennych globalnych.
Matlab – deklarowanie zmiennych i przypisywanie wartości
• zadeklarujmy zmienną skalarną (macierz 1x1), np:
» X=1
X =
1
»
umieszczenie średnika na
końcu instrukcji powoduje, iż
wartość zmiennej nie zostaje
wyświetlona
» X=1;
»
znak
zachęty
kolejny
znak
zachęty
• możemy rozszerzyć zadeklarowaną powyżej zmienną X np. do macierzy 3x3 instrukcją:
» X(3,3)=2
X =
1 0 0
0 0 0
0 0 2
możemy jeszcze zwiększyć liczbę wymiarów, tworząc macierz 3x3x2 następująco:
» X(3,1,2)=5
X(:,:,1) =
1 0 0
0 0 0
0 0 2
X(:,:,2) =
0 0 0
0 0 0
5 0 0
operator : symbolizuje
wszystkie indeksy
danego wymiaru
zbadajmy rozmiar macierzy X:
» size(X)
ans =
3 3 2
Matlab – właściwości nazw zmiennych
• rozpoznawane są małe i wielkie litery
• nazwy mogą się składać maksymalnie z 31 znaków, znaki powyżej tej granicy są
ignorowane
• nazwy muszą się zaczynać od liter, kolejne znaki mogą być literami, cyframi lub
podkreśleniami: „ _ ”
• nazwy nie mogą być tożsame ze słowami kluczowymi języka. Zastrzeżonymi
sekwencjami znaków są:
• nazwy nie powinny pokrywać się z nazwami funkcji, jakich użytkownik będzie miał zamiar
używać po zadeklarowaniu zmiennej. Np. deklaracja clear=4; zablokuje dostęp do
funkcji clear usuwającej wszystkie zmienne z pamięci. Wywołanie „ clear” jedynie
spowoduje wyświetlenie:
zaś wywołanie „clear;” w ogóle niczym się nie objawi
• nazwy zmiennych nie powinny pokrywać się z nazwami zmiennych specjalnych
break case catch continue else elseif end for function
global if otherwise persistent return switch try while
clear =
4
Matlab – wybrane zmienne specjalne
liczba argumentów wejściowych funkcji, lista argumentów wejściowych funkcji
nargin,
varargin
liczba argumentów wyjściowych funkcji, lista argumentów wyjściowych funkcji
nargout,
varargout
największa dodatnia całkowita liczba w formacie zmiennoprzecinkowym, najczęściej
2
53
-1, dla liczb większych od bitmax nie ma gwarancji, iż po dodaniu 1 zmienią swoją
wartość, np.
» bitmax + 5 == bitmax + 6
ans =
1
bitmax
największa dodatnia liczba zmiennoprzecinkowa
realmax
najmniejsza dodatnia liczba zmiennoprzecinkowa
realmin
jednostka urojona, np. » sqrt(-1)
ans =
0 + 1.0000i
i lub j
symbol nieoznaczony, np. 0/0, 0*inf, inf/inf, 0*NaN
NaN lub nan
nieskończoność, np. 1/0, 1.1*realmax, 2*inf
Inf lub inf
określa precyzję pewnych obliczeń, np. rzędu macierzy
eps
stosunek obwodu koła do jego średnicy
pi
przechowuje wynik ostatnio obliczonego wyrażenia, jeżeli wynik ten nie był
przypisany do żadnej innej zmiennej, np.
» 2+2
ans =
4
ans
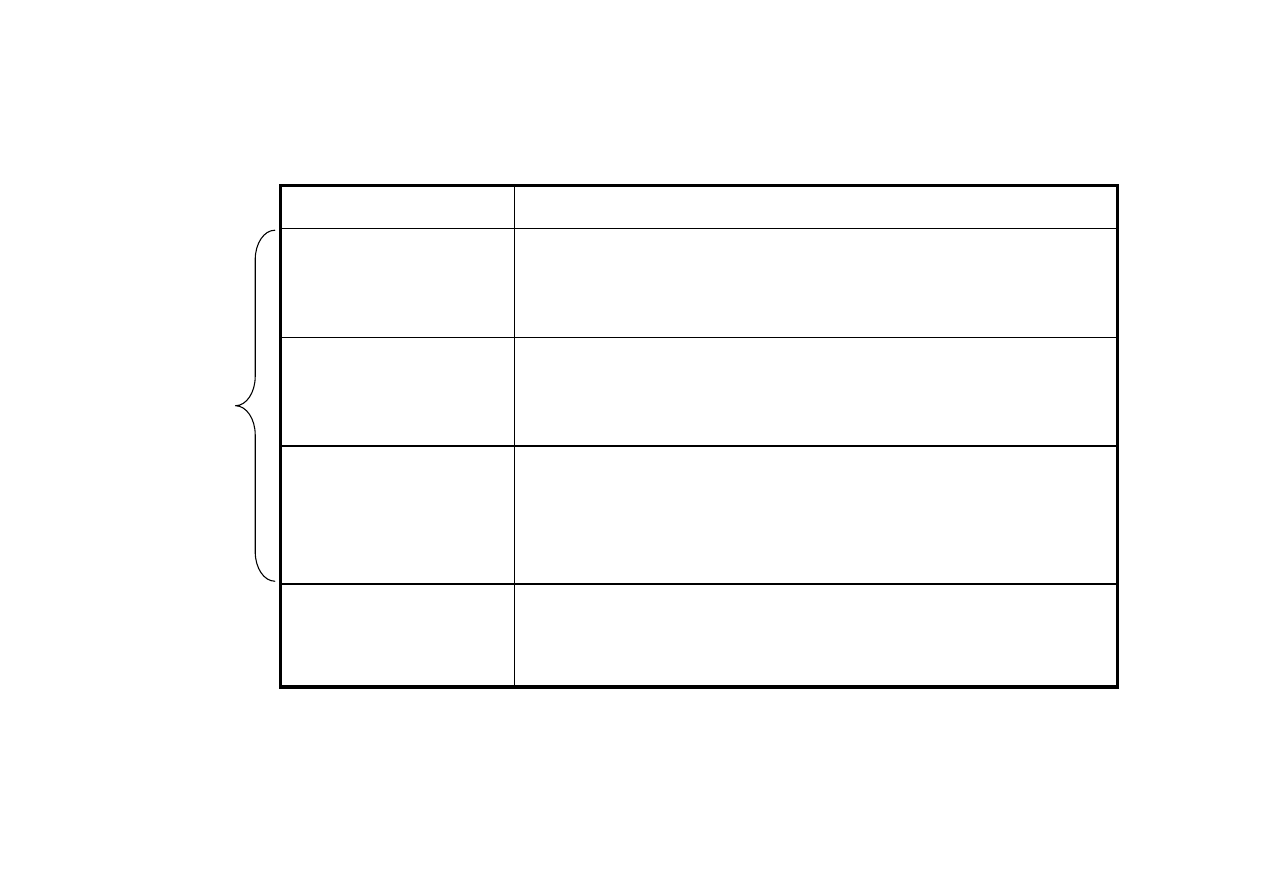
funkcja clear przywraca domyślne wartości zmiennych
przedstawionych w wierszach od 1 do 9 tabeli
Matlab – działania na macierzach (1)
• ręczne wprowadzanie elementów macierzy:
• elementy można także odczytać z pliku dyskowego, Matlab domyślnie tworzy nową
zmienną o nazwie identycznej z nazwą pliku bez rozszerzenia.
• macierz może zostać zapisana jako wartość wyjściowa funkcji, np:
• sposoby odwoływania się do elementów macierzy (indeksowania):
» A=[1 2 3; 4 5 6; 7 8 9]
A =
1 2 3
4 5 6
7 8 9
średniki oddzielają
wiersze
odstępy (lub przecinki)
oddzielają kolumny
» load proba.txt
» who
Your variables are:
proba
w pliku tekstowym umieszcza się liczby
oddzielone spacjami (lub przecinkami)
oraz znakami nowej linii
» A=rand(2,3)
A =
0.4565 0.8214 0.6154
0.0185 0.4447 0.7919
(2,3)
6
(2,2)
4
(2,1)
2
(1,3)
5
(1,2)
3
(1,1)
1
» A(6)
ans =
0.7919
» A(2,3)
ans =
0.7919
poprzez podanie
numeru wiersza i
kolumny:
poprzez
indeksowanie
liniowe:
Próba odwołania się do nieistniejącego elementu, np
» A(3,3)
zakończy się wyświetleniem
komunikatu o błędzie:
???
Index exceeds matrix dimensions.
Matlab – działania na macierzach (2)
•
działania wykonywane element po elemencie:
operandy muszą być tych samych rozmiarów
• działania oparte na algebrze macierzy:
+
-
.*
./
.\
.^
*
/
\
^
‘
prawostronne
dzielenie macierzy
A/B = A*(B^-1)
lewostronne
dzielenie macierzy
A\B = (A^-1)*B
transpozycja
macierzy
Należy zwrócić uwagę, aby nie pomylić funkcji pobierających jako argumenty wejściowe macierze,
ale liczących element po elemencie, z funkcjami macierzy wykorzystującymi algebrę macierzy.
Rozważmy następujący przykład. Funkcja
polyval(
p
,
x
)
zwraca wartość wielomianu o
współczynnikach zawartych w wektorze
p
w punkcie
x
w następujący sposób:
polyval(p,x)= p
1
x
n-1
+ p
2
x
n-2
+ ... + p
n-1
x
1
+ p
n
x
0
gdzie
n
to rozmiar wektora
p
, zaś stopień zdefiniowanego przez ten wektor wielomianu to
n-1
.
Pierwszy element wektora
p
jest współczynnikiem przy najwyższej potędze. Prosty przykład
zastosowania to np.
Jeżeli jako drugi argument funkcji
polyval
podamy macierz, obliczenia zostaną wykonane element
po elemencie, np:
» A=[0 0 1; 0 1 0; 0 0 1]
A =
0 0 1
0 1 0
0 0 1
» polyval([1 2 3],A)
ans =
3 3 6
3 6 3
3 3 6
» polyval([1 2 3],2)
ans =
11
ponieważ
1·2
2
+ 2·2
1
+ 3·2
0
= 4 + 4 + 3 = 11
Inaczej zachowuje się funkcja
polyvalm
, która obliczy wartość
wielomianu podnosząc macierze do odpowiednich potęg:
polyvalm(p,X)= p
1
X
n-1
+ p
2
X
n-2
+ ... + p
n-1
X
1
+ p
n
X
0
Analogicznie zachowują się funkcje exp i expm
» A=[0 0 1; 0 1 0; 0 0 1]
A =
0 0 1
0 1 0
0 0 1
» polyvalm([1 2 3],A)
ans =
3 0 3
0 6 0
0 0 6
Matlab – funkcje macierzy
Matlab – operatory relacji
warunek uzyskania 1 w wyniku
operacja
A równe B
A == B
A mniejsze lub równe B
A <= B
A większe lub równe B
A >= B
A mniejsze od B
A < B
A większe od B
A > B
A różne od B
A ~= B
przykład:
» A=[1 2; 3 4]
A =
1 2
3 4
» B=[4 1; 3 2]
B =
4 1
3 2
» A>=B
ans =
0 1
1 1
Macierze A i B muszą być tych samych rozmiarów.
Operatory relacji porównują odpowiadające sobie
elementy macierzy i zapisują wynik do nowej macierzy,
wypełnionej wyłącznie wartościami 0 lub 1.
Operatory relacji porządkujących mają sens tylko dla
liczb rzeczywistych. W przypadku czterech ostatnich
operatorów Matlab porównuje części rzeczywiste liczb.
Matlab – operatory i funkcje logiczne dwuargumentowe
opis
operacja
zwracana jest macierz, której element (i, j) jest równy
• 0 – jeżeli A(i, j) · B(i, j)
=0
• 1 – w przeciwnym wypadku
A & B
zwraca 1 jeżeli wszystkie elementy A są równe
odpowiadającym im elementom macierzy B
(tzn. sprawdza, czy A
=B)
isequal(A, B)
zwracana jest macierz, której element (i, j) jest równy
• 0 – jeżeli A(i, j)
=0 oraz B(i, j)=0 lub jeżeli A(i, j)−0
oraz B(i, j)
−0
• 1 – w przeciwnym wypadku
xor(A,B)
zwracana jest macierz, której element (i, j) jest równy
• 0 – jeżeli A(i, j)
=0 oraz B(i, j)=0
• 1 – w przeciwnym wypadku
A | B
A i B muszą
być tych
samych
rozmiarów
Matlab – operatory i funkcje logiczne jednoargumentowe
zwracany jest wektor, którego n-ta współrzędna przyjmuje
wartość: 1 – jeżeli w n-tej kolumnie macierzy A wszystkie
wartości są niezerowe; 0 – w przeciwnym wypadku
all(A)
zwraca wartość 1, jeżeli macierz A jest pusta, np.
isempty(A)
zwracany jest wektor, którego n-ta współrzędna przyjmuje
wartość: 1 – jeżeli w n-tej kolumnie macierzy A wszystkie
wartości są niezerowe; 0 – w przeciwnym wypadku
all(A)
zwracany jest wektor, którego n-ta współrzędna przyjmuje
wartość: 1 – jeżeli w n-tej kolumnie macierzy A wystąpiła
choć jedna niezerowa wartość; 0 – w przeciwnym wypadku
any(A)
zwraca wektor kolumnowy zawierający liniowe indeksy
niezerowych elementów, np:
find(A)
zwracana jest macierz, której element (i, j) jest równy
• 0 – jeżeli A(i, j)
−0
• 1 – jeżeli A(i, j)
=0
~A
» A=[0 1 2; 0 i 1]
A =
0 1.0000 2.0000
0 0 + 1.0000i 1.0000
» find(A)'
ans =
3 4 5 6
» A=ones(0)
A =
[]
» isempty(A)
ans =
1
Matlab – wizualizacja wektorów
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-1
-0.5
0
0.5
1
-1
-0.5
0
0.5
1
0
5
10
15
20
0
1
2
3
4
5
6
7
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
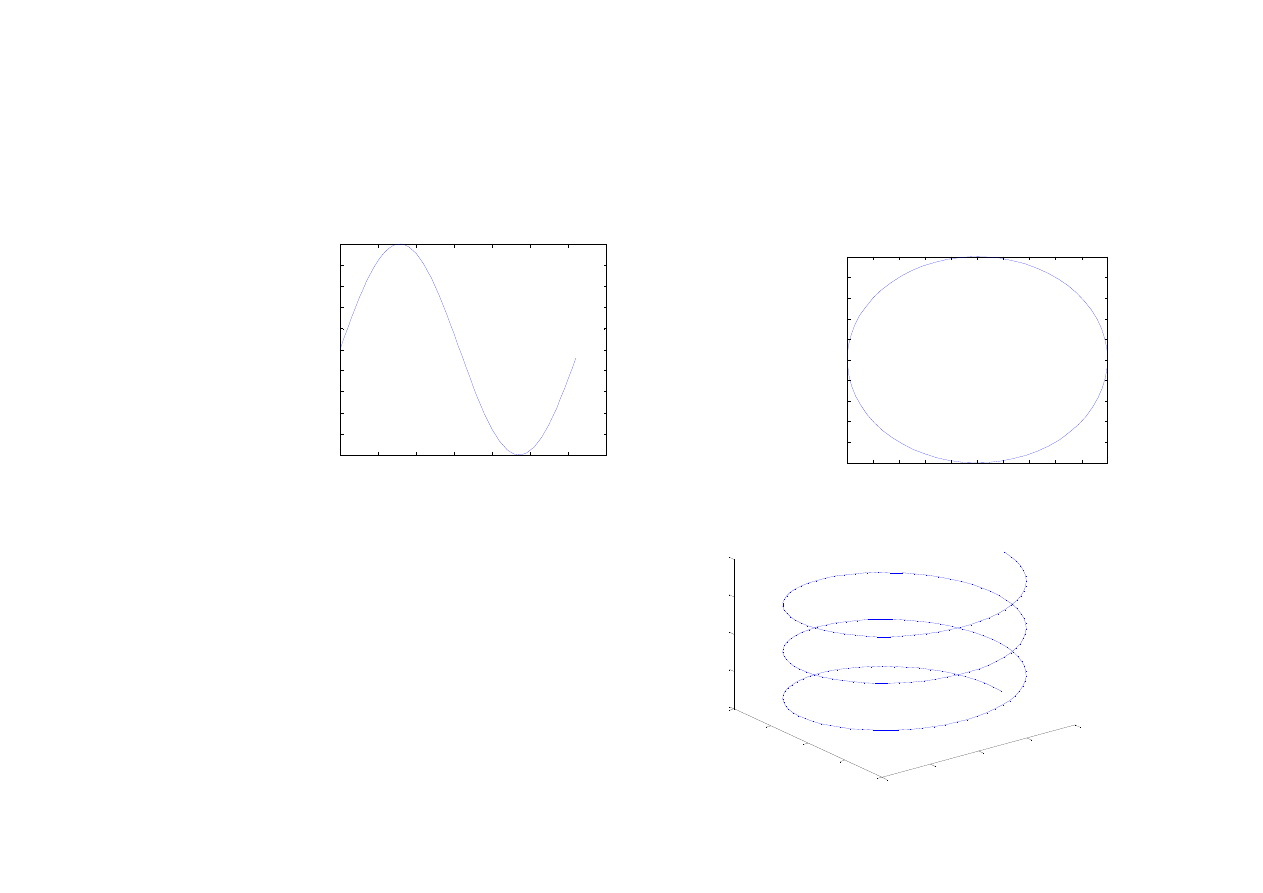
krzywa w przestrzeni dwuwymiarowej
opisana parametrycznie:
» t=0:0.1:2*pi;
» x=cos(t);
» y=sin(t);
» plot(x,y)
» x=0:0.1:2*pi;
» y=sin(x);
» plot(x,y)
krzywa w przestrzeni trójwymiarowej
opisana parametrycznie:
wykres funkcji jako przykład krzywej w
przestrzeni dwuwymiarowej:
» t=0:0.1:6*pi;
» x=cos(t);
» y=sin(t);
» z=t;
» plot3(x,y,z)
Matlab – wykreślanie powierzchni trójwymiarowych
-2
0
2
-2
0
2
0
2
4
6
x
y
z
-2
-1
0
1
2
-2
-1
0
1
2
0
1
2
3
4
5
-2
-1
0
1
2
-2
-1
0
1
2
0
1
2
3
4
5
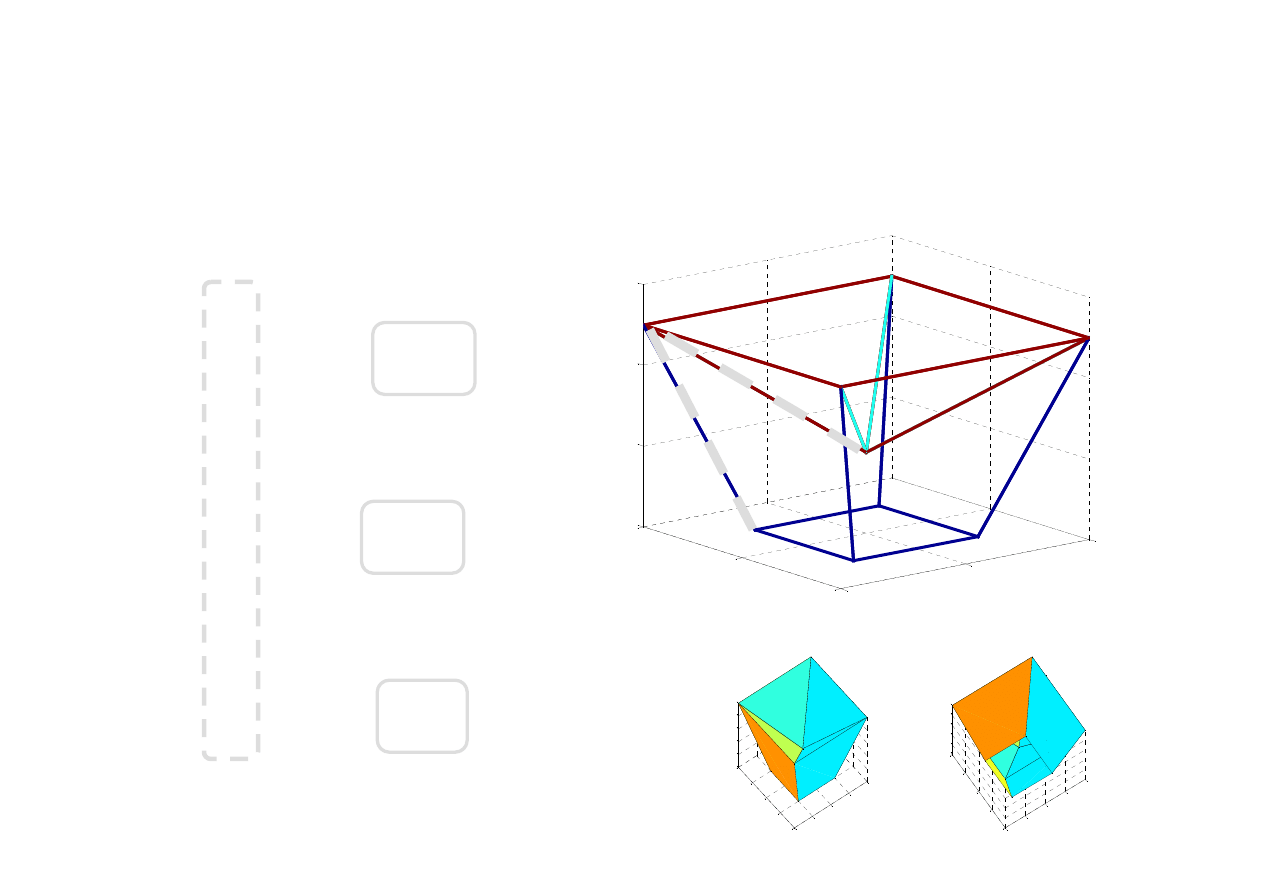
Powierzchnie trójwymiarowe o dowolnym kształcie składane są z płaskich, sąsiadujących
ze sobą czworokątów. Współrzędne ich wierzchołków można zapisać do trzech odrębnych
macierzy (np. X, Y, Z) i wykreślić używając np. funkcji mesh(X,Y,Z) lub surf(X,Y,Z).
-1 1 1 -1 –1
-2 2 2 -2 –2
0 0 0 0 0
X
1 1 -1 -1 1
2 2 -2 -2 2
0 0 0 0 0
Y
0 0 0 0 0
5 5 5 5 5
2 2 2 2 2
Z
linia 1 linia 2
zamykamy
bryłę - ponownie
linia 1
zaznaczono przykładowy czworokąt,
zbiegający się do trójkąta