Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 1 z 26

DUALIZM KORPUSKULARNO-FALOWY

1.

Źródła światła i ich światłość

Najczęstszymi źródłami światła są ciała posiadające wysoką temperaturę, np.
Słońce, rozgrzane metale itp. Oczywiście istnieją także ciała, które świecą w
stosunkowo niskich temperaturach (np. neonówki). Źródła światła różnią się
także między sobą kształtem i wielkością (rozciągłe, liniowe, punktowe itp.)
oraz ilością wysyłanego światła w danym kierunku i w danym czasie.
Oceną źródeł światła pod względem ich zdolności do świecenia i oświetlania
przedmiotów zajmuje się dział optyki zwany fotometrią. Fotometria
energetyczna zajmuje się całym zakresem widma fal elektromagnetycznych, a
fotometria wizualna tylko jego częścią widzialną.
W fotometrii energetycznej podstawową wielkością charakteryzującą źródło jest
natężenie promieniowania źródła – ilość energii ∆E wysyłanej przez źródło
promieniowania w jednostce czasu ∆t w jednostkowy kąt przestrzenny ∆

ω

.

sr

W

s

sr

J

∆t

∆ω

∆E

J









=

⋅

⋅

=

Natomiast w fotometrii wizualnej wielkościami charakteryzującymi dane źródło
światła (oczywiście oprócz natężenia promieniowania źródła) są :

a)

światłość źródła

światła w danym kierunku

Światłość – podstawowa wielkość fotometrii wizualnej (natężenie światła)
określona

przez

porównanie

wrażeń

wzrokowych

wywołanych

promieniowaniem przedmiotu i promieniowaniem wzorca jednostki
światłości.

Innymi słowy, bierzemy latarkę jako wzorzec i drugi przedmiot świecący
i porównujemy „na oko” : nasz przedmiot świeci jak 2,5 latarki.
Oczywiście w fizyce nie stosujemy latarki jako źródła światłości ale ....
świecę. Oczywiście jest to żart, ale jednostką światłości jest kandela ( z
łac. candela – świeca )

1 kandela

( 1 cd ) jest to światłość, jaką ma w określonym kierunku

źródło emitujące promieniowanie o częstotliwości 540* 10

12

Hz (barwa

żółto-zielona) i którego natężenie promieniowania w tym kierunku jest
równe

1

/

683

W

/

sr

.

Jest to podstawowa jednostka układu SI.

Wracając do naszej świecy, jej światłość w kierunku prostopadłym do
płomienia wynosi około ¾ cd.

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 2 z 26

b)

strumień światła wysyłany ze źródła w określony kąt bryłowy.

Strumień światła

Φ

- moc promieniowania świetlnego oceniania na

podstawie wywołanego przez nie wrażenia świetlnego.
Definicja jest może zbyt enigmatyczna, ale weźmy okrągłą latarkę z
regulowanym reflektorem. Światłość latarki jest identyczna, ale możemy
sterować strumieniem światła : albo będzie to wąska wiązka światła albo
rozbieżna. Oczywiście wąska wiązka wywoła inne wrażenie wzrokowe
(oślepi) niż rozbieżna.
Logicznym wydaje się tu wspomnieć, że strumień światła będzie zależał
także od rozmiarów źródła. Jednak ze względu na złożoność tego
zagadnienia powiemy sobie tu tylko o punktowym źródle światła o
światłości J, które wysyła w głąb kąta bryłowego ∆

ω

strumień światła o

∆

Φ

równy :

∆ω

J

∆

⋅

=

Φ

Przypominam,

że 1 sr (steradian) to kąt bryłowy stożka wycinającego z

kuli o promieniu R=1 m pole S=1 m

2

. Pełny kąt bryłowy wynosi 4

π

sr.

Stąd możemy zapisać :

2

R

∆S

J

∆Φ

⋅

=

Jednostką strumienia światła jest lumen ( 1 lm ).
1 lm jest to strumień światła płynący z punktowego źródła o światłości 1
cd w obrębie kąta bryłowego 1 sr.

Punktowe i izotropowe źródło światła o światłości 1 cd wysyła we
wszystkie strony strumień 4

π

lm.

2.

Natężenie oświetlenia

Światło wychodzace ze źródła i padające na pewną powierzchnię oświetla ją
silniej lub słabiej. Wtedy mówimy o natężeniu oświetlenia.

Natężeniem oświetlenia

nazywamy stosunek strumienia świetlnego ∆

Φ

padającego ze źródła na daną powierzchnię do pola tej powierzchni.

(luks)

lx

1

m

1

lm

1

∆S

∆Φ

E

2









=

=

Jeżeli powierzchnia jest oświetlana przez źródło punktowe to istnieją dwa prawa
pozwalające obliczyć natężenie oświetlenia.

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 3 z 26

Natężenia oświetlenia E

1

i E

2

dwóch powierzchni ustawionych prostopadle do

promieni świetlnych są odwrotnie proporcjonalne do kwadratów ich odległości
od punktowego źródła światła.

2

1

2

2

2

1

r

r

E

E

=

Natężenie oświetlenia E’ powierzchni ∆S’, na którą promienie padają pod kątem

α

, jest przy stałej odległości źródła proporcjonalne do kosinusa tego kąta.

α

cos

E

E

'

⋅

=

gdzie E – natężenie oświetlenia powierzchni ustawionej prostopadle do
promieni.


3.

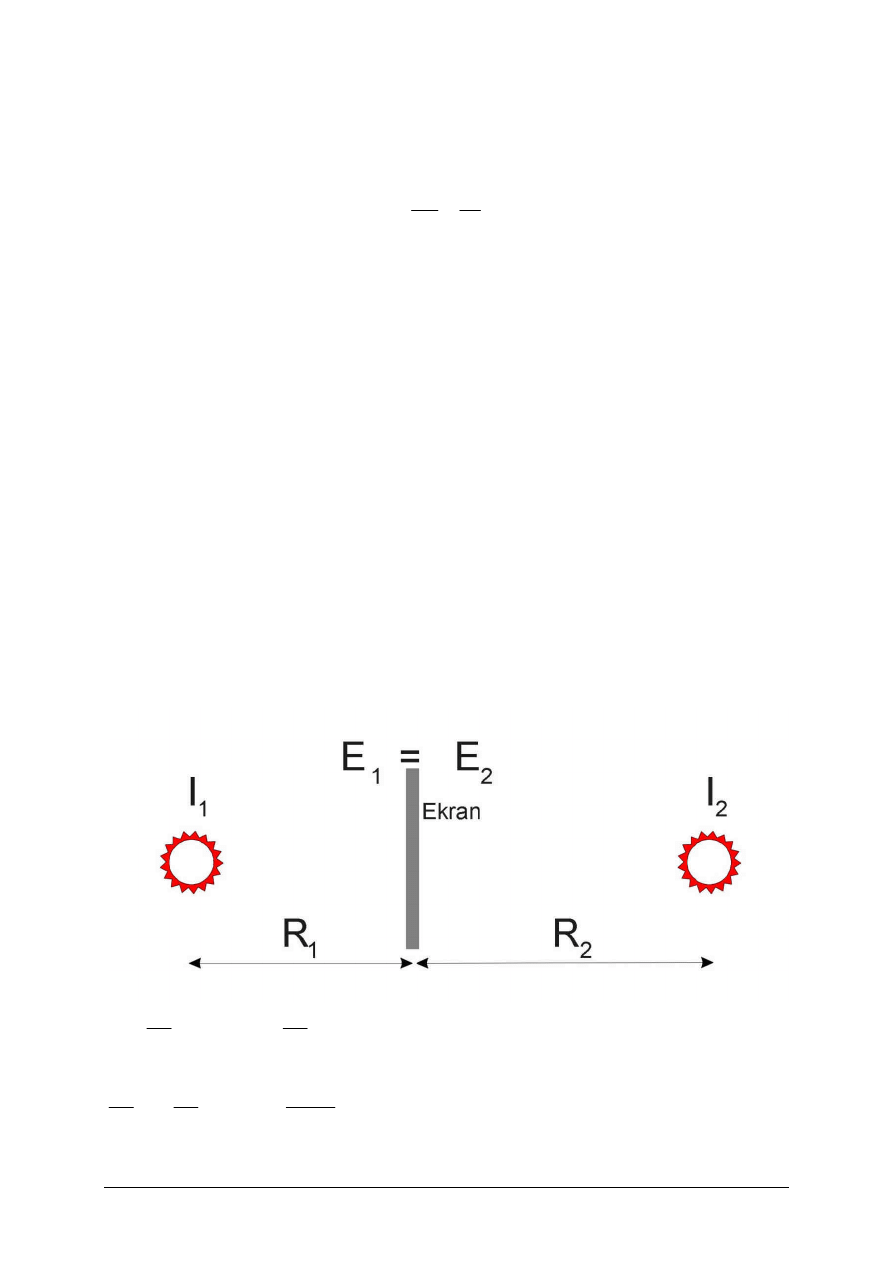
Zasada fotometru

Znajomość praw dotyczących natężenia oświetlenia pozwala w dosyć prosty
sposób rozwiązać problem porównania różnych natężeń źródeł światła, czyli
skonstruować prosty fotometr.

Fotometr Bunsena składa się z dwóch źródeł światła, z których natężenie
jednego znamy (np. J

1

) , a drugie chcemy wyznaczyć (J

2

) oraz półprzeroczytego

ruchomego ekranu. Ekranem sterujemy tak, aby natężenie oświetlenia na nim
było jednakowe (z dwóch stron) – po to jest półprzezroczysty.

2

1

2
2

2

2

2

1

1

1

E

E

R

J

E

R

J

E

=

=

=

stąd

R

R

J

J

R

J

R

J

2

1

2
2

1

2

2
2

2

2

1

1

⋅

=

→

=

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 4 z 26

4.

Promieniowanie termiczne ciał

Jak poprzednio wspomniałem, niektóre źródła światła wysyłają promieniowanie
termiczne, tzn. świecenie wywołane jest dosyć wysoką temperaturą ciała.
Promieniowanie widzialne pojawia się przy temperaturze około 950 K (światło
czerwone). W miarę wzrostu temperatury ciała, widmo widzialne rozszerza się
od czerwonego poprzez żółty do zielonego przy temperaturze 1500 K , a w
temperaturze około 1800 K obejmuje ono już cały zakres promieniowania
widzialnego.
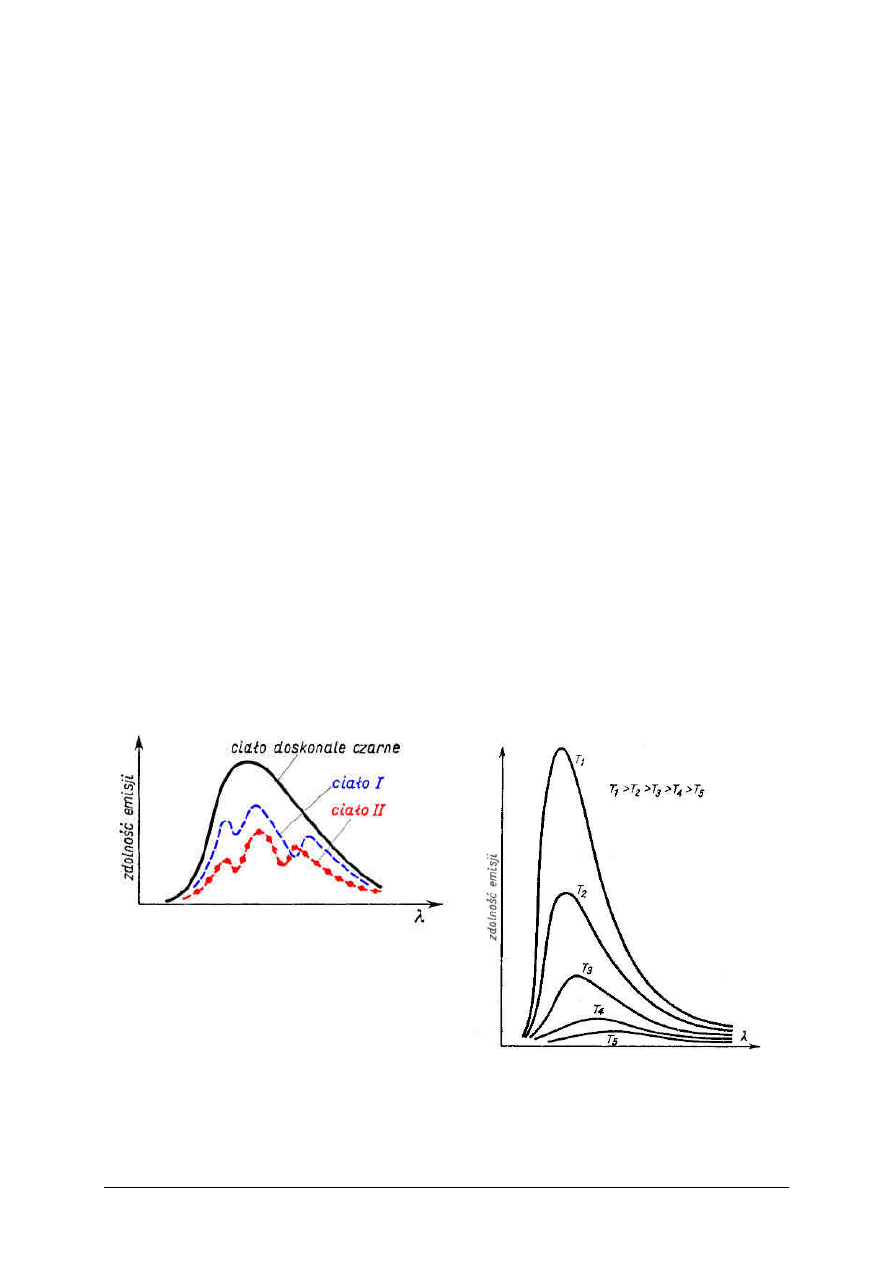
Wyniki badań promieniowania termicznego można przedstawić na wykresie,
odkładając na osi X długość lub częstotliwość fali, a na osi Y tzw. zdolność
emisji (rys. 2 i 3 ).

Zdolność emisji – ilość energii promienistej odpowiadającej wąskiemu
zakresowi długości fali od

λ

do

λ

+

∆λ

wysyłanej w jednostce czasu przez

jednostkę powierzchni źródła. Oznaczamy ją symbolem e (

λ

, T ) , jednostką

jest W/m

2

.

Wykresy mogą odnosić się do różnych źródeł badanych w tej samej
temperaturze (rys. 2) lub do tego samego źródła badanego w różnych
temperaturach (rys. 3).

Rys. 2

Rys. 3

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 5 z 26

Zauważmy, że na rysunku 2 mamy zdolność emisyjną dwóch ciał o tej samej
temperaturze. Widać z niego, że rodzaj ciała ma wpływ na przebieg emisji, co
utrudnia wyciągnięcie jakichkolwiek ogólnych wniosków. Jednak okazuje się,
że można sztucznie wytworzyć źródło o maksymalnej emisji w każdej
temperaturze i dodatkowo o 100% absorpcji padającego promieniowania – ciało
doskonale czarne.

Wydrążona kula z małym otworem, przez który wpada
wiązka promieniowania. Kula jest w środku wydrążona
i poczerniona. Promień wpadający przez otwór zostaje
całkowicie pochłonięty i nie wyjdzie z kuli. Wykres
zdolności emisyjnej takiego otworu przedstawiony jest
na rysunku 2 (ciało doskonale czarne).

Rys. 4 – schemat ciała doskonale czarnego


Krzywa ta jest niezależna od charakteru źródła, zależy tylko od temperatury.
Ilość energii wypromieniowanej przez ciało doskonale czarne została
doświadczalnie wyznaczona przez Stefana, natomiast teoretyczne opracowanie
zawdzięczamy Boltzmannowi.

Prawo Stefana – Boltzmanna

Całkowita energia promieniowania widzialnego i niewidzialnego wysyłana
przez jednostkę powierzchni ciała doskonale czarnego w jednostce czasu wynosi

4

T

σ

E

⋅

=

gdzie : T – temperatura bezwzględna ciała doskonale czarnego

4

2

8

K

m

W

10

5,669

σ

⋅

⋅

=

−

- stała Stefana - Boltzmanna

Wzór ten można zmodyfikować i po uwzględnieniu dowolnego pola
powierzchni S i dowolnego czasu t, energia wypromieniowana przez ciało
doskonale czarne będzie wynosiła :

t

S

T

σ

E

4

⋅

⋅

⋅

=

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 6 z 26

Spójrzmy teraz na wykresy znajdujące się na rys. 3. Ciało doskonale czarne
badane jest w różnych temperaturach. Widzimy, że w miarę wzrostu
temperatury pole pod krzywą rośnie (zgodnie z prawem Stefana-Boltzmanna)
i jest równe energii promieniowania. Oprócz tego maksimum krzywej przesuwa
się w lewo (przy wzroście temperatury). Wilhelm Wien stwierdził, że
obowiązuje przy tym zależność :

K

m

10

2,897

const

T

λ

3

max

⋅

⋅

=

=

⋅

−

gdzie :

λ

max

– długość fali w metrach, przy której następuje maksimum zdolności

emisji w danej temperaturze T.
Jest to prawo przesunięć Wiena.

W przeglądzie praw rządzących promieniowaniem termicznym nie może
zabraknąć prawa Kirchhoffa. Prawo to, wyprowadzone na podstawie rozważań
termodynamicznych,

podaje

zależność

między

zdolnością

emisji

promieniowania o długości

λ

i zdolnością absorpcji tego promieniowania w tej

samej temperaturze.

Zdolność absorpcji – liczba wskazująca jaka część promieniowania padającego
na ciało zostaje pochłonięta (liczba niemianowana). Oznaczamy ją symbolem

α

(

λ

, T ).

Dla ciała doskonale czarnego

α

(

λ

, T ) = 1, dla innych ciał jest ułamkiem

właściwym.

W przypadku padania energii promienistej na dowolną powierzchnię, część z
niej ulega odbiciu, część jest przepuszczana, a część pochłaniana. Możemy więc
zdefiniować sobie zdolność odbijania

ρ

(

λ

, T ) , zdolność przepuszczania

τ

(

λ

, T )analogicznie do zdolności absorpcji. Otrzymamy wtedy związek :

α

+

ρ

+

τ

= 1

Przejdźmy jednak do prawa Kirchhoffa.
Stosunek zdolności emisji do zdolności absorpcji danego ciała nie zależy od
rodzaju ciała, to znaczy dla wszystkich ciał jest funkcją częstotliwości
(długości) promieniowania i temperatury bezwzględnej ciała.

)

T

λ,

(

ε

)

T

λ,

(

α

)

T

,

λ

(

e

=

Aby znaleźć sens fizyczny wielkości

ε

(

λ

, T ) zapiszmy prawo Kirchhoffa dla

ciała doskonale czarnego :

1

)

T

λ,

(

α

ale

)

T

λ,

(

ε

)

T

λ,

(

α

)

T

,

λ

(

e

o

o

o

=

=

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 7 z 26

)

T

λ,

(

ε

)

T

,

λ

(

e

o

=

Wynika stąd, że

ε

(

λ

, T ) jest równa zdolności emisji ciała doskonale czarnego

dla długości fali

λ

i temperatury T.

)

T

λ,

(

e

)

T

λ,

(

α

)

T

,

λ

(

e

o

=

Wynika stąd, że ciało doskonale czarne ma maksymalną zdolność emisji
każdego z rodzajów promieniowania w każdej temperaturze.
Pamiętajmy jednak, że stosowalność prawa Kirchhoffa ogranicza się wyłącznie
do promieniowania termicznego.

Ważnym wnioskiem wynikającym z prawa Kirchhoffa jest to, że jeśli jakieś
ciało w pewnej temperaturze T emituje promieniowanie o długości

λ

, to

absorbuje ono ten sam rodzaj promieniowania. Z odwróceniem tego wniosku
należy jednak być ostrożnym – absorpcja promieniowania o długości

λ

w

temperaturze T nie musi iść w parze z emisją tego promieniowania gdyż
zdolność emisji e (

λ

, T ) może być równa zero ( o ile dla danego

λ

i T zdolność

emisji ciała doskonale czarnego wynosi 0 ).


5.

Kwantowość promieniowania. Wzór Plancka.

Dla dalszego rozwoju teorii promieniowania kolosalne znaczenie miała krzywa
przedstawiająca zdolność emisji ciała doskonale czarnego w funkcji długości
fali (rys. 2 i 3). Otóż podobna krzywa występuje w termodynamice i przedstawia
rozkład prędkości cząstek – tzw. rozkład Maxwella. Podobieństwo tyc
wykresów skłoniło Wiena do poczynienia prób dostosowania równania
Maxwella do opisu promieniowania ciała doskonale czarnego ( przez analogię
!!! ). I udało mu się ustalić wzór empiryczny z dwiema stałymi tak dobranymi,
że zgadzał się on z wynikami eksperymentalnymi w zakresie fal krótkich.
Niezgodność wzoru w zakresie fal długich była tłumaczona złym doborem
stałych – pamiętajmy : był to wzór empiryczny !
Jednocześnie, niezależnie od Wiena, prace nad tym samym zagadnieniem
prowadził Rayleigh. Na podstawie rozważań na gruncie fizyki klasycznej
doszedł on do odmiennego równania niż Wien, które dawało wyniki zgodne z
doświadczeniem ale tylko w zakresie fal długich. Natomiast w zakresie fal
krótkich równanie to dawało wyniki zupełnie niezgodne z doświadczeniem. Tą
niezgodność z doświadczeniem prawa wyprowadzonego na podstawie ścisłych
rozważań na gruncie fizyki klasycznej nazwaną katastrofą w nadfiolecie. Stało

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 8 z 26

się bowiem jasne, że fizyka klasyczna nie jest w stanie wytłumaczyć faktów
doświadczalnych.

dλ

e

λ

'

C

dλ

)

T

,

λ

(

e

T

λ

"

C

5

⋅

−

⋅

=

- równanie Wiena

Następny fizyk, Planck rozwiązał problem Wiena w sposób dosyć przypadkowy
– wprowadził on kilka poprawek, zmieniając między innymi stałe. Otrzymał w
ten sposób równanie, które na granicy fal długich przechodziło w równanie
Wiena, a w całym zakresie promieniowania było zgodne z doświadczeniem.

dλ

1)

-

e

(

λ

C

dλ

)

T

,

λ

(

e

T

λ

C

5

1

2

⋅

−

⋅

=

- równanie Plancka

Następnym krokiem Plancka było poszukiwanie poprawnej z punktu fizyki
i matematyki metody uzasadnienia tego równania. Żadna z prób opartych na
założeniach fizyki klasycznej nie dała pozytywnego wyniku. Dlaczego ? W
ujęciu klasycznym zakłada się, że energia może przyjmować wszystkie
wartości, a zatem zmiany energii mogą zachodzić w sposób ciągły (patrz :
spadanie swobodne ciał – E

p

zamieniana jest w E

k

). Planck odrzucił założenia

mechaniki klasycznej wprowadzając nowy obraz mechanizmu promieniowania.
Jego zdaniem zmiany energii źródła wysyłającego promieniowanie mogą
zachodzić tylko określonymi porcjami, tzn. w sposób nieciągły. Porcja
wypromieniowanej energii (kwant promieniowania, foton) wyraża się wzorem :

ν

h

E

⋅

=

gdzie :

ν

- częstotliwość emitowanego promieniowania

s

J

10

6,626

h

34

⋅

⋅

=

−

- stała Plancka

Cecha kwantowości promieniowania okazała się niesłychanie ważna dla
rozwoju fizyki współczesnej.

6.

Zjawisko fotoelektryczne zewnętrzne

Mniej więcej w tym samym czasie (1900 r.) gdy starano się „usunąć” katastrofę
w nadfiolecie, odkryte zostało zjawisko zwane fotoelektrycznym, którego
wyjaśnienie na gruncie fizyki klasycznej, a więc i teorii falowej światła było
niemożliwe.
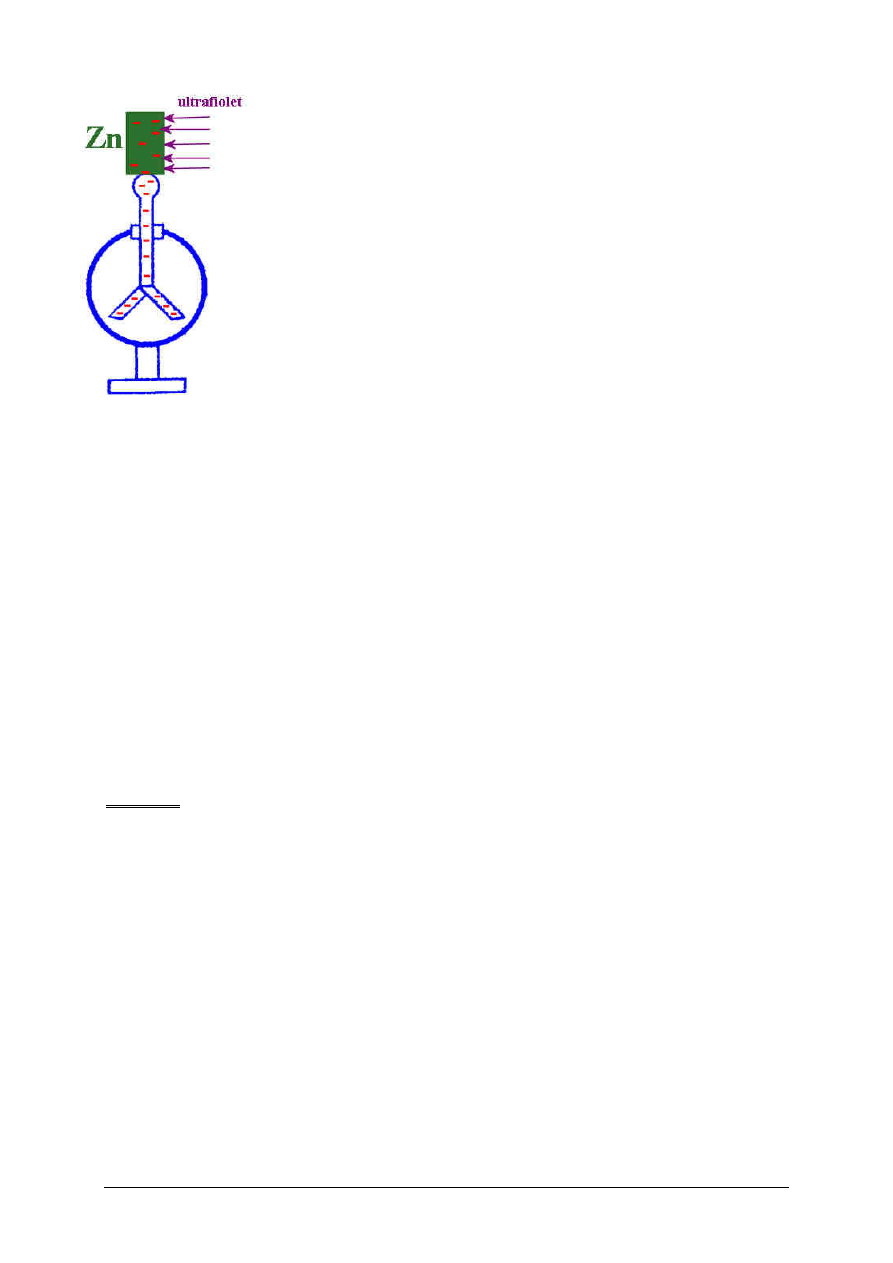
Na początek omówmy to zjawisko.

Naelektryzowaną ujemnie płytkę cynkową oświetlamy promieniowaniem
nadfioletowym. Listki gwałtownie opadają. Tą samą płytkę elektryzujemy
dodatnio i ponownie oświetlamy ją nadfioletem – listki nie opadają.

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 9 z 26

Wniosek : pod wpływem promieniowania nadfioletowego
płytka traci ładunki ujemne (elektrony).

Emisję

elektronów

z

ciała

naświetlonego

promieniowaniem

elektromagnetycznym nazywamy zjawiskiem fotoelektrycznym, a elektrony
emitowane w tym zjawisku fotoelektronami.
Metal, z którego emitowane są fotoelektrony nazywany jest fotokatodą.
Badając zjawisko fotoelektryczne zewnętrze otrzymujemy następujące wyniki :

dla danego metalu ilość emitowanych fotoelektronów jest proporcjonalna
do natężenia padającego na ten metal światła;

dla każdego metalu istnieje najniższa częstotliwość promieniowania

ν

o

,

poniżej której zjawisko fotoelektryczne nie zachodzi;

maksymalna prędkość fotoelektronów zależy jedynie od częstotliwości
promieniowania padającego na metal;

fotoelektrony wylatują z metalu bez opóźnienie (pojawia się
promieniowanie – elektrony wylatują natychmiast).

Wyjaśnienie zjawiska fotoelektrycznego na gruncie teorii klasycznej
(błędne).
Aby elektron mógł opuścić metal, musi on posiadać dosyć duży zapas energii
aby pokonać siły elektrostatycznego przyciągania, które powstają gdy elektron
opuszcza metal. Oczywiście siła ta maleje wraz z odległością, dlatego tak zwana
praca wyjścia (energia) ma skończoną wartość. Aby elektron zgromadził
wystarczającą ilość energii do wyjścia musi upłynąć pewien okres czasu. Czas
ten zależy od ilości dostarczanej w sposób ciągły energii, tak więc dla słabych
źródeł światła czas ten jest dłuższy niż dla źródeł silniejszych. Pamiętamy, że
natężenie fali (światła) jest proporcjonalne do amplitudy i częstotliwości fali ( w
tym wypadku elektromagnetycznej )

2

2

ν

A

~

J

⋅

.

Istnienie granicznego natężenia światła wywołującego zjawisko fotoelektryczne
wskazywałoby na ewentualną zależność ilości emitowanych fotoelektronów
(prąd fotoelektryczny) od kwadratu amplitudy i częstotliwości promieniowania.
Tymczasem doświadczenie tego nie stwierdza, a wykazuje istnienie granicznej
częstotliwości, co w żaden sposób nie wynika z klasycznej teorii światła. Mało

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 10 z 26

tego, doświadczenie pokazuje, że elektrony wylatują bez żadnego opóźnienie,
czyli nie „zbierają” energii na pokonanie sił elektrostatycznego przyciągania.

W celu wyjaśnienia zjawiska fotoelektrycznego zewnętrznego w 1905 roku
Einstein wykorzystał hipotezę kwantów promieniowania czyli wzór Plancka

ν

h

E

⋅

=

.

Według Einsteina, zjawisko fotoelektryczne zewnętrzne należy traktować jako
przekazywanie elektronowi związanemu z atomem ściśle określonej ilości
energii przez foton, który po jej przekazaniu przestaje istnieć. Padając na metal,
foton dostarcza elektronowi energii w ilości E=h

ν

, przy czym jej część zużyta

jest na wyrwanie elektronu z fotokatody – W (praca wyjścia), a pozostała część
energii o wartości E-W przeznaczona jest na energię kinetyczną fotoelektronu.

W

h

)

h(

2

v

m

o

2
max

−

=

−

=

⋅

ν

ν

ν

równanie Einsteina-Millikana

Zauważmy, że zjawisko fotoelektryczne zachodzi wtedy, gdy

W

h

≥

ν

. Dla

W

h

=

ν

spełniona jest zależ

no

ść

ν

o

=

ν

.

Poza tym Einstein przyj

ą

ł,

ż

e nie tylko emisja i absorpcja odbywaj

ą

si

ę

kwantowo (porcjami), ale tak

ż

e rozchodzenie si

ę

energii jest skwantowane

(rozchodzi si

ę

porcjami).

Nat

ęż

enie

ś

wiatła zwi

ą

zane jest z ilo

ś

ci

ą

fotonów, a energia tych fotonów z

cz

ę

stotliwo

ś

ci

ą

. Ka

ż

dej energii fotonów odpowiada inna cz

ę

stotliwo

ść

.

Zwró

ć

my uwag

ę

,

ż

e skoro foton posiada energi

ę

to musi posiada

ć

tak

ż

e p

ę

d.

Energia promieniowania dana jest wzorem

ν

h

E

⋅

=

, a jednocze

ś

nie z teorii

wzgl

ę

dno

ś

ci

2

f

c

m

E

⋅

=

, st

ą

d

2

f

c

m

h

⋅

=

⋅

ν

. Wobec tego p

ę

d fotonu mo

ż

na

wyrazi

ć

za pomoc

ą

λ

h

c

h

c

m

p

f

=

⋅

=

⋅

=

ν

.

Zauwa

ż

my,

ż

e w tym wzorze foton traktowany jest jednocze

ś

nie jako fala (

λ

)

oraz jako cz

ą

stka (p) – czyli mamy do czynienia z dwoist

ą

struktur

ą

promieniowania (dualizm korpuskularno-falowy).

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 11 z 26

Praca wyjścia i maksymalna długość fali światła wywołującej zjawisko
fotoelektryczne w nanometrach [nm] dla wybranych metali

Lp.

pierwiastek

- metal

symbol

chemiczny

maksymalna długość

fali światła

wywołującej zjawisko

fotoelektryczne [nm]

1. Cez

Cs

581

2. Rubid

Rb

575

3. Sód

Na

452

4. Glin

Al.

280

5. Cynk

ZN

287

6. Miedź

Cu

267

7. Żelazo

Fe

264

8. Platyna

Pt

220

7.

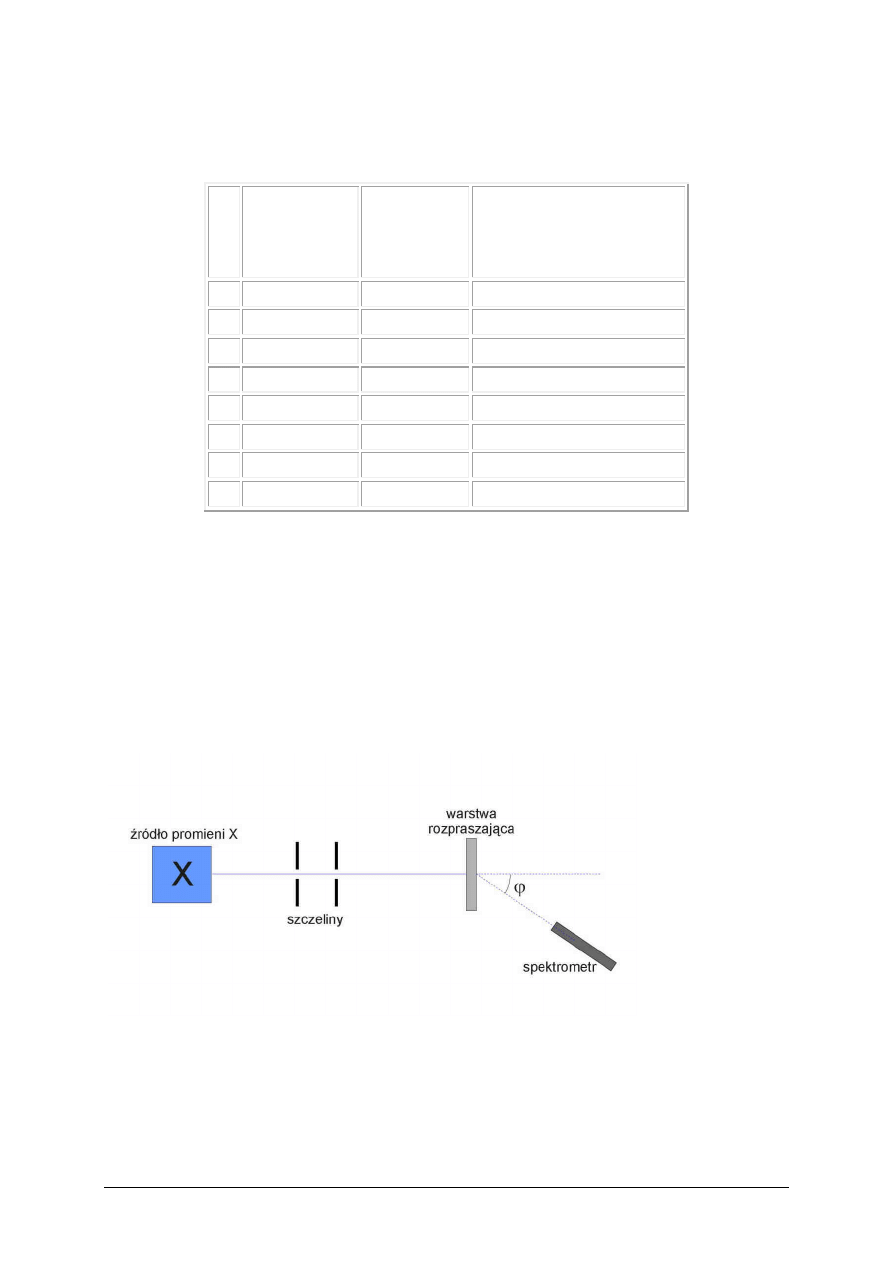
Zjawisko Comptona

Kwantowe właściwości promieniowania elektromagnetycznego potwierdza
również odkryte 1923r. przez Comptona rozproszenie promieni X na
elektronach. Compton odkrył, że oprócz promieni rozproszonych o
niezmienionej długości, istnieje jeszcze promieniowanie rozproszone połączone
ze zmianą długości, a dokładniej o długości większej od promieniowania

padającego.




Schemat
doświadczenia
Comptona

Monochromatyczna wiązka promieni X przechodzi przez dwie szczeliny i pada
na materiał rozpraszający. Spektrometr, który służy do pomiaru długości fali,
można przesuwać po okręgu wokół próbki rozpraszającej. Okazuje się, że

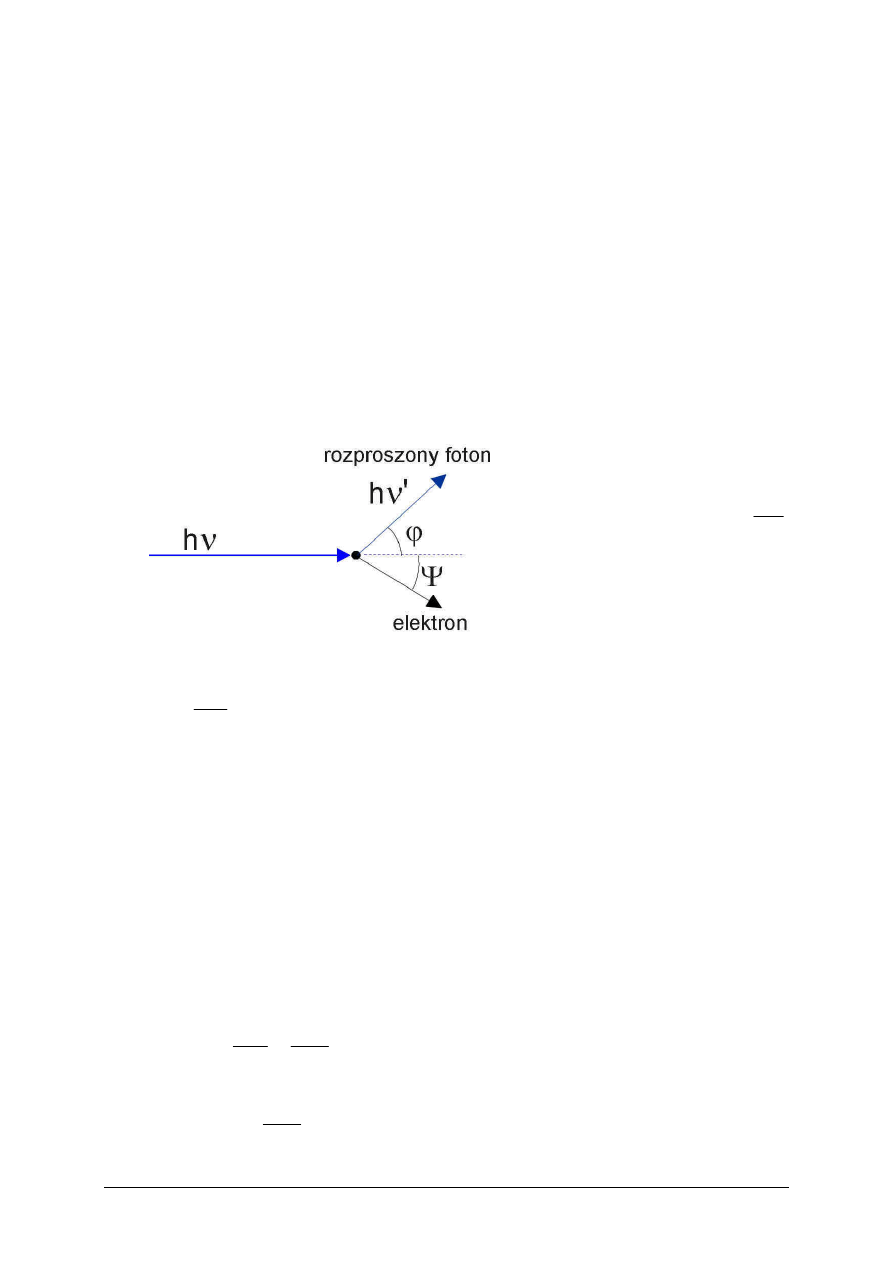
Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 12 z 26

spektrometr w ruchu po kole rejestruje co najmniej dwie różne długości fali.
Zjawisko to jest niewytłumaczalne z punktu widzenia teorii klasycznej. Zgodnie
z tą teorią, fale elektromagnetyczne pobudzają do drgań atomy, które jako
oscylatory stają się źródłem promieniowania rozproszonego. Ponieważ są to
drgania wymuszone, więc częstotliwość promieniowania rozproszonego musi
być równa częstotliwości promieniowania padającego. Doświadczenie pokazuje
jednak istnienie dodatkowego promieniowania. Dlaczego ?
Otóż według teorii kwantowej zjawisko Comptona polega na zderzeniu się
fotonu
z elektronem swobodnym, podczas którego, w odróżnieniu od zjawiska
fotoelektrycznego zewnętrznego, foton traci tylko część swojej energii. Jest to
zderzenie doskonale sprężyste a więc zostaje zachowana zasada zachowania

energii i oczywiście także
pędu.

Foton, posiadający energię

ν

h

E

⋅

=

oraz pęd

c

h

p

ν

⋅

=

zderzając się z elektronem
swobodnym przekazuje mu
część

swojej

energii

zmieniając

jednocześnie

swój bieg o kąt

ϕ

od

pierwotnego kierunku ruchu. Energia fotonu maleje do

ν'

h

⋅

, a jego pęd do

wartości

c

'

h ν

⋅

. Elektron będący przed zderzeniem w spoczynku uzyskuje

prędkość v i porusza się w kierunku tworzącym z kierunkiem fotonu padającego
kąt

Ψ

.

Oznaczmy energię spoczynkową przez m

o

c

2

, a jego pęd i energię całkowitą po

zderzeniu odpowiednio przez p i E.



Zasada zachowania energii dla tego układu ma postać :

E

'

h

2

c

o

m

h

+

⋅

=

+

⋅

ν

ν

natomiast zasada zachowania pędu (dla kierunków prostopadłych) :

X)

(oś

cos

p

cos

c

'

h

c

h

Ψ

⋅

+

⋅

⋅

=

⋅

ϕ

ν

ν

Y)

(oś

sin

p

sin

c

'

h

0

Ψ

⋅

−

⋅

⋅

=

ϕ

ν

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 13 z 26

Rozwiązując układ równań otrzymujemy :

)

cos

(1

Λ

λ

λ'

∆λ

ϕ

−

⋅

=

−

=

gdzie

m

10

2,426

c

m

h

Λ

12

-

o

⋅

≈

⋅

=

- komptonowska długość fali

Ze wzoru Comptona wynika, że zmiana długości fali w tym zjawisku nie zależy
od długości fali promieniowania padającego, a jedynie jest funkcją kąta
rozproszenia fotonu. Zmiana długości fali w zjawisku Comptona staje się łatwa
do wykrycia w przypadku, gdy długość fali padającej jest porównywalna z
komptonowską długością fali. Długość promieniowania rozproszonego jest
większa niż długość promieniowania padającego. Zauważmy, że dla kąta

ϕ

=

π

/2 ∆

λ

=

Λ

. Wobec tego, jeśli nasze ciało rozprasza promieniowanie z

zakresu widzialnego to zmiana o

Λ

jest praktycznie niewykrywalna. Natomiast

dla promieni X zmiana długości fali o

Λ

jest już bardzo dużą zmianą. Tak

naprawdę wynika stąd, że ważna jest dla nas względna

λ

∆λ

, a nie bezwzględna

zmiana długości. Spektrometry rentgenowskie wykrywają zmianę względną
rzędu 10

-3

czyli

Λ

jest łatwa do wykrycia.

Na zakończenie należy wspomnieć, że zjawisko Comptona zachodzi wyraźnie
wtedy, gdy :

częstotliwość promieniowania padającego jest duża

fotony zderzają się z elektronami słabo związanymi z atomami
(wtedy można je uznać za swobodne).

8.

Fale materii

W

poprzednich

rozdziałach

wykazaliśmy,

że

promieniowanie

elektromagnetyczne ma dwojaką (dualną) strukturę : falową (dyfrakcja,
interferencja i polaryzacja) oraz korpuskularną (zjawisko fotoelektryczne,
zjawisko Comptona). Wykazaliśmy także, że foton posiada dwoistą strukturę :
korpuskularną (pęd) i falową (

λ

- długość fali) :

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 14 z 26

=

ℎ

=

ℎ

gdzie

λ

- długość fali promieniowania, które polega na rozchodzeniu się

fotonów z prędkością c.

Einstein był ciekawy, czy jego zasada dualizmu może być zastosowana do

opisu materii, tak jak to było w przypadku światła. Podczas wykładu w 1909
roku wykazał, że światło ma dwoistą naturę, że może wykazywać zarówno
właściwości cząstek, jak i fal. Chociaż pomysł wydawał się heretycki, został on
w pełni potwierdzony danymi eksperymentalnymi. Dualistyczny program
badawczy Einsteina stał się inspiracją dla młodego doktoranta - księcia Louisa
de Broglie'a, który w 1923 roku zaczął się zastanawiać, czy sama materia nie ma
właściwości zarazem cząstek i fal. Była to koncepcja odważna i rewolucyjna,
gdyż przekonanie, że materia składa się z cząstek, było mocno ugruntowane. De
Broglie przedstawił wyjaśnienie niektórych tajemniczych cech atomu,
przyjmując koncepcję, że ma on właściwości falowe.
W 1924r. Louis de Broglie wysunął dosyć śmiałą hipotezę, że dualizm
korpuskularno falowy jest zjawiskiem powszechnym. Skoro foton, cząstka o
masie spoczynkowej równej zero, może być opisany za pomocą pędu i długości
fali, to cząstka (ciało) może być także opisany za pomocą p i

λ

.

„Każda poruszająca się materialna cząstka (cząsteczka, ciało) niesie ze sobą
falę”.
Według de Broglie’a z każdą materialną cząstką poruszającą się ruchem
jednostajnym prostoliniowym skojarzona jest fala płaska, której parametry

λ

i

ν

są związane z wielkościami „mechanicznymi” : energią E oraz pędem p
identycznymi związkami jak foton :

= ℎ =

ℎ

=

ℎ

W 1927r. hipoteza de Broglie’a została doświadczalnie potwierdzona

przez C. Davissona i L.Germera, którzy otrzymali obraz dyfrakcyjny
elektronów. Niezależnie od nich, George Thomson uzyskał obraz
interferencyjno-dyfrakcyjny elektronów. Rozkład pierścieni interferencyjnych
okazał się zgodny z teorią. W 1929r. de Broglie otrzymał nagrodę nobla za „za
stworzenie teorii o falowej naturze materii”.

Oprócz obrazów interferencyjnych elektronów otrzymano także obrazy

dyfrakcyjno-interferencyjne neutronów, atomów i molekuł. Zaobserwowano
także dla elektronów zjawisko odbicia i załamania, czyli prawie wszystkie
zjawiska jakim podlegają fale.

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 15 z 26

Związanie elektronu z falą stojącą materii umożliwiło podanie

odpowiedzi na pytanie, dlaczego elektron krążący po orbicie nie emituje
promieniowania elektromagnetycznego. (Fale stojące nie przenoszą energii -
jest na stałe zmagazynowana w poszczególnych punktach przestrzeni).

Postulat de Broglie'a mówiący, że ruch cząstki mikroskopowej (np. elektronu)
opisywany jest przez zachowanie się stowarzyszonej z nią fali materii stworzył
fundament współczesnej teorii opisu stanów atomowych.

Einstein poparł tą teorię. Ale jeśli materia ma właściwości falowe, to jakim
równaniom podlegają te fale? Tym problemem zajął się miedzy innymi
austriacki fizyk Erwin Schrödinger. Jak głosi anegdota, Erwin Schrödinger,
podczas bożonarodzeniowego urlopu, który w 1925 roku spędzał z jedną ze
swoich niezliczonych przyjaciółek w pensjonacie Villa Herwig w Arosie
(Szwajcaria), stworzył równanie, które jako falowe równanie Schrödingera
wkrótce zyskało największą sławę w całej fizyce kwantowej.
W ciągu kilku następnych miesięcy Schrödinger w znakomitej serii artykułów
wykazał, że opisane przez Nielsa Bohra dziwne reguły rządzące atomem
wodoru są prostą konsekwencją jego równania. Po raz pierwszy fizycy
otrzymali szczegółowy obraz wnętrza atomu, na podstawie którego mogli w
zasadzie wyliczyć właściwości bardziej złożonych atomów, a nawet cząstek.

Dzisiaj, kiedy uczniowie mają zapamiętać śmieszne niczym piłka do

rugby orbitale otaczające jądro, które zawierają dziwne oznaczenia i liczby
kwantowe, to w gruncie rzeczy zapamiętują wyniki rozwiązania falowego
równania Schrödingera). Rozwój fizyki kwantowej uległ teraz niesamowitemu
przyspieszeniu. Paul Dirac, który zwrócił uwagę, że równanie Schrödingera nie
uwzględnia teorii względności, zaledwie w dwa lata później dokonał
uogólnienia równania Schrödingera, doprowadzając do stworzenia w pełni
relatywistycznej teorii elektronu. Ponadto równanie Diraca automatycznie
wyjaśniało pewne niejasne właściwości elektronu, łącznie z czymś, co nazywa
się spinem. Wiadomo było z wcześniejszych eksperymentów Ottona Sterna i
Waltera Gerlacha, że elektron w polu magnetycznym zachowuje się jak
wirujący bąk, a jego moment pędu określa się liczbą ½ (w jednostkach stałej
Plancka). Elektron Diraca dawał w rezultacie spin wynoszący dokładnie ½, tak
jak w eksperymencie Sterna-Gerlacha. Pole Maxwella przedstawiające foton ma
spin równy 1, a fale grawitacyjne Einsteina mają spin wynoszący 2. Dzięki
pracy Diraca stało się jasne, że spin cząstek subatomowych będzie jedną z ich
najważniejszych właściwości.

Następnie Dirac poszedł o krok dalej. Badając energie elektronów, odkrył,

że Einstein pominął jedno z rozwiązań swojego własnego równania. Zazwyczaj,
kiedy wyciągamy pierwiastek kwadratowy z jakiejś liczby, wpisujemy wynik
zarówno dodatni, jak i ujemny. Ponieważ Einstein nie wziął pod uwagę
pierwiastka kwadratowego w zastosowaniu do swoich równań, jego słynne

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 16 z 26

równanie E = mc

2

było niezupełnie prawidłowe. Prawidłowe równanie powinno

mieć postać E = ±mc

2

. Ten dodatkowy znak minus, argumentował Dirac,

sprawiał, że stawało się możliwe istnienie nowego rodzaju lustrzanego
wszechświata, w którym cząstki miałyby nową postać, formę antymaterii.

W pierwszej chwili radykalne idee Diraca spotkały się z ogromnym

sceptycyzmem. Idea całego wszechświata lustrzanych cząstek, która wynikała z
równania E = ±mc

2

, wydawała się pomysłem cudacznym. Jednakże fizycy

musieli powściągnąć swoją dumę, kiedy antyelektron czy pozyton został w
końcu odkryty w 1932 roku, za co Dirac otrzymał później Nagrodę Nobla.
Jednakże mimo swoich niezaprzeczalnych sukcesów fizyka kwantowa wciąż
zmagała się z kłopotliwymi filozoficznymi pytaniami. Jeżeli materia jest falą, to
co właściwie faluje? Chociaż owe kwantowe fale odniosły graniczący z cudem
sukces w opisie atomu wodoru, nie wydawało się możliwe, aby fala
Schrödingera mogła być wykorzystana do opisu elektronu poruszającego się w
swobodnej przestrzeni. W istocie gdyby fala Schrödingera rzeczywiście
reprezentowała elektron, uległaby powolnemu rozproszeniu, a wszechświat
uległby rozcieńczeniu.

Gdzieś tkwił poważny błąd. W końcu długoletni przyjaciel Einsteina Max

Born zaproponował jedno z najbardziej kontrowersyjnych rozwiązań tej
łamigłówki. W 1926 roku Born zdecydował się na śmiały krok i ogłosił, że fala
Schrödingera w ogóle nie opisuje elektronu, lecz tylko prawdopodobieństwo
odnalezienia się elektronu. Wykazał on, że „ruch cząstek podlega prawom
rachunku prawdopodobieństwa, ale samo prawdopodobieństwo rozprzestrzenia
się zgodnie z prawami przyczynowości". Według tej nowej wizji materia
rzeczywiście składa się z cząstek, a nie z fal. Znaki utrwalone na kliszach
fotograficznych są śladami pozostawionymi przez punktowe cząstki, a nie przez
fale. Ale już szansa znalezienia się cząstki w danym punkcie dana jest poprzez
falę. Nie ma zatem znaczenia fakt, że fala Schrödingera rozprzestrzenia się wraz
z upływem czasu. Oznacza to po prostu, że jeśli zostawimy elektron samemu
sobie na jakiś czas, będzie on wędrował tu i tam i nie będziemy wiedzieli
dokładnie, gdzie on się znajduje. Wszystkie paradoksy zostały teraz rozwiązane
- sama fala Schrödingera nie była cząstką, ale dawała szansę na jej znalezienie.
Werner Heisenberg poszedł w tym kierunku jeszcze dalej, zadając sobie pytanie,
jak to możliwe, że nie można poznać dokładnego położenia elektronu. Jak
położenie elektronu może być niepewne, co twierdził Bohr, jeżeli można je po
prostu zmierzyć?
I nagle wszystko stało się jasne. Aby się dowiedzieć, gdzie jest elektron,
musimy na niego spojrzeć. Oznacza to konieczność oświetlenia go wiązką
światła. Ale fotony z wiązki światła zderzą się z elektronem i sprawią, że jego
położenie stanie się niemożliwe do oznaczenia. Innymi słowy, akt obserwacji z
konieczności wprowadza nieoznaczoność. Heisenberg przekuł problem w nową
zasadę fizyki, zasadę nieoznaczoności, która stanowi, że nie można jednocześnie

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 17 z 26

zmierzyć położenia i prędkości cząstki w tym samym momencie. Nie jest to po
prostu produkt uboczny niedoskonałości naszych przyrządów. Jest to
fundamentalne prawo natury.
Nie istnieje taki stan cząstki, w którym miałaby ona jednocześnie dokładnie
określone położenie i pęd. Również nie można wtedy dokładnie wyznaczyć jej
energii w dowolnie krótkim czasie.

∆ ∙ ∆ ≥

ℎ

4

∆ ∙ ∆ ≥

ℎ

4

Był to decydujący moment. Teoria kwantowa wypłynęła na głębokie,
całkowicie niezbadane wody. Do tej pory można było argumentować, że
zjawiska kwantowe mają charakter statystyczny i reprezentują uśrednione ruchy
bilionów elektronów. Teraz nawet ruchy pojedynczego elektronu nie mogły być
definitywnie określone. Einstein był przerażony. Poczuł się prawie zdradzony,
gdy się dowiedział, że jego dobry przyjaciel Max Born porzucił determinizm,
jedną z najbardziej hołubionych idei w całej fizyce klasycznej. Determinizm
stanowi, mówiąc w skrócie, że możemy określić przyszłość, jeśli wiemy
wszystko o teraźniejszości. Na przykład wielkim wkładem Newtona w fizykę
było to, że mógł on przewidzieć ruchy komet, księżyców i planet na podstawie
swoich zasad dynamiki, jeśli tylko znał aktualny stan Układu Słonecznego.
Przez stulecia fizycy zachwycali się precyzją zasad Newtona, dzięki którym
można było przewidzieć pozycje ciał niebieskich w zasadzie miliony lat
naprzód. Faktem jest, że do tej chwili cała wiedza była oparta na determinizmie,
to znaczy, że naukowcy mogli przewidywać wyniki eksperymentów, jeśli tylko
znali położenie i prędkość wszystkich cząstek.

Przykład 1.
Jeśli chcemy obserwować ruch protonu i odbijemy od niego światło, to
zaburzenie ruchu protonu wcale nie jest małe. Oczywiście zmiany ruchu protonu
pod wpływem uderzenia w niego fotonu nie można ani uniknąć ani dokładnie
ocenić. Możemy natomiast minimalne niepewności (błędy pomiarowe)
korzystając z zasady nieoznaczoności Heisenberga. Załóżmy, że proton ma
prędkość kuli karabinowej (v = 500m/s) określoną z dokładnością do 0,01%. Ile
wynosi nieokreśloność położenia protonu ? Masa protonu m = 1,67 · 10

-37

kg.

Rozwiązanie :
Z niepewności położenia i pędu otrzymujemy :

∆ =

ℎ

4 ∙ ∆

Ale

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 18 z 26

∆ =

∙ ∆

Stąd

∆ =

ℎ

4 ∙

∙

∆

∙

=

6,626 ∙ 10

4 ∙ 3,14 ∙ 1,7 ∙ 10

∙ 10

∙ 500

≈ 6,2 ∙ 10

Jeśli porównamy nieokreśloność położenia ∆x = 6,2·10

-7

m z rozmiarami protonu

r

p

= 2,82·10

-15

m to zobaczymy, ze jest ona około 300 mln razy większa od

protonu. Zatem mówienie o torze protonu w takich warunkach jest bardzo
dużym przybliżeniem.

Przykład 2.
Pocisk o masie m=10g został wystrzelony z prędkością v = 500m/s określoną
z taka sama dokładnością jak proton w poprzednim przykładzie, tj. 0,01%. Ile
wynosi nieokreśloność położenia pocisku ?
Rozwiązanie.

∆ =

ℎ

4 ∙

∙

∆

∙

=

6,626 ∙ 10

4 ∙ 3,14 ∙ 10

∙ 10

∙ 500

≈ 1,06 ∙ 10

!

Nieokreśloność położenia jest w tym przypadku dużo mniejsza od wielkości,
którą w ogóle potrafimy zmierzyć, gdyż stanowi ona

1

/

10

16

część rozmiarów

jadra atomowego.

Widzimy stad, że chociaż zasadę nieokreśloności Heisenberga możemy
zastosować do obiektów makroskopowych, to nie ma ona praktycznie żadnego
znaczenia i pojecie toru w odniesieniu do tych obiektów jest w pełni
uzasadnione.

Fizycy podzielili się na dwa obozy. Einstein przewodził jednemu

obozowi, w którym znaleźli się także Schrödinger i de Broglie, który wciąż
propagował determinizm oraz na obóz dużo większy z Nielsem Bohrem na
czele, który opowiadał się za nową wersją przyczynowości. Do ostatecznej
rozgrywki miedzy Einsteinem a Bohrem doszło podczas VI Konferencji Solvaya
w Brukseli w 1930 roku. Stawką była ni mniej, ni więcej tylko sama natura
rzeczywistości. Einstein nieustannie krytykował Bohra, który poddany
krzyżowemu ogniowi pytań wił się jak piskorz, ale dobrze sobie radził, broniąc
mądrze swoich pozycji. W końcu Einstein zaprezentował elegancki eksperyment
myślowy, który, jak sądził, rozniesie w pył zasadę nieoznaczoności.

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 19 z 26

Wyobraźmy sobie pudełko wypełnione promieniowaniem. W pudełku jest

dziurka zasłonięta migawka. Kiedy migawka zostaje na krótki moment otwarta,
z pudelka wydostanie się pojedynczy foton. Zatem z wielką dokładnością
możemy zmierzyć czas, w którym foton został wyemitowany. Dużo później
pudełko może zostać zważone. Z powodu uwolnienia fotonu pudełko waży
mniej niż wcześniej. Biorąc pod uwagę równoważność materii i energii,
możemy teraz powiedzieć, także z wielką dokładnością, ile całkowitej energii
zawiera pudełko. Tak więc znamy teraz wielkość całkowitej energii i czas
otwarcia migawki z żądaną dokładnością, bez żadnej niepewności, a z tego
wynika, że zasada nieoznaczoności jest błędna. Einstein myślał, że w końcu
znalazł narzędzie do obalenia nowej teorii kwantowej.

Początkowo Bohr nie był w stanie znaleźć żadnego rozwiązania tego

problemu. Ale po pełnej napięcia, bezsennej nocy Bohr znalazł w końcu defekt
w rozumowaniu Einsteina i użył jego własnej teorii względności, by go
pokonać. Bohr zauważył, że ponieważ pudełko waży mniej niż przedtem,
uniesie się ono nieco, zgodnie z zasadami ziemskiej grawitacji. Ale ogólna
teoria względności mówi, że gdy grawitacja ulega osłabieniu, czas przyspiesza
(na przykład czas płynie szybciej na Księżycu). Zatem każda minimalna
niepewność w pomiarze czasu migawki będzie się przekładała na niepewność w
pomiarze położenia pudełka. Dlatego nie będzie można zmierzyć położenia
pudełka z absolutną pewnością. Poza tym każda niepewność dotycząca wagi
pudełka odbije się na niepewności co do jego energii oraz pędu, z czego wynika
niemożność określenia pędu pudełka z absolutną pewnością. Gdy to wszystko
weźmie się pod uwagę, niepewność położenia i niepewność pędu - będą w pełni
zgodne z zasadą nieoznaczoności. Bohr obronił teorię kwantową.

Schrödinger, zaproponował słynny problem kota, aby podważyć zasadę
nieoznaczoności (do tej pory nie jest on rozwiązany w sposób
satysfakcjonujący). Kota zamknięto w pudełku, wewnątrz którego jest butelka z
trującym gazem, cyjanowodorem, podłączona do młotka zwalnianego poprzez
licznik Geigera, który z kolei ma połączenie z atomem radioaktywnego uranu.
Nie ma wątpliwości, że rozpad radioaktywny ma charakter kwantowy. Jeżeli
uran nie ulegnie rozpadowi, to kot pozostanie żywy. Jeśli jednak nastąpi rozpad,
uruchomi się licznik, który zwolni młotek, a ten rozbije butelkę, powodując
śmierć kota. Jednak zgodnie z teorią kwantową nie możemy przewidzieć, kiedy
nastąpi rozpad atomu uranu. W zasadzie może on istnieć w obu stanach
jednocześnie, i w stanie nienaruszonym, i w stanie rozpadu. Jeżeli zaś atom
uranu może istnieć jednocześnie w obu stanach, to kot także musi istnieć w obu
stanach. Powstaje więc pytanie: czy kot jest żywy, czy martwy?

W normalnych okolicznościach byłoby to głupie pytanie. Nawet jeśli nie

możemy otworzyć pudełka, zdrowy rozsądek mówi nam, że kot jest albo żywy,
albo martwy. Nie można być żywym i martwym jednocześnie. Byłoby to

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 20 z 26

sprzeczne z całą naszą wiedzą, jaką mamy o wszechświecie i fizycznej
rzeczywistości. Jednakże teoria kwantowa daje nam dziwną odpowiedź:
naprawdę nie wiemy. Zanim otworzymy pudełko, kot jest reprezentowany przez
falę, a fale można dodawać tak jak liczby. Musimy dodać funkcję falową
martwego kota do funkcji falowej żywego kota. Zatem przed otwarciem pudełka
kot nie jest ani żywy, ani martwy. O kocie zamkniętym w pudełku możemy
powiedzieć tylko tyle, że istnieją fale przedstawiające kota zarówno martwego,
jak i żywego w tym samym czasie.
Kiedy w końcu otworzymy pudełko, możemy dokonać pomiaru i zobaczyć czy
kot jest żywy, czy martwy. Proces pomiaru dokonany przez zewnętrznego
obserwatora pozwala na „załamanie" funkcji falowej i precyzyjne zdefiniowanie
stanu kota. Teraz wiemy, czy kot jest żywy, czy martwy. Kluczowy jest tu
proces dokonania pomiaru przez zewnętrznego obserwatora. Wskutek
oświetlenia wnętrza pudełka funkcja falowa zostaje załamana, a obiekt nagle
uzyskuje określony stan.
Innymi słowy, proces obserwacji determinuje końcowy stan obiektu. Słabość
kopenhaskiej interpretacji Bohra sprowadza się do kwestii, czy obiekt
rzeczywiście istnieje przed dokonaniem pomiaru. Według Einsteina
i Schrödingera wszystko to wydaje się absurdalne. Przez resztę swojego życia
Einstein nieustannie zmagał się z tym głębokim filozoficznym problemem, który
i dzisiaj jest przedmiotem gwałtownych dyskusji.

Po długich przemyśleniach Einstein wystąpił z kontrargumentem, którym

chciał definitywnie rozprawić się z teorią kwantową. W 1933 roku wraz ze
swoimi studentami Borisem Podolskim i Nathanem Rosenem zaproponował
nowy eksperyment, który nawet dzisiaj jest przyczyną bólu głowy wielu
fizyków kwantowych i filozofów. Eksperyment EPR (Einstein-Podolski-Rosen)
nie podważył teorii kwantowej, jak się tego Einstein spodziewał, ale pozwolił na
wykazanie, że teoria kwantowa, która i dotąd była wystarczająco dziwna, jest
jeszcze dziwniejsza. Przypuśćmy, że atom emituje dwa elektrony w
przeciwnych kierunkach. Każdy elektron wiruje jak bąk i wskazuje albo górę,
albo dół. Przypuśćmy dalej, że wirują one w przeciwnych kierunkach, tak że
całkowity spin równa się zero, chociaż nie wiemy, jak każdy z nich wiruje. Na
przykład spin jednego elektronu może być skierowany do góry, a drugiego w
dół. Jeśli poczekamy dostatecznie długo, oba elektrony oddalą się od siebie o
miliardy mil. Przed dokonaniem jakiegokolwiek pomiaru nie wiemy, jakie są
spiny tych elektronów. Teraz załóżmy, że w końcu mierzymy spin jednego z
elektronów. Okazuje się na przykład, że jest on skierowany do góry. Stąd
natychmiast poznajemy spin drugiego elektronu, odległego o lata świetlne,
ponieważ jego spin jest przeciwny do spinu jego partnera i musi być skierowany
w dół. Oznacza to, że pomiar w jednej części wszechświata natychmiast
determinuje stan elektronu w innej części wszechświata, co, jak się wydaje,
stanowi naruszenie szczególnej teorii względności. Einstein nazwał to upiornym

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 21 z 26

oddziaływaniem na odległość. Może oznaczać to, że niektóre atomy naszego
ciała mogą być powiązane niewidoczną siecią z atomami w innej części
wszechświata, a więc ruchy naszego ciała mogą natychmiast mieć wpływ na
stan atomów odległych o miliardy lat świetlnych, co pozornie narusza założenia
szczególnej teorii względności. Einstein odnosił się z niechęcią do tej idei,
ponieważ jej konsekwencją była teza, że wszechświat jest nielokalny, co
oznacza, że zdarzenia tu, na Ziemi, natychmiast oddziałują na inną część
wszechświata, przemieszczając się szybciej niż światło.

Przez lata, eksperyment ten był przedmiotem nieporozumień, gdyż

wywołał liczne spekulacje, na przykład takie, że można zbudować EPR-radio
szybsze od światła lub że możemy wysyłać sygnały do przeszłości albo że
możemy ten efekt wykorzystać do telepatii.
Jednakże eksperyment EPR nie negował teorii względności ponieważ nie
pozwala na transmisję żadnej użytecznej informacji. Fizyk John Bell użył
następującego przykładu, aby wyjaśnić problem. Opisał on matematyka
zwanego Bertlmann, który zawsze nosił jedną skarpetkę różową, a drugą
zieloną. Jeżeli wiemy, że na jednej jego stopie jest skarpetka zielona, to wiemy
też, że druga skarpetka musi być różowa. Jednak żaden sygnał nie przebiegał od
jednej stopy do drugiej. Innymi słowy, posiadanie wiedzy o czymś jest czym
innym niż przesyłanie tej wiedzy. Jest kolosalna różnica pomiędzy posiadaniem
informacji a jej transmisją.
Zatem eksperyment EPR nie obala mechaniki kwantowej, lecz jedynie ujawnia,
że jest ona rzeczywiście zwariowana.

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 22 z 26

9.

Przykładowe zadania

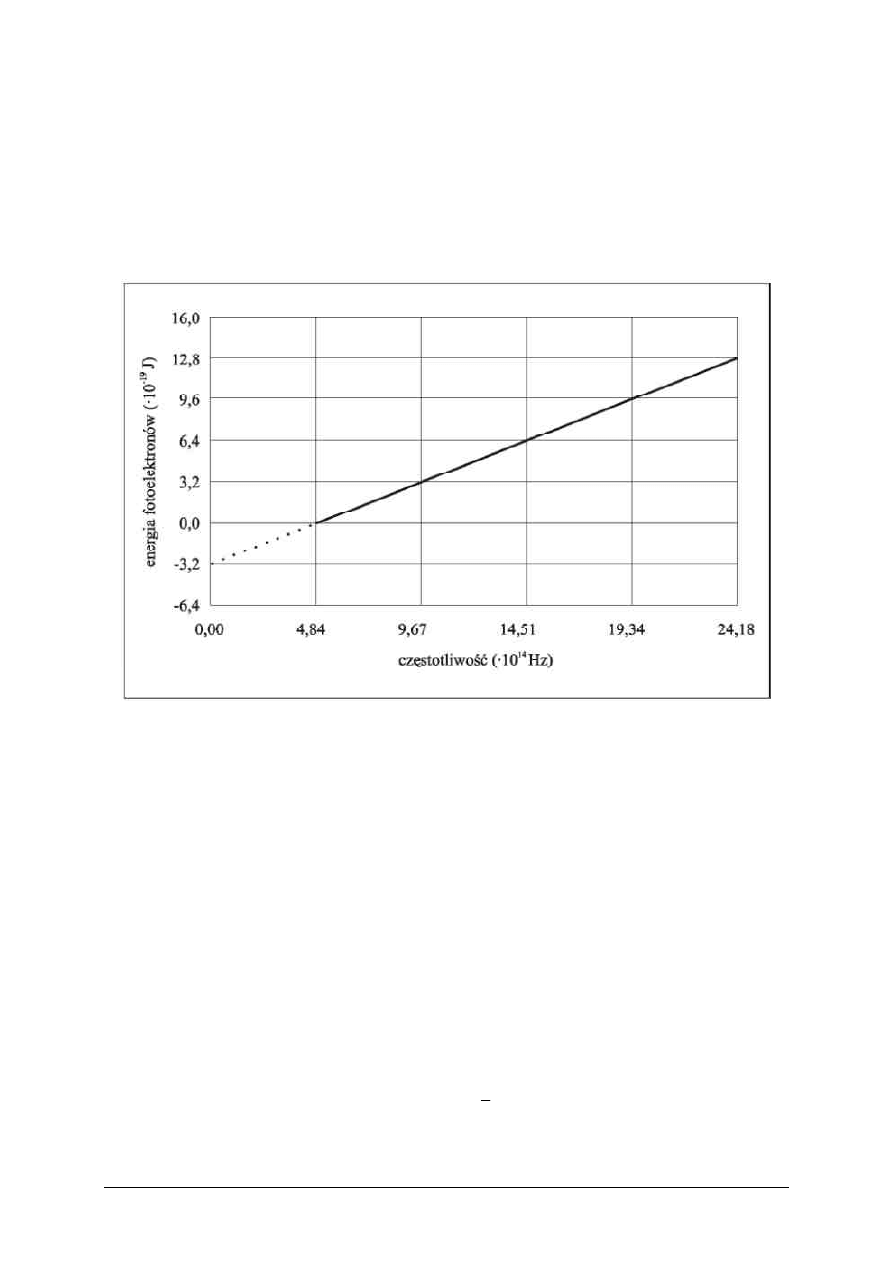
(Matura 2006 - arkusz 2) W pracowni fizycznej wykonano doświadczenie mające na
celu badanie zjawiska fotoelektrycznego i doświadczalne wyznaczenie wartości stałej
Plancka. W oparciu o wyniki pomiarów sporządzono poniższy wykres. Przedstawiono
na nim zależność maksymalnej energii kinetycznej uwalnianych elektronów od
częstotliwości światła padającego na fotokomórkę.

a)

Odczytaj z wykresu i zapisz wartość częstotliwości granicznej
promieniowania dla tej fotokatody.
Rozwiązanie :
Pamiętajmy, że cała energia fotonu zamieniana jest na pracę wyjścia oraz na
energię kinetyczną fotoelektronów. Zjawisko fotoelektryczne zajdzie, gdy
elektrony opuszczą fotokatodę, wcale nie muszą dalej się poruszać.
Stąd E

k

= 0 . Z wykresu odczytujemy wartość, dla której energia

fotoelektronów jest równa zero. Odpowiedź :

Hz

10

4,84

14

o

⋅

=

ν

b)

Oblicz, korzystając z wykresu, pracę wyjścia elektronów z fotokatody.
Wynik podaj w elektronowoltach.
Rozwiązanie :
Posługując się rozważaniami z punktu a) możemy zapisać r-nie Einsteina-
Millikana w postaci :

W

h

=

ν

(E

k

= 0). Odczytując z wykresu

Hz

10

4,84

14

o

⋅

=

ν

i podstawiając do wzoru otrzymujemy :

J

10

3,21

s

1

10

4,84

s

J

10

6,626

W

19

14

34

−

−

⋅

=

⋅

⋅

⋅

⋅

=

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 23 z 26

2eV

10

1,602

10

3,21

W

19

19

≈

⋅

⋅

=

−

−

c)

Oblicz doświadczalną wartość stałej Plancka, wykorzystując tylko dane
odczytane z wykresu oraz zależność

h

W

E

max

kin

ν

=

+

.

Rozwiązanie :
W zadaniu zaznaczone jest wyraźnie, że musimy korzystać z danych
odczytanych z wykresu, a więc nie możemy skorzystać z rozwiązania z
podpunktu b) !
Wobec tego zapisujemy układ równań w postaci :







=

+

=

+

2

2

kin

1

1

kin

h

W

E

h

W

E

ν

ν

i rozwiązujemy go otrzymując

2

kin

1

kin

2

1

E

E

)

h(

−

=

−

ν

ν

. Stąd

2

1

2

kin

1

kin

E

E

h

ν

ν

−

−

=

. Odczytujemy dane z wykresu :

np.

ν

1

= 4,84*10

14

Hz , E

k1

= 0

ν

2

= 9,67*10

14

Hz , E

k2

= 3,2*10

-19

J i podstawiamy do wzoru

otrzymując : h = 6,625 * 10

-34

J s

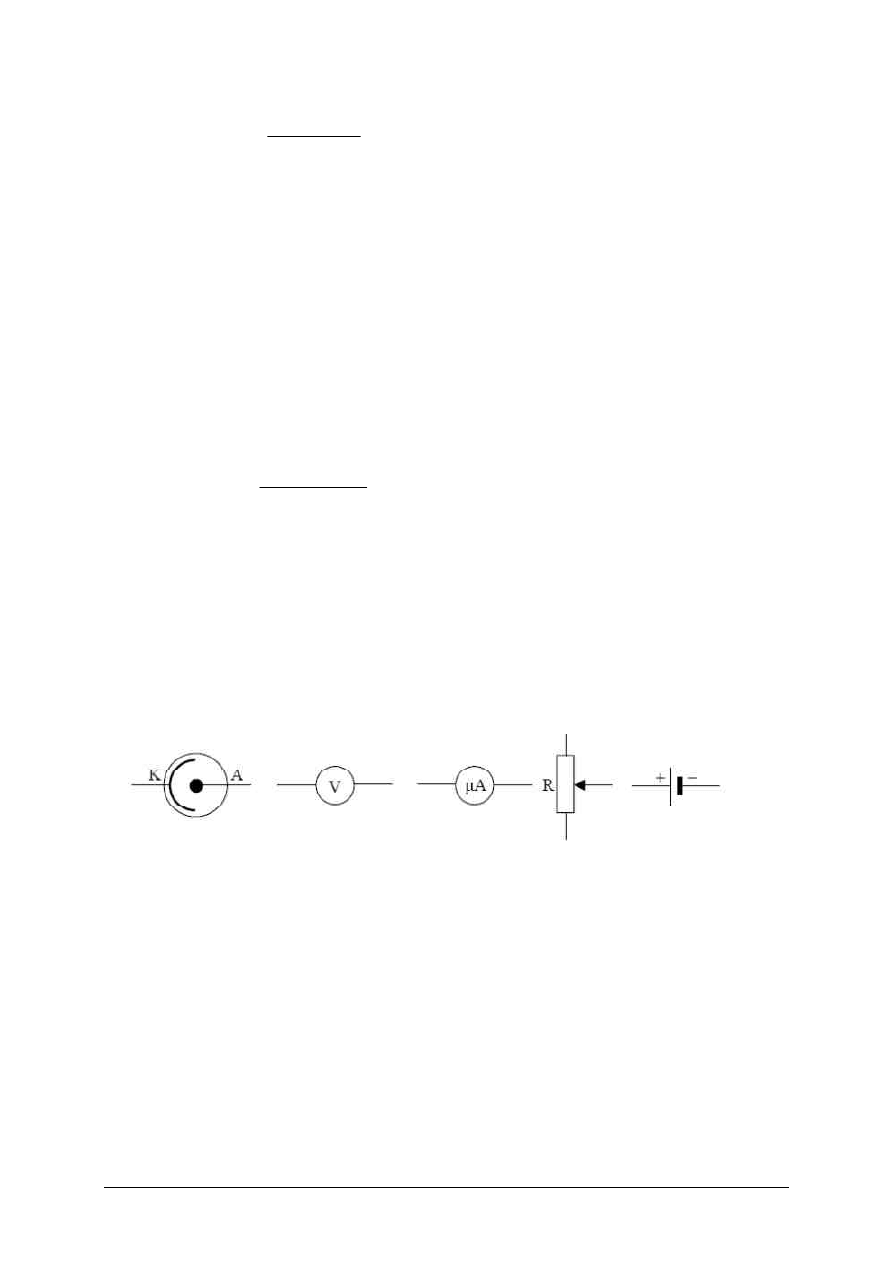
d)

Narysuj

schemat

układu

elektrycznego

pozwalającego

wyznaczyć

doświadczalnie wartość napięcia hamowania fotoelektronów. Masz do
dyspozycji elementy przedstawione poniżej oraz przewody połączeniowe.

Rozwiązanie :

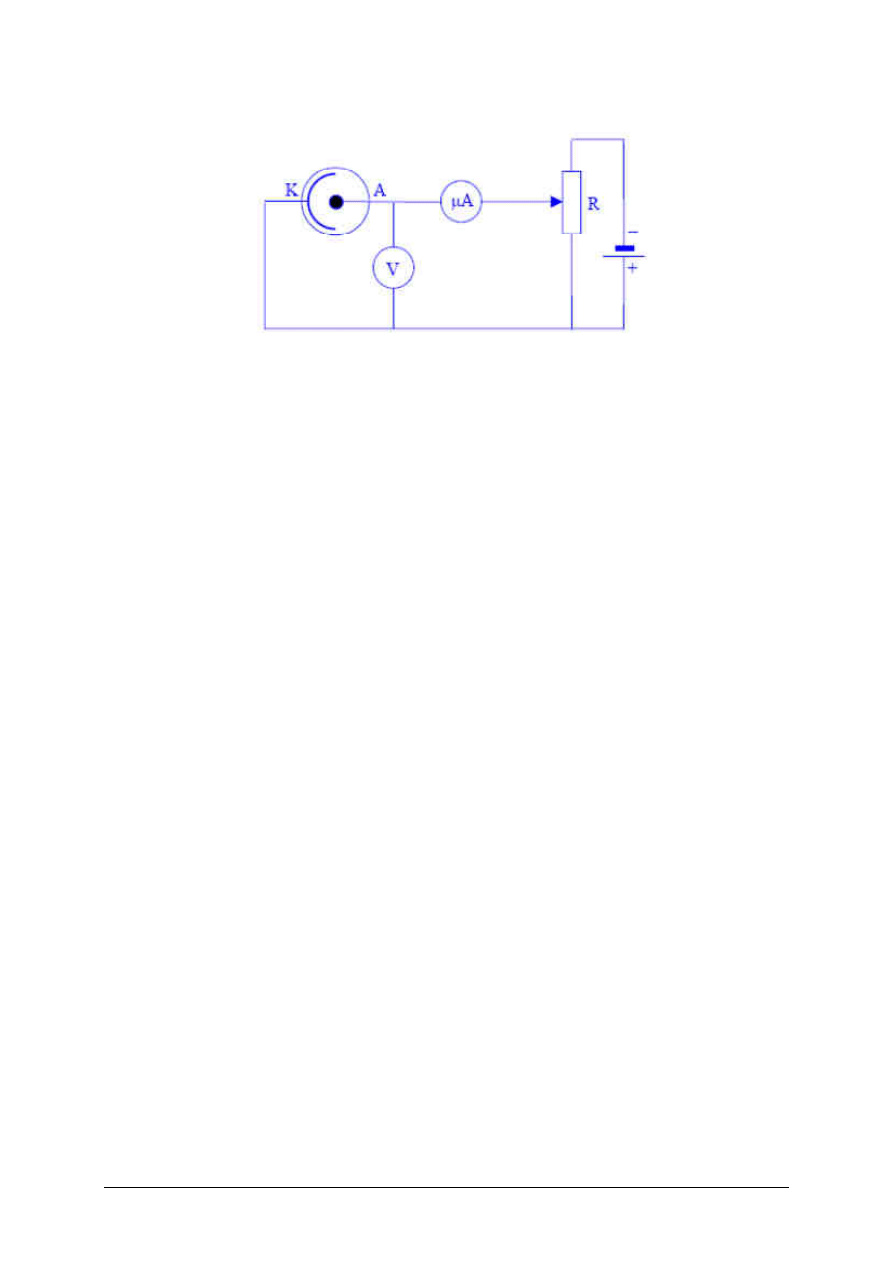
Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 24 z 26

Uwaga: dopuszcza się wstawienie woltomierza za amperomierz , a nie jak na
schemacie przed.

1)

Praca wyjścia cezu wynosi 1,8eV. Jaka jest maksymalna długość fali
światła, które może spowodować wyrzucenie z cezu elektronu o energii
2 eV ?

2)

Oko ludzkie wykrywa światło zielono-żółte (λ = 520nm), jeżeli moc
dostarczana do siatkówki oka wynosi P = 1,5 ·10

-17

W. Ile fotonów w ciągu

czasu t = 1s wpada wtedy na siatkówkę oka ?

3)

Obliczyć energie fotonów odpowiadające granicom widma światła
widzialnego (40•10

-8

m - 76•10

-8

m). Energie wyrazić w dżulach

i elektronowoltach.

4)

Za pomocą betatronu (indukcyjnego akceleratora elektronów) otrzymuje się
fotony promieniowania

γ

o energii E = 50 MeV. Jaka jest długość fali tych

promieni ? Podać wartość liczbową.

5)

Strumień promieniowania słonecznego padający na powierzchnię Ziemi
wynosi

Φ

= 7,96 J/cm

2

• min). Przeliczyć ten strumień na liczbę

fotonów/cm

2

• min zakładając, że średnia długość fali promieniowania

słonecznego dochodzącego do powierzchni Ziemi wynosi

λ

sr = 55 • 10

-8

m.

Podać wartość liczbową.

6)

Ile razy energia fotonu światła fioletowego (

λ

= 40•10

-8

m) jest większa od

średniej energii kinetycznej ruchu postępowego cząsteczki tlenu
w temperaturze pokojowej (t = 20°C)? Podać wartość liczbową.

7)

Ciśnienie promieniowania monochromatycznego wywierane na zwierciadło
płaskie wynosi p = 0,2 • 10

-6

Pa. Znaleźć strumień padającego

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 25 z 26

promieniowania świetlnego, jeżeli zwierciadło pochłania x=1/2 padającego
nań prostopadle promieniowania.

8)

Płytka sodu jest napromieniowywana monochromatyczną wiązką światła.
Obliczyć długość fali odpowiadającą częstotliwości progowej fotoefektu,
jeżeli praca wyjścia dla sodu wynosi W = 2,3 eV. Naszkicuj zależność
fotoprądu od potencjału hamującego, przyłożonego do anody fotoelementu,
dla fal o częstotliwościach

ν

1

i

ν

2

,

ν

1

<

ν

2

oraz równych natężeniach.

9)

Długofalowa granica zjawiska fotoelektrycznego dla platyny wynosi około

λ

1

= 198 • 10

-9

m. Po ogrzaniu platyny do wysokiej temperatury granica ta

wyniosła

λ

2

= 210 • 10

-9

m. O ile ogrzewanie zmniejszyło pracę wyjścia?

Podać wartość liczbową w elektronowoltach.

10)

Na fotokatodę wykonaną z materiału o pracy wyjścia W pada
promieniowanie o częstotliwości

ν

. Znaleźć maksymalną wartość pędu

przekazywaną fotokatodzie przy emisji każdego elektronu. Porównać ten
pęd z pędem padającego fotonu.

11)

Na powierzchnię niklu pada promieniowanie monochromatyczne o
długości fali

λ

= 100 • 10

-9

m. Długofalowa granica zjawiska

fotoelektrycznego dla niklu wynosi

λ

g

= 248 • 10

-9

m. Znaleźć energię

padających fotonów E

f

, pracę wyjścia W oraz maksymalną energię

kinetyczną elektronów E

max

i ich prędkość v

max

. Podać dane liczbowe, a

energie podać w eV.

12)

Powierzchnię cezu naświetlamy promieniowaniem ultrafioletowym a
następnie promieniami

γ

. Znaleźć maksymalną prędkość fotoelektronów w

obu przypadkach, jeśli długość fali promieniowania ultrafioletowego

λ

f

= 15 • 10

-8

m, długość fali promieniowania

γ

λγ

= 25 • 10

-13

m, praca

wyjścia W= 3,05 • 10

-19

J.

Uwaga: W przypadku, gdy energia padającego fotonu jest porównywalna z
energią spoczynkową elektronu, należy uwzględnić efekty relatywistyczne.

13)

Obliczyć i porównać ze sobą długości fal de Broglie'a neutronu i elektronu
o energiach odpowiadających temperaturze T = 300 K.

Opracowanie : Dariusz Nyk dla uczniów I LO im. Ks. Elżbiety w Szczecinku

Strona 26 z 26

14)

Z jaką prędkością powinna poruszać się cząstka o masie spoczynkowej m

0

,

aby jej długość fali de Broglie’a równała się komptonowskiej długości
fali?

15)

Znaleźć długość fali de Broglie'a protonu przyspieszonego różnicą
potencjałów U = 50 kV.

16)

Laser o mocy 0,1 W emituje w próżni monochromatyczną wiązkę światła o
długości fali 633 nm i kołowym przekroju.

a)

Oszacuj liczbę fotonów zawartych w elemencie wiązki światła o długości
jednego metra.

b)

Oblicz wartość siły, jaką wywierałaby ta wiązka światła laserowego
padająca w próżni prostopadle na wypolerowaną metalową płytkę. Do
obliczeń przyjmij, że w ciągu jednej sekundy na powierzchnię płytki pada
1017 fotonów. Załóż, że płytka odbija w całości padające na nią
promieniowanie.

c)

Oblicz najwyższy rząd widma, jaki można zaobserwować po skierowaniu
tej wiązki prostopadle na siatkę dyfrakcyjną posiadającą 400 rys/mm.

17)

Louis de Broglie przewidział, że cząstki elementarne wykazują własności
falowe – cząstka o pędzie p jest falą o długości h/ p Oblicz długość fali
powolnego neutronu o energii kinetycznej E = 1,6⋅10

-21

J. (Pomiń efekty

relatywistyczne).

18)

Na powierzchnię metalu, dla którego praca wyjścia wynosi W = 1,8 eV,
pada:

a) 500 fotonów o energii 2 eV każdy,
b) 1000 identycznych fotonów o energii 1,7 eV każdy.
Oblicz, ile elektronów zostanie wybitych w każdym z podanych
przypadków oraz jaka będzie energia kinetyczna każdego z nich.
Odpowiedź krótko uzasadnij.