X L V I I I K O N F E R E N C J A N AU K O W A
KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN
I KOMITETU NAUKI PZITB
Opole – Krynica
2002
Roman LEWANDOWSKI
1
Tomasz SZYMKOWIAK
2
WPŁ YW UKŁ ADU POMIAROWEGO NA EFEKTY
AKTYWNEJ REGULACJI DRGAŃ KONSTRUKCJI RAMOWYCH
1. Wstęp
Stałą tendencją jest dą żenie do budowy konstrukcji lekkich, o wię kszej rozpię tości, optymal-
nie zaprojektowanych i wykonywanych z materiałó w o wyższej wytrzymałości. Ró wnocześ-
nie konstrukcje te są bardziej wrażliwe na działanie obcią żeń dynamicznych. Drgania
wywołane tymi obcią żeniami mogą w sposó b istotny zmniejszać komfort użytkowania lub,
w skrajnych przypadkach, zagrażać bezpiecznej eksploatacji tych obiektó w. Konieczne staje
się wię c doskonalenie metod redukcji drgań konstrukcji budowlanych. Jednym ze sposobó w
redukcji drgań jest zastosowanie układó w automatycznej regulacji.
Ogó lnie rzecz ujmują c, układ aktywnej regulacji składa się z pewnej liczby czujnikó w
mierzą cych odpowiedź dynamiczną w wybranych punktach konstrukcji, komputera wyzna-
czają cego potrzebne siły aktywnego sterowania oraz siłownikó w wywołują cych wspomniane
siły regulacji. Opis ró żnych układó w aktywnej regulacji umożliwiają cych redukcję drgań
budynkó w można znaleźć w pracy [1].
Analizę dynamicznego zachowania konstrukcji z zainstalowanym układem aktywnej regu-
lacji przeprowadza się zakładając zazwyczaj, że mierzony jest stan dynamiczny całej konstrukcji
gdy tymczasem, ze wzglę dó w technicznych poprzestaje się na pomiarze stanu dynamicznego kilku
wybranych punktó w. Może to w istotny sposó b zmienić działanie rzeczywistego układu regulacji w
poró wnaniu z zachowaniem wynikającym z analizy modelu obliczeniowego.
Niniejsza praca jest poświę cona analizie wpływu rozmieszczenia czujnikó w drgań , ich
ilości i rodzaju na efekty redukcji drgań konstrukcji ramowych poddanych działaniu wiatru.
Wykazano, że rozmieszczenie czujnikó w drgań ma zasadniczy wpływ na efekty regulacji
drgań . W poró wnaniu do przypadku w któ rym mierzy się stan dynamiczny całej konstrukcji
można uzyskać zaró wno zwię kszenie jak i zmniejszenie efektó w regulacji. Niestety przez
nieodpowiedni wybó r punktó w pomiaru można ró wnież spowodować, że układ aktywnej
regulacji stanie się niestabilny.
1
Dr hab. inż., Politechnika Poznań ska
2
Mgr inż., Studio projektowe ADS
118
2. Ró wnania ruchu konstrukcji ramowej
Ró wnanie ruchu rozpatrywanej konstrukcji ramowej daje się zapisać w postaci:
)
(
)
(
)
(
)
(
)
(
1
t
t
t
t
t
p
u
B
Kq
q
D
q
M
+
=
+
+
&
&
&
,
(1)
gdzie symbolami q
u
( ), ( )
t
t
oraz p( )
t oznaczono odpowiednio wektory przemieszczeń , sił
aktywnej regulacji i obcią żeń wę złowych. Wymiar wektoró w
)
(
),
(
t
t p
q
jest ró wny n, a
wektor sił aktywnej regulacji ma wymiar r. Ponadto symbole
K
D
M
,
,
oraz
1
B oznaczają
odpowiednio macierz mas, macierz tłumienia, macierz sztywności oraz prostoką tną macierz o
wymiarze (nxr) określają cą punkty przyłożenia sił aktywnej regulacji. Modelem
obliczeniowym ramy jest tzw. rama ścinana opisana mię dzy innymi w monografii [2]. Rygle
tej ramy są nieskoń czenie sztywne, a masa konstrukcji jest skoncentrowana na poziomie
rygli. Przemieszczenia poziome rygli są jedynymi stopniami dynamicznej swobody ramy.
Obcią żeniem ramy są siły wywołane dynamiczną czę ścią parcia wiatru. Zakłada się , że
obcią żenie to ma charakter losowego procesu ergodycznego wzglę dem czasu. Obcią żenie nie
jest skorelowane przestrzennie. Siłę wymuszają cą działają cą na poziomie stropu i-tej
kondygnacji, któ ra jest ró wnocześnie i-tym elementem wektora
)
(
t
p
, oblicza się ze wzoru:
)
(
)
(
t
w
V
A
C
t
p
i
i
i
z
i
r
=
,
(2)
gdzie symbole
r
,
z
C ,
i
V
,
)
(t
w
i
oraz A
i
oznaczają odpowiednio gę stość powietrza,
wspó łczynnik opływu, średnią prę dkość wiatru i jego losowe fluktuacje na poziomie i-tego
stropu oraz pole ekspozycji stowarzyszone z i-tą kondygnacją . Funkcje opisują ce losowe
fluktuacje prę dkości wiatru wyznacza się w sposó b opisany w pracy [3] na podstawie funkcji
gę stości widmowej zaproponowanej przez Davenporta. Ostatecznie przykładowe fluktuacje
prę dkości wiatru dają się opisać za pomocą wzoru o postaci:
å
=
+
=
N
j
j
j
jk
k
t
t
w
1
)
cos(
)
(
q
w
a
,
(3)
gdzie wspó łczynniki
a
jk
są określone w sposó b podany w pracy [3], a
q
j
to losowe ką ty
fazowe o rozkładzie ró wnomiernym z przedziału
<
>
,
0 2
p
. Ponadto
w
dw
j
i
= -
(
)
1
,
dw w
=
max
/ N gdzie
w
max
jest tzw. czę stością obcię cia funkcji gę stości widmowej, a
N
liczbą harmonicznych uwzglę dnionych w rozwinię ciu (3).
Analizę układó w automatycznej regulacji czę sto przeprowadza się używając ró wnań ruchu
zapisanych za pomocą zmiennych stanu. W rozpatrywanym przypadku ró wnania te mają postać:
&
( )
( )
( )
( )
x
Ax
Bu
Hp
t
t
t
t
=
+
+
,
(4)
gdzie x
q q
( )
( , & )
t
col
=
, a ponadto
ú
ú
û
ù
ê
ê
ë
é
-
-
=
-
-
1
1
D
M
K
M
I
0
A
,
ú
ú
û
ù
ê
ê
ë
é
=
-
1
1
B
M
0
B
,
ú
ú
û
ù
ê
ê
ë
é
=
-
1
M
0
H
.
(5)
3. Metoda automatycznej regulacji drgań
Zgodnie z teorią liniowej regulacji kwadratowej (LQR) wskaźnik jakości sterowania przyję to
w postaci:
119
(
)
ò
¥
+
=
0
)
(
)
(
)
(
)
(
dt
t
t
t
t
J
T
T
Ru
u
Qx
x
,
(6)
gdzie symbolami Q i
R
oznaczono macierze wagowe. Macierz Q jest symetryczna i
pó łdodatnio określona, a macierz
R
jest symetryczna i dodatnio określona.
Oznaczmy ponadto symbolem
)
(t
y
c-wymiarowy wektor zawierają cy te wspó łrzę dne
wektora stanu
)
(t
x
któ re mierzy się za pomocą czujnikó w. Można teraz napisać dodatkowe
ró wnanie o postaci:
)
(
)
(
t
t
Cx
y
=
,
(7)
gdzie C jest zerojedynkową macierzą transformacji o wymiarze (cx2n).
Zakładamy dalej, że siły aktywnej regulacji są określane na podstawie tylko tych
wspó łrzę dnych wektora stanu któ re są znane z pomiaru. Można wię c napisać:
)
(
)
(
)
(
t
t
t
GCx
Gy
u
=
=
,
(8)
gdzie G jest chwilowo nieznaną macierzą sprzę żenia zwrotnego.
Omawiany problem jest traktowany jako zadanie optymalizacji w któ rym należy
wyznaczyć macierz G w taki sposó b aby wskaźnik jakości sterowania (6) osią gną ł wartość
minimalną oraz aby ró wnocześnie były spełnione ograniczenia wyrażone ró wnaniami (4), (7)
i (8). Zadanie to rozwią zano za pomocą metody opisanej w pracy [4]. Po jej zastosowaniu
otrzymuje się do rozwią zania układ trzech macierzowych ró wnań o postaci:
,
)
(
1
1
2
1
-
-
-
=
T
T
T
CLC
PLC
B
R
G
(9)
,
2
2
)
(
)
(
0
RGC
G
C
Q
P
BGC
A
BGC
A
P
=
+
+
+
+
+
T
T
T
(10)
.
)
(
)
(
0
I
L
BGC
A
BGC
A
L
=
+
+
+
+
T
(11)
W ró wnaniach (9) – (11) niewiadomymi są macierze
P
G , oraz
L
.
Można pokazać, że jeżeli znany jest cały wektor stanu to układ ró wnań (9) – (11) jest
ró wnoważny ró wnaniu Riccati’ego. Wtedy
I
C
=
, a ró wnanie (9) przyjmuje postać (12)
,
1
2
1
P
B
R
G
T
-
-
=
(12)
z któ rej to postaci wynika, że rozwią zanie ró wnania (11) staje się nieistotne ponieważ
macierz G nie zależy teraz od
L
. Podstawiają c z kolei (12) do (10) otrzymuje się
nastę pują ce ró wnanie Riccati’ego:
0
P
B
PBR
Q
P
A
PA
=
-
+
+
-
T
T
1
2
1
2
.
(13)
Należy ró wnież zaznaczyć, że postę pują c w opisany powyżej sposó b, w istocie rzeczy,
otrzymuje się rozwią zanie suboptymalne ponieważ w trakcie wyprowadzania ró wnań
(9) – (11) pomija się wpływ wymuszenia zewnę trznego na warunki optymalności. Taki
sposó b postę powania jest czę sto stosowany przy projektowaniu regulatoró w drgań (patrz
prace [1] lub [5]).
Układ ró wnań (9) – (11) rozwią zuje się za pomocą pewnej procedury iteracyjnej któ ra
zostanie kró tko opisana poniżej. Oznaczmy indeksem i numer iteracji, a symbolami
i
i
P
G ,
oraz
i
L i-te przybliżenia macierzy
P
G , i
L
. Na począ tku procesu iteracyjnego należy
przyją ć
0
G (poczatkowe przybliżenie macierzy G ) w ten sposó b aby były spełnione
120
warunki stabilności ruchu konstrukcji z zainstalowanym układem regulacji. Warunki te bę dą
spełnione jeżeli czę ści rzeczywiste wszystkich wartości własnych macierzy
BGC
A
A
+
=
~
bę dą ujemne. Znają c macierz
i
G można rozwią zać ró wnanie (10) wzglę dem
P
, a ró wnanie
(11) wzglę dem
L
otrzymują c w ten sposó b ich nowe przybliżenia
1
+
i
P i
1
+
i
L
. Po
podstawieniu macierzy
i
G w miejsce macierzy G ró wnania (10) i (11) stają się liniowymi
ró wnaniami Lapunowa. Ró wnania te rozwią zuje się za pomocą metody Bartelsa - Stewarta
opisanej w pracy [6]. Nowe przybliżenie macierzy G oblicza się z ró wnania:
1
1
1
1
1
2
1
1
)
(
-
+
+
+
-
+
-
=
T
i
T
i
i
T
i
C
CL
C
L
P
B
R
G
.
(14)
Jeżeli dwa kolejne przybliżenia macierzy
P
G , i
L
niewiele ró żnią się od siebie to
proces iteracyjny koń czy się , a ostatnio otrzymane przybliżenie macierzy G traktuje się jako
poszukiwane rozwią zanie problemu. Przyję to nastę pują ce warunki zakoń czenia iteracji:
1
1
e
£
-
+
i
i
G
G
,
2
1
e
£
-
+
i
i
P
P
,
3
1
e
£
-
+
i
i
L
L
,
(15)
gdzie symbolami
3
2
1
,
,
e
e
e
oznaczono założone dokładności obliczeń .
4. Rozwiązanie ró wnania ruchu
Podstawiają c zależność (8) do ró wnania (4) możemy napisać:
)
(
)
(
~
)
(
t
t
t
Hp
x
A
x
+
=
&
,
(16)
Rozwią zanie ró wnania ruchu (16) można przedstawić w nastę pują cy sposó b [5]:
t
t
t
d
t
t
t
t
t
ò
-
+
=
0
0
)
(
)
(
)
(
)
(
)
(
Hp
x
x
F
F
(17)
gdzie
)
(t
F
jest macierzą fundamentalną obliczaną w nastę pują cy sposó b [5]:
( )
.....
~
~
~
~
exp
)
(
3
3
!
3
1
2
2
!
2
1
+
+
+
+
=
=
A
A
A
I
A
t
t
t
t
t
F
. (18)
Całkę wystę pują cą we wzorze (17) oblicza się numerycznie. Zakłada się , że w małym
przedziale czasu
k
k
t
t
h
-
=
+
1
siły wymuszają ce mają wartość stałą ró wną wartości w chwili
k
t . Można teraz łatwo obliczyć wspomnianą całkę i przedstawić stan układu w chwili t
k
+
1
w
sposó b nastę pują cy:
k
k
k
Hp
x
x
G
F
+
=
+
1
,
(19)
gdzie
.....
~
~
~
3
4
!
4
1
2
3
!
3
1
2
!
2
1
+
+
+
+
=
A
A
A
I
h
h
h
h
G
.
(20)
W powyższych wzorach wielkości z indeksem k są określone w chwili t
k
.
Znają c warunki począ tkowe ruchu oraz siły wymuszają ce można wyznaczyć stan układu
w kolejnych chwilach czasu korzystają c z ró wnania rekurencyjnego (19).
5. Wyniki przykładowych obliczeń
Wykonano przykładowe obliczenia dla ramy jednoprzę słowej budynku ośmiokondygnacyj-
nego. Przyję to nastę pują ce podstawowe dane do obliczeń : wysokość kondygnacji h = 3,0 m,
121
masa stropu
kg
0
,
34560
=
M
, sztywność słupa na zginanie
2
kNm
0
,
191475
=
EJ
,
rozpię tość rygla ramy l=9,0 m, rozstaw ram d=12,0 m. Bezwymiarowy wspó łczynnik
tłumienia 1 i 2 postaci drgań wynosi 2% tłumienia krytycznego. Macierz tłumienia
konstrukcji ma postać:
K
M
D
2
1
a
a
+
=
.
(21)
Założono, że na 1, 4, 6 i 8 kondygnacji są zainstalowane aktywne, cię gnowe tłumiki
drgań . Przyję to ponadto, że macierze Q i
R
są diagonalne, a elementy diagonalne tych
macierzy są ró wne
1300
=
ii
q
oraz
00000001
,
0
=
ii
r
.
Przyję to nastę pują ce wartości parametró w funkcji gę stości widmowej Davenporta:
s
m
V
/
0
,
27
=
,
0
,
10
=
z
C
,
3
/
23
,
1
m
kg
=
r
. Pole ekspozycji stowarzyszone z typową
kondygnacją jest ró wne
2
m
0
,
36
=
A
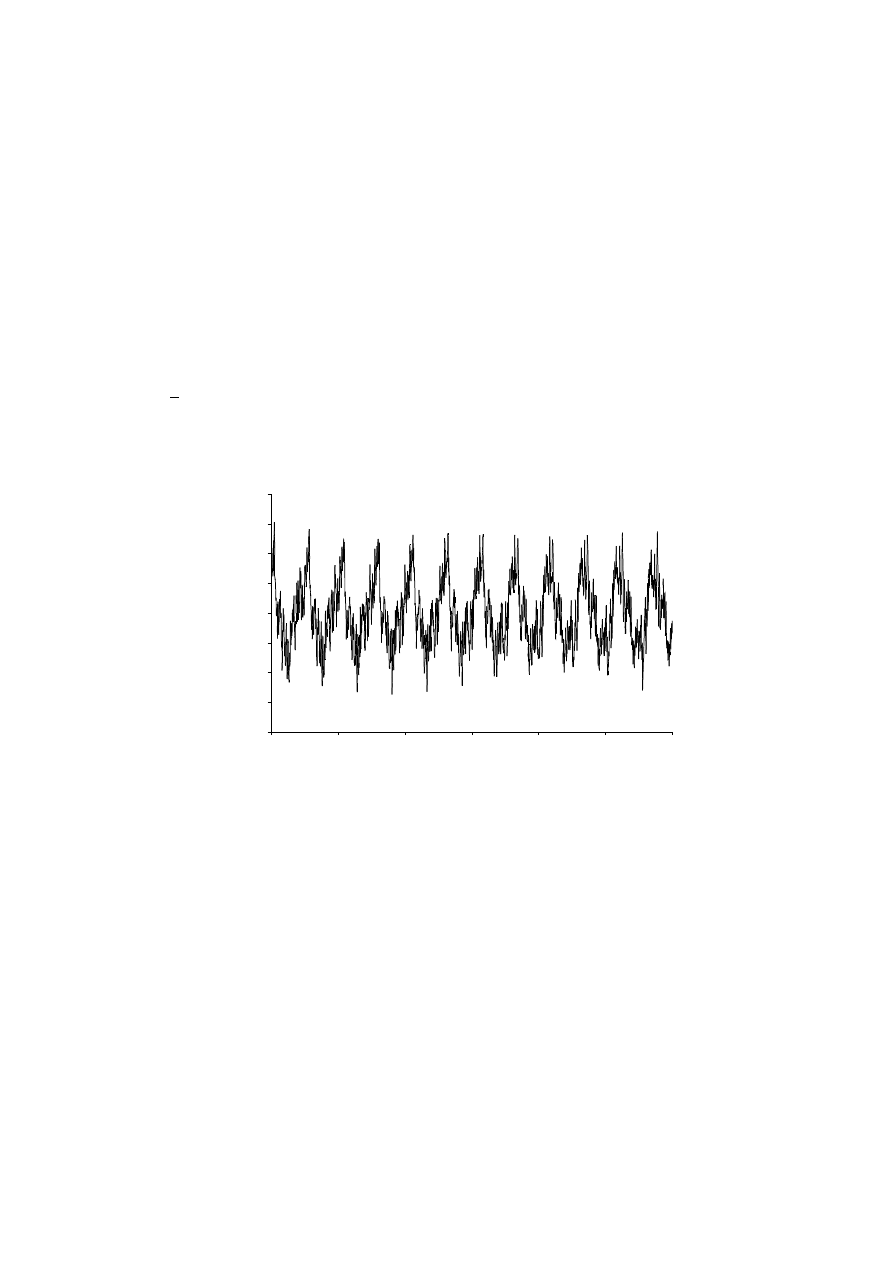
. Przykładowy przebieg siły dynamicznej (na poziomie
rygla 7 kondygnacji) wywołanej fluktuacjami prę dkości średnich wiatru pokazano na rys. 1.
-40000
-30000
-20000
-10000
0
10000
20000
30000
40000
0
20
40
60
80
100
120
czas t [sek]
o
b
c
ią
że
n
ie
w
ia
tr
e
m
(
7
k
o
n
d
y
g
n
a
c
ja
)
[N
]
Rys. 1. Obcią żenie wiatrem na poziomie stropu 7 kondygnacji
Wykonano obliczenia dynamiczne ramy dla ró żnych sposobó w rozmieszczenia czujni-kó w
na konstrukcji. Założono, że można instalować czujniki mierzące przemieszczenia poziome i
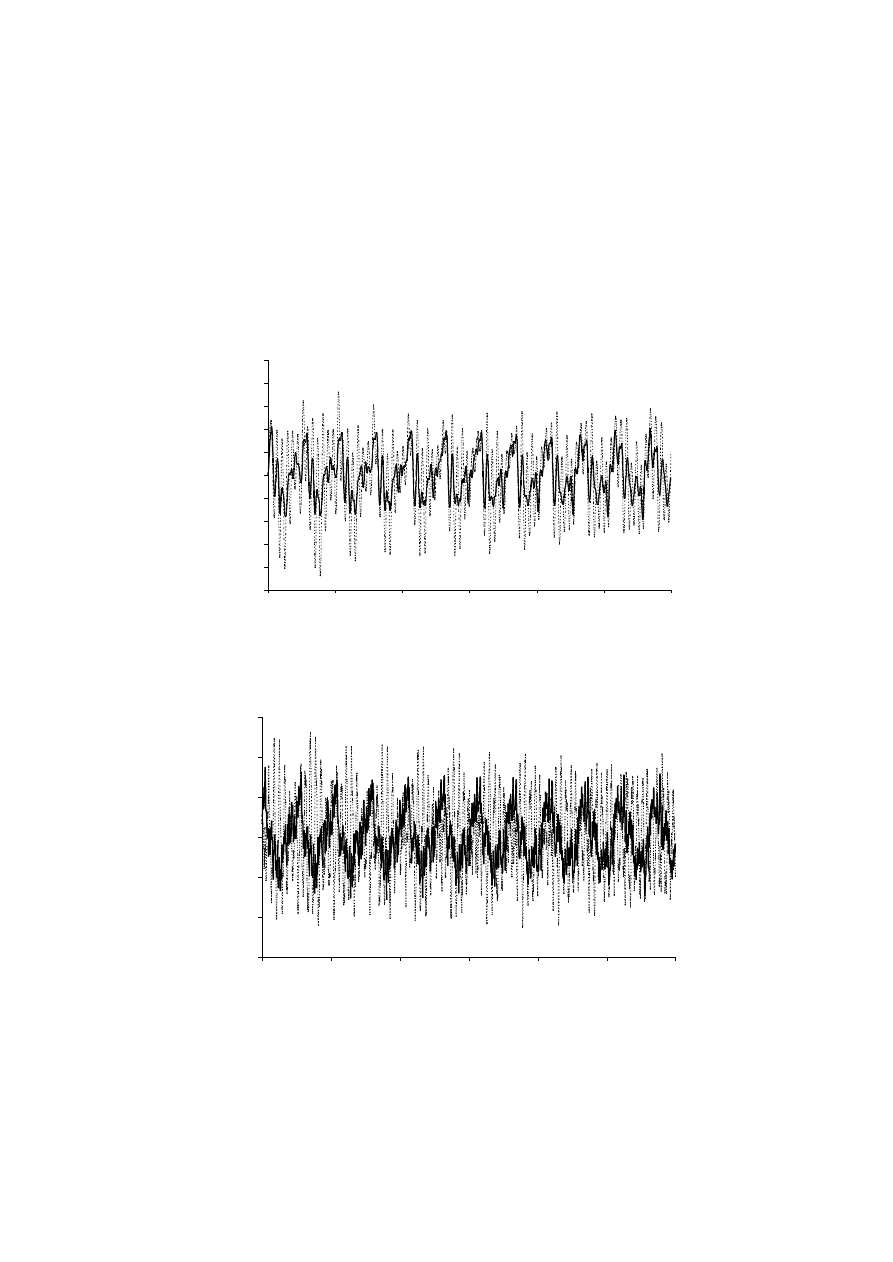
prę dkości stropó w. Na rys. 2 pokazano poró wnanie przemieszczeń poziomych stropu 7
kondygnacji. Linią przerywaną pokazano przemieszczenia konstrukcji bez układu aktywnej
regulacji, a linią ciągłą przemieszczenia ramy na któ rej zainstalowano układ regulacji. Czujniki
tego układu regulacji mierzą prę dkości poziome wszystkich stropó w. Na rys. 3 dokonano
poró wnania przyspieszeń stropu 7 kondygnacji ramy bez układu regulacji z przyspieszeniami
ramy na któ rej zainstalowano układ regulacji. Widać, że zaproponowany układ regulacji
umożliwia znaczną redukcję drgań ramy. Istotna jest znaczna redukcja przyspieszeń ponieważ w
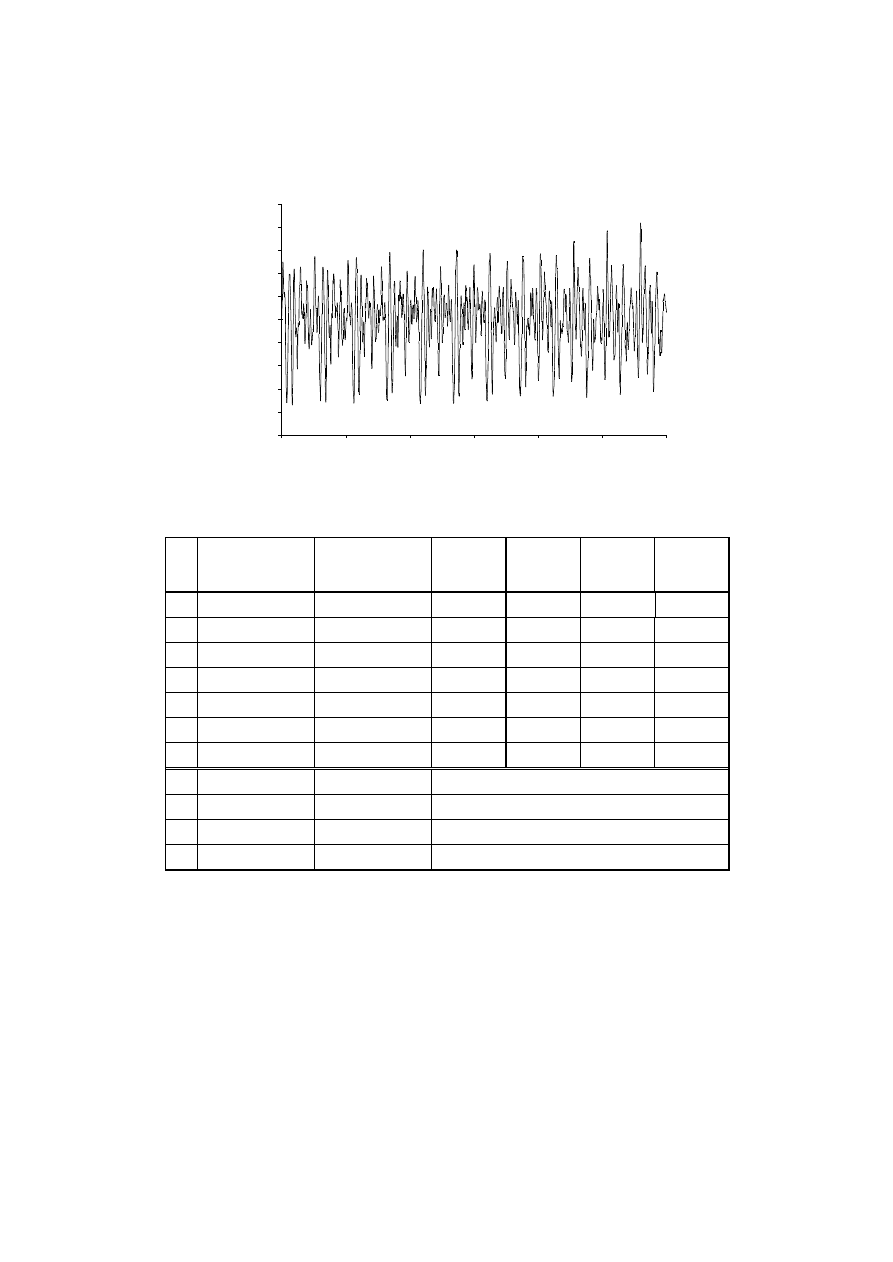
ten sposó b zwię ksza się komfort użytkowania budynku. Na rys. 4 pokazano przebieg siły
regulacji wywoływanej przez siłownik umieszczony na 1 kondygnacji.
W tab. 1 zestawiono najistotniejsze informacje umożliwiają ce poró wnanie efektyw-
ności kilku układó w regulacji ró żnią cych się od siebie rozmieszczeniem czujnikó w.
122
W kolumnach 2 i 3 podano liczbę czujnikó w oraz numery rygli ramy na któ rych te czujniki
są zamontowane. Zauważmy, że przypadek 5 opisuje ramę dla któ rej mierzymy cały wektor
stanu (tzn. przemieszczenia poziome i prę dkości wszystkich rygli ramy), a przypadek 7
dotyczy ramy bez układu regulacji. W kolejnych kolumnach omawianej tablicy zestawiono
maksymalne wartości przemieszczeń , prę dkości, przyspieszeń oraz sił aktywnej regulacji.
Analiza danych zawartych w tablicy upoważnia do sformułowania nastę pują cych wnioskó w:
·
rozmieszczenie czujnikó w na konstrukcji ma istotny wpływ na efekty regulacji,
-0,01
-0,008
-0,006
-0,004
-0,002
0
0,002
0,004
0,006
0,008
0,01
0
20
40
60
80
100
120
czas t [sek]
p
rz
e
m
ie
s
z
c
z
e
n
ie
(
7
k
o
n
d
y
g
n
a
c
ja
)
[m
]
Rys. 2. Poró wnanie przemieszczeń stropu 7 kondygnacji. Linia przerywana – wyniki dla ramy
bez układu regulacji, linia cią gła - wyniki dla ramy z zainstalowanym układem regulacji
-0,15
-0,1
-0,05
0
0,05
0,1
0,15
0
20
40
60
80
100
120
czas t [sek]
p
rz
y
s
p
ie
s
z
e
n
ie
(
7
k
o
n
d
y
g
n
a
c
ja
)
[m
/s
2
]
Rys. 3. Poró wnanie przyspieszeń stropu 7 kondygnacji. Linia przerywana – wyniki dla ramy
bez układu regulacji, linia cią gła – wyniki dla ramy z zainstalowanym układem regulacji
123
-100000
-80000
-60000
-40000
-20000
0
20000
40000
60000
80000
100000
0
20
40
60
80
100
120
czas t [sek]
s
iła
r
e
g
u
la
c
ji
(1
k
o
n
d
y
g
n
a
c
ja
)
[
N
]
Rys. 4. Siła regulacji wywoływana przez siłownik umieszczony na 1 kondygnacji
Tablica 1. Poró wnanie układó w regulacji ró żnią cych się rozmieszczeniem czujnikó w
Lp
Liczba czujnikó w
przemieszczeń
(nr kondygnacji)
Liczba czujnikó w
prę dkości
(nr kondygnacji)
Amplituda
przem.
[m]
Amplituda
prę dkości
[m/s]
Amplituda
przysp.
[m/s
2
]
Amplituda
siły regul.
[N]
1
0
8(1,2,3,4,5,6,7,8) 0,00422
0,01182
0,08761
83484,0
2
4(1,4,6,8)
4(1,4,6,8)
0,00596
0,01898
0,08726
6190,7
3
2(1,8)
2(1,8)
0,00615
0,02272
0,08719
5941,8
4
0
2(1,8)
0,00615
0,02290
0,08720
4651,5
5 8(1,2,3,4,5,6,7,8) 8(1,2,3,4,5,6,7,8) 0,00638
0,01724
0,08723
22304,0
6
0
4(1,4,6,8)
0,00707
0,01893
0,08727
4846,6
7
0
0
0,00875
0,02746
0,13026
0,0
8 8(1,2,3,4,5,6,7,8)
0
układ niestabilny
9
4(1,4,6,8)
0
układ niestabilny
10
4(2,3,5,7)
4(2,3,5,7)
układ niestabilny
11
0
1(8)
układ niestabilny
·
nie jest konieczny pomiar całego wektora stanu po to by uzyskać istotną redukcję drgań ,
·
niektó re konfiguracje czujnikó w są szczegó lnie korzystne, umożliwiają wię kszą redukcję
drgań za pomocą mniejszych sił regulacji w poró wnaniu z układem regulacji któ ry
mierzy cały wektor stanu,
·
istnieją ró wnież konfiguracje czujnikó w destabilizują ce działanie układu regulacji,
·
problem optymalnego rozmieszczenia czujnikó w pomiarowych wymaga dalszych szcze-
gó łowych badań ,
·
informacje podane w tab. 1 sugerują , że racjonalnymi konfiguracjami czujnikó w dla
rozpatrywanej ramy są konfiguracje oznaczone numerami 2, 3 i 4.
124
6. Zakoń czenie
W niniejszej pracy omó wiono pewną metodę aktywnej regulacji drgań konstrukcji ramowych
umożliwiają cą analizę wpływu liczby, rodzaju i rozmieszczenia czujnikó w pomiarowych na
efekty aktywnej regulacji drgań . W szczegó lności badano możliwości redukcji drgań
budynkó w poddanych działaniu sił wywołanych działaniem silnych wiatró w. Wykazano, że
efekty aktywnej regulacji w znacznym stopniu zależą od konfiguracji układu mierzą cego stan
dynamiczny konstrukcji. Problem ten ma istotne znaczenie, a pełne jego rozwią zanie wymaga
przeprowadzenia dalszych badań .
Literatura
[1] SOONG T., Active structural control, Longman Scientific & Technical, New York, 1990.
[2] PAZ M.: Structural dynamics: theory and computation, Van Nostrand Reihold Company,
New York, 1985.
[3] LEWANDOWSKI R.,
Application of semi-empirical model to analysis of votex-excited
vibrations of beams near synchronisation region, in Computational Civil and Structural
Engineering (eds. G.De Roeck and B.H.V. Topping), Civil-Comp Press, Edinburgh, 2000,
s. 133-141.
[4] LEVINE W. S., ATHANS M., On the determinations of the optimal constant output
feedback gains for linear multivariable systems, IEEE Transactions on Automatic
Control, Vol. AC-15, No1, 1970, s. 44-48.
[5] MEIROVITCH L., Dynamics and control of structures, John Wiley, New York, 1990.
[6] BARTELS R., STEWART G., Solution of the matrix equation AX+XB=C; Algorithm
432, Communications of ACM, Vol.15, 1972, s. 820-826.
INFLUENCE OF MEASURMENTS SYSTEM ON EFFECTS
OF ACTIVE VIBRATION CONTROL OF FRAME STRUCTURES
Summary
In this paper, the influence of sensor placements on effects of active control of vibration of
planar frameworks is investigated. In particular, the reduction of vibration caused by wind
loads is of interest. The wind loads are numerically simulated on a basis of well-known
Davenport power spectral density. The linear quadratic regulator theory and the method
proposed by Levine and Athanes [4] are used to design the control system with the reduced-
order state system observer. Results of example calculations for the eighth story framework
with and without control system are presented and discussed. Different sensor placements are
taken into account and it is found that a strong relation between effectiveness of control
system and the sensor configuration exists.
Praca została wykonana w ramach programu badań naukowych finansowanych przez Komitet
Badań Naukowych (BW-11-168/02).