74

Szeregując wielkości

i

F

od największej do najmniejszej i uwzględniając różnice między

kolejnymi wyrazami szeregu wnioskuje się o ich wpływie na wynik końcowy. Jeżeli wyraźnie
widać różnicę między dwoma kolejnymi wyrazami szeregu, z sieci można usunąć wejścia
odpowiadające tym małym wielkościom

i

F

.

3.6.

Sieci neuronowe o radialnych funkcjach bazowych

W najpopularniejszych wielowarstwowych sieciach neuronowych typu perceptronowego

stosuje się zazwyczaj sigmoidalne funkcje aktywacji. Konsekwencją tego faktu jest to, że
neuron pozostaje aktywny wówczas, gdy suma jego sygnałów wejściowych jest większa od
pewnej wartości progowej. W rezultacie, wszystkie neurony aktywne uczestniczą w
formowaniu sygnału wyjściowego sieci. Klasyczne sieci neuronowe nazywa się czasami
aproksymatorami globalnymi [29].

Podejściem alternatywnym jest aproksymacja lokalna, w której sygnał wyjściowy sieci jest

sumą odwzorowań lokalnych. Neurony ukryte stanowią zbiór funkcji bazowych typu
lokalnego. Poszczególne neurony są aktywne tylko w wąskim obszarze przestrzeni danych. W
opisywany sposób działają sieci neuronowe o radialnych funkcjach bazowych (RBF – ang.
Radial Basis Function). Neurony ukryte realizują funkcje zmieniające się radialnie wokół
centrum c i przyjmujące wartości niezerowe wyłącznie w otoczeniu centrum. Ogólna postać
radialnych funkcji bazowych jest następująca

(

)

i

c

x

x

−

=

ϕ

ϕ

)

(

(3.76)

Zakładając dla uproszczenia, że sieć ma tylko jedno wyjście, jest ono opisane zależnością

(

)

∑

=

−

+

=

K

i

i

i

w

w

y

1

0

)

(

c

x

x

ϕ

(3.77)

przy czym K jest liczbą neuronów ukrytych, natomiast wagi sieci oznaczone są przez

i

w

(

K

i

,

,

1 K

=

). Wektory podawane na wejścia sieci mają, analogicznie jak w sieciach

perceptronowych,

długość

N

,

tzn.

[

]

T

2

1

N

x

x

x

K

=

x

.

Wektory

[

]

T

,

2

,

1

,

N

i

i

i

i

x

x

c

K

=

c

reprezentują centra poszczególnych funkcji bazowych. Ogólna

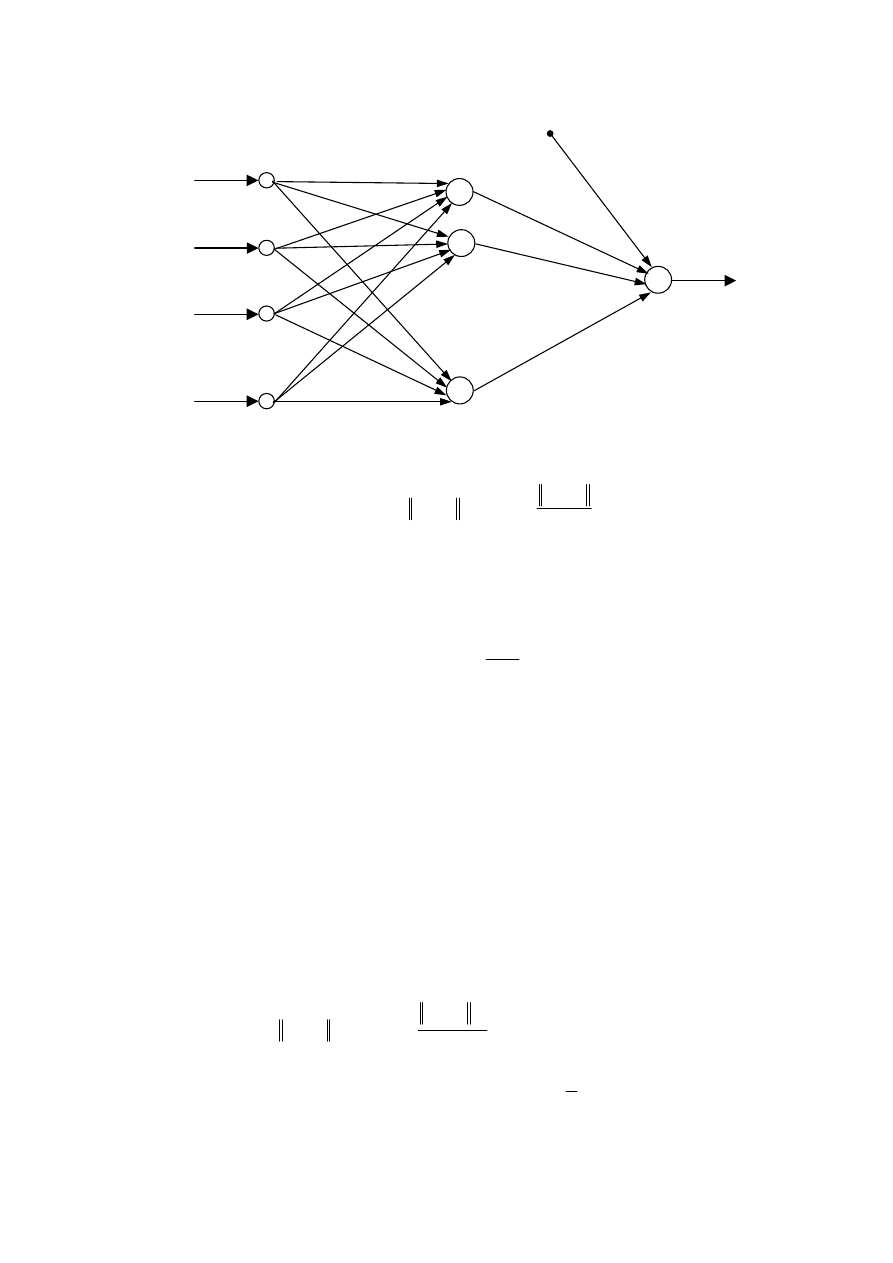
struktura sieci radialnej została przedstawiona na rys. 3.23. Otrzymana sieć ma strukturę
dwuwarstwową, neurony ukryte o radialnych funkcjach bazowych są oczywiście nieliniowe,
natomiast węzeł wyjściowy (sumator) jest liniowy. Analogicznie jak w sieciach
perceptronowych dodatkowe wejście

1

0

=

x

jest polaryzacją sieci.

75

M

3

x

N

x

2

x

1

x

M

y

Polaryzacja

ϕ

ϕ

ϕ

1

0

=

x

K

w

0

w

1

w

2

w

+

Rys. 3.23. Ogólna struktura radialnej sieci neuronowej

Najczęściej używaną funkcją radialną jest funkcja Gaussa

(

)















−

−

=

−

=

2

2

exp

)

(

i

i

i

σ

ϕ

ϕ

c

x

c

x

x

(3.78)

gdzie parametry

i

σ

(

K

i

,

,

1 K

=

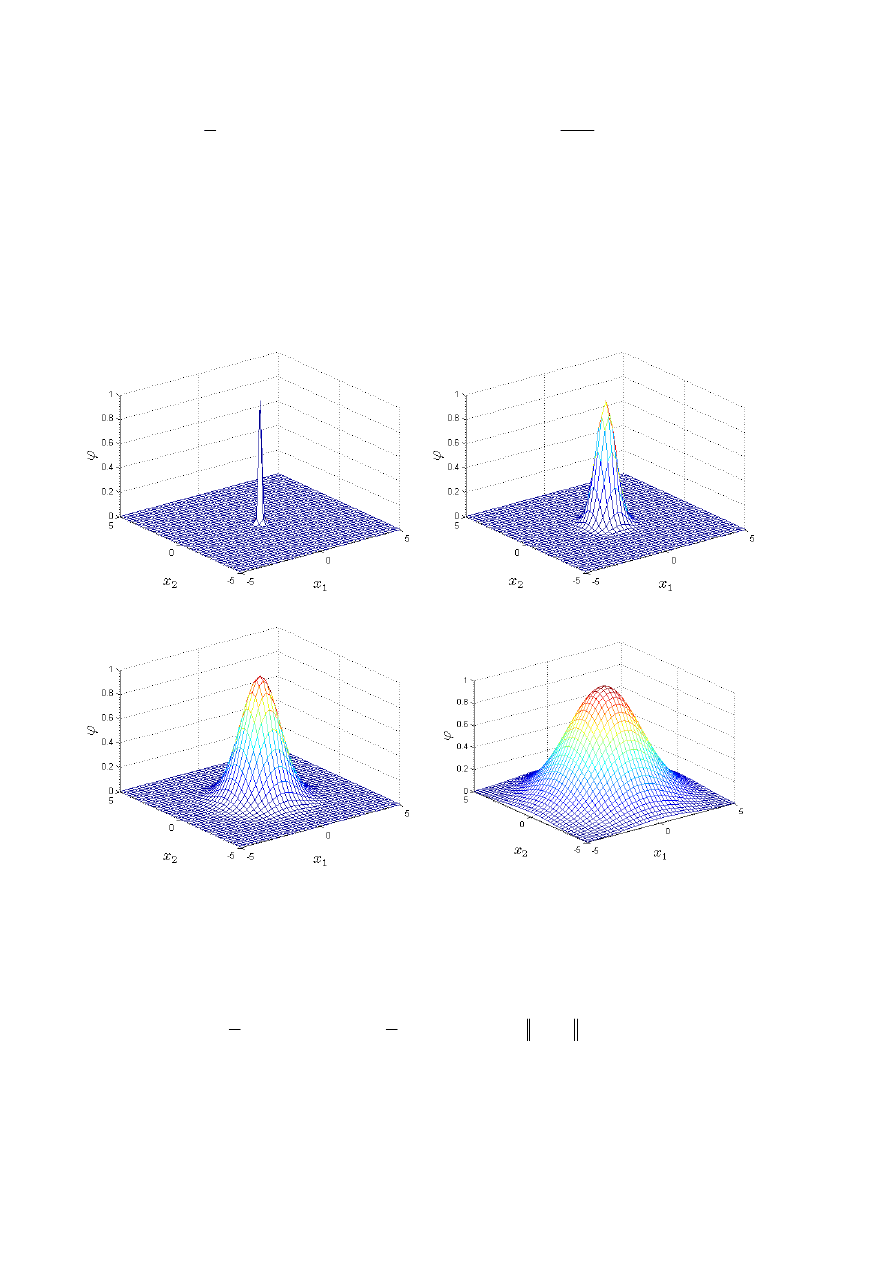
) decydują o szerokości funkcji. Wpływ tego parametru na

kształt funkcji Gaussa przedstawiono na rys. 3.24. Wyjście sieci z radialną funkcją Gaussa
można również zapisać w następujący sposób

∑

∑

=

=















−

−

+

=

K

i

N

j

j

i

j

i

i

c

x

w

w

y

1

1

2

,

2

0

)

(

2

1

exp

)

(

σ

x

(3.79)

W przeciwieństwie do sieci perceptronowych, które mogą mieć dowolną liczbę warstw, sieć
radialna ma stałą strukturę. Co więcej, wszystkie nieliniowe neurony warstwy ukrytej
stosowane w sieciach perceptronowych mają zazwyczaj taką samą funkcję aktywacji, o takich
samych parametrach (np. tangens hiperboliczny), natomiast parametry

i

c funkcji radialnych

poszczególnych neuronów są, z definicji, inne. W przeciwnym wypadku wszystkie neurony
działałyby lokalnie wokół tych samych punktów przestrzeni wielowymiarowej wektora
wejściowego. Parametry

i

σ

poszczególnych funkcji radialnych też są zazwyczaj różne,

jedynie w uproszczonych przypadkach są one stałe.

Ponieważ rząd poszczególnych składowych wektora wejściowego może być różny, dobrze

jest zastosować skalowanie funkcji aktywacji poszczególnych neuronów. Macierze skalujące
o wymiarowości

N

N

×

oznaczone są przez

i

Q (

K

i

,

,

1 K

=

). Otrzymuje się wówczas

uogólnioną funkcję Gaussa postaci

(

)

(

)













−

−

−

=

−

−

−

=

















−

−

=

−

=

)

(

)

(

2

1

exp

)

(

)

(

exp

2

exp

)

(

T

T

T

2

i

i

i

i

i

i

i

i

i

i

i

c

x

C

c

x

c

x

Q

Q

c

x

c

x

c

x

x

i

Q

Q

σ

ϕ

ϕ

(3.80)

76

gdzie macierz

i

i

Q

Q

C

i

T

2

1

=

pełni rolę skalarnego czynnika

2

2

1

i

σ

standardowej funkcji

Gaussa (3.78). Sieci, w których wykorzystuje się macierze skalujące nazywane są sieciami
HRBF (ang. Hyper Radial Basis Function). Elementy macierzy skalujących są dodatkowymi
parametrami modelu neuronowego, ich dobór pozwala dopasować sieć do rozwiązywanego
problemu. Z drugiej jednak strony, wprowadzenie macierzy skalujących powoduje, że liczba
parametrów sieci gwałtownie wzrasta, co ma duże znaczenie podczas uczenia. Dlatego też
największe praktyczne znacznie mają sieci HRBF o diagonalnych macierzach skalujących

)

,

,

(

diag

,

1

,

N

i

i

i

q

q

K

=

Q

.

a)

b)

c)

d)

Rys. 3.24. Wykresy funkcji bazowej Gaussa: a)

1

,

0

=

σ

, b)

5

,

0

=

σ

, c)

1

=

σ

, d)

2

=

σ

3.6.1.

Uczenie sieci neuronowych o radialnych funkcjach bazowych

Uczenie, czyli dobór parametrów sieci radialnych można sformułować jako minimalizację

błędu modelu dla wszystkich S próbek

(

)

∑

∑

∑

=

=

=













−

−

+

=

−

=

S

s

K

i

i

i

S

s

s

d

w

w

s

d

s

y

E

1

2

1

0

1

2

)

(

2

1

))

(

)

(

(

2

1

c

x

ϕ

(3.81)

W wyniku rozwiązania powyższego zadania optymalizacji wyznacza się wagi sieci, centra
funkcji bazowych oraz parametry określające kształt funkcji bazowych. W przypadku
klasycznych sieci RBF będą to współczynniki

i

σ

(

K

i

,

,

1 K

=

), dla sieci HRBF będą to

77

macierze

i

Q (

K

i

,

,

1 K

=

), natomiast dla uproszczonych sieci HRBF będą to diagonalne

macierze

i

Q .

Uwzględniając wyłącznie wagi sieci, funkcja błędu jest kwadratowa, a więc jeżeli

optymalizacji podlegają tylko wagi, to zadanie optymalizacji można bardzo efektywnie
numerycznie (bez iteracji, znajdując minimum globalne) rozwiązać metodą najmniejszych
kwadratów. Spostrzeżenie to jest podstawą algorytmu hybrydowego uczenia radialnych sieci
neuronowych. Składa się on z dwóch, powtarzających się etapów. Struktura algorytmu jest
następująca:

1.

Wybór początkowych wartości wag (zwykle w sposób losowy), wybór centrów funkcji

bazowych, wybór parametrów

i

σ

lub macierzy

i

Q .

2.

Dobór wag sieci przy wykorzystaniu metody najmniejszych kwadratów.

3.

Optymalizacja parametrów

i

σ

lub

i

Q na drodze nieliniowej optymalizacji.

4.

Przejście do kroku 2.

Inicjalizacja parametrów funkcji bazowych ma bardzo duże znaczenie, nawet większe niż

w przypadku sieci perceptronowych. Jest to spowodowane tym, że funkcje wykładnicze
charakteryzują się bardzo silnymi nieliniowościami, prawdopodobieństwo utknięcia w
minimum lokalnym jest bardzo duże. Dlatego też stosuje się bardzo efektywne algorytmy
samoorganizacji [29].

W drugim kroku algorytmu hybrydowego parametry

i

σ

lub

i

Q są zamrożone, wyznacza

się wyłącznie wagi sieci. Dla S próbek uczących można sformułować układ równań

























=

















































)

(

)

2

(

)

1

(

))

(

(

))

(

(

))

(

(

1

))

2

(

(

))

2

(

(

))

2

(

(

1

))

1

(

(

))

1

(

(

))

1

(

(

1

1

0

2

1

2

1

2

1

S

y

y

y

w

w

w

S

S

S

K

K

K

K

M

M

K

M

O

M

M

M

K

K

x

x

x

x

x

x

x

x

x

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

(3.82)

który można zapisać jako

y

Gw

=

. Podstawiając w miejsce wektora wyjściowego wzorce

[

]

T

2

1

S

d

d

d

K

=

d

można wyznaczyć analitycznie optymalny wektor wag

d

G

w

+

=

(3.83)

Do obliczenia macierzy pseudoodwrotnej

+

G można zastosować rozkład SVD.

W trzecim kroku algorytmu hybrydowego wagi zostają zamrożone, optymalizacji

podlegają jedynie parametry mające nieliniowy wpływ na wyjście sieci. Stosuje się do tego
celu dowolną procedurę nieliniowej optymalizacji, analogicznie jak ma to miejsce w
przypadku klasycznej sieci jednokierunkowej wielowarstwowej, np. procedurę zmiennej
metryki lub gradientów sprzężonych. Podczas obliczeń składowe wektora gradientu funkcji
kryterialnej E względem parametrów

i

σ

lub

i

Q oblicza się w sposób analityczny. Na

przykład, dla klasycznej sieci radialnej pochodne względem parametrów

i

σ

mają postać

∑

∑

∑

=

=

=















−















−

−

−

=

∂

∂

−

=

∂

∂

S

s

i

j

i

j

N

j

j

i

j

i

i

j

i

S

s

j

i

c

x

c

x

w

s

d

s

y

c

s

y

s

d

s

y

c

E

1

2

,

1

2

,

2

,

1

,

)

(

)

(

2

1

exp

))

(

)

(

(

)

(

))

(

)

(

(

σ

σ

(3.84)

78

dla wszystkich

K

i

,

,

1 K

=

,

N

j

,

,

1 K

=

, oraz

∑

∑

∑

=

=

=





























−

−

−

=

∂

∂

−

=

∂

∂

S

s

i

N

j

j

i

j

i

i

S

s

i

i

c

x

w

s

d

s

y

s

y

s

d

s

y

E

1

3

1

2

,

2

1

1

)

(

2

1

exp

))

(

)

(

(

)

(

))

(

)

(

(

σ

σ

σ

σ

(3.85)

dla

K

i

,

,

1 K

=

.

Uczenie sieci radialnych można również zorganizować tak samo jak sieci

perceptronowych, gdzie wszystkie parametry sieci są optymalizowane jednocześnie. Wagi
względem wag dla

0

=

i

oblicza się ze wzoru

∑

∑

=

=

−

=

∂

∂

−

=

∂

∂

S

s

S

s

s

d

s

y

w

s

y

s

d

s

y

w

E

1

1

0

0

))

(

)

(

(

)

(

))

(

)

(

(

(3.86)

natomiast dla

K

i

,

,

1 K

=

∑

∑

∑

=

=

=





























−

−

−

=

∂

∂

−

=

∂

∂

S

s

N

j

j

i

j

i

i

S

s

i

i

c

x

w

s

d

s

y

w

s

y

s

d

s

y

w

E

1

1

2

,

2

1

)

(

2

1

exp

))

(

)

(

(

)

(

))

(

)

(

(

σ

(3.87)

W praktyce jednak najskuteczniejszy okazuje się algorytm hybrydowy.

3.6.2.

Sieci perceptronowe a radialne

Jak już wspomniano na wstępie, klasyczne sieci wielowarstwowe (perceptronowe) są

aproksymatorami globalnymi, podczas gdy sieci radialne, w których stosuje się funkcje
aktywacji mające wartości niezerowe jedynie w pewnym otoczeniu centrów, są
aproksymatorami lokalnymi. Sieci perceptronowe, ze względu na globalny charakter funkcji
aktywacji, nie mają wbudowanego mechanizmu pozwalającego zidentyfikować region, w
którym aktywność danego neuronu jest największa. Bardzo trudno jest powiązać obszar
aktywności poszczególnych neuronów z odpowiednim obszarem danych uczących. Oznacz
to, że trudno jest wyznaczyć wartości początkowe wag. Uczenie sieci perceptronowej
sprowadza się do nieliniowej optymalizacji, w której podstawowym problemem jest
występowanie minimów lokalnych.

Ponieważ stosowane w sieciach radialnych funkcje aktywacji są funkcjami lokalnymi,

stosunkowo łatwo można powiązać ich parametry z fizycznym rozmieszczeniem danych
uczących. W rezultacie można wyznaczyć wartości początkowe parametrów modelu. Stosując
hybrydowy algorytm uczenia sieci radialnych można oddzielić etap doboru parametrów
funkcji bazowych od etapu dobory wag, co znacznie upraszcza i przyspiesza uczenie. Można
dodatkowo zastosować bardzo skuteczną metodę kontroli liczby neuronów ukrytych –
algorytm ortogonalizacji Grahama-Schmidta [29]. Dzięki temu, w odróżnieniu od sieci
perceptronowych gdzie architektura sieci dobierana jest zwykle na drodze eksperymentalną
metodą prób i błędów (należy zwykle nauczyć wiele sieci o różnej architekturze), dla sieci
radialnych kształtowanie architektury jest integralnym fragmentem procesu uczenia.