I zasada termodynamiki



U = q + w

II zasada termodynamiki

T

dq

dS



ENERGIA WEWNĘTRZNA U

ENTALPIA H = U + pV

ENTROPIA S

Nowe funkcje termodynamiczne

Energia swobodna

Helmholtza

F =

U

– TS

TERMODYNAMICZNE FUNKCJE STANU

Entalpia swobodna

Gibbsa

G =

H

- TS

Josiah Willard Gibbs

(1839 –1903)

Hermann Ludwig Ferdinand von Helmholtz
(1821-1894)

Energia swobodna Helmholtza F = U – TS

I zasada termodynamiki : dU = q

el

+ w

el

= đq + đw

II zasada termodynamiki: đq ≤T ∙dS

dU ≤ T dS + đw

dU – T dS ≤ đw

T = const

dU – d(TS) ≤ đw

d ( U – TS) ≤ đw

dF ≤ đw

w = w

obj

+ w

nieobj

V = const

w

obj

= 0 dF ≤ đw

nieobj

T

dq

dS



ΔF = (F

k

– F

p

) ≤ w

nieobj

W warunkach izotermiczno-izochorycznych różnica pomiędzy energią swobodną Helmholtza dla

dwóch stanów układu, stanu koocowego i początkowego, określa pracę, którą układ może

wymienid z otoczeniem.

ΔF jest potencjałem termodynamicznym w procesie izotermiczno-izochorycznym.

w = w

obj

+ w

nieobj

Entalpia swobodna Gibbsa G = H - TS

Entalpia H = U + pV

dH = dU + pdV + Vdp

I zasada termodynamiki: dU = đq+ đw

II zasada termodynamiki: dq ≤T ∙dS

dU ≤ T dS + đ w

dH = dU + pdV + Vdp

dH ≤ T dS + đw + pdV + Vdp ,

p = const

dH ≤ T dS + đw + pdV

dH – T dS ≤ đw+ pdV

T= const

d(H – TS) ≤ đw + pdV

w = w

obj

+ w

nieobj

w

nieobj

= w - w

obj

dw

nieobj

= dw –(-pdV)

dG ≤ đw + pdV

dw + pdV = dw

nieobj

dG ≤ dw

nieobj

T

dq

dS



W warunkach izotermiczno-izobarycznych różnica pomiędzy entalpią swobodną Gibbsa dla dwóch

stanów układu, stanu koocowego i początkowego, określa pracę, którą układ może wymienid z

otoczeniem.

ΔG jest potencjałem termodynamicznym w procesie izotermiczno-izobarycznym.

w = w

obj

+ w

nieobj

ΔF i ΔG jako kryteria określające charakter procesu

Zdolnośd układu do wykonania pracy jest miarą tendencji do SAMORZUTNEGO przebiegu procesu .
Gdy układ nie wykonuje pracy – znajduje się w stanie równowagi

.

Procesy izotermiczno-izochoryczne ΔF ≤ w

nieobj

Ponieważ praca oddana przez układ do otoczenia w procesie samorzutnym jest ujemna, stąd
możliwe jest samorzutne przejście układu ze stanu początkowego do koocowego gdy ΔF < 0,
co oznacza, że F

k

< F

p

w procesach samorzutnych energia swobodna Helmholtza maleje

.

Proces jest odwracalny (układ znajduje się

w stanie równowagi

) gdy F

k

= F

p

, czyli gdy nie ma

zmiany energii swobodnej Helmholtza

ΔF=0

.

Procesy izotermiczno-izobaryczne ΔG ≤ w

nieobj

Ponieważ praca oddana przez układ do otoczenia w procesie samorzutnym jest ujemna, stąd
możliwe jest samorzutne przejście układu ze stanu początkowego do koocowego gdy ΔG < 0,
co oznacza, że G

k

< G

p

w procesach samorzutnych entalpia swobodna Gibbsa maleje.

Proces jest odwracalny (układ znajduje się

w stanie równowagi

) gdy G

k

= G

p

, czyli gdy nie ma

zmiany entalpii swobodnej Gibbsa

ΔG=0

.

Wpływ temperatury i objętości na energię swobodną F

F = U – TS

F= f(T,V)

dV

V

F

dT

T

F

dF

T

V





































dF = dU – TdS – SdT

dF = dq + dw –TdS – SdT

Gdy dq =TdS (proces odwracalny) i

dw = -pdV (możliwe jest wykonanie tylko pracy objętościowej)

dF= - SdT

– pdV

Z porównania różniczek funkcji otrzymujemy zależnośd:

p

V

F

oraz

S

T

F

T

V









































Wpływ temperatury i ciśnienia na entalpię swobodną G

G= H – TS

G= f(T,p)

dp

p

G

dT

T

G

dG

T

p





































dG = dH – TdS – SdT

dG = dU + pdV + Vdp –TdS –SdT

dG = dq + dw + Vdp – TdS - SdT

Gdy dq =TdS (proces odwracalny) i
dw = -pdV (możliwe jest wykonanie tylko pracy objętościowej)

dG = - SdT + Vdp

Z porównania różniczek funkcji otrzymujemy zależnośd:

V

p

G

oraz

S

T

G

T

p







































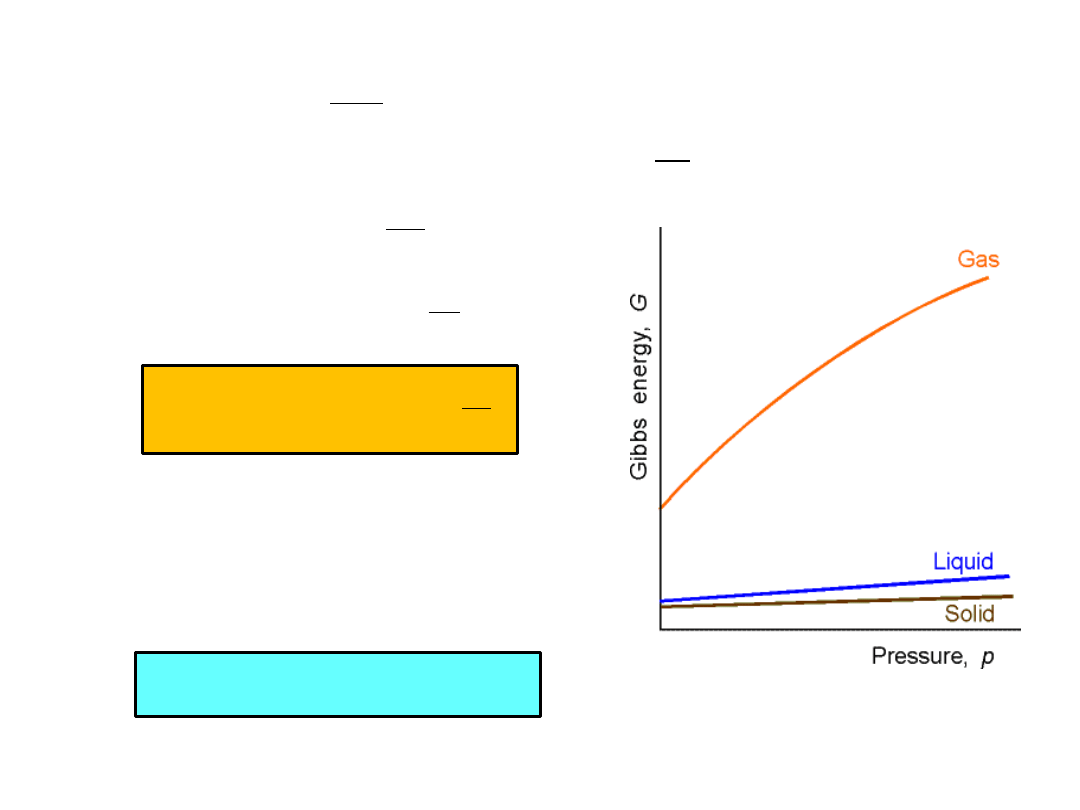
Wpływ ciśnienia na molową entalpię swobodną Gibbsa (T=const)

m

T

m

V

p

G



















Gdy gaz spełnia równanie stanu gazu doskonałego

p

RT

V

m



dp

p

RT

dp

V

dG

m

m











2

1

p

p

1

m

2

m

p

dp

RT

)

(p

G

)

(p

G



















1

2

1

m

2

m

p

p

ln

RT

)

(p

G

)

(p

G

dla cieczy i ciał stałych V

m



const.

)

p

(p

V

)

(p

G

)

(p

G

1

2

m

1

m

2

m







Entalpia swobodna wzrasta ze wzrostem ciśnienia





2

1

p

p

m

1

m

2

m

dp

V

)

(p

G

-

)

(p

G

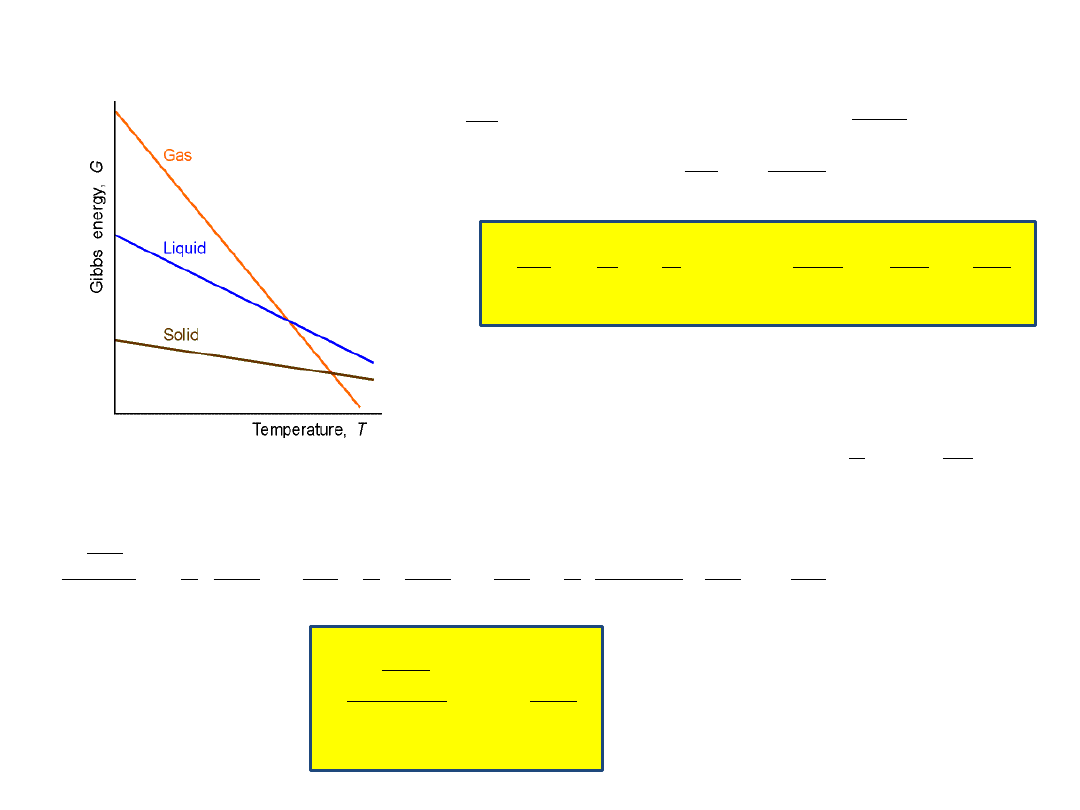
Wpływ temperatury na entalpię swobodną Gibbsa (p=const):

S

T

G

p





















G = H

– T S

S

T

H

G







T

H

G

T

G

p





















T

ΔH

T

ΔG

T

ΔG

lub

T

H

T

G

T

G

p

p













































W procesie izobarycznym (p= const) zmiana entalpii
swobodnej Gibbsa zależy tylko od zmian temperatury

Równania (



) można zapisad w innej formie, wprowadzając nową wielkośd:

(



)

T

ΔG

lub

T

G

Pod stałym ciśnieniem zmiany tych wielkości są skutkiem zmian temperatury, stąd

2

p

2

p

p

T

ΔH

T

ΔG

T

ΔH

ΔG

T

1

T

ΔG

T

ΔG

T

1

T

ΔG

T

ΔG

T

1

T

T

ΔG



















































































































2

p

T

ΔH

T

T

ΔG













































Równanie Gibbsa- Helmholtza

Funkcje termodynamiczne

Energia wewnętrzna U I zasada termodynamiki dU = q

el

+ w

el

Entalpia H

H = U + pV

Entropia S

II zasada termodynamiki

Energia swobodna F F = U - TS

Entalpia swobodna G G = H - TS

T

dq

dS



U

H

F

G

+ pV

- T S

- T S

+ pV

G = H – TS = U + pV – TS = F + pV

Różniczki zupełne funkcji termodynamicznych

Energia wewnętrzna U

dU = q

el

+ w

el

U = f(T,V) dU = c

V

dT

– pdV

U = f(S,V) dU = TdS - pdV

Entalpia H

H = U + pV

H = f(T,p) dH = c

p

dT + Vdp

H = f(S,p) dH = TdS + Vdp

Entropia S

S = f(T,V)

S = f(T,p)

T

dq

dS



Energia swobodna F

F = U - TS

F = f(T,V) dF= -SdT

– pdV

Entalpia swobodna G

G = H - TS

G = f(T,p) dG = -SdT + Vdp

dV

V

R

dT

T

c

dS

V





dp

p

R

dT

T

c

dS

p





Funkcje termodynamiczne układu wieloskładnikowego

W układzie wieloskładnikowym funkcje termodynamiczne zależą od ciśnienia,
temperatury, objętości i ilości składników tworzących układ

(składu układu)

.

F = f ( V, T,

n

1

, n

2

, .........n

k

); G = f ( p, T,

n

1

, n

2

, ...........n

k

)

Zmiana liczby moli składników powoduje zmianę wartości funkcji termodynamicznej:

...

dn

n

F

dT

T

F

dV

V

F

dF

1

,...

n

,

n

T,

V,

1

,...

n

V,

,..

n

T,

3

2

1

1

























































.

..

dn

n

G

dT

T

G

dp

p

G

dG

1

,...

n

,

n

T,

p,

1

,...

n

p,

,...

n

T,

3

2

1

1

























































dF = – pdV – SdT

układ jednoskładnikowy

dG = + Vdp – SdT

układ jednoskładnikowy

Entalpia swobodna układu wieloskładnikowego

)

n

T,

p,

i

i

n

G

μ



















.

..

dn

n

G

dT

T

G

dp

p

G

dG

1

,...

n

,

n

T,

p,

1

,...

n

p,

,...

n

T,

3

2

1

1

























































Potencjał chemiczny składnika

określa zmianę entalpii swobodnej



G układu,

gdy zmieniamy ilośd tego składnika w układzie w warunkach stałego składu innych składników
oraz p = const i T = const









i

i

i

dn

μ

SdT

Vdp

dG

Różniczka zupełna entalpii swobodnej układu wieloskładnikowego

V -S

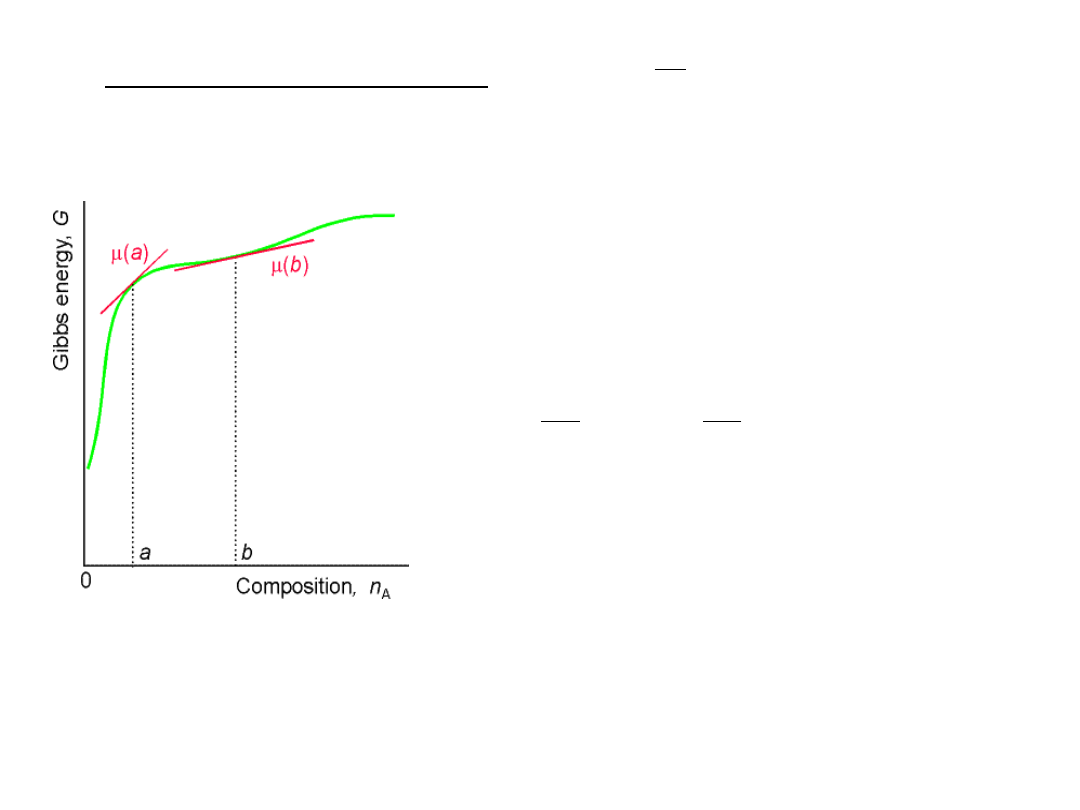
Potencjał chemiczny składnika układu

)

n

T,

p,

i

i

n

G

μ



















jest cząstkową molową entalpią swobodną

tzn. jest nachyleniem wykresu entalpii swobodnej jako funkcji ilości
składnika,( np. A) gdy p i T oraz ilości pozostałych składników są stałe

B

B

A

A

B

n

T,

p,

B

A

n

T,

p,

A

dn

μ

dn

μ

dn

n

G

dn

n

G

dG

A

B









































W warunkach izotermiczno-izobarycznych zmiana
entalpii swobodnej układu dwuskładnikowego
spowodowana zmianą składu układu wynosi:

całkowita entalpia swobodna dwuskładnikowej mieszaniny
w warunkach izotermiczno-izobarycznych

G = n

A



A

+ n

B



B

Potencjał chemiczny substancji w mieszaninie jest wkładem jaki substancja ta wnosi do
całkowitej entalpii swobodnej układu

T = const
p = const

Równanie Gibbsa- Duhema









i

i

i

dn

μ

SdT

Vdp

dG

W układzie wieloskładnikowym zmianę entalpii swobodnej Gibbsa może spowodowad
zmiana temperatury, ciśnienia lub składu mieszaniny





i

i

i

dn

μ

dG

W warunkach

izotermiczno-izobarycznych entalpia swobodna Gibbsa

zależy tylko od

składu: od rodzaju składników i ich ilości, czyli

jest funkcją potencjałów chemicznych i liczby

moli

:





i

i

i

μ

n

G

Entalpię swobodną Gibbsa można zmieniad

zmieniając albo potencjały chemiczne

składników, albo liczbę moli składników

i

i

i

i

i

i

d

μ

n

dn

μ

dG













0

d

μ

n

i

i

i





0

d

μ

n

SdT

Vdp

i

i

i











Równanie Gibbsa-Duhema wiąże zmiany
temperatury, ciśnienia i potencjałów
chemicznych składników

gdy p,T = const

W warunkach izotermiczno-izobarycznych, potencjały
chemiczne składników są od siebie uzależnione.

Potencjał chemiczny jednego ze składników mieszaniny nie
może się zmieniad w sposób niezależny od potencjałów
chemicznych pozostałych składników

.

POTENCJAŁ CHEMICZNY składnika w stanie gazowym

)

n

T,

p,

i

i

n

G

μ



















Potencjał chemiczny jest funkcją termodynamiczną określającą zmianę entalpii swobodnej



G układu,

gdy dodajemy do niego substancji w warunkach p=const i T=const

dla substancji czystych

potencjał chemiczny jest

molową entalpią swobodną



i

= (G

m,

)

i

,

określa pracę, jaką może wymienid z otoczeniem 1 mol składnika w warunkach izotermiczno-izobarycznych.

potencjał chemiczny gazu A wynosi:



i

0

- standardowy potencjał chemiczny gazu – potencjał chemiczny czystego

gazu w warunkach standardowych czyli pod ciśnieniem p

0

= 1 bar



















1

2

1

m

2

m

p

p

ln

RT

)

(p

G

)

(p

G

Zależnośd molowej entalpii swobodnej gazu doskonałego

od ciśnienia

Jeżeli przyjmiemy jako stan początkowy gazu(A) stan standardowy, czyli p

1

= p

0

, a p

2

= p

A

,

to molowa entalpia swobodna gazu (A) pod ciśnieniem p

A

wynosi

 



















0

A

0

m

m

p

p

ln

RT

(A)

G

A

G



















0

A

0

A

A

p

p

ln

RT

μ

μ



















0

i

0

i

i

p

p

ln

RT

μ

μ

Potencjał chemiczny substancji (składnika) „i”
w stanie gazowym

Entalpia swobodna reakcji chemicznej

aA + bB ⇌ cC + dD

Zmiana entalpii swobodnej dla reakcji  entalpia swobodna reakcji

∆

r

G = ∆G

prod

- ∆G

substr

b

0

B

a

0

A

d

0

D

c

0

C

p

p

p

p

p

p

p

p

Q























































Potencjał chemiczny każdego reagenta wyraża zależnośd:

standardowa entalpia swobodna reakcji

)

b

μ

(a

μ

d

μ

c

μ

G

Δ

B

A

D

C

r



























0

i

0

i

i

p

p

ln

RT

μ

μ









































0

B

o

B

0

A

o

A

0

D

o

D

0

C

o
C

r

p

p

bRTln

b

μ

p

p

aRTln

a

μ

p

p

dRTln

d

μ

p

p

cRTln

c

μ

G

Δ



 



b

0

B

a

0

A

d

0

D

c

0

C

o

B

o

A

o

D

o
C

r

p

p

p

p

p

p

p

p

RTln

b

μ

a

μ

d

μ

c

μ

G

Δ































































RTlnQ

G

Δ

G

Δ

o

r

r







 



o

B

o

A

o

D

o
C

o

r

b

μ

a

μ

d

μ

c

μ

G

Δ









Iloraz reakcji Q

Reakcja zachodzi w fazie gazowej, a
wszystkie reagenty zachowują się jak gaz
doskonały

Stała równowagi reakcji chemicznej

Gdy reakcja chemiczna osiąga stan równowagi ∆G = 0,
a

ciśnienia cząstkowe reagentów gazowych przyjmują wartości równowagowe

b

r

0

B

a

r

0

A

d

r

0

D

c

r

0

C

p

p

p

p

p

p

p

p

RTln

0

r

ΔG

0

























































r

0

B

r

0

A

r

0

D

r

0

C

p

p

,

p

p

,

p

p

,

p

p

















































aA + bB ⇌ cC + dD

b

r

0

B

a

r

0

A

d

r

0

D

c

r

0

C

p

p

p

p

p

p

p

p

p

K























































Stała równowagi reakcji chemicznej
wyrażona za pomocą ciśnieo
cząstkowych reagentów

∆G

r

0

= - RT ln K

p

związek między standardową entalpią
swobodną reakcji chemicznej
i stałą równowagi reakcji

.

RT

ΔG

p

o

r

e

K





Jeśli znamy

standardową entalpię swobodną reakcji ΔG

0

r

– możemy obliczyd stałą równowagi reakcji K

p

Stała równowagi reakcji chemicznej

∆G

r

0

= - RT ln K

p





































substraty

o

i

i

produkty

o

j

j

o

r

ΔH

ν

ΔH

ν

H

Δ





































substraty

o

i

i

produkty

o

j

j

o

r

S

ν

S

ν

S

Δ

o

r

o

r

o

r

S

Δ

T

H

Δ

G

Δ







I sposób

obliczamy:

standardową entalpię reakcji



r

H

o

standardową entropię reakcji



r

S

o

standardową entalpię swobodną reakcji



G

r

o

korzystając z tablic termochemicznych

Δ

r

G

0

można obliczyd dwoma sposobami

:

0

i

tw

substr

i

0

j

tw

prod.

j

0

r

G

Δ

ν

G

Δ

ν

G

Δ









II sposób

Na podstawie wartości ∆

tw

G

0

reagentów można obliczyd

wartośd standardowej entalpii swobodnej dowolnej reakcji ∆

r

G

0

Standardowa ENTALPIA SWOBODNA tworzenia

analogicznie do ENTALPII



tw

H tworzenia związku chemicznego wprowadza się pojęcie

ENTALPII SWOBODNEJ tworzenia

( potencjału termodynamicznego tworzenia) związków chemicznych

Standardowa ENTALPIA SWOBODNA tworzenia ∆

tw

G

0

jest to
zmiana ENTALPII SWOBODNEJ towarzysząca reakcji tworzenia związku chemicznego z
pierwiastków w ich stanach podstawowych ( stabilnych )

Standardowy potencjał termodynamiczny G

0

trwałej odmiany pierwiastka wynosi 0.

Na podstawie wartości ∆

tw

G

0

z tabel termodynamicznych można obliczyd

wartośd standardowej entalpii swobodnej dowolnej r-cji ∆

r

G

0

0

i

tw

substr

i

0

j

tw

prod.

j

0

r

G

Δ

ν

G

Δ

ν

G

Δ









W tablicach fizyko-chemicznych zamieszczone są
standardowe entalpie swobodne tworzenia reagentów



tw

G

0

RÓWNOWAGA CHEMICZNA W FAZIE GAZOWEJ - OBLICZENIA

Zadanie
Standardowe entalpie i entropie reakcji

CO

(g)

+ H

2

O

(g)

 CO

2 (g)

+ H

2 (g)

w temperaturze 300 K i 1200 K są następujące:



H

0

300K

= - 41,16 kJ/mol;



H

0

1200K

= - 32,93 kJ/mol



S

0

300K

= - 42.4 J/mol K;



S

0

1200K

= - 29,6 J/ mol K

W jakim kierunku reakcja będzie przebiegad samorzutnie a) w temp.300K i b) w temp.1200K, jeżeli
ciśnienie mieszaniny w stanie równowagi wynosi 1 x 10

5

N/m

2

.Obliczyd wartości K

p

dla podanej

reakcji w każdej z tych dwóch temperatur.

Obliczenie



G

0



G

0

T

=



H

0

T

– T



S

0

T



G

0

300

= - 28440 J/mol



G

0

1200

= 2590 J/mol



G

0

300

< 0 r-cja przebiega samorzutnie w prawo powstaje CO

2

i H

2



G

0

1200

> 0 r-cja przebiega samorzutnie w lewo powstaje CO i H

2

O

Obliczenie K

p



G

0

= - RT ln K

p

ln K

p300

= -



G

0

300

/ RT = 11,4



K

p300

= 8,95 x 10

4

ln K

p1200

= -



G

0

1200

/ RT = -0,26 K

p1200

= 0,77

Zadanie
Standardowa molowa entalpia spalania fenolu C

6

H

5

OH

(s)

w 25

0

C wynosi -3054 kJ



mol

-1

, a jego

standardowa molowa entropia jest równa 146 J



K

-1



mol

-1

. Obliczyd

standardową molową entalpię

swobodną

spalania fenolu w temperaturze 25

0

C .

Rozwiązanie:

C

6

H

5

OH

(s)

+ 7 O

2(g)

= 6CO

2(g)

+ 3H

2

O

(c)

∆

r

G

0

= ∆

r

H

0

- T



∆

r

S

0

∆

r

S

0

sp

(obliczamy na podst. tablic)=-89,80 JK

-1

,

Odp. ∆G

0

= -3027 kJ



mol

-1

Zadanie
Obliczyd

entalpię swobodną

dla reakcji spalania gazowego propanu w temperaturze 298K i pod

ciśnieniem 1 atm.

C

3

H

8(g)

+ 5O

2(g)

= 3CO

2(g)

+ 4H

2

O

(c)

Rozwiązanie:
I metoda:

∆

r

G

0

= ∆

r

H

0

- T



∆

r

S

0

∆S

0

(obliczamy z tablic)=-374,74J



K

-1

, ∆H

0

odczytujemy z tablic = -2220kJ; ∆G

0

= -2108,3 kJ.

II metoda: Obliczmy na podstawie ∆G

0

tw

wziętych z tablic. ∆G

0

= -2108kJ

RÓWNOWAGA CHEMICZNA W FAZIE GAZOWEJ - OBLICZENIA

0

im

substraty

i

0

j m

produkty

j

0

S

ν

S

ν

S











r

Stałe równowagi reakcji K

p

, K

x

b

r

0

B

a

r

0

A

d

r

0

D

c

r

0

C

p

p

p

p

p

p

p

p

p

K























































K

p

stała równowagi wyrażona za pomocą ciśnieo

cząstkowych reagentów gazowych p

i

(ciśnieniowa stała równowagi).

aA + bB

⇌ cC + dD

p

0

- ciśnienie standardowe =1bar

Jeżeli reagenty spełniają prawo Daltona to ich ciśnienia cząstkowe są proporcjonalne do

ułamka molowego reagenta x

i

(p- ciśnienie całkowite w układzie)

p

i

= x

i

p

Δn

p

p

b
r

)

(x

a

r

)

(x

d

r

)

(x

c

r

)

(x

b

r

0

p

p

x

a

r

0

p

p

x

d

r

0

p

p

x

c

r

0

p

p

x

0

B

A

D

C

B

A

D

C

p

K





























































































Δ n

0

x

p

p

p

K

K

















gdzie ∆n = ( c + d ) – ( a + b )
jest zmianą liczby moli reagentów gazowych

K

x

stała równowagi chemicznej wyrażona za

pomocą ułamków molowych reagentów

   

   

b
r

B

a

r

A

d

r

D

c

r

C

x

x

x

x

x

K







Stałe równowagi reakcji K

p

, K

c

aA + bB

⇌ cC + dD

p V = nRT

jeżeli założymy że reagenty spełniają założenia modelu gazu doskonałego

p = (n/V) RT

p

i

= c

i

RT

Δn

0

p

RT

b
r

)

B

(c

a

r

)

A

(c

d

r

)

D

(c

c

r

)

C

(c

b

r

0

p

RT

B

c

a

r

0

p

RT

A

c

d

r

0

p

RT

D

c

c

r

0

p

RT

C

c

p

K





























































































b

r

c

c

a

r

c

c

d

r

c

c

c

r

c

c

K

0

B

0

A

0

D

0

C

c































































K

c

stała równowagi chemicznej wyrażona

za pomocą stężeo molowych c

i

c

0

= 1 mol dm

-3

stężenie standardowe

Δ n

0

0

c

p

p

RT

c

K

K

















Stałe równowagi chemicznej K

p

, K

c

i K

x

są liczbami bez miana

Zależności pomiędzy K

p

, K

c

i K

x

dotyczą

układów doskonałych

lub takich, które w

przybliżeniu zachowują się jak doskonałe ( gazy lub roztwory)

Termodynamiczna stała równowagi

W przypadku układów rzeczywistych należy stosowad termodynamiczną stałą równowagi, w której

ilośd reagentów wyraża się za pomocą

aktywności

.

Aktywnośd

określa efektywne stężenie reagenta

jest proporcjonalna do jego stężenia

a

i

=



i



x

i



- współczynnik aktywności

c

0

= 1 mol/L, m

0

=1 mol/kg – stężenia normalizujące

,

aktywnośd jest wielkością bezwymiarową

aA + bB ⇌ cC + dD

   

   

b

r

B

a

r

A

d

r

D

c

r

C

a

a

a

a

a

K







Dla gazów rzeczywistych
aktywnośd ciśnieniowa nazywana
jest lotnością f

i

0

i

i

i

m

m

γ

a





i

0

i

i

i

f

p

p

γ

a







0

i

i

i

c

c

γ

a





RÓWNOWAGA CHEMICZNA W FAZIE GAZOWEJ - OBLICZENIA

Zadanie
Stopieo dysocjacji jodowodoru w temperaturze 1500 K wynosi 0,33 pod ciśnieniem 1,013x10

5

Pa. Obliczyd K

p

dla reakcji:

1). HJ

(g)

 ½ H

2 (g)

+ ½ J

2(g)

odp K

p1

=



/2(1-



)=0,25

2). 2 HJ

(g)

 H

2 (g)

+ J

2(g)

odp. K

p2

= (K

p1

)

2

= 0,0625

3). H

2 (g)

+ J

2(g)

 2HJ

(g)

odp. K

p3

= 1/K

p2

= 16









































0

HI

0

I

1/2

0

H

p1

p

p

p

p

p

p

K

2

2

2

1/

2

2

0

HI

0

I

0

H

p2

p1

2

2

K

p

p

p

p

p

p

K











































p2

0

H

0

I

2

0

HI

p3

K

1

p

p

p

p

p

p

K

2

2











































