
Materiały przygotowane w ramach projektu „Uruchomienie
unikatowego kierunku studiów Informatyka Stosowana odpowiedzią
na zapotrzebowanie rynku pracy” ze środków Programu Operacyjnego
Kapitał Ludzki współfinansowanego ze środków Europejskiego
Funduszu Społecznego nr umowy UDA – POKL.04.01.01-00-011/09-00
Wprowadzenie do matematyki
Materiały do zajęć (1):
Elementy logiki matematycznej.
Definicja zdania logicznego.
Spójniki logiczne.
Tautologie.
Formy zdaniowe i kwantyfikatory.
Formułowanie twierdzeń i definicji.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
14
4. Materiały do zajęć
Temat 1: Elementy logiki matematycznej i teorii mnogości
1. Definicja zdania logicznego.
Zdania w sensie logiki matematycznej oznaczamy małymi literami: p, q, itp.
Przykłady zdań logicznych:
2. Spójniki logiczne.
Zdania utworzone za pomocą funktorów zdaniowych mają znaczenia:
q
p
: p i q,
q
p
: p lub q,
q
p
: jeśli p, to q; p nazywamy poprzednikiem implikacji, q następnikiem,
q
p
: p wtedy i tylko wtedy, gdy q,
p
~
: nieprawda, że p.
Definicja.
Zdaniem w sensie logiki matematycznej nazywamy zdanie orzekające, któremu
w jednoznaczny sposób można przypisać jedną z ocen: prawdę („1”) lub fałsz („0”).
Funktory zdaniowe (spójniki logiczne): koniunkcja
, alternatywa
, implikacja
,
równoważność
, negacja (zaprzeczenie)
, służą do budowy zdań złożonych.
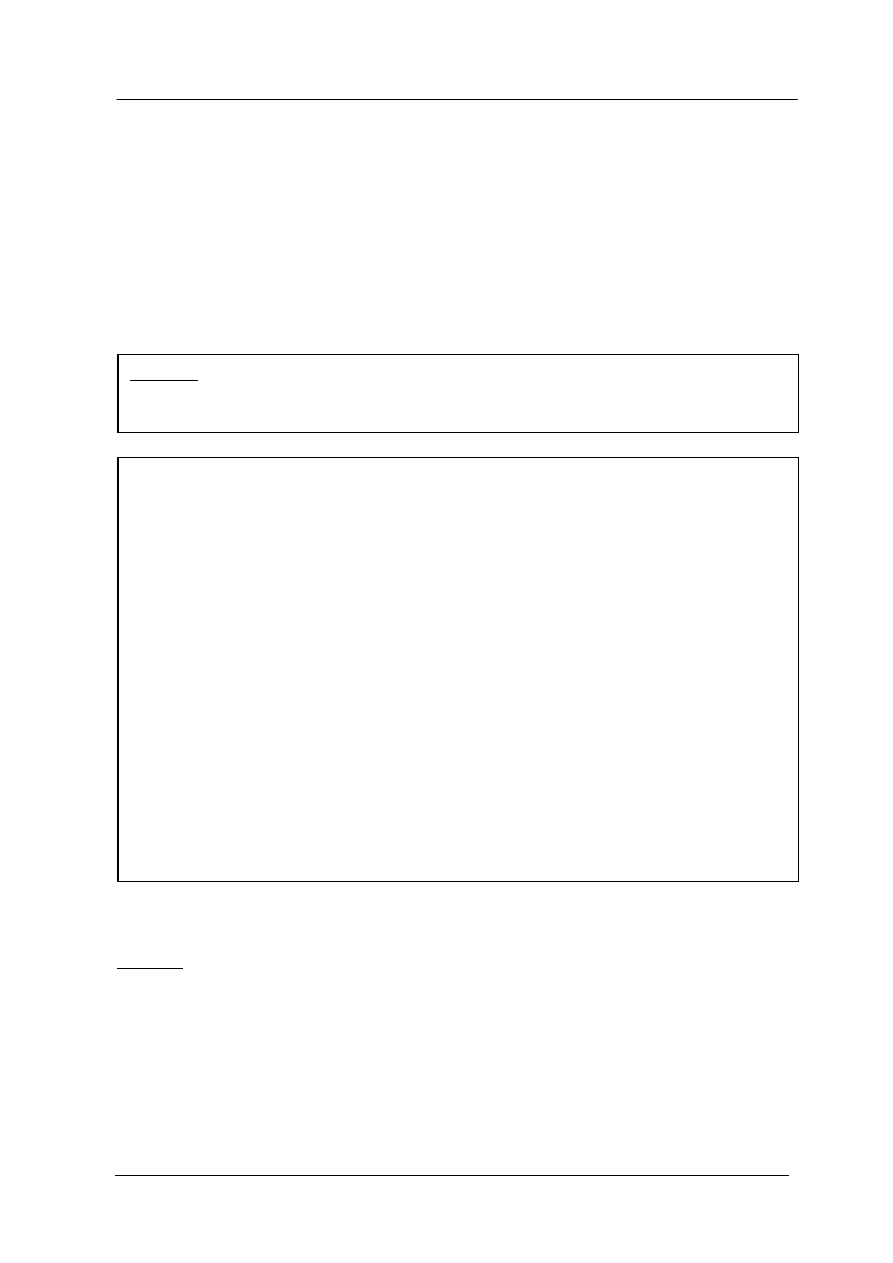
Wartości logiczne
p
q
q
p
q
p
q
p
q
p
p
~
1
1
1
1
1
1
0
1
0
0
1
0
0
0
0
1
0
1
1
0
1
0
0
0
0
1
1
1
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
15
3. Tautologie.
Na podstawie tautologii można sprawdzać poprawność rozumowania.
Przykład.
Sprawdzić, czy poprawne jest rozumowanie: „jeśli pewna liczba rzeczywista x jest mniejsza
od 3, to
3
x
.
Rozwiązanie:
Definicja.
Tautologią (prawem logiki) nazywamy zdanie, które jest prawdziwe, niezależnie od
wartości logicznych zdań, z których jest zbudowane.
Przykłady tautologii:
Prawa przemienności:
)
(
)
(
p
q
q
p
,
)
(
)
(
p
q
q
p
.
Prawa łączności:
)
(
)
(
r
q
p
r
q
p
,
)
(
)
(
r
q
p
r
q
p
.
Prawa rozdzielności:
)
(
)
(
)
(
r
p
q
p
r
q
p
,
)
(
)
(
)
(
r
p
q
p
r
q
p
.
Prawa de Morgana:
)]
(~
)
(~
[
)
(
~
q
p
q
p
,
)]
(~
)
[(~
)
(
~
q
p
q
p
.
Prawa pochłaniania:
p
q
p
)
(
,
)
(
q
p
p
.
Prawo podwójnego zaprzeczenia:
p
p
)
(~
~
.
Prawo zaprzeczenia implikacji:
)
~
(
)
(
~
q
p
q
p
.
Prawo (zasada) kontrapozycji:
)
~
(~
)
(
p
q
q
p
.
Prawo wyłączonego środka:
)
(~ p
p
.
Prawo niesprzeczności:
)
~
(
~
p
p
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
16
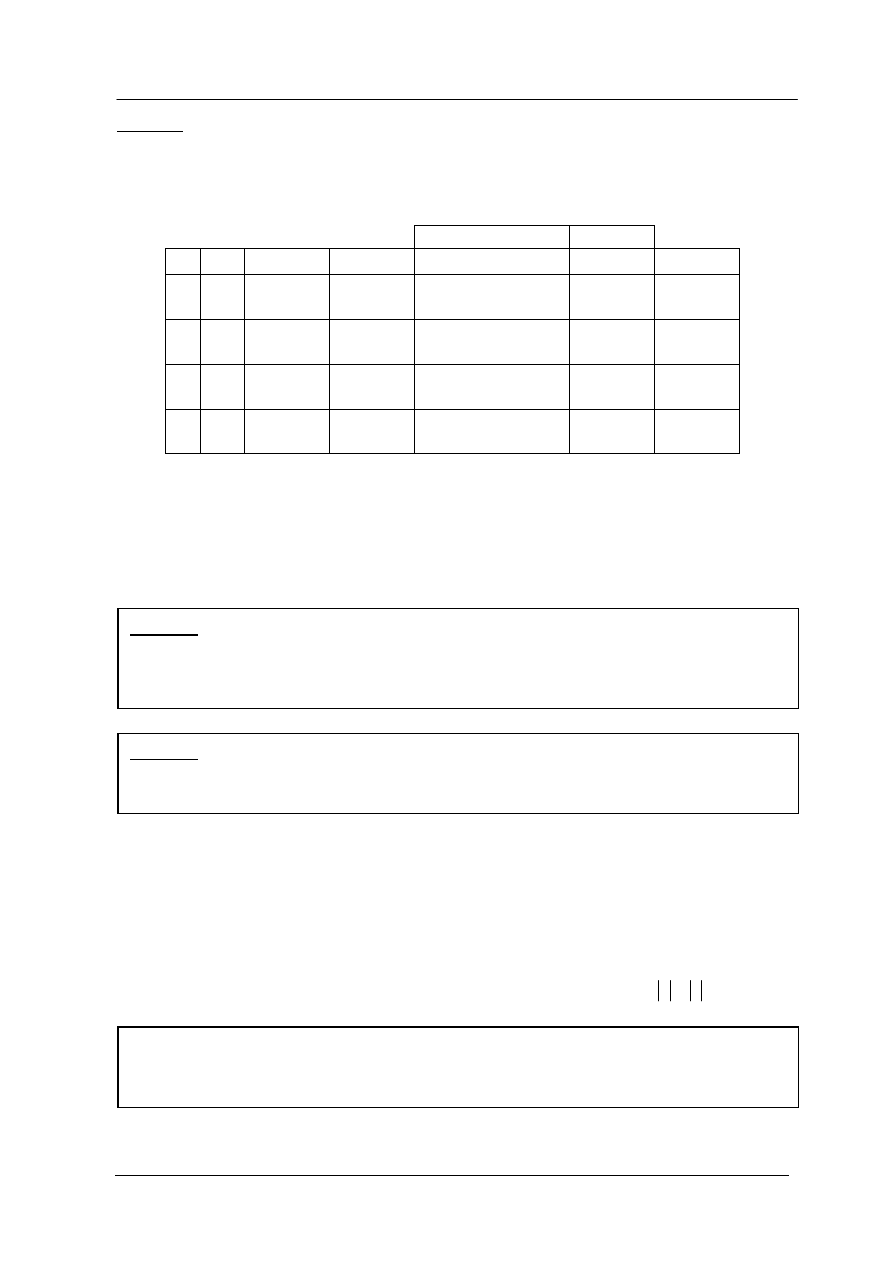
Przykład.
Sprawdzić, czy jest tautologią zdanie:
)
(~
)]
(~
)
[(
p
q
q
p
.
Rozwiązanie:
L
P
p
q
q
p
q
~
)]
(~
)
[(
q
q
p
p
~
P
L
1
1
1
0
0
1
0
0
Odpowiedź:
……………………………………………………………………………………………………………………………
4. Formy zdaniowe i kwantyfikatory.
Formy zdaniowe mogą zawierać jedną lub więcej zmiennych i oznaczamy je
symbolami
)
(x
p
,
)
,
( y
x
r
itp. Formę zdaniową nazywamy tożsamością, jeżeli spełnia ją każdy
element dziedziny, tzn. jeżeli dla każdego elementu z dziedziny otrzymujemy zdanie
prawdziwe. Tożsamościami w zbiorze liczb rzeczywistych są np. formy zdaniowe:
0
2
x
1
cos
sin
2
2
x
x
. Formę zdaniową nazywamy sprzeczną, jeżeli nie spełnia jej żaden
element z dziedziny (gdy dla każdego elementu z dziedziny otrzymujemy zdanie fałszywe).
W zbiorze liczb rzeczywistych sprzeczne są np. formy zdaniowe:
2
sin
x
,
0
y
x
.
Definicja.
Formą zdaniową nazywamy wyrażenie, które zawiera zmienną i staje się zdaniem
logicznym, gdy zmienną zastąpimy dowolnym elementem pewnego niepustego zbioru lub
skwantyfikujemy.
Definicja.
Dziedziną formy zdaniowej jest zbiór tych elementów, dla których staje się ona zdaniem
logicznym.
Rodzaje kwantyfikatorów:
kwantyfikator duży (ogólny)
zastępuje zwrot „dla każdego”,
kwantyfikator mały (szczegółowy)
zastępuje zwrot „istnieje”.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
17
Przykład.
Niech dane będą dwie formy zdaniowe
)
(x
p
:
1
3
x
i
)
(x
q
:
1
x
.
Zdaniami prawdziwymi są:
Zdaniami fałszywymi są:
Przykład.
Zaprzeczyć zdanie:
)]
(
)
(
[~
x
q
x
p
A
x
.
Rozwiązanie:
5. Formułowanie twierdzeń i definicji.
Spójniki logiczne
,
mają zastosowanie w formułowaniu twierdzeń i definicji
oraz dowodach twierdzeń.
Niech zbiór
A
oraz
)
(x
p
oznacza formę zdaniową.
Zdania z kwantyfikatorem:
)
(x
p
A
x
czytamy: dla każdego
A
x
zachodzi
)
(x
p
,
)
(x
p
A
x
czytamy: istnieje
A
x
taki, że zachodzi
)
(x
p
.
Prawa de Morgana dla kwantyfikatorów:
)
(
~
)]
(
[
~
x
p
A
x
x
p
A
x
,
)
(
~
)]
(
[
~
x
p
A
x
x
p
A
x
.
Dla twierdzenia w postaci:
q
p
:
p jest założeniem twierdzenia, q jest tezą twierdzenia;
q jest wnioskiem z p;
zdanie q jest warunkiem koniecznym dla p;
zdanie p jest warunkiem wystarczającym dla q.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
18
Twierdzenie sformułowane w postaci implikacji można wypowiedzieć równoważnie
na kilka sposobów.
Przykład.
Twierdzenie: „Jeśli liczba naturalna jest podzielna przez 4, to jest podzielna przez 2” można
sformułować następująco:
Twierdzenie w postaci
q
p
można udowodnić przeprowadzając dowód wprost
lub dowód nie wprost. W pierwszej metodzie przyjmujemy wszystkie założenia wymienione
w poprzedniku implikacji za prawdziwe i korzystając ze znanych twierdzeń oraz własności
przeprowadzamy wnioskowanie oparte na prawach logiki do momentu stwierdzenia
prawdziwości tezy. Metoda dowodzenia nie wprost opiera się na wykorzystaniu zasady
kontrapozycji
)
~
(~
)
(
p
q
q
p
. Wówczas za prawdziwe przyjmujemy zdanie
q
~
i postępując jak w metodzie pierwszej dążymy do wykazania prawdziwości zdania
p
~
(lub
wykazania sprzeczności ze znanym twierdzeniem).
Twierdzenie
w
postaci
q
p
można
udowodnić
………………………………………………………
Dla twierdzenia lub definicji w postaci:
)]
(
)
[(
)]
[(
p
q
g
p
q
p
:
zdanie q jest warunkiem koniecznym i wystarczającym dla p;
zdanie p jest warunkiem koniecznym i wystarczającym dla q.

Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
19
Zadania
zad. 1) Ocenić wartość logiczną zdań:
a)
1
5
,
0
1
2
cos
2
,
b)
1
0
90
s in
2
ctg
,
c)
0
1
tg
15
sin
17
2
0
2
,
d)
0
45
ctg
45
cos
2
3
10
3
.
zad. 2) Sprawdzić (metodą zero-jedynkową), czy zdanie jest tautologią:
a)
p
q
q
p
~
~
,
b)
q
p
q
p
q
p
~
~
,
c)
q
p
q
p
p
~
~
~
.
Zapisać jego zaprzeczenie.
zad. 3) Wyznaczyć wszystkie wartości rzeczywiste
x , dla których forma zdaniowa:
a)
0
5
4
21
5
7
2
x
x
x
x
stanie się zdaniem fałszywym,
b)
2
8
6
2
5
2
0
4
4
2
x
x
x
x
x
x
x
stanie się zdaniem prawdziwym.
zad. 4) Ocenić wartość logiczną zdań:
a)
1
2
0
2
x
x
x
x R
,
b)
2
1
0
~
x
x
x R
,
c)
9
0
4
~
2
2
x
x
x R
.
zad. 5) Wypowiedzieć twierdzenia na różne sposoby:
a) Jeżeli się nauczyłem to zdam egzamin.
b) Jeżeli funkcje
f i g są całkowalne w przedziale
]
,
[ b
a
to funkcja
g
f
jest
całkowalna w
]
,
[ b
a
.
c) Warunkiem koniecznym istnienia ekstremum funkcji
)
(x
f
y
w punkcie
f
D
x
0
jest
0
)
(
'
0
x
f
.
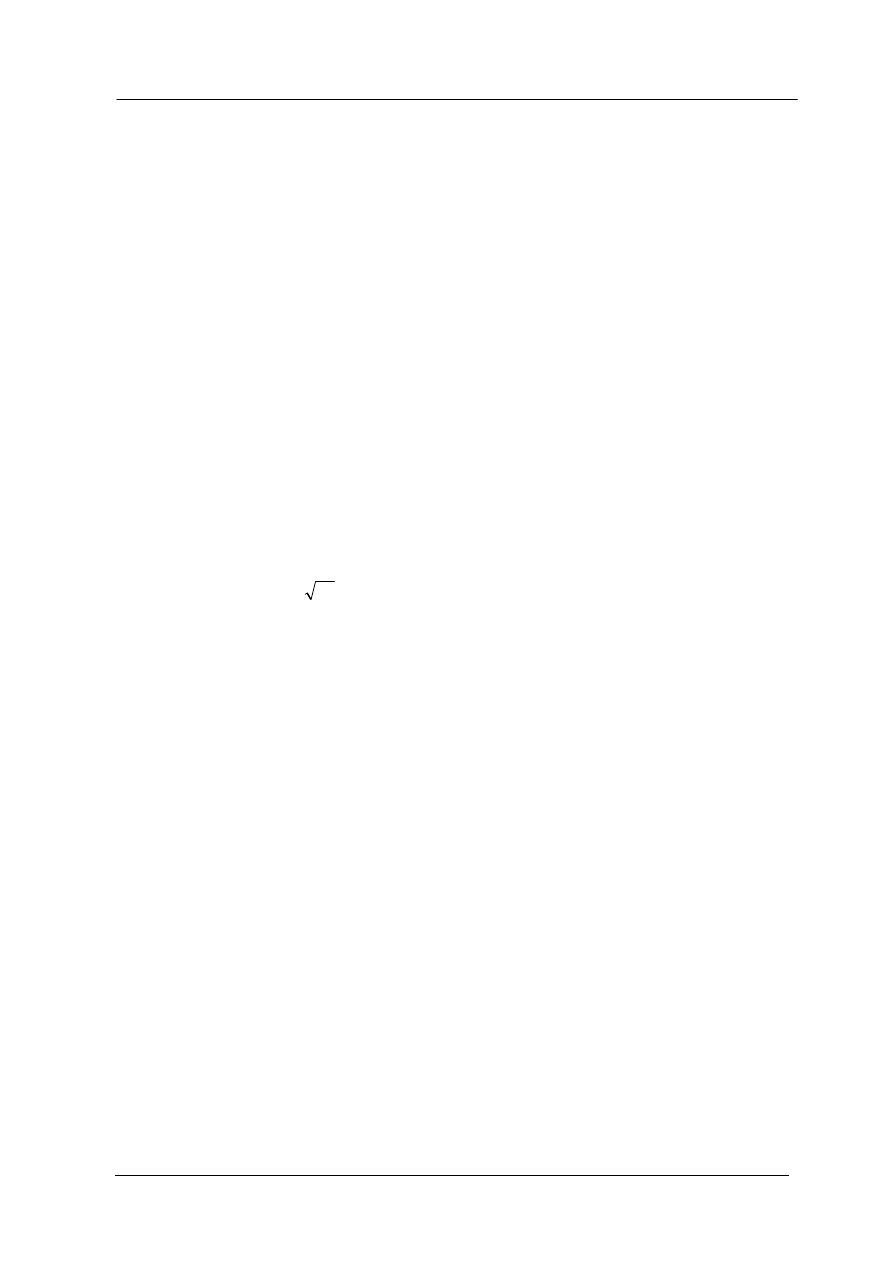
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
20
Zadania do samodzielnego rozwiązania
zad. 1) Sprawdzić (metodą zero-jedynkową), czy zdanie jest tautologią:
a)
q
p
q
p
q
p
~
~
,
b)
p
p
p
~
~
,
c)
q
p
p
q
p
~
~
~
d)
q
p
q
p
~
.
Zapisać jego zaprzeczenie.
Odpowiedź:
a) nie jest tautologią,
q
p
q
p
q
p
~
~
,
b) jest tautologią,
p
p
p
~
,
c) jest tautologią,
q
p
p
q
p
~
~
~
d) jest tautologią,
q
p
q
p
~
~
zad. 2) Ocenić wartość logiczną zdań:
a)
4
16
3
21
log
7
,
b)
3
4
0
0
sin
3
log
2
,
c)
0
2
2
x
x
x
x R
,
d)
4
2
~
2
x
x
x R
,
e)
2
3
~
x
x
x R
,
f)
5
1
3
15
5
x
x
x
x R
.
Odpowiedź:
a) prawda,
b) fałsz,
c) fałsz,
d) fałsz,
e) prawda,
f) prawda.
zad. 3) Wyznaczyć wszystkie wartości rzeczywiste x , dla których forma zdaniowa:
a)
0
30
0
4
2
2
x
x
x
stanie się zdaniem prawdziwym;
b)
2
2
2
0
2
4
x
x
x
x
stanie się zdaniem fałszywym.
Odpowiedź:
a)
,
2
2
,
x
,
b)
}
2
{
\
R
x
.

Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
21
zad. 4) Wypowiedzieć twierdzenia na różne sposoby:
a) Jeżeli funkcja
)
(x
f
y
jest ciągła w przedziale
]
,
[ b
a
to jest w tym przedziale
całkowalna.
b) Jeżeli
0
)
(
'
x
f
w przedziale
]
,
[ b
a
to funkcja
)
(x
f
y
jest rosnąca w tym
przedziale.
Literatura
(do zajęć: 1, 2)
1) Gryglaszewska A., Kosiorowska M., Paszek B. [2009], „Ćwiczenia z matematyki, część
1”, wydanie 6, Wydawnictwo Uniwersytetu Ekonomicznego w Krakowie, Kraków.
2) Gurgul H., Suder M. [2009], „Matematyka dla kierunków ekonomicznych. Przykłady
i zadania wraz z repetytorium ze szkoły średniej”, Wydawnictwo Wolters Kluwer
Polska Sp. z o. o., Kraków.
3) Kłaczkow K., Kurczab M., Świda E. [2002], „Matematyka, podręcznik do liceów
i techników klasa I, zakres podstawowy i rozszerzony”, wydanie I, Oficyna
Edukacyjna * Krzysztof Pazdro Spółka z o. o., Warszawa.
4) Marek W., Onyszkiewicz J. [2008], „Elementy logiki i teorii mnogości w zadaniach”,
wydanie XII, Wydawnictwo Naukowe PWN, Warszawa.
Wyszukiwarka
Podobne podstrony:
IS Matematyka C S 01 logika
Analiza Wyklad 01 Logika id 59757 (2)
matematyka 01
Wykład z dnia 10.05.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
IS Matematyka C S 05 wielomiany f wymierna
IMiR gzamin I z matematyki 01-02-2013
IMiR gzamin I z matematyki 01-02-2013
Ćwiczenia IV (relacje porządkujące), Matematyka stosowana, Logika
Zakres materialu obowiazujacego do egzaminu ze Wstepu do Matematyki, Matematyka stosowana, Logika
wmd4, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Matematyka Dyskretna i logika
jakobczak, mdl egz, Matematyka Dyskretna i Logika - egzamin
MATEMATYKA! 01 2011
Mat Dyskr i Log, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka Dyskretna i logika, MD
IMiR gzamin I z matematyki 01-02-2013 niebieski, Barbasze IMiR mibm
IS Matematyka C S 06 f trygonometryczne
IMiR gzamin I z matematyki 01-02-2013, Barbasze IMiR mibm
więcej podobnych podstron