Materiały przygotowane w ramach projektu „Uruchomienie
unikatowego kierunku studiów Informatyka Stosowana odpowiedzią
na zapotrzebowanie rynku pracy” ze środków Programu Operacyjnego
Kapitał Ludzki współfinansowanego ze środków Europejskiego
Funduszu Społecznego nr umowy UDA – POKL.04.01.01-00-011/09-00
Wprowadzenie do matematyki
Materiały do zajęć (5):
Funkcje elementarne.
Wielomiany.
Funkcja wymierna.
Funkcja homograficzna.
Funkcja potęgowa.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
46
5. Wielomiany.
Dziedziną funkcji wielomianowej jest zbiór R.
Stałe
n
a
a
a
...,
,
,
1
0
nazywamy współczynnikami wielomianu,
0
a jest wyrazem wolnym.
Liczbę
N
n
nazywamy stopniem wielomianu W.
Dwa niezerowe wielomiany W oraz Q są równe wtedy i tylko wtedy, gdy
)
(
)
(
x
Q
x
W
dla każdego
x R. Oznacza to, że wielomiany W oraz Q są tego samego stopnia
i mają równe współczynniki przy odpowiednich potęgach zmiennej.
Przykład.
Podzielić wielomian
1
5
12
5
)
(
2
3
4
x
x
x
x
x
W
przez dwumian
1
)
(
x
x
P
oraz
rozwiązać nierówność
0
1
5
12
5
2
3
4
x
x
x
x
.
Definicja.
Wielomianem stopnia
N
n
nazywamy funkcję określoną wzorem:
0
1
1
1
.....
)
(
a
x
a
x
a
x
a
x
W
n
n
n
n
, gdzie
n
a
a
a
...,
,
,
1
0
R,
0
n
a
,
x R.
Definicja.
Pierwiastkiem wielomianu W nazywamy liczbę
0
x , dla której
0
)
(
0
x
W
.
Twierdzenie Bézout.
Liczba
0
x jest pierwiastkiem wielomianu W wtedy i tylko wtedy, gdy wielomian W jest
podzielny przez dwumian
)
(
0
x
x
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
47
Przykład.
Sprowadzić do najprostszej postaci wyrażenie
9
7
4
3
8
)
(
x
x
x
x
.
Rozwiązanie:
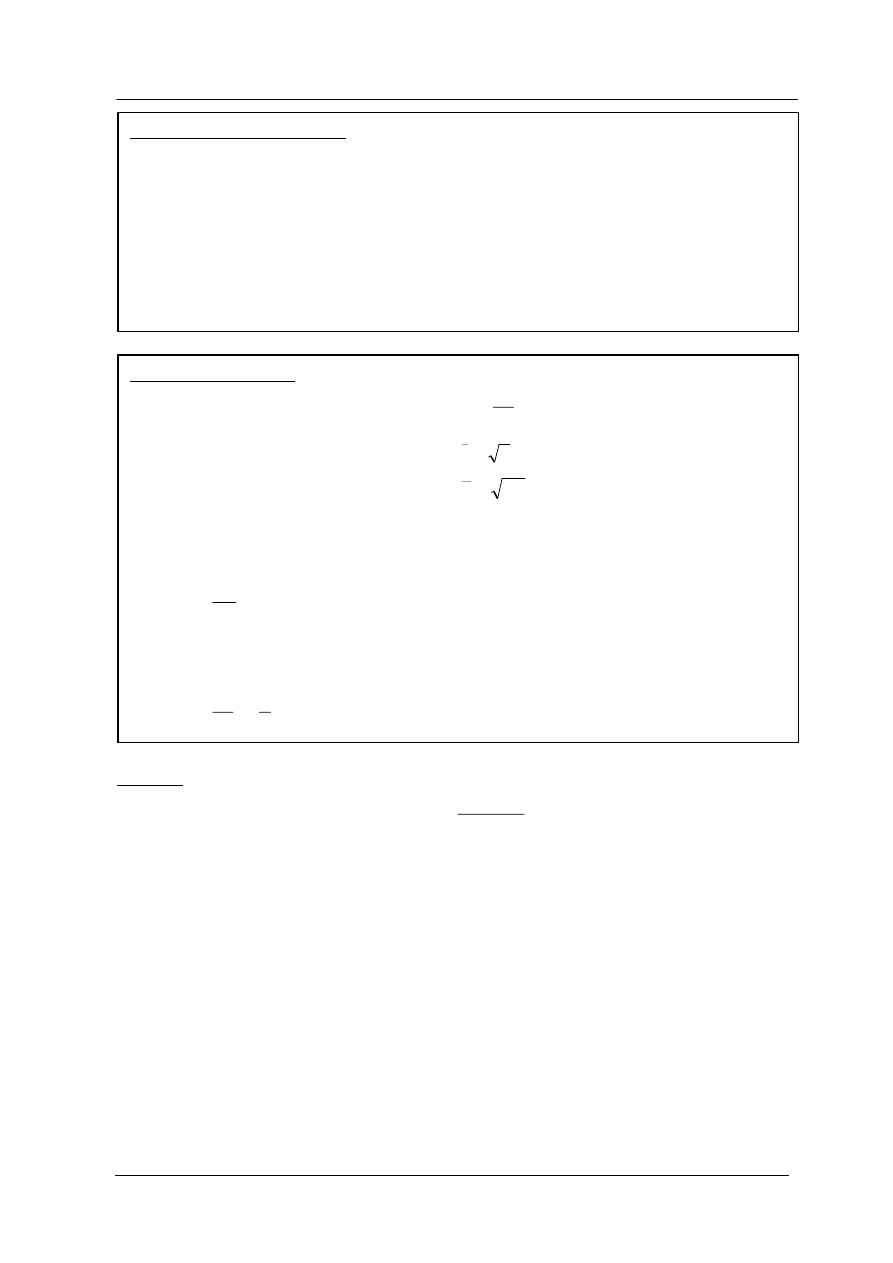
Wzory skróconego mnożenia:
2
2
2
2
)
(
b
ab
a
b
a
,
2
2
2
2
)
(
b
ab
a
b
a
,
)
)(
(
2
2
b
a
b
a
b
a
,
3
2
2
3
3
3
3
)
(
b
ab
b
a
a
b
a
,
3
2
2
3
3
3
3
)
(
b
ab
b
a
a
b
a
,
)
)(
(
2
2
3
3
b
ab
a
b
a
b
a
,
)
)(
(
2
2
3
3
b
ab
a
b
a
b
a
.
Działania na potęgach:
dla
0
x
i
n N:
n
n
x
x
1
,
dla
0
x
oraz
n N i
1
n
:
n
n
x
x
1
,
dla
0
x
,
m Z oraz
n N i
1
n
:
n
m
n
m
x
x
,
dla dowolnych liczb
0
,
y
x
oraz
n
m,
R (lub
0
,
y
x
i
n
m,
Z) prawdziwe są
zależności:
a)
n
m
n
m
x
x
x
,
b)
n
m
n
m
x
x
x
,
c)
n
m
n
m
x
x
,
d)
n
n
n
y
x
y
x
)
(
,
e)
n
n
n
y
x
y
x
.
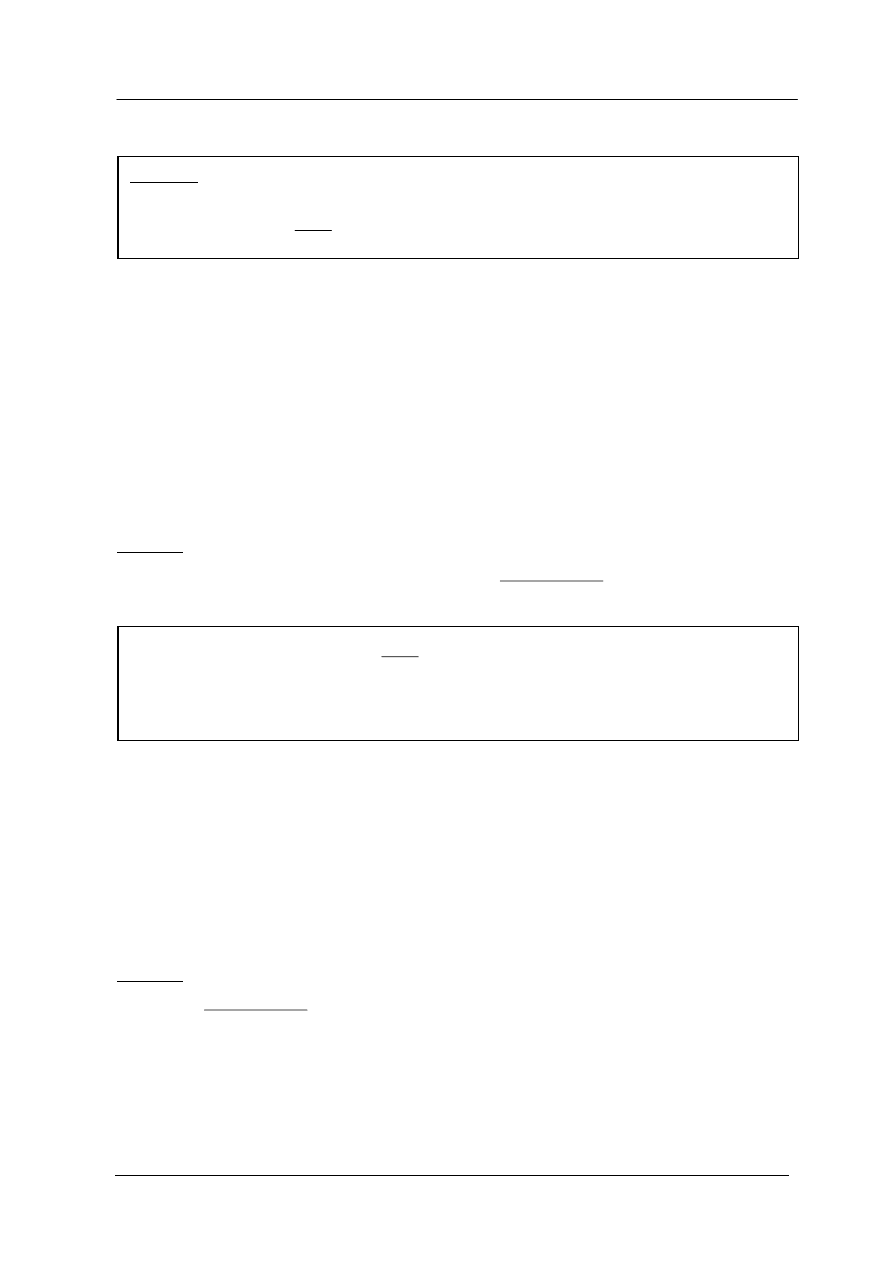
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
48
6. Funkcja wymierna.
Dziedziną funkcji wymiernej jest zbiór liczb rzeczywistych takich, że
0
)
(
x
P
,
}
0
)
(
:
{
x
P
x
D
f
R
.
Przykład.
Wyznaczyć dziedzinę i miejsca zerowe funkcji
4
3
2
)
(
2
4
2
3
x
x
x
x
x
x
f
.
Przykład.
Rozwiązać:
0
4
3
2
2
4
2
3
x
x
x
x
x
.
Definicja.
Funkcją wymierną nazywamy funkcję postaci:
)
(
)
(
)
(
x
P
x
W
x
f
, gdzie W oraz P są wielomianami i
0
)
(
x
P
.
Wartości funkcji wymiernej
)
(
)
(
)
(
x
P
x
W
x
f
dla
0
)
(
x
P
:
f przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy
0
)
(
)
(
x
P
x
W
;
f przyjmuje wartości ujemne wtedy i tylko wtedy, gdy
0
)
(
)
(
x
P
x
W
.
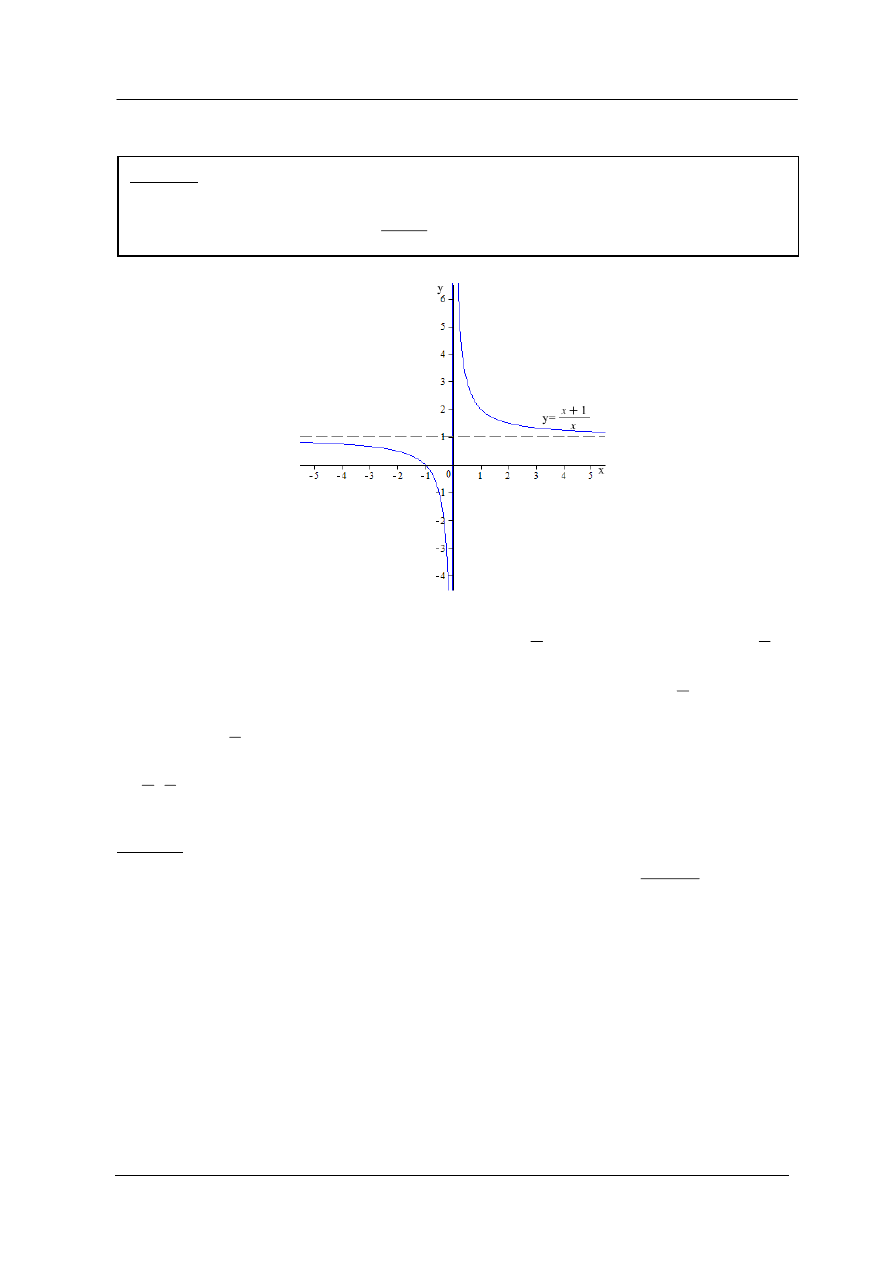
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
49
7. Funkcja homograficzna.
Dziedziną funkcji homograficznej jest zbiór
c
d
\
R
, zbiorem wartości
c
a
\
R
.
Wykresem funkcji homograficznej jest hiperbola o asymptotach
c
d
x
(asymptota
pionowa),
c
a
y
(asymptota pozioma). Hiperbola jest symetryczna względem punktu
c
a
c
d
,
.
Przykład.
Wyznaczyć dziedzinę, zbiór wartości i asymptoty wykresu funkcji
2
5
3
)
(
x
x
x
f
.
Definicja.
Funkcją homograficzną nazywamy funkcję wymierną określoną wzorem:
d
cx
b
ax
x
f
)
(
,
0
bc
ad
i
0
c
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
50
Położenie hiperboli w układzie współrzędnych zależy od znaku liczby
0
s
. Dla
0
s
wykres funkcji
x
s
x
g
)
(
znajduje się w I i III ćwiartce układu współrzędnych, dla
0
s
w ćwiartce II i IV.
Przykład.
Narysować wykres funkcji
2
5
3
)
(
x
x
x
f
.
Przedziały monotoniczności funkcji homograficznej
0
,
)
(
s
q
p
x
s
x
f
zależą od
znaku współczynnika s:
8. Funkcja potęgowa.
Własności funkcji potęgowej zależą od wykładnika potęgi
R
a
.
Wzór każdej funkcji homograficznej można zapisać w postaci:
0
,
)
(
s
q
p
x
s
x
f
.
Definicja.
Funkcją potęgową nazywamy funkcję postaci
R
a
x
x
f
a
,
)
(
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
51
Przykład.
Określić dziedzinę funkcji:
a)
3
)
(
x
x
f
,
f
D
…………………………………………………………………………………………………………………
b)
2
2
1
)
(
x
x
x
f
,
f
D
………………………………………………………………………………………………………
c)
x
x
x
f
2
1
)
(
,
f
D
……………………………………………………………………………………………………….
d)
7
5
7
5
)
(
x
x
x
f
,
f
D
………………………………………………………………………………………………………
e)
8
3
8
3
)
(
x
x
x
f
,
f
D
……………………………………………………………………………………………………..
f)
5
3
5
3
1
)
(
x
x
x
f
,
f
D
……………………………………………………………………………………………………
g)
4
4
1
1
)
(
x
x
x
f
,
f
D
……………………………………………………………………………………………………..
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
52
Zadania
Wielomiany
zad. 1) Obliczyć:
a)
0
3
2
5
,
1
1
1500
27
9
5
,
1
9
,
b)
7
3
7
3
7
7
5
5
7
5
4
,
1
5
,
1
5
,
1
2
1
2
1
2
1
2
1
5
5
,
c)
3
3
2
1
2
1
2
2
3
a
ab
b
a
dla
2
2
a
i
3
2
1
b
.
zad. 2) Dany jest wielomian
8
)
(
2
3
4
nx
mx
x
x
W
, wartość tego wielomianu dla
2
x
jest taka sama jak dla
2
x
. Natomiast
82
)
3
(
W
. Wyznaczyć wartość liczb
m i
n .
zad. 3) Wiedząc, że wielomian
10
9
)
(
2
3
x
bx
ax
x
W
jest podzielny przez dwumian
2
x
i przez dwumian
1
x
znaleźć współczynniki a i
b
.
zad. 4) Rozłożyć wielomiany na czynniki i podać ich pierwiastki:
a)
6
9
2
3
)
(
2
3
x
x
x
x
W
,
b)
7
9
2
)
(
2
4
x
x
x
P
,
c)
2
4
2
)
(
x
x
x
Q
,
d)
6
4
)
(
2
3
x
x
x
x
S
.
zad. 5) Dany jest wielomian
2
4
10
2
4
)
(
2
3
x
x
x
x
W
.
a) Obliczyć
)
2
(
W
,
b) Ile różnych pierwiastków ma wielomian W ?
c) Wyznaczyć resztę z dzielenia wielomianu W przez wielomian
2
)
(
x
x
P
.
zad. 6) Dla jakich wartości parametru k równanie
0
1
2
1
2
3
5
x
k
x
k
x
ma
dokładnie trzy pierwiastki?
zad. 7) Rozwiązać nierówności:
a)
0
3
1
3
2
x
x
x
,
b)
0
7
4
2
2
x
x
,
c)
0
16
4
x
,
d)
1
1
2
2
2
x
x
,
e)
0
15
3
5
2
3
x
x
x
,
f)
x
x
x
3
3
,
g)
0
2
7
2
3
x
x
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
53
Funkcja wymierna
zad. 8) Wyznaczyć dziedzinę funkcji:
a)
x
x
x
x
x
x
f
3
7
2
)
(
2
3
2
,
b)
2
3
2
1
)
(
2
2
x
x
x
x
f
,
c)
2
16
2
7
)
(
x
x
x
f
.
zad. 9) Rozwiązać równania:
a)
2
1
7
2
x
x
,
b)
4
4
2
2
2
x
x
x
,
c)
x
x
x
2
2
1
1
,
d)
0
1
2
4
2
2
x
x
x
.
zad. 10) Rozwiązać nierówności:
a)
2
1
3
1
5
x
x
x
x
,
b)
0
4
3
4
2
2
x
x
,
c)
0
1
1
2
2
x
x
x
x
,
d)
1
1
2
2
x
x
.
zad. 11) Dana jest funkcja
8
2
3
6
)
(
x
x
x
f
a) zapisać wzór funkcji
f w postaci kanonicznej,
b) wyznaczyć dziedzinę i zbiór wartości funkcji
f ,
c) wyznaczyć miejsca zerowe funkcji
f ,
d) wyznaczyć asymptoty funkcji f ,
e) wyznaczyć przedziały monotoniczności funkcji
f ,
f) narysować wykres funkcji
f .
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
54
Zadania do samodzielnego rozwiązania
zad. 1) Obliczyć:
a)
2
3
1
3
75
,
0
125
,
0
3
2
1
:
625
81
,
b)
2
4
1
3
3
81
16
3
9
375
,
0
,
c)
2
2
1
2
2
2
1
2
2
2
1
2
2
2
1
2
2
a
x
a
x
a
x
a
x
dla
2
1
2
2
2
mn
n
m
a
x
,
0
,
0
m
n
a
.
Odpowiedź:
a) 4,
b)
2
1
10 ,
c)
2
2
n
m
.
zad. 2) Wykonać dzielenie wielomianu W przez wielomian P:
a)
4
2
2
3
)
(
2
3
4
x
x
x
x
x
W
,
1
)
(
x
x
P
,
b)
10
7
4
2
)
(
2
3
x
x
x
x
W
,
2
)
(
x
x
P
.
Odpowiedź:
a)
4
3
5
3
2
3
x
x
x
,
b)
2
4
7
2
2
x
x
.
zad. 3) Wielomian W przy dzieleniu przez
)
5
(
x
daje resztę 1, a przy dzieleniu przez
)
3
(
x
daje resztę
)
7
(
. Wyznaczyć resztę z dzielenia wielomianu W przez wielomian
15
2
)
(
2
x
x
x
P
.
Odpowiedź:
4
)
(
x
x
R
.
zad. 4) Dla jakich wartości parametru
R
m
reszta z dzielenia wielomianu
m
x
x
m
x
W
5
8
)
(
3
6
2
przez dwumian
)
1
(
x
jest równa 2?
Odpowiedź:
}
2
,
3
{
m
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
55
zad. 5) Rozłożyć na czynniki wielomiany i podać ich pierwiastki:
a)
1
)
(
4
2
x
x
x
W
,
b)
6
13
2
)
(
2
4
x
x
x
W
,
c)
x
x
x
x
W
36
7
)
(
2
2
3
,
d)
2
3
2
3
)
(
4
5
x
x
x
x
W
.
Odpowiedź:
a)
1
2
1
)
(
2
3
4
2
2
5
1
2
5
1
x
x
x
x
x
x
x
x
W
,
2
5
1
2
5
1
,
x
,
b)
6
6
2
)
(
2
2
2
2
x
x
x
x
x
W
,
6
,
,
,
6
2
2
2
2
x
,
c)
)
3
)(
3
)(
2
)(
2
)(
1
)(
1
(
)
(
x
x
x
x
x
x
x
x
W
,
}
3
,
2
,
1
,
0
,
1
,
2
,
3
{
x
,
d)
)
2
3
)(
1
(
)
(
4
x
x
x
W
,
3
2
x
.
zad. 6) Rozwiązać nierówności:
a)
0
)
2
(
)
3
)(
5
(
2
3
x
x
x
,
b)
0
12
8
2
3
4
x
x
x
,
c)
0
3
7
4
3
x
x
,
d)
0
4
3
x
x
,
e)
0
2
4
2
2
3
x
x
,
f)
x
x
x
x
4
4
3
3
.
Odpowiedź:
a)
)
,
3
[
}
2
{
]
5
,
(
x
,
b)
,
0
0
,
2
6
,
x
,
c)
1
,
2
1
2
3
,
x
,
d)
)
,
2
(
)
2
,
(
x
,
e)
]
6
,
2
[
x
,
f)
)
2
,
0
(
)
2
,
(
x
.
zad. 7) Wyznaczyć dziedzinę oraz miejsca zerowe funkcji:
a)
9
6
4
)
(
2
x
x
x
x
f
,
b)
x
x
x
x
x
x
f
6
5
6
2
)
(
2
3
2
.
Odpowiedź:
a)
}
3
{
\
R
f
D
, miejsce zerowe
4
x
,
b)
}
3
,
2
,
0
{
\
R
f
D
, funkcja nie ma miejsc zerowych.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
56
zad. 8) Rozwiązać równania:
a)
x
x
x
5
2
5
5
,
b)
1
1
2
2
1
x
x
,
c)
2
3
1
2
x
x
x
.
Odpowiedź:
a)
2
5
5
,
2
5
5
x
,
b)
x
,
c)
}
2
,
1
{
x
.
zad. 9) Rozwiązać równania:
a)
1
3
2
3
x
,
b)
2
1
1
3
x
.
Odpowiedź:
a)
3
,
0
x
,
b)
2
7
,
2
3
x
.
zad. 10) Rozwiązać nierówności:
a)
0
9
6
5
2
2
x
x
x
,
b)
2
3
x
,
c)
x
x
1
9
,
d)
2
2
3
4
5
x
x
.
Odpowiedź:
a)
)
,
3
(
)
3
,
2
[
)
3
,
(
x
,
b)
)
,
0
(
]
5
,
1
;
(
x
,
c)
3
1
,
0
3
1
,
x
,
d)
3
2
,
0
x
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
57
zad. 11) Wyznaczyć dziedzinę, zbiór wartości, asymptoty oraz określić przedziały
monotoniczności funkcji:
a)
1
2
3
)
(
x
x
f
,
b)
1
3
2
)
(
x
x
x
f
,
c)
3
4
3
)
(
x
x
x
f
.
Odpowiedź:
a)
}
2
{
\
R
f
D
,
}
1
{
\
1
R
f
D
, asymptoty:
1
,
2
y
x
, funkcja jest malejąca
w przedziałach:
)
,
2
(
),
2
,
(
,
b)
}
1
{
\
R
f
D
,
}
2
{
\
1
R
f
D
, asymptoty:
2
,
1
y
x
, funkcja jest rosnąca
w przedziałach:
)
,
1
(
),
1
,
(
,
c)
}
3
{
\
R
f
D
,
}
3
{
\
1
R
f
D
, asymptoty:
3
,
3
y
x
, funkcja jest rosnąca
w przedziałach:
)
,
3
(
),
3
,
(
.