Materiały przygotowane w ramach projektu „Uruchomienie
unikatowego kierunku studiów Informatyka Stosowana odpowiedzią
na zapotrzebowanie rynku pracy” ze środków Programu Operacyjnego
Kapitał Ludzki współfinansowanego ze środków Europejskiego
Funduszu Społecznego nr umowy UDA – POKL.04.01.01-00-011/09-00
Wprowadzenie do matematyki
Materiały do zajęć (6):
Funkcje elementarne.
Funkcje trygonometryczne.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
58
9. Funkcje trygonometryczne.
Dziedziną funkcji
x
x
f
cos
)
(
jest zbiór liczb rzeczywistych, zbiorem wartości jest
przedział
]
1
,
1
[
. Jest to funkcja parzysta i okresowa o okresie podstawowym
2
. Ma
nieskończenie wiele miejsc zerowych,
k
x
2
dla
Z
k
.
Podstawowe własności funkcji:
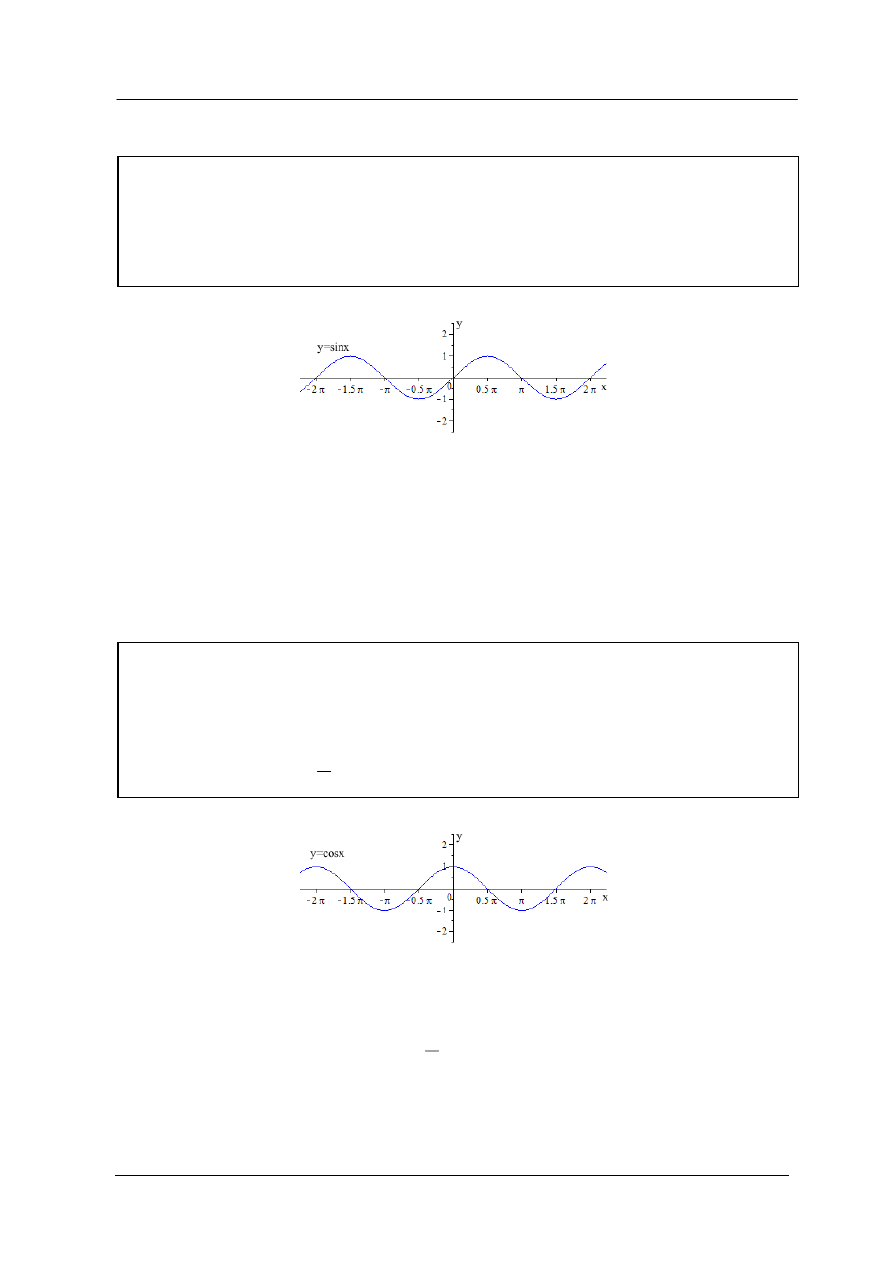
x
x
f
sin
)
(
,
R
x
1
sin
1
x
,
x
x
sin
)
sin(
,
x
k
x
sin
)
2
sin(
dla
Z
k
,
k
x
x
0
sin
dla
Z
k
.
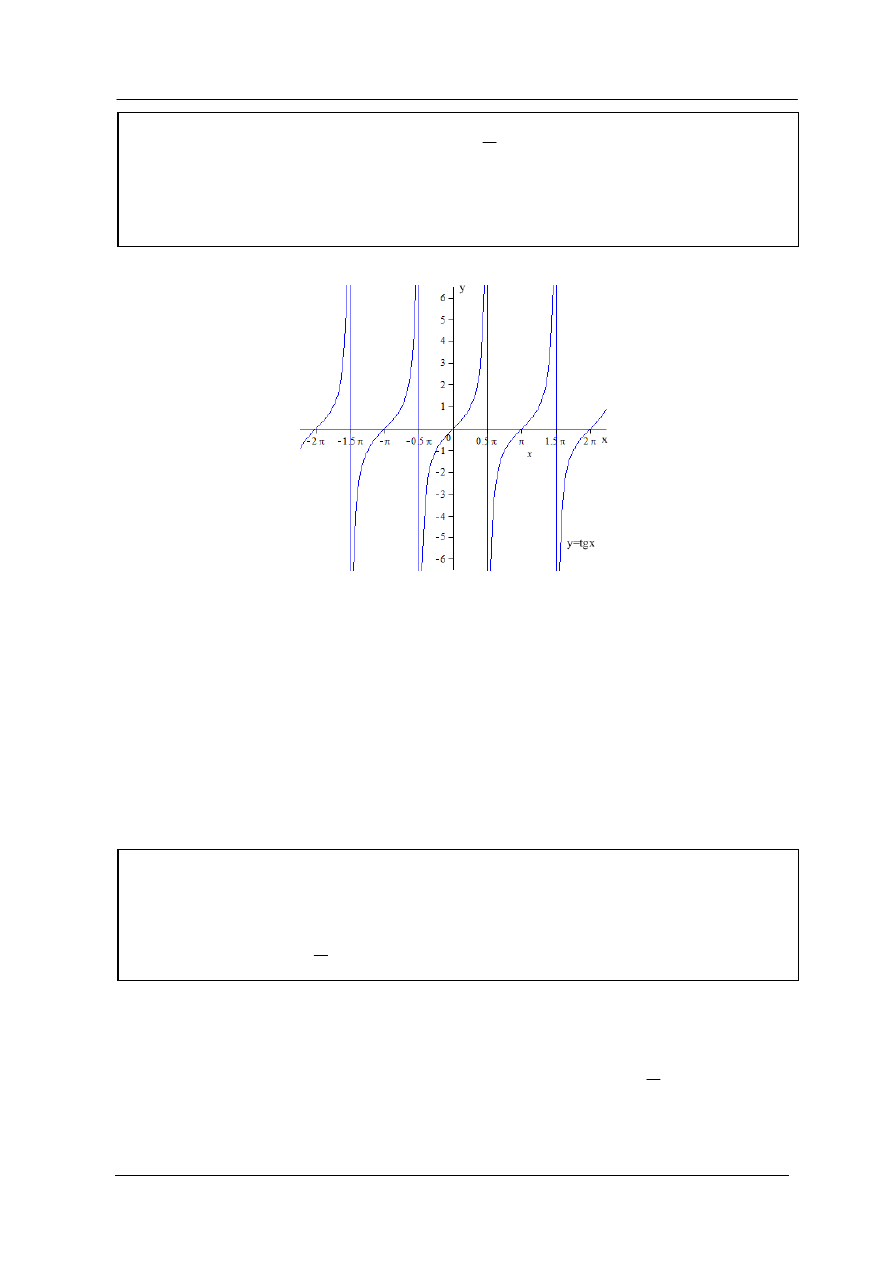
Podstawowe własności funkcji:
x
x
f
cos
)
(
,
R
x
1
cos
1
x
,
x
x
cos
)
cos(
,
x
k
x
cos
)
2
cos(
dla
Z
k
,
k
x
x
2
0
cos
dla
Z
k
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
59
Dziedziną funkcji
x
x
f
ctg
)
(
jest zbiór
,
dla
:
Z
R
k
k
x
x
≠
czyli suma
mnogościowa przedziałów
Z
k
k
k
,
,
, zbiorem wartości jest zbiór R. Jest to funkcja
nieparzysta, okresowa o okresie podstawowym
oraz malejąca w każdym z przedziałów
Z
k
k
k
,
,
. Ma nieskończenie wiele miejsc zerowych,
k
x
2
dla
Z
k
.
Wykres funkcji ma asymptoty pionowe o równaniach
k
x
dla
Z
k
.
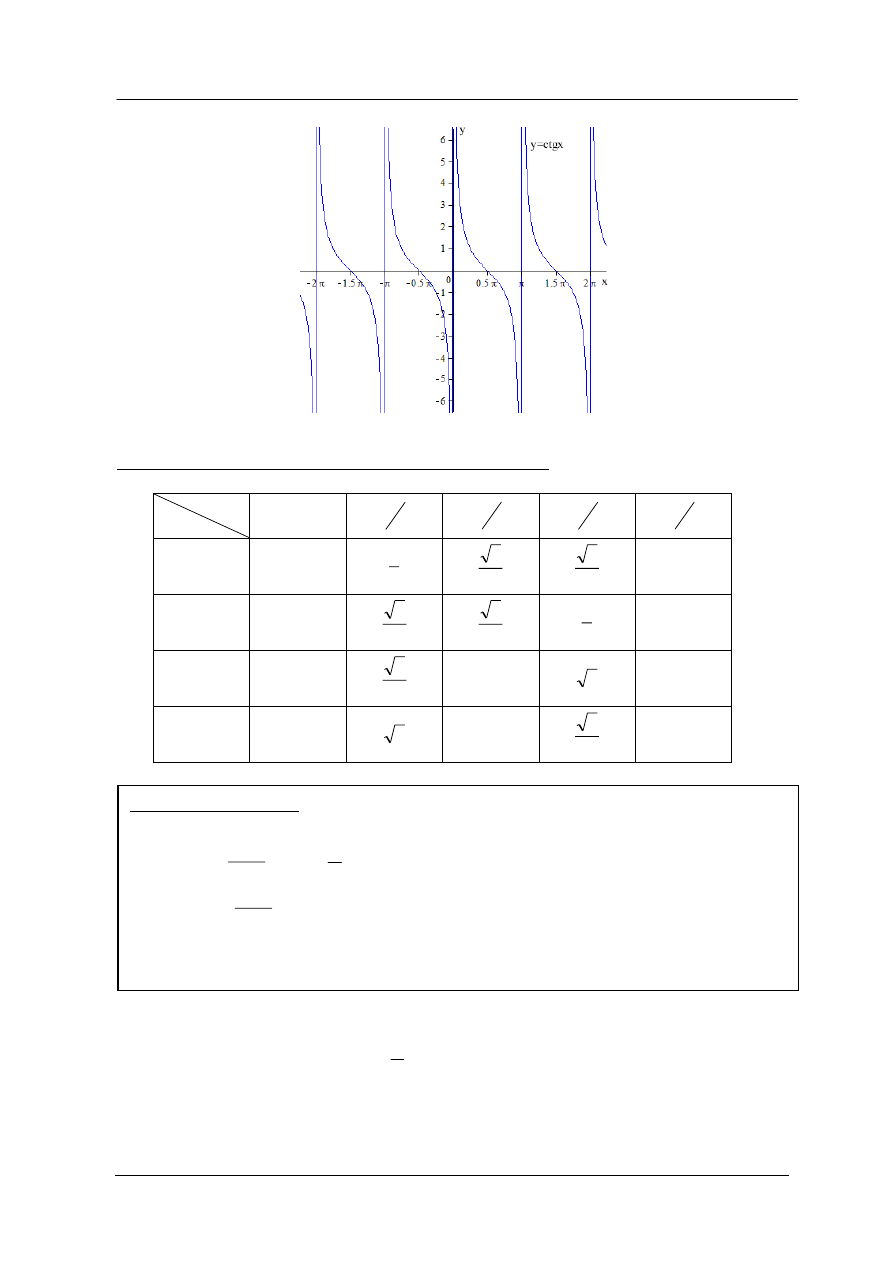
Podstawowe własności funkcji:
x
x
f
tg
)
(
,
k
x
2
dla
Z
k
x
x
tg
)
tg(
,
x
k
x
tg
)
tg(
dla
Z
k
,
k
x
x
0
tg
dla
Z
k
.
Podstawowe własności funkcji:
x
x
f
ctg
)
(
,
k
x
dla
Z
k
x
x
ctg
)
ctg(
,
x
k
x
ctg
)
ctg(
dla
Z
k
,
k
x
x
2
0
ctg
dla
Z
k
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
60
Wartości funkcji trygonometrycznych dla wybranych kątów
x
y
0
6
4
3
2
x
y sin
0
2
1
2
2
2
3
1
x
y cos
1
2
3
2
2
2
1
0
x
y tg
0
3
3
1
3
nie istnieje
x
y ctg
nie istnieje
3
1
3
3
0
Z przedstawionych własności wynikają zależności:
1
ctg
tg
x
x
dla
k
x
i
k
x
2
i
Z
k
,
x
x
2
sin
2
1
2
cos
oraz
1
cos
2
2
cos
2
x
x
.
Podstawowe własności dla
R
x
:
1
cos
sin
2
2
x
x
,
x
x
x
cos
s in
tg
dla
Z
k
k
x
,
2
,
x
x
x
s in
cos
ctg
dla
Z
k
k
x
,
,
x
x
x
cos
sin
2
2
sin
,
x
x
x
2
2
sin
cos
2
cos
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
61
Powyższe
zależności
są
podstawą
rozwiązywania
równań
i
nierówności
trygonometrycznych.
Przypadki szczególne:
równanie
a
x
sin
,
R
x
dla
1
a
ma rozwiązania
k
x
2
2
i
Z
k
, dla
1
a
ma
rozwiązania
k
x
2
2
i
Z
k
, dla
0
a
rozwiązaniami są miejsca zerowe funkcji
x
x
f
sin
)
(
, dla
)
,
1
(
)
1
,
(
a
nie ma rozwiązań,
równanie
a
x
cos
,
R
x
dla
1
a
ma rozwiązania
k
x 2
i
Z
k
, dla
1
a
ma
rozwiązania
)
2
1
(
2
k
k
x
i
Z
k
, dla
0
a
rozwiązaniami są miejsca zerowe
funkcji
x
x
f
cos
)
(
, dla
)
,
1
(
)
1
,
(
a
nie ma rozwiązań.
Przykład.
Rozwiązać równania:
a)
2
1
s i n
x
,
b)
3
ctg
x
,
c)
1
)
3
tg(
x
.
Przykład.
Rozwiązać równania:
a)
3
3
4
ctg
tg
x
x
,
)
2
,
0
(
x
,
b)
0
cos
sin
x
x
.
Własności:
Jeżeli
0
x jest jednym z rozwiązań równania
a
x
sin
,
]
1
,
1
[
a
, to dla każdego
R
x
k
x
x
k
x
x
a
x
2
)
(
2
sin
0
0
,
Z
k
.
Jeżeli
0
x jest jednym z rozwiązań równania
a
x
cos
,
]
1
,
1
[
a
, to dla każdego
R
x
k
x
x
k
x
x
a
x
2
2
cos
0
0
,
Z
k
.
Jeżeli
0
x jest jednym z rozwiązań równania
a
x
tg
,
R
a
, to dla każdego
k
x
2
,
Z
k
,
k
x
x
a
x
0
tg
,
Z
k
.
Jeżeli
0
x jest jednym z rozwiązań równania
a
x
ctg
,
R
a
, to dla każdego
k
x
,
Z
k
,
k
x
x
a
x
0
ctg
,
Z
k
.
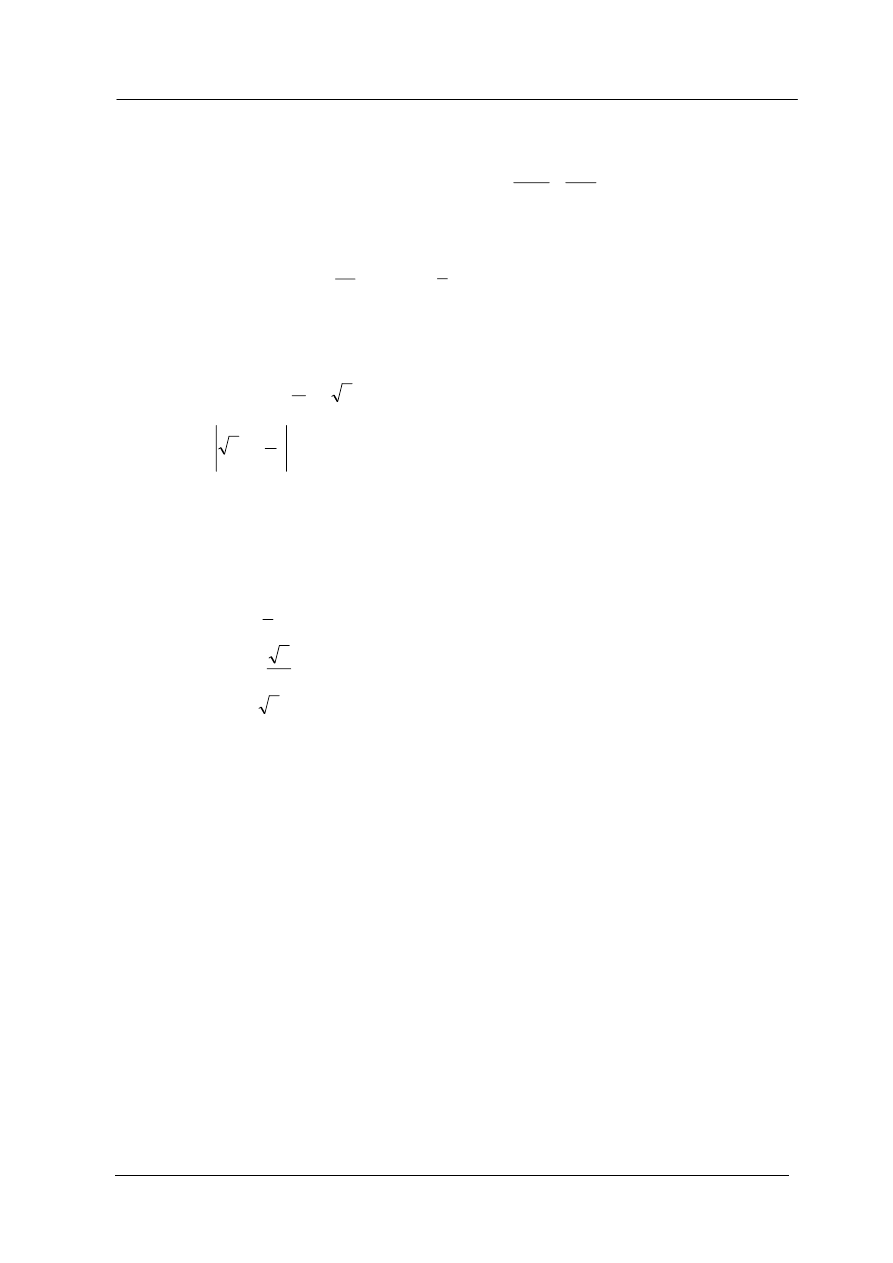
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
62
Zadania
zad. 1) Sprawdzić, czy podana równość:
s in
tg
1
s in
1
cos
1
jest tożsamością
trygonometryczną. Podać konieczne założenia.
zad. 2) Wiedząc, że
60
11
ctg
x
i
2
3
,
x
wyznaczyć wartości pozostałych funkcji
trygonometrycznych.
zad. 3) Rozwiązać równania:
a)
3
2
2
cos
2
x
,
b)
1
3
tg
3
x
,
,
x
,
c)
1
3
cos
5
,
0
3
sin
2
x
x
,
d)
0
cos
cos
sin
2
sin
2
2
x
x
x
x
,
e)
0
sin
2
2
sin
x
x
.
zad. 4) Rozwiązać nierówności:
a)
2
1
s i n
x
,
b)
2
2
cos
x
,
c)
3
tg
x
,
d)
1
ctg
x
.
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
63
Zadania do samodzielnego rozwiązania
zad. 1) Wiedząc, że
2
tg
obliczyć wartości pozostałych funkcji trygonometrycznych dla
2
3
,
.
Odpowiedź:
2
1
ctg
,
5
5
cos
,
5
5
2
sin
x
x
x
.
zad. 2) Obliczyć
x
2
sin
wiedząc, że
25
24
s i n
x
i
,
2
x
.
Odpowiedź:
625
336
.
zad. 3) Rozwiązać równania:
a)
]
2
,
2
[
,
2
2
cos
x
x
,
b)
1
)
3
(
tg
x
,
c)
1
3
2
cos
x
,
2
3
,
2
x
.
Odpowiedź:
a)
4
7
,
4
3
,
4
3
,
4
7
x
,
b)
Z
k
k
x
,
3
12
,
c)
6
5
x
.
zad. 4) Rozwiązać równania:
a)
0
1
sin
sin
2
2
x
x
,
b)
0
3
cos
3
sin
2
x
x
,
c)
x
x
ctg
3
ctg
3
,
)
,
0
(
x
,
d)
3
2
3
sin
2
2
x
,
e)
]
,
[
,
0
1
2
sin
2
cos
x
x
x
.
Odpowiedź:
a)
Z
k
k
x
k
x
k
x
,
2
6
5
2
6
2
2
,
b)
Z
k
k
x
,
)
1
2
(
,
Materiały pomocnicze dla studentów
Wprowadzenie do matematyki
© Uniwersytet Ekonomiczny w Krakowie
64
c)
6
5
,
2
,
6
x
,
d)
Z
k
k
x
,
,
e)
2
,
4
,
2
,
4
3
x
.
zad. 5) Dla jakich wartości parametru
R
m
równanie:
a)
m
x
2
)
3
cos (
,
b)
0
1
sin
4
)
sin
1
(
2
x
m
x
m
ma rozwiązania?
Odpowiedź:
a)
)
,
2
[
]
2
,
(
m
,
b)
)
,
2
[
2
1
,
0
m
.
zad. 6) Rozwiązać nierówności:
a)
2
3
s in
x
,
b)
2
1
cos
x
,
c)
3
3
x
tg
,
d)
3
x
ctg
.
Odpowiedź:
a)
k
k
x
2
3
2
,
2
3
,
Z
k
,
b)
k
k
x
2
3
5
,
2
3
,
Z
k
,
c)
k
k
x
6
,
2
,
Z
k
,
d)
k
k
x
3
2
,
,
Z
k
.