1
Reprezentacja informacji w
komputerze
1
Reprezentacja informacji w
komputerze
2
Forma informacji
• Komunikat zawierający tę samą informację
może mieć różną formę, np.:
– 100 mil/h = 44.4 m/sek,
• Ten sam komunikat może być zapisany:
– alfabetem łacińskim,
– Arabskim
– albo pismem Brailla
• itd.
3
Dane:
• Dane to obiekty posiadające:
– jednoznaczną nazwę
– i określoną wartość.
• Dane stanowią reprezentację informacji.
• Przykładowe typy danych:
– dane typu logicznego: „tak” lub „nie”,
– dane alfanumeryczne (alfabet + liczby),
– dane numeryczne,
– dane graficzne,
– dane alfanumeryczne o ustalonej strukturze – rekordy.
– etc.
4
Format danych
• Organizacja każdego komputera zależy w dużej mierze od
sposobu, w jaki zapisywane są w nim liczby, znaki i
informacje sterujące.
– Z jednej strony, reprezentacja danych wykorzystywanych w
procesie automatycznego przetwarzania powinna być dogodna dla
wykonywania na nich operacji przez procesor.
– Z drugiej, dane muszą być czytelne i łatwe do interpretacji przez
człowieka.
• Np. jak podzielić dwie liczby zapisane rzymskimi cyframi?
• W historii rozwoju informatyki wypracowano standardy i
konwencje odnoszące się do organizacji komputerów.
5
Format danych
• Większość danych przetwarzanych przez komputer ma postać tekstu
zapisanego znakami alfabetu stosowanego w życiu codziennym.
• Alfabet, w którym przedstawiane są dane wewnątrz maszyny
cyfrowej, zawiera dwa symbole: zero i jeden.
• Urządzenie elektroniczne korzystające z takiego dwuznakowego
alfabetu jest prostsze i bardziej niezawodne niż w przypadku
alfabetów o większej liczbie symboli.
• Fizyczną realizację tego dwuznakowego alfabetu stanowią:
– dziurka lub jej brak na karcie perforowanej,
– impuls i brak impulsu elektrycznego lub świetlnego,
– określony zwrot polaryzacji pozostałości magnetycznej lub jej zwrot
przeciwny,
– stan przewodzenia i nie przewodzenia tranzystora,
– 1 i 0 na papierze.
6
Systemy liczbowe
• W połowie XVI wieku Europejczycy za pośrednictwem
Arabów przyjęli dziesiątkowy system liczbowy, z którego
Hindusi korzystali już od 1000. lat.
• Ogólne założenia pozycyjnych systemów liczbowych:
– wartość liczby reprezentowana jest przez kolejne potęgi
podstawy systemu,
– liczba znaków stosowanych w każdym pozycyjnym
systemie liczbowym jest taka sama, jak jego podstawa,
– największa stosowana cyfra ma wartość o 1 mniejszą
od podstawy systemu.
7
Przykłady
• W systemie dziesiątkowym mamy 10 cyfr -
od 0 do 9,
• W systemie o podstawie 3 wykorzystuje się
3 cyfry: 0, 1 i 2.
• Aby zaznaczyć, w jakim systemie została
zapisana dana liczba, piszemy obok niej
podstawę np.:
– liczba 44
(10)
to dziesiętnie 44.
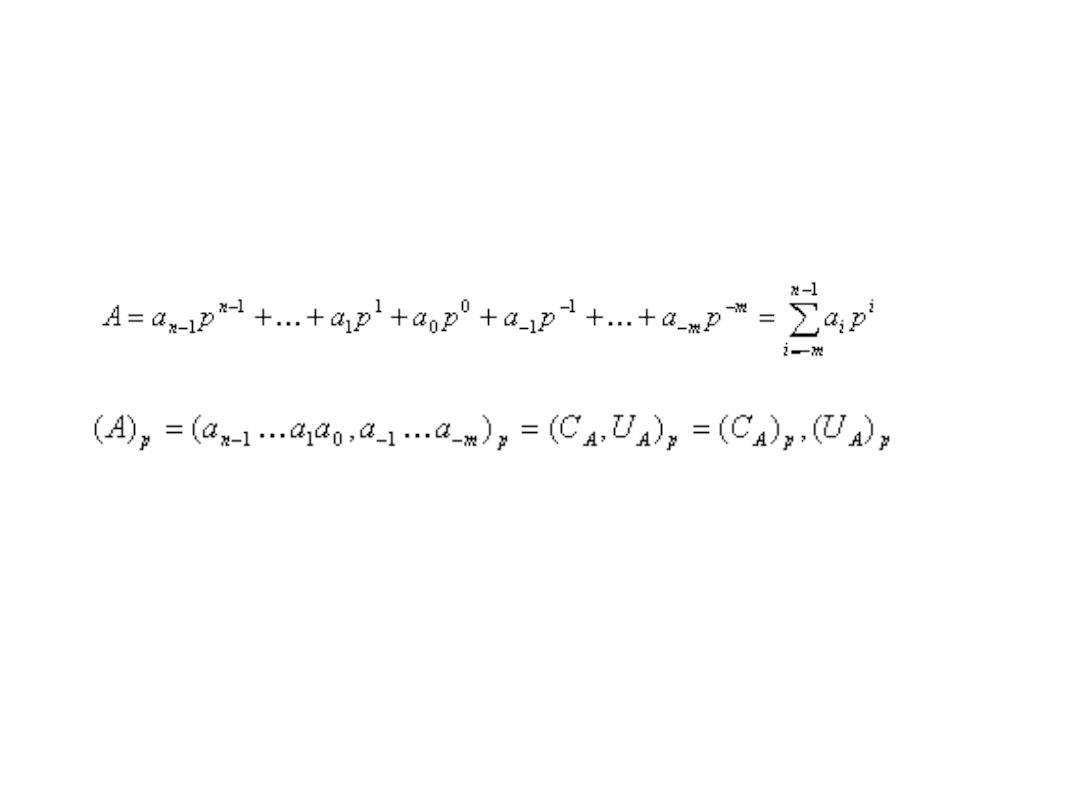
8
Pozycyjne systemy liczbowe o
dodatniej podstawie.
•
W systemie pozycyjnym nieujemną (n+m) pozycyjną liczbę A:
zapisuje się w postaci :
gdzie:
p – jest podstawą systemu liczbowego; |p|>1, p
∈
{2, 3, ...};
a
i
– cyfra na i-tej pozycji liczby A, a
i
∈
{0, 1, ..., p – 1};
n – liczba cyfr części całkowitej liczby A;
m – liczba cyfr części ułamkowej liczby A.
•
Przecinek lub kropka oddziela część całkowitą C
A
liczby A od jej części
ułamkowej U
A
9
Przykłady kodowania liczb
• Trzy liczby wyrażone przez wyrazy będące potęgami wybranej
podstawy:
Podstawa=10
243,56
10
=2·10
2
+4·10
1
+3·10
0
+5·10
-1
+6·10
-2
Podstawa=3
100000,12
3
≈
1·3
5
+0·3
4
+0·3
3
+0·3
2
+0·3
1
+0·3
0
+1·3
-1
+2·3
-
2
≈
243,555
10
...
Podstawa=2
11110011,10011
2
≈
1·2
7
+1·2
6
+1·2
5
+1·2
4
+0·2
3
+0·2
2
+1·2
1
+1·2
0
+1·2
-1
+0·2
-
2
+ 0· 2
-3
+1· 2
-4
+1· 2
-5
+..
≈
243,59375
10
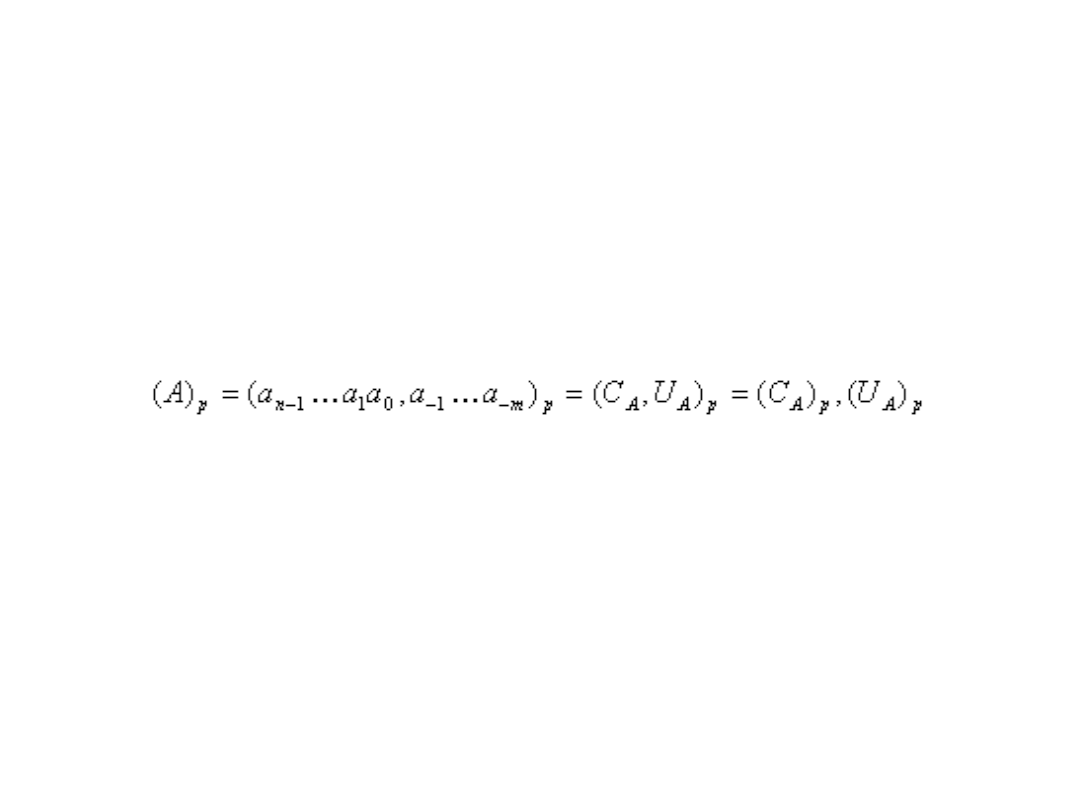
10
Cyfry znaczące
• Podstawa pozycyjnego systemu liczbowego odpowiada
liczbie cyfr wykorzystywanych do przedstawienia danej
liczby w tym systemie:
– jeżeli m = 0, to A jest liczbą całkowitą,
– jeżeli n = 0 , to ułamkowa.
– jeśli natomiast m i n są niezerowymi liczbami całkowitymi, to A
jest liczbą mieszaną,
– a
n-1
jest cyfrą najbardziej znaczącą (Most Significant Digit -
MSD),
– a
-m
to cyfra najmniej znacząca (Least Significant Digit - LSD).
11
System dwójkowy
• Dwójkowy system liczenia kojarzy się
nieodłącznie z informatyką.
– Historia binarnego systemu liczenia sięga 3000 lat
p.n.e..
– W czasach nowożytnych systemu binarnego używał już
John Napier w XVI wieku, przy czym 0 i 1 zapisywał
jako a i b.
– Gottfried Leibniz (1646 - 1716), jako pierwszy
zaproponował rozszerzenie założeń obowiązujących w
systemie dziesiętnym na systemy liczbowe o innych
podstawach.
12
System dwójkowy w informatyce
• Idea zastosowania układu dwójkowego w maszynach
cyfrowych nie była wcale oczywista.
– Pierwsza elektroniczna maszyna cyfrowa ENIAC wykonywała
operacje na liczbach dziesiętnych.
– System binarny został zastosowany po raz pierwszy przez Johna
von Neumana w maszynie cyfrowej EDVAC.
• Obecnie system dwójkowy stanowi podstawę każdego
urządzenia elektronicznego sterowanego cyfrowo.
Ponieważ dzięki swej prostocie może być on z łatwością
obsługiwany przez układy elektroniczne.
13
System dwójkowy
• Podstawa rozwinięcia równa się
w tym przypadku 2, a zbiór
możliwych cyfr składa się z a
i
∈
{0, 1}.
• Kod binarny prosty – służy do
kodowania liczb dodatnich:
Potęgi 2
2
-2
=1/4= 0,25
2
-1
=1/2= 0,5
2
0
= 1
2
1
= 2
2
2
=4
2
3
=8
2
4
= 16
2
5
=32
2
6
= 64
2
7
= 128
2
8
= 256
2
9
= 512
2
10
= 1024
2
15
= 32768
==== 32 768
2
16
= 65 536
∑
−
=
=
1
0
2
n
i
i
i
a
L
[
]
1
2
,
0
−
∈
n
L
14
System dwójkowy
• Zapis liczby
11110011,100112
(2)
odczytujemy, patrząc od lewej
strony, następująco:
1·2
7
+1·2
6
+1·2
5
+1·2
4
+0·2
3
+0·2
2
+1·2
1
+1·2
0
+1·2
-1
+0·2
-2
+
0· 2
-3
+1· 2
-4
+
1· 2
-5
+...
≈
243,59375
10
MSB
- Most Significant Bit,
LSB
- Least Significant Bit.
• Liczba zapisana w systemie dwójkowym jako
11110011,100112
(2)
odpowiada liczbie 243,59375
10
w systemie dziesiętnym.
15
Konwersja całkowitej liczby
dziesiętnej na liczbę dwójkową
• Konwersja liczby 147
10
na system dwójkowy:
2|147
1
2 mieści się w 147, 73 razy, reszta 1
2|73
1
2 mieści się w 73, 36 razy, reszta 1
2|36
0
2 mieści się w 36, 18 razy, reszta 0
2|18
0
2 mieści się w 18, 9 razy, reszta 0
2|9
1
2 mieści się w 9, 4 razy, reszta 1
2|4
0
2 mieści się w 4, 2 razy, reszta 0
2|2
0
2 mieści się w 2, 1 raz, reszta 0
2|1
1
2 mieści się w 1, 0 razy, reszta 1
0
•
Odczytując reszty od dołu do góry, otrzymujemy: 147
10
=
10010011
2
16
Konwersja całkowitej liczby
dziesiętnej na liczbę dwójkową
• Konwersja liczby 147
10
na system dwójkowy:
147 = 146 +
1
73 = 72 +
1
36 = 36 +
0
18 = 18 +
0
9 = 8 +
1
4 = 4 +
0
2 = 2 +
0
1 = 0 +
1
• Odczytując reszty od dołu do góry, otrzymujemy: 147
10
=
10010011
2
17
Reasumując
• W celu konwersji daną liczbę całkowitą w układzie dziesiętnym,
przedstawiamy w postaci sumy
liczby parzystej
i
jedności lub zera
:
11 =
10
+
1
5 =
4
+
1
2 =
2
+
0
1 =
0
+
1
• Po zakończeniu operacji jedynki i zera kolejnych sum stanowią
poszukiwaną liczbę w zapisie dwójkowym.
– Jedynka bądź zero wyznaczone w pierwszym kroku odpowiada najmniej
znaczącej pozycji 2
0
.
– Cyfra wyznaczona w ostatnim kroku odpowiada najbardziej znaczącej
pozycji.
• Otrzymujemy więc liczbę
1011
(2)
.
18
Operacje na liczbach dwójkowych
• Stosując zapis binarny na N bitach można
zapisać liczby całkowite bez znaku z
przedziału od 0 do 2
N-1
, np. :
– na 2 bitach można zapisać wartości dziesiętne
od 0 do 3,
– na 4 bitach można zapisać wartości dziesiętne
od 0 do 15,
– na 8 - od 0 do 255.
19
Zjawisko przepełnienia
• Zakres wartości, które mogą być przedstawiane za pomocą
danej liczby bitów, ma znaczenie przy wykonywaniu operacji
arytmetycznych na liczbach dwójkowych.
– Np. załóżmy, że liczby dwójkowe mogą składać się z 4 bitów.
– Dodajemy: 15
(10)
+ 15
(10)
= 30
(10)
1111
(2)
+ 1111
(2)
= ?
liczby 30 nie da się zapisać, mając do dyspozycji jedynie 4 bity.
• Sytuację taką nazywamy przepełnieniem,
– pojawia się ona przy binarnym zapisie liczby będącej wynikiem
operacji arytmetycznej, przekraczającym zakres liczb, które można
przedstawić za pomocą określonej liczby bitów.
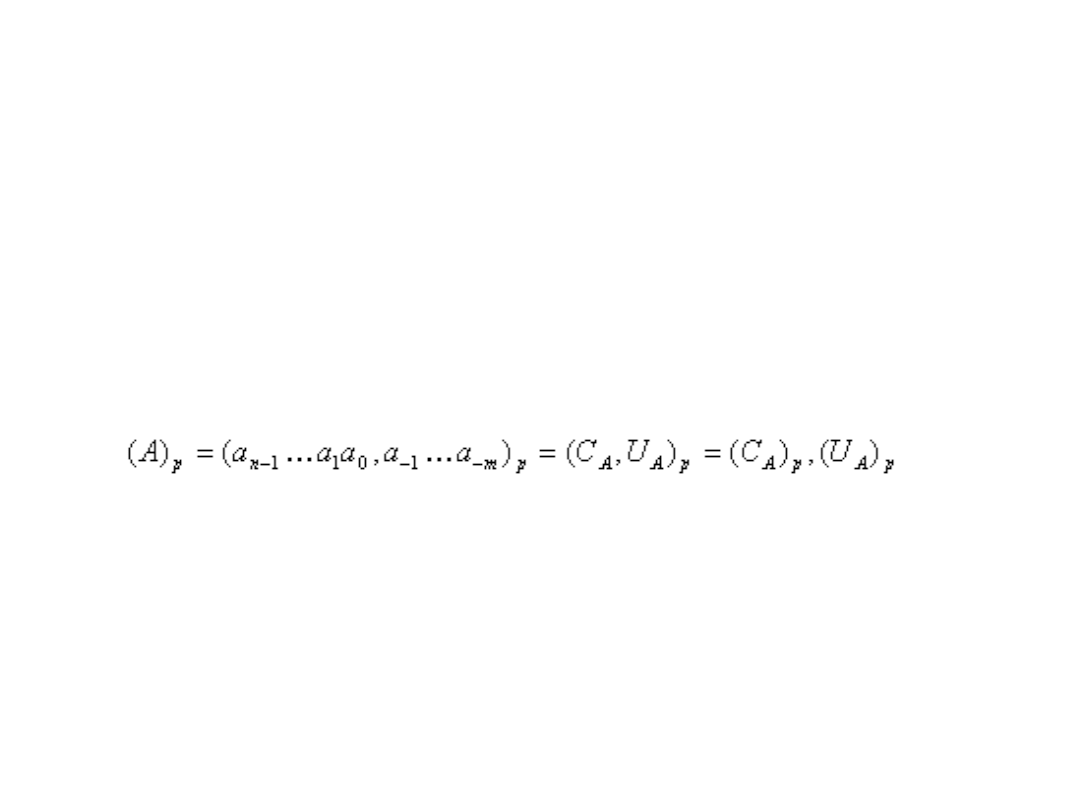
20
Przeliczanie ułamków
• Ułamki występujące we wszystkich systemach
liczbowych mogą być z pewnym przybliżeniem
przedstawiane w innym systemie jako ujemne
potęgi podstawy.
• Przecinek (kropka) bazowa oddziela całkowitą
część liczby od części ułamkowej.
– W system dziesiętnym przecinek bazowy nazywamy po
prostu przecinkiem dziesiętnym, natomiast w systemie
dwójkowym - przecinkiem dwójkowym.
21
Uwaga
• Ułamki, które w jednym systemie
liczbowym są okresowe, w innym systemie
mogą być dokładnie określone.
• Na przykład:
– liczba 2/3
(10)
=0,6666… w systemie
dziesiętnym jest ułamkiem okresowym,
– a w systemie trójkowym ma skończoną postać:
0,2
(3)
=2·3
-1
=2·1/3.
22
Przeliczanie ułamków
• Ułamki można przeliczać między różnymi systemami, korzystając z
metod kolejnych odejmowań i dzieleń.
• Przykładowe przeliczanie ułamka
0.4304
10
na system liczbowy o
podstawie 5:
0.4304
x 5
2.
1520 Część całkowita jest równa 2. Pomijamy ją przy kolejnym mnożeniu.
.1520
x 5 Część całkowita jest równa 0. Będzie ona potrzebna do wypełnienia
0.
7600 pustego miejsca.
.7600
x 5
3.
8000 Część całkowita jest równa 3. Pomijamy ją przy kolejnym mnożeniu.
.8000
x 5
4.
0000 Część całkowita = 4, a ułamkowa = zero.
Czytając od góry do dołu, otrzymamy: 0.4304
10
=
0.2034
5
.
23
Skończona dokładność konwersji
• Często z powodu ograniczenia dostępnej
liczby bitów, zadowalająca jest część
rozwiązania, która mieści się w założonym
zakresie dokładności.
24
Przykład
• Przeliczanie ułamka 0,34375
10
na system dwójkowy z precyzją do 4
bitów po przecinku.
0,34375
x 2
0
,68750
(wypełniacz)
,68750
X 2
1
,37500 ,
,37500
X 2
0
,75000
,75000
X 2
1
,50000
(przerywamy rachunki przy 4 bicie)
...........
•
Czytając od góry do dołu stwierdzamy, że 0,34375
10
≈
0,0101
2
...
z
dokładnością do 4 miejsc po przecinku.
25
Kod szesnastkowy
(heksadecymalny)
• Zapis binarny nie jest czytelny dla człowieka,
natomiast zapis dziesiętny wymaga każdorazowej
konwersji z zapisu binarnego.
• Dlatego do wymiany komunikatów pomiędzy
maszyną i człowiekiem stosuje się często kod
szesnastkowy (hexadecimal).
• Podstawą rozwinięcia tego systemu jest liczba
16=2
4
26
Kod szesnastkowy
• Zbiór cyfr jest rozszerzony o litery alfabetu A =
10, B = 11, ... , F = 15,
• a
i
∈
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}.
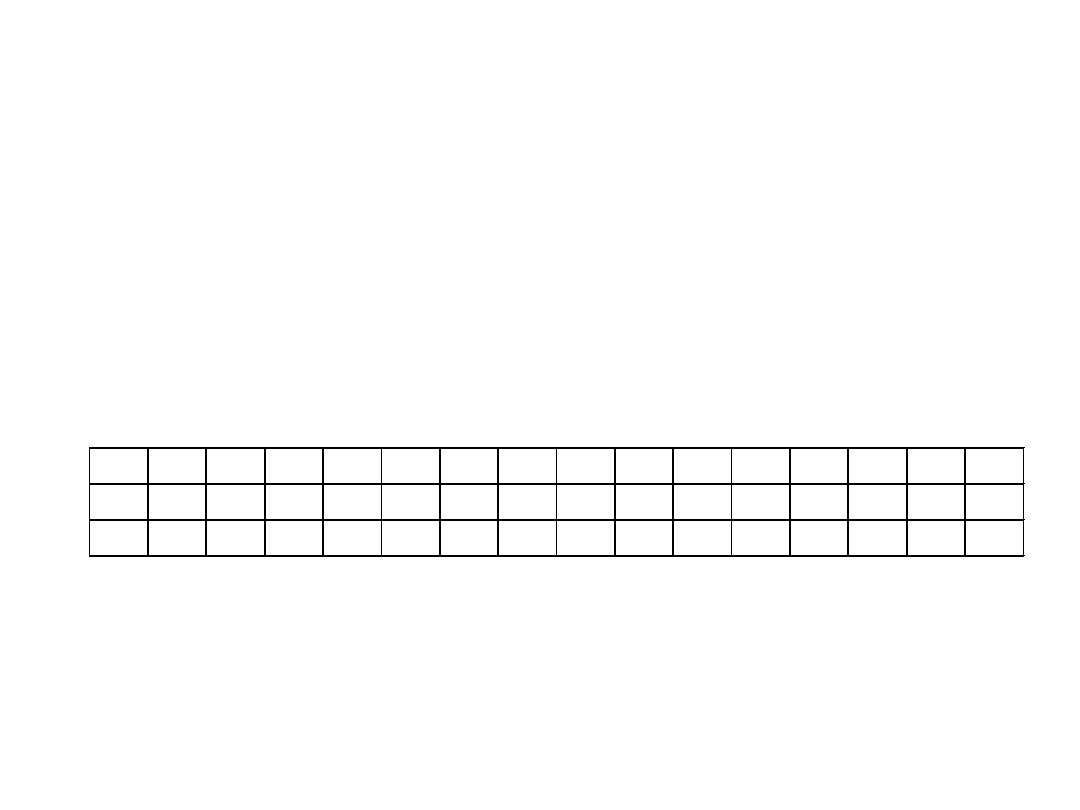
• Z tabeli wynika, że konwersja liczb
szesnastkowych na binarne i na odwrót jest prosta.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
27
Przeliczanie liczb między systemami
o podstawach 2N
• Ponieważ 16 = 2
4
, grupę 4 bitów (hekstet) można
traktować jako jedną cyfrę szesnastkową.
• Podobnie, 8 = 2
3
, grupę trzech bitów (oktet)
można traktować jak jedną cyfrę w systemie
ósemkowym.
• Zależności te pozwalają w prosty przeliczać liczby
z systemu dwójkowego na ósemkowy i
szesnastkowy.
28
Przeliczanie liczb między systemami
o podstawach 2
N
• Ponieważ 16 = 2
4
, grupę 4 bitów (hekstet) można traktować
jako jedną cyfrę szesnastkową.
• Podobnie, 8 = 2
3
, grupę trzech bitów (oktet) można
traktować jak jedną cyfrę w systemie ósemkowym.
• Zależności te pozwalają w prosty przeliczać liczby z
systemu dwójkowego na ósemkowy i szesnastkowy.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
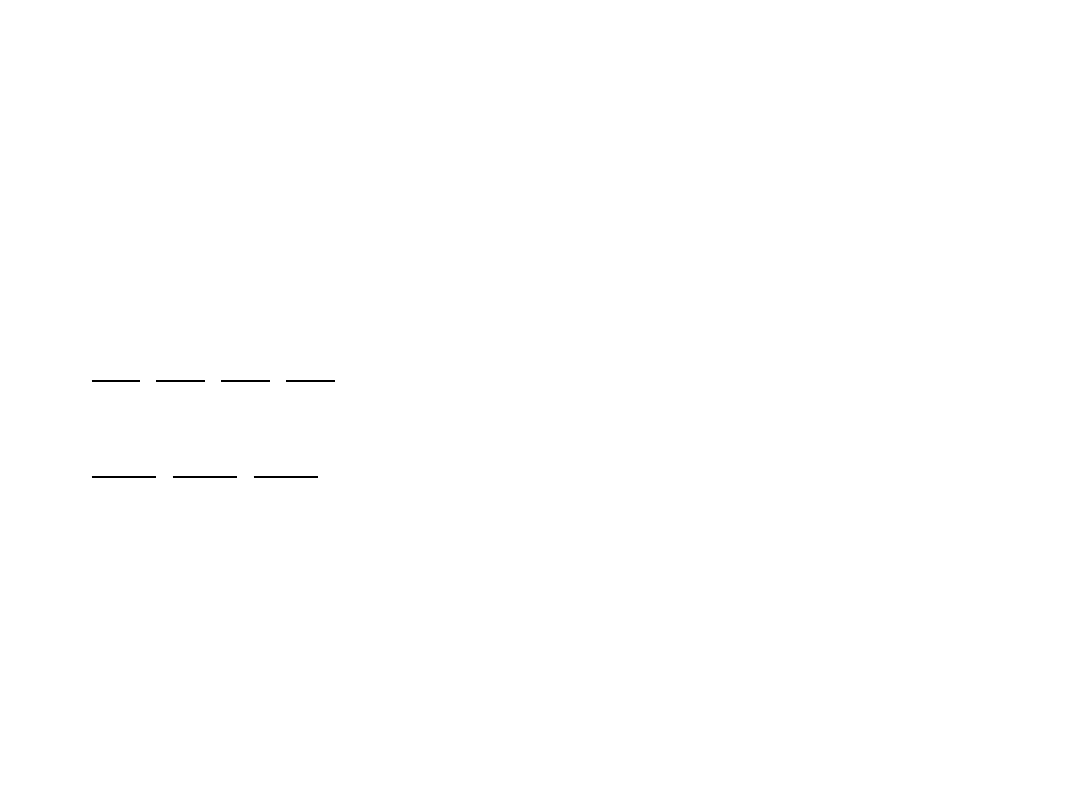
29
Przykład
• Przeliczanie liczby 110010011101
2
na system ósemkowy i
szesnastkowy.
110 010 011 101
Grupując bity po 3
6 2 3 5
110010011101
2
= 6235
8
1100 1001 1101 Grupując bity po 4,
C 9 D
110010011101
2
= C9D
16
• Wynik odczytujemy jako: (C dziewięć D).
• Jeżeli liczba dwójkowa ma za mało bitów, na jej początku można
wstawić odpowiednią liczbę zer.
30
Konwersja liczby szesnastkowej na
dwójkową
• Wykonuje się ją odwrotnie jak dwójkową na
szesnastkową.
– Kolejne cyfry w zapisie szesnastkowym zapisujemy
jako cztery cyfry w zapisie dwójkowym.
– Ewentualnie należy pozbyć się zer znajdujących się na
pozycji wysuniętej najbardziej w lewo, aż napotkamy
tam jedynkę, gdyż kod binarny zawsze zaczyna się od
1.
– Np. jeśli wyjdzie wynik 0001100101110 to można
go zapisać jako 1100101110 pozbywając się zer z
początku.
31
Konwersja liczby szesnastkowej na
dziesiętną
• Konwersja ta odbywa się podobnie jak w przypadku liczb
binarnych, z tym, że podstawą jest nie 2, a 16.
– Weźmy dowolną liczbę w zapisie szesnastkowym, np. : AB12
(16)
– Bierzemy cyfrę wysuniętą najbardziej w prawo i postępujemy tak
samo jak w przypadku liczb dwójkowych, ale zamiast mnożnika 2
mamy 16:
2*16
0
+ 1*16
1
+ 11*16
2
+ 10*16
3
,
otrzymamy
2 + 16 + 2816 + 40960,
a więc w zapisie dziesiętnym jest to liczba:
43794
(10)
.
32
Konwersja liczby dziesiętnej na
szesnastkową
• Odwróćmy teraz na powrót liczbę 43794
(10)
w zapisie dziesiętnym na
AB12
(16)
w szesnastkowym.
• Kolejne wielokrotności liczby 16 są następujące:
16
0
= 1, 16
1
= 16, 16
2
= 256, 16
3
= 4096, 16
4
= 65536 itd.
• Wybrana liczba w systemie dziesiętnym znajduje się w przedziale:
4096 < 43794 < 65536.
• Bierzemy pod uwagę liczbę mniejszą od konwertowanej, czyli 4096.
– Jest ona czwartą wielokrotnością 16, więc konwertowana liczba w
systemie szesnastkowym będzie miała 4 cyfry.
• Sprawdzamy, ile razy liczba 4096 mieści się w liczbie konwertowanej,
czyli: 43794: 4096=10.691894
– Okazuje się, że mieści się ona 10 razy.
– 10 w systemie szesnastkowym to A, zatem pierwsza cyfra to A.
33
Konwersja liczby dziesiętnej na
szesnastkową c.d.
• Skoro liczba 4096 zmieściła się dziesięć razy w 43794, to jeszcze
zapewne została jakaś reszta.
• Obliczamy tę resztę.
– Mnożymy 4096*10 = 40960.
– Odejmujemy wynik od naszej liczby:
43794 - 40960 = 2834.
• Z resztą postępujemy podobnie, jak na początku konwersji.
256<2834<4096
• W następnym kroku sprawdzamy ile razy 256 mieści się w 2834.
2834:256=11.070312
– Mieści się 11 razy, zatem kolejna cyfra szukanego zapisu to B.
• Następnie znowu: obliczamy resztę, itd.
• Wynik powinien wynosić: AB12.
34
Reprezentacja liczb całkowitych ze
znakiem
• Wzór pozwala przedstawiać jedynie liczby
dodatnie.
• Główny problem z zapisywaniem liczb ze znakiem w
systemie dwójkowym polega na tym, że nie bardzo
wiadomo, gdzie i w jaki sposób zapisać znak liczby.
– W wielu językach programowania automatycznie rezerwowany jest
określony obszar pamięci, którego pierwszy bit określa znak liczby.
– Przyjęło się, że jeżeli najbardziej znaczący bit ma wartość „1”, to
pozostałe bity przedstawiają liczbę ujemną.
i
n
m
i
i
p
a
A
∑
−
−
=
=
1
35
Kod prosty
• Intuicyjnym rozwiązaniem jest kod prosty,
– pierwszy bit z lewej (nazywany też najbardziej
znaczącym) służy do przechowywania
informacji o znaku,
– bity występujące po bicie znaku przechowują
wartość bezwzględną liczby.
• Na przykład:
– w 8-bitowym słowie liczba -1 byłaby zapisana
jako 10000001, natomiast +1 jako 00000001.
36
Kod prosty c.d.
• W przypadku kodu prostego wartości liczb
całkowitych są zapisane jedynie na 7 bitach.
• Oznacza to, że największą liczbą całkowitą,
jaką można przechowywać w 8-bitowym
słowie, jest:
– 2
7-1
, czyli 127 = 01111111
2,
– najmniejsza liczba to -127=11111111
2
.
– Na N bitach można zapisać liczby ze znakiem
od -2
N-1
– 1 do 2
N-1
– 1.
37
Arytmetyka z zastosowaniem kodu
prostego
• Arytmetyka liczb zapisanych w kodzie prostym
jest realizowana w sposób podobny, w jaki
liczymy na kartce ołówkiem.
• Reguły rządzące dodawaniem:
– Jeżeli znaki obu liczb są takie same, dodaj ich wartości
bezwzględne i pozostaw znak bez zmian.
– Jeżeli liczby mają różne znaki, musisz ustalić, która z
nich ma większą wartość bezwzględną, jej znak
powinien mieć wynik całego dodawania.
• Wyznacza się go, odejmując (nie dodając) mniejszą liczbę od
większej.
38
Przykład
• Dodawanie 01001111
2
+ 00100011
2
w arytmetyce kodu prostego:
1 1 1 1
<=przeniesienia
0 1 0 0 1 1 1 1 (79)
0 + 0 1 0 0 0 1 1 +(35)
0 1 1 1 0 0 1 0 (114)
• Wszystkie „nie mieszczące się" wartości przenosimy do kolejnej
kolumny, aż do osiągnięcia siódmego bitu od prawej.
• Jeżeli i na tej pozycji trzeba wykonać przeniesienie, mówimy, że
nastąpił błąd przepełnienia i odrzucamy przeniesienie, co skutkuje
otrzymaniem nieprawidłowej sumy.
• W tym przykładzie nie nastąpiło przepełnienie i w kodzie prostym
wynik dodawania wynosi: 01001111
2
+ 00100011
2
= 01110010
2
.
39
Przykład
• Dodawanie 01001111
2
+ 01100011
2
w arytmetyce
kodu prostego.
1 1 1 1 1
0 1 0 0 1 1 1 1 (79)
0 + 1 1 0 0 0 1 1 +(99)
0 0 1 1 0 0 1 0 (50)
• Trzeba wykonać przeniesienie z siódmego bitu,
oznacza to błąd przepełnienia i wynik będzie
nieprawidłowy.
40
Odejmowanie w kodzie prostym
• Podobnie jak w przypadku dodawania,
odejmowanie liczb zapisanych w kodzie
prostym odbywa się podobnie do
dziesiętnego odejmowania na papierze.
• Przy tej operacji zachodzi niekiedy potrzeba
pożyczenia niektórych cyfr z odjemnej.
41
Przykład
• Odejmowanie 01100011
2
- 01001111
2
w
arytmetyce kodu prostego.
0 1 1 2
pożyczenia
0 1 1 0 0 0 1 1 (99)
0 - 1 0 0 1 1 1 1 -(79)
0 0 0 1 0 1 0 0 (20)
• W wyniku otrzymujemy: 01001111
2
-01100011
2
= 00010100
2
.
42
Kody uzupełnieniowe
• Z teorii liczb wynika, że można odjąć od siebie
dwie liczby dziesiętne w następujący sposób:
– odejmując odjemnik od „samych dziewiątek",
– dodając wynik do odjemnej,
– a następnie dodając z powrotem przeniesienie.
• Proces ten nosi nazwę poszukiwania uzupełnienia
zmniejszonej podstawy odjemnika.
43
Kod odwrotny
(notacja uzupełnieniowa)
• Dla d-cyfrowej liczby N w systemie liczbowym o
podstawie p, uzupełnienie zmniejszonej
podstawy liczby N definiujemy jako:
(p
d
- 1) - N.
– W przypadku liczb dziesiętnych p = 10, więc
zmniejszona podstawa wynosi:10 - 1 = 9.
– W przypadku liczb dwójkowych zmniejszona podstawa
jest o jeden mniejsza od podstawy systemu p = 2, czyli
jest równa 1.
44
Przykład
• Obliczmy różnicę: 167 – 52.
• W układzie dziesiętnym zmniejszona podstawa
odjemnika = 9, czyli (p
d
- 1) = (10
3
-1) = 999.
• Liczymy w arytmetyce dopełnieniowej dziewiątek :
– odejmujemy odjemnik: 999 – 52= 947.
– Otrzymany wynik dodajemy do odjemnej:
167 - 52 = 167 + 947 =
1
114.
– 1
przeniesienie z kolumny setek trafia z powrotem do
kolumny jedności,
– co daje prawidłowy wynik: 167 - 52 = =114+
1
=115.
45
Kody uzupełnieniowe
• Metodę tę zastosowano w odniesieniu do liczb
dwójkowych, co pozwoliło uprościć (?!) operacje
arytmetyczne dokonywane przez ... komputery.
• Zaletą kodów dopełnieniowych w porównaniu z
kodem prostym jest to, że nie wymagają one
osobnego przetwarzania bitów znaków, a mimo to
z wartość najbardziej znaczącego bitu, nadal
wskazuje, czy liczba jest dodatnia czy ujemna!
46
Notacja uzupełnieniowa do 1
• W przypadku notacji uzupełnieniowej do 1
liczba 0101
2
to:
1111
2
-0101
2
=1010
2
.
– Przedstawienie liczby dwójkowej w kodzie
odwrotnym sprowadza się do zamiany
wszystkich zer na jedynki i vice versa.
– Proste odwrócenie bitów ułatwia sprzętowe
implementowanie kodu odwrotnego.
47
Liczby ujemne w notacji
uzupełnieniowej. Podsumowanie
• Notacja uzupełnieniowa pozwala zapisywać liczby ujemne bez
konieczności przeznaczenia osobnego bitu na reprezentację znaku
liczby
– Co było konieczne w kodzie prostym.
• Liczbę ujemną, należy przekształcić na jej dopełnienie do
zmniejszonej podstawy.
– Najstarszy bit liczb ujemnych powinien mieć wartość 1.
• Nie jest konieczne zastępowanie liczby dodatniej jej uzupełnieniem.
– Najstarszy bit liczb dodatnich powinien mieć wartość 0.
• Notacja uzupełnieniowa pozwala uprościć odejmowanie poprzez
przekształcenie go w dodawanie.
– Np. odejmowanie: 10 – 7 możemy zastąpić dodawaniem liczby o
przeciwnym znaku, w tym przypadku 10 + (–7).
48
Przykład
• Odejmowanie liczb 23
10
i -9
10
w kodzie odwrotnym.
• Liczby 23
10
i -9
10
zapisujemy w kodzie odwrotnym, na 8
bitach,
23
10
= +(00010111
2
) = 00010111
2
-9
10
= -(00001001
2
) = 11110110
2
•
Obliczamy różnicę 23
10
+(-9
10
) w arytmetyce kodu odwrotnego.
• 1 1 1 1 1
<-przeniesienia
0 0 0 1 0 1 1 1 (23)
+1 1 1 1 0 1 1 0 +(-9)
0 0 0 0 1 1 0 1 (14)
+1
0 0 0 0 1 1 1 0 14
10
•
Przeniesienie najbardziej znaczącego bitu dodamy do najmniej
znaczącego bitu sumy.
49
Przykład
• Dodawanie 9
10
do -23
10
w arytmetyce kodu
odwrotnego.
1
Ostatnie 0 0 0 0 1 0 0 1 (9)
przeniesienie ma +1 1 1 0 1 0 0 0 +(-23)
wartość 0, a więc 1 1 1 1 0 0 0 1 -14
10
skończyliśmy działania.
• Skąd wiadomo, że liczba 11110001
2
to -14
10
?
– Jest to liczba ujemna ponieważ jej MSB=1,
– Obliczamy dopełnienie 11110001
2
do 11111111
2
,
które wynosi 00001110
2
, czyli 14
10
.
50
Wada kodu odwrotnego
• Zasadniczą wadą kodu odwrotnego jest
niejednoznaczność przedstawienia zera
jako: 0000...0000 lub 1111...1111.
• Dlatego zarzucono notację uzupełnieniową
do 1 na rzecz bardziej efektywnej notacji
uzupełnieniowej do 2.
51
Kod dopełnieniowy
notacja uzupełnieniowa do 2
• Uzupełnieniem do podstawy d-cyfrowej liczby N
zapisanej w systemie liczbowym o podstawie p
nazywamy liczbę w postaci p
d
- N dla N różnych
od zera i zero dla N = 0.
– Uzupełnianie do podstawy jest może bardziej intuicyjne
od uzupełniania do zmniejszonej podstawy.
– Np. uzupełnieniem do podstawy 4-bitowej liczby
0011
2
, jest 2
4
- 0011
2
=10000
2
-0011
2
=1101
2
.
52
Notacja uzupełnieniowa do 2
• Notacja uzupełnieniowa do 2 jest notacją
uzupełnieniową do 1 powiększoną o 1.
• W celu przedstawienia liczby w kodzie
dopełnieniowym do 2, należy:
– zanegować wszystkie jej bity,
– do uzyskanego wyniku dodać l.
53
Notacja uzupełnieniowa do 2
upraszcza dodawanie i odejmowanie
• Ponieważ odjemnik (czyli liczba, którą dopełniamy i dodajemy) jest
na końcu powiększana, nie musimy przejmować się bitem
przeniesienia, który trzeba by dodać do uzyskanego wyniku.
• Pomijamy wszelkie przeniesienia wychodzące z najbardziej
znaczących bitów.
• Na kod dopełnieniowy muszą być przekształcane jedynie liczby
ujemne.
• Np. liczby 23
10
, -23
10
i -9
10
w 8 bitowym kodzie dopełnieniowym
przedstawiają się następująco:
23
10
= +(00010111
2
) = 00010111
2
-23
10
= -(00010111
2
) = 11101000
2
+1= 11101001
2
-9
10
= -(00001001
2
) = 11110110
2
+1= 11110111
2
54
Konwersja kodu dopełnieniowego na
system dziesiętny
•
Z liczbami dodatnimi nie ma żadnego problemu.
– Np. chcąc poznać wartość liczby 00010111
2
zapisanej w kodzie dopełnieniowym,
przeliczamy ją z systemu dwójkowego na dziesiętny, otrzymując 23.
•
Przeliczanie liczb ujemnych wymaga wykonania w odwrotnej kolejności
kroków procedury, która przypomina konwersję z systemu dziesiętnego na
dwójkowy.
– Np. liczba 11110111
2
jest zapisana w kodzie dopełnieniowym i chcemy poznać
jej dziesiętną wartość.
– Jest to liczba ujemna, przedstawiona w notacji uzupełnieniowej do 2.
– Znajdujemy jej postać w kodzie odwrotnym, negując wszystkie bity, a następnie
dodajemy 1:
00001000
2
+ 1 = 00001001
2
= 9
10
.
– Ponieważ liczba, wyjściowa była ujemna, należy pamiętać o zmianie znaku, czyli
11110111
2
= -9
10
.
55
Przykład operacji w kodzie
dopełnieniowym
•
Liczby ujemne są przedstawiane w postaci uzupełnień do 2 ich wartości bezwzględnych,
np.:
125
(10)
= 1111101
(2)
Najstarszy bit uzupełniamy 0
01111101
(2)
uzupełnienie do 1 ma postać
10000010
(2)
uzupełnienie do 2 tworzy się przez dodanie liczby 1 do jej uzupełnienia do 1.
10000010
(2)
00000001
(2)
-125
(10)
= 10000011
(2)
•
Liczby 8-bitowe mieszczą się z zakresie od –128 do 127.
•
Liczby dodatnie mają MSB=0, a liczby ujemne MSB=1.
56
Zastosowania
• Kod dopełnieniowy jest najpopularniejszym
sposobem zapisu liczb ze znakiem:
– Operacja uzupełnienia do 1 może być dokonana przez
prosty obwód logiczny TTL – bramkę NOT.
– Koncepcja ta pozwala na uniwersalność konstrukcji
komputera.
• Operacja odejmowania danej liczby jest zastąpiona
dodawaniem liczby komplementarnej.
• Większość komputerów używa komplementarnej
(uzupełnieniowej) arytmetyki dla reprezentacji
liczb całkowitych.
57
Własności kodu dopełnieniowego
• Zalety
– Liczby w postaci dopełnieniowe łatwo się dodaje i odejmuje,
– Zero ma jednoznaczną reprezentację
• same zera,
– System kodowania można dopasować do potrzeb liczb
zapisywanych na większej liczbie bitów.
• Wady
– Asymetria zakresów liczb, które można zapisać na N bitach:
• w kodzie prostym 4 bity pozwalają zapisać wartości od -7 do +7,
• w kodzie dopełnieniowym wartości od -8 do +7.
– Pierwszy bit liczby dodatniej musi mieć wartość 0, więc gdy wszystkie
pozostałe bity będą miały wartość 1, otrzymamy 0111
2
, czyli +7.
58
Reprezentacja stałoprzecinkowa
• W większości komputerów zakres liczb na których
wykonywane są operacje ogranicza się do ułamków
właściwych,
– tzn. ustala się przecinek bezpośrednio po pozycji znaku.
• Liczby przetwarzane przez maszynę są sprowadzane do
zakresu [–1, 1] poprzez skalowanie.
• Znając zakres danych i wyników ustalić można wartość
skalującą 2
S
stosowaną podczas wprowadzania i
wyprowadzanie liczb do i z komputera.
– Na przykład, gdy S=16, dopuszczalne liczby zawierają się w
zakresie: –65536 < x < 65536
59
Wada reprezentacji
stałoprzecinkowej
• W obliczeniach naukowo-technicznych często mamy do czynienia z
bardzo dużymi lub bardzo małymi liczbami.
– Np.: stała grawitacji G = 6.67 ·10
-11
N m
2
kg
-2
lub stała występująca w
prawie Coulomba k = 9 ·10
9
N m
2
C
-2
.
• W przypadku reprezentacji stało przecinkowej działania na takich
liczbach mogą prowadzić do wytworzenia liczby nadmiarowej, nie
mieszczącej się w przyjętym zakresie (overflow).
– Np. przyjmując zakres zmienności liczb równy 10
20
,
• przy około 3.17 b/10 (bitu na rząd),
• daje to około 2
63
.
• Reprezentacja oparta na liczbach całkowitych wymaga ponad 60
bitów, aby przedstawić te liczby, ale nawet wówczas dokładność
obliczeń będzie niewielka.
60
Mnożenie i dzielenie liczb
całkowitych
• Tabliczka mnożenia liczb binarnych jest prosta:
– zero razy zero to zero,
– a jeden pomnożone przez dowolną liczbę równa się tej liczbie.
• Metoda mnożenia bezpośredniego podobnie jak w mnożeniu
pisemnym liczb dziesiętnych, jest ono zastąpione wielokrotnym
dodawaniem odpowiednio przesuniętej mnożnej.
• Mechanizm mnożenia:
– każdy składnik iloczynu zapisujemy w osobnej komórce pamięci,
– wynik umieścimy w trzeciej komórce,
– począwszy od najmniej znaczącego bitu, ustawiamy specjalny wskaźnik
na każdy bit mnożnika po kolei,
– dla każdego bitu mnożnika „przesuwamy" mnożną o jeden bit w lewo.
– gdy wskazywany bit mnożnika ma wartość l, „przesunięta" mnożna jest
dodawana do bieżącej sumy iloczynów cząstkowych.
61
Przykład
•
Pomnożyć binarnie liczbę 1101
2
przez 1011
2
.
•
Obie liczby umieszczamy jedna pod drugą tak, aby ich cyfry znalazły się w kolumnach o
tych samych wagach:
1101
×1011
•
Każdą cyfrę mnożnej mnożymy przez poszczególne cyfry mnożnika zapisując wyniki
mnożeń w odpowiednich kolumnach:
1101
×1011
0001101
0011010
0000000
1101000
10001111
•
Ponieważ przesuwamy mnożną o jeden bit na każdy bit mnożnika, wyznaczenie iloczynu
wymaga dwa razy szerszej przestrzeni adresowej niż przestrzeń zajmowana przez
mnożną (mnożnik).
62
Dzielenie binarne
• Dzielenie może być realizowane na dwa sposoby:
– iteracyjnie odejmować dzielnik od dzielnej,
– stosować metodę „prób i błędów".
• Jak w przypadku mnożenia, nie przedstawiamy bardziej
zaawansowanych algorytmów dzielenia binarnego (są one trudne).
• Dzielenie może doprowadzić do „zawieszenia" komputera
przy próbie dzielenia przez zero, a także w sytuacji, gdy
operandami są dwie liczby o diametralnie różnej
wielkości.
– Gdy dzielnik jest znacznie mniejszy od dzielnej, mamy do
czynienia z sytuacją nazywaną błędem niedomiaru przy dzieleniu,
która jest postrzegana przez komputera jako próba dzielenia przez
zero.
63
Reprezentacja zmiennoprzecinkowa
(Floating-Point Representation)
•
Często w obliczeniach stosuje się notację normalną (naukową) mająca
postać kilku cyfr po przecinku razy 10 podniesione do odpowiedniej potęgi
X = ± liczba
⋅
10
wykładnik
.
– W notacji naukowej liczba
∈
{1.0, 9.9999999…}.
•
Reprezentacja zmiennoprzecinkowa wykorzystuje podobną koncepcję.
•
Standardowo liczbę zmiennoprzecinkową stanowi para liczb całkowitych i bit
znaku:
x = znak * ułamek * 2
wykładnik
– w notacji zmiennoprzecinkowej 0.1 ≤ |ułamek| ≤1.0,
– każda liczba ma swoją "własną skalę" w postaci wykładnika.
•
Ułamek zapisany jest w kodzie dwójkowym o określonej długości, a
wykładnik jest liczba całkowitą, dodatnią lub ujemną.
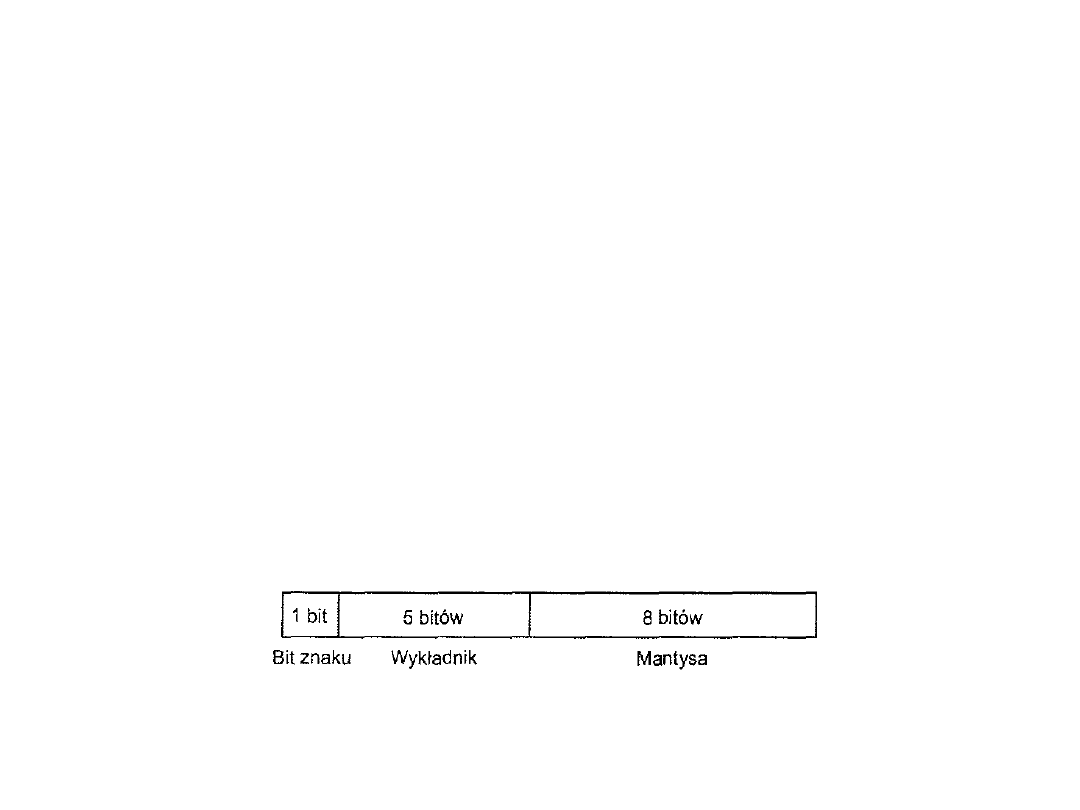
64
Implementacja arytmetyki
zmiennoprzecinkowej
•
W komputerach liczby zmiennoprzecinkowe składają się z trzech części:
– bitu znaku,
– części wykładniczej
• reprezentującej wykładnik potęgi dwójki,
– części ułamkowej
• mantysy.
•
Liczba bitów przechowujących część wykładniczą i mantysę zależy od tego,
czy bardziej zależy nam szerokości dostępnego przedziału liczb
– więcej bitów na wykładnik,
czy na precyzji
– więcej bitów na mantysę.
– Np.
– Binarna reprezentacja części ułamkowej i wykładnika jest przechowywana w
jednym słowie.
65
Ograniczenia reprezentacji
zmiennoprzecinkowej
• Za pomocą reprezentacji zmiennoprzecinkowej wyrazić można
jedynie ograniczony zbiór liczb.
• Na przykład ustalamy:
– rozmiar części ułamkowej na 4 bity,
– Rozmiar wykładnika na 3 bity włączając w to znak wykładnika.
– jeden bit reprezentuje znak ułamka
w sumie 8 bitów.
• Największa liczba zapisana w ten sposób to 0.9375*2
3
, a kolejna po
niej to tylko 0.875*2
3
, różnica tych liczb wynosi Δ= 0.9375*2
3
-
0.875*2
3
=0.0625*2
3
.
• Widać dlaczego liczba bitów użytych w obliczeniach jest istotna!
66
Przykład
• Liczba 17 w postaci dziesiętnej:
17 = 17,0 * 10
0
= 1,7 * 10
1
= 0,17 * 10
2
.
• Analogicznie, w systemie dwójkowym:
17
10
= 10001
2
* 2
0
= 1000,1
2
* 2
1
= 100,01
2
* 2
2
= 10,001
2
* 2
3
= 1,0001
2
* 2
4
=
0,10001
2
* 2
5
.
• Jeżeli zdecydujemy się wykorzystać tę ostatnią postać,
część ułamkowa: 10001000, a część wykładnicza:
00101.
• Mając do dyspozycji 14 bitów, liczba 17 przyjmie więc
postać:
67
Przykład
• W przyjetej postaci zmiennoprzecinkowej można zapisać
znacznie większe liczby niż w zapisie stałoprzecinkowym
na 14 bitach,
– w którym wykorzystuje się 14 bitów plus kropkę pozycyjną.
• Np. zapisana w tej postaci liczba 65 536
10
= 0.1
2
·2
17
,
wyglądałaby następująco:
68
Problem ujemnych wykładników
• Nie przewidzieliśmy miejsca na ujemne wykładniki.
• Nie możemy zapisać w żaden sposób liczby np. 0,25,
ponieważ 0,25 to 2
-2
, a nie mamy jak zapisać wykładnika
-2.
• Możliwe rozwiązania problemu:
– dodając do wykładnika bit znaku,
– stosować tak zwane przesunięte wykładniki,
• W drugim przypadku do porównywania wartości dwóch
liczb zmiennoprzecinkowych można zastosować proste
układy elektroniczne.
69
Przesuwane wykładniki
• Liczby całkowite w pożądanym zakresie
wykładników są najpierw dostosowywane
w ten sposób, że do każdego wykładnika
dodaje się pewną stałą wartość
przesunięcia.
• Jest to liczba leżąca mniej więcej na środku
dozwolonego zakresu wartości, co do której
umawiamy się, że będzie oznaczała zero.
70
Przesuwane wykładniki
• Przykładowo:
– wykładnik ma 5 bitów, co pozwala na przypisanie mu 2
5
=32
wartości.
– jako przesunięcie wybieramy wartość 16, leży ona na osi
liczbowej w połowie odległości między 0 a 31.
– Każda liczba mająca wykładnik większy od 16 będzie traktowana
przez nas jako dodatnia, zaś pozostałe będziemy uznawali za
liczby ujemne.
• Nazywa się to „notacją z nadmiarową szesnastką”,
ponieważ chcąc poznać rzeczywistą wartość wykładnika,
musimy odjąć od niego 16.
• Uwaga:
– wykładniki złożone z samych zer lub z samych jedynek są
zazwyczaj zarezerwowane dla reprezentacji symboli specjalnych,
takich jak zero lub nieskończoność.
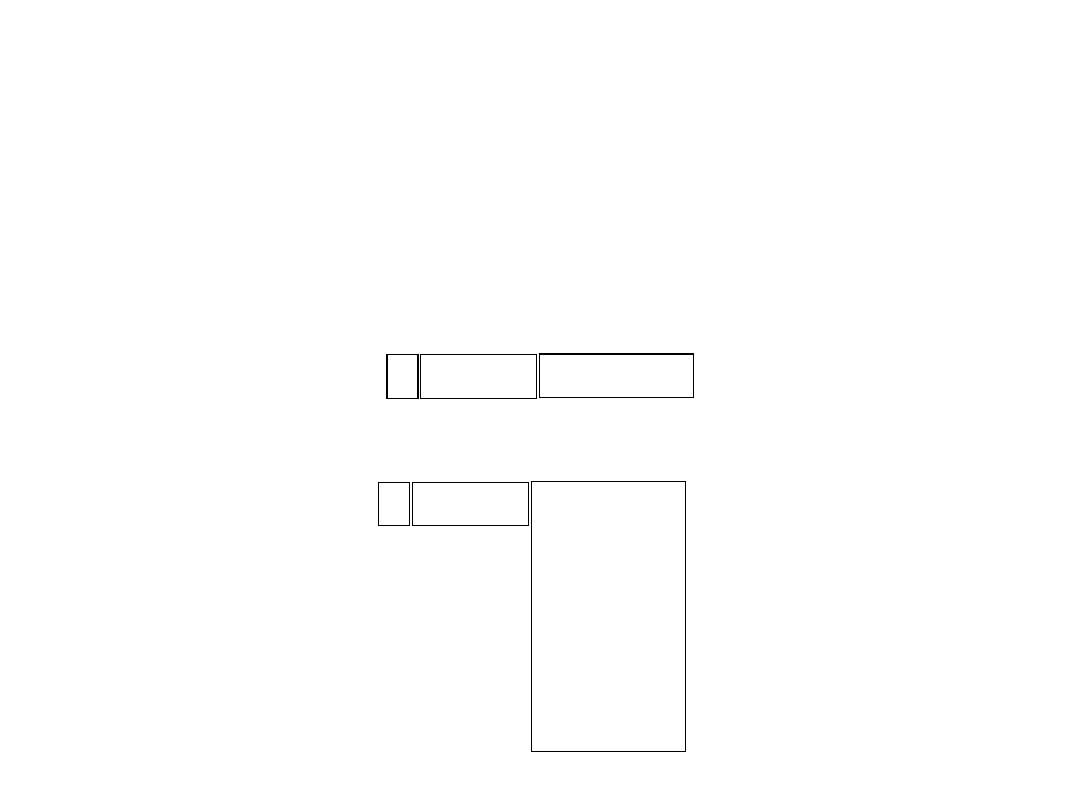
71
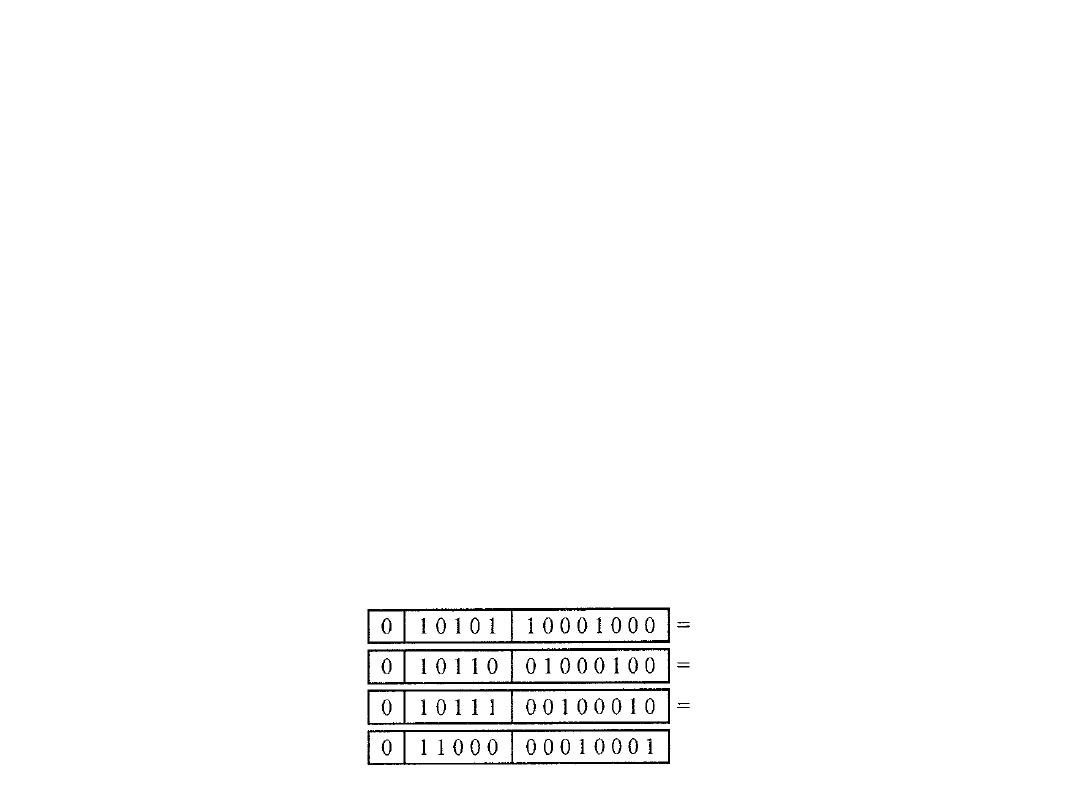
Przykład
• Wróćmy do naszego przykładu z zapisem liczby 17:
obliczyliśmy, że 17
10
= 0,10001
2
* 2
5
.
• Przesunięty wykładnik będzie teraz wynosił: 16 + 5 = 21:
0 10101
10001000
0 00101
10001000
72
Niejednoznaczność reprezentacji
• Wciąż mamy poważny problem - nie
wszystkie liczby mają jednoznaczną
reprezentację.
– Np. przedstawione niżej liczby mają tę samą
wartość: 17
10
= 0,10001
2
* 2
5
=
0,010001
2
* 2
6
= 0,0010001
2
* 2
7
=
0,00010001
2
* 2
8
.
73
Rozwiązanie problemu
niejednoznaczności
• W celu usunięcia niejednoznaczności
reprezentacji liczb przyjęto, normalizację:
– najbardziej znaczący bit mantysy będzie miał
zawsze wartość 1.
• Rozwiązanie to ma tę dodatkową zaletę, że
występowanie jedynki na pierwszej pozycji
jest pewne, dzięki czemu zyskuje się jeden
dodatkowy bit mantysy, co zwiększa
precyzję.
74
Przykład
• Zapiszemy liczbę 0,03125
10
w postaci
zmiennoprzecinkowej, w notacji „z nadmiarową
szesnastką”:
0,03125
10
= 0,00001
2
* 2
0
= 0,0001
2
* 2
-1
= 0,001
2
* 2
-2
= 0,01
2
* 2
-3
= 0,1
2
* 2
-4
• Po dodaniu „przesunięcia" pole wykładnika będzie
przechowywało wartość 16 - 4 = 12.
75
Arytmetyka
zmiennoprzecinkowa
• Aby dodać do siebie dwie liczby zapisane w notacji
wykładniczej, np. 1,5 * 10
2
+ 3,5 10
3
, należy
przekształcić je w taki sposób, aby obie miały taki sam
wykładnik.
1,5*10
2
+3,5*10
3
=0,15*10
3
+3,5*10
3
=3,65*10
3
• Dodawanie i odejmowanie liczb zmiennoprzecinkowych
przebiega w podobny sposób
76
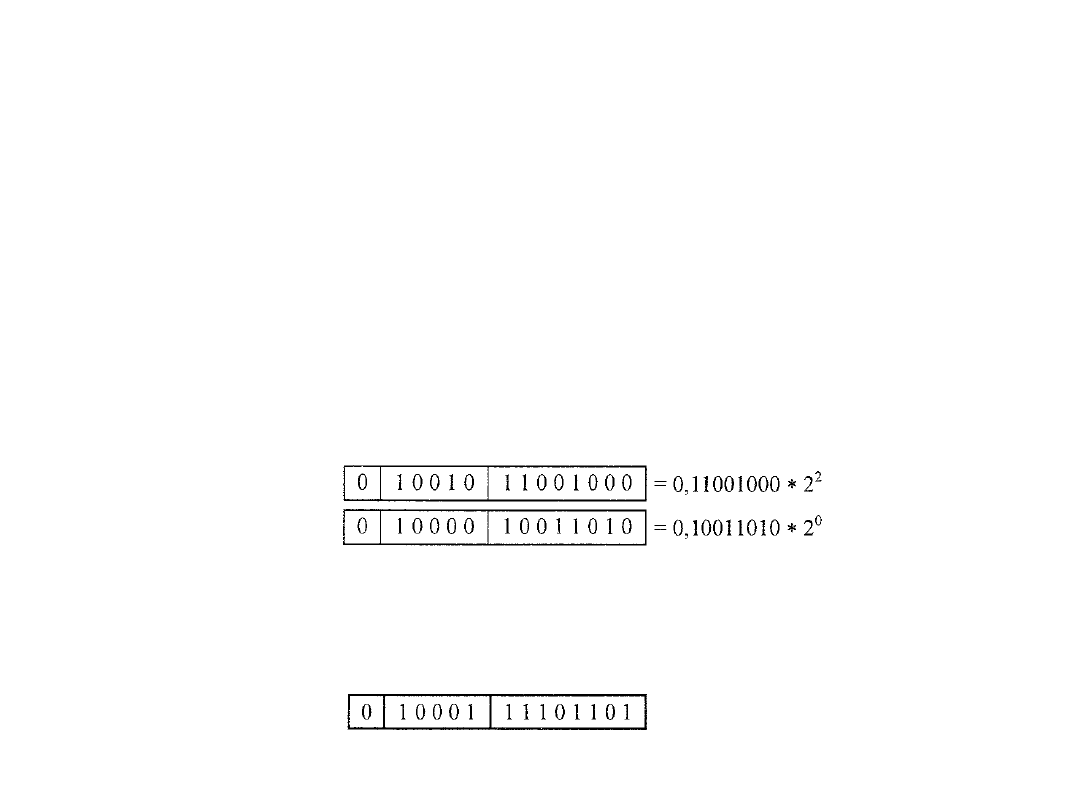
Przykład
• Dodajemy liczby dwójkowe, zapisane w znormalizowanej notacji 14-
bitowej z przesunięciem równym 16.
– Jeden ze składników dodawania jest podniesiony do potęgi pierwszej, a
drugi do zerowej.
– Wyrównanie obu tych wartości względem kropki ułamkowej daje
:
1,1001000
+0,10011010
10,00101010
– Dokonując ponownie normalizacji, zachowujemy większy wykładnik i odrzucamy
najmniej znaczący bit:
77
Mnożenie i dzielenie
• Mnożenie i dzielenie przeprowadzane jest zgodnie z tymi
samymi regułami dotyczącymi wykładników stosowanymi
dla liczb dziesiętnych
– np. 2
-3
* 2
4
= 2
1
.
• Przykład mnożenia:
• Iloczyn:
0,11001000*0,10011010 = 1,11011011,
po ponownej normalizacji i odpowiednim przesunięciu
wykładnika wynik ma postać:
78
Precyzja obliczeń
zmiennoprzecinkowych
• Wykonując obliczenia intuicyjnie rozumiemy, że
operujemy na nieskończonym zbiorze liczb rzeczywistych.
– Dla każdej pary liczb rzeczywistych potrafimy zawsze znaleźć
liczbę większą od największej i mniejszą od najmniejszej z nich.
• Komputery są w tym zakresie ograniczone.
– Odwzorowuje nieskończony zbiór liczb rzeczywistych na
skończony zbiór liczb całkowitych.
• Komputer dysponuje jedynie pewnym przybliżeniem
zbioru liczb rzeczywistych.
– Im więcej bitów mamy do dyspozycji, tym jest ono dokładniejsze.
– Jednak niezależnie od liczby użytych bitów zawsze jest ono
obarczone błędem.
79
Przykład
• W przedstawionym modelu możemy zapisywać znormalizowane
liczby z zakresu od -0,11111111
2
* 2
15
do +0,11111111
2
* 2
15
.
– Oczywistym jest, że duże liczby, jak 2
-1
, nie zmieszczą się w tym
zakresie.
– Nie możemy także zapewnić precyzyjnej reprezentacji liczby 128.5
10
,
która jak najbardziej mieści się w dozwolonym zakresie.
• 128,5
10
= 10000000,1
2
, liczba ta ma 9 bitów długości, a mantysa może
przechowywać tylko 8.
• Zazwyczaj najmniej znaczący bit jest odrzucany lub zaokrąglany do
sąsiedniego bitu.
• Błąd zaokrąglenia można oszacować wyznaczając stosunek
bezwzględnej wartości błędu do prawdziwej wartości liczby.
– Dla liczby 128,5 błąd procentowy wynosi: 128,5-128|/128,5 = 0,003906
≈
0,39%
80
Kumulacja błędów
• Z każdym kolejnym działaniem tego rodzaju błędy będą się
potęgować, co doprowadzi do wyraźnego spadku precyzji
obliczeń.
– Np. kumulacja błędu obliczeniowego dla 14-bitowej liczby zmienno
przecinkowej.
Mnożna
Mnożnik
14-bitowy
wynik
Prawidłowy
wynik
Błąd
1000,001
* 0,11101000= 1110,1001 14,7784
1,46%
(16,125)
(0,90625)
(14,5625)
1110,1001 * 0,11101000= 1101,0011 13,4483
1,94%
(14,5625)
(13,1885)
1101,0011 * 0,11101000= 1011,1111 12,2380
2,46%
(13,1885)
(11,9375)
1011,1111 * O,l1101000= 1010,1101 11,1366
2,91%
(11,9375)
(10,8125)
1010,1101 * 0,11101000= 1001,1100 10,1343
3,79%
(10,8125)
(9,75)
1001,1100 * 0,11101000= 1000.1101 8,3922
4,44%
(9,75)
(8,8125)
81
Standard zmiennoprzecinkowy
IEEE-754
• Do lat osiemdziesiątych XX w. firmy komputerowe
samodzielnie decydowały o formacie przechowywania
liczb zmiennoprzecinkowych, na rynku istniało równolegle
wiele niezgodnych ze sobą systemów.
• W roku 1985 Instytut Inżynierów Elektryków i
Elektroników (IEEE) opublikował standard regulujący
zagadnienia związane z reprezentacją liczb
zmiennoprzecinkowych o pojedynczej i podwójnej
precyzji.
– Jest on znany jako IEEE-754 (1985).
• Obecnie wszystkie komputery są zgodne z modelem IEEE-
754.
– Do roku 1998 komputery IBM zbudowane były w oparciu o
architekturę zmiennoprzecinkową, Systemu/360 z 1964 roku.
82
Standard IEEE-754 (1985)
• Dla liczb o pojedynczej precyzji standard zaleca:
– 8-bitowy wykładnik,
– przesunięcie o 127,
– mantysa liczy 23 bity,
– po uwzględnieniu bitu znaku całkowita długość słowa
wynosi 32 bity.
• Dla liczb o podwójnej precyzji:
– zapisywane są na 64-bitowych słowach,
– wykładnik liczy 11 bitów,
– mantysa 52 bity.
– przesunięcie wynosi 1023.
83
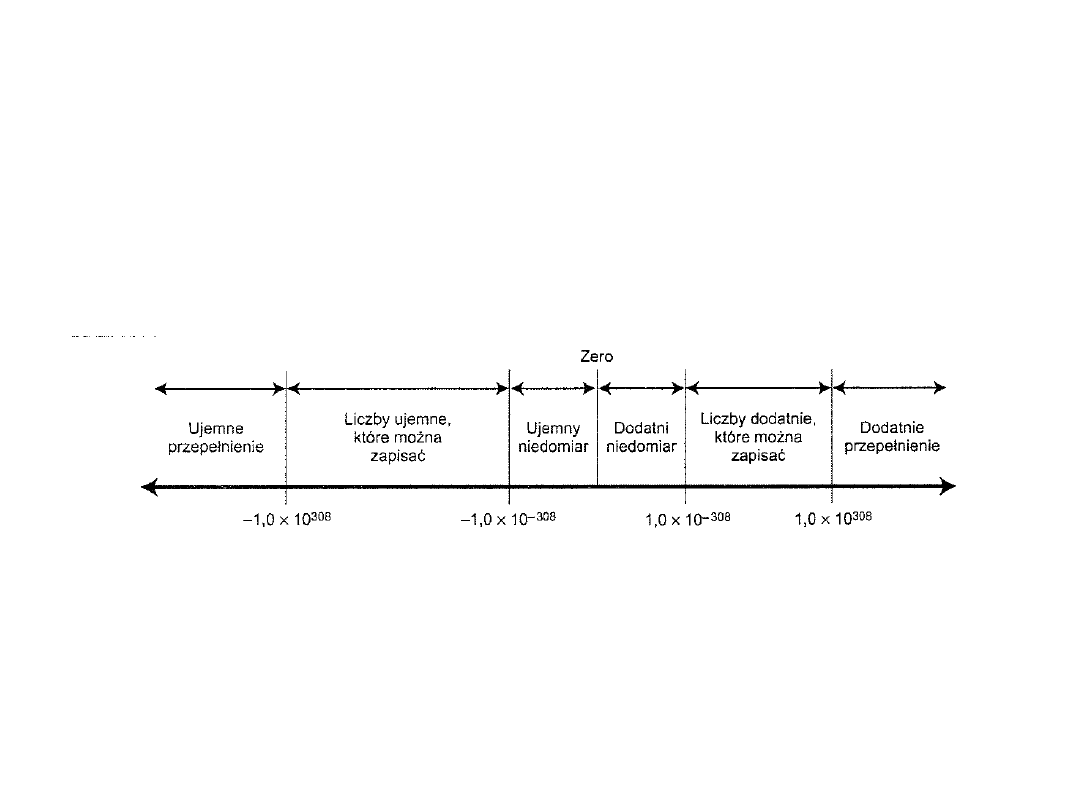
Standard zmiennoprzecinkowy
IEEE-754
• Zakres wartości, jakie mogą przyjmować liczby o podwójnej precyzji
w rozumieniu standardu IEEE.
• Jeżeli wykładnik ma wartość 255 oznacza to:
– plus bądź minus nieskończoność, mantysa = zero,
– wartość nieliczbowa NaN (not a number), mantysa
≠
zera.
• Wartość NaN służy do oznaczania wartości, które nie są liczbami
rzeczywistymi. Najczęściej oznacza to wystąpienie błędu.
84
Dane alfanumeryczne
• Dane alfanumeryczne – tekstowe mają postać znaków
pisarskich – liter, cyfr, znaków przestankowych i innych
symboli .
• W komputerze są one reprezentowane przez liczby,
określające pozycję danego symbolu w tablicy kodowej.
• Standardy kodowania znaków pisarskich:
– EBCDIC (Extended Binary-Coded-Decimal Interchange Code) -
7 bitów.
– ASCII (American Standard Code for Information Exchange) -
7 bitów lub 8 bitów.
– ISO – (International Organization for Standarisation) – pełne 8
bitów
– UNICODE – 16 bitów
85
Kod ASCII
• Kod ASCII (American Standard Code for Information
Interchange) został opracowany w 1963.
• Na 128 pozycjach kodowych zawiera on:
• na pozycjach (32 – 127). znaki widoczne,
– cyfry, znaki interpunkcyjne, podstawowe symbole matematyczne
oraz małe i wielkie litery alfabetu łacińskiego,
• na pozycjach (0 – 31) znaki niewidoczne,
– kody formatujące, kody sterujące wymianą informacji i
urządzeniami.
• W oryginalnej wersji ASCII do reprezentacji tej liczby
kodów koniecznych jest 7 bitów, 8 bit służył kontroli
poprawności zapisu
– bit parzystości.
86
EBCDIC
• Kody rodziny EBCDIC są używane w
systemach firmy IBM.
• Bazują one na binarnym kodowaniu liczb
dziesiętnych reprezentujących pozycje
kodowe znaków.
87
Znaki ASCII
0 – 31 – kody sterujące
32 – 47 – znaki pomocnicze ( ,!,+,-, ...)
48 – 57 – cyfry 0 – 9
58 – 64 – znaki pomocnicze (:,;,>,=,<,?,@)
65 – 90 – A, B, ... , Z
91 – 96 – znaki specjalne
97 – 122 – a, b, ... , z
123 – 126 – znaki specjalne
127 – DEL
88
Znak można zapisać w postaci dwójkowej, np.:
J
a
c
e
k
11010001
10000001
10000011
10000101
10000010
10101010
11100001
11100011
11100101
11101011
W sumie możliwych jest 128 symboli jest to wystarczająca liczba
symboli dla US/UK English, nie wystarczyło to jednak aby ASCII stał
się kodem uniwersalnym ze względu na:
– francuskie (è, é, etc.), niemieckie (ä, ß, etc.),
– polskie (ą, ę,etc), czeskie (ĉ, ŝ etc),
_ japońskie i chińskie (Kanji).
89
Kod ASCII c.d.
• Gdy kontrolę poprawności zapisu zaczęto
realizować innymi metodami
– kody z korekcją błędów
powstał rozszerzony kod ASCII liczący 256
znaków.
– pierwsze 128 pozycji jest identyczne, jak w kodzie
ASCII,
– kolejne 128 pozycji zawiera znaki dodatkowe,
• np. litery akcentowane, rozszerzony zestaw symboli
matematycznych, litery alfabetów narodowych.
90
Inne systemy kodowania
• Istnieje wiele kodów tej rodziny, używanych w różnych
częściach świata.
– DOS: Code Page, czyli strona kodowa 852, zwana Latin 2
– Windows 3/95: CP-1250, Central-European encoding
– ISO-8859-2.
– Unicode, 2 bajty/znak czyli 65536 znaków.
• Alfabet polski ma 35 liter, uwzględniając małe i duże
litery oraz znaki specjalne jest to w sumie około 100
znaków.
• W Polsce najpowszechniej używa się kodów ISO8859-2
oraz Microsoft CP1250.
91
UNICODE
• UNICODE jest uniwersalnym kodem znakowym,
umożliwiającym reprezentację wszystkich znaków
pisarskich zapisu fonetycznego używanych na całym
świecie
• UNICODE wykorzystuje do reprezentacji znaku 16 bitów
(2 B/znak)
– w sumie można zakodować 65536 znaków.
– to wystarcza dla zakodowania dużych, małych oraz specjalnych
form liter każdego ze znaczących alfabetów: łacińskiego,
greckiego, cyrylicy, hebrajskiego, etc.
– w zakresie języka angielskiego UNICODE jest zgodny z kodem
ASCII.
• Pozostał jednak problem. Dostępnych jest tylko 20992
kodów dla ideogramów Han, których jest ponad 50000.
92
UNICODE
• Każdy znak diakrytyczny
– np. ogonki, akcenty, umlaut
ma swój własny kod, więc dla liter z którymi
znaki te występują używane są kombinacje
kodów.
• W odróżnieniu od kodu ASCII kody te
jednoznacznie identyfikują symbol.
• Daje to możliwość swobodnego mieszania znaków
różnych krajów bez obawy o niejednoznaczność.
93
Bity i bajty
przypomnienie
• „Bit” = binary unit, czyli jednostka informacji.
• w układzie dwójkowym.
– Używając 1 bit można skonstruować 2 znaki: 0, 1.
– Z 2 bitów da się złożyć 4 znaki: 00, 01, 10, 11.
– Z 3 bitów 8 znaków: 000, 001, 010, 011, 100, 101, 110,
111.
– Z 4 bitów 16 znaków: 0000, 0001, 0010, 00011, ...,
1111.
– 8 bitów pozwala odróżnić 28 = 16 x 16 = 256 znaków.
• Ciąg 8 bitów = 1 bajt, [8b]=[1B] podstawowa
jednostka struktury pamięci.
94
Wielkość danych
• Przedrostek kilo oznacza w informatyce nie 1000, a potęgę
liczmy 2 najbliższą liczbie 1000, czyli 1024 = 2
10
.
• 2
10
=1024=1K, kilobajt, typowa strona tekstu to kilka KB;
• 2
20
=1024K=1M, megabajt, książka bez grafiki lub minuta
muzyki;
• 2
30
=1024M=1G, gigabajt, film cyfrowy, sporo grafiki,
ludzki genom;
• 2
40
=1024G=1T, terabajt,
– Biblioteka Kongresu USA zawiera około 20 TB informacji
tekstowej, tyle co kilka dużych dysków magnetycznych.
• 2
50
=1024T=1P, petabajt, ludzka pamięć?
95
Rozróżnienie B i b:
• B=bajty, KB=kilobajty, MB=megabajty, GB=gigabajty, ...
• b=bity, Kb=kilobity, Mb-megabity, ....
• Słowo (word) jest podstawową jednostka danych przetwarzanych
przez CPU.
– Składa się ono z 8, 16, 32, 48, 64, 128 lub 256 bitów, na których
wykonywana jest jednocześnie operacja logiczna lub arytmetyczna.
• Jest ono zwykle określone rozmiarem rejestru pamięci danych MDR.
– The Memory Data Register (MDR) is the register of a computer's control
unit that contains the data to be stored in the computer storage (e.g.
RAM), or the data after a fetch from the computer storage.
– It acts like a buffer and holds anything that is copied from the memory
ready for the processor to use it.
96
1
97
Istnieje różnica między dzieleniem liczb całkowitych, a dzieleniem
zmiennoprzecinkowym:
•przy dzieleniu liczb całkowitych wynik podawany jest w dwóch
częściach, to znaczy w postaci ilorazu i reszty,
•Z kolei przy dzieleniu zmiennoprzecinkowym wynik jest ułamkiem
zapisanym w systemie dwójkowym.
Obliczenia zmiennoprzecinkowe wykonywane są przez wydzielone
obwody, nazywane wspólnie jednostką zmiennoprzecinkową (FPU).