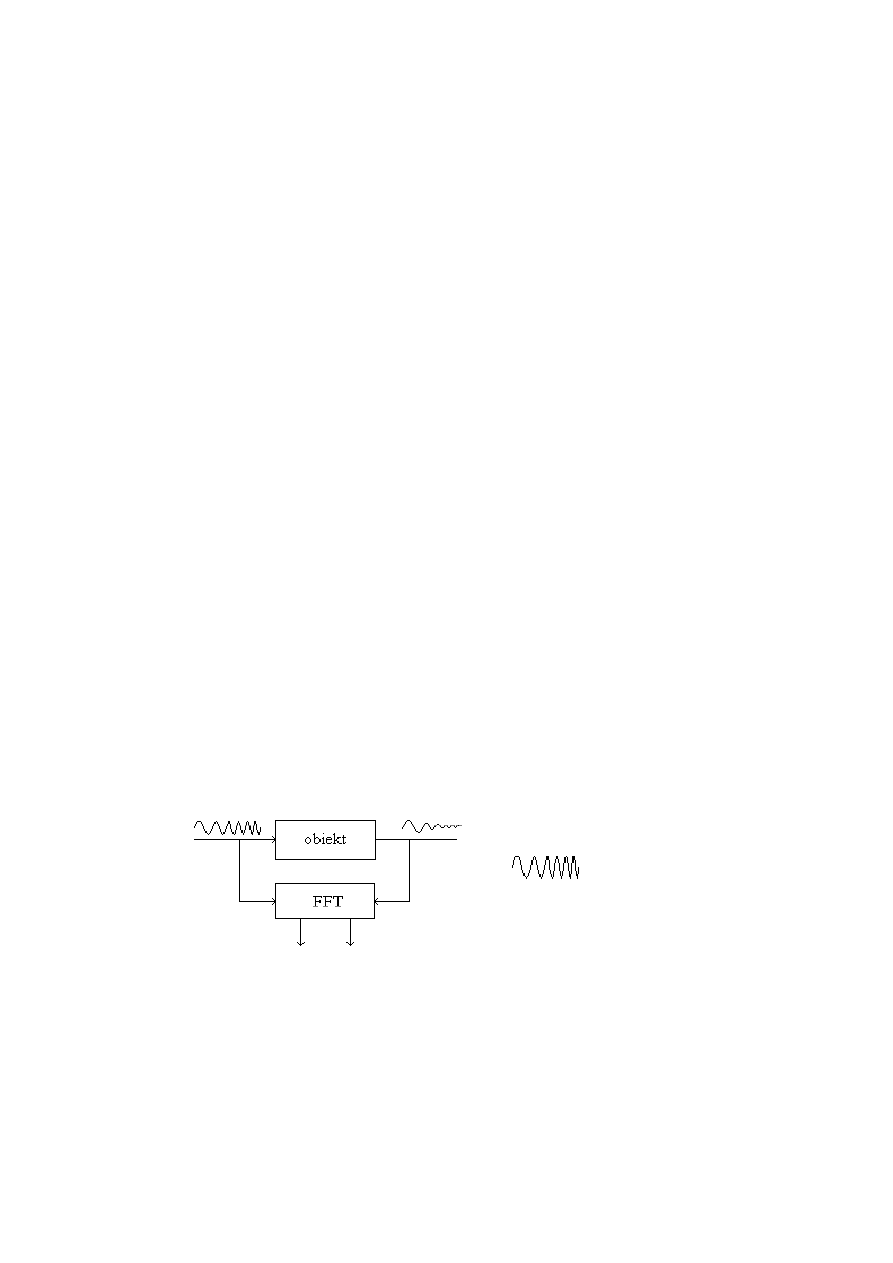
1
PRz – AiS – W9
METODY CZĘSTOTLIWOŚCIOWE
Charakterystyka ogólna. Zapas fazy i zapas modułu. Przeregulowanie i czas regulacji. Obiekt
z opóźnieniem. Twierdzenie Nyquista. Dobór wzmocnienia. Automatyczny eksperyment
Zieglera–Nicholsa.
CHARAKTERYSTYKA OGÓLNA
1.
Historia i cechy metod częstotliwościowych
•
Historia
1932 – Nyquist – badanie stabilności na podstawie charakterystyk częstotliwościowych
1942 – Bode – charakterystyki logarytmiczne i dobór wzmocnienia
1943 – Ziegler i Nichols – eksperymentalny dobór nastaw regulatorów PID po
doprowadzeniu do granicy stabilności.
•
Cechy metod częstotliwościowych
1.
Do projektowania służą charakterystyki częstotliwościowe a nie transmitancja, nie
ma więc ograniczeń na rząd obiektu (aproksymacja niepotrzebna).
2.
Charakterystyki częstotliwościowe otrzymuje się eksperymentalnie za pomocą
szybkiej transformaty Fouriera (FFT) pobudzając obiekt sygnałem o rosnącej
częstotliwości (chirp).
3.
Samostrojenie częstotliwościowe można przeprowadzić dla złożonych obiektów z
wzajemnymi interakcjami, gdzie odpowiedzi skokowe nie są powtarzalne (nie można
nastrajać na podstawie odpowiedzi skokowej).
4.
Metody częstotliwościowe są rozpowszechnione w pokrewnych dziedzinach – teoria
sygnałów, telekomunikacja, elektronika.
Wady
2.
Instrukcje Matlaba
•
w = logspace(d1,d2,n) – generowanie n punktów częstotliwości
ω
rozmieszczonych
równomiernie w skali logarytmicznej w przedziale
10
d1
...10
d2
w =logspace(d1,d2)
– standardowo 50 punktów
- chirp
FFT – Fast Fourier Transform
(Matlab, Java for Process Control)
moduł - M(
ω
)
F(
ω
) - faza
2
•
[M,F] = bode(l,m,w)
– wyznaczenie modułu M i fazy F transmitancji
m
l
dla
częstotliwości
ω
, gdzie F jest w stopniach
•
subplot(211)
– wybór górnej połowy ekranu do umieszczenia wykresu
semilogx(w,M), grid
– wykres modułu w skali półlogarytmicznej
subplot(212)
– wybór dolnej połowy ekranu
semilogx(w,F), grid
– wykres fazy
clg
– ekran standardowy (następny wykres pojedynczy, np. step()).
•
Zalecenia
1.
W typowych problemach wystarczy 50 punktów na dekadę.
2.
Przedział 10
d1
...10
d2
powinien objąć częstotliwości charakterystyczne lub graniczne,
którymi są odwrotności najmniejszej i największej stałej czasowej.
3.
Transmitancja II rzędu
2
2
2
2
)
(
n
n
n
s
s
s
G
ω
ξω
ω
+
+
=
)
2
(
)
2
(
)
(
2
)
(
2
2
2
2
2
2
2
2
2
2
4
4
4
4
3
4
4
4
4
2
1
4
4
4
4
3
4
4
4
4
2
1
ω
ω
ω
ξω
ω
ξω
ω
ω
ω
ω
ω
ξω
ω
ω
ω
−
−
+
−
=
+
+
−
=
=
n
n
arctg
j
e
j
j
s
G
n
n
n
n
n
n
Matlab -
ω
n
= 1
l = 1
w = logspace(-1,1,100);
ksi = 1
m = [1 2*ksi 1]
[M, F] = bode(l,m,w);
subplot(211)
semilogx(w,M), grid
subplot(212)
semilogx(w,F), grid
ksi = 0.6
..............
ksi = 0.4
..............
ksi = 1.5
..............
ξξξξ
= 0.4
ξξξξ
= 1.5
ξξξξ
= 0.4
ξξξξ
= 1.5
M(
ω
)
- moduł
F(
ω
)
- faza
3
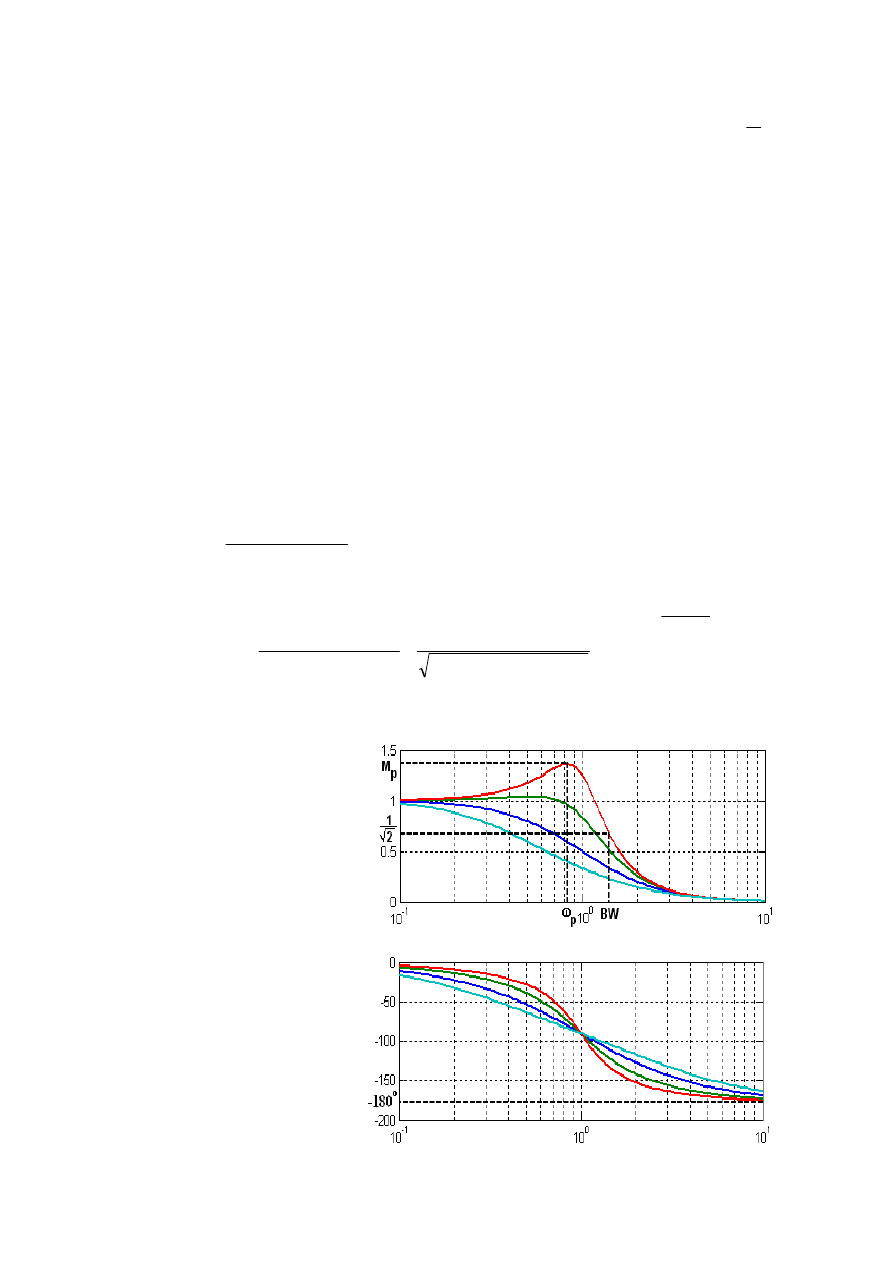
Częstotliwością charakterystyczną jest
ω
n
= 1. Przedział 0.1...10 w logspace (-1,1,100)
obejmuje ją po dekadzie z lewej i prawej strony.
Wnioski
1.
Wzrost tłumienia
ξ
powoduje:
– zmniejszenie modułu szczytowego M
p
(peak) i jego częstotliwości
ω
p,
– zmniejszenie pasma przenoszenia BW (band-width), gdzie
.
707
.
0
2
/
1
≅
=
M
2.
Częstotliwość
ω
p
jest nieco niższa niż częstotliwość naturalna
ω
n
= 1.
3.
Faza F ustala się na wartości -180
°
, ponieważ stopnie licznika i mianownika
różnią się o 2
)
180
)
90
(
2
(
o
o
−
=
−
⋅
.
4.
Dla częstotliwości
ω
n
faza wynosi - 90
°
(niezależnie od
ξ
).
ZAPAS FAZY I ZAPAS MODUŁU
Są to pojęcia związane z układem otwartym.
1.
Serwomechanizm napięciowy
,
)
2
(
)
1
(
)
1
(
)
(
2
n
n
otw
s
s
T
s
s
T
k
Ts
s
k
s
G
ξω
ω
+
=
+
=
+
=
gdzie:
T
T
k
n
n
1
2
,
2
=
=
ξω
ω
2
2
2
2
2
2
)
2
(
1
)
2
(
)
(
n
n
n
n
n
n
n
zam
s
s
s
s
s
s
s
G
ω
ξω
ω
ξω
ω
ξω
ω
+
+
=
+
+
+
=
•
Charakterystyki układu otwartego
4
4 3
4
4 2
1
4
4
4
3
4
4
4
2
1
−
−
⋅
⋅
+
=
+
=
n
j
M
n
n
n
n
otw
e
j
j
j
G
ξω
ω
ξω
ω
ω
ω
ξω
ω
ω
ω
ω
2
arctan
90
2
2
2
2
)
2
(
)
2
(
)
(
Dane:
1
,
1
=
=
n
ω
ξ
(czyli p
%
= 0, t
r
= 4 ).
Matlab
l = 1
m = [1 2 0]
w = logspace(-1,1,100);
[M, F] = bode(l,m,w);
subplot(211)
semilogx(w,M), grid
– standardowy układ II rzędu
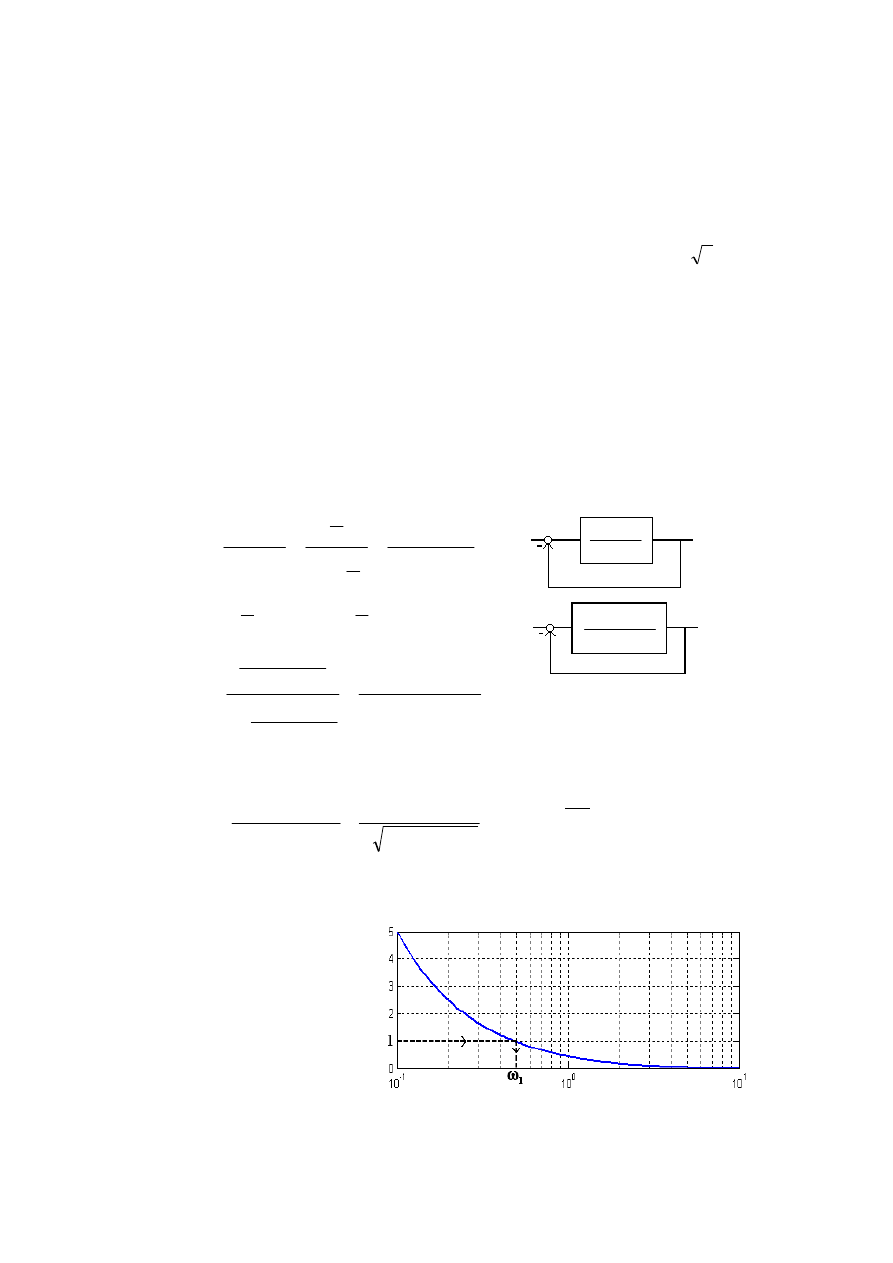
„omega dla jedynki”
)
2
(
2
n
n
s
s
ξω
ω
+
)
1
(
+
Ts
s
k
F
4
subplot(212)
semilogx(w,F), grid
[ w’ M F ]
..........................
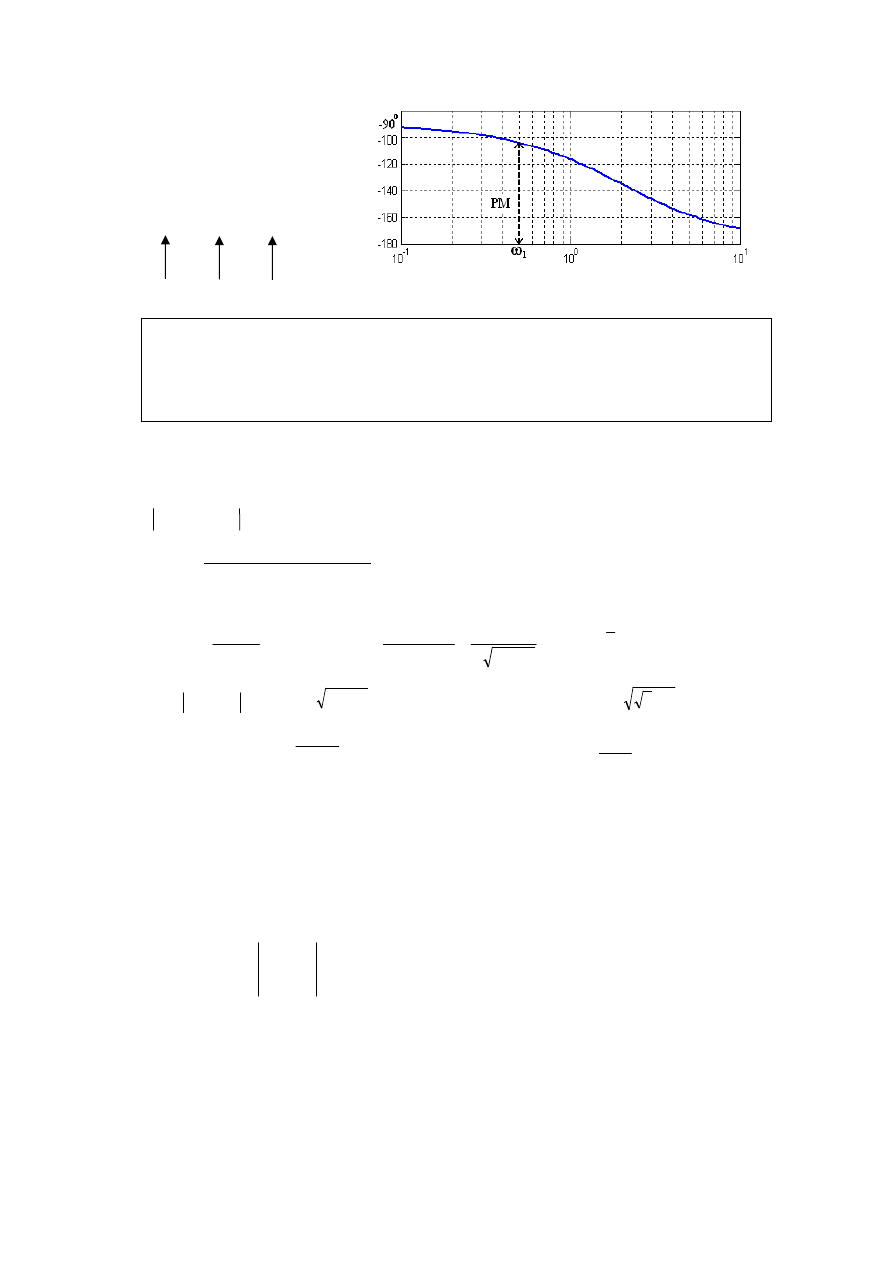
0.4863 0.9991 -103.6
Tok obliczeń
PM=180
°
-103.6
°
= 76.4
°
•
Obliczenia „ręczne”
)
2
arctg
90
(
2
4
1
)
2
(
1
)
(
,
)
2
(
1
)
(
ω
ω
ω
ω
ω
ω
−
−
+
=
+
=
+
=
o
j
otw
otw
e
j
j
j
G
s
s
s
G
4858
.
0
2
5
0
1
4
1
4
1
)
(
1
2
4
2
1
≅
−
=
→
=
−
+
→
=
+
→
=
ω
ω
ω
ω
ω
ω
ω
j
G
:
otw
o
o
o
o
o
4
.
76
6
.
103
180
PM
6
.
103
2
4858
.
0
atan
90
)
(
1
=
−
=
→
−
=
−
−
=
∠
ω
j
G
2.
Układ III rzędu
•
Stabilność wg. Hurwitza (pierwiastki wielomianu ujemne lub o ujemnych częściach
rzeczywistych).
Układ zamknięty 3-go rzędu o dodatnich współczynnikach a
0
…a
3
w mianowniku
0
1
2
2
3
3
a
s
a
s
a
s
a
+
+
+
jest stabilny wtedy i tylko wtedy jeśli wyznacznik
0
0
3
1
2
1
0
3
2
2
>
−
=
=
∆
a
a
a
a
a
a
a
a
jest dodatni. Inaczej mówiąc, iloczyn współczynników środkowych ma być większy od
iloczynu wyrazów skrajnych.
Niech M(
ω
), F(
ω
) będą charakterystykami częstotliwościowymi układu otwartego,
a
ω
1
częstotliwością, taką że M(
ω
1
) =1. Zapasem fazy PM (phase margin)
nazywamy kąt określony wzorem
)
(
180
1
ω
F
PM
+
=
o
)
(
180
PM
)
(
1
)
(
1
1
1
1
ω
ω
ω
ω
j
G
j
G
j
G
otw
otw
otw
∠
+
=
→
∠
→
→
=
o
ω
1
1
≅
F(
ω
1
)
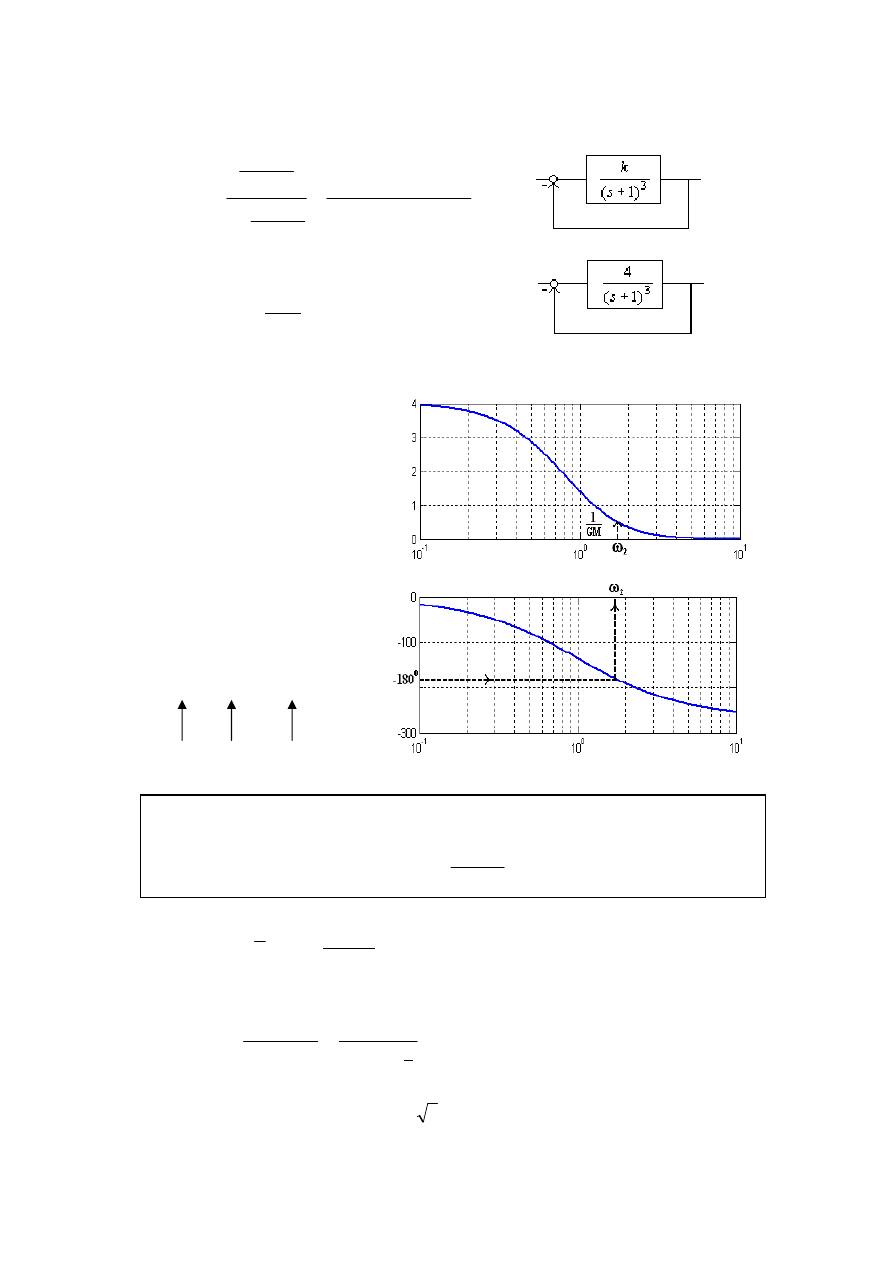
5
•
Określenie
k
kr
1
3
3
)
1
(
1
)
1
(
)
(
2
3
3
3
+
+
+
+
=
+
+
+
=
k
s
s
s
k
s
k
s
k
s
G
zam
Hurwitz:
8
,
8
1
3
3
=
<
→
+
>
⋅
kr
k
k
k
Wybieramy np. k = 4, aby układ był stabilny.
•
Charakterystyki układu otwartego
Matlab
l = 4; m = [1 3 3 1];
w = logspace(-1,1,200);
[M, F] = bode(l,m,w);
subplot(211)
semilogx(w,M), grid
subplot(212)
semilogx(w,F), grid
[ w’ M F ]
..........................
1.722 0.5062 -179.59
Powyżej
,
2
1
≅
M
zatem GM = 2.
•
Obliczenia „ręczne”
)
arctg
3
(
2
3
2
3
)
1
(
4
)
1
(
4
)
(
ω
ω
ω
ω
−
+
=
+
=
j
e
j
j
G
otw
ω
2
:
3
180
arctg
3
2
=
→
−
=
−
ω
ω
o
ω
2
≅
1/2 -180
°
Niech
ω
2
będzie częstotliwością, taką że F(
ω
2
) = –180
°
.
Zapasem modułu GM
nazywamy odwrotność modułu
M(
ω
2
), tzn.
)
(
1
2
ω
M
GM
=
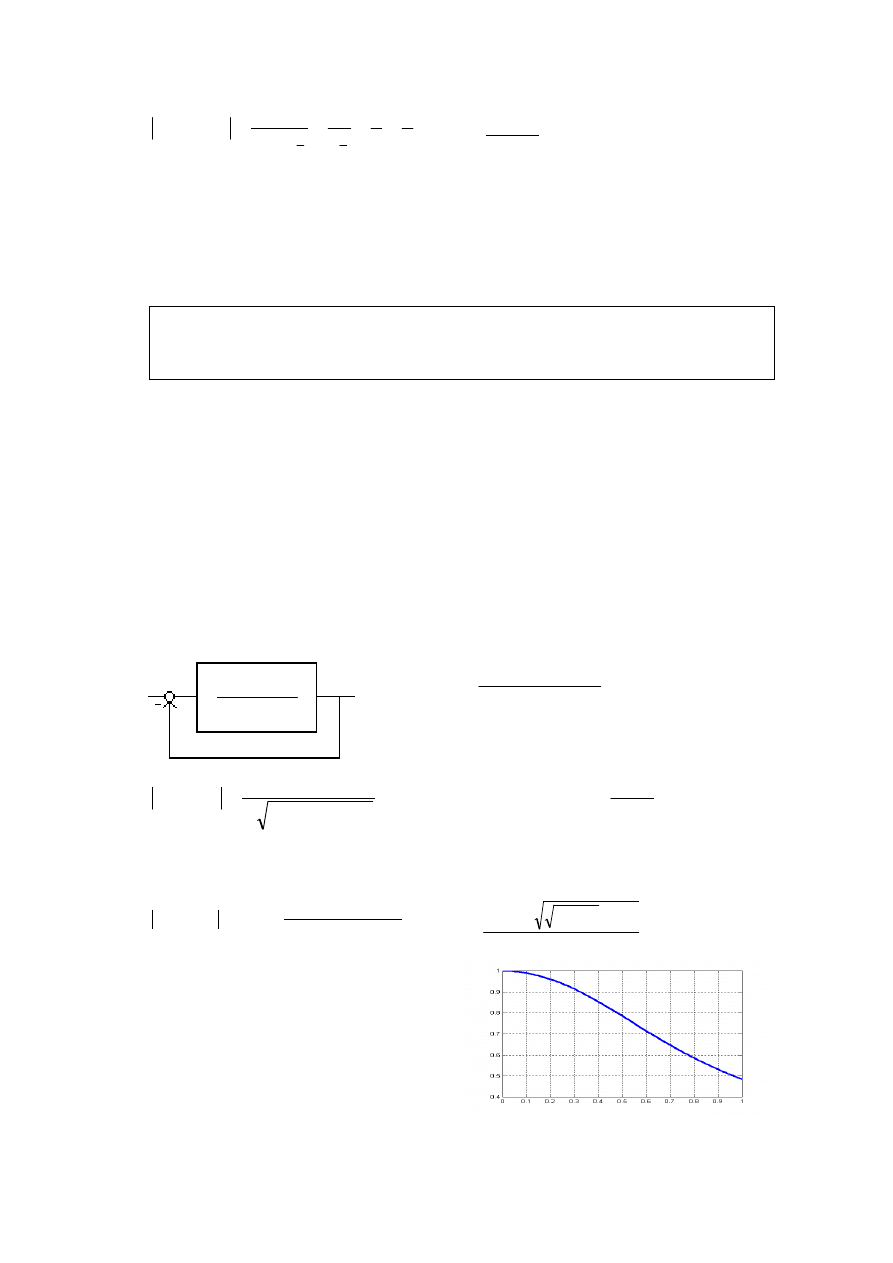
6
→
=
=
=
+
=
2
1
8
4
4
4
)
3
1
(
1
)
(
2
3
2
3
2
ω
j
G
otw
GM = 2
Uwaga. Zapas modułu mówi, ile razy należy zwiększyć wzmocnienie, aby osiągnąć
granicę stabilności, tzn.
.
kr
k
GM
k
=
⋅
Z kryterium Hurwitza:
8
2
4
8
=
⋅
→
=
kr
k
Zapas modułu rozważa się tylko wtedy, gdy różnica stopni licznika i mianownika
transmitancji układu otwartego wynosi przynajmniej 3, albo gdy w układzie występuje
opóźnienie. Wtedy bowiem charakterystyka fazowa schodzi poniżej -180
°
i można
wyznaczyć częstotliwość
ω
2
.
PRZEREGULOWANIE I CZAS REGULACJI
1.
Przeregulowanie a zapas fazy
•
Układ II rzędu – serwomechanizm napięciowy
n
n
n
j
G
j
G
otw
otw
ξω
ω
ω
ξω
ω
ω
ω
ω
2
arctg
90
)
(
,
)
2
(
)
(
2
2
2
−
−
=
∠
+
=
o
•
Częstotliwość
ω
1
2
4
1
2
2
1
2
1
4
1
2
1
4
1
]
)
2
(
[
1
)
(
ξ
ξ
ω
ω
ξω
ω
ω
ω
ω
−
+
=
→
=
+
→
=
n
n
n
otw
j
G
Matlab
ksi = 0:0.01:1;
KW=ksi
.* ksi;
w1=sqrt(sqrt(4*KW
.*KW+1)-2*KW);
clg - pełen ekran
plot(ksi,w1), grid
W typowych układach sterowania zapas fazy PM wynosi 40
°
...75
°
, a zapas modułu
GM od 2 do 4. Im którykolwiek zapas mniejszy, tym większa skłonność do
oscylacji.
2
2
2
2
)
(
n
n
n
zam
s
s
s
G
ω
ξω
ω
+
+
=
)
2
(
2
n
n
s
s
ξω
ω
+
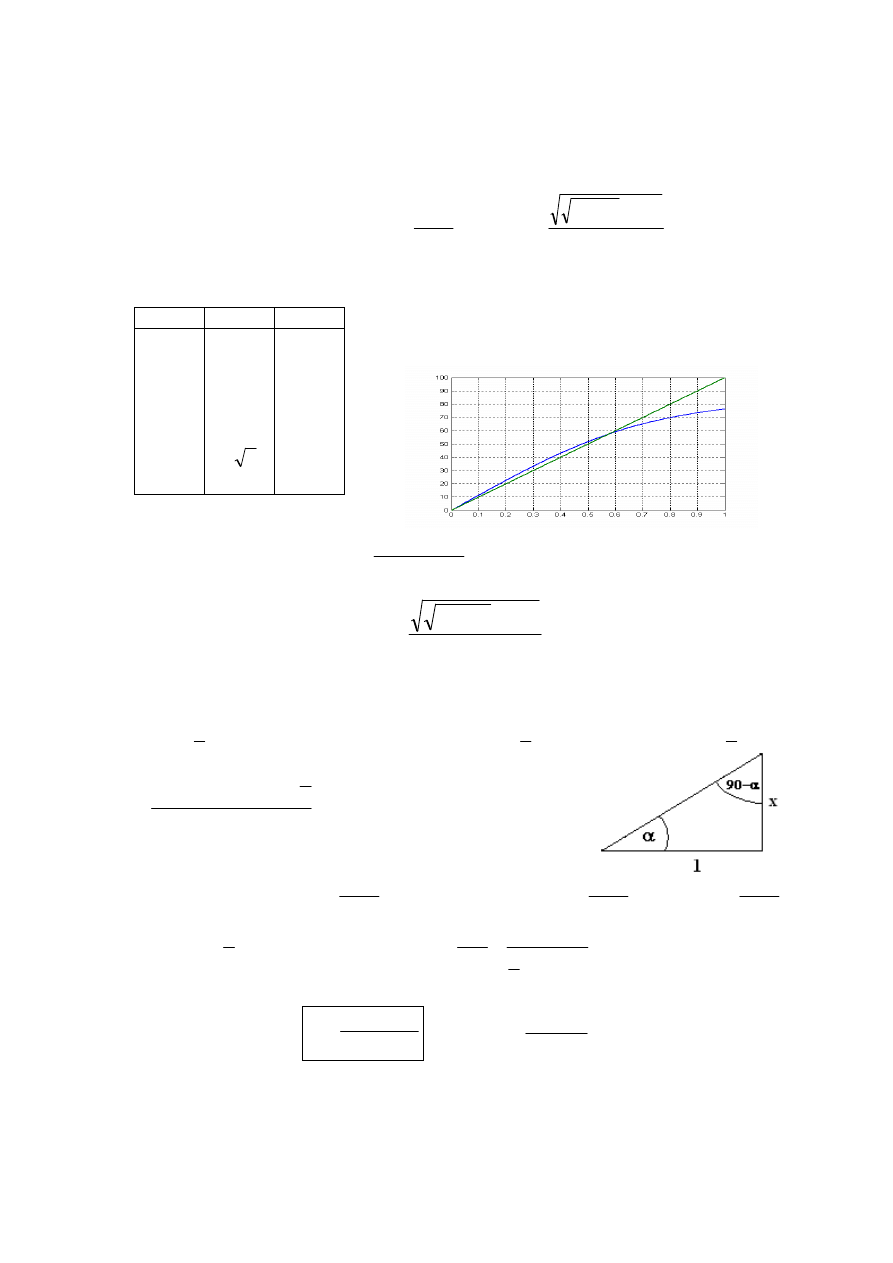
7
Wniosek. Im większe tłumienie
ξ
tym niższa częstotliwość
ω
1
, dla której układ
osiąga zapas fazy.
•
Zapas fazy PM
ξ
ξ
ξ
ξω
ω
ω
2
2
1
4
arctan
90
2
arctan
90
)
(
180
2
4
1
1
−
+
−
°
=
−
=
<
+
=
n
j
G
PM
otw
o
o
Przeregulowanie a zapas fazy
p
%
ξ
PM
37.2
25.4
16.3
9.5
4.6
4.3
0
0.3
0.4
0.5
0.6
0.7
1/
2
1
33.3
43.1
51.8
59.2
65.1
65.5
76.3
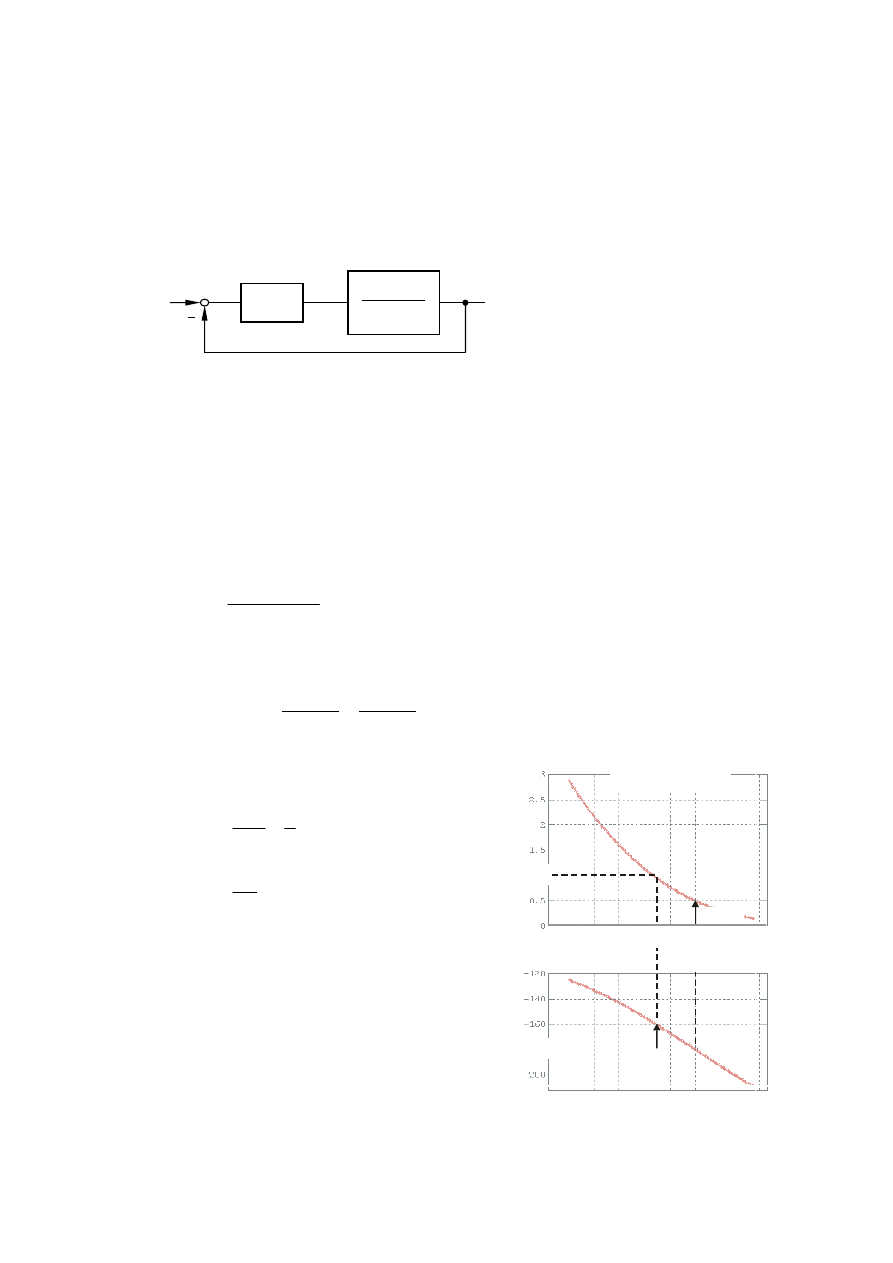
Wniosek. „Inżynierski” wzór
ξ
⋅
≅
100
PM
jest dobrym przybliżeniem pełnego wzoru
na zapas fazy PM, ale tylko dla przeregulowań nie mniejszych niż 10%
)
0.6
(
≤
ξ
.
ξ
ξ
ξ
ξ
⋅
≅
−
+
−
°
=
100
2
2
1
4
atan
90
PM
2
4
2.
Czas regulacji a częstotliwość
α
α
=
→
=
=
x
x
x
arctg
1
tg
,
x
x
1
arctg
90
1
)
tg(90
=
−
→
=
−
α
α
o
o
x
x
1
arctg
arctg
90
=
−
o
Ponieważ
,
2
arctg
90
PM
1
n
ξω
ω
−
=
o
więc również
1
2
arctg
PM
ω
ξω
n
=
albo
1
2
tg
ω
ξω
n
PM
=
oraz
PM
n
tg
2
1
1
ω
ξω
=
. Czas regulacji:
PM
t
n
r
tg
2
1
4
4
1
ω
ξω
=
=
PM
t
r
tg
8
1
ω
=
lub
PM
t
r
tg
8
1
=
ω
Matlab
PM=90-atan(w1
./(2*ksi))*180/pi;
plot(ksi, PM, ksi, 100*ksi), grid
8
•
Idea projektowania
Podobnie mając charakterystyki częstotliwościowe układu otwartego w dziedzinie
częstotliwości wyznaczamy z nich PM i
ω
1
. Na podstawie powyższych wzorów
określamy
100
PM
≅
ξ
, przeregulowanie p
%
i czas regulacji t
r
.
– p
%
a
ξ
:
OBIEKT Z OPÓŹNIENIEM
1.
Przykład
s
s
G
e
s
s
G
52
.
0
)
(
1
2
56
.
0
)
(
−
′
+
=
3
2
1
,
π
ω
ω
ω
180
52
.
0
)
(
)
(
−
′
∠
=
∠
j
G
j
G
Częstotliwości charakterystyczne:
5
.
0
2
1
=
,
92
.
1
52
.
0
1
=
→
zakres 0.1 ... 10
2.
Matlab
w = logspace(-1,1,100);
[M, Fprim] = bode(0.56,[2 1],w);
F=Fprim-0.52*w'*180/pi;
subplot(211)
semilogx(w,20*log10(M)), grid
subplot(212)
semilogx(w,F), grid
20*log10(M) – dB (decyble)
Uwaga. Charakterystyka fazowa obiektu z opóźnieniem osiąga silnie ujemne
wartości dla wyższych częstotliwości.
Mając dane p
%
i t
r
za pomocą powyższych wzorów przechodzimy na PM i
ω
1
w
dziedzinie częstotliwości.
%,
100
2
1
%
ξ
πξ
−
−
=
e
p
100
%
2
ln
2
100
%
ln
p
p
+
=
π
ξ
9
TWIERDZENIE NYQUISTA
Nyquist – 1932, Bell Telephone Laboratories, USA (telekomunikacja)
4.
Przykład. Układ III rzędu
•
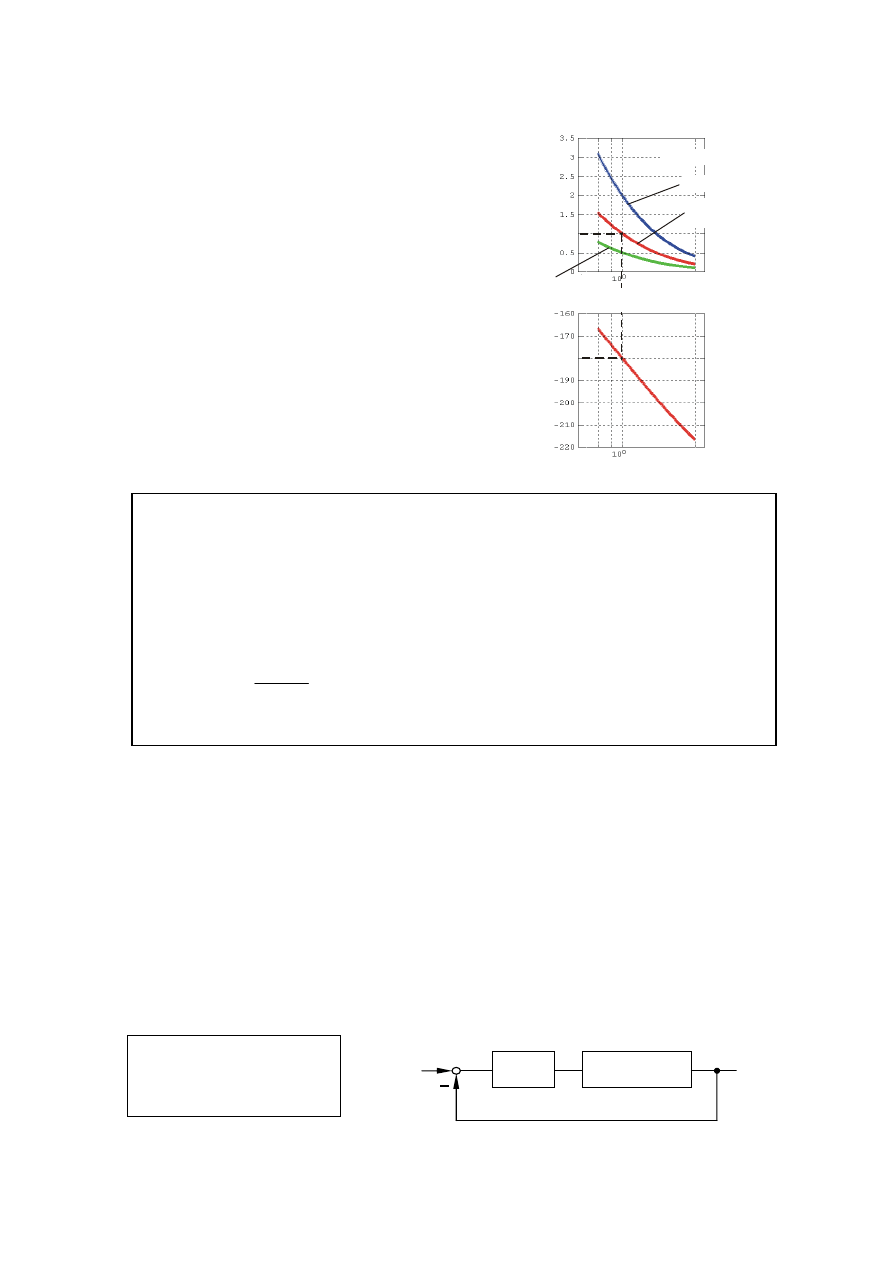
Dany jest układ jak na rysunku
Wykreślić charakterystyki częstotliwościowe:
a)
układu na granicy stabilności
b)
układu stabilnego z zapasem modułu GM=2
c)
układu niestabilnego z „zapasem” GM=0.5.
•
Rozwiązanie
ad a) Granica stabilności – mianownik układu zamkniętego – pierwiastki urojone
0
)
(
1
=
+
s
G
otw
→
ω
j
s
=
→
0
)
(
1
=
+
ω
j
G
otw
0
)
1
(
1
2
=
+
+
ω
ω
j
j
k
→
kr
k
,
kr
ω
0
)
2
1
(
2
=
+
−
+
k
j
j
ω
ω
ω
→
Re:
0
2
2
=
+
−
k
ω
, Im:
0
)
1
(
2
=
−
ω
ω
1
=
kr
ω
,
2
=
kr
k
ad b)
GM
k
k
kr
⋅
=
1
2
2
=
=
=
GM
k
k
kr
ad c)
4
5
.
0
2
=
=
k
Uwaga. Wszystkie warianty układu
mają jednakowe charakterystyki fazowe.
k
2
)
1
(
1
+
s
s
Układ otwarty
M
1
ω
1
-180
F
PM
1/GM
ω
2
ω
ω
10
0
10
0
10
Matlab
w=logspace(-0.1,0.3,200);
995
.
1
10
3
.
0
=
l=2
m=[1 2 1 0]
[M1,F]=bode(l,m,w);
[M2,F]=bode(0.5*l,m,w);
[M3,F]=bode(2*l,m,w);
subplot(211)
semilogx(w,M1, w,M2, w,M3), grid
subplot(212)
semilogx(w,F), grid
•
Wykresy powyższe ilustrują następujące twierdzenie:
Twierdzenie Nyquista
Jeśli charakterystyki
),
(
ω
M
)
(
ω
F
układu otwartego, który nie ma biegunów w
prawej półpłaszczyźnie (tzn. jest stabilny przynajmniej granicznie), przechodzą
przez punkty:
−
°
−
=
180
)
(
2
ω
F
,
1
)
(
2
=
ω
M
, to układ zamknięty znajduje się na granicy
stabilności
oscylując z częstotliwością
kr
ω
ω
=
2
,
−
°
−
=
180
)
(
2
ω
F
,
1
)
(
2
<
ω
M
, to układ zamknięty jest stabilny, a zapas modułu
GM wynosi
)
(
1
2
ω
M
,
−
°
−
=
180
)
(
2
ω
F
,
1
)
(
2
>
ω
M
, to układ zamknięty jest niestabilny.
Wnioski
−
O stabilności układu zamkniętego wnosi się na podstawie charakterystyk układu
otwartego (inaczej niż u Hurwitza).
−
Potrzebne są charakterystyki częstotliwościowe, które można otrzymać eksperymentalnie
(transmitancja służy tutaj tylko do wykreślenia charakterystyk).
DOBÓR WZMOCNIENIA
1.
Dane przeregulowanie p
%
– lub zapas fazy PM
Problem
−
dane
%
p
,
)
(
ω
M
,
)
(
ω
F
−
szukane
,
k
r
t
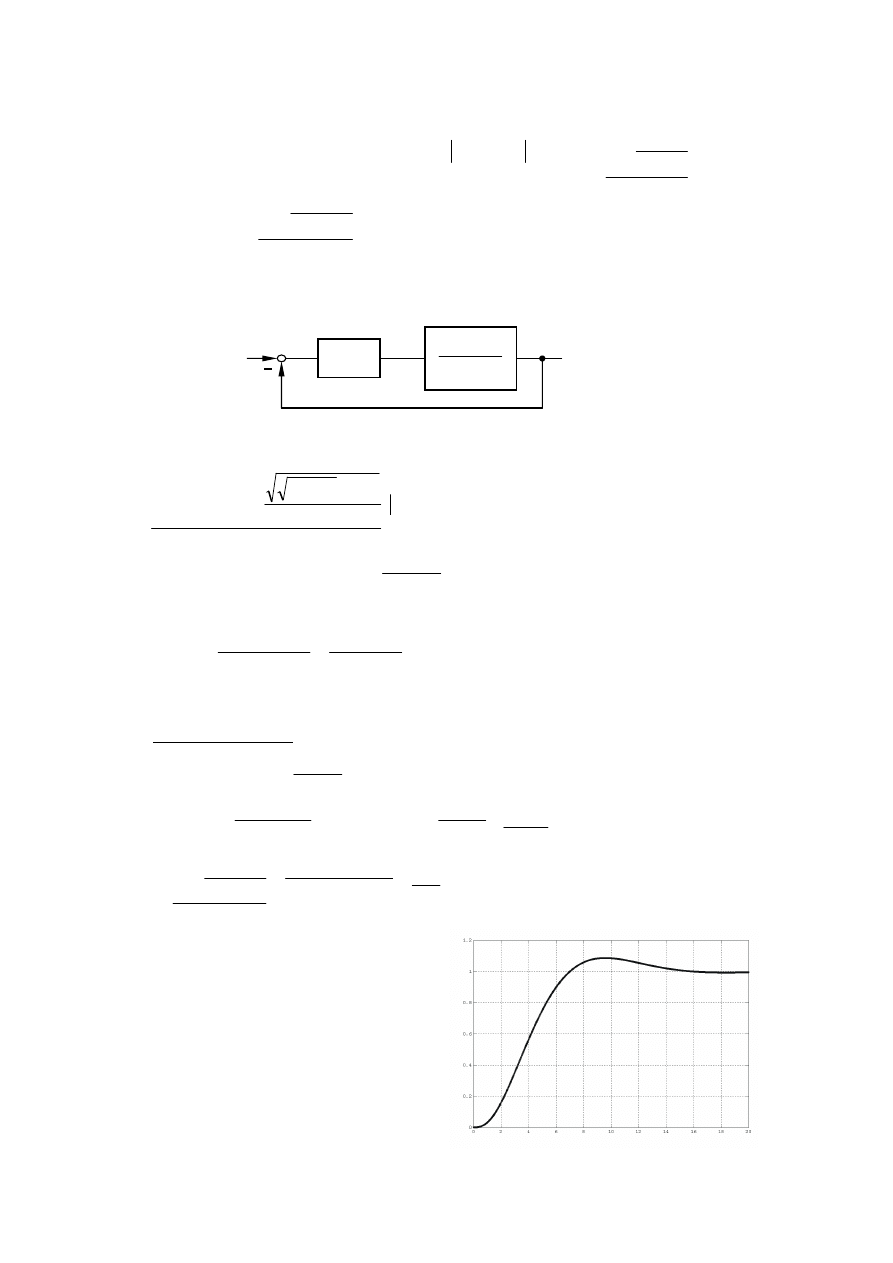
Charakterystyki układu otwartego
M
F
ω
ω
1
ω
2
=
= 1
ω
kr
-180
niestabilny
Układ zamknięty:
na granicy
stabilności
stabilny
k
)
(
),
(
ω
ω
F
M
Obiekt
11
•
Tok projektowania
)
(
1
1
)
(
:
)
(
1
)
(
1
1
1
%
1
)
(
)
(
ω
ω
ω
ω
ξ
ω
ω
ω
M
k
j
G
M
PM
p
M
k
otw
M
F
=
→
=
→
→
→
→
⋅
43
42
1
tgPM
t
r
1
8
ω
=
Przykład. Układ jak poprzednio
.
5
.
9
%
=
p
6
.
0
5
.
9
%
=
→
=
ξ
p
,
2
.
59
2
2
1
90
6
.
0
2
°
=
−
+
−
=
=
ξ
ξ
ξ
ξ
4
4
arctg
PM
)
(
)
(
s
G
k
s
G
otw
=
,
2
)
1
(
1
)
(
+
=
s
s
s
G
)
)
(
2
90
(
)
(
2
2
)
1
(
1
)
1
(
1
)
(
4
4 8
4
4 7
6
4
3
42
1
ω
ω
ω
ω
ω
ω
ω
ω
F
arctg
j
M
e
j
j
j
G
−
−
+
=
+
=
)
(
180
1
ω
F
PM
+
=
,
°
=
→
−
−
=
4
.
15
2
90
180
2
.
59
1
1
ω
ω
arctg
arctg
2754
.
0
4
.
15
1
=
=
tg
ω
2962
.
0
)
(
1
375
.
3
)
1
(
1
)
(
1
2
1
1
1
=
=
→
=
+
=
ω
ω
ω
ω
M
k
M
3
.
17
2
.
59
2754
.
0
8
8
1
=
⋅
=
=
tg
tgPM
t
r
ω
•
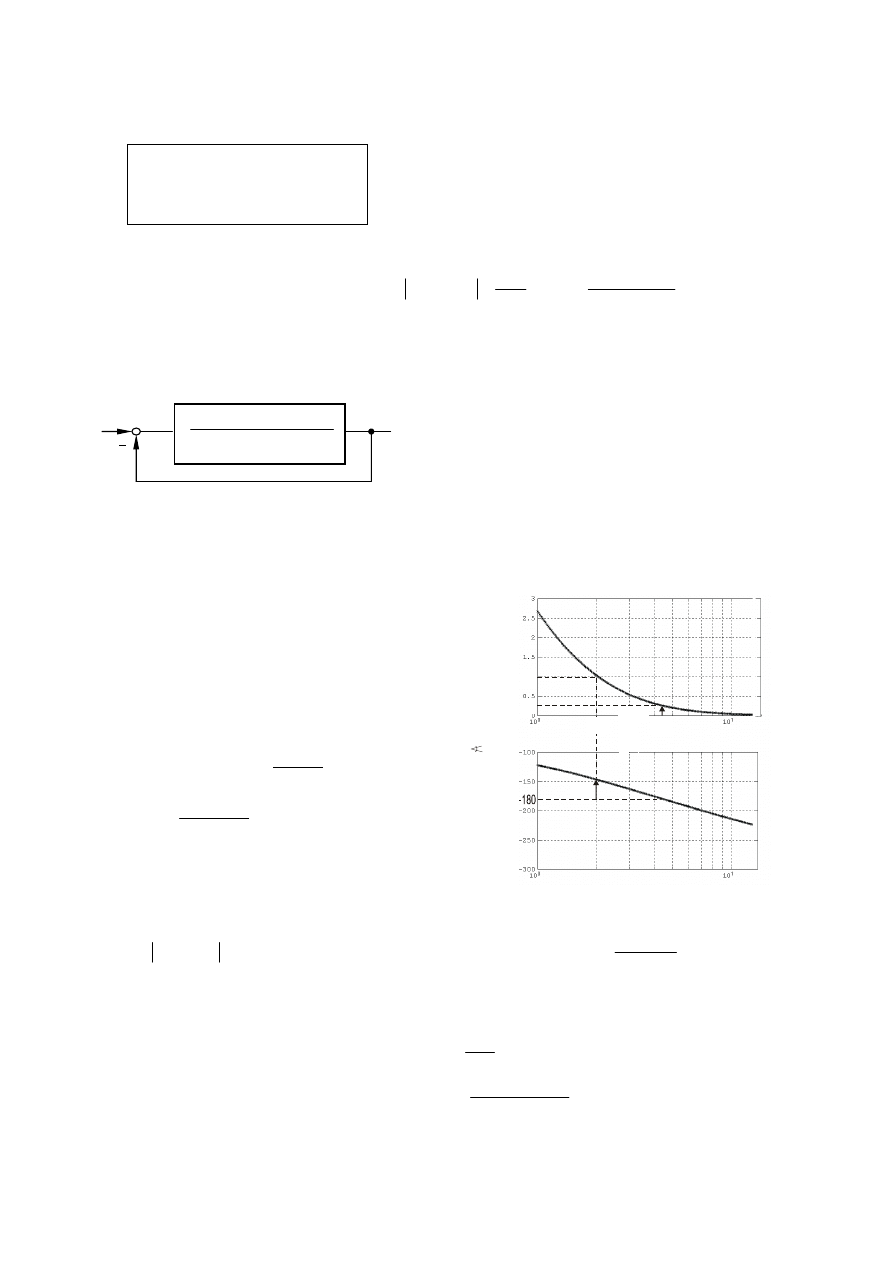
Matlab
clg
l=0.2962*[0 0 0 1];
m=[1 2 1 0];
t=0:0.2:20;
y=step(l, l+m, t);
plot(t, y), grid
max(y)
54
.
8
%
=
p
k
2
)
1
(
1
+
s
s
ew.
°
=
≅
60
100
ξ
PM
12
2.
Dany zapas modułu GM
Problem
−
dane
,
GM
),
(
ω
M
)
(
ω
F
−
szukane
,
k
,
%
p
r
t
•
Tok projektowania
)
(
1
1
)
(
:
)
(
180
)
(
2
2
2
2
2
)
2
(
)
(
)
(
ω
ω
ω
ω
ω
ω
ω
ω
M
GM
k
GM
j
G
M
F
M
k
M
F
otw
⋅
=
→
=
→
→
°
−
=
⋅
43
42
1
•
Przykład. Układ – jak na rysunku,
dB
12
=
dB
GM
roots([0.05, 0.6, 1])
→
2, 10
zakres
ω
1...100
•
Matlab
w=logspace(0, 2, 200);
l=1
m=[0.05, 0.6, 1, 0]
[M,F]=bode(l,m,w);
[w’, M, F]
...
4.50 0.0823 –180.27
2
ω
)
(
2
ω
M
180
−
≅
3
03
.
3
0873
.
0
4
1
≅
=
⋅
=
k
•
Określenie p
%
i t
r
%
1
1
1
100
)
(
)
(
3
)
(
180
1
)
(
p
F
PM
j
G
F
M
otw
→
→
+
=
→
→
=
⋅
ξ
ω
ω
ω
ξ
ω
ω
,
tgPM
t
r
1
8
ω
=
c.d. Matlab
[w’,
3*M,
F]
2.049 1.0018
-147.27
1
ω
1
≅
)
(
1
ω
F
73
.
32
27
.
147
180
=
−
=
PM
7
.
33
327
.
0
100
%
=
→
=
≅
p
PM
ξ
08
.
6
7
.
32
049
.
2
8
=
⋅
=
tg
t
r
)
1
6
.
0
05
.
0
(
2
+
+
s
s
s
k
GM
GM
dB
log
20
=
4
98
.
3
10
10
20
/
12
20
/
≅
=
=
=
dB
GM
GM
1
ω
1
PM
ω
ω
|G
otw
|
G
otw
3M
F
0.25
ω
2
1/GM
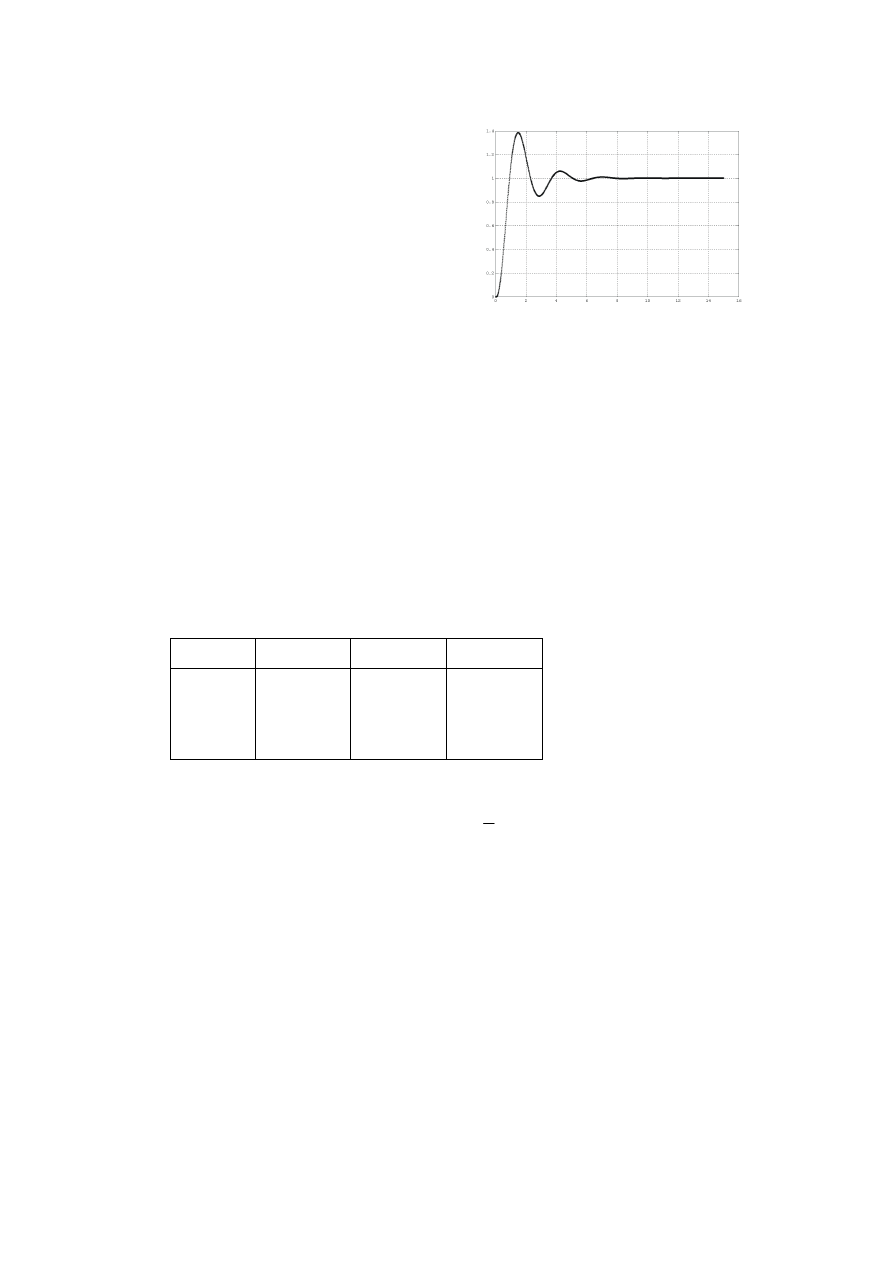
13
t=0:0.15:15;
l=3*[0,0,0,l]
y=step(l,l+m,t);
plot(t,y), grid
max(y)
39
.
38
%
=
p
AUTOMATYCZNY EKSPERYMENT ZIEGLERA–NICHOLSA
1.
Reguły Zieglera-Nicholsa
Ziegler i Nichols – 1943 – eksperymentalny dobór nastaw regulatora PID przez
doprowadzenie do granicy stabilności, a potem przez odpowiednią redukcję nastaw.
•
Kroki eksperymentu Z-N
1.
Ustawić regulator na działanie proporcjonalne P.
2.
Stopniowo zwiększając
p
k
doprowadzić układ zamknięty do granicy stabilności.
3.
Zapisać wzmocnienie krytyczne
kr
p
k
,
i okres oscylacji
kr
T .
4.
Określić nastawy według reguł podanych w tabeli dla wybranego typu regulatora.
Regulator
p
k
i
T
d
T
P
kr
p
k
,
5
.
0
–
–
PI
kr
p
k
,
45
.
0
kr
T
85
.
0
–
PID
kr
p
k
,
6
.
0
kr
T
5
.
0
kr
T
125
.
0
Uwagi
−
Regulator PID ma podwójne zero, bo
i
d
T
T
4
1
=
.
−
Reguły Z-N nie określają jakiego przeregulowania, ani czasu regulacji można się
spodziewać. Zazwyczaj przebiegi są oscylacyjne.
−
Obecnie eksperyment Z-N jest wykonywany automatycznie przez regulatory
niektórych firm (np. regulator RF-537 – laboratorium).
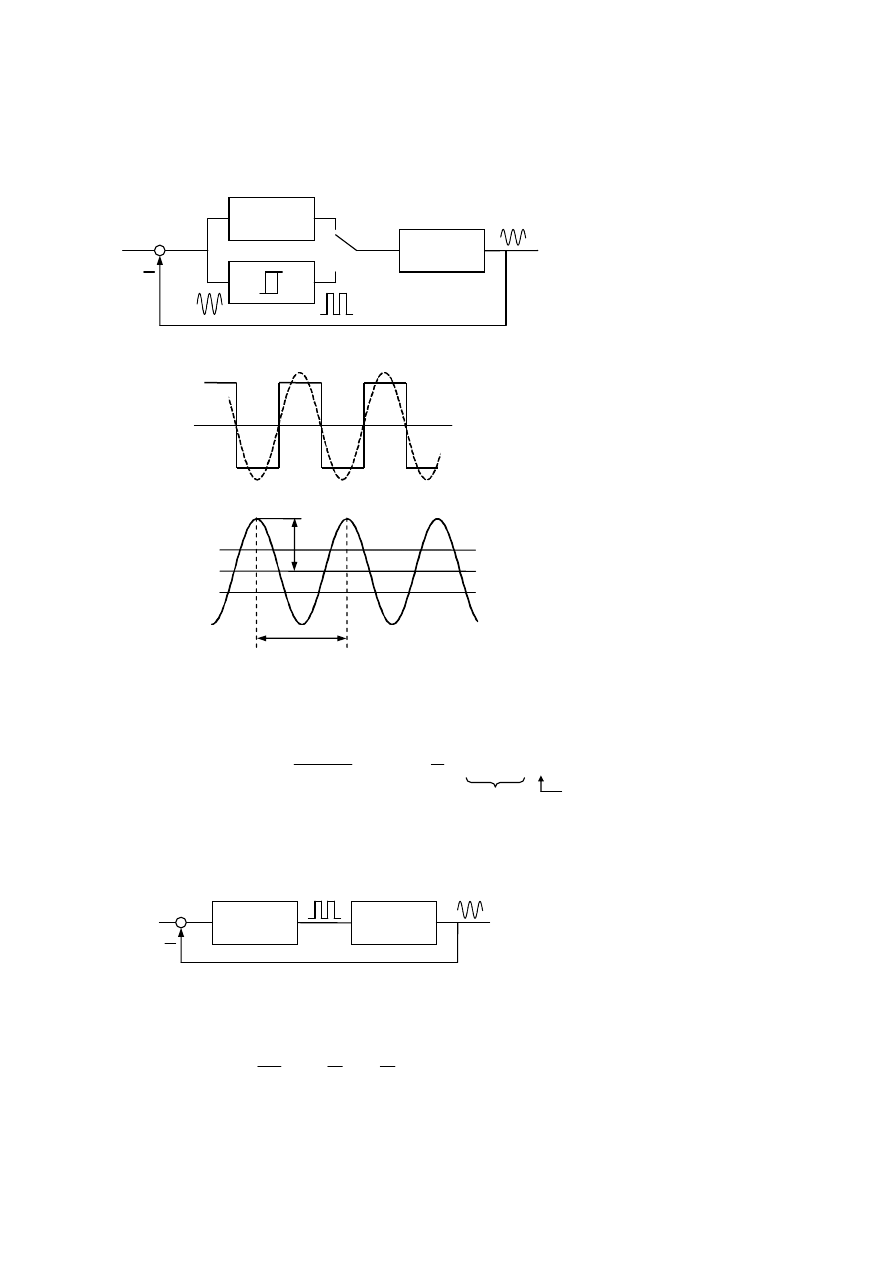
14
2.
Sterowanie przekaźnikowe
•
1984 – Åstrӧm i Hägglund
T – Tune (nastrajanie)
Regulator firmy Satt Control
(obecnie ABB)
Sterowanie przekaźnikowe ±U
i aproksymacja pierwszą harmoniczną
A
kr
– amplituda, T
kr
– okres
±H – histereza przekaźnika
•
Idea – ze względu na odporność układu ze sprzężeniem zwrotnym na przybliżenia
można ograniczyć się do pierwszej harmonicznej sygnału u(t) (szereg Fouriera) i
wyznaczyć „transmitancję” (tzw. funkcją opisującą)
A
jC
B
A
N
1
1
)
(
+
=
,
∫
=
A
d
sin
sin
A
f
B
0
1
)
(
1
φ
φ
φ
π
kr
A
A
=
Przybliżenie układu
←
granica stabilności
•
Przekaźnik idealny – bez histerezy (wystarcza dla obiektów inercyjnych,
nieodpowiedni dla całkujących)
kr
p
k
A
U
A
U
A
U
A
N
,
3
.
1
27
.
1
4
)
(
=
≅
=
=
π
Wniosek. Na podstawie
kr
p
k
,
i
kr
T
z reguł Zieglera–Nicholsa można dobrać nastawy
regulatora typu PID.
N(A)
Obiekt
U
+H
-H
A
kr
T
kr
y
+U
-U
u
PID
Obiekt
w
e
u
T
A, M
funkcja
przeka
ź
nika
cosφ dla C
1
15
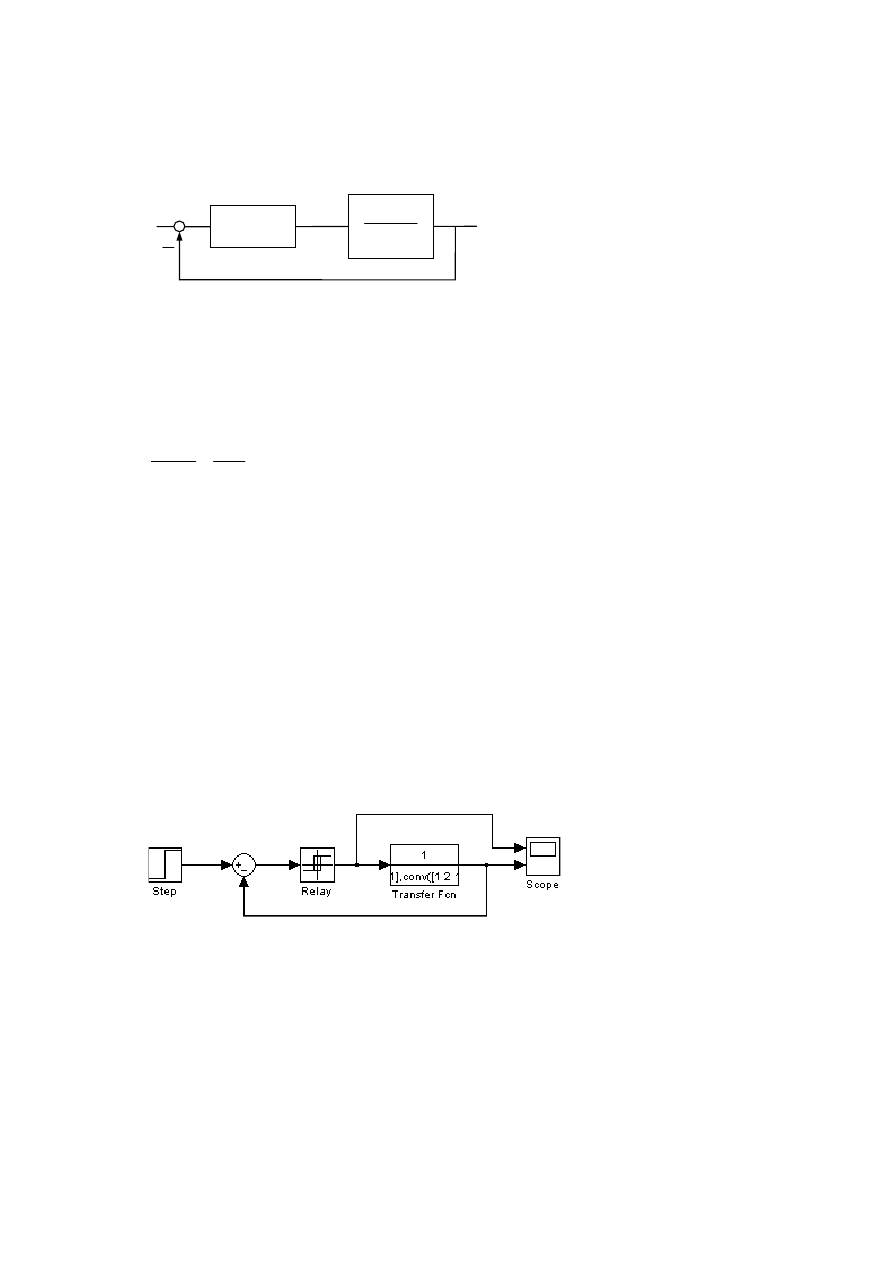
3.
Redukcja wzmocnienia względem granicy stabilności
•
Przykład – obiekt „trudny” z regulatorem PID
zob. Przebiegi oscylacyjne
PID:
77
.
0
=
p
k
,
69
.
1
2
⋅
=
i
T
,
4
/
i
d
T
T
=
5
=
D
– bezpieczne
nastawy
(przebiegi
aperiodyczne krytyczne)
•
Można sprawdzić, że powyższy układ znajdzie się na granicy stabilności przy
wzmocnieniu regulatora PID wynoszącym
.
08
.
4
,
=
kr
p
k
– ponad 5–krotny wzrost wzmocnienia w stosunku do
wzmocnienia bezpiecznego.
Wniosek. Nastawy Zieglera–Nicholsa, które odpowiadają 2–krotnej redukcji
czułości regulatora względem granicy stabilności, dają w wyniku przebiegi
oscylacyjne. W celu uzyskania przebiegów bliskich aperiodycznym
krytycznym, należy jeszcze 2–krotnie zmniejszyć wzmocnienie
p
k
w stosunku
do wzmocnienia wynikającego z reguł Zieglera–Nicholsa (4–krotnie względem
wzmocnienia krytycznego).
•
Sterowanie przekaźnikowe
step: S.t.1 Relay:
S.on p eps, S.off p. – eps
I.v.0
Out. on 1
Out. off 0
F.v. 0.5
PID
(
)
5
1
1
+
s
29
.
5
77
.
0
08
.
4
.
,
,
=
=
bezp
p
kr
p
k
k
16
Ziegler-Nichols:
2U = 1.0, U=0.5
2A=0.446, A=0.223
T
kr
=8.8
•
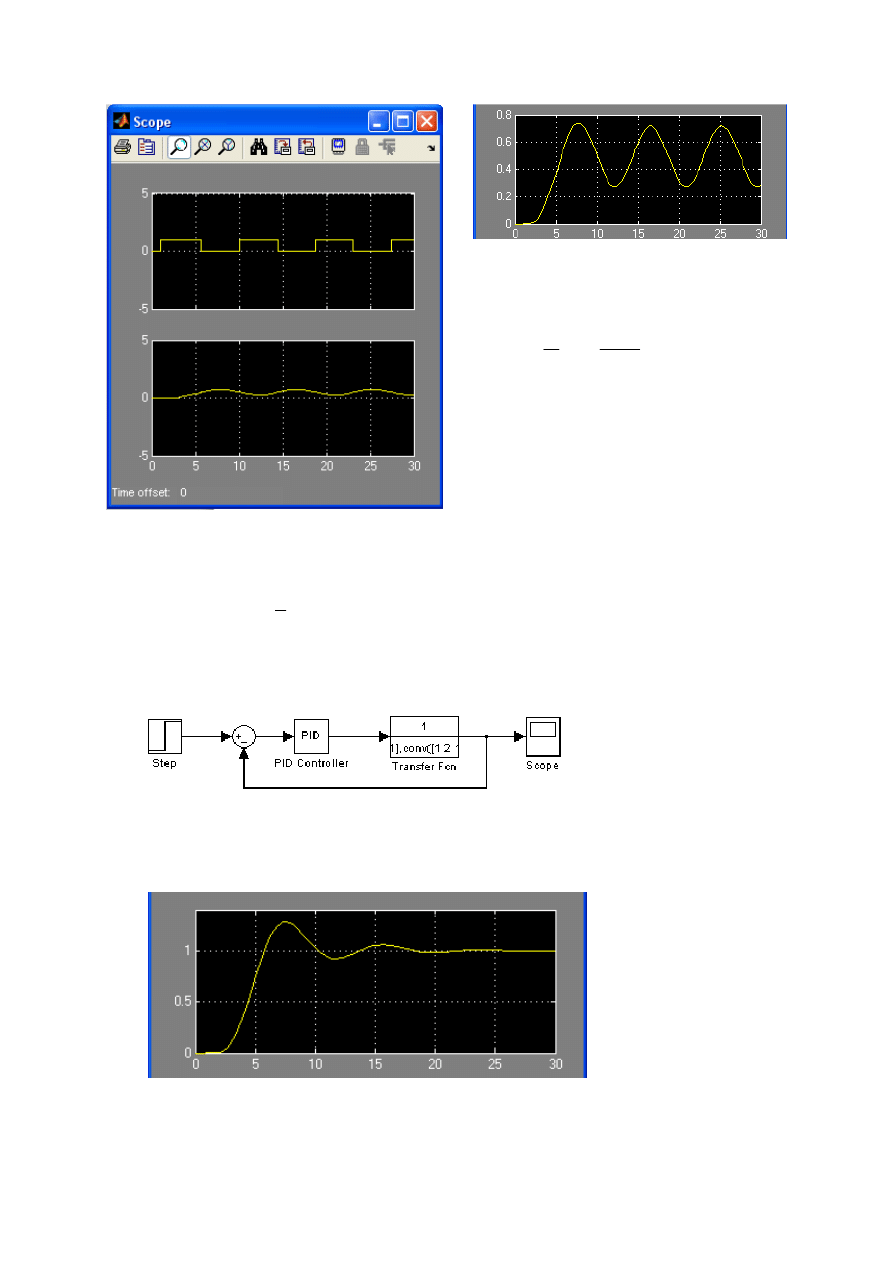
Układ z regulatorem PID
P=1.75, I=1.75/4.4, D=1.75·1.1
91
.
2
223
.
0
5
.
0
3
.
1
3
.
1
,
=
=
=
A
U
k
kr
p
75
.
1
91
.
2
6
.
0
64
.
0
,
=
⋅
=
=
kr
p
p
k
1
.
1
4
1
,
4
.
4
5
.
0
=
=
=
=
i
d
ur
i
T
T
T
T