PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W CHEŁMIE
INSTYTUT NAUK TECHNICZNYCH

Laboratorium Mechaniki Płynów

Ćwiczenie 4

Pomiar oporu profilu o kształcie opływowym metodą

Jones'a ("Wake survey").

Opracował: dr inż. Dariusz Mika

1. Wprowadzenie teoretyczne.

Analizie poddane zostanie zachowanie brył zanurzonych w nieograniczonym,

jednorodnym strumieniu płynu. Jest oczywistym, że siły wywierane przez ośrodek płynny na
ciało stałe są takie same dla ruchu ciała stałego w nieruchomym ośrodku, jak przy opływie
nieruchomego ciała płynem, którego pole prędkości w dużej odległości od przeszkody jest
jednorodne. W obu przypadkach obserwujemy ruch względny ośrodka płynnego i
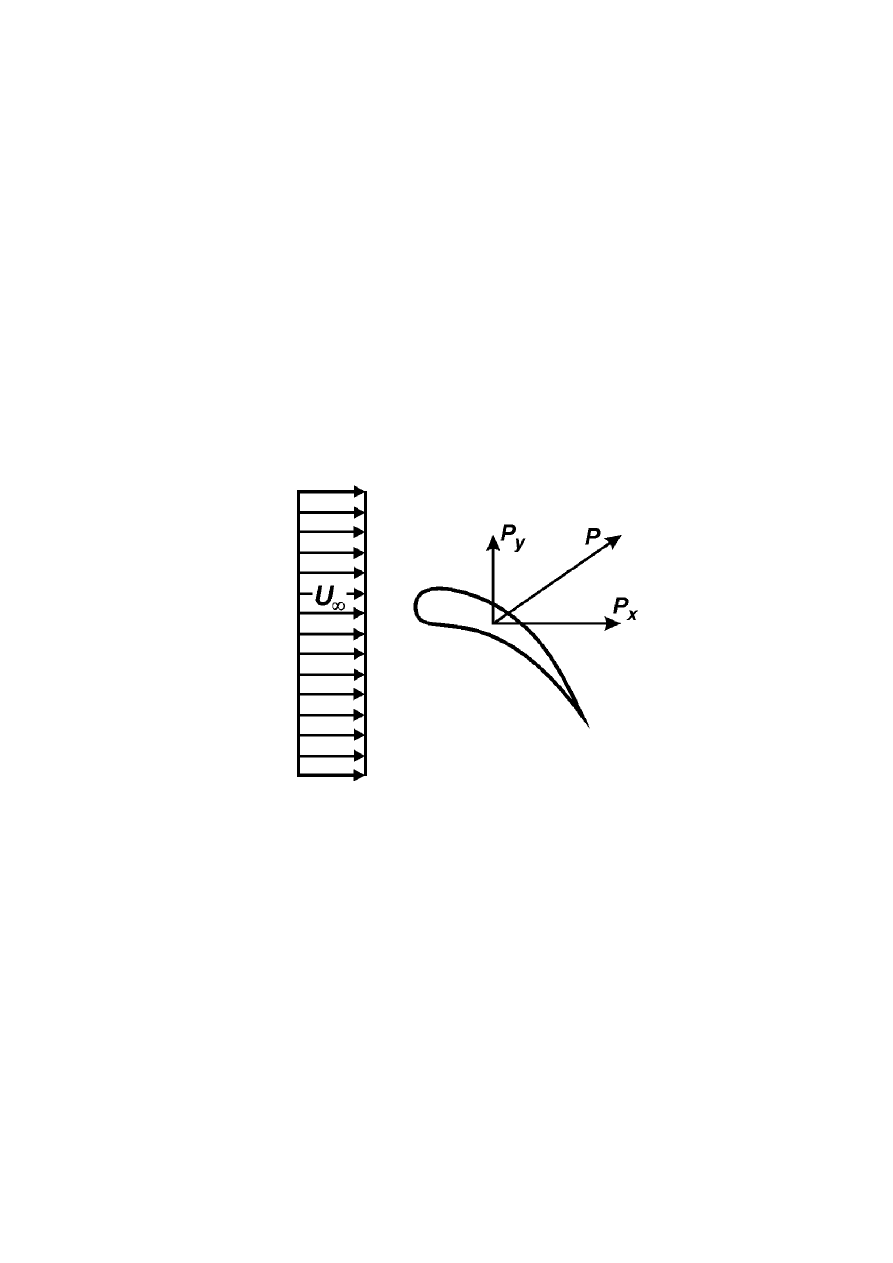
opływanego ciała, który powoduje siły wzajemnego oddziaływania. Siły te, przedstawione
schematycznie na rys. 1, nazywamy siłami aerodynamicznymi. Składowa P

x

wypadkowej siły

aerodynamicznej równoległa do kierunku przepływu niezakłóconego, scharakteryzowanego
tzw. prędkością w nieskończoności



U , nazywana jest oporem, natomiast składowa

P

y

prostopadła do tego kierunku nosi nazwę siły nośnej. Dla brył mających przynajmniej jedną
płaszczyznę symetrii zorientowaną równolegle do kierunku przepływu nie występuje trzecia
składowa prostopadła do P

x

i P

y

a wypadkowa sił aerodynamicznych leży wówczas w

płaszczyźnie symetrii.

Rys. 1. Siły aerodynamiczne działające na ciało stałe

Przypomnieć należy, że dla płynów nielepkich istotną treścią tzw. paradoksu

d’Alamberta jest fakt, że nie potrafimy znaleźć takiej analitycznej interpretacji opływu, przy
której można by uzyskać rozkład ciśnień na powierzchni bryły dający opór różny od zera. W
przypadku płynów lepkich występuje zawsze opór przy ruchu względnym ciała stałego i
opływającego je płynu. Reakcja wywierana na ciało jest sumą wypadkowych sił stycznych
występujących na jego powierzchni, a wywołanych lepkością płynu oraz sił ciśnieniowych,
skierowanych normalnie do poszczególnych elementów powierzchni opływanego ciała. Siły
styczne działające na powierzchnię ciała zwrócone są zgodnie z kierunkiem prędkości
względnej płynu, a ich składowa w kierunku



U nazywa się oporem tarcia P

xt

. Jednocześnie

siły tarcia występujące na powierzchni opływanych ciał wywołują ukształtowanie opływu
odmienne, niż w przypadku przepływu płynu nielepkiego. Wypadkowa sił pochodzących od
naprężeń normalnych (ciśnień) na powierzchni ciała opływanego płynem lepkim ma w

związku z tym różną od zera składową zwróconą zgodnie z



U . Tę składową nazywa się

oporem ciśnieniowym P

xc

.

Dla każdej bryły opływanej istnieje takie jej usytuowanie w stosunku do



U przy

którym nie występuje siła nośna (P

y

= 0). Dla brył osiowosymetrycznych lub mających co

najmniej dwie płaszczyzny symetrii zachodzi to wówczas, gdy prędkość



U jest równoległa

do osi symetrii lub linii przecięcia płaszczyzn symetrii. We wszystkich innych położeniach

bryły względem



U siła nośna jest różna od zera (

0



y

P

). Dla P

y

= 0, siłę P

x

= P

xt

+ P

xc

=

P

xp

nazywamy oporem profilowym. Siły aerodynamiczne wyraża się zwykle przez

współczynniki sił c

x

i c

y

opierające się na wyprowadzonych w analizie wymiarowej

zależnościach [2]:

S

U

c

P

x

x

2

2







(1)

S

U

c

P

y

y

2

2







(2)

gdzie:

c

x

- współczynnik oporu,

c

y

- współczynnik siły nośnej,

ρ - gęstość czynnika,

S -umowna powierzchnia odniesienia.

W ogólnym przypadku współczynniki c

x

i c

y

są zależne od kształtu ciała i jego

ustawienia, a ponadto od liczb kryterialnych Reynoldsa i Macha. Wyniki badań
doświadczalnych wskazują, że w zakresie niskich liczb Macha możemy pominąć wpływ
ściśliwości na wartości współczynników c

x

i c

y

, tzn.

4

,

0



Ma



)

(

,

Ma

f

c

c

y

x



W zakresie małych prędkości istotnymi stają się zależności c

x

=f(Re) i c

y

=f(Re).

Ostatnie zależności mają różny charakter dla brył opływowych, charakteryzujących

się

małymi wartościami współczynnika oporu c

x

oraz dla brył o kształtach nieopływowych, dla

których przyjmują one znacznie większe wartości.

Kształty opływowe charakteryzują się tym, że w pewnym zakresie położeń w stosunku

do kierunku ruchu nie występuje na powierzchni bryły zjawisko oderwania warstwy
przyściennej. Typowymi przykładami kształtów opływowych w technice są łopatki maszyn
przepływowych (turbin, sprężarek itp.) oraz skrzydło samolotu (tzw. profil lotniczy).
Wymienione ciała charakteryzują się posiadaniem ostrej krawędzi spływowej (zapobiegającej
oderwaniu warstwy przyściennej w tylnej części ciała) oraz obłym czołem (zapewniającym

nieczułość ciała na oderwanie warstwy przyściennej w pewnym zakresie zmienności kąta
napływu strugi). Zaburzenie, jakie obserwuje się za przeszkodami o kształtach opływowych,
ogranicza się do stosunkowo niewielkiego śladu powstałego ze spływających warstw
przyściennych. Przy takim opływie i śladzie aerodynamicznym można zastosować dla
określenia siły oporu lub jej współczynnika metody badań modelowych oparte o zasadę
zmiany ilości ruchu strumienia opływającego. Jedną z nich jest metoda Jones'a, stosowana do
wyznaczania wartości współczynnika c

x

ciał w strumieniach nieograniczonych.

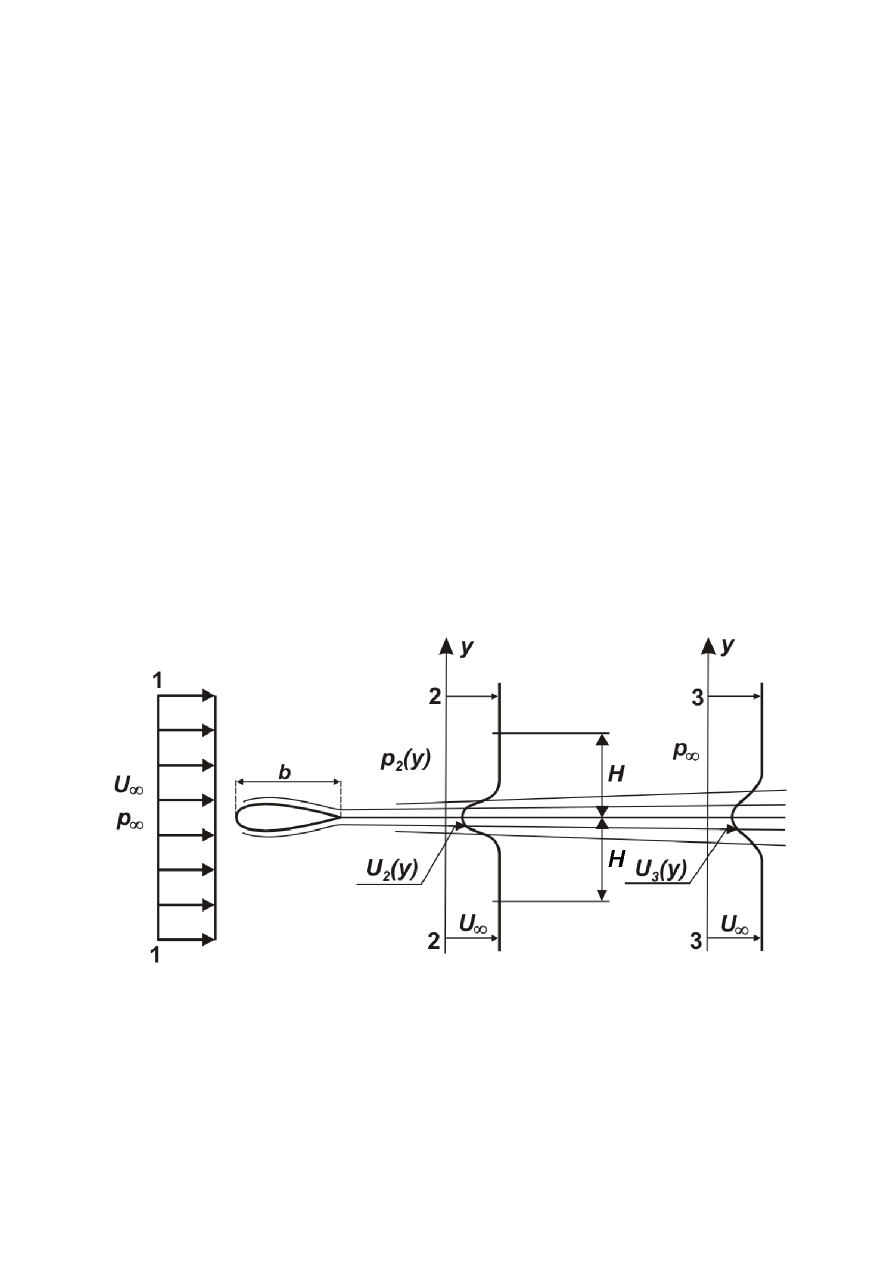
Rozpatrzmy trzy poprzeczne przekroje kontrolne przepływu płaskiego, w których

umieszczony jest model płata o nieskończonej rozpiętości (rys. 2):



przekrój 1-1 jest usytuowany przed modelem; panuje w nim ciśnienie statyczne



p , a prędkość równa jest



U , i ich rozkłady są jednorodne,



przekrój 2-2 zlokalizowany jest tuż za opływanym ciałem; prędkość przepływu
U

2

jak i ciśnienie statycznep

2

są funkcjami współrzędnej poprzecznej U

2

= f (y)

oraz p

2

= f (y),



przekrój 3-3 zlokalizowany jest w takiej odległości za modelem, że panujące w
nim ciśnienie statyczne jest stałe i równe ciśnieniu w przepływie niezakłóconym





p

p

3

, natomiast profil prędkości nadal wykazuje defekt, tzn. U

3

= f (y);

przekrój 3-3 jest przekrojem pomiarowym.

Rys. 2. Rozmieszczenie przekrojów kontrolnych

Warto nadmienić, iż zgodnie z wynikami pomiarów zamieszczonymi w pracy [4],

zaburzenie pola ciśnień statycznych obecnością ciała zanika już w odległości 0.3b za
krawędzią spływu.

Siłę oporu przypadającą na jednostkę długości modelu (w kierunku z) można określić

wzorem uzyskanym z przekształcenia równania zmiany pędu [1] pomiędzy przekrojami 1-1 i
3-3 (wyprowadzenie zostało przedstawione w dodatku A do niniejszego ćwiczenia):





dy

y

U

U

y

U

P

H

H

xj











)

(

)

(

3

3



(3)

Uwzględniając fakt, iż w przepływie płaskim umowna powierzchnia odniesienia

(powierzchnia jednostkowa odniesiona do jednostki długości profilu, wyrażona w m

2

/m)

równa jest cięciwie b profilu:

S

j

=b (4)

związek definicyjny współczynnika oporu c

x

dla przypadku przepływu płaskiego

przyjmuje postać:

b

U

c

P

x

xj

2

2







(5)

Wykorzystując związek (5) współczynnik oporu określony będzie następującą

zależnością:

dy

p

p

p

p

b

c

d

d

H

H

d

d

x



























3

3

1

2

(6)

gdzie:

3

d

p

- ciśnienie dynamiczne w przekroju pomiarowym,



d

p - ciśnienie dynamiczne w przepływie niezakłóconym (przekrój 1-1).

2. Cele ćwiczenia

Celem ćwiczenia jest wyznaczenie siły oporu aerodynamicznego oraz współczynnika

oporu profilowego wykorzystując metodę zmiany ilości ruchu strumienia opływającego
"wake survey".

3. Zadania.

a) wyznaczyć profil tzw. "defektu prędkości" wzdłuż profilu pomiarowego,

b) na podstawie otrzymanych wyników obliczyć wartość siły oporu oraz

współczynnik oporu profilowego dla badanego profilu.

4 Przebieg ćwiczenia.

Ćwiczenie przeprowadzane jest z wykorzystaniem tunelu aerodynamicznego

edukacyjnego Aerolab typu otwartego. Profil ćwiczeniowy oraz sondę pomiarową "wake
rake" należy umieścić w sekcji testowej tunelu (stosowanie do instrukcji obsługi tunelu).
Drugie końce wężyków sondy "wake rake" należy połączyć z odpowiednimi gałązkami
(kanałami) multi-manometru będącego wyposażeniem tunelu. Drugie gałązki manometru są
otwarte do atmosfery w związku z tym manometr mierzy różnicę ciśnienia całkowitego na
przekroju pomiarowym i ciśnienia atmosferycznego. Należy pamiętać o odpowiedniej
konwencji znakowej odczytywania wysokości słupków cieczy w manometrach. Wysokości
powyżej przyjętego poziomu zerowego bierzemy ze znakiem (-) (podciśnienie w stosunku do
ciśnienia atmosferycznego) natomiast wysokości poniżej poziomu zerowego ze znakiem (+)
(nadciśnienie). Aby obliczyć ciśnienie dynamiczne w śladzie aerodynamicznym otrzymane
wyniki pomiaru ciśnienia należy odnieść do ciśnienia statycznego sekcji testowej (ciśnienie
dynamiczne jest różnicą między ciśnieniem całkowitym a ciśnieniem statycznym). Do
otrzymanych wyników należy dodać więc różnicę między ciśnieniem otoczenia a ciśnieniem
statycznym sekcji testowej

st

P

p

p

p









0

1

0

. Różnicę tych ciśnień odczytujemy korzystając

z sondy Prandtla umieszczonej w sekcji testowej tunelu. Otrzymane wyniki będą wówczas
stanowiły ciśnienie dynamiczne p

d3

=Δp+Δp

P0-1=

(p-p

0

)+(p

0

-p

st

)=p-p

st.

. Za pomocą sondy

Prandtla wyznaczamy dodatkowo ciśnienie dynamiczne przepływu niezakłóconego

2

1

025

,

0









P

d

z

g

p



.

5. Opracowanie wyników pomiaru.

Dla wyznaczenia wartości współczynnika oporu modelu ciała opływowego należy

określić doświadczalnie rozkład ciśnienia dynamicznego w przekroju poprzecznym
położonym za badanym ciałem (przekrój pomiarowy III).

Przyjmuje się, że potrzebna w obliczeniach wartość ciśnienia dynamicznego w

strumieniu niezakłóconym jest równa maksymalnej wartości ciśnienia dynamicznego w
przekroju pomiarowym (punkt pomiarowy dostatecznie daleko odsunięty od strefy zakłóceń
wywołanej opływem modelu). Wartość całki występującej we wzorze (6) można określić w
sposób przybliżony za pomocą metody prostokątów:

























































d

i

d

n

i

d

i

d

d

d

H

H

d

d

p

p

p

p

y

dy

p

p

p

p

3

1

3

3

3

1

1



(8)

gdzie:

n - ilość punktów pomiarowych,

Δy - elementarny przedział całkowania wynoszący

1







n

L

y

r

(9)

gdzie: L

r

- szerokość sondy "wake rake".

Wartość współczynnika oporu profilowego c

x

wyznacza się z zależności:



b

c

x

2



(10)

Literatura

1.

Bukowski J, Kijkowski P.: Kurs mechaniki płynów, PWN, Warszawa 1980

2.

Duckworth R.A.: Mechanika płynów, WNT, Warszawa 1983

3.

Jones, B.M., 1936, “The Measurement of Profile Drag by the Pitot-Traverse Method”,
ARC Reports and Memoranda No. 1688, Teddington,UK.

4.

Martynov A.: Eksperimentalnaja aerodynamika, GIOP, Moskwa 1958

Zadanie do wykonania:

1. Wyznaczyć profil "defektu prędkości" w przekroju pomiarowym,

2.Na podstawie otrzymanych wyników pomiaru wyznaczyć siłę oporu P

xj

oraz

współczynnik oporu profilowego c

x.

Tabela ćwiczeniowa:
t

ot

=.......°C; p

ot

=...........Pa; b=...........m; Δy=............m; ρ=1000 [kg/m

3

];

..........

025

,

0

1

0

0

1

0



















P

P

z

g

p

p

p



;

.........

025

,

0

2

1











P

d

z

g

p



;

1

0





P

z

-

wysokość słupa cieczy manometru odpowiadająca różnicy ciśnienia

atmosferycznego i ciśnienia statycznego sekcji testowej [cal].

2

1





P

z

- różnica wysokości słupa cieczy manometrycznej odpowiadająca różnicy

ciśnień wskazywanej przez rurkę Prandtla [cal].

Lp.

z





d

p



i

d

i

p

v

3

3

2



1

0

3

025

,

0











P

i

d

p

z

g

p























d

i

d

d

i

d

p

p

p

p

3

3

1

[cal]

[Pa]

[m/s]

[Pa]

1

2

3

4

5

Państwowa Wyższa Szkoła Zawodowa w Chełmie

Laboratorium

Mechaniki Płynów

Laboratorium mechaniki płynów, ćwiczenie nr 4

Temat ćwiczenia: „ Pomiar oporu ciśnieniowego profilu o kształcie opływowym metodą Jones'a
("Wake survey")"

Imię i nazwisko

Grupa

Semestr/rok akademicki

Prowadzący

Data wykonania ćwiczenia/godz.

Ocena

6

7

8

9

10

11

12

13

14

15

16

17

18





























d

i

d

i

d

i

d

p

p

p

p

y

3

18

1

3

1



=................



b

c

x

2



=............

Przelicznik jednostek:
1[mBar]=100 [Pa];
1 [cal] = 0,025 [m];

Dodatek A:

Wyznaczanie sił powstających przy opływie ciał stałych na podstawie rozkładu

prędkości w śladzie aerodynamicznym

Zasadę zmiany pędu w mechanice płynów dla przypadku przepływu płynu doskonałego

(tzn. przy pominięciu naprężeń stycznych) można wyrazić następującym wzorem:







S

n

dS

n

p

U

U

0

)

(







(A1)

gdzie:

U



- wektor prędkości,

U

n

- składowa wektora prędkości normalna do powierzchni kontrolnej,

p - ciśnienie,

n



- jednostkowy wektor normalny do powierzchni kontrolnej,

S - powierzchnia kontrolna, ograniczająca rozważaną objętość płynu.

W zależności (A1) nie uwzględniono również sił masowych, które w przypadku

przepływu gazu są bardzo małe.

W przypadku opływu ciała stałego płynna objętość kontrolna (patrz rys. A1)

ograniczona jest:



dwoma płaszczyznami prostopadłymi do kierunku przepływu niezakłóconego,
położonymi przed (element powierzchni S

1

) i za (element powierzchni S

2

)

opływanym ciałem,



powierzchniami prądu (elementy powierzchni S

3

i S

4

) tworzącymi z poprzednimi

płaszczyznami przestrzeń zamkniętą,



powierzchnią ciała S

5

.

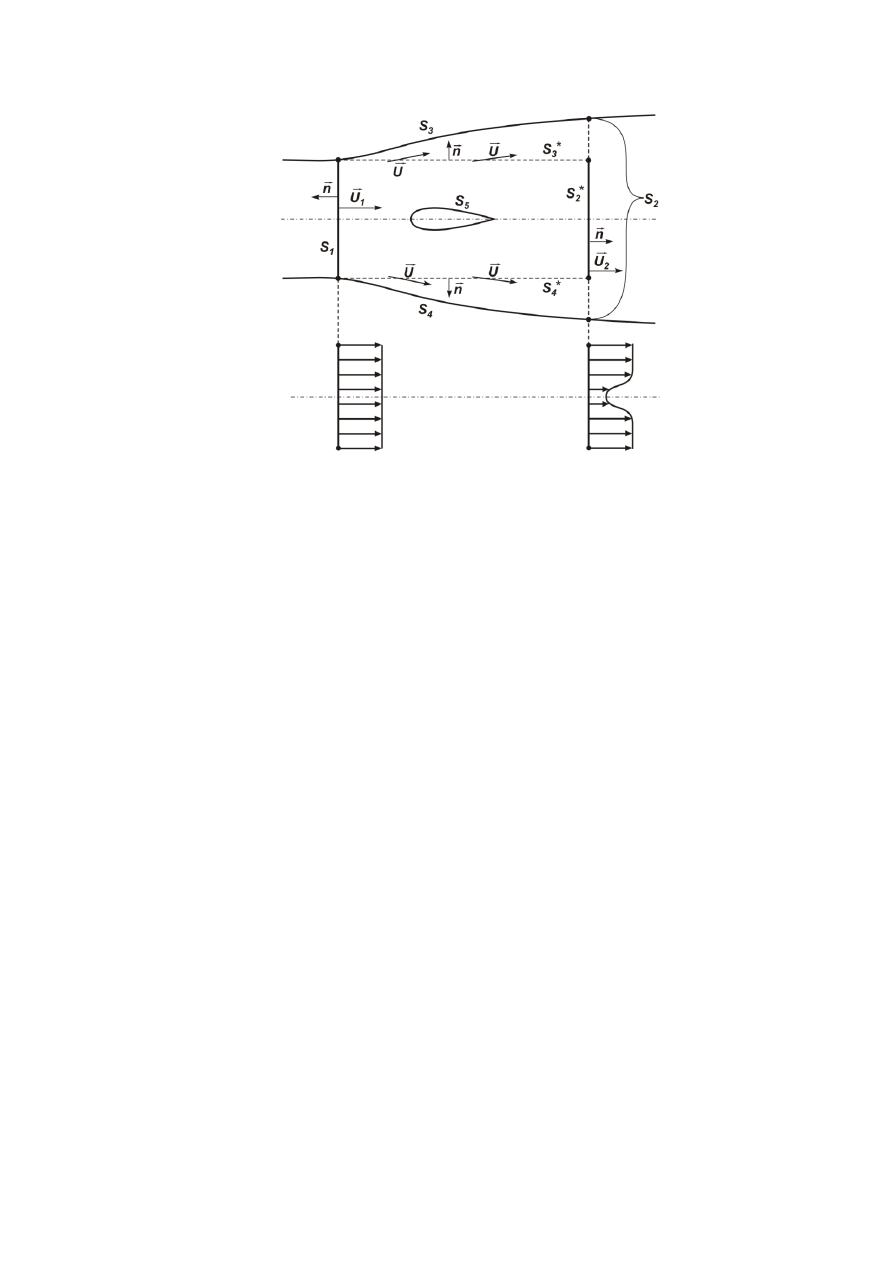
Rys. A1. Definicja objętości kontrolnej wokół opływanego ciała

Dla tak zdefiniowanej powierzchni kontrolnej zasada zmiany pędu (A1) przyjmuje

następującą postać:











i

S

i

n

i

dS

n

p

U

U

0

)

(

5

1







(A2)

Jeśli przyjąć, iż wszystkie elementy powierzchni S są odpowiednio oddalone od

powierzchni ciała, to panujące na nich ciśnienia można przyjąć za stałe i równe ciśnieniu
strugi niezakłóconej





p

p

i

; dla i = 1,2,3,4

(A3)

W związku z tym suma składników ciśnieniowych



i

S

i

dS

n

p



dla 4 powierzchni

zewnętrznych rozpatrywanej objętości kontrolnej wynosi 0.

Na powierzchni S

5

występuje natomiast niejednorodny rozkład ciśnienia i suma

elementarnych sił ciśnieniowych daje wypadkową siłą ciśnieniową P oddziaływania
przepływającego płynu na zanurzone w nim ciało, równą co do wartości i skierowaną
przeciwnie do reakcji hydrodynamicznej R.









5

5

S

dS

n

p

R

P







(A4)

Ponieważ składowa normalna prędkości U

n

na powierzchniach prądu S

3

i S

4

oraz na

powierzchni ciała S

5

(również będącej linią prądu) równa jest zero, zatem przez powierzchnie

te nie odbywa się wymiana pędu:

0

5

4

3

5

4

3













S

n

S

n

S

n

dS

U

U

dS

U

U

dS

U

U













(A5)

Wziąwszy pod uwagę powyższe założenia zasadę zmiany pędu można zapisać w

uproszczonej postaci skalarnej:













2

1

2

2

1

2

S

S

x

dS

U

dS

U

R

P





(A6)

gdzie:

P

x

-

składowa siły ciśnieniowej w kierunku przepływu, tzw. siła oporu,

U

-

składowa prędkości w kierunku przepływu.

Z uwagi na oddziaływanie ciała na przepływ otaczające je linie prądu ulegają

odkształceniu od linii prostych, i w konsekwencji powierzchnie S

1

i S

2

są różne, co może

prowadzić do trudności rachunkowych. Trudności te można wyeliminować poprzez nieco
odmienne zdefiniowanie objętości kontrolnej. Wybierając w miejsce powierzchni S

3

i S

4

powierzchnie

*

3

S

oraz

*

4

S równoległe do kierunku przepływu uzyskuje się objętość kontrolną

o przekroju prostokątnym, której dopełnieniem jest powierzchnia

*

2

S równa powierzchni

wlotowej S

1

. Jak wynika z doświadczenia prędkość w przekroju

*

2

S jest funkcją położenia

wykazując zmniejszenie w obszarze śladu aerodynamicznego (tzw. defekt prędkości). Wynika
stąd, że pomiędzy przekrojami S

1

i

*

2

S następuje odprowadzenie strumienia objętości:





















*

2

*

2

1

*

2

*

2

1

)

(

S

S

S

dS

U

U

UdS

dS

U

Q

(A7)

Strumień

Q



zostaje wyprowadzony z objętości kontrolnej poza obszarem śladu

(poprzez elementy powierzchni S

3

oraz S

4

) czyli w strefie przepływu niezakłóconego, z czego

wynika, że towarzyszący mu ubytek pędu wynosi:

















*

3

*
4

*

4

*

S

S

n

s

n

Q

U

dS

U

U

dS

U

U

M











(A9)

Zgodnie z powyższym pęd przenikający przez powierzchnię S

2

w związku (A6) należy

zastąpić pędem czynnika opuszczającego objętość kontrolną przez powierzchnie

*

2

S ,

*

3

S

oraz

*

4

S uzyskując:





































1

*
2

*
2

*
2

1

*

2

*

2

2

1

2

*

2

2

1

2

)

(

S

S

S

S

S

x

dS

U

U

U

dS

U

dS

U

M

dS

U

dS

U

P











(A8)

Identyczność powierzchni S

1

i

*

2

S pozwala na ostateczne wyrażenie siły oporu

ciśnieniowego w następujący sposób









*

2

*

2

)

(

S

x

dS

U

U

U

P



(A9)

Biorąc pod uwagę, że rozważany przepływ jest płaski, siła przypadająca na jednostkę

długości ciała (w kierunku z ) znajdującego się w przepływie wyraża się równaniem:











H

H

xj

dy

U

U

U

P

2

)

(



(A10)

gdzie H - połowa szerokości śladu aerodynamicznego.