Patrycja Grabowska
Weronika Hasslinger

Kinematyka i Dynamika Układów

Mechatronicznych

Laboratorium nr 2

Sprawozdanie

Prowadzący:
dr inż. Jarosław Bednarz

IMIR, Mechatronika,
Projektowanie
Mechatroniczne,
Gr. nr 7

Temat:

Model geometryczny – rozwiązanie

symboliczne

Data zajęć:
12.03.2015r.

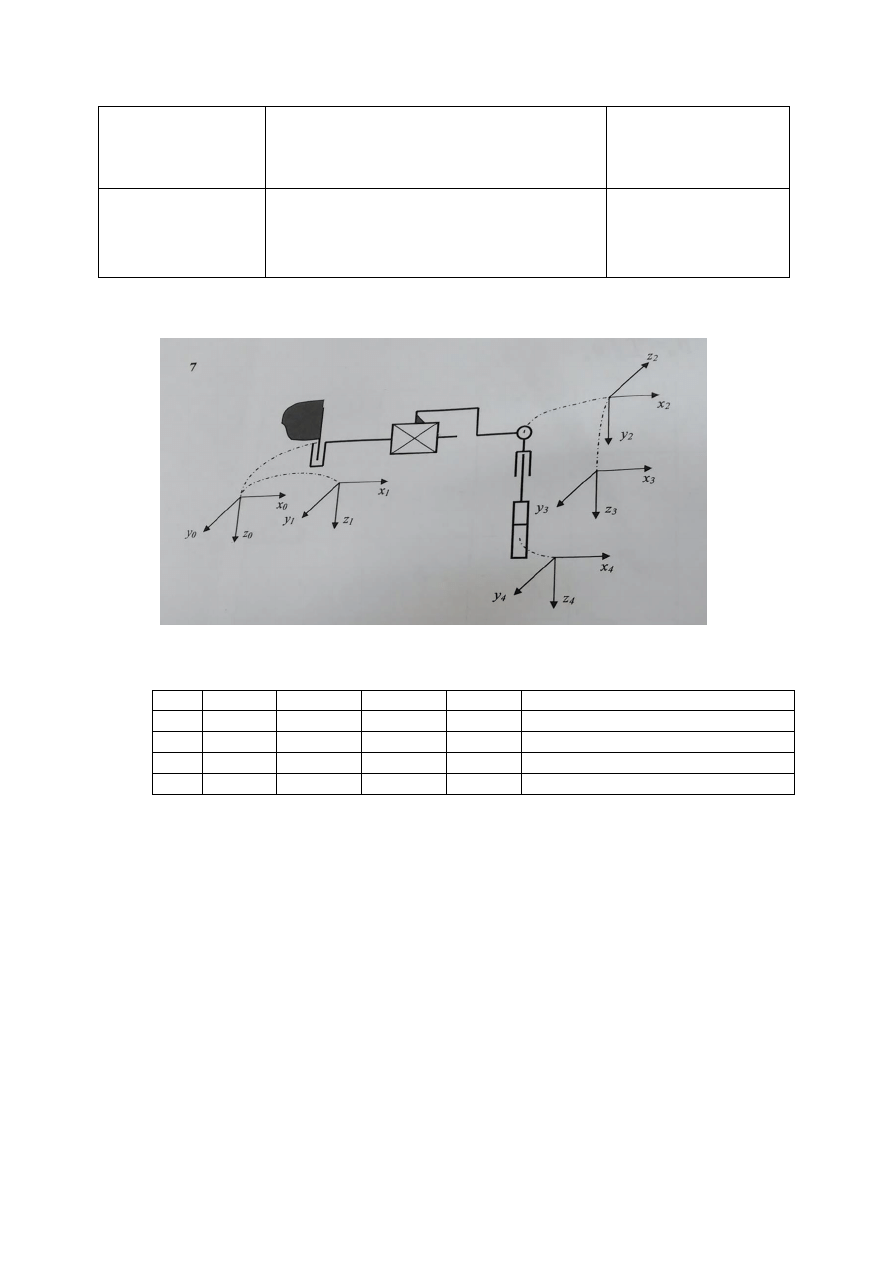
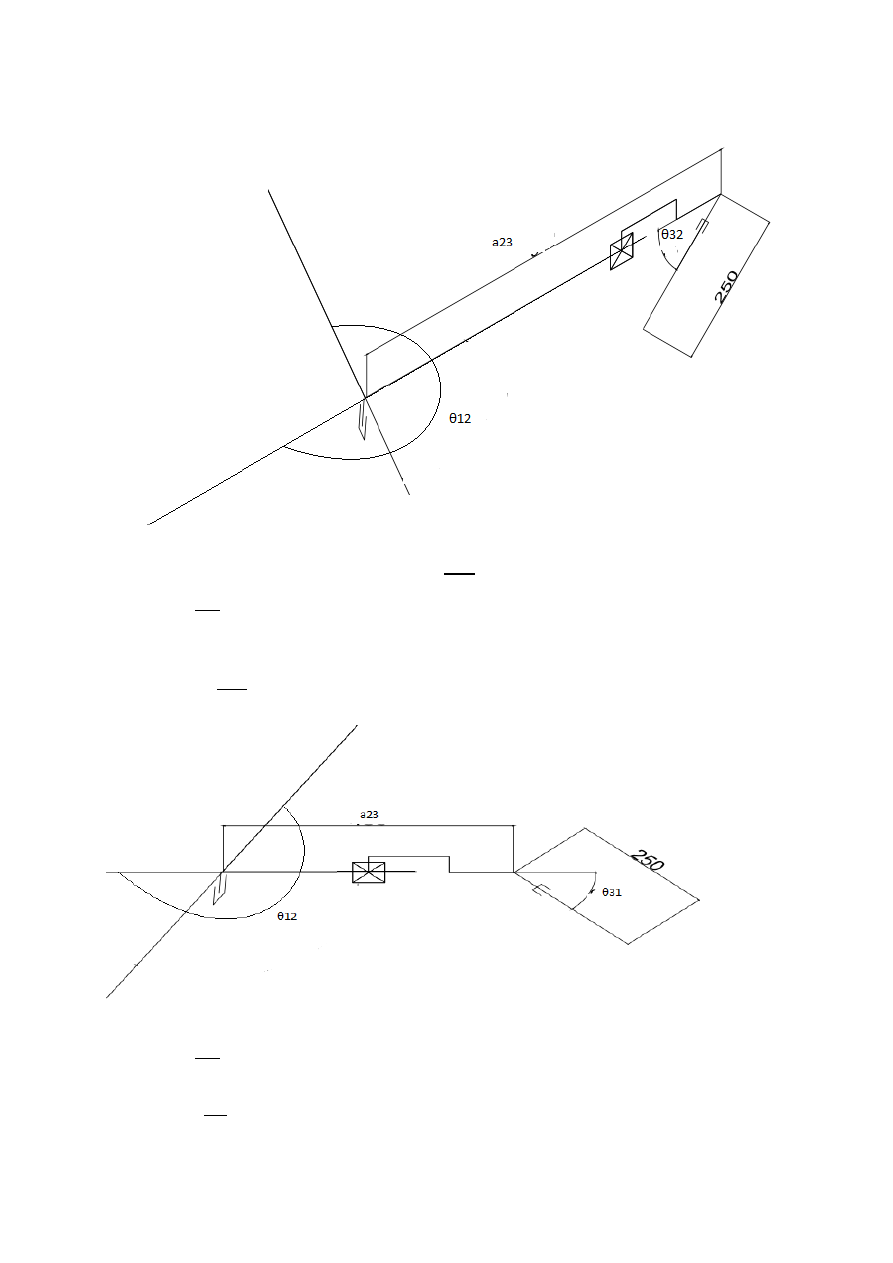
1. Schemat kinematyczny manipulatora

2. Tabela parametrów modelu geometrycznego:

Nr

θ

i

d

i

a

i

α

i

Zakresy wartości zmiennych

1.

θ

1v

0

0

0

± 180 [

O

]

2.

0

0

a

2v

90

O

300 ÷ 600[mm]

3.

θ

3v

0

0

-90

O

± 90 [

O

]

4.

θ

4v

d

4

0

0

± 90 [

O

]

Wartości stałe:
d

4

=0.250 [m]

Przyjęte wartości zmiennych (z uwagi na występowanie we wcześniejszym doborze wartości 90
stopni, zmieniono wartości współrzędnych złącowych):
θ

1v

= 60 [

O

], a

2v

=0.450 [m], θ

3v

=-45 [

O

], θ

4v

=-45 [

O

]

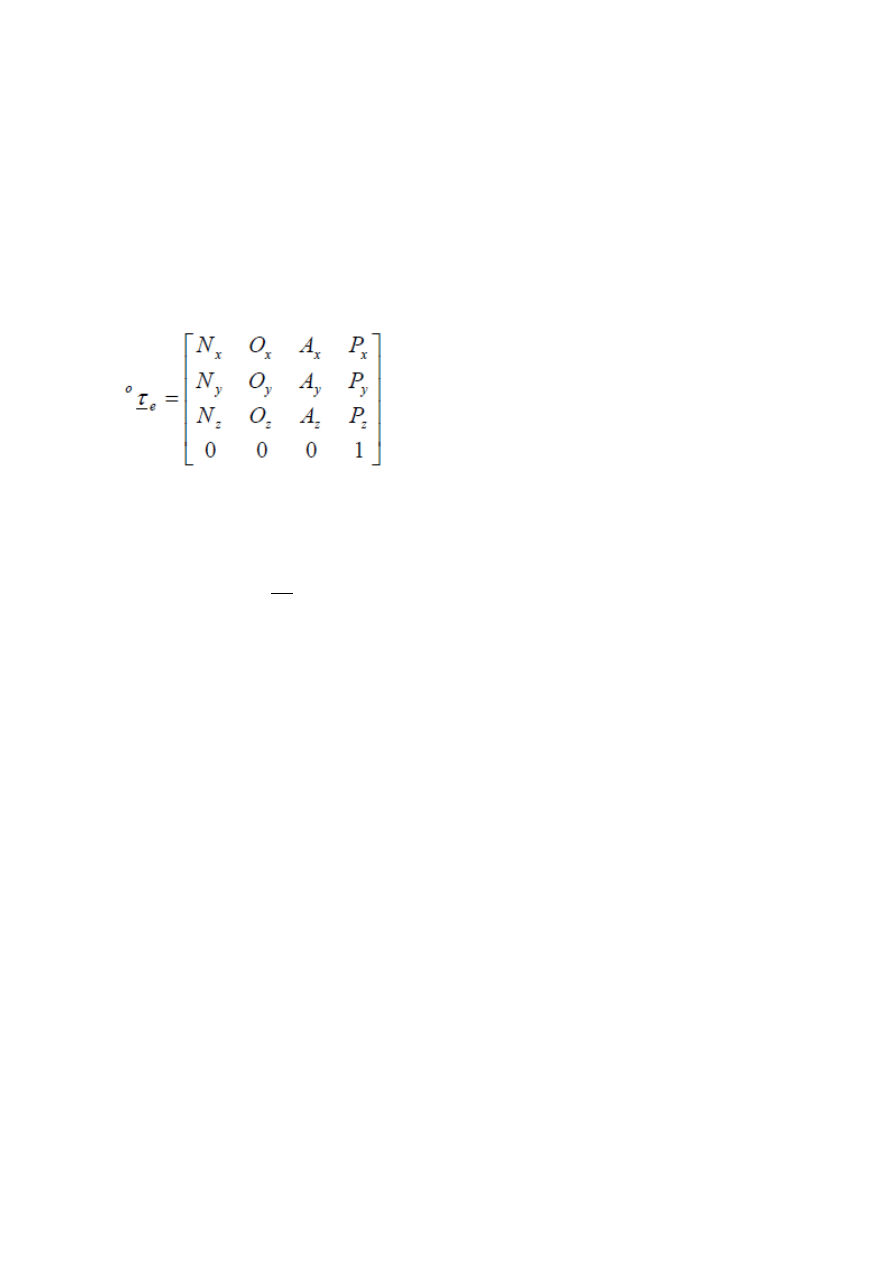
Z1.

Macierz otrzymana w wyniku z poprzednich zajęć:

𝑇

4

0

= [

𝐶1 ∗ 𝐶3 ∗ 𝐶4 − 𝑆1 ∗ 𝑆4 − 𝐶4 ∗ 𝑆1 − 𝐶1 ∗ 𝐶3 ∗ 𝑆4 −𝐶1 ∗ 𝑆3 𝐶1 ∗ (𝑎2 − 𝑆3 ∗ 𝑑4)

𝐶1 ∗ 𝑆4 + 𝐶3 ∗ 𝐶4 ∗ 𝑆1

𝐶1 ∗ 𝐶4 − 𝐶3 ∗ 𝑆1 ∗ 𝑆4

−𝑆1 ∗ 𝑆3 𝑆1 ∗ (𝑎2 − 𝑆3 ∗ 𝑑4)

0. 𝐶4 ∗ 𝑆35

−𝑆3 ∗ 𝑆4

𝐶3

𝐶3 ∗ 𝑑4

0

0

0

1

]

jednocześnie znano położenie i orientacje ostatniego członu w postaci

Algorytm wyznaczania współrzędnych końca trzeciego członu.
Dane: Macierz T04 oraz stałe modelu geometrycznego.

Wyznaczenie wektora Pw

𝑃

𝑊

= [

𝐴𝑥

𝐴𝑦

𝐴𝑧

] ∗ |0| = [

0

0
0

]

Wyznaczenie wektora P

𝑃 = [

𝑃𝑥

𝑃𝑦

𝑃𝑧

]

Wyznaczenie wektora Pa

Pa = P – Pw = Pa

więc

𝑃

𝑎

= [

𝑃𝑎𝑥
𝑃𝑎𝑦
𝑃𝑎𝑧

] = P = [

𝑃𝑥

𝑃𝑦

𝑃𝑧

]

Zależności współrzędnych Pax , Pay , Paz końca 3-o członu od współrzędnych złączowych
otrzymane przy pomocy macierzy T04

Pax = C1*(a2 - S3*d4)

Pay = S1*(a2 - S3*d4)

Pax = C3*d4

Z trzeciego równania:

𝜃

3

= +

−

𝑎𝑟𝑐𝑐𝑜𝑠

𝑃𝑎𝑧

𝑑4

Podnosząc do kwadratu pierwsze i drugie równanie otrzymano:

𝑃𝑎𝑥

2

= 𝑎

2

2

∗ 𝑐𝑜𝑠

2

𝜃

1

− 2𝑎

2

∗ 𝑐𝑜𝑠

2

𝜃

1

∗ 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

+ 𝑑

4

2

∗ 𝑐𝑜𝑠

2

𝜃

1

∗ 𝑠𝑖𝑛

2

𝜃

3

𝑃𝑎𝑦

2

= 𝑎

2

2

∗ 𝑠𝑖𝑛

2

𝜃

1

− 2𝑎

2

∗ 𝑠𝑖𝑛

2

𝜃

1

∗ 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

+ 𝑑

4

2

∗ 𝑠𝑖𝑛

2

𝜃

1

∗ 𝑠𝑖𝑛

2

𝜃

3

Dodając oba równani otrzymano:

𝑃𝑎𝑦

2

+ 𝑃𝑎𝑥

2

= 𝑎

2

2

∗ (𝑠𝑖𝑛

2

𝜃

1

+ 𝑐𝑜𝑠

2

𝜃

1

) − 2𝑎

2

∗ (𝑠𝑖𝑛

2

𝜃

1

+ 𝑐𝑜𝑠

2

𝜃

1

) ∗ 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

+ 𝑑

4

2

∗ (𝑠𝑖𝑛

2

𝜃

1

+ 𝑐𝑜𝑠

2

𝜃

1

) ∗ 𝑠𝑖𝑛

2

𝜃

3

𝑃𝑎𝑦

2

+ 𝑃𝑎𝑥

2

= 𝑎

2

2

− 2𝑎

2

∗ 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

+ 𝑑

4

2

∗ 𝑠𝑖𝑛

2

𝜃

3

𝑃𝑎𝑦

2

+ 𝑃𝑎𝑥

2

= (𝑎

2

− 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

)

2

𝑎

2

= 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

+

−

√𝑃𝑎𝑦

2

+ 𝑃𝑎𝑥

2

Z równań pierwszego i drugiego:

𝜃

1

= arcsin (

𝑃𝑎𝑦

𝑎

2

− 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

)

𝜃

1

= arccos (

𝑃𝑎𝑥

𝑎

2

− 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

)

𝜃

1

= 𝑎𝑟𝑐𝑡𝑔

𝑃𝑎𝑦
𝑃𝑎𝑥

+ 𝑁 ∗ 𝜋

N=-1,0,1

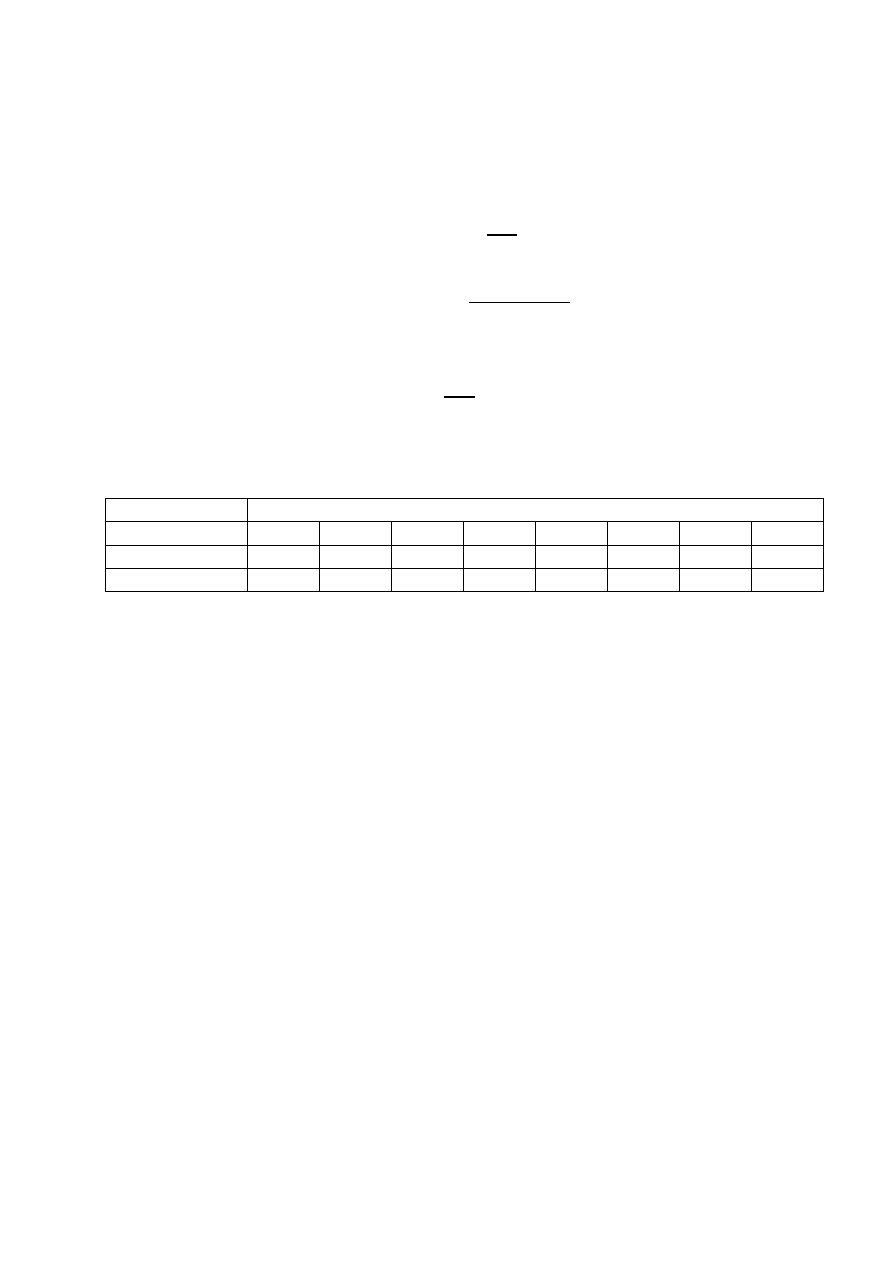
Z.2

Opis liczby rozwiązań zadania odwrotnego

Wyznaczone równania

𝜃

3

= +

−

𝑎𝑟𝑐𝑐𝑜𝑠

𝑃𝑎𝑧

𝑑4

tworzy 2 rozwiązania

𝑎

2

= 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

+

−

√𝑃𝑎𝑦

2

+ 𝑃𝑎𝑥

2

tworzy 2 rozwiązania dla każdego θ3

𝜃

1

= 𝑎𝑟𝑐𝑡𝑔

𝑃𝑎𝑦
𝑃𝑎𝑥

+ 𝑁 ∗ 𝜋

tworzy 2 rozwiązania dla n=1 i n=0

8 rozwiązań

ROZWIĄZANIA

równanie dla θ3

θ31

θ31

θ31

θ31

θ32

θ32

θ32

θ32

równanie dla a2

a21

a21

a22

a22

a23

a23

a24

a24

równanie dla θ1

θ11

θ12

θ11

θ12

θ11

θ12

θ11

θ12

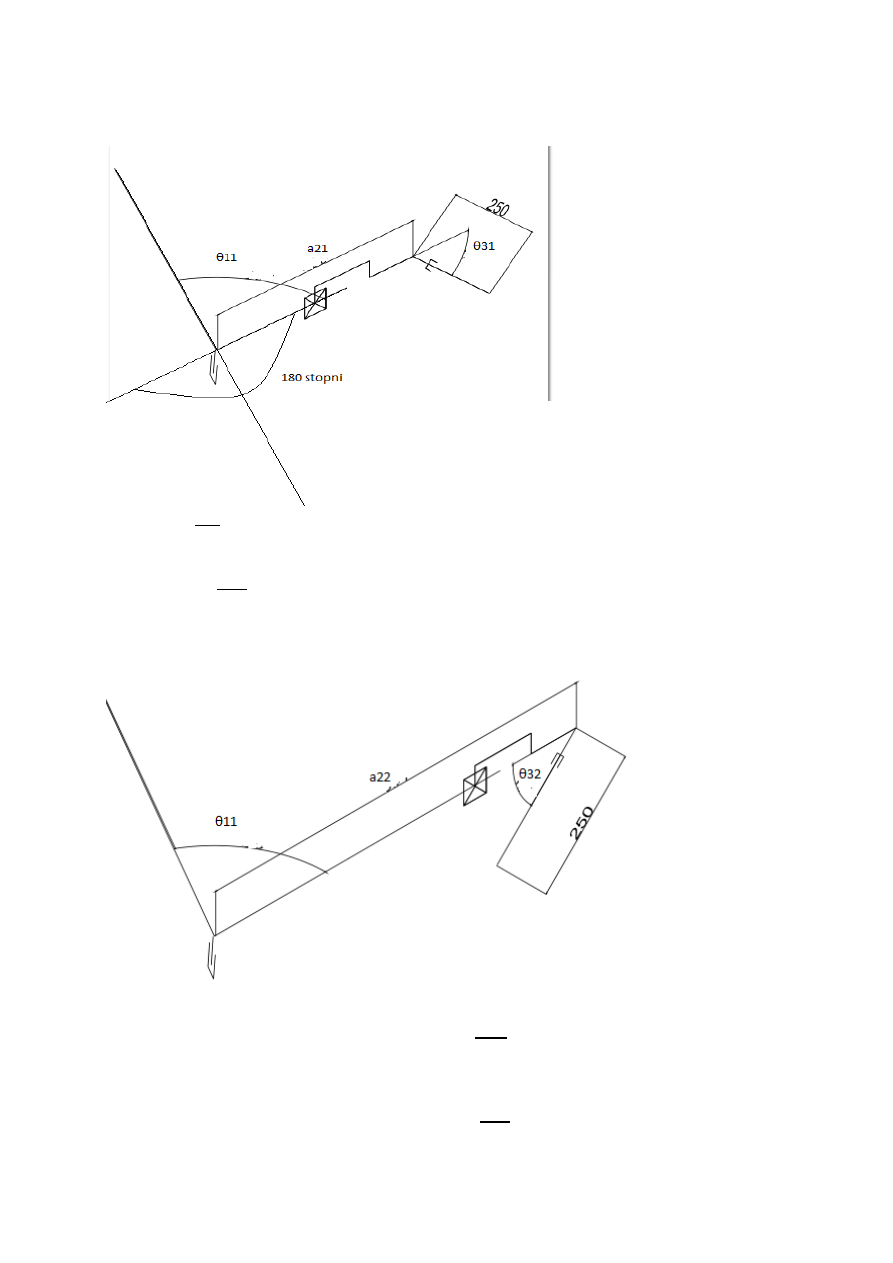
4 rozwiązania prawidłowe

𝜃

1

= 𝑎𝑟𝑐𝑡𝑔

𝑃𝑎𝑦
𝑃𝑎𝑥

a21>0

𝜃

3

= −𝑎𝑟𝑐𝑐𝑜𝑠

𝑃𝑎𝑧

𝑑4

Jedyne rozwiązanie znajdujące się w zakresie ruchu.

𝜃

1

= 𝑎𝑟𝑐𝑡𝑔

𝑃𝑎𝑦
𝑃𝑎𝑥

a22>0

𝜃

3

= 𝑎𝑟𝑐𝑐𝑜𝑠

𝑃𝑎𝑧

𝑑4

𝜃

1

= 𝑎𝑟𝑐𝑡𝑔

𝑃𝑎𝑦
𝑃𝑎𝑥

+ 𝑁 ∗ 𝜋

𝜃

1

= 𝑎𝑟𝑐𝑡𝑔

𝑃𝑎𝑦
𝑃𝑎𝑥

− 𝜋

a23<0

𝜃

3

= −𝑎𝑟𝑐𝑐𝑜𝑠

𝑃𝑎𝑧

𝑑4

𝜃

1

= 𝑎𝑟𝑐𝑡𝑔

𝑃𝑎𝑦
𝑃𝑎𝑥

− 𝜋

a24<0

𝜃

3

= 𝑎𝑟𝑐𝑐𝑜𝑠

𝑃𝑎𝑧

𝑑4

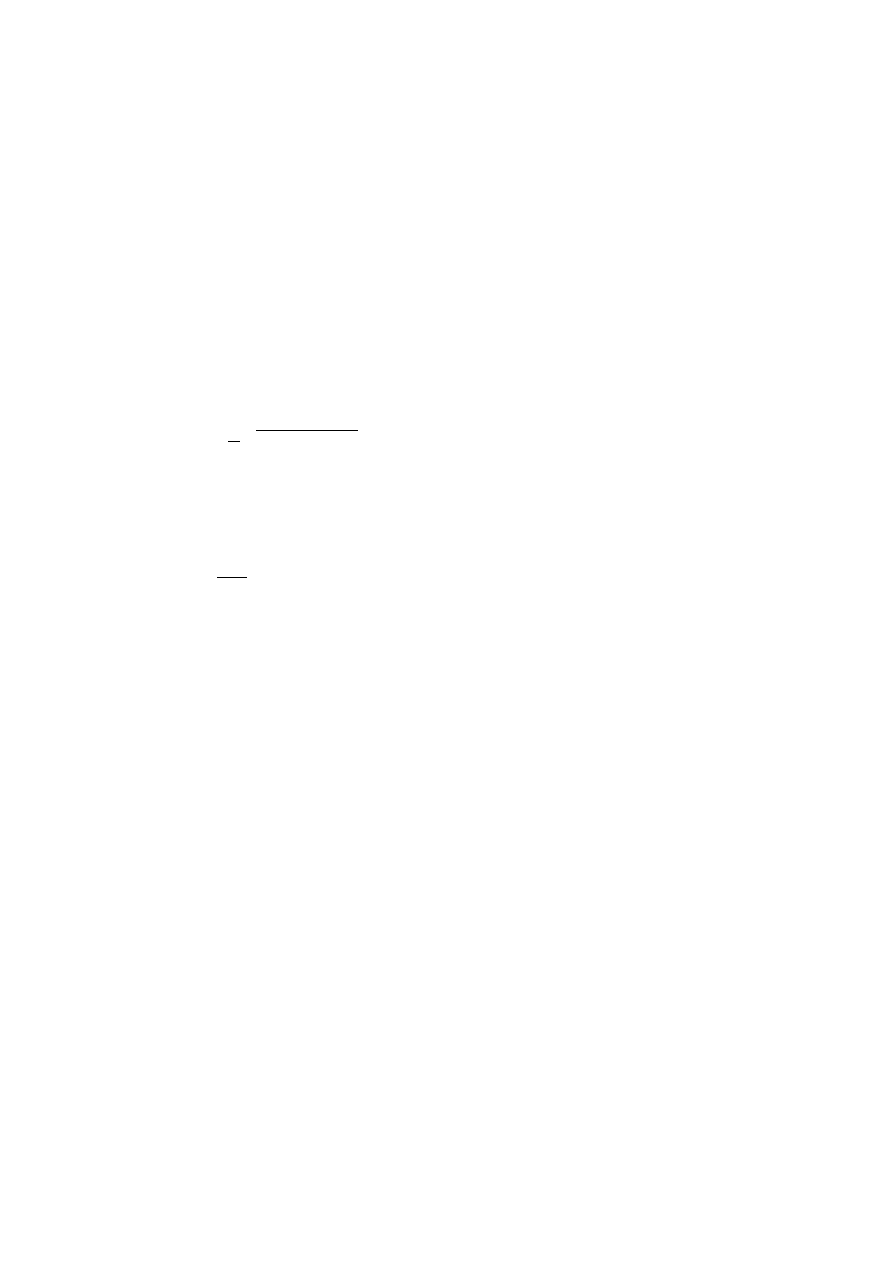
Z.3

Warunki istnienia rozwiązania

Z3.1

Pax = 0

Pay = 0

Tg(0/0) = Tg (Pay/Pax) Nieskończona liczba rozwiązań ; kąt th1 może być dowolny
Ponieważ w takim przypadku a2=d4 a d4>0,25 [m] więc nie można osiągnąć tego rozwiązania,
znajduje się ono poza zakresem ruchu

Z3.2

𝑎

2

= 𝑑

4

∗ 𝑠𝑖𝑛𝜃

3

+

√𝑃𝑎𝑦

2

+ 𝑃𝑎𝑥

2

Rozwiązanie a2 zawsze istnieje

Z3.3

𝜃

3

= +

−

𝑎𝑟𝑐𝑐𝑜𝑠

𝑃𝑎𝑧

𝑑4

Rozwiązanie th3 zawsze istnieje ponieważ d4>0.

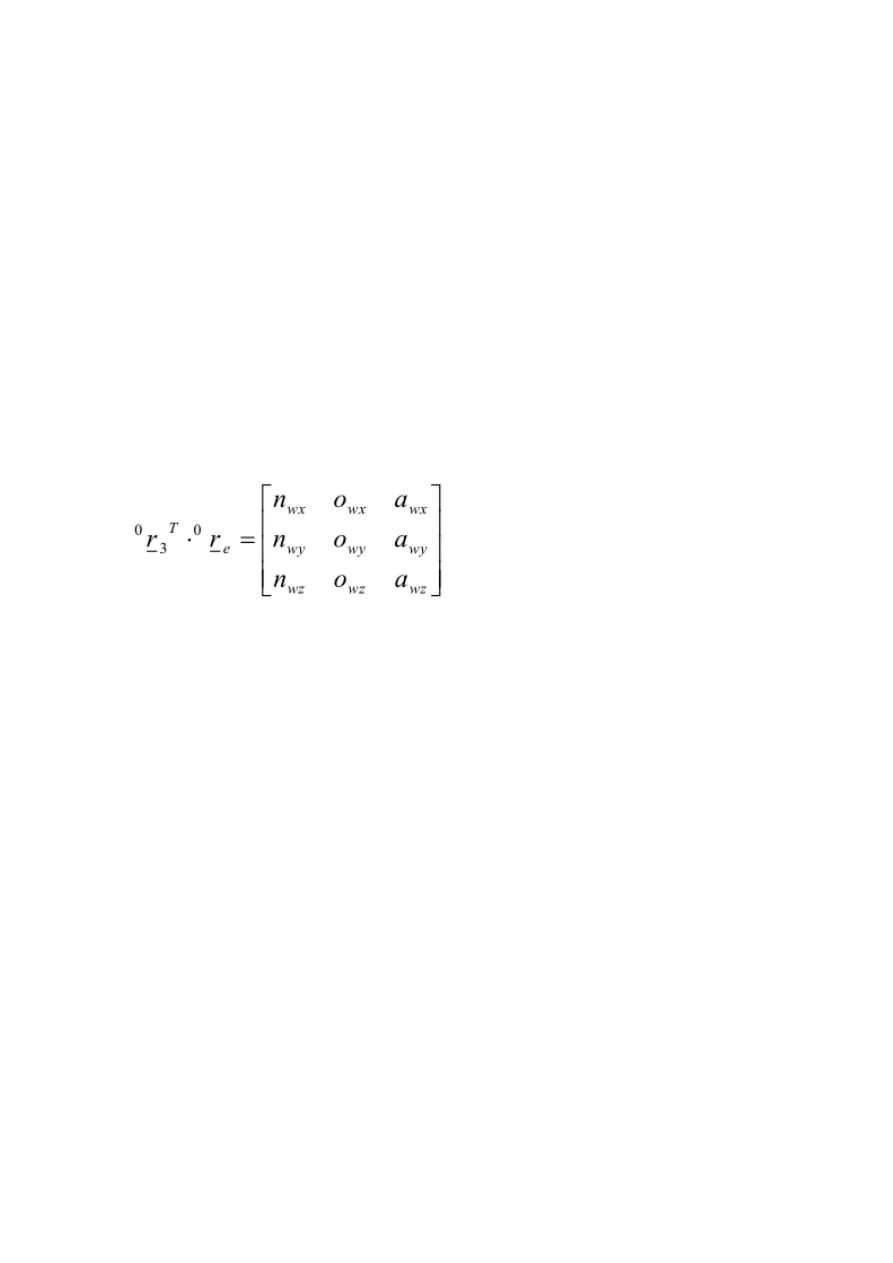
Z.4

Z poprzednich zajęć:

R3e=[

cos(th4) − sin(th4) 0

sin(th4) cos(th4) 0

0 0 1

]

𝑅04 = [

0,8624 −0,3624 03536

0,0795 0,7866 0,6124

−0,5 −0,5 0,7071

]

𝑅03 = [

cos(th1) ∗ cos(th3) − sin(th1) − cos(th1) ∗ sin(th3)

cos(th3) ∗ sin(th1) cos(th1) − sin(th1) ∗ sin(th3)

in(th3) 0 cos(th3)

]

Korzystając z matlaba:

R3e = transpose(R03)*R04

R3e =

0.7071 0.7071 0.0000

-0.7071 0.7071 0.0000

0 -0.0000 1.0000

Otrzymano równania:

cos(𝑡ℎ4) = 0,7071

sin(𝑡ℎ4) = −0,7071

Z powyższych równań:

th4 = - π/4

Z.5

Kod wykonany w matlabie:

syms

th1

a2

th3

%macierz pobrana z poprzednich zajęć

T04 =[ cos(th1)*cos(th3)*cos(th4) - sin(th1)*sin(th4), - cos(th4)*sin(th1)
- cos(th1)*cos(th3)*sin(th4), -cos(th1)*sin(th3), a2*cos(th1) -
d4*cos(th1)*sin(th3);

cos(th1)*sin(th4) + cos(th3)*cos(th4)*sin(th1), cos(th1)*cos(th4) -
cos(th3)*sin(th1)*sin(th4), -sin(th1)*sin(th3), a2*sin(th1) -
d4*sin(th1)*sin(th3);

cos(th4)*sin(th3),
-sin(th3)*sin(th4), cos(th3), d4*cos(th3);

0,
0, 0, 1]

%macierz z wynikami

T04w =[ (2^(1/2)*3^(1/2))/4 + 1/4, 1/4 - (2^(1/2)*3^(1/2))/4,
2^(1/2)/4, 2^(1/2)/16 + 9/40;

3^(1/2)/4 - 2^(1/2)/4, 2^(1/2)/4 + 3^(1/2)/4, (2^(1/2)*3^(1/2))/4,
(2^(1/2)*3^(1/2))/16 + (9*3^(1/2))/40;

-1/2, -1/2, 2^(1/2)/2,
2^(1/2)/8;

0, 0, 0,
1]

%zadeklarowanie użytej stałej

d4=0.25;

%z uwagi na P=[0;0;0], Pa=P

%przypisanie poszczególnym liczbom wartości z macierzy

pax=T04w(1,4)

pay=T04w(2,4)

paz=T04w(3,4)

% obliczanie rozwiązań

rozw=solve(pax==T04(1,4),pay==T04(2,4),paz-T04(3,4),th1,a2,th3)

%Wywołanie otrzymanych wyników

Rth1=rozw.th1

Ra2=rozw.a2

Rth3=rozw.th3

W wyniku otrzymano:

Rozwiązania

th1 (stopnie)

a2 [m]

th3(stopnie)

1

-120

-0,8036

-45

2

60

0,45

-45

3

-120

-0,45

45

3

60

0,8036

45

W celu sprawdzenia obliczeń, do macierzy wyznaczonej na poprzednich zajęciach
podstawiono wynik i porównano go z otrzymanym na poprzednich zajęciach.

Z.6

Rozwiązyjąc numerycznie wykorzystano funkcję „vpasolve”

% obliczanie rozwiązań

ro_numero=vpasolve(pax==T04(1,4),pay==T04(2,4),paz==T04(3,4),t
h1,a2,th3)

%Wywołanie otrzymanych wyników

R_n_th1=ro_numero.th1
R_n_a2=ro_numero.a2
R_n_th3=ro_numero.th3

Otrzymany wynik:

R_n_th1 =1.0471975511965977352760098566071

R_n_a2 =0.45000000000000003913244479732864

R_n_th3 =-0.78539816339744830961566084581988

Wszystkie wartości są praktycznie takie same jak założone I otrzymane we wcześniejszych
rozwiązaniach. Różnice występują, ale są pomijalne. Funkcja służąca do wyznaczania
wyników numerycznie przedstawia tylko jeden wynik, w tym przypadku zgodny z
oczekiwanymi wartościami.