Patrycja Grabowska
Weronika Hasslinger

Kinematyka i Dynamika Układów

Mechatronicznych

Laboratorium nr 5

Sprawozdanie

Prowadzący:
dr inż. Jarosław Bednarz

IMIR, Mechatronika,
Projektowanie
Mechatroniczne,
Gr. nr 7

Temat: Dynamika – formułowanie

dynamicznych równań ruchu
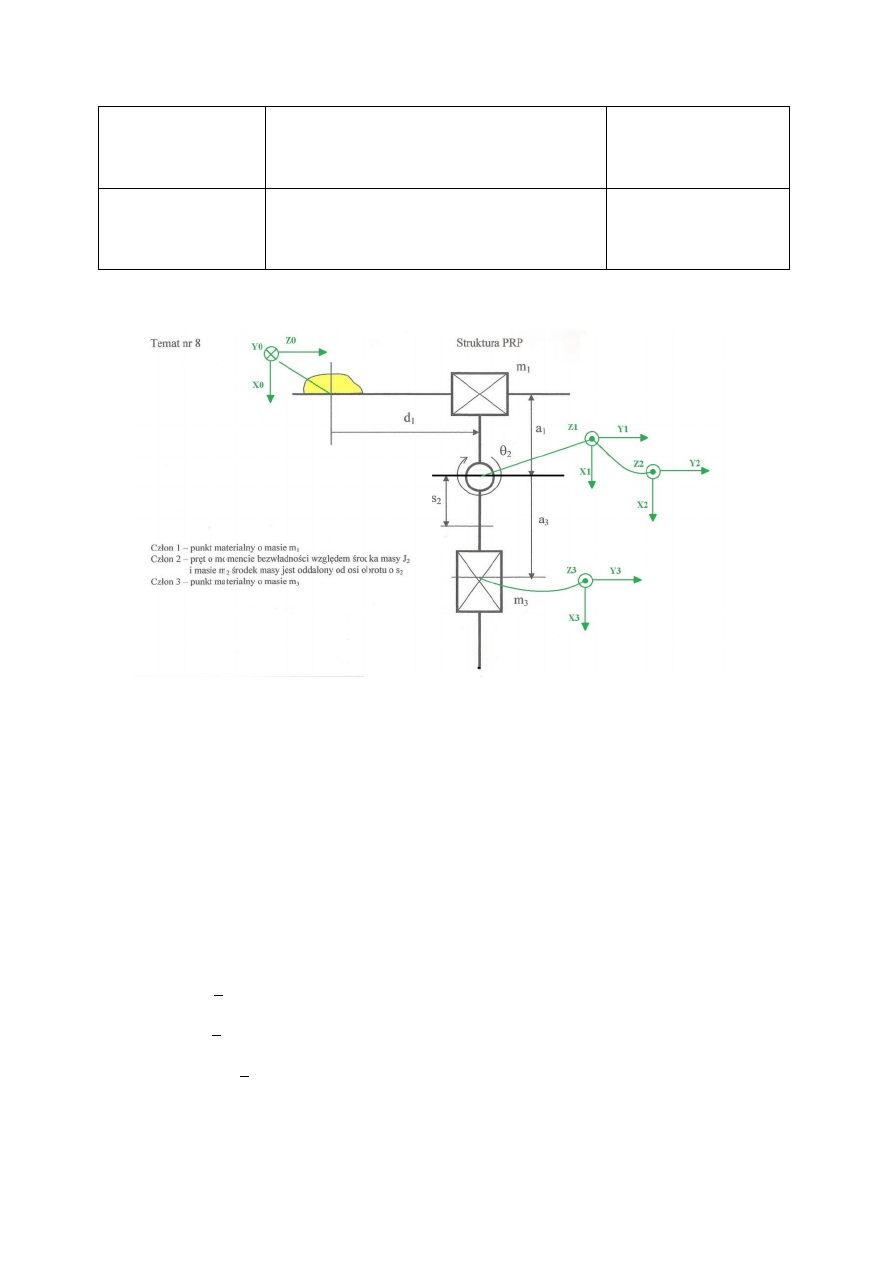
Temat nr 8

Data zajęć:
9.04.2015r.

1. Model

2. Określenie przestrzennego rozkładu masy

Energia potencjalna jest obliczana względem płaszczyzny Y

0

Z

0

.

2.1. Dla członu 1.:

J

1yy

= 𝑚

1

∗ 𝑎

1

2

J

1zz

= 𝑚

1

∗ 𝑎

1

2

𝑚

1

∗ 𝑥

1

= −𝑚

1

∗ 𝑎

1

J

1

=

[

𝑚

1

∗ 𝑎

1

2

0

0

−𝑚

1

∗ 𝑎

1

0

𝑚

1

∗ 𝑎

1

2

0

0

0

0

𝑚

1

∗ 𝑎

1

2

0

−𝑚

1

∗ 𝑎

1

0

0

𝑚

1

]

2.2. Dla członu 2.:

J

2yy

=

4
3

𝑚

2

∗ 𝑠

2

2

J

2zz

=

4
3

𝑚

2

∗ 𝑠

2

2

𝑚

2

∗ 𝑥

2

=

1
2

𝑚

2

∗ 𝑠

2

J

2

=

[

4
3

𝑚

2

∗ 𝑠

2

2

0

0

1
2

𝑚

2

∗ 𝑠

2

0

4
3

𝑚

2

∗ 𝑠

2

2

0

0

0

0

4
3

𝑚

2

∗ 𝑠

2

2

0

1
2

𝑚

2

∗ 𝑠

2

0

0

𝑚

2

]

2.3. Dla członu 3.:

J

2

= [

0 0 0

0

0 0 0

0

0 0 0

0

0 0 0

𝑚

3

]

3. Określenie energii kinetycznej i potencjalnej członów mechanizmu

3.1. Człon 1- ruch postępowy:

𝑣

1

= 𝑑

1

̇

𝐸

𝐾1

=

1
2

𝑚

1

𝑑

1

̇

2

𝐸

𝑃1

= 0

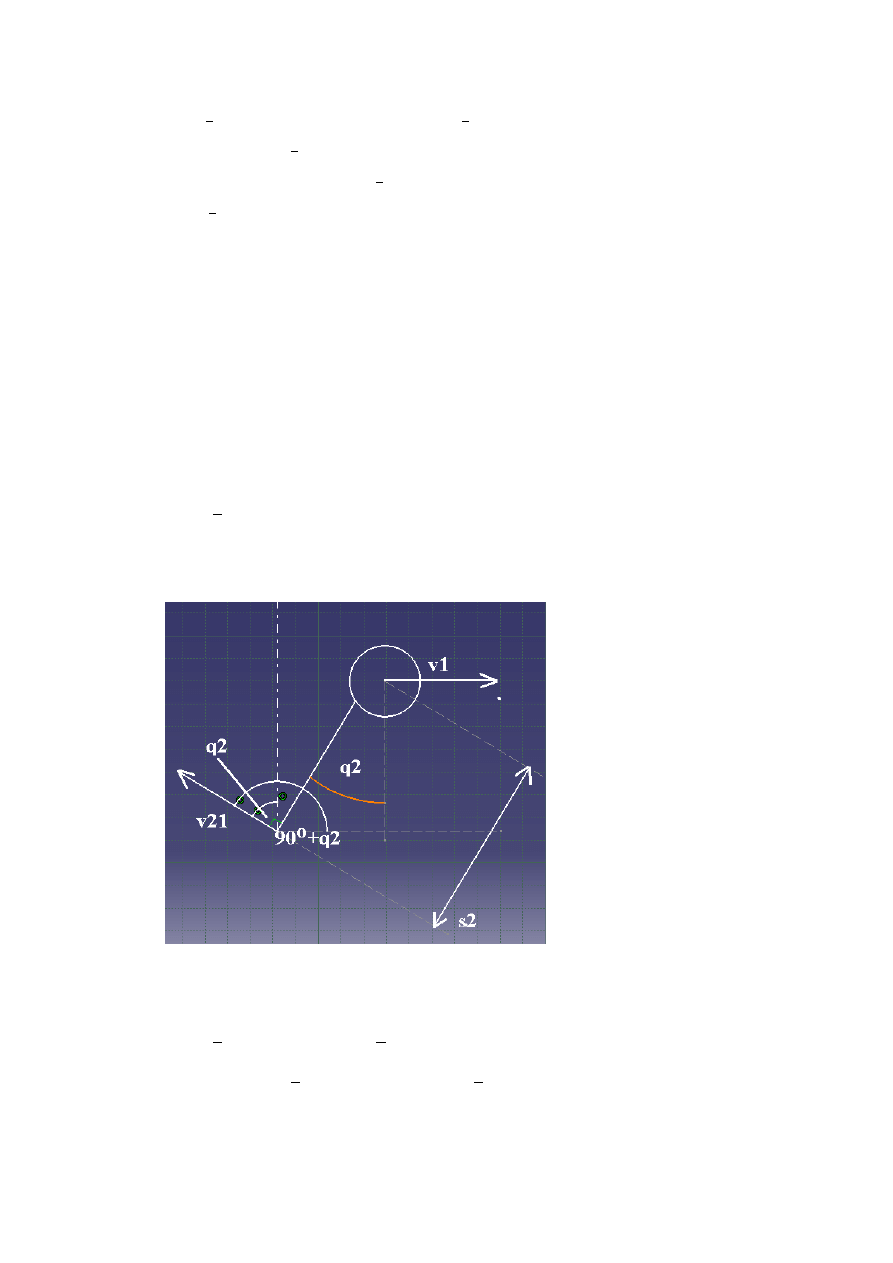
3.2. Człon 2- ruch płaski:

𝑣

2

̅̅̅ = 𝑣

1

̅̅̅ + 𝑣

21

̅̅̅̅

𝑣

21

= 𝜃

2

̇ ∗ 𝑠

2

𝑣

2

2

= 𝑣

1

2

+ 𝑣

21

2

− 2 ∗ 𝑣

1

∗ 𝑣

21

∗ cos

2

𝜃

2

= 𝑑

1

̇

2

+ 𝜃

2

̇

2

∗ 𝑠

2

2

− 2 ∗ 𝑑

1

̇ ∗ 𝜃

2

̇ ∗ 𝑠

2

∗ cos 𝜃

2

𝐸

𝐾2

=

1
2

(𝐼

2

+ 𝑚

2

∗ 𝑠

2

2

) ∗ 𝜃

2

2

̇ +

1
2

∗ 𝑚

2

∗ (𝑑

1

̇

2

+ 𝜃

2

̇

2

∗ 𝑠

2

2

− 2 ∗ 𝑑

1

̇ ∗ 𝜃

2

̇ ∗ 𝑠

2

∗ cos 𝜃

2

)

=

1
2

𝐼

2

∗ 𝜃

2

2

̇ + 𝑚

2

∗ 𝑠

2

2

∗ 𝜃

2

2

̇ +

1
2

∗ 𝑚

2

∗ 𝑑

1

̇

2

− 𝑚

2

∗ 𝑑

1

̇ ∗ 𝜃

2

̇ ∗ 𝑠

2

∗ cos 𝜃

2

𝐸

𝑃2

= −𝑚

2

∗ 𝑔 ∗ 𝑎

1

− 𝑚

2

∗ 𝑔 ∗ 𝑠

2

∗ cos 𝜃

2

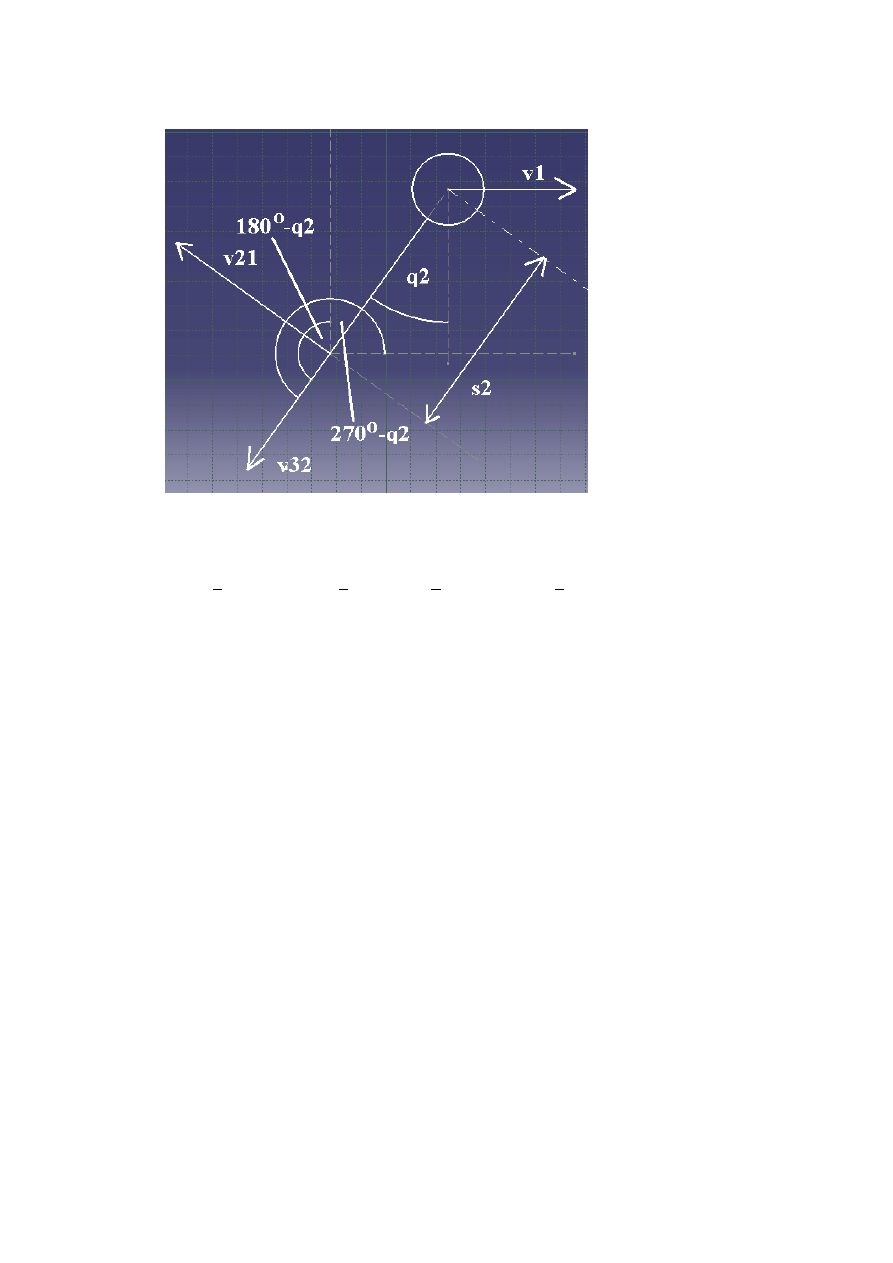
3.3. Człon 3- ruch płaski:

𝑣

3

̅̅̅ = 𝑣

2

̅̅̅ + 𝑣

32

̅̅̅̅

𝑣

32

= 𝑎

3

̇

𝑣

3

2

= 𝑑

1

̇

2

+ 𝜃

2

̇

2

∗ 𝑠

2

2

+ 𝑎

3

2

̇ − 2 ∗ 𝑑

1

̇ ∗ 𝜃

2

̇ ∗ 𝑠

2

∗ cos 𝜃

2

+ 2 ∗ 𝑑

1

̇ ∗ 𝑎

3

̇ ∗ sin 𝜃

2

𝐸

𝐾3

=

1
2

𝑚

3

∗ 𝑎

3

2

∗ 𝜃

2

2

̇ +

1
2

𝑚

3

∗ 𝑑

1

̇

2

+

1
2

𝑚

3

∗ 𝜃

2

̇

2

∗ 𝑠

2

2

+

1
2

𝑚

3

∗ 𝑎

3

2

̇ − 𝑚

3

∗ 𝑑

1

̇ ∗ 𝜃

2

̇ ∗ 𝑠

2

∗ cos 𝜃

2

+ 𝑚

3

∗ 𝑑

1

̇ ∗ 𝑎

3

̇ ∗ sin 𝜃

2

𝐸

𝑃3

= −𝑚

3

∗ 𝑔 ∗ 𝑎

1

−𝑚

3

∗ 𝑔 ∗ 𝑎

3

∗ cos 𝜃

2

4.

Skrypt utworzony w Matlabie:

% formulowanie rownan dynamicznych ruchu

% dla struktury kinematycznej PRP

clear

all

clc
syms

Ek1

Ek2

Ek3

Ek

m1

a1

J2

m2

s2

m3

q1

q2

q3

dq1

dq2

dq3

real

syms

Ep1

Ep2

Ep3

g

real

syms

L

t

ddq1

ddq2

ddq3

S1

S2

S3

S4

real

%człon 1

Ek1=1/2*m1*((dq1)^2+(0)^2)
Ep1=0

% człon 2

Ek2=1/2*(J2+ m2*s2^2)*dq2^2 + 1/2*m2*((dq1+
dq2*s2*cos(sym(pi)-q2))^2+(dq2*s2*cos(sym(pi/2)-q2))^2)
Ep2=-m2*g*(a1+s2*cos(q2))

%człon 3

Ek3=1/2*(m3*q3^2)*dq2^2 + 1/2*m3*((dq1+ dq2*s2*cos(sym(pi)-
q2)+dq3*cos(sym(3/2*pi)-q2))^2+(dq2*s2*cos(sym(pi/2)-
q2)+dq3*cos(sym(pi)-q2))^2)
Ep3=-m3*g*(a1+q3*cos(q2))

%energia kinetyczna

Ek=simplify(Ek1+Ek2+Ek3)

% energia potencjalna

Ep=simplify(Ep1+Ep2+Ep3)

% potencjal kinetyczny L

L=Ek-Ep;

% rownania Lagrange’a drugiego rodzaju

% pochodna L wzgledem dqi i=1,2,3

f11=diff(L,

'dq1'

);

f21=diff(L,

'dq2'

);

f31=diff(L,

'dq3'

);

% wprowadzenie zmiennej czasowej t

S1={

'q1'

,

'q2'

,

'q3'

,

'dq1'

,

'dq2'

,

'dq3'

};

S2={

'q1(t)'

,

'q2(t)'

,

'q3(t)'

,

'dq1(t)'

,

'dq2(t)'

,

'dq3(t)'

};

f12=subs(f11,S1,S2);
f22=subs(f21,S1,S2);
f32=subs(f31,S1,S2);

% pochodna fi2 wzgledem t - czasu i=1,2,3

f13=diff(f12,

't'

);

f23=diff(f22,

't'

);

f33=diff(f32,

't'

);

% ujednolicenie oznaczen i usuniecie zmiennej t

S3={

'diff(q1(t),t)'

,

'diff(q2(t),t)'

,

'diff(q3(t),t)'

,

'diff(dq

1(t),t)'

,

'diff(dq2(t),t)'

,

'diff(dq3(t),t)'

};

S4={

'dq1'

,

'dq2'

,

'dq3'

,

'ddq1'

,

'ddq2'

,

'ddq3'

};

f14=subs(f13,S3,S4);
f24=subs(f23,S3,S4);
f34=subs(f33,S3,S4);
S5={

'dq1(t)'

,

'dq2(t)'

,

'dq3(t)'

};

S6={

'dq1'

,

'dq2'

,

'dq3'

};

f15=subs(f14,S5,S6);
f25=subs(f24,S5,S6);
f35=subs(f34,S5,S6);
S7={

'q1(t)'

,

'q2(t)'

,

'q3(t)'

};

S8={

'q1'

,

'q2'

,

'q3'

};

r11=subs(f15,S7,S8);
r21=subs(f25,S7,S8);
r31=subs(f35,S7,S8);

% pochodna L wzgledem qi i=1,2,3

r12=diff(L,

'q1'

);

r22=diff(L,

'q2'

);

r32=diff(L,

'q3'

);

% zestawienie prawej stony rownan dynamicznych ruchu

r1=simplify(r11-r12)
r2=simplify(r21-r22)
r3=simplify(r31-r32)

5. Wyprowadzone równania dynamiczne ruchu w postaci macierzowej oraz charakterystyka

postaci i składników tych równań:

[

𝑓

1

𝜏

2

𝑓

3

] = [

𝑚

1

+ 𝑚

2

+ 𝑚

3

−( 𝑚

2

+ 𝑚

3

) ∗ 𝑠

2

∗ 𝑐𝑜𝑠(𝜃

2

)

−𝑚

3

∗ 𝑠𝑖𝑛(𝜃

2

)

−( 𝑚

2

+ 𝑚

3

) ∗ 𝑠

2

∗ 𝑐𝑜𝑠(𝜃

2

) 𝐽

2

+ 𝑚

3

∗ 𝑎

3

2

+ (2 ∗ 𝑚

2

+ 𝑚

3

) ∗ 𝑠

2

2

0

−𝑚

3

∗ sin(𝜃

2

)

0

𝑚

3

]

∗ [

𝑑

1

̈

𝜃

2

̈

𝑎

3

̈

] + [

−𝜃

2

̇ ∗ 𝑎

3

̇ ∗ 𝑚

3

∗ 𝑐𝑜𝑠(𝜃

2

) + 𝜃

2

̇

2

∗ ( 𝑚

2

+ 𝑚

3

) ∗ 𝑠

2

∗ 𝑠𝑖𝑛(𝜃

2

)

(2 ∗ 𝜃

2

̇ ∗ 𝑎

3

+ 𝑑

1

̇ ∗ 𝑐𝑜𝑠(𝜃

2

)) ∗ 𝑎

3

̇ ∗ 𝑚

3

−𝑚

3

∗ 𝜃

2

̇ (𝑎

3

∗ 𝜃

2

̇ + 𝑑

1

̇ ∗ cos (𝜃

2

))

]

+ [

0

(𝑚

3

∗ 𝑎

3

+ 𝑚

2

∗ 𝑠

2

) ∗ 𝑠𝑖𝑛(𝜃

2

)

−𝑚

3

∗ cos(𝜃

2

)

] ∗ 𝑔

gdzie:
𝑚

1

, 𝑚

2

, 𝑚

3

- masy członów 1, 2 i 3

𝑠

2

- odległość środka ciężkości członu 2 od osi obrotu w przegubie [m]

a

3

- odległość członu 3 od osi obrotu [m]

J

2

– moment bezwładności członu 2

θ

2

- przemieszczenie kątowe w członie 2

𝑑

1

̇ -prędkość liniowa członu 1względem bazowego układu współrzędnych

𝜃

2

̇ − prędkość kątowa członu względem lokalnego układu współrzędnych

𝑓

1

–siła przyłożona do członu nr 1 [N]

𝜏

2

- moment siły przyłożony do członu nr 2 [Nm]

𝑓

3

–siła przyłożona do członu nr 3 [N]

6. Wnioski:

6.1. Metoda Lagrange’a pozwala w szybki sposób wyznaczyć zewnętrzne siły i momenty sił

oddziaływujących na poszczególne człony.

6.2. Przedstawienie równań dynamiki w postaci macierzowej pozwala zaobserwować, jaki wpływ

ma prędkość i przyspieszenie oraz położenie danego członu na ruch pozostałych elementów
mechanizmu .

6.3. Energia potencjalna jest wielkością względną, zależy od przyjętego poziomu zerowego.