Kierunek: Informatyka
rok akademicki: 2009/2010
Semestr: 1
Grupa: 4

Nr ćwiczenia: 10

Bartosz Ogrodowicz

Busola stycznych

Indukcja magnetyczna:
Indukcja magnetyczna w fizyce wielkość wektorowa opisująca pole magnetyczne. Jest ona
określana przez siłę Lorentza, czyli siłę działającą na ładunek elektryczny poruszający się w polu
magnetycznym:

→

→

→

×

=

B

v

q

F

gdzie:

•

→

F

- siła działająca na ładunek elektryczny

•

q - ładunek elektryczny

•

→

v

prędkością

•

→

B

indukcja magnetyczna pola magnetycznego

Jednostką indukcji magnetycznej jest jedna tesla (1 T).
Skalarnie wzór ten można zapisać:

α

sin

qvB

F

=

gdzie α - kąt pomiędzy wektorem prędkości a wektorem indukcji.
Wartość indukcji magnetycznej jest równa sile działającej na ładunek jednego kulomba poruszający
się w polu magnetycznym z prędkością 1 metra na sekundę, prostopadle do jego linii sił, wówczas:

qv

F

B

=

Z powyższego wzoru dla natężenia prądu płynącego w prostoliniowym przewodzie wynika:

Is

F

B

=

Wtedy wartość indukcji magnetycznej jednorodnego pola magnetycznego wyrażać się będzie przez
siłę działającą na przewodnik o długości s = 1 m , przez który płynie prąd I = 1 A.
Z punktu widzenia matematycznego wektor indukcji magnetycznej jest pseudowektorem.

Natężenie pola magnetycznego:
Natężenie pola magnetycznego, H, wielkość wektorowa charakteryzująca pole magnetyczne,
definiowana poprzez prawo Biota-Savarta.

Natężenie pola magnetycznego związane jest z indukcją magnetyczną B równaniem:

I

B

H

−

=

0

µ

,

gdzie:

•

I - wektor namagnesowania

•

µo - przenikalność magnetyczna próżni.

Natężenie pola magnetycznego wyraża się w układzie Si w

m

A

(amper na metr), dawniej stosowaną

jednostką był ersted.

Pole magnetyczne wokół przewodnika z prądem, prawa: Ampera i Biota – Savarta:
W przestrzeni otaczającej przewodnik, przez który płynie prąd elektryczny, istnieje pole

magnetyczne.
Kierunek natężenia pola magnetycznego wytworzonego w jakimś punkcie przestrzeni otaczającej
bardzo krótki i prostoliniowy odcinek przewodnika, przez który płynie prąd jest prostopadły do
płaszczyzny przechodzącej przez dany punkt przestrzeni i dany odcinek przewodnika. Jest to prawo
Biota-Savarta. Natężenie tego pola zgodnie z tym prawem wynosi:

,

sin

4

2

α

π

⋅

=

r

dl

I

dH

gdzie:

•

I jest natężeniem prądu

•

dl – długość odcinka przewodnika

•

r – odległość między punktem, w którym rozpatruje się natężenie pola a środkiem odcinka
dl

•

α – kąt między odcinkiem dl i r.

Jeżeli przewodnik, przez który płynie prąd, ma kształt okręgu, natężenie pola magnetycznego, które
powstaje w środku tego okręgu, wyznacza się następująco. Każdy odcinek dl okręgu wytwarza
w środku tego okręgu pole o natężeniu:

2

4 r

dl

I

dH

π

=

Wartość natężenia pola w środku koła równa się:

2

4 r

dl

I

dH

π

=

∫

=

r

dl

r

I

H

π

π

2

0

2

4

r

I

H

2

=

Jeżeli zamiast pojedynczego przewodnika kołowego rozpatrujemy obwód złożony z N blisko siebie
położonych identycznych przewodników kołowych, które mają poprzeczne rozmiary (grubość
drutów
i izolacji) znikomo małe w stosunku do promienia koła, natężenie pola w środku okręgu wynosi:

,

2r

NI

H

=

gdy przez każdy przewodnik płynie prąd o natężeniu I (tzn. gdy są one połączone szeregowo,
stanowiąc poszczególne zwoje wspólnego uzwojenia).

Obecność pola magnetycznego można wykazać za pomocą swobodnie zawieszonej igły
magnetycznej, która ustawia się równolegle do kierunku pola. Jeżeli rozpatrywane poprzednio
uzwojenie kołowe ustawione jest pionowo i w jego środku zawieszona jest igła magnetyczna,
mająca swobodę obrotu w płaszczyźnie poziomej, to podczas przepływu prądu przez uzwojenie igła
ta ustawia się prostopadle do płaszczyzny uzwojenia. W tym przypadku na igłę magnetyczną działa
w płaszczyźnie poziomej tylko pole magnetyczne wytworzone przez uzwojenie kołowe. Jeżeli
jednocześnie igła magnetyczna poddana zostaje działaniu jeszcze jednego poziomego pola
magnetycznego, które posiada kierunek odmienny od kierunku pola magnetycznego wytworzonego
przez uzwojenie, igła ustawia się wzdłuż linii sił pola wypadkowego, powstałego w miejscu,
w którym się ona znajduje. Jeżeli oba wspomniane pola są prostopadłe do siebie, igła ustawia się
wzdłuż przekątnej prostokąta, którego boki są wektorami tych pól. Znając natężenie pola
magnetycznego H wytworzonego przez uzwojenie kołowe i kąt α, jaki tworzy igła z kierunkiem
prostopadłym do tego pola, można wyznaczyć wartość natężenia drugiego składowego pola.
Oznaczymy je przez H

z

w zależności:

α

tg

H

H

z

=

.

Przyrządem, który umożliwia porównanie natężenia tych dwóch pól magnetycznych jest busola
stycznych.

Pole magnetyczne Ziemi, inklinacja, deklinacja:
Pole magnetyczne ziemskie jest ukośne w stosunku do (poziomej) powierzchni Ziemi. Kąt, jaki
tworzy jego kierunek z płaszczyzną poziomą, nie jest więc prosty, a wartość tego kąta nazywamy
inklinacją magnetyczną w danym punkcie powierzchni kuli ziemskiej.

Natomiast deklinacja magnetyczna to odchylenie igły magnetycznej od kierunku północ-południe.
Wektor natężenia pola magnetycznego ziemskiego można rozłożyć na dwa wektory składowe:
poziomy i pionowy.
Jeżeli płaszczyzna uzwojenia busoli stycznych leży w płaszczyźnie południka magnetycznego
ziemskiego, to kierunek pola magnetycznego wytworzonego przez prąd płynący w uzwojeniu jest
prostopadły do kierunku pola magnetycznego ziemskiego. Pomiar kąta wychylenia igły α
umożliwia wyznaczenie składowej poziomej natężenia pola ziemskiego.
Oznaczając przez H

z

natężenie składowej poziomej, przez H – natężenie pola wytworzonego przez

uzwojenie otrzymujemy:

α

α

tg

r

NI

tg

H

H

z

2

=

=

Moment magnetyczny, dipol magnetyczny:
Moment magnetyczny jest własnością danego ciała opisującą pole magnetyczne wytwarzane przez
to ciało a tym samym i jego oddziaływanie z polem magnetycznym.
M=I*S
M- moment magnetyczny I- natężenie S- pole powierzchni
Z reguły mówi się o dipolowym momencie magnetycznym, choć można zaobserwować także
wyższą multipolowość momentu magnetycznego. Pole magnetyczne jest bezźródłowe, z czego
wynika, że nie istnieją monopole magnetyczne.
W fizyce kwantowej moment magnetyczny wyraża się w jednostkach zwanych magnetonem Bohra
(dla atomów) lub magnetonem jądrowym (dla jąder atomowych).

Mikroskopowy moment magnetyczny jest związany z ruchem orbitalnym naładowanej cząstki (co
można interpretować jak prąd płynący w przewodzącej pętli) lub ze spinem, przy czym należy
pamiętać, że moment magnetyczny to nie to samo co spin, choć jest z nim nierozerwalnie związany.

Dipol magnetyczny, układ 2 blisko siebie położonych różnoimiennych ładunków (mas)
magnetycznych; pole magnetyczne wytwarzane przez dipol magnetyczny nosi nazwę pola
dipolowego; wielkością charakteryzującą dipol magnetyczny jest dipolowy moment magnetyczny;
w skali mikroskopowej dipolem magnetycznym są cząstki elementarne o niezerowym spinie, w
skali makroskopowej — magnesy sztabkowe, kołowe obwody z prądem elektrycznym; swobodne
ładunki magnetyczne w przyrodzie nie występują.

-------------------------------------------------------------------------------------------------------

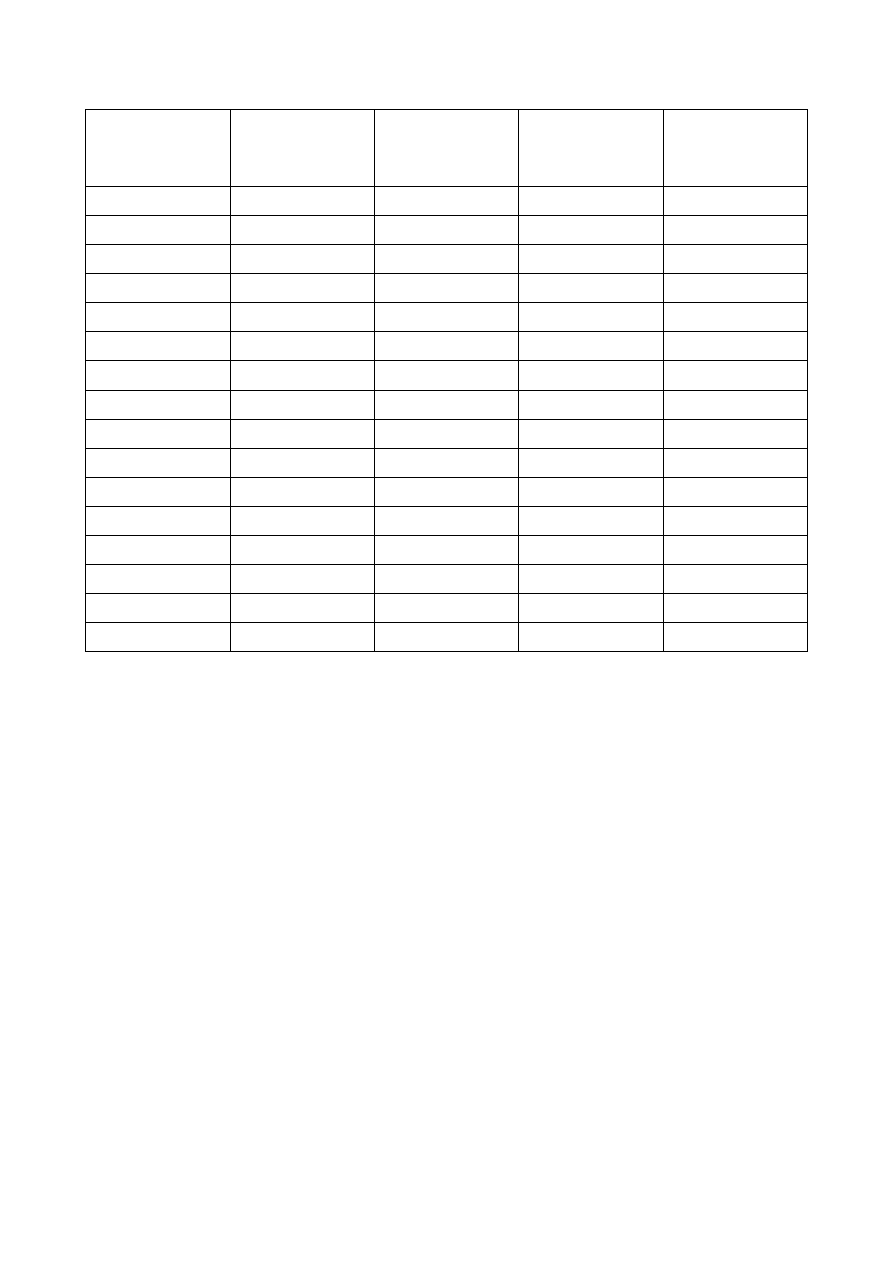
50 zwojów

Liczba zwojów

Napięcie [V]

Natężenie [A]

Wychylenie

Wartość składowej

poziomej ziemskiego

pola magnetycznego

[A/m]

50

0,5 V

76 A

71

87,15 A/m

50

0,5 V

76 A

68

102,35 A/m

50

0,6 V

84,3 A

72

91,30 A/m

50

0,7 V

102,3 A

75

91,37 A/m

50

0,7 V

102,3 A

74

97,78 A/m

50

0,8 V

110,5 A

76

91,84 A/m

50

0,8 V

110,5 A

77

85,04 A/m

50

0,9 V

131 A

78

92,82 A/m

50

1 V

140,3 A

79

90,91 A/m

50

1,1 V

155 A

80

91,10 A/m

50

1,1 V

155 A

81

81,83 A/m

50

1,2 V

163,7 A

81

86,43 A/m

50

1,3 V

176 A

80

103,45 A/m

50

1,3 V

176 A

81

92,92 A/m

500 zwojów

Liczba zwojów

Napięcie [V]

Natężenie [A]

Wychylenie

Wartość składowej

poziomej ziemskiego

pola magnetycznego

[A/m]

500

0,5 V

3,31 A

40

131,49 A/m

500

0,5 V

3,31 A

55

77,26 A/m

500

1 V

6,19 A

60

119,13 A/m

500

1 V

6,19 A

70

75,1 A/m

500

1,5 V

9 A

69

115,16 A/m

500

1,5 V

9 A

75

80,39 A/m

500

2 V

12,16 A

75

108,61 A/m

500

2 V

12,16 A

78

86,16 A/m

500

2,5 V

15 A

85

43,74 A/m

500

2,5 V

15 A

80

88,16 A/m

500

3 V

18,15 A

83

74,28 A/m

500

3 V

18,15 A

82

85,03 A/m

500

3,5 V

22,2 A

81

117,20 A/m

500

3,5 V

22,2 A

85

64,74 A/m

500

3,9 V

24,8 A

83

101,5 A/m

500

3,9 V

24,8 A

85

72,32 A/m

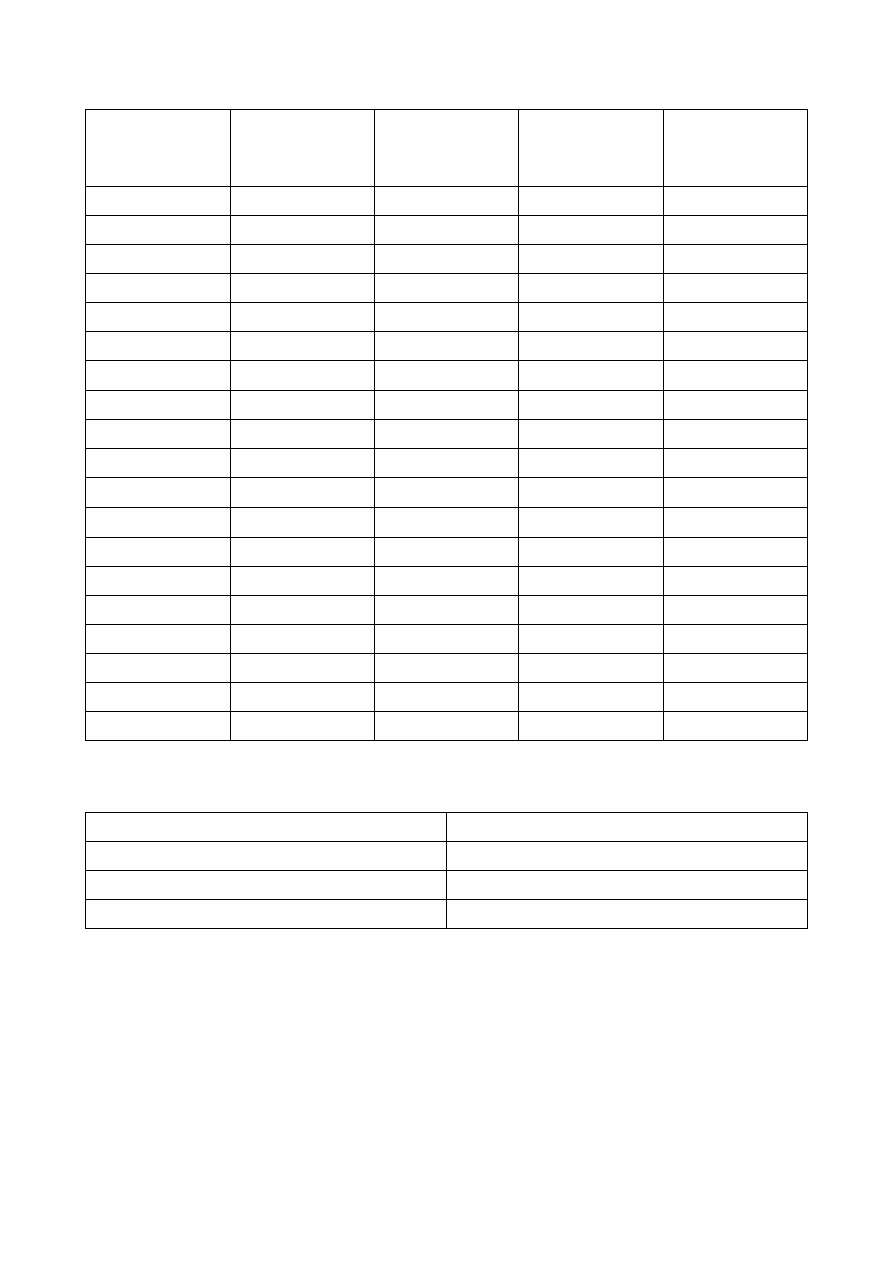
550 zwojów

Liczba zwojów

Napięcie [V]

Natężenie [A]

Wychylenie

Wartość składowej

poziomej ziemskiego

pola magnetycznego

[A/m]

550

0,5 V

2 A

37

55,29 A/m

550

0,5 V

2 A

38

57,27 A/m

550

0,9 V

3 A

50

92,29 A/m

550

0,9 V

3 A

57

71,39 A/m

550

1,2 V

4 A

50

123,05 A/m

550

1,2 V

4 A

57

95,19 A/m

550

1,8 V

8 A

60

169,25 A/m

550

1,8 V

8 A

65

136,69 A/m

550

3,3 V

11 A

72

131,08 A/m

550

3,3 V

11 A

77

93,17 A/m

550

4,2 V

14 A

75

137,57 A/m

550

4,2 V

14 A

78

109,34 A/m

550

4,8 V

16 A

76

146,08 A/m

550

4,8 V

16 A

81

92,69 A/m

550

5,1 V

17 A

72

202,58 A/m

550

5,1 V

17 A

82

87,89 A/m

550

5,7 V

19 A

89

11,34 A/m

550

6,6 V

22 A

83

99,22 A/m

550

6,6 V

22 A

85

70,18 A/m

-------------------------------------------------------------------------------------------------------

Liczba zwojów

Średnia

50

91,87785714

500

90,015875

550

104,3189474

Wniosek, analiza wyników:
Po wykonaniu danego mi ćwiczenia zaobserwowałem, że przy zmianie kierunku
prądu natężenia były inne ( wraz ze zmianą wychylenia ). Mogę przypuszczać, że
wpływ na to mogło mieć pole magnetyczne panujące w laboratorium tworzone przez
inne urządzenia, oraz stan techniczny przyrządu pomiarowego. W niektórym etapie
ćwiczenia wartości były zbliżone. Wartości są prawie zbliżone do tabelarycznych,
pomijając granicę błędu poprzez wymienione wcześniej przyczyny.