R E G U L A R A RT I C L E

The opportunity cost of social relations:
On the effectiveness of small worlds

Lorenzo Cassi

&

Lorenzo Zirulia

Published online: 16 October 2007

# Springer-Verlag 2007

Abstract The aim of this paper is to extend the theoretical literature on knowledge
and network structure by studying the use of social networks as a learning
mechanism. The novelty of this approach is suggested by the empirical evidence on
informal trading of know-how. In the model, we consider a set of actors who create
and diffuse knowledge with the aim of increasing their own personal knowledge.
They are located on a lattice (identifying the social space) and are directly connected
to a small number of other individuals. We assume that individuals can learn
individually or socially, and that individuals choose how to learn on the basis of a
cost-benefit comparison. Within this framework, we compare network structures in
terms of efficiency and equity. We find that the opportunity cost of using the network
affects its optimal structure in terms of aggregate performance and that the small
world does not emerge unambiguously as being the most efficient.

Keywords Knowledge . Networks . Small worlds . Diffusion . Learning

J Evol Econ (2008) 18:77

–101

DOI 10.1007/s00191-007-0073-5

A previous version of this paper has circulated under the title

“Social networks as option and the creation

and diffusion of knowledge

”. We thank participants in the I-NECK meeting, May 2004, Pompeu Fabra

University, Barcelona, the Druid PhD conference, January 2004, Aalborg, and a seminar at GREQAM,
Marseille, November, 2005, for useful comments and suggestions. Moreover, we are indebted to two
anonymous referees for valuable comments. The usual disclaimers apply.

L. Cassi
ADIS, Université Paris Sud, Paris, France

L. Cassi

:

L. Zirulia

CESPRI, Bocconi University, Milan, Italy

L. Zirulia (

*)

Department of Economics, University of Bologna, Bologna, Italy
e-mail: [e-mail]

L. Zirulia
RCEA, Rimini, Italy

JEL classification D83 . O33 . Z13

1 Introduction

The role of (social) networks in the economy has been a central concern of late in
economics (Kirman

1998

), and in particular in the economics of innovation. From an

empirical point of view, the systemic approach to innovation (Lundvall et al.

2002

;

Malerba

2002

), the notions of networks as loci of innovation (Powell et al.

1996

) and

collective invention (Allen

1983

) build on the idea that connections among agents

matter. From a theoretical point of view, some recent studies, building on the seminal
work by Cowan and Jonard (

2004

), have investigated the role of network structure in

the process of knowledge creation and diffusion, embodying contributions from
sociology (Coleman

1988

; Burt

1992

) and physics (Watts and Strogatz

1998

).

In this paper, we extend the theoretical literature. We start from the following

consideration that economic agents, while being embedded in social networks,
interact with their social contacts only if it is convenient for them to do so. In other
words, the use of networks can be conceived as an economic choice based on cost-
benefit comparisons.

The novelty of this approach is supported by the empirical literature on know-

how trading (Von Hippel

1987

). Informal know-how trading can be defined in terms

of technical knowledge that engineers and other technically oriented personnel
exchange with peers in other firms without any formal collaboration arrangements
between the firms that employ them (Carter

1989

). Faced with a technical problem,

an engineer might contact another network member in the expectation of drawing on
his experience of having confronted the same or a similar problem in the past. This is
what we define as the use of networks. However, there is another option, which is
for the engineer to develop this know-how himself. The benefits and costs associated
with these options are different, and, as long as the choice is based on a cost-benefit
comparison, the decision is an economic one.

On this basis, we develop a model in which a population of rational and self-

interested agents, active in an exogenously given social structure, can choose to use
the social network (i.e., knowledge exchange), or not (i.e., individual learning). We
assume that, within each learning episode, the two mechanisms are mutually
exclusive. The value which can be obtained from individual learning represents the
opportunity cost of using the network. Furthermore, we assume that returns from
individual learning are increasing in the level of knowledge agents already possess.
Consequently, as the (average) knowledge level increases, so does the (average)
opportunity cost of using the network.

In this framework, we study how network structure affects over time: (i) the overall

efficiency of the system, as measured by the average knowledge level across the
economy; (ii) its equity, as measured by the coefficient of variation across agents; (iii)
the degree of individuals

’ specialization; and (iv) the intensity in the use of the network.

We focus on two structural properties of networks, which are at the center of

debates in sociology and also in recent economics and business studies. Coleman
(

1988

), and many others after him, have argued that being embedded in a very

dense, interconnected,

“cliquish” network brings benefits by enhancing the trust

78

L. Cassi, L. Zirulia

among individuals and thereby encouraging joint activities and the sharing of tacit
and complex knowledge. However, Burt (

1992

) has argued that when the objective

is to access new knowledge, being embedded in a very dense and strongly cohesive
network may harm individual learning processes, and that efficiency in accessing
knowledge is achieved by occupying structural holes, i.e. by being linked to
individuals who are not connected to each other. The recent literature on small
worlds can be seen as reconciling these two views. Watts and Strogatz (

1998

)

developed a formal model to show that it is possible to build networks that are both
“cliquish” (consistent with Coleman’s argument) and characterized by short average
distances, consistent with Burt

’s view. Then, we could expect what Watts and Strogatz

term small worlds to emerge, because they exploit the benefits of both structures.

The main result of our study is that the opportunity cost of using the network

affects its optimal structure in terms of aggregate performance. For a low level of the
opportunity cost, networks with the lowest average distance maximize efficiency; for
an intermediate level of the opportunity cost, networks with relatively low of average
distance and relatively high level of average cliquishness (i.e. small worlds)
maximize efficiency; for a high level of the opportunity cost, networks with the
highest average distance maximize efficiency. Thus, in contrast to the claims made
by Cowan and Jonard (

2004

), the small world does not emerge as unambiguously

the most efficient network structure. However, the small world structure does appear
to be the most equal in terms of knowledge distribution and therefore a trade-off
emerges between efficiency and equity. While in our model, opportunity cost is
associated with ease of individual learning and with time (it increases over time), we
propose two additional interpretations that relate to the degree of competition among
agents and to the content of what is exchanged.

The paper is organized as follows: Section

2

stresses the element of novelty in our

work relative to the existing theoretical literature. Section

3

provides a description of

Watts and Strogatz

’s (

1998

) small world model, which is the foundation for the

comparative dynamics exercises in this paper. Section

4

describes our model, and

Section

5

discusses the results of the numerical simulations. Section

6

concludes.

2 Knowledge creation and diffusion, and social networks as opportunities

The aim of this section is to highlight the importance of our contribution. First, we
provide a brief review of the theoretical literature in which our model is situated.
Second, we provide a rationale for our modification. In particular, we refer to the
empirical literature on know-how trading, which constitutes a motivation for our work.
Third, we formulate our research question, and we discuss how, in answering it, we are
contributing to the ongoing debate on social capital and the properties of small worlds.

The recent stream of theoretical literature investigating the relationship between

networks and the creation and diffusion of knowledge builds on two basic elements.
First, it represents the economy as a heterogeneous population of agents involved in
the creation and diffusion of knowledge. Second, it assumes that these agents are
located within a network, which implies that each agent can

“interact” (in the

process of both knowledge creation and diffusion) with only a subset of other agents
in the society (his

“neighborhood”). Given these two commonalities, the existing

The opportunity cost of social relations: On the effectiveness of small worlds

79

models differ in several dimensions. The network can be exogenous or endogenous.
If endogenous, it can be a

“virtual” network, resulting from the historical sequence

of one-period pair-wise relationships, formed through a matching algorithm (Cowan
et al.

2002

), or it can be an

“actual” network, in which agents form and sever links

following a kind of

“reinforcement learning” mechanism (Morone and Taylor

2004

).

Knowledge has been represented in several ways: by a stock (Morone and Taylor

2004

), by a vector of real positive scalars (Cowan and Jonard

2004

), by a pair

constituting a scalar and an angle (Cowan et al.

2004b

), and by a

“tree” of activated

nodes (Morone and Taylor

2003

). Diffusion can occur though pair-wise barter

(Cowan and Jonard

2004

), through broadcasting, in which agents in turn share their

knowledge with their neighbors (Cowan and Jonard

2003a

), or through

“narrow-

casting

”, in which an agent shares its knowledge with only one agent at a time

(Morone and Taylor

2004

). Creation can occur through recombination, when the

receiver in an interaction recombines existing knowledge with the knowledge he has
received, in order to create new knowledge (Cowan and Jonard

2003a

); or by

innovation, when agents increase their knowledge (usually stochastically) through an
unmodeled process of learning (Cowan et al.

2004a

). Finally, the models can include

additional elements to characterize the process of knowledge creation and diffusion
in specific institutional contexts, such as scientific communities (Cowan and Jonard

2003b

), or be calibrated to reproduce specific historical and geographical cases

(Morone and Taylor

2003

).

Given these differences, what all these models have in common is that they do not

consider the use of the network as a true economic choice. By an

“economic choice”

we mean a decision process based on a cost-benefit comparison, even though prices
and payments are not involved. If agents (firms or individuals) aim at increasing
their knowledge, there will typically be several options available, each associated
with different benefits and costs. Some of these options may imply use of the
network, others may not. It is exactly discussion of this type of choice that is missing
in the current literature.

In this paper, we model a simple situation in which an economic choice involving

the use of the network emerges. We model a population of individuals who aim at
increasing their knowledge. Individuals can learn in two ways: individually, by
improving their personal knowledge; or socially, by interacting and exchanging
knowledge with other individuals in their social neighborhood.

An economic choice emerges because we assume that individuals have an

endowment of time and resources that can be allocated to one option or the other.
Thus, it is possible to consider explicitly the opportunity cost of using the network.
The opportunity cost of any decision can defined as the value of the next best
alternative that the decision forces the decision maker to forgo (Baumol and Blinder

2004

). Since the only alternative to the use of the network is individual learning, the

opportunity cost of using the network is the value that accrues to agent from
individual learning.

We would make two comments concerning our contribution. First, from a

substantive viewpoint, the novelty is in the spirit of the sociological perspective of
“embeddedness” (Granovetter

1985

; Uzzi

1997

). We assume that agents are nodes in

a social web of relations. Such a web does not determine agents

’ behavior (as in an

“oversocialized” view), but does constitute a set of opportunities and constraints that

80

L. Cassi, L. Zirulia

influence behavior, which is in any case driven by a cost-benefit comparison. The
network constitutes an opportunity because it enables an alternative way of learning
to individual one; at the same time, it constitutes a constraint because it selects the
subset of agents out of the entire population, with whom an individual can interact.

Second, with respect to the existing literature, we can locate our work at an

intermediate position along the dimension of exogenous vs. endogenous networks. On
the one hand, we assume the existence of a (social) network that is exogenous and time-
invariant, and, consequently, independent of agents

’ incentives to barter knowledge. In

particular, agents cannot form new links with other agents even if this is convenient. On
the other hand, agents

’ choices endogenously determine the actual network, which is

given by the subset of links that are activated by agents. This actual network changes
over time and clearly depends on agents

’ incentives to barter knowledge. In fact, they

are motivated by an

“economic”, self-interested reasoning, since agents interact with

their neighbors only if this maximizes their learning opportunities.

Our contribution to the existing theoretical literature is based on insights from the

empirical literature. In particular, we were inspired by the phenomenon defined as
know-how trading (Von Hippel

1987

; Carter

1989

) or information trading (Schrader

1991

). Evidence of this phenomenon was found in the US specialty steel and mini-

mill industry (Von Hippel

1987

; Carter

1989

), in the wireless communication cluster

in Northern Denmark (Dahl and Pedersen

2004

) and in the Chilean wine sector

(Giuliani and Bell

2005

).

Informal know-how trading can be defined as technical assistance provided by

engineers and other technically oriented personnel to peers in other firms without
there being any formal collaboration arrangements between the firms (Carter

1989

).

Based on empirical case studies, several authors have shown that know-how trading
has some recurrent specificities in both the content and modality of exchange. The
three main ones are: (1) exchange of knowledge works as barter; (2) effective
exchange depends on the comparison of benefits and costs; (3) exchange occurs
between socially connected individuals. These three elements drive the theoretical
exercise in this paper.

The object of know-how trading is practical knowledge typically associated with

production processes. Faced with a technical difficulty, an engineer can activate a
contact who might have faced a similar problem in the past and should possess the
relevant expertise. Quoting from Von Hippel:

A firm

’s staff of engineers is responsible for obtaining or developing the know-

how its firm needs. When required know-how is not available in-house, an
engineer typically cannot find what he needs in publications either: much is very
specialized and not published yet. He must either develop it himself or learn what
he needs to know by talking to other specialists. (Von Hippel

1987

, p. 293)

The specificities of information make know-how trading a very special form of

exchange. As suggested by Carter (

1989

), non-rivalry of information (i.e. the

provider of a piece of information does not lose it), uselessness of duplication and
the difficulties in imputing money values to know-how, make the use of pricing
mechanisms problematic. Consequently, know-how trading takes the form of barter,
where the equivalence of what is given and received must hold only in the long run.
The relation between the two agents is informal (i.e. no contract is signed involving

The opportunity cost of social relations: On the effectiveness of small worlds

81

the exchange of know-how), and it is based on personal knowledge and reputation.
While contemporaneous barter is rarely observed, reciprocity is the rule: if individual
A helps individual B, the latter is expected to return the favor in the future:
“Information must be given in order to be obtained” (Rogers

1982

, p. 114).

In relation to the effectiveness of the exchange, the literature has underlined that

the decision to provide help or not is based on a cost-benefit comparison,

1

in which

the engineer takes into account the constraints deriving from his belonging to an
institution (i.e. employment in a firm). While benefits are associated with the
possibility of asking for help in the future, the literature has underlined the cost of
“competitive backlash”, i.e. the reduction in the rent from that piece of knowledge.
As argued by Schrader (

1991

), three factors are involved: the degree of competition,

the availability of alternative sources of information, and the domain of information
trade. The higher the degree of competition between firms, the higher will be the
cost of transmitting information due to the reduction in rent. If the information can
be obtained by the engineer from another source, then the cost of providing the
knowledge is low, because the rent would be lost in any case. Finally, know-how
trading is more likely to occur if it involves knowledge domains that do not
constitute key sources of competitive advantage. Based on a sample of 294
technically oriented middle level managers in the US specialty steel and mini-mill
industries, Schrader found confirmation of the negative effect of competition and the
positive effect of the existence of alternative sources of information on the
probability of information being revealed to other firms.

Finally, in informal know-how trading, social relations (e.g. friendships) play a

central role, since trust between individuals is required to be sure that help will be
returned when asked. Therefore, social networks matter because they define the set
of agent pairs that can exchange know-how. In other words, an engineer

’s social

networks delimit the set of agents from whom he can request assistance. Since
know-how trading is based on trust and reputation, social connections cannot be
formed for the purpose of finding the solution to a specific problem: an engineer
must choose which person to ask for help within a social neighborhood. In their
sample of 259 engineers in the Northern Denmark wireless communications cluster,
Dahl and Pedersen (

2004

) reported that 66% of engineers have personal contacts

who were former colleagues, 50% who were classmates and 47% who were
considered personal friends. Schrader (

1991

), while finding that friendship has no

significant effect on the probability that information is traded, argues that it may
define the network within which information is exchanged.

To summarize, the aim of our contribution is to extend the theoretical literature on

networks and knowledge. We develop a model of creation and diffusion of
knowledge in which agents can choose between learning individually or bartering
knowledge, and, consequently, where the use of social networks is one of the options
available. In this framework, our research question is related to investigating the role
of social networks in the creation and diffusion of knowledge. More precisely, we
study how network structure affects over time: (1) the overall efficiency of the
system, as measured by the average knowledge level across the economy; (2) its

1

“Given that the amount of time and energy that a given individual has available for trading is limited

each is likely to try to maximize the useful yield of his trading

” (Carter

1989

, p. 157).

82

L. Cassi, L. Zirulia

equity, as measured by the coefficient of variation across agents; (3) the degree of
individuals

’ specialization; and (4) the intensity in the use of the network.

Given our emphasis on the properties of different network structures, the results

we obtained should be seen as a contribution to the rich discussion in the literature
on social capital, and a reassessment of the effectiveness of small world networks.

The long debate in sociology on the strategy of network positioning has recently

spilled over into business studies and economics. Two opposing views have
emerged. The first is based on the work of Coleman (

1988

) and its basic argument is

that being embedded in a very dense, interconnected, highly cohesive network
brings benefits by enhancing trust among individuals and thus encouraging joint
activities and the sharing of tacit and complex knowledge (e.g., Walker et al.

1997

;

Uzzi and Spiro

2005

).

The second view derives from Burt

’s (e.g.

1992

) work on structural holes. The

basic argument here is that when the objective is to access new knowledge, being
embedded in a very dense and strongly cohesive network may be harmful to
individual learning processes as it produces high levels of redundancy, thereby
reducing the amount and quality of accessible information. According to this view,
efficiency in accessing knowledge is achieved by limiting the number of redundant
contacts, and positioning across structural holes, i.e. linking to individuals that are not
connected to one another. Individuals positioned in structural holes are able to broker
knowledge flows across unconnected groups (e.g., Gargiulo and Benassi

2000

).

The recent literature on small worlds can be seen as reconciling these two views

(Verspagen and Duysters

2004

). The idea of small worlds dates back to Milgram

(

1967

), who demonstrated the low average distance that characterizes social

networks. More recently, Watts and Strogatz (

1998

) developed a formal model to

show that the

“small world property” can exist in networks with high levels of

clustering, which is a typical feature of observed social networks. Watts and
Strogatz

’s model, on which our exercise is based, is discussed in the next section.

Since high clustering is associated with closure and low average distance capture,

Burt

’s idea of non-redundancy, the perspectives on social capital and structural holes

are not incompatible in the sense that a (severe) trade-off does not exist. If we
assume the existence of advantages from location in a clique and (some) non-
redundant contacts, we could expect a small world (à la Watts and Strogatz) to
emerge as the most efficient structure. Empirical support for this hypothesis is
provided by those studies that have identified the existence of small worlds in
several networks where knowledge creation and diffusion is relevant, such as
networks of strategic alliances (Breschi and Cusmano

2004

; Verspagen and Duysters

2004

) and networks of scientists (Goyal et al.

2006

).

2

2

The discussion on cliques, structural holes and small worlds can be related to the concept of strong and

weak ties (Granovetter

1973

), where the strength of a tie depends on a combination of time, emotional

intensity, intimacy and reciprocal service. Granovetter

’s argument is based on the following assumption: if

an individual (say A) has strong ties with other two persons (say B and C), then it is not possible for the tie
between B and C to be absent. This assumption, based on some empirical results, has a logical
implication: only weak ties can bridge two subsets of the network.

“If each person’s close friends know

one another, they form a closely knit clique. Individuals are then connected to other cliques through their
weak rather than their strong ties. Thus, from an aerial view of social networks, if cliques are connected to
one another, it is mainly by weak ties.

” (Granovetter

2005

, p. 34). Therefore it seems plausible to consider

links inside cliques to be strong ties, and links outside cliques (bridging structural holes) as weak ties.

The opportunity cost of social relations: On the effectiveness of small worlds

83

3 Network structure: Watts and Strogatz

’s model

As already mentioned, our model considers the network as exogenous. Therefore, in
this section we describe Watts and Strogatz

’s (

1998

) small world model, which is the

common starting point for the theoretical literature that considers the network
structure to be taken as given. This model is particularly suitable for our analysis for
two reasons. First, it can parsimoniously generate different structures as a function of
one parameter only. Second, and more importantly, it can generate both small worlds
and network structures consistent with Coleman

’s and Burt’s views.

In Watts and Strogatz

’s model, network density (i.e., the number of total existing

links) is kept fixed, while its topology varies. Network structure is characterized by
two properties: average path length, and average cliquishness. Average path length is
a global concept, defined as the average number of steps separating two randomly
chosen agents. Average cliquishness is a local concept, measuring the degree of link
redundancy in an agent

’s neighbourhood.

Consider a set of agents I={1,...N}. For any i,j define the variable

χ(i, j), which

takes the value 1 if the two agents are connected, and 0 otherwise. The network G=
{

χ(i, j);i, j ∈ I} corresponds to the list of all pair-wise relationships between agents.

Then the neighborhood of agent i is formally defined as

Γ

i

¼ j 2 I= i

f g :

f

χ i; j

ð Þ ¼ 1g. A path connecting two agents i and j is defined as a set of pair-wise

relationships {(i,i

i

),...;(i

k

, j)} such that

χ(i,i

i

)=...=

χ(i

k

,j)=1; the distance between i and

j d(i,j) is given by the number of steps in the shortest path between i and j. Given this,
we can define the average path length as:

L

¼

X

i

;j2I

d i

; j

ð Þ

N N

1

ð

Þ=2

ð

Þ

ð1Þ

The cliquishness of a set S

⊆ I is defined as the proportion of pair-wise

relationships in S over the total number of possible number of relationships,
formally:

cl S

ð Þ ¼

P

i

;j2S

χ i; j

ð Þ

#S #S

1

ð

Þ=2

ð2Þ

In the model, average cliquishness is given by the average value of cl(S) for S=

Γ

i

,

i

∈ I, that is:

C

¼

X

i

2I

cl

Γ

i

ð Þ

N

ð3Þ

Watts and Strogatz consider a family of graphs with a given number of nodes N

and an average number of links n. Then, the total number of links is fixed, and equal
to

n

*

N

2

. They start from a ring of N vertices, i.e. a regular periodic lattice with n

nearest neighbors (n even). Loosely speaking, they consider N agents located on a
circle, each of them connected (by undirected edges) with their n nearest neighbors.

The next step is to implement the following algorithm: choose a vertex and the

edge that connects it to its nearest neighbor in a clockwise sense. With probability p,
reconnect this edge randomly to a vertex chosen over the entire ring, with duplicate
edges not allowed; with probability 1-p, leave the edge in place. The process is

84

L. Cassi, L. Zirulia

repeated by moving clockwise around the ring, considering each vertex in turn until
one lap is completed. Next, consider the edges that connect vertices to their second
nearest clockwise neighbors. As before, randomly rewire each of these edges with
probability p, and continue the process, circulating around the ring and proceeding
outward to more distant neighbors after each lap, until each edge in the original
lattice has been considered once.

Varying p, it is possible to build graphs with different values for average path length

and average cliquishness, L(p) and C(p). Both L(p) and C(p) are monotonically
decreasing in p. At one extreme, for p=0, we have a regular network, characterized by
high average cliquishness and high average path length. This network structure is
consistent with Coleman

’s interpretation of social capital. At the other extreme, for

p=1, we have a random network, where both average path length and average
cliquishness are low. This structure, in which link redundancy is minimized, is
consistent with the structural holes argument. The importance of Watts and Strogatz

’s

contribution lies in their demonstrating that the trade-off between the local concept of
cliquishness and the global notion of average distance is not as severe as might appear
at first sight. For a non-negligible region of parameter p

’s space (approximately, the

interval [0.01; 0.1]), they show that L(p)

≈ L(1), but C(p) ≫ C(1). When in a regular

network some "shortcuts" are created connecting distant parts of the graph, average
path length is dramatically reduced, but cliquishness is substantially preserved. Watts
and Strogatz call this network structure

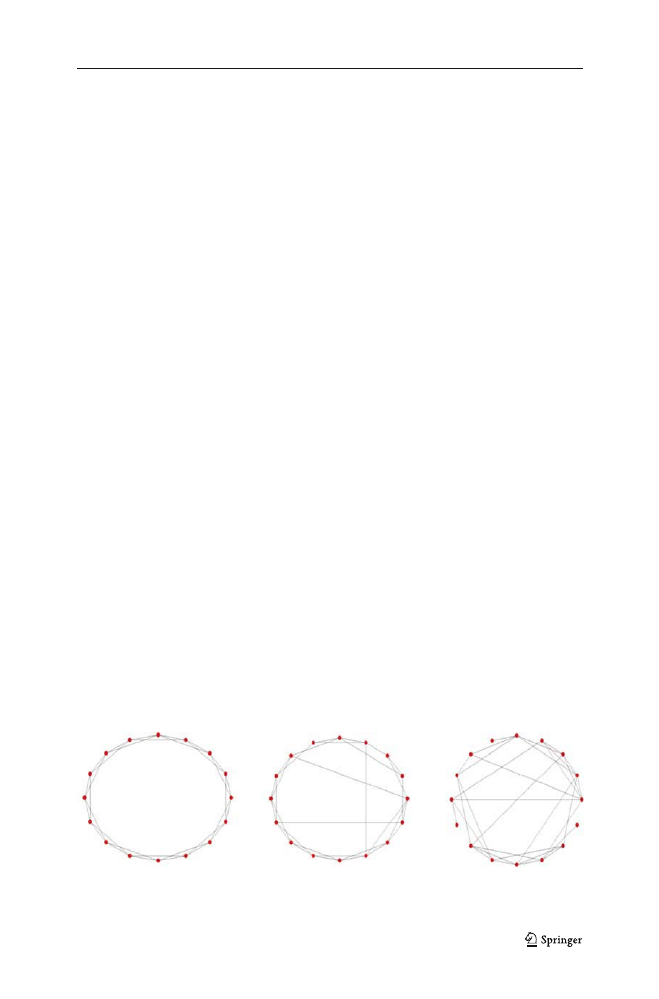
“small world.” Fig.

1

reports the three main

kinds of networks we consider: a regular network, a small world, and a random
network. Each graph has 16 nodes and 32 edges. In section

5

, we investigate the

properties of our model for three values of p, each corresponding to one of these
structures.

4 The model

Our model builds on Cowan and Jonard (

2004

), and introduces into their framework

the choice that economic agents have between learning individually and bartering
with others in their social neighborhood. We consider an economy populated by N
agents located on a graph G. For each agent, the graph identifies the subset of agents
with whom he can exchange knowledge. The graph is exogenously derived and is

regular network

small world

random network

Fig. 1 The three social structures

The opportunity cost of social relations: On the effectiveness of small worlds

85

kept fixed over time. Agents aim to increase their own knowledge. This can be
achieved in two ways: through knowledge barter between directly connected agents,
and through individual learning.

Knowledge is represented by a vector V

i

t

ð Þ 2 <

K

þ

; where the K components

represent different categories of knowledge. V

i,k

(t) is the level of knowledge in

category k for agent i at time t.

Agents

’ pay-offs are represented by the utility function:

U V

i

t

ð Þ

ð

Þ ¼

P

k

V

i

;k

t

ð Þ

K

ð4Þ

Agents aim at maximizing the average level of their knowledge in different

categories; they are risk-neutral and they are not affected by other agents

’ levels of

knowledge (i.e. there is no competition in this economy). Each agent starts with a
given level of knowledge in each category at time t=0. Then in each period, one link
(i.e. two directly connected agents) is picked at random with uniform probability.
These two connected agents can choose to barter knowledge or engage in individual
learning.

3

Opportunities for increasing agent i

’s knowledge from a knowledge barter with j,

or through individual learning, are, respectively:

V

B

i

;k

t

þ 1

ð

Þ ¼ V

i

;k

t

ð Þ þ a max V

j

;k

t

ð Þ V

i

;k

t

ð Þ; 0

ð5Þ

V

I

i

;k

t

þ 1

ð

Þ ¼ V

i

;k

t

ð Þ 1 þ b

i

;k

t

þ 1

ð

Þ

ð6Þ

In equation (

5

),

α ∈ (0;1) measures the ease of knowledge transfer through face-

to-face interactions. Since

α<1, we assume that knowledge is only partially

assimilable, due to imperfect absorptive capacity. In equation (

6

),

β

i,k

(t+1) is

uniformly distributed on 0

; b

, where

b is a measure of opportunities (i.e., easiness)

for individual learning. Consistent with the literature on knowledge creation, we
assume that the process of individual learning is cumulative, i.e. it is based on
agents

’ existing knowledge.

4

Knowledge barter occurs if

max

k

2K

V

B

r

;k

t

þ 1

ð

Þ V

r

;k

t

ð Þ

n

o

max

k

2K

E V

I

r

;k

t

þ 1

ð

Þ V

r

;k

t

ð Þ

h

i

n

o

ð7Þ

where r = i,j.

In the case of both individual learning and barter, agents will learn only in one

category, i.e. in the category where the (expected) gain is the highest. In the case of

3

The empirical literature on informal know-how trading often claims that individuals ask for help when

they have to solve some technical or practical problem (e.g. which material is better to use). Our
representation of a learning episode as the increase of an argument of vector V

i

(t) can be interpreted as the

accumulation of a piece of knowledge that could be useful for the solution of a problem.

4

In the long run, it is reasonable to assume that decreasing returns in learning prevail, so that the rate at

which knowledge is accumulated through individual learning decreases. However, since we intend to
model a situation of rapid technological or scientific change, we ignore this issue.

86

L. Cassi, L. Zirulia

ties, the knowledge category for individual learning or barter is randomly chosen
with uniform probability.

After knowledge barter or individual learning has occurred, the economy moves

to the next period and the previous steps are repeated.

The proposed decision rule has a number of implications. We assume that agents

have a cognitive and time endowment constraint in the sense that they can learn in
only one category each period. Agents are rational, but myopic, in that they
maximize only current period pay-offs. When mutually beneficial barter can occur,
we select the Pareto superior outcome (which holds for both the agents involved and
the economy as whole), in which agents completely exhaust the knowledge trading
opportunities. It should also be noticed that when barter occurs, it is necessarily the
Pareto superior option, since the consent of both players is required. This is not
necessarily true in the case of individual learning: if the difference between the
returns from individual learning and the returns from bartering is positive but small
for one agent, and negative and large for the other, barter does not occur even if it is
socially desirable.

5

It is fair to say that some of the characteristics of know-how trading phenomenon

summarized above are not taken into account by the hypotheses underlying our
model. Indeed, the objective of this paper is not to provide a model fully capturing
the details of know-how trading. Instead, we intend to contribute to the theoretical
literature on networks and knowledge adding one aspect which is both conceptually
relevant and inspired by the empirical literature (i.e., knowledge exchange depends
on the comparison of benefits and costs, while occurring between socially connected
individuals). Doing so, we try to stay as close as possible to the existing theoretical
literature (in particular Cowan and Jonard

2004

), in order to favor the comparability

of results.

In particular, three hypotheses of our model do not directly correspond to the

empirical literature. First, the hypothesis that individuals have to invest time and
resources in internal or external learning implies that the two activities are
considered to be substitutes. This implies that, in our model, there is no room for
complementarities between internal and external learning (Giuliani and Bell

2005

).

For instance, we exclude a role for absorptive capacity à la Cohen and Levinthal
(

1990

). Indeed, in our model, an agent can learn more in a specific category of

knowledge through bartering with others, the lower is his knowledge in such a
category. That is the opposite of what an absorptive capacity argument would imply.

However, while there is a static trade-off between internal and external learning

within a learning episode, a dynamic trade-off may fail to exist. Knowledge
exchange through bartering implies that an agent can provide useful knowledge to
the other party, and this is more likely if the individual has performed (successful)
individual learning in the past. In other words: it is true that, in our model, agents

5

Suppose, for instance, that there are five knowledge categories,

α=0.5 and β ¼ 0:02

.

For agent i,

V

i

;1

t

ð Þ ¼ 10 and V

i

;k

t

ð Þ ¼ 8 for all the other k. For agent j, V

i

;k

t

ð Þ ¼ 8 for all k. Total gain from bartering

is 1; expected total gain from individual learning is 0.18. In this case, bartering does not occur, even if it is
socially desirable. Side-payments are not allowed in this model. Consistent with the empirical evidence,
we assume that the agent who gains more from the barter cannot compensate through monetary transfer
the agent who gains less.

The opportunity cost of social relations: On the effectiveness of small worlds

87

with low levels of knowledge have more to learn from other agents. However, this
does not imply that they actually exchange more, since they also have less
knowledge to provide, and mutual consent is required for barter to occur.

6

Second, we have seen that, in most real-world examples of knowledge trading,

exchange of knowledge does not occur simultaneously. Typically, agent i releases a
piece of knowledge to agent j today because i expects to receive useful knowledge
from j tomorrow. Modelling the dynamic game through which agents build a
reputation is beyond the scope of this paper, and in fact has never been considered in
this literature. In our model, as in Cowan and Jonard (

2004

), the double coincidence

of wants within the period captures the idea of mutual convenience in the barter.
Related to this, agents in our model do not search purposely for the agent who
possesses the knowledge they lack (indeed, each period, two directly connected
agents are picked at random with uniform probability). However, in our model,
agents exchange knowledge only when this is convenient for them, i.e. the other
agent is knowledgeable in categories in which they are not. Over sufficiently long
period of time, then, what we observe in the model is that agents effectively interact
only with those neighbors who have knowledge they do not have. This is also what
we observe in real world know-how trading.

Third, as mentioned in Section

2

, the empirical literature claims that one of the

most relevant costs of bartering derives from the cost of competitive backlash. Of
course, this cannot explicitly captured by our model, since it requires at least some
degree of competition in knowledge accumulation and we have assumed that the
individuals (the firms they belong to) are not competitors. However, it is possible to
provide an interpretation for parameter

b that takes account of the competitive

backlash cost. Since this parameter captures the ease of individual learning, the higher
the value of

b the higher will be the gain from individual learning, and therefore the

higher the opportunity cost of bartering. Because competitive backlash is also a
component in the opportunity cost of bartering, variations in

b may be interpreted as

capturing formally variations in the degree of competition between agents.

Our model differs from Cowan and Jonard

’s (

2004

) in three respects. First, they

consider a pure diffusion model, in which the knowledge possessed by a limited
number of

“experts” in one of the categories is spread throughout the population. Our

model is one of both creation and diffusion of knowledge. Second, they assume that
agents barter only if it is convenient for both in at least one category. If this condition
is not satisfied, nothing happens, even if the absence of competition between agents
implies no cost of giving knowledge to other agents. In our model, agents have the
alternative of individual learning, and choose the option that maximizes their expected
gain. Finally, and differently from Cowan and Jonard, agents are fully able to evaluate
the knowledge held by other agents, or, if we see the model as a

“mean field

approximation

”, they do not commit systematic errors in making such an evaluation.

In our model, we fully exploit the representation of knowledge as a vector of real
numbers, since the cardinality of V

i

(t) plays an important role in agents

’ decisions.

6

For instance, Giuliani and Bell (

2005

) show that firms with more absorptive capacity have more external

links. In their paper, absorptive capacity is proxied by education and experience of technical personnel and
firms

’ R&D intensity. Then, their result can also be interpreted in terms of firms’ capability to provide

useful knowledge to their partners.

88

L. Cassi, L. Zirulia

This increases the hiatus between the appreciative discussions on the nature of
“knowledge” (see for instance, Cowan et al.

2000

) and its formal representation, but it

helps to keep the model simple, and allows us to focus on the key aspect of the model:
the notion of social networks as an option.

5 Simulation results

This section describes the numerical implementation and results of the model.

Most parameters in the model are the same for all the numerical exercises we

performed. That is, in all the simulations, we considered a population of 500 agents
(N=500), each with an average of 10 links (n=10), and five categories of knowledge
(K=5).

7

The value of parameter

α, i.e. the ease of knowledge transmission, is equal

to 0.5. Initial value in each knowledge category is 1 for all agents. The simulation
number of periods is fixed to T=100000.

8

However, two parameters do vary. The first parameter is p, the rewiring

probability in the Watts and Strogatz model; we considered three values of p, in
order to build graphs with features of regular, small world and random networks.
The values of p were 0.007, 0.07 and 0.7, respectively.

The second parameter that was varied is

b. b is a measure of the opportunities for

individual learning, and is thus related to the opportunity cost of using the network.
We considered two values for this parameter:

“low” opportunities for individual

learning

b ¼ 0:01

and

“high” opportunities for individual learning b ¼ 0:03

.

Overall, we obtained six combinations for the two parameters. For each of these six
combinations, we ran 50 simulations with different random seeds. We report the
average of the 50 runs.

9

For each case, we consider the patterns of four statistical measures, capturing

different dimensions: efficiency, equity, specialization, and use of the network.

In line with Cowan and Jonard (

2004

), we consider two statistics in order to

measure the efficiency and equity of networks in creating and diffusing knowledge.
These two measures, respectively, are average level of knowledge and the coefficient
of variation.

Agent i

’s average knowledge level is:

V

i

t

ð Þ ¼

P

K

k

¼1

V

i

;k

t

ð Þ

K

ð8Þ

7

This parameterization is the same as that adopted in Cowan and Jonard (

2004

).

8

In terms of interpreting the time horizon, we note the following. Since each agent has a probability 1/250

to be drawn each period, in expected value every agent will have an opportunity to learn every 250
periods. Then, it is plausible to define this as the basic unit of time. If the empirical counterpart of this
basic unit is one week, the time horizon considered will correspond to approximately 8 years.

9

We ran other numerical experiments, but without any other economic insights than those reported in this

paragraph. We also computed confidence intervals for the statistics reported in the paper, but since these
turned out to be very small, we omit them from the graph for the sake of readability.

The opportunity cost of social relations: On the effectiveness of small worlds

89

The average level of knowledge in the economy at time t is:

m t

ð Þ ¼

P

N

i

¼1

V

i

t

ð Þ

N

ð9Þ

The variance in knowledge levels is:

σ

2

t

ð Þ ¼

X

i

2I

V

2

i

t

ð Þ

N

μ

2

t

ð Þ

ð10Þ

from which the coefficient of variation

σ t

ð Þ

μ t

ð Þ

is derived.

As a measure of average specialization of individuals, we used the average

Herfindhal index, computed as follows. s

ik

t

ð Þ ¼

V

i

;k

t

ð Þ

V

i

t

ð Þ

is the share of total knowledge

that agent i possesses in category k. Then

H

i

t

ð Þ ¼

X

k

2K

s

2
i

;k

t

ð Þ

ð11Þ

and

H t

ð Þ ¼

P

i

H

i

t

ð Þ

N

ð12Þ

This is the statistic we report here.

Finally, we considered another indicator to measure the use of the network. For

each period t, we used S(t) to indicate the number of times that the network is used
up to t. We obtained:

RS t

ð Þ ¼

S t

ð Þ

t

ð13Þ

This measure is relevant for the exercise because it captures the effects of our

original assumption on networks as an option.

Before commenting on the numerical results, we need to clarify one point. In

contrast to Cowan and Jonard (

2004

), our model does not reach a steady state; our

model is not a pure model of diffusion, but also includes knowledge creation. Over
time, average knowledge diverges. This has clear implications for our simulation
results. In our exercise, what is relevant is not the long run outcome to which the
system converges (since the system does not converge), but its transient properties.
In particular, it is the interaction between social and individual learning that is
relevant or, in other words, the use or non-use of the network. Consequently, our
comments will focus on system dynamics.

We start by considering jointly the efficiency of the three different network

structures (Fig.

2

), the use of network (Fig.

3

) and knowledge specialization (Fig.

4

).

In order for the results to be readily comparable with respect to the different values
of the parameters, Figs.

2

and

4

report the data using the regular network as a

benchmark. In particular, for average knowledge levels and average knowledge
specialization, the values for the three series (regular network, small world, random
network) are divided by the value for the regular network.

90

L. Cassi, L. Zirulia

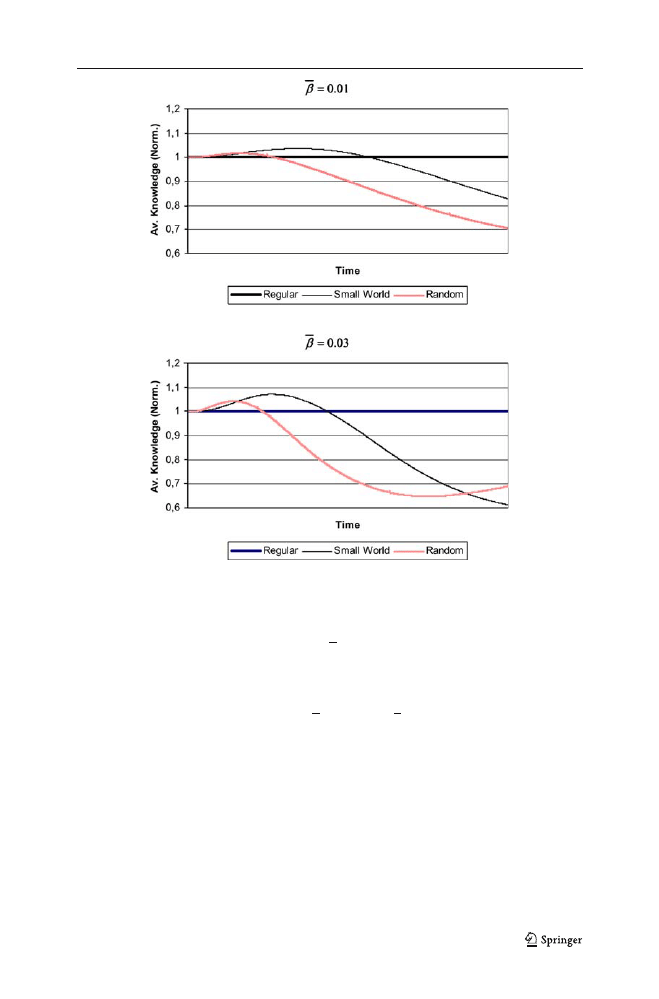
In terms of average knowledge levels, the dynamics of the ordering of the three

networks are the same for both values of

b. We can distinguish three phases. In the

first, the random network is the most efficient network, followed by the small world
and the regular network. In the second phase, the small world maximizes average
knowledge. In the third phase, the regular network becomes more efficient. This
timing is the same for both value of

b, but when b is higher the changes in the

efficiency of the network occur earlier.

These results can be interpreted in terms of the two main properties of the graphs:

average distance and average cliquishness. Low average distance is the key property
for efficiency in the beginning (when the average level of knowledge is low), while
high cliquishness becomes crucial later (when the average level of knowledge is
high). In other words, initially, the most efficient network is depicted in the graph as
having the lowest average distance; later, the most efficient network is depicted on
the graph showing relatively high cliquishness and relatively low average distance;
finally, the most efficient network is the one with the highest cliquishness.

Also in terms of use of the network (Fig.

3

), the three network structures present

different dynamics, which resemble the behavior of average knowledge series. Since

Fig. 2 Simulation results: average knowledge levels

The opportunity cost of social relations: On the effectiveness of small worlds

91

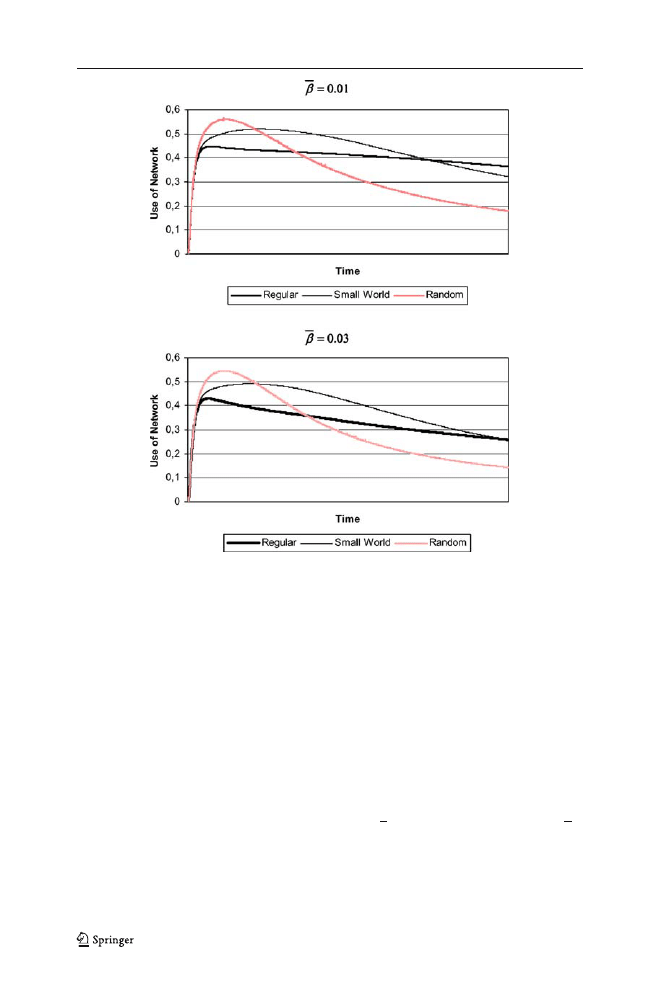
we plot average use of the network until period t, the tendency in the use of the
network in a given period of time can be seen in the slope of the curve. Initially, the
random network exhibits the highest use, which is overtaken by the small world.
which in turn is overtaken by the regular network. The three networks also differ in
the way their use varies over time: the random network is intensively used at the
beginning of the simulations, but its use declines at a quite rapid rate. The regular
network shows lower use initially, but then this stabilizes over the simulation
horizon. The small world graph is an intermediate case. The peak in the use of the
small world network is lower than for the random network, but the decline in use is
less severe.

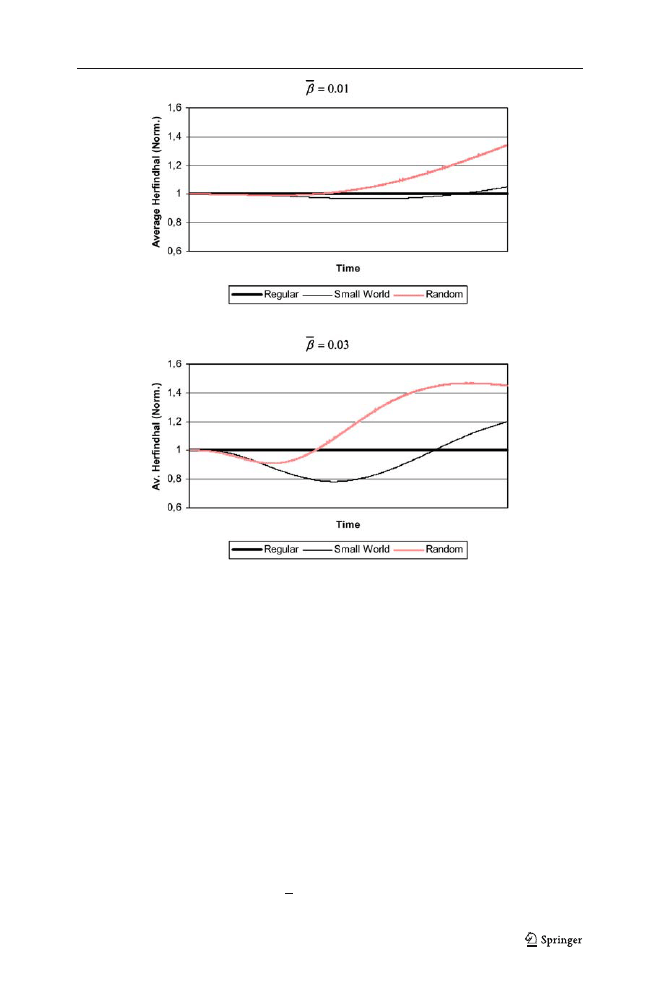
Finally, the average Herfindhal index (Fig.

4

) seems very similar for the different

network structures, but on closer inspection, for

b=0.01 and more clearly for b=

0.03, it can be shown that specialization is highest for the regular network, followed
by the small world and the random network graph. Over time, the random network
emerges as the structure with the highest level of specialization, even though there is
some evidence of convergence with the small world network at the end of the
simulation time horizon.

Fig. 3 Simulation results: use of the network

92

L. Cassi, L. Zirulia

It is possible to account for the joint dynamics of these variables over time.

However, we first need to detail the effects of average distance and cliquishness, as
identified by Cowan and Jonard (

2004

) in their diffusion model. The advantages of

short average distances are clear: knowledge flows more rapidly and, if we assume
dispersion of knowledge when passing from one agent to the other, short average
distances increase the overall efficiency of the system. Also, cliquishness has a
positive effect on the diffusion of knowledge. Cliquishness allows circumvention of
the limitations imposed by the

“double coincidence of wants” that barter implies. If

agent i and agent j are linked, agent i possesses knowledge that is valuable to agent j,
but the reverse is not true; cliquishness guarantees that there are several paths
through which knowledge can indirectly flow from agent i to agent j. The small
world is the optimal structure in Cowan and Jonard

’ model, since both high

cliquishness and low average distances have a positive effect on knowledge
diffusion.

The dynamics of our model can be explained as follows. Initially, the average

knowledge level is low. The level of knowledge (in the category in which the agent
knows the most) is, together with

b, the key determinant of the opportunity cost of

using the network. In equation (

6

), we assume that the return from individual

Fig. 4 Simulation results: Herfindhal index

The opportunity cost of social relations: On the effectiveness of small worlds

93

learning is increasing in the maximum of knowledge levels. Then, the higher is this
value, the higher will be the opportunity cost of using the network. This means that,
when the average knowledge level in the economy is low, then the (average)
opportunity cost of using the network is also low. It turns out that, in this situation,
networks with short path lengths are effective in terms of knowledge accumulation,
because they diffuse globally, and with low dispersion, the successfully innovative
episodes that occur in an economy where knowledge levels among agents are very
similar. Networks with low average distances are intensively used for this reason, and
use of the network, by diffusing knowledge, leads to low levels of specialization.

As the average knowledge increases, the opportunity cost of using the network

progressively increases. The return from individual learning increases and this is the
alternative to using the network. Over time, first the small world and then the regular
network become more efficient due to the higher cliquishness of these networks. As
we have already mentioned, cliquishness enables to circumvent the limitation
imposed by the double coincidence of wants. As the opportunity cost increases, the
likelihood of this coincidence decreases, so that cliquishness becomes crucial for
sustaining use of the network. This is socially important because, while barter, when
it is used, is always a Pareto superior option, this is not the case for individual
learning. At the end of the simulations, the regular network is seen to be the most
efficient network because cliquishness becomes crucial in diffusing knowledge
through the social network.

We have also seen that, in graphs with low average distance, the level of

specialization is relatively low at the beginning, because of the intense use of the
network. Since barter requires some degree of heterogeneity, this reinforces the
tendency towards individual learning in the random and in small world graphs.
Then, this low use of networks in the random graphs (and to a lesser extent, in the
small world graphs) will tend to favor specialization and, consequently, an increase
in the Herfindhal index, since agents learn in the category in which they are already
specialized.

If we compare runs for different values of

b, we need to recall that higher values

for this parameter are associated with higher opportunity costs of using the network.
For this reason, we can apply the argument used in relation to the changes that occur
within a given simulation over the time horizon. For a higher value of

b (0.03 vs

0.01), the opportunity cost of using the network is ceteris paribus higher. This
implies that cliquishness is relatively more important than average distance in
guaranteeing efficiency of the economy, and consequently, more cliquish networks
emerge as being more efficient, earlier.

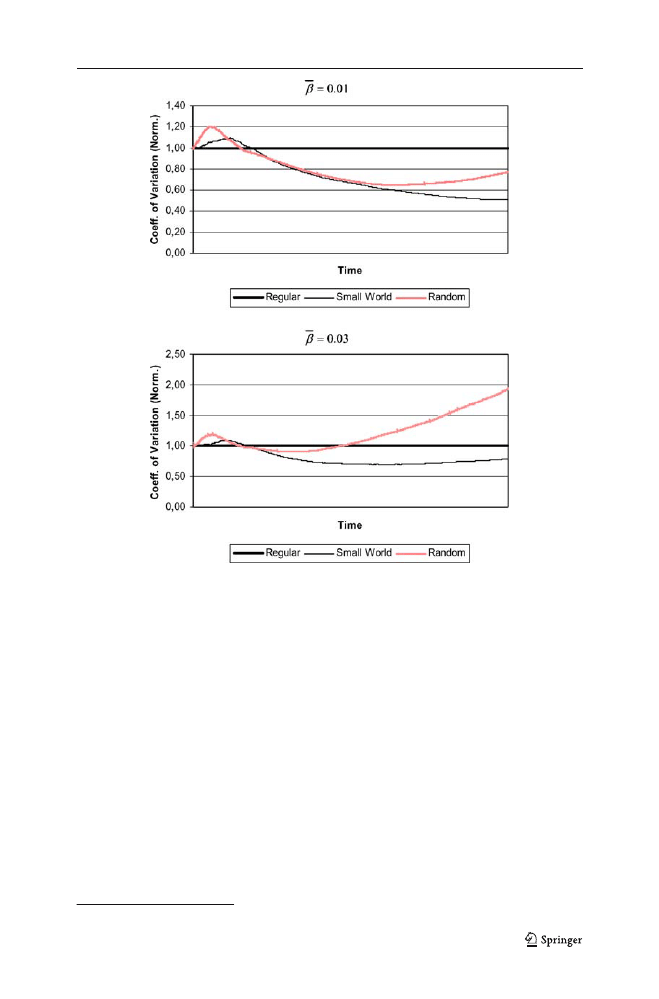
We now consider the equity properties of the three different network structures

(Fig.

5

). In this case, the order among the different networks changes several times

over the simulation horizon, and it is dependent on

b.

The basis for this is that the effect of a learning episode on the coefficient of

variation can be decomposed. First, it can increase or reduce the differences in
average knowledge between the two individuals involved in the learning episode.
Second, it can increase or reduce the differences between the two individuals and the
rest of the population.

Concerning the first point, if the two agents learn individually, the coefficient of

variation at the pair level increases if the individual with the greatest amount of

94

L. Cassi, L. Zirulia

knowledge in one field also has the greatest average level of knowledge. This is
because the agent

’s expected gain from individual learning depends only on the

amount of knowledge in the category with which he is most familiar (Eq.

7

). This

condition may fail when one individual is very specialized (he knows a lot in one
category, but little in the others); while the other is not (i.e. his knowledge across all
the categories is fairly uniform). However, the assumption that agents learn
individually in the category in which they are best informed, tends to favor
specialization, such that non-specialized agents tend not be observed.

10

Therefore, it

could be concluded that, if agents opt for individual learning (i.e. not using the
network), the coefficient of variation between them will probably increase.

The reverse will be true if the two individuals decide to barter. In this case, the

coefficient decreases if the individual that gains more from bartering also has the
lowest average knowledge. This tends to occur if the individual with the greatest

Fig. 5 Simulation results: coefficient of variation of knowledge levels

10

This can be seen in the graphs for the non normalized Herfindhal index, not reported here.

The opportunity cost of social relations: On the effectiveness of small worlds

95

amount of knowledge in one field (which is likely to be the type of knowledge he
provides in barter) also has the highest average level of knowledge. As discussed
above, this condition is likely to be satisfied and then barter will reduce the
coefficient of variation at the dyadic level.

Concerning the second point, it is clear that the coefficient of variation increases

(decreases) if the two individuals involved in the learning episode have an average
knowledge greater (lower) than the average knowledge of other agents.

For both value of

b, Fig.

5

initially shows a greater coefficient of variation for

random and small world networks: the coefficient of variation is greater for networks
characterized by low average distance, and greater for networks that are initially
more used. This can be explained as follows. At the beginning of our simulation
exercise, all individuals are equal in terms of their knowledge, and therefore they can
only learn individually; social learning will not start to occur until differences among
individuals start to increase. The intensive use of individual learning, combined with
its stochastic and cumulative nature, increases the coefficient of variation at the
population level. The increase is more pronounced for network structures that are
more intensively used. Although barter reduces the coefficient of the variation within
the pair, barter is more likely to occur among agents who have been particularly
successful in individual learning at the beginning, and who consequently have an
average knowledge greater than the population average. For such agents, bartering is
the way to learn fast in categories in which they are not specialized. As a result, the
coefficient of variation increases with use of the network.

As times elapses, the dynamics of the coefficient of variation depend on the value

of

b. For a low value of b, the regular network, followed by the random network,

become the more unequal structures over the time considered. For a high value of

b,

the regular network is initially the most unequal structure, but by the end of the
simulation time, the most unequal is the random network. In both cases, the small
world is the least unequal network at the end of the simulation horizon.

These results can be explained as follows. As we have seen, members of a clique

tend to use the network more intensively and this makes them became both more
knowledgeable and promotes more uniformity among them. This causes the
coefficient of variation inside the clique to decrease, while the difference between
cliques tends to increase. This is due to the stochastic nature of individual learning:
in some areas of the network, but not in others, there will be a number of successful
innovative episodes with positive effects at local level. Since the average distance is
high, knowledge will not flow easily across regions in the network. This generates
high levels of inequality in regular networks. In random networks, individual
learning is largely predominant. As we have argued, individual learning tends per se
to increase the coefficient of variation, and this effect is reinforced by the cumulative
nature of individual learning. This generates a high level of inequality in random
networks. For a low value of

b, the first effect prevails until the end of the

simulation, while for a high value of

b the regular network is initially the most

unequal, and then, over time, the random network takes over. This is due to the
impact of limited network use on the coefficient of variation, which is more
pronounced when the expected gain from individual learning is higher.

In conclusion, and in contrast to Cowan and Jonard (

2004

), the small world does

not emerge as the most efficient network structure when the opportunity cost of

96

L. Cassi, L. Zirulia

using the network is considered. As the opportunity cost increases, both within a
simulation and for a variation in

b, more cliquish networks are the most efficient

from a knowledge accumulation point of view. For a low level of opportunity cost,
networks with the lowest average distance maximize efficiency of knowledge
accumulation; for an intermediate level of the opportunity cost, networks with
relatively low average distance and relatively high level of average cliquishness
maximize efficiency; and for a high level of opportunity cost, networks with the
highest average distance maximize knowledge accumulation.

Interestingly, the small world emerges as the most equal structure, because it

enables the knowledge accumulated to be spread locally. Cowan and Jonard (

2004

)

produced a similar result when agent heterogeneity was measured by the coefficient
of variation. In our model, however, a trade-off emerges between efficiency and
equity, something that is absent in Cowan and Jonard.

11

It is interesting to compare our results with those in the literature on knowledge

and networks (Cowan et al.

2004a

). Cowan et al. model knowledge creation and

diffusion through broadcasting. Their results show that cliquish networks are optimal
when technological opportunities are high or, in another interpretation, when
innovation is relatively more important than imitation. Our results are substantially
the same, even though the rationale behind them is different. In Cowan et al.

’s

model, the redundancy of links in the clique favors a self-reinforcing mechanism in
which knowledge is created and diffused at the local level. In our model, when
opportunities at the individual level are high (both because knowledge levels are
high and because expected

β is high), cliquish networks become more efficient.

As we argued in Section

2

, our findings contribute to the debate on the optimal

structural properties of social networks, in our case with reference to the processes of
knowledge creation and diffusion. In light of our results, we identified the
opportunity cost of using the network as a variable which affects the optimal
network structure. For a low level of the opportunity cost, Burt

’s view of structural

holes applies; for a high level of the opportunity cost, Coleman

’s view related to

social capital applies; for an intermediate level, the small world is the optimal
structure.

Our results have additional implications. First, we argued in Section

2

that the

parameter

b also captures determinants of the opportunity cost in addition to the ease

of individual learning. In particular, we referred to the notion of competitive
backlash costs discussed in the empirical literature on know-how trading, to argue
that the stronger the competition (and consequently, the higher the competitive
backlash cost), the higher is the opportunity cost of using the network. This implies
that, although the model does not explicitly consider competition among the agents,
the greater the competition, the more cliquish must be the optimal network. Second,
the notion of opportunity cost can also be discussed and related to the content of
what is exchanged on networks. In this respect, we propose two interpretations.

11

Figure

5

shows that. for high

β

,

the coefficient of variation of small world increases compared to the

coefficient of variation for the regular network; the trade off then presumably will vanish. What we
maintain, however, is that, for a significant period of time, such a trade-off exists.

The opportunity cost of social relations: On the effectiveness of small worlds

97

The first refers to the value of what is exchanged. Based on our assumptions, the

opportunity cost of using the network depends positively on average knowledge: the
cost of using the network increases over time, i.e. the system of incentives is
endogenously modified. Thus, if the network continues to be used, this implies that
what is exchanged is of great value. Then, as the value of what is exchanged
increases, cliques become increasingly important with respect to short distances for
knowledge accumulation.

The second interpretation refers to the type of knowledge that is exchanged. Initially,

agents are not specialized in any particular knowledge category. Knowledge levels
across categories, and among agents, are relatively similar, and barter occurs, involving
an amount of knowledge that is relatively small. In this case, we would claim that
generic knowledge is exchanged. However, over time, specialization increases.
Typically, each agent becomes knowledgeable in a particular category (the one in
which the agent has performed individual learning), and when these agents later engage
in bartering, it is likely that they reveal knowledge in the category in which in they are
specialized. In this case, we would claim that specific knowledge is being exchanged,
i.e. knowledge where one agent has the advantage over the others. When specific
knowledge is exchanged, cliques are more important than short distances for knowledge
accumulation, while the opposite is true when generic knowledge is being exchanged.

We conclude by discussing the empirical test of our proposition. To our

knowledge, there are no existing studies that provide direct evidence in relation to
our propositions. Testing them would involve the construction of social networks of
individuals engaged in know-how trading in different regions and sectors, and
subsequent analysis of the link between the structure of the networks and some
measures of aggregate performance, controlling for a number of variables, including
those capturing the opportunity cost of know-how trading. However, there are two
empirical studies papers that show some relation to our work.

Giuliani and Bell (

2005

) examined the Chilean wine cluster. Through an original

survey, they built a network of know-how trading in the cluster. However, their focus
was on the roles of the different firms in the network and the relationship between
the firms

’ characteristics and their position in the network, and not on the relation

between network structure and aggregate performance. Furthermore, their network
was too small to apply the Watts and Strogatz model.

Fleming et al. (

2006

) share our focus on the relationship between network

structure and aggregate performance. Using data on US patents, the authors
constructed networks of inventors for 337 Metropolitan Statistical Areas, and
assumed that two inventors are socially linked if they are listed as the patent
inventors. They regressed the number of patents at regional area on the structural
properties of the network (average distance and average cliquishness). Interestingly,
they found that the degree of

“smallworldness” (i.e. how much the network mirrors a

small world) did not significantly affect aggregate performance (in terms of patents),
which, in principle, is consistent with our predictions that the network structure
effect depends on the opportunity costs of network use and, then, presumably, on
sectoral specificities. There are two caveats here: first, patents are a rough measure
of true social networks, and probably underestimate them. Second, there is evidence
that know-how trading occurs in some sectors, but not in others. Thus, ignoring the
sectoral composition at regional level could bias the results.

98

L. Cassi, L. Zirulia

6 Conclusions

This paper contributes to the theoretical literature on the relationship between
network structure and creation and diffusion of knowledge. The novelty of our study
is in integrating these theoretical studies with insights from the empirical work on
know-how trading. This literature has some recurrent specificities related to both
content and modality of exchange. First, exchange of knowledge can occur as a
barter; second, effective exchange depends on benefit and cost comparison; third,
knowledge exchange occurs between socially connected individuals. This empirical
evidence motivated us to develop a theoretical framework to account for these
specificities. In particular, since the existing theoretical studies do not consider the
use of the network as a true economic choice (i.e. a choice based on cost-benefit
analysis), we developed a simulation model in which a population of rational and
self-interested agents, active in an exogenously given social structure, can choose to
use the social network, or, alternatively, can choose to learn individually.

Based on this framework, we studied how network structure affects the aggregate

performance of the economy in terms of the overall efficiency of the system and in
terms of its equity in diffusing knowledge. Our main result is that we identified the
opportunity cost of using the network as a key variable determining its optimal
structure in terms of aggregate performance. For a low level of opportunity cost,
networks with the lowest average distance maximize efficiency of knowledge
exchange; for an intermediate level of opportunity cost, networks with relatively low
average distance and relatively high average cliquishness maximize efficiency of
knowledge exchange; and for a high level of opportunity cost, networks with the
highest average distance maximize efficient knowledge exchange. In contrast to
Cowan and Jonard

’s (

2004

) finding, the small world does not emerge as being

unambiguously the most efficient network structure. However, the small world
structure does appear to be the most equal in terms of knowledge distribution, since
the knowledge accumulated locally is diffused relatively more quickly among the
other agents. Therefore, a trade-off emerges between efficiency and equity.

While in our model opportunity cost is associated with ease of individual learning

and with time (it increases over time), we have offered two additional interpretations
of the results. The first is related to the degree of competition among agents.
Although the model does not explicitly consider competition, a different reading of
the key parameter allows us to claim that the more intense the competition, the more
cliquish is the optimal network. The second concerns how the content of the
exchange influences the optimal network structure: when the value of the knowledge
exchanged is high, or when specific knowledge is exchanged, cliquish networks are
the most efficient; conversely, when the value of the knowledge exchanged is low, or
when generic knowledge is exchanged, random networks are socially optimal.

Thus, our paper improves on the existing literature since it avoids an

“oversocialized” view of economic action. In our exercise, the social relations
among agents do not determine their behavior, but constitute a set of opportunities
and constraints which influence their behavior, which, in any case, is driven by a
benefit and cost comparison.

The main limitations of our study fall under two categories. The first is related to

the link to the empirical evidence. As we said, we included in the model only a few

The opportunity cost of social relations: On the effectiveness of small worlds

99

aspects of the know-how trading phenomenon. This has been done because we
wanted to focus on and to model in a simple way the decision of using the network
or not, while keeping the similarity with the previous theoretical literature to favor
results comparability. However, we plan now to include new details of know-how
trading, in particular by modelling explicitly the issue of diachronic learning and
reciprocity and taking into account the role played by agents

’ absorptive capacity.

The second limitation is related to the hypothesis of an exogenous network. It

would be worthwhile for future research to develop a framework able to take
account of how economic behavior might affect or modify the social environment in
which individuals are embedded. For instance, as some individuals become expert in
particular fields of knowledge, the incentives for other individuals to interact socially
increase. Thus, the fact that social networks and knowledge change at different
speeds, and that the opportunities to modify the network depend on the existing set
of relations, should be taken into account. Our future agenda involves progressing in
this direction, building partially on recent contributions in the econo-physics
literature (e.g. Ehrhardt et al.

2006

), to investigate the co-evolution between

individuals

’ attributes, their social relations and more generally the overall social

structure of the network.

References

Allen R (1983) Collective invention. J Econ Behav Organ 4:1

–24

Baumol WJ, Blinder AS (2004) Economics: principles and policy. Thompson -South Western
Breschi S, Cusmano L (2004) Unveiling the Texture of a European Research Area: emergence of

oligarchic networks under EU Framework Programmes. Int J Technol Manag 27:747

–772

Burt RS (1992) Structural holes. The social structure of competition. Harvard University Press, Cambridge MA
Carter AP (1989) Know-how trading as economic exchange. Res Policy 18:155

–163

Cohen WM, Levinthal DA (1990) Absorptive capacity: a new perspective on learning and innovation.

Adm Sci Q 35(1):128

–152

Coleman JC (1988) Social capital in the creation of human capital. Am J Sociol 94:95

–120

Cowan R, Jonard N (2003a) The dynamics of collective invention. J Econ Behav Organ 52(4):513

–532

Cowan R, Jonard N (2003b) The workings of scientific communities. In: Geuna A, Salter A, Steinmueller

E (eds) Science and innovation. Rethinking the rationales for funding and governance. Edward Elgar,
Cheltenham, pp 309

–334

Cowan R, Jonard N (2004) Network structure and the diffusion of knowledge. J Econ Dyn Control 28

(8):1557

–1575

Cowan R, David P, Foray D (2000) The explicit economics of knowledge codification and tacitness. Ind

Corp Change 9(2):211

–253

Cowan R, Jonard N, Zimmermann JB (2002) The joint dynamics of networks and knowledge. In: Cowan

R, Jonard N (eds) Heterogeneous agents interactions and economic performance. Lecture notes in
economics and mathematical systems 521. Springer, pp 155

–174

Cowan R, Jonard N, Ozman M (2004a) Knowledge dynamics in a network industry. Technol Forecast Soc

Change 71:469

–484

Cowan R, Jonard N, Zimmermann JB (2004b) On the creation of networks and knowledge. In: Gallegati

M, Kirman A, Marsili M (eds) The complex dynamics of economic interaction. Springer, pp 337

–353

Dahl M, Pedersen C (2004) Knowledge flows through informal contacts in industrial clusters: Myth or

reality? Res Policy 33:1673

–1686

Ehrhardt G, Marsili M, Vega-Redondo F (2006) Phenomemological models of socio-economic network

dynamics. Phys Rev E 74

Fleming L, King C, Juda A (2006) Small worlds and regional innovation. Organization Science

forthcoming

100

L. Cassi, L. Zirulia

Gargiulo M, Benassi M (2000) Trapped in your own net: Network cohesion, structural holes, and the

adaptation of social capital. Organ Sci 11:183

–196

Giuliani E, Bell M (2005) The micro-determinants of meso-level learning and innovation: Evidence from

a Chilean wine cluster. Res Policy 34:47

–68

Goyal S, Moraga JL, van der Leij M (2006) Economics: An emerging small world? J Polit Econ 114:

403

–412

Granovetter M (1973) The strength of weak ties. Am J Sociol 78(6):1360

–1380

Granovetter M (1985) Economic action and social structure: The problem of embeddedness. Am J Sociol

91:481

–510

Granovetter M (2005) The impact of social structure on economic outcomes. J Econ Perspect 19(1):33

–50

Kirman A (1998) The economy as an interactive system. In: Arthur WB, Durlauf S, Lane D (eds) The

economy as an evolving complex system II. Addison Wesley, Reading, MA, pp 491

–531

Lundvall B, Johnson B, Andersen ES, Dalum B (2002) National systems of production, innovation and

competence building. Res Policy 31(2):213

–231

Malerba F (2002) Sectoral systems of innovation and production. Res Policy 31(2):247

–264

Milgram S (1967) The small world problem. Psychol Today 2:60

–67

Morone P, Taylor R (2003) Small world dynamics and the process of knowledge diffusion: The case of the

metropolitan area of greater Santiago de Chile. JASSS 7(2)

Morone P, Taylor R (2004) Knowledge creation and network properties of face to face interactions. J Evol

Econ 14(3):327

–351

Powell WW, Koput KW, Smith-Doerr L (1996) Interorganizational collaboration and the locus of

innovation: networks of learning in biotechnology. Adm Sci Q 41:116

–145

Rogers E (1982) Information exchange and technological innovation. In: Sahal D (ed) The transfer and

utilization of technical knowledge. Lexington, Mass, pp 105

–123

Schrader S (1991) Informal technology transfer between firms: co-operation through information trading.

Res Policy 20:153

–170

Uzzi B (1997) Social structure and competition in interfirm networks: the paradox of embeddedness. Adm

Sci Q 42:35

–67

Uzzi B, Spiro J (2005) Collaboration and creativity: The small world problem. Am J Sociol 111:447

–504

Verspagen B, Duysters GM (2004) The small worlds of strategic technology alliances. Technovation

24:563

–571

von Hippel E (1987) Cooperation between rivals: informal know-how trading. Res Policy 16:291

–302

Walker G, Kogut B, Shan W (1997) Social capital, structural holes and the formation of an industry

network. Organ Sci 8:109

–125

Watts D, Strogatz SH (1998) Collective dynamics of

“small world” networks. Nature 393:440–442

The opportunity cost of social relations: On the effectiveness of small worlds

101

Reproduced with permission of the copyright owner. Further reproduction prohibited without permission.