Convective air drying characteristics of thin layer carrots

_IIbrahim Doymaz

*

Department of Chemical Engineering, Yildiz Technical University, Davutpasa Cad No 127, Esenler, 34210 Istanbul, Turkey

Received 6 August 2002; accepted 21 April 2003

Abstract

The effects of air temperature, air-flow rate and sample thickness on drying kinetics of carrot cubes were investigated. Convective

air drying characteristics of carrot cubes were evaluated in a cabinet dryer. Drying was carried out at 50, 60, 65, 70

C and drying

data were analyzed to obtain diffusivity values from the period of falling drying rate. In the falling rate period, moisture transfer
from carrot cubes was described by applying the FickÕs diffusion model, and effective moisture diffusion coefficients were calculated.
Effective diffusivity increased with increasing temperature. An Arrhenius relation with an activation energy value of 28.36 kJ/mol
expressed effect of temperature on the diffusivity. Two mathematical models available in the literature were fitted to the experimental
data. The Page model is given better prediction than the Henderson and Pabis model and satisfactorily described drying charac-
teristics of carrot cubes.
2003 Elsevier Ltd. All rights reserved.

Keywords: Carrot; Drying; Rehydration; Mathematical modelling; Diffusivity; Activation energy

1. Introduction

Carrot is one of the most commonly used vegetables

for human nutrition due to high vitamin and fibre
content. Since higher temperature causes wilt and have a
poor appearance on the carrots, refrigeration and con-
trolled atmosphere storage have been used (Negi & Roy,
2000). Alternatively, the keeping ability of carrot can be
enhanced by drying and subsequent storage. Drying
operations are important steps in food processing in-
dustry. Drying is one of the oldest methods of food
preservation, and it represents a very important aspect
of food processing. Sun drying is the most common
method used to preserve agricultural products in most
tropical countries. However, this technique is extremely
weather dependent, and has the problems of contami-
nation with dust, soil, sand particles and insects, and
being weather dependent. Also, the required drying time
can be quite long. Therefore, using solar and hot-air
dryers, which are far more rapid, providing uniformity
and hygiene are inevitable for industrial food drying
processes (Diamante & Munro, 1993; Ratti & Mujum-
dar, 1997).

Many studies were done to process carrot by air

drying (Mulet, Berna, & Rosello, 1989), sun drying
(Mulet, Berna, Rosello, & Canellas, 1993), convection-
microwave drying (Prabhanjan, Ramaswamy, & Ragh-
avan, 1995; Sanga, Mujumdar, & Raghavan, 2002), and
combination of freeze drying, microwave heating and air
or vacuum drying (Lin, Durance, & Scaman, 1998;
Litvin, Mannheim, & Miltz, 1998) and solar drying
(Ratti & Mujumdar, 1997).

Several studies have been conducted to the influence

of some process parameters such as temperature, sample
thickness and air-flow rate, etc. Cordova-Quiroz, Ruiz-
Cabrera, and Garcia-Alvarado (1996) investigated the
effect of carrot slices with 0.5 cm thickness and 0.5–1.0
m/s of air-flow rate on the drying kinetics. Ruiz-
Cabrera, Salgado-Cervantes, Waliszewski-Kubiak, and
Garcia-Alvarado (1997) studied the effect of path dif-
fusion on the average moisture diffusivity in carrot
samples (cylinders and slices) temperatures ranging from
50 to 70

C. Mulet, Berna, Borras, and Pinaga (1987)

indicated that when air mass flow is higher than 4200 kg/
(m

2

h) it has not effect over 1 cm carrot cubes drying at

30

C.

The aim of this research was (1) to observation of

the effect of process parameters such as drying temper-
ature, air-flow rate and simple thickness, (2) to estimate
the constants of selected model equations as well as

Journal of Food Engineering 61 (2004) 359–364

www.elsevier.com/locate/jfoodeng

*

Tel.: [phone]; fax: [phone].

E-mail address:

[e-mail]

(_II. Doymaz).

0260-8774/$ - see front matter

2003 Elsevier Ltd. All rights reserved.

doi:10.1016/S0260-8774(03)00142-0

diffusion coefficient and activation energy, for drying of
carrot.

2. Modelling

A constant rate-drying period was not observed in

any of the experiments of this study. In most studies
carried out on drying, diffusion is generally accepted to
be the main mechanism during the transport of moisture
to the surface to be evaporated. The solution of FickÕs
equation, with the assumptions of moisture migration
being by diffusion, negligible shrinkage, constant diffu-
sion coefficients and temperature and for a sphere
(Crank, 1975; Pala, Mahmutoglu, & Saygi, 1996):

MR

¼

m

m

e

m

0

m

e

¼

6

p

2

X

1

n

¼1

1

n

2

exp

p

2

n

2

D

eff

t

r

2

ð1Þ

where m, m

0

and m

e

are the local, initial and equilbrium

moisture content, respectively, r is the radius, t is the
time and D

eff

is the effective diffusivity (m

2

/s).

The Henderson and Pabis model is first term of

general series solution of FickÕs second law (Henderson
& Pabis, 1961; Ozdemir & Devres, 1999). The moisture
ratio,

MR

¼

m

m

e

m

0

m

e

¼

6

p

2

exp

p

2

D

eff

t

r

2

ð2Þ

Eq. (2) can also be written in a more simplified form as:

ln

m

m

e

m

0

m

e

¼ k exp ð ctÞ

ð3Þ

Other widely applied empirical equation is the Page

equation. PageÕs model has been widely advocated for
thin layer drying of solids under constant drying con-
ditions. This model has produced good fits in predicting
drying of sweet potato (Diamante & Munro, 1993),
garlic (Madamba, Driscoll, & Buckle, 1996), apricot
(Pala et al., 1996), seedless grapes (Doymaz & Pala,

2002), and mint leaves (Park, Vohnikova, & Brod,
2002). It is written in this form:

MR

¼

m

m

e

m

0

m

e

¼ expðzt

N

Þ

ð4Þ

The values of the equilibrium moisture content, m

e

, are

relatively small compared to m or m

0

. Thus

ðm m

e

Þ=

ðm

0

m

e

Þ is simplified to m=m

0

MR

¼

m

m

0

¼ k exp ð ctÞ

ð5Þ

MR

¼

m

m

0

¼ expðzt

N

Þ

ð6Þ

3. Material and methods

The drying of carrot slices was investigated in cabinet

dryer installed in the Chemical Engineering Department
of Yildiz Technical University. Cabinet dryer is pro-
duced by APV and PASILAC (England). The dryer
basically consist of a centrifugal fan to supply the air-
flow, an electric heater, an air filter and an electronic
proportional controller. The air temperature was con-
trolled by means of a proportional controller. During
the drying experiments, air-flow rates of 0.5 and 1.0 m/s
were measured with TESTO 440 Vane Probe Ane-
mometer, and flowed perpendicular to the bed. The
samples were dried in the perforated square chamber,
which had a flow cross-section of 30 cm

· 30 cm. The air

was circulated by a variable speed fan and heated by
electricity.

Carrots (Daucus carota L.) procured from the local

market were used in the studies. Samples were stored in
a refrigerator at 4

C prior to the drying experiments. At

the start of each experiment, the carrots were washed
and cut into cubes, which are consisted both orange
exterior and yellow core, having the dimensions of
1

· 1 · 1 and 2 · 2 · 2 cm using a kitchen slicer. These

Nomenclature

c

constant (Eq. (3)), 1/s

D

eff

effective moisture transfer diffusion coeffi-
cient, m

2

/s

D

0

pre-exponential factor, m

2

/s

d

diameter, cm

E

a

activation energy, kJ/mol

k

constant (Eq. (3)), dimensionless

MR

moisture ratio

m

moisture content, kg moisture/kg dry matter

m

0

initial moisture content, kg moisture/kg dry
matter

m

e

equilibrium moisture content, kg moisture/kg
dry matter

N

constant (Eq. (4)), dimensionless

R

gas constant, kJ/mol K

R

2

correlation coefficient

RC

rehydration capacity

r

radius, cm

T

temperature (

C or K)

t

drying time, h

v

air-flow rate, m/s

z

constant (Eq. (4)), s

N

360

_II. Doymaz / Journal of Food Engineering 61 (2004) 359–364

cubes were blanched at 100

C for 5 min, immediately

cooled in 15

C water for 5 min to remove excess heat,

and then the surface water was absorbed with filter
paper. The carrot cubes were spread in a square cham-
ber in a single layer. The sample size was kept constant
at 200 g for all runs. The initial moisture content of
carrots was about 87.5% (w/w) (AOAC, 1990). Weight
loss of samples was measured by means of a load cell
(REVERE SHBXM CC) and was recorded at 0.5–1 h
intervals during drying. Four inlet air temperatures of
50, 60, 65 and 70

C were used for the runs. Drying tests

were replicated three times at each inlet air temperature,
and averages are reported.

Drying of carrot cubes were finalized when the

moisture content decreased to 6% from an initial value
of 87.5% (w/w). The product was cooled for 10 min after
drying, and kept in air glass jars.

The rehydration ratio of dried carrot cubes was de-

termined by immersing 20 g samples in water at 95

C.

Samples were drained and weighed at 10 min for those
at 95

C. Rehydration Capacity (RC) in described as

(Lewicki, 1998):

RC

¼

Weight of water absorbed during rehydration

Weight of water removed during drying

100

ð7Þ

4. Results and discussion

4.1. Influence of process parameters

The drying times according to experimental condi-

tions selected were presented in Table 1. The moisture
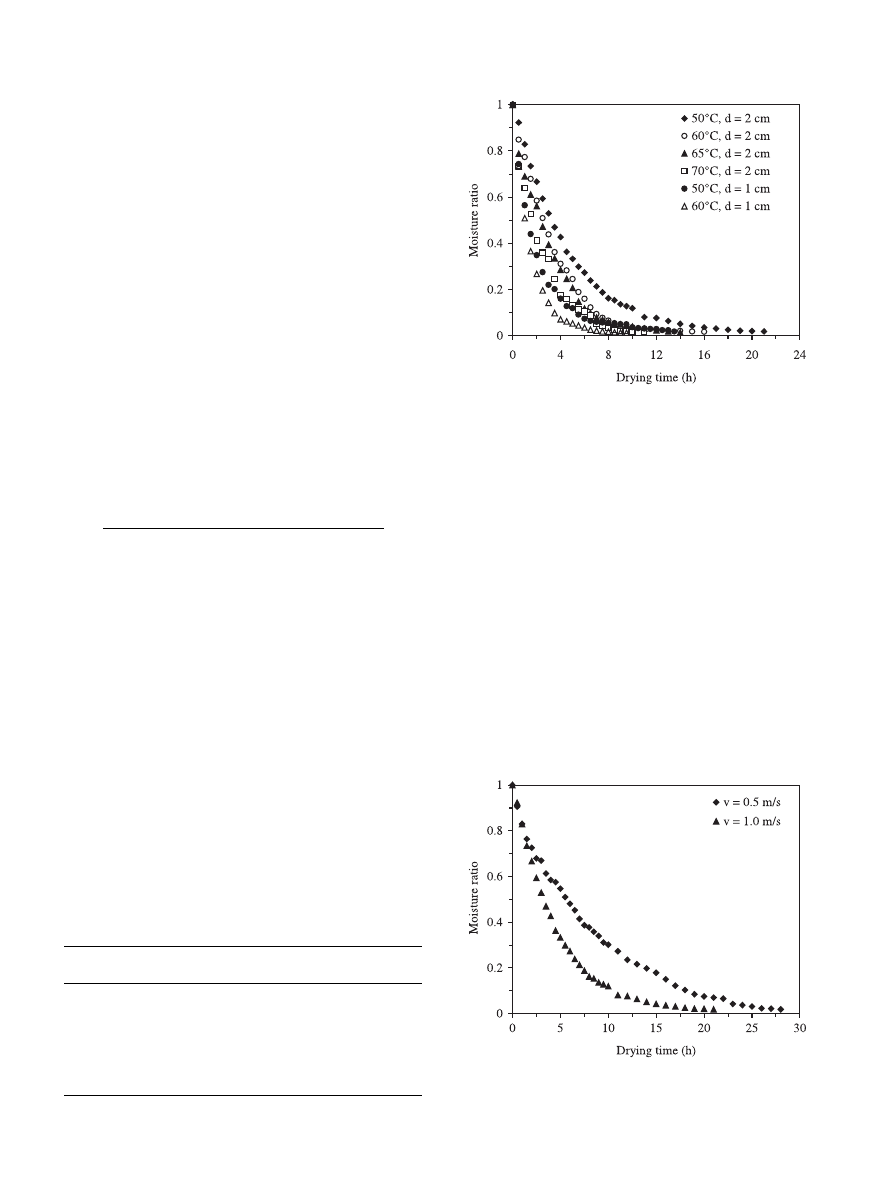
ratio versus time curves for thin layer drying of carrots
as influenced by temperature (50–70

C) is shown in

Fig. 1. As can be observed, increasing the drying tem-
perature caused an important increase in the drying rate,
thus the drying time is decreased. The curves typically
demonstrated smooth diffusion-controlled drying be-
havior under all run conditions.

In general, the time required to reduce the moisture

ratio to any given level was dependent on the drying

condition, being the highest at 50

C and lowest 70 C.

With drying, the time taken to reduce moisture content
of carrot cubes (d

¼ 2 cm) from the initial 87.5% to a

final 6% was 21, 16, 14 and 11 h at 50, 60, 65 and 70

C,

respectively. The drying times for carrot cubes (d

¼

1 cm) at 50 and 60

C were 13.5 and 9.5 h, respectively.

Consequently, the effect of air temperature has been
reflected in drying rate. However, at higher than 70

C,

the dried product was partially lost its fresh product
characteristics (Mulet et al., 1987). Similar results were
reported by Prabhanjan et al. (1995), and by Ozdemir
and Devres (1999).

The results obtained in runs of E1 and E2 were used

to analyze the effect of air-flow rate on moisture ratio.
Fig. 2 shows the effect of air-flow rate on drying rate.
The drying time for the E1 run was 28 h, whereas E2 run

Table 1
Drying conditions versus drying times observed

Run

Diameter
(cm)

Air-flow
rate (m/s)

Tempera-
ture (

C)

Drying
time (h)

E1

2.0

0.5

50

28.0

E2

2.0

1.0

50

21.0

E3

2.0

1.0

60

16.0

E4

2.0

1.0

65

14.0

E5

2.0

1.0

70

11.0

E6

1.0

1.0

50

13.5

E7

1.0

1.0

60

9.5

Fig. 1. Variation of carrot cubes moisture ratio with time at different
temperatures.

Fig. 2. Drying curves at different air-flow rates for carrot cubes (d

¼

2 cm, T

¼ 50 C).

_II. Doymaz / Journal of Food Engineering 61 (2004) 359–364

361

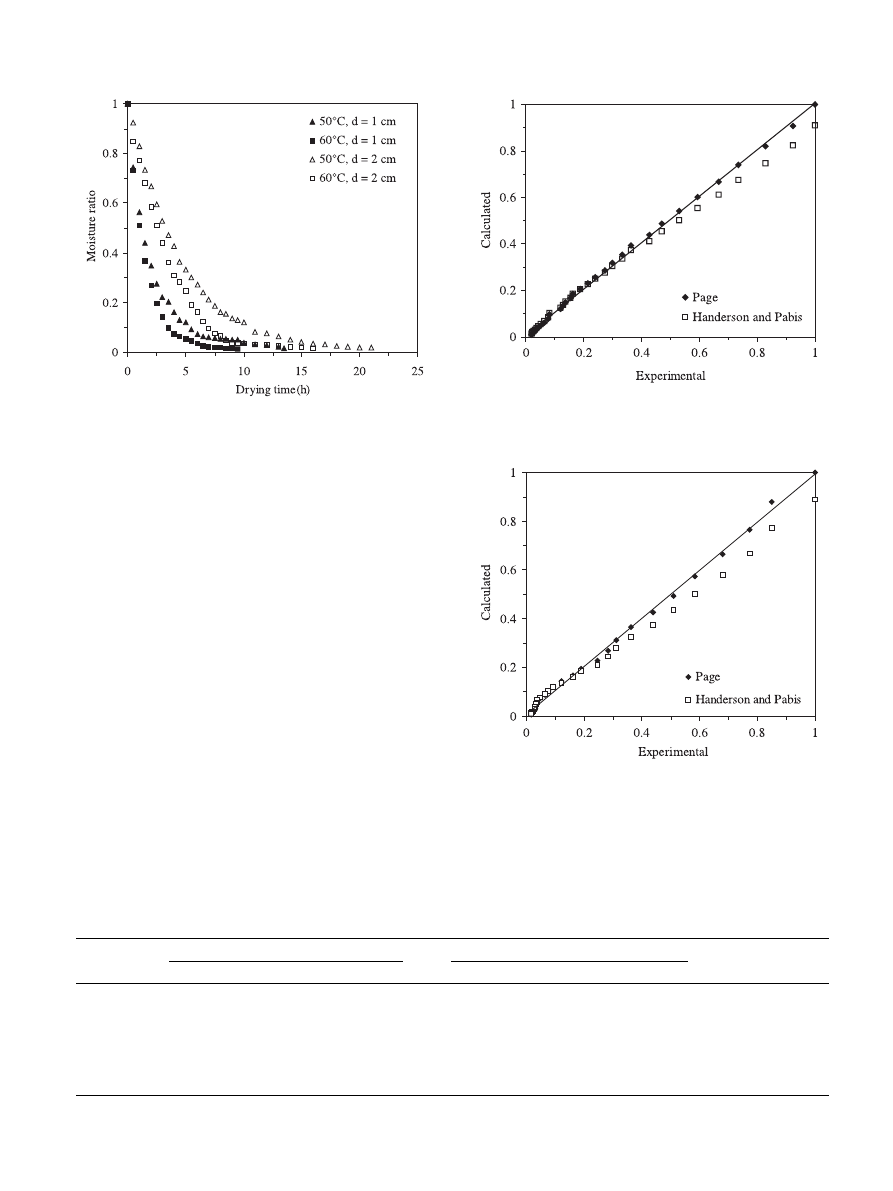
was 21 h. These results demonstrated that the drying
time was decreased than 25% depend on higher air-flow
rate. As a result, the drying rate increased with the air-
flow rate. It must be noted that the air-flow at which
water leaves the solid matrix.

The results obtained in runs E2, E3, E6 and E7 were

used to analyze the effect of sample diameter on mois-
ture ratio. The results were presented in Fig. 3. As dia-
meter of sample increases, the drying time increases
due to increased diffusion path.

Moreover, the some part of product (E3) that is dried

at 60

C, is drained in water for 10 min at 95 C. As a

result of the treatment rehydration ratio is obtained as
93%.

4.2. Evaluation of the models

In order to determine the moisture content as a

function of drying time, empirical Henderson and Pabis
(Eq. (5)) and Page (Eq. (6)) equations were fitted and
correlation coefficients (R

2

) were calculated. The coeffi-

cients of correlation and estimated parameters for the
two models are presented in Table 2. The values of R

2

obtained from Page equation are higher than those at-
tained by Henderson and Pabis equation. The R

2

values

of Page equation vary between 0.985 and 0.995 and

Fig. 3. Effect of simple thickness on air drying of carrot cubes at 50
and 60

C.

Fig. 4. Comparison of experimental and calculated moisture ratios of
carrot cubes (d

¼ 2 cm, T ¼ 50 C, v ¼ 1:0 m/s).

Fig. 5. Comparison of experimental and calculated moisture ratios of
carrot cubes (d

¼ 2 cm, T ¼ 60 C, v ¼ 1:0 m/s).

Table 2
Results of diffusion coefficients and regression analysis for constants and correlation coefficients of the Page with the Handerson and Pabis equations

Run

Page equation

Handerson and Pabis equation

D

eff

10

9

(m

2

/s)

z

N

R

2

k

c

R

2

E1

0.0164

0.8682

0.991

1.0777

0.1359

0.987

0.776

E2

0.1989

1.0281

0.995

0.9096

0.1988

0.993

1.304

E3

0.2672

1.0628

0.987

0.8899

0.2872

0.956

1.882

E4

0.3282

0.9985

0.989

0.9233

0.3147

0.988

2.072

E5

0.4716

0.9166

0.988

0.9655

0.4012

0.987

2.418

E6

0.6089

0.7449

0.985

0.6625

0.4614

0.967

5.980

E7

0.6872

0.8773

0.986

0.5516

0.2667

0.959

9.335

362

_II. Doymaz / Journal of Food Engineering 61 (2004) 359–364

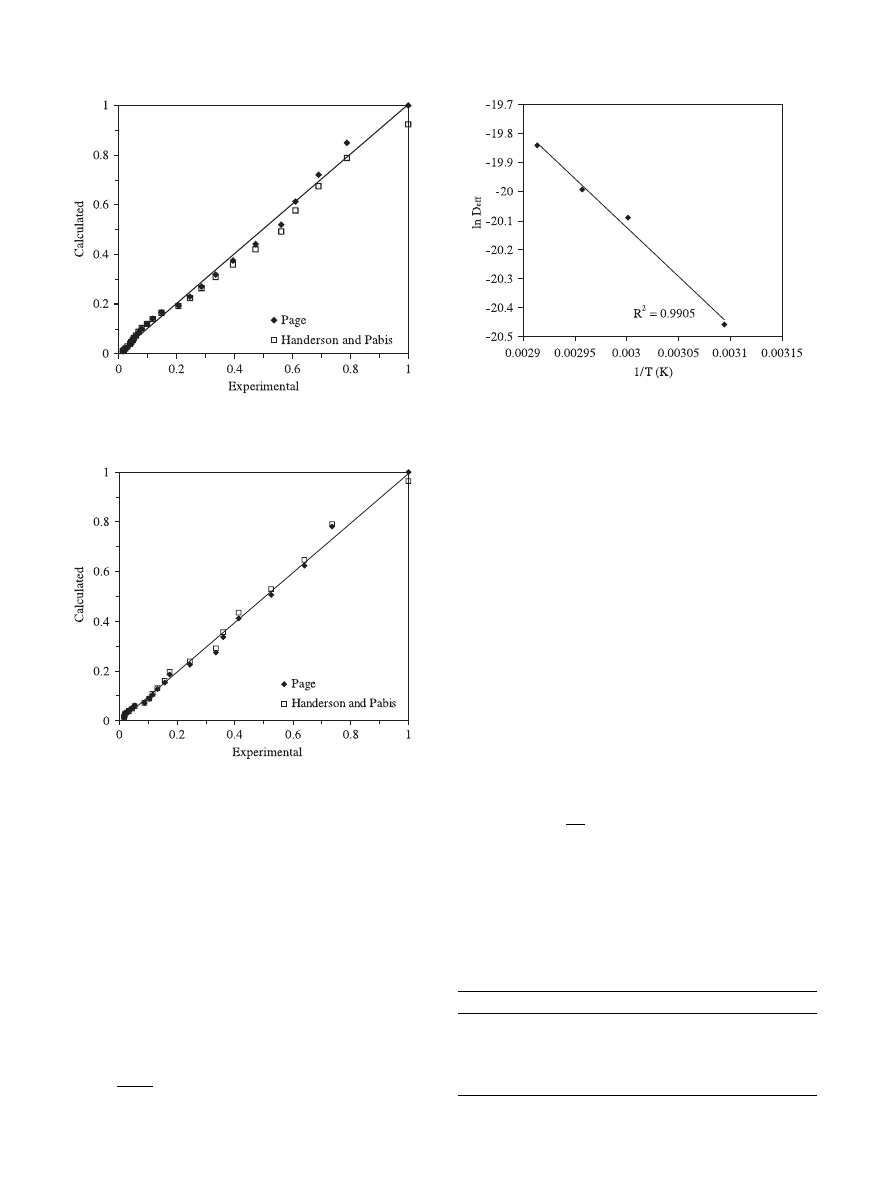
between 0.956 and 0.993 for the Henderson and Pabis
equation (Table 2). In Figs. 4–7 are reported the cal-
culated versus the experimental moisture data. Good
agreement between the former variables is observed.
Similar findings were reported by Madamba et al. (1996)
for garlic slices, and by Doymaz and Pala (2002) for
grape drying.

4.3. Calculation of moisture diffusivity and activation
energy

From Eq. (2), a plot of ln MR versus time gives a

straight line with a slope of:

slope

¼

p

2

D

eff

r

2

ð8Þ

Values of D

eff

for different temperatures are presented in

Table 1. These values of diffusivity in the range of
0.776

· 10

9

–9.335

· 10

9

m

2

/s

are

comparable

to

1.371

· 10

7

m

2

/s for drying 4 mm thick fresh carrot

slices in air at 60

C (Markowski, 1997), 1–3 · 10

11

m

2

/s

for apricot in temperature range of 50–80

C (Abdelhaq

& Labuza, 1987), 1.5

· 10

-9

m

2

/s for raisin (Lomauro,

Bakshi, & Labuza, 1985), 2

· 10

9

–29

· 10

9

m

2

/s for

blanched mushroom in temperature range of 40 and
70

C (Sahbaz, Uzman, & Palazoglu, 2000). These values

are consistent with the present estimated D

eff

values for

carrot cubes.

Effect of temperature on effective diffusivity is de-

scribed using Arrhenius relationship to obtain better
agreement of the predicted curve with experimental data
(Madamba et al., 1996; Ozdemir & Devres, 1999). Val-
ues of D

eff

calculated Eq. (2) for different drying exper-

iments were plotted in Fig. 8. The plot was found to be
essentially a straight line in the range of temperatures
investigated, indicating Arrhenius dependence.

D

eff

¼ D

0

exp

E

a

RT

ð9Þ

where D

0

is the pre-exponential factor (m

2

/s), E

a

is the

activation energy (kJ/mol), T is the temperature of air
(K) and R is the gas constant (kJ/mol K).

From the slope of the straight line described by

the Arrhenius equation, the activation energy, E

a

was

Fig. 6. Comparison of experimental and calculated moisture ratios of
carrot cubes (d

¼ 2 cm, T ¼ 65 C, v ¼ 1:0 m/s).

Fig. 7. Comparison of experimental and calculated moisture ratios of
carrot cubes (d

¼ 2 cm, T ¼ 70 C, v ¼ 1:0 m/s).

Fig. 8. Effect of temperature on moisture diffusivity in carrot cubes
(d

¼ 2 cm, v ¼ 1:0 m/s).

Table 3
Activation energies of carrot and other products

Product

E

a

(kJ/mol)

References

Corn

27.61

Tolaba and Suarez (1988)

Potato

20.00

Bon, Simal, Rossell

o

o, and Mulet (1997)

Mint

82.93

Park et al. (2002)

Prune

57.00

Sabarez and Price (1999)

Carrot

28.36

Present work

_II. Doymaz / Journal of Food Engineering 61 (2004) 359–364

363

determined as 28.36 kJ/mol. The comparison with lit-
erature values for various fruits and vegetables is shown
in Table 3.

5. Conclusions

The most important characteristics of carrot required

for simulation and optimization of the drying were
studied. The values of calculated effective diffusivity for
drying at 50, 60, 65 and 70

C of air temperature and 0.5

and 1.0 m/s of air flow rates ranged from 0.776

· 10

9

to

9.335

· 10

9

m

2

/s. The effective diffusivity increases as

air-flow rate and temperature increases. Temperature
dependence of the diffusivity coefficients was described
by Arrhenius-type relationship. The activation energy
for moisture diffusion was found as 28.36 kJ/mol.
Comparable with the reported values of various food
materials. PageÕs empirical model showed a good fit
curves than the Henderson and Pabis model.

References

Abdelhaq, E. H., & Labuza, T. P. (1987). Air drying characteristics of

apricots. Journal of Food Science, 52(2), 342–345.

AOAC (1990). Official method of analysis. Association of Official

Analytical Chemists (No. 934.06), Arlington, VA.

Bon, J., Simal, S., Rossell

o

o, C., & Mulet, A. (1997). Drying

characteristics of hemispherical solids. Journal of Food Engineering,
34, 109–122.

Cordova-Quiroz, V. A., Ruiz-Cabrera, M. A., & Garcia-Alvarado, M.

A. (1996). Analytical solution of mass transfer equation with
interfacial resistance in food drying. Drying Technology, 14(7–8),
1815–1826.

Crank, J. (1975). The mathematics of diffusion (2nd ed.). Oxford, UK:

Clarendon Press.

Diamante, L. M., & Munro, P. A. (1993). Mathematical modelling of

the thin layer solar drying of sweet potato slices. Solar Energy,
51(4), 271–276.

Doymaz, I., & Pala, M. (2002). The effects of dipping pretreatments

on air-drying rates of seedless grapes. Journal of Food Engineering,
52(4), 413–417.

Henderson, S. M., & Pabis, S. (1961). Grain drying theory I:

Temperature effect on drying coefficient. Journal of Agricultural
Research Engineering, 7, 85–89.

Lewicki, P. P. (1998). Some remarks of rehydration of dried foods.

Journal of Food Engineering, 36, 81–87.

Lin, T. M., Durance, T. D., & Scaman, C. H. (1998). Characterization

of vacuum microwave, air and freeze dried carrot slices. Food
Research International, 31(2), 111–117.

Litvin, S., Mannheim, C. H., & Miltz, J. (1998). Dehydration of

carrots by a combination of freeze drying, microwave heating and
air or vacuum drying. Journal of Food Engineering, 36, 103–111.

Lomauro, C. J., Bakshi, A. S., & Labuza, T. P. (1985). Moisture

transfer properties of dry and semimoist foods. Journal of Food
Science, 50, 397–400.

Madamba, P. S., Driscoll, R. H., & Buckle, K. A. (1996). The thin-

layer drying characteristics of garlic slices. Journal of Food
Engineering, 29, 75–97.

Markowski, M. (1997). Air drying of vegetables: Evaluation of mass

transfer coefficient. Journal of Food Engineering, 34, 55–62.

Mulet, A., Berna, A., Borras, M., & Pinaga, F. (1987). Effect of air

flow rate on carrot drying. Drying Technology, 5(2), 245–258.

Mulet, A., Berna, A., & Rosello, S. (1989). Drying of carrots. I. Drying

models. Drying Technology, 7(3), 537–557.

Mulet, A., Berna, A., Rosello, S., & Canellas, J. (1993). Analysis of

open sun drying experiments. Drying Technology, 11(6), 1385–
1400.

Negi, P. S., & Roy, S. K. (2000). Effect of low-cost storage and

packaging on quality and nutritive value of fresh and dehydrated
carrots. Journal of the Science of Food Agriculture, 80(15), 2169–
2175.

Ozdemir, M., & Devres, Y. O. (1999). The thin layer drying

characteristics of hazelnuts during roasting. Journal of Food
Engineering, 42, 225–233.

Pala, M., Mahmutoglu, T., & Saygi, B. (1996). Effects of pretreatments

on the quality of open-air and solar dried apricots. Nahrung, 40(3),
137–141.

Park, K. J., Vohnikova, Z., & Brod, F. P. R. (2002). Evaluation of

drying parameters and desorption isotherms of garden mint leaves
(Mentha crispa L.). Journal of Food Engineering, 51, 193–199.

Prabhanjan, D. G., Ramaswamy, H. S., & Raghavan, G. S. V. (1995).

Microwave-assisted convective air drying of thin layer carrots.
Journal of Food Engineering, 25, 283–293.

Ratti, C., & Mujumdar, A. S. (1997). Solar drying of foods. Modeling

and numerical simulation. Solar Energy, 60(3–4), 151–157.

Ruiz-Cabrera, M. A., Salgado-Cervantes, M. A., Waliszewski-Kubiak,

K. N., & Garcia-Alvarado, M. A. (1997). Effect of path diffusion
on the effective moisture diffusivity in carrot slabs. Drying
Technology, 15(1), 169–181.

Sabarez, H. T., & Price, W. E. (1999). A diffusion model for prune

dehydration. Journal of Food Engineering, 42(3), 167–172.

Sahbaz, F., Uzman, D., & Palazoglu, T. K. (2000). Drying kinetics of

blanched and unblanched mushrooms. Nahrung, 44(4), 283–284.

Sanga, E. C. M., Mujumdar, A. S., & Raghavan, G. S. V. (2002).

Simulation of convection-microwave drying for a shrinking mate-
rial. Chemical Engineering and Processing, 41, 487–499.

Tolaba, M., & Suarez, C. (1988). Simulation of the thin-layer drying of

corn by means of the diffusional model. Lebensmittel-Wissenschaft
und-Technologie, 21, 83–86.

364

_II. Doymaz / Journal of Food Engineering 61 (2004) 359–364