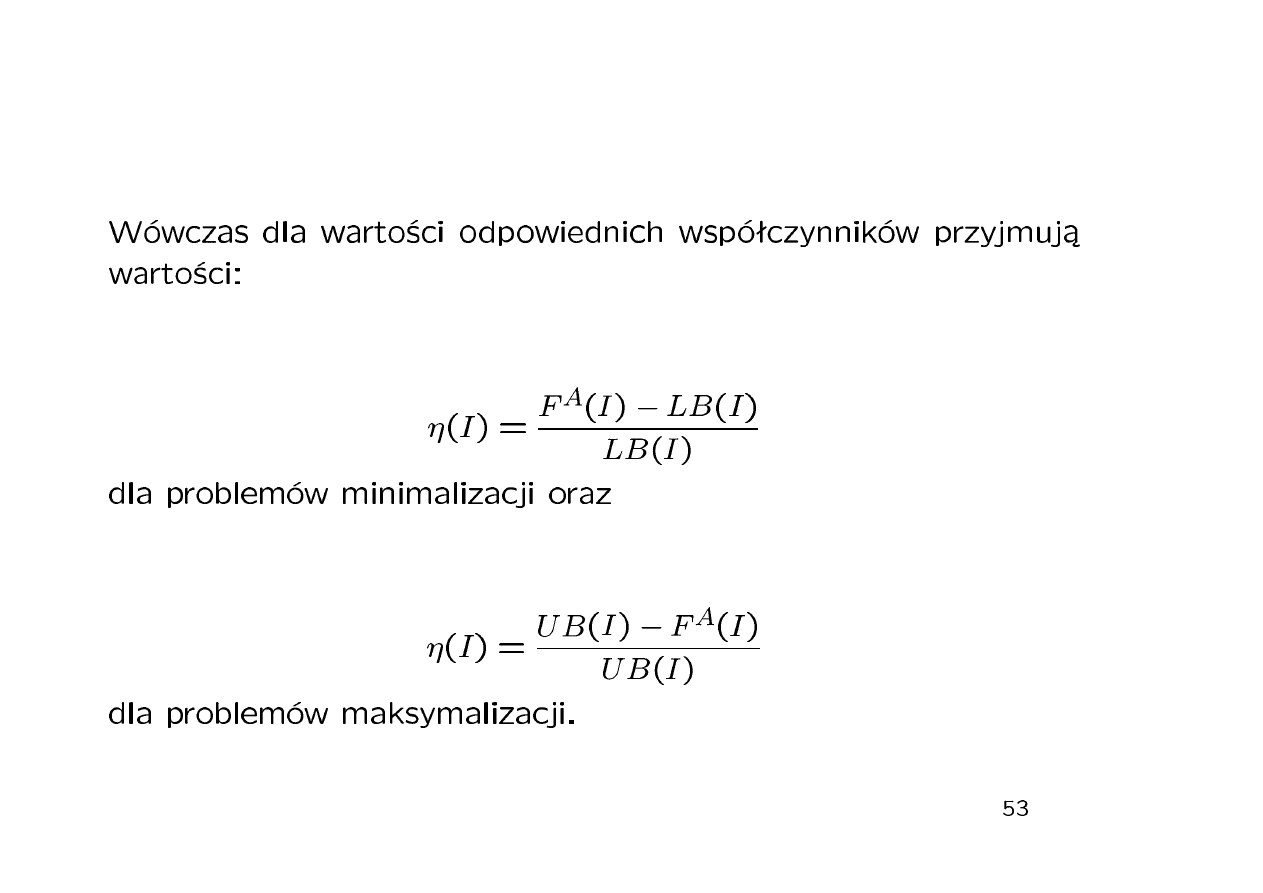
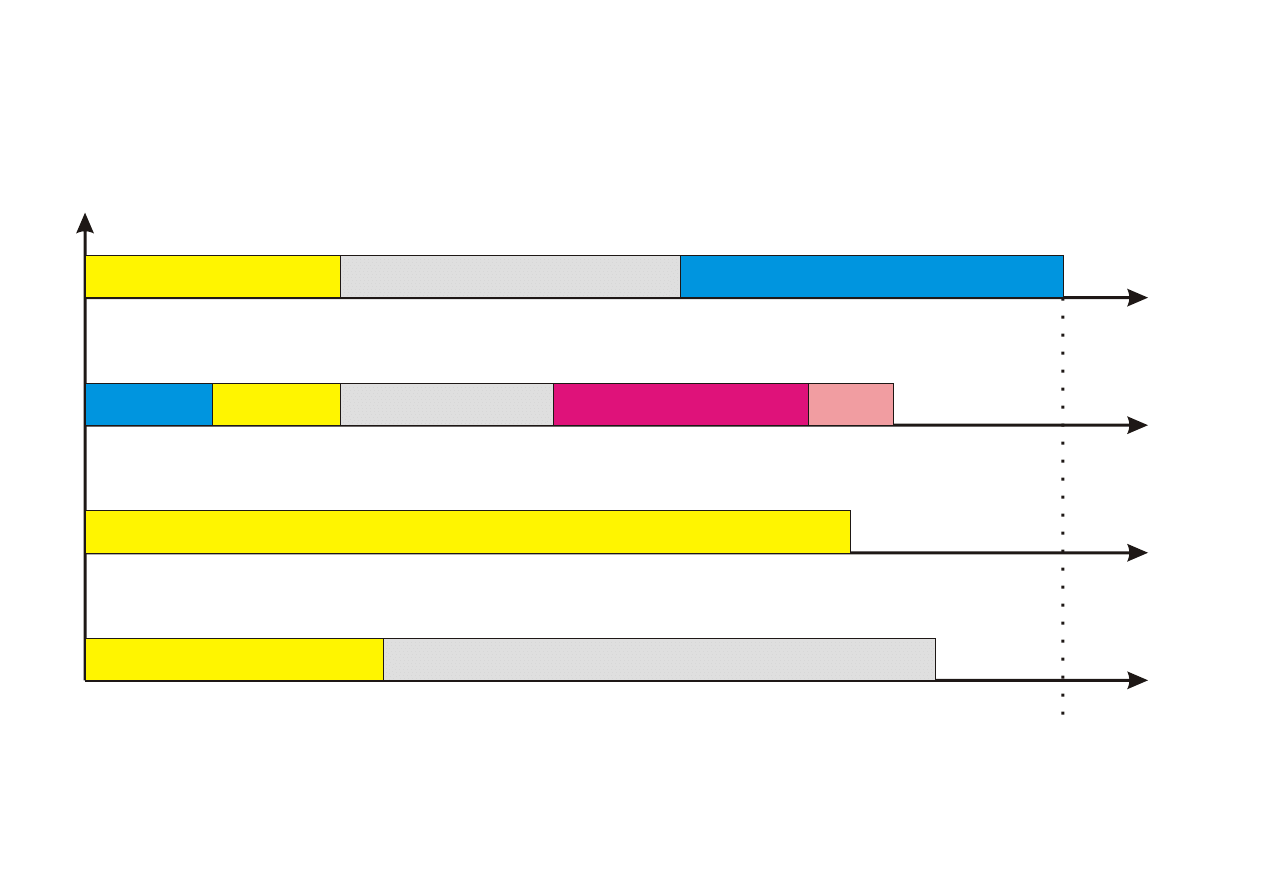
1

2

3

4

czas

procesor

C

max

1

2

3

4

5

6

7

8

9

10

11

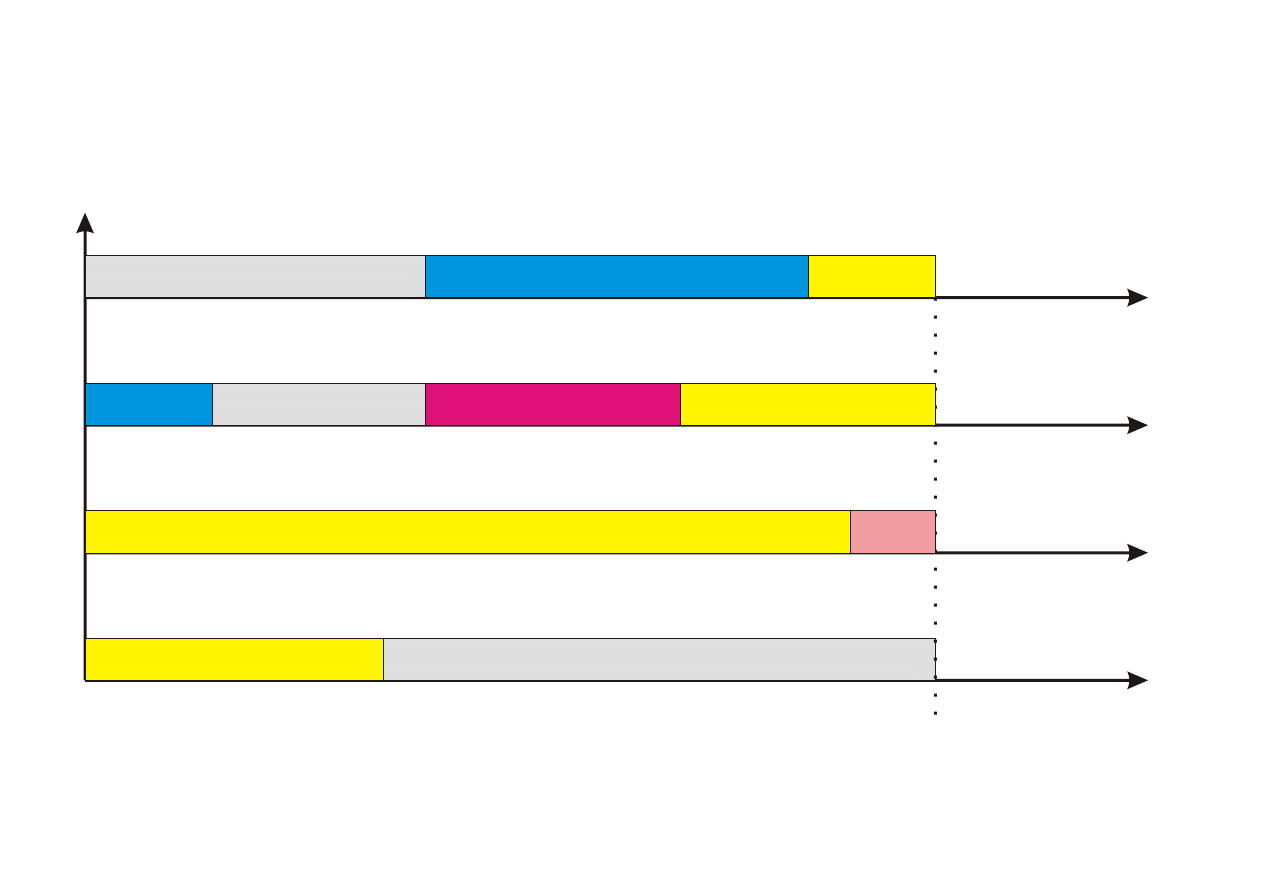
1

2

3

4

czas

procesor

C

max

2

3

1

4

5

6

7

8

9

10

11

1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

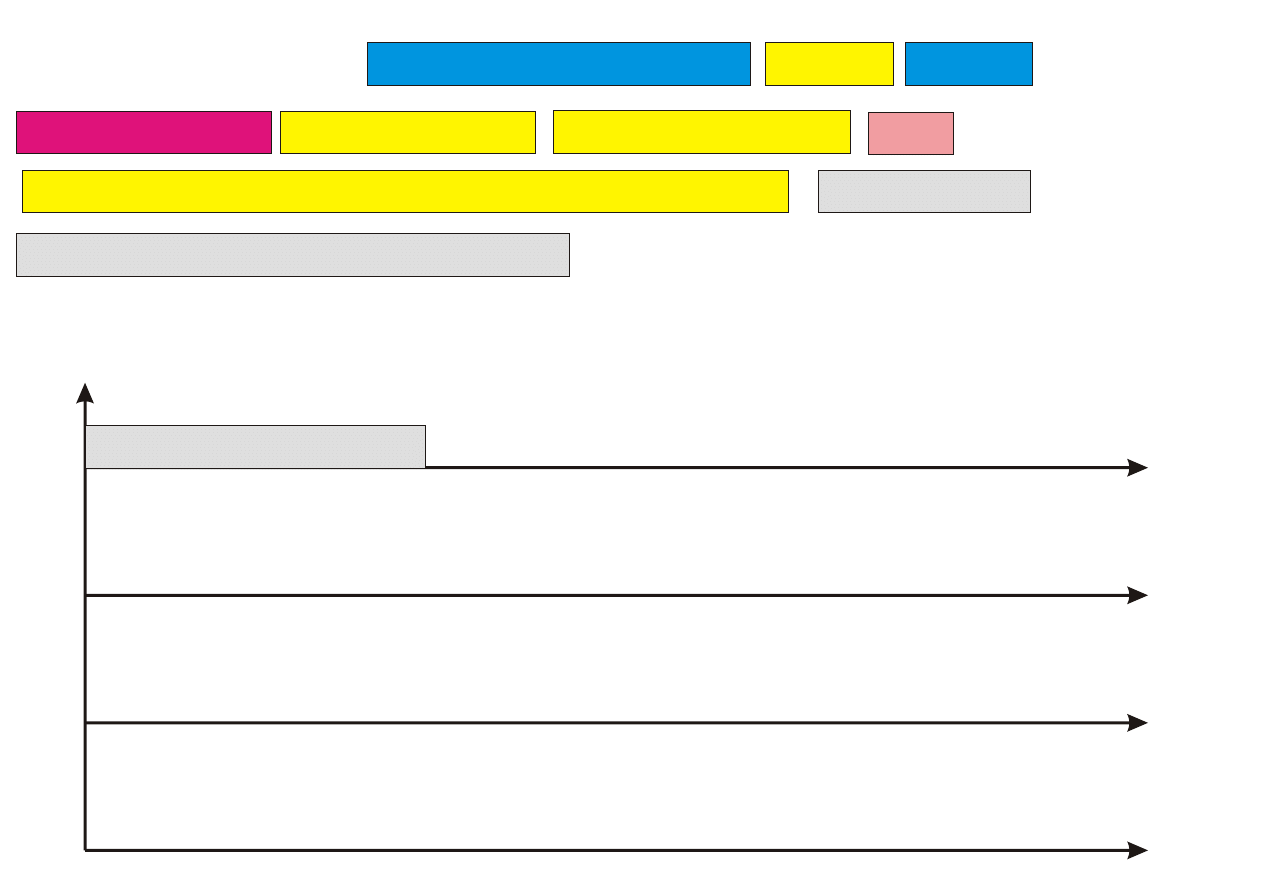
1

2

3

4

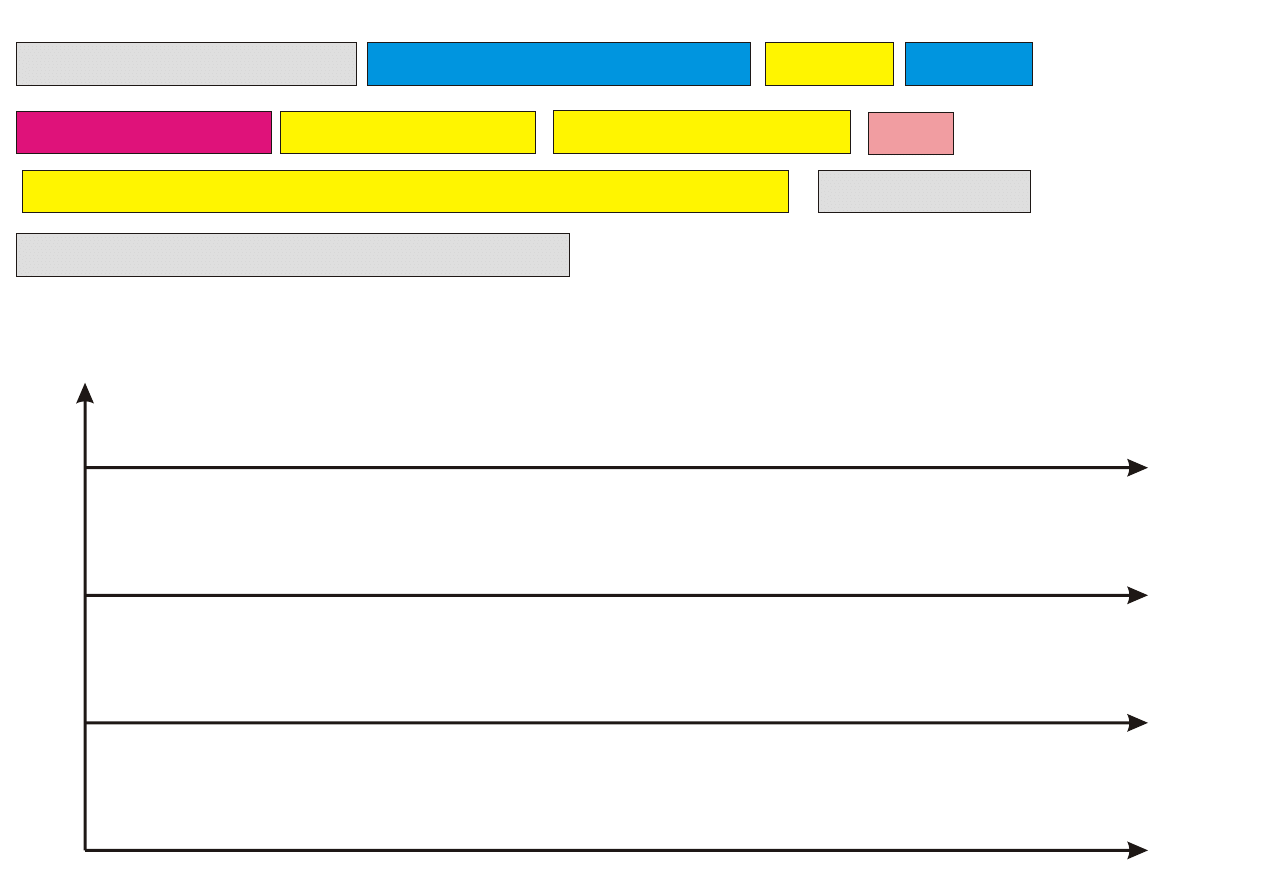
procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

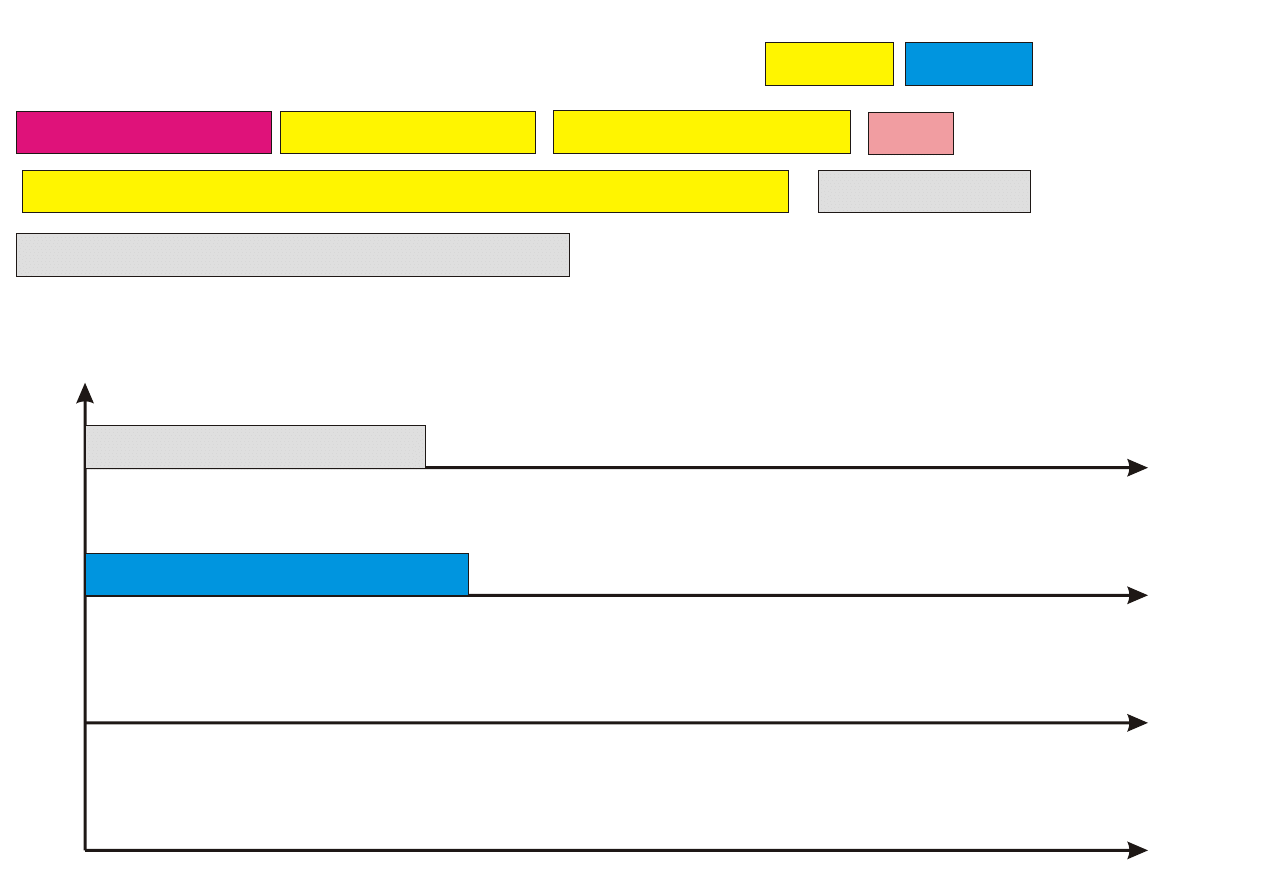
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

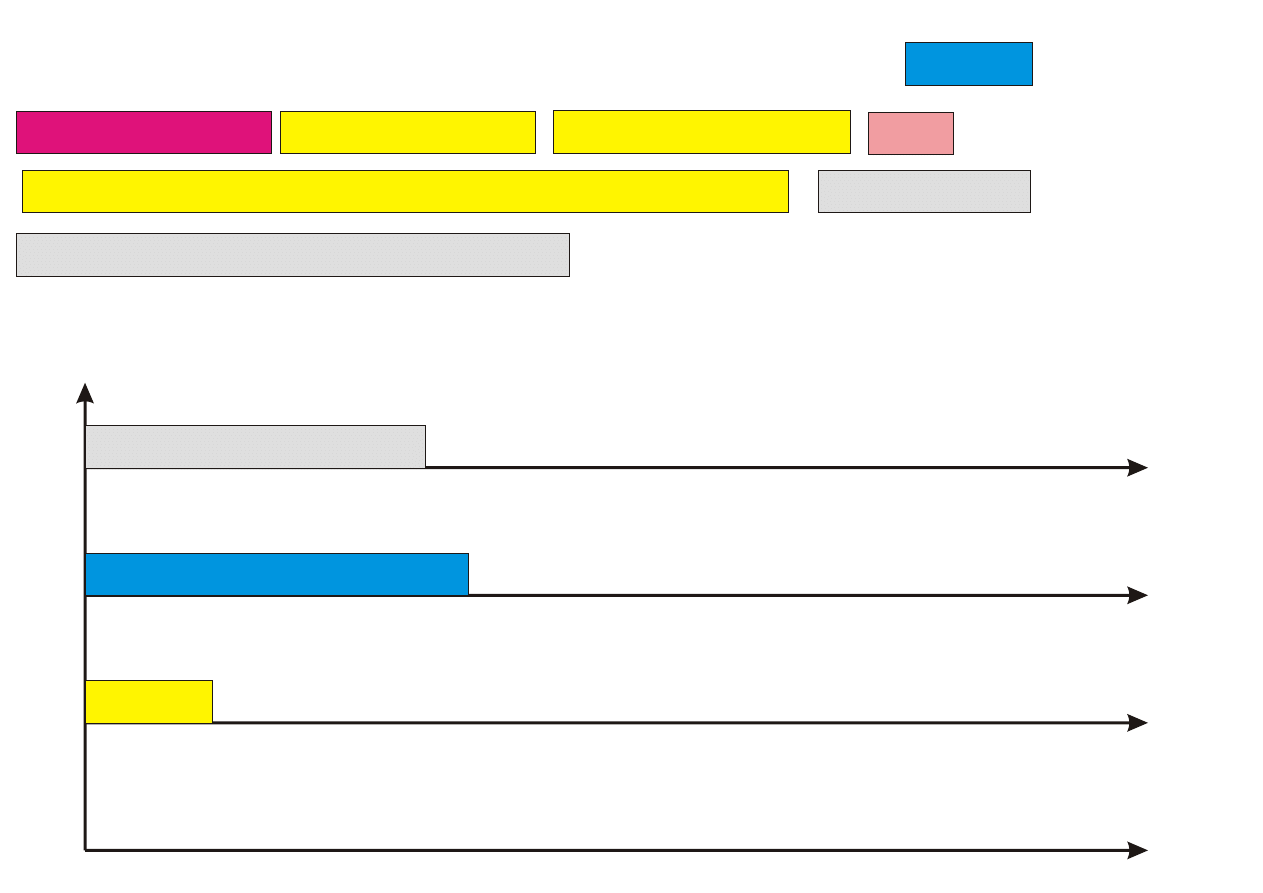
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

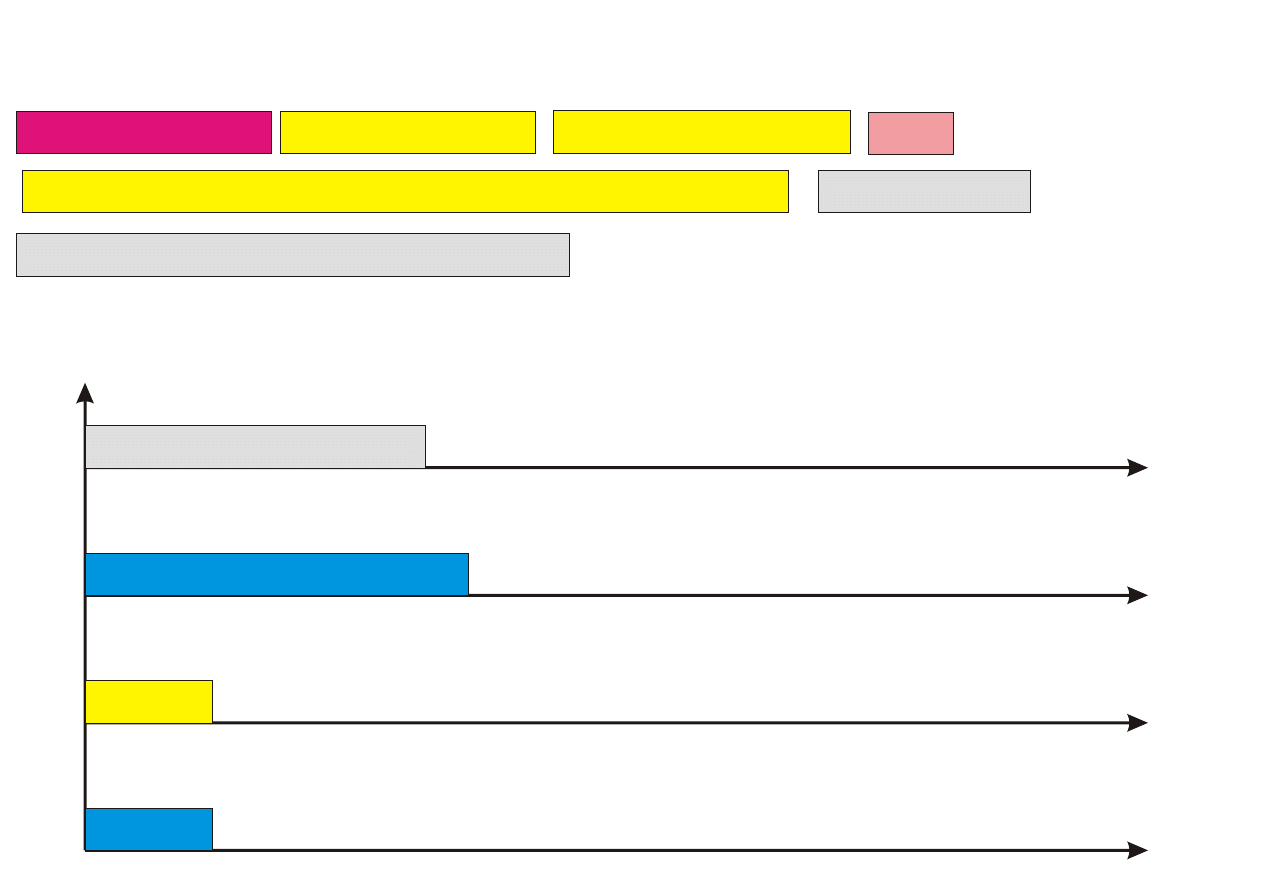
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

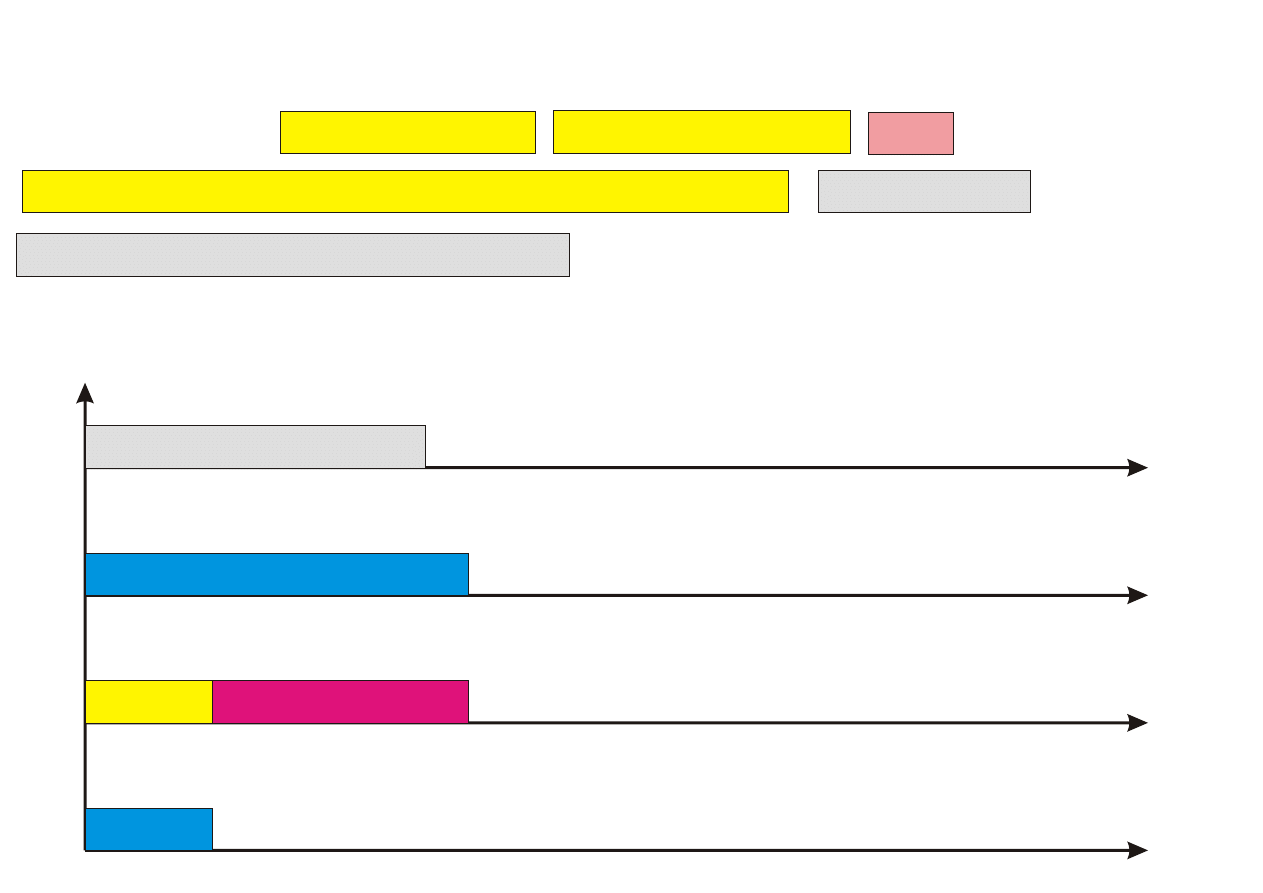
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

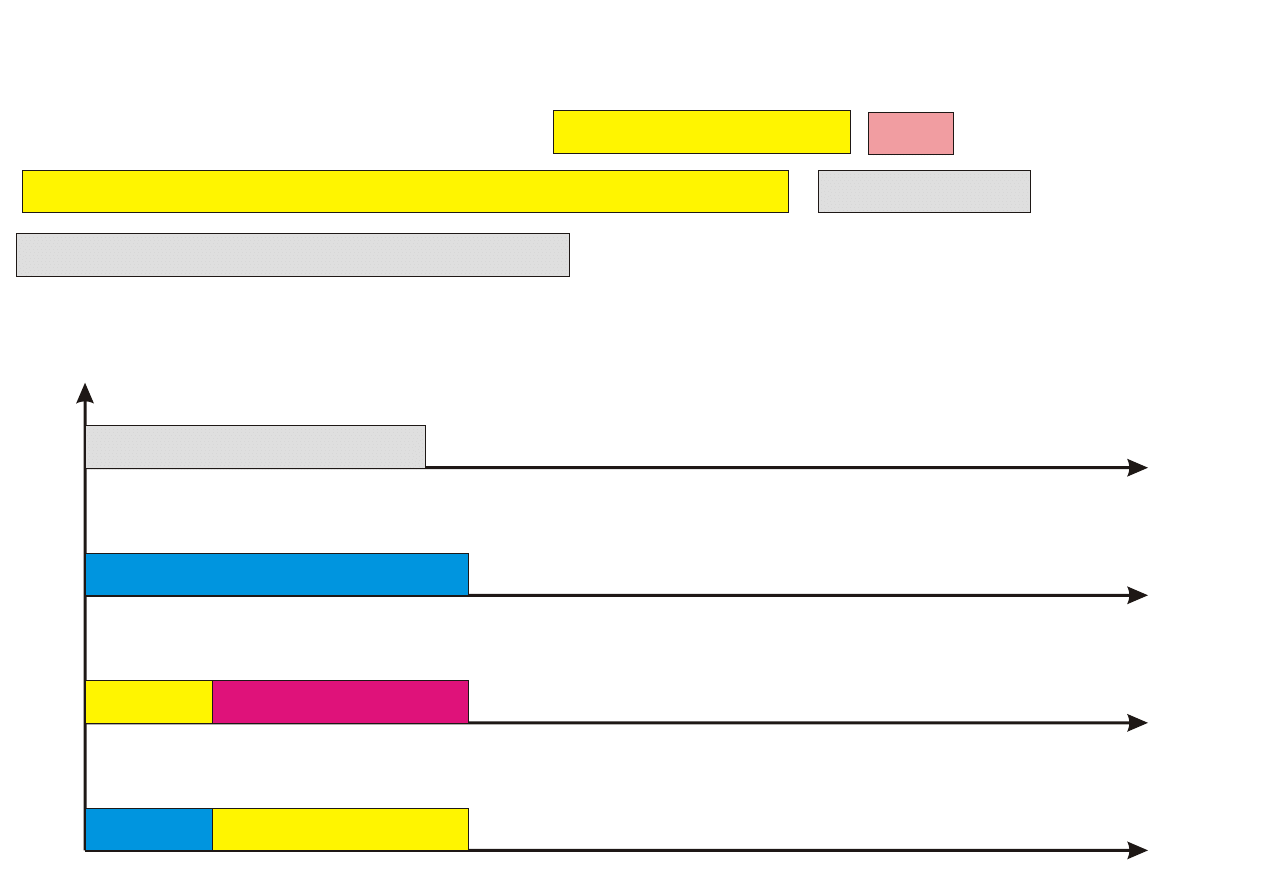
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

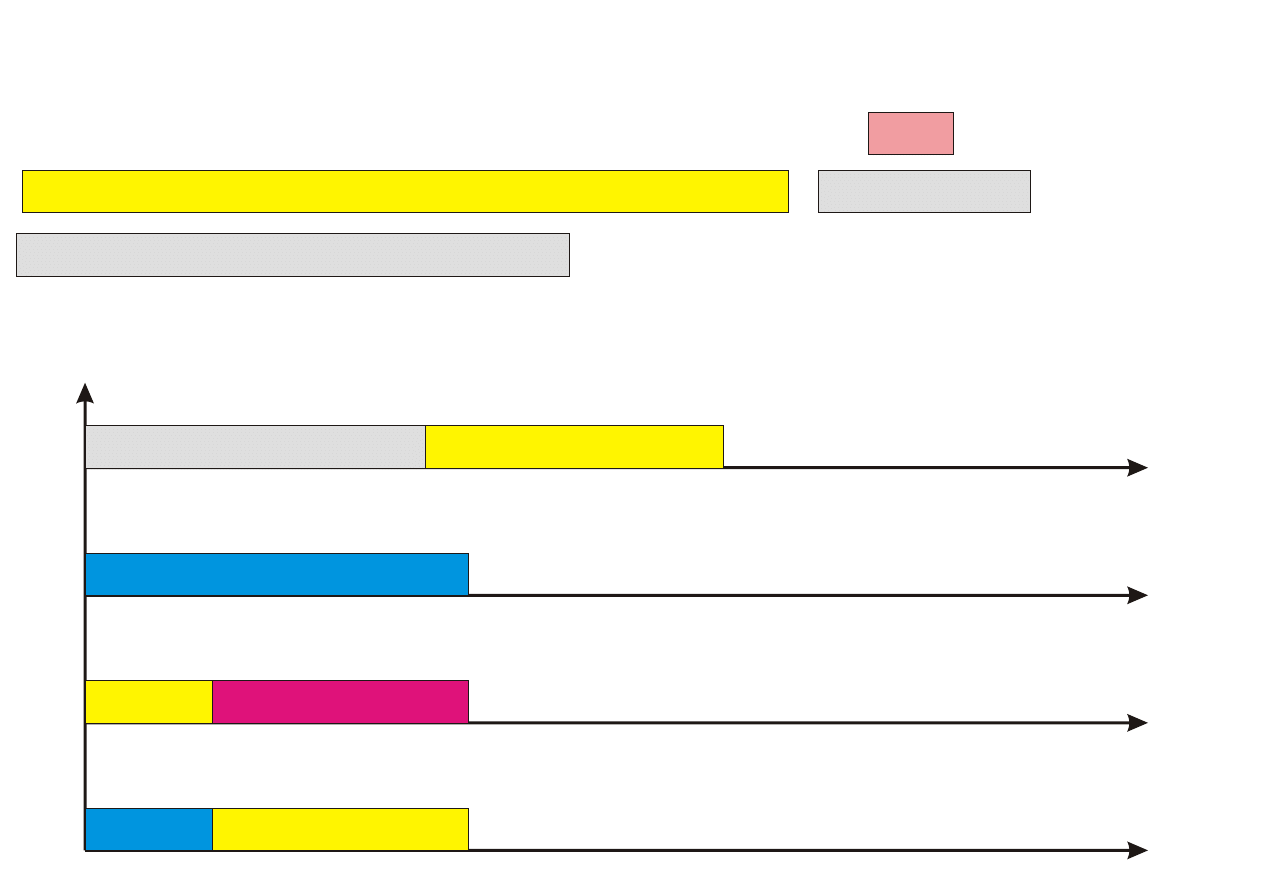
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

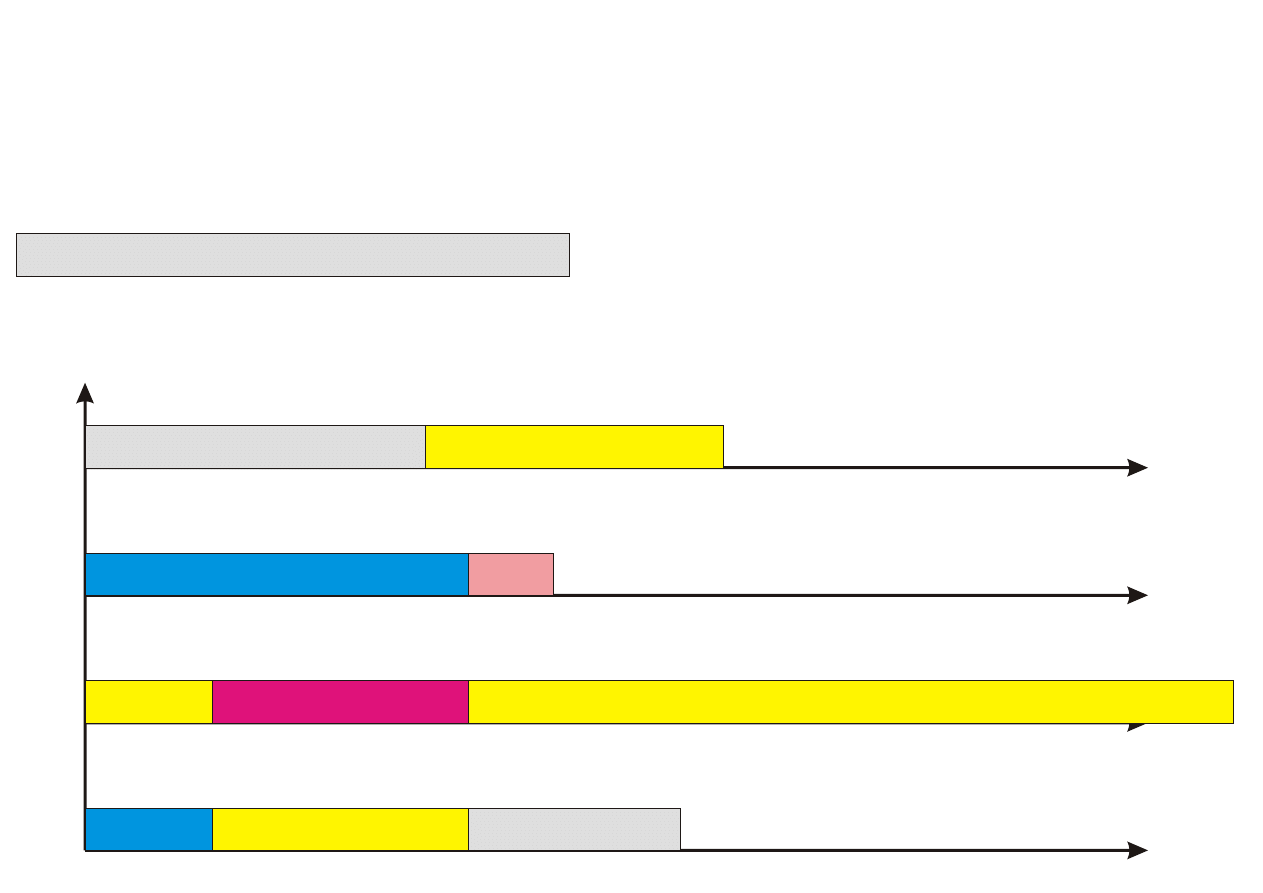
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

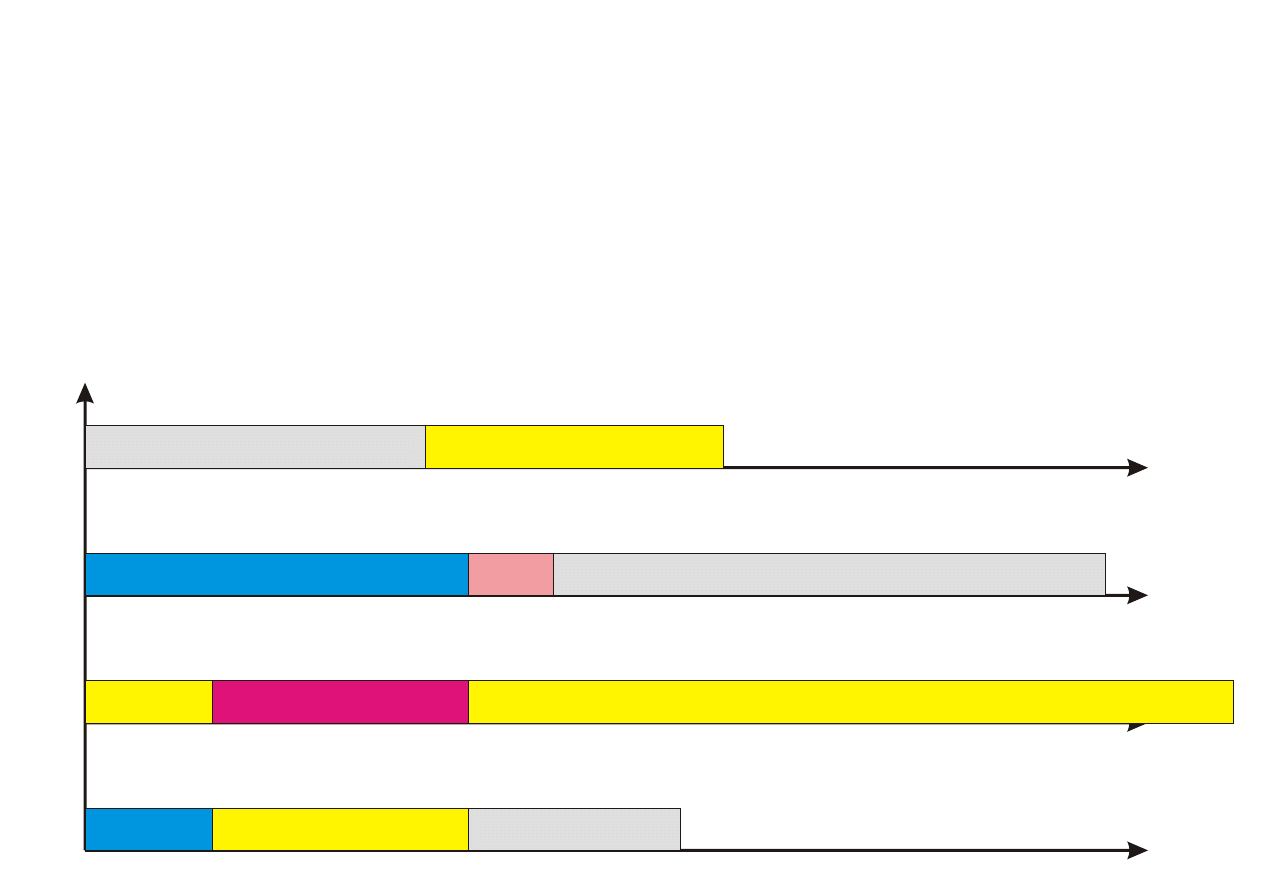
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(3,2,8,10,5,1,9,7,11,4,6)

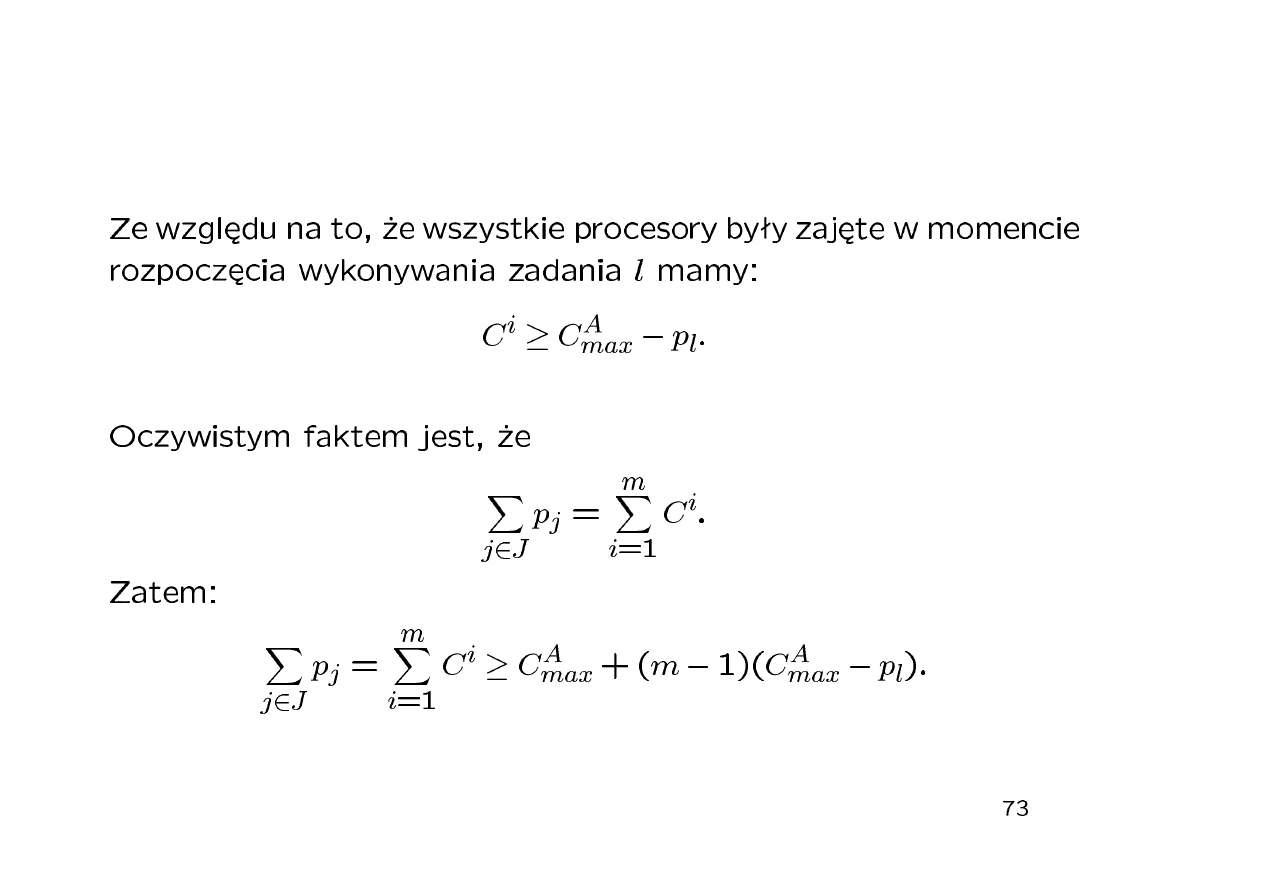
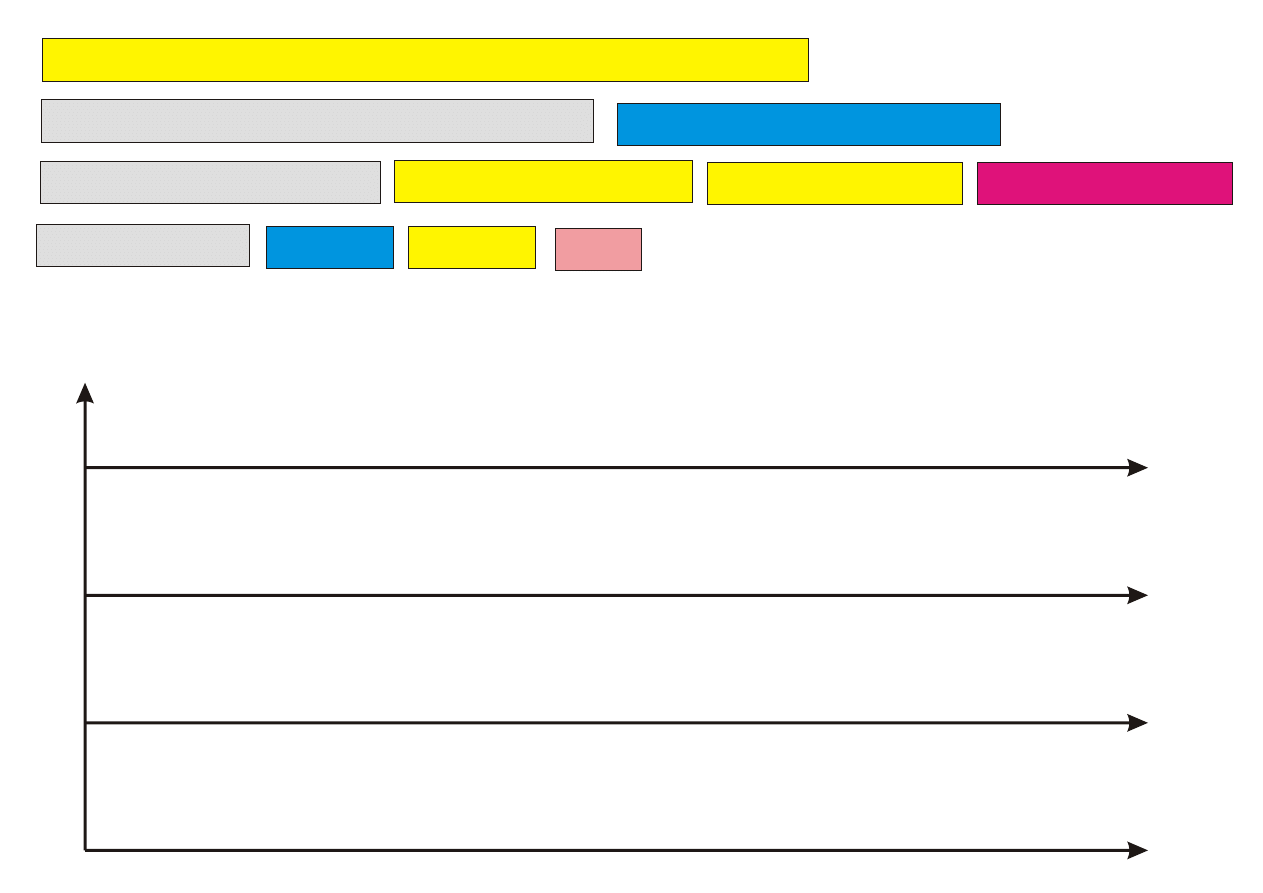
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

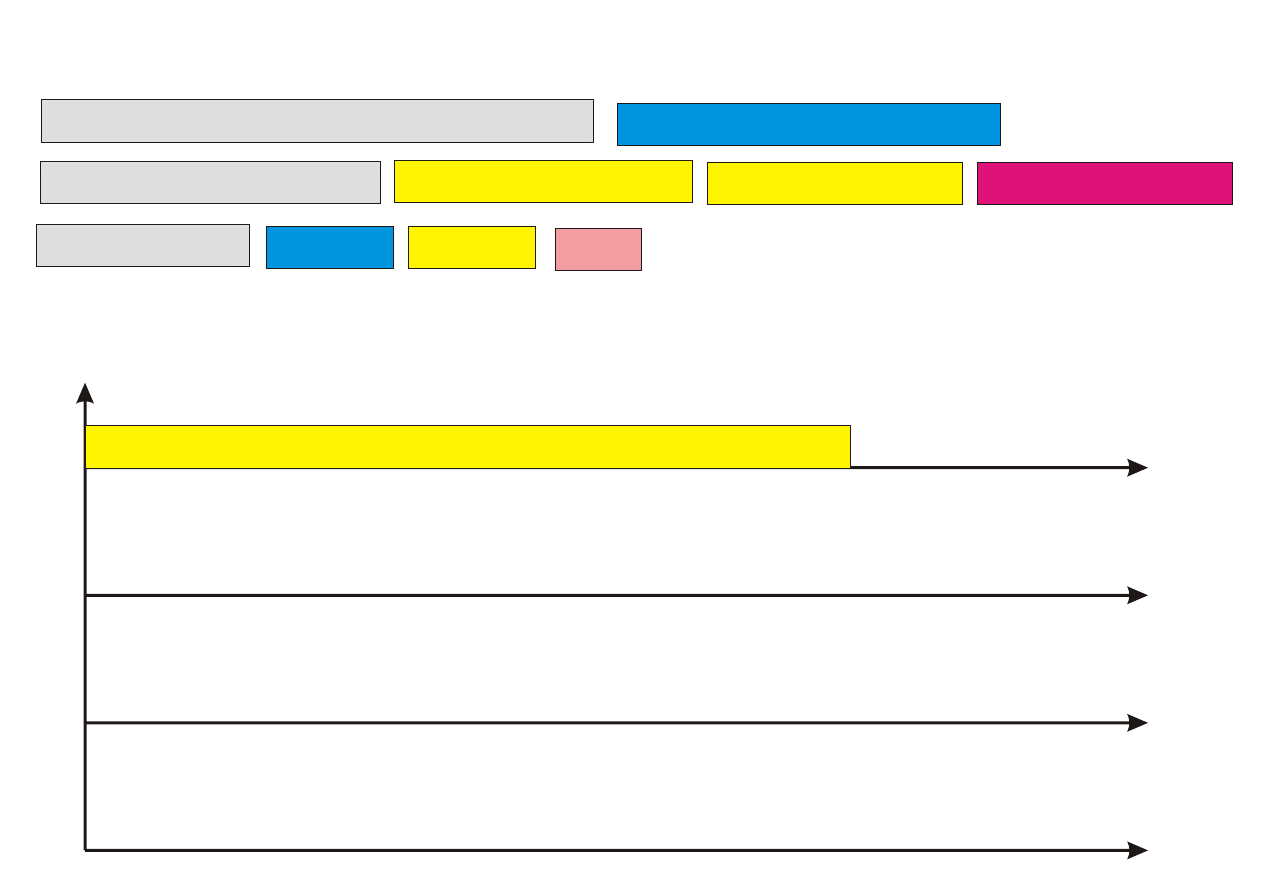
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

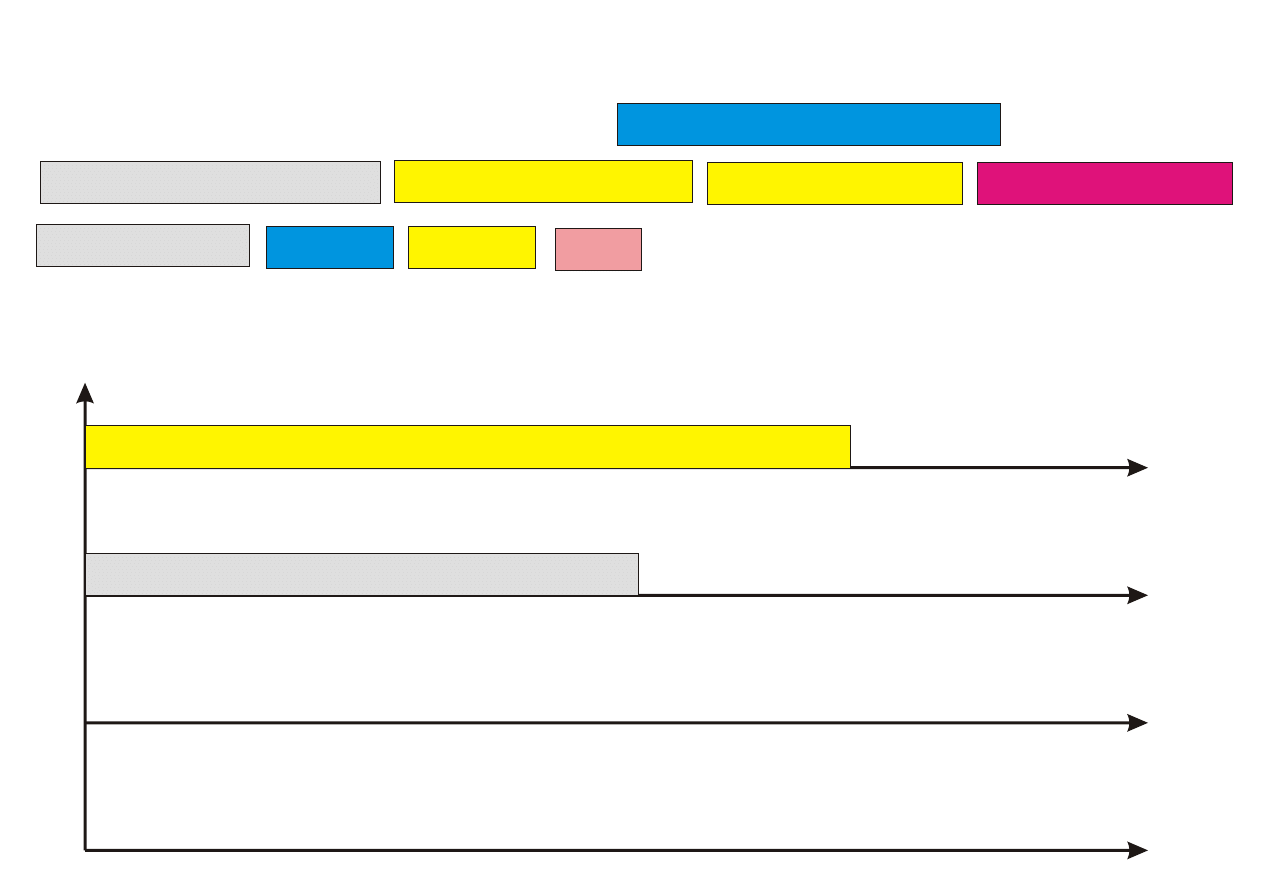
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

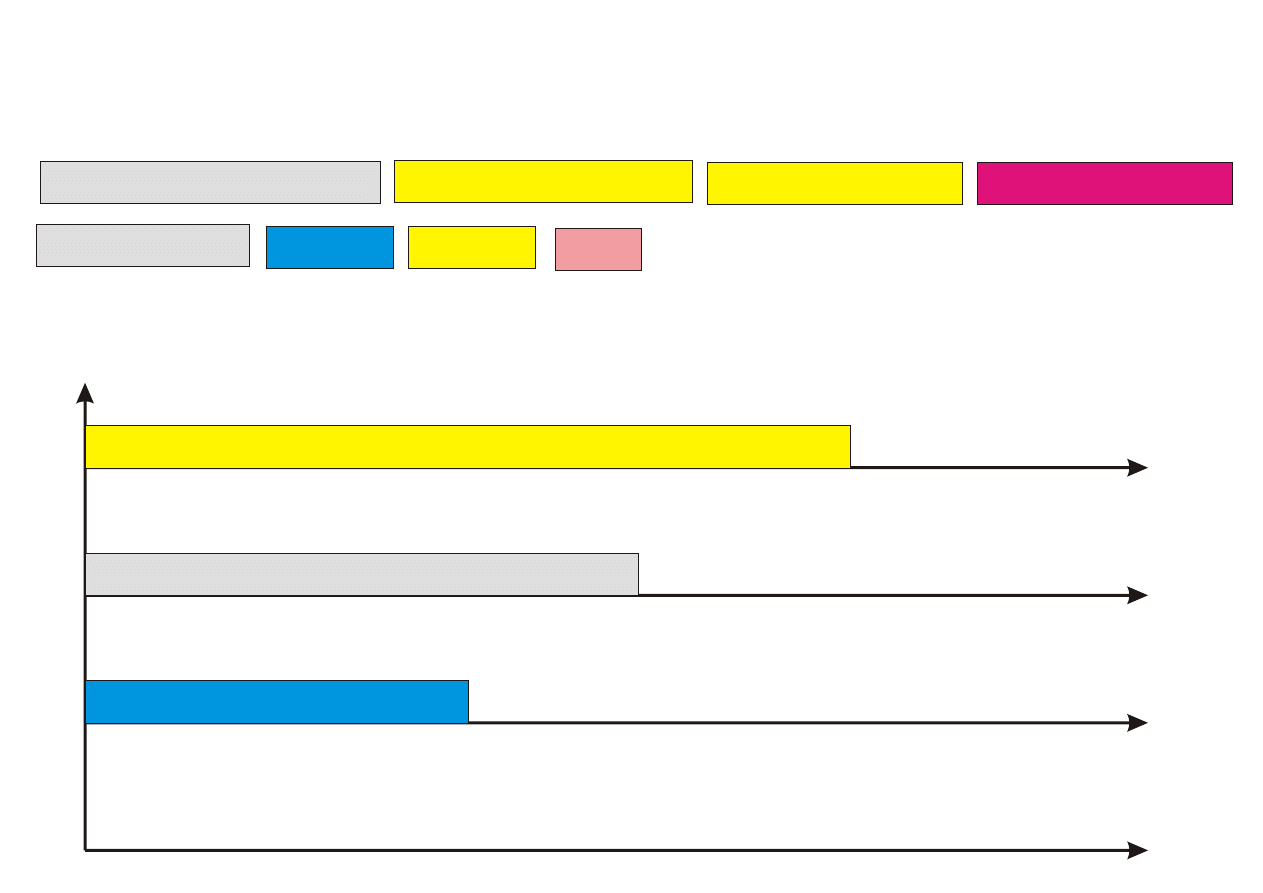
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

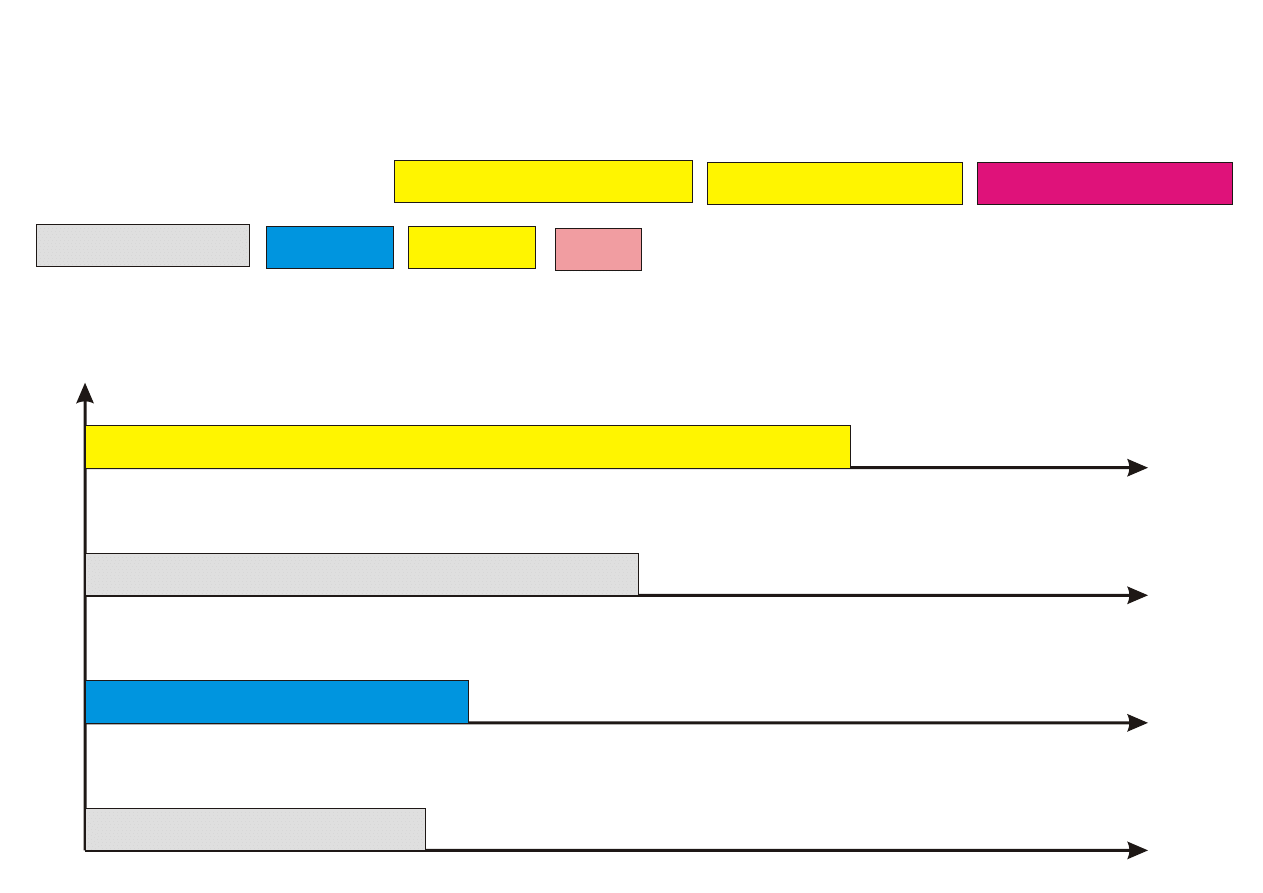
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

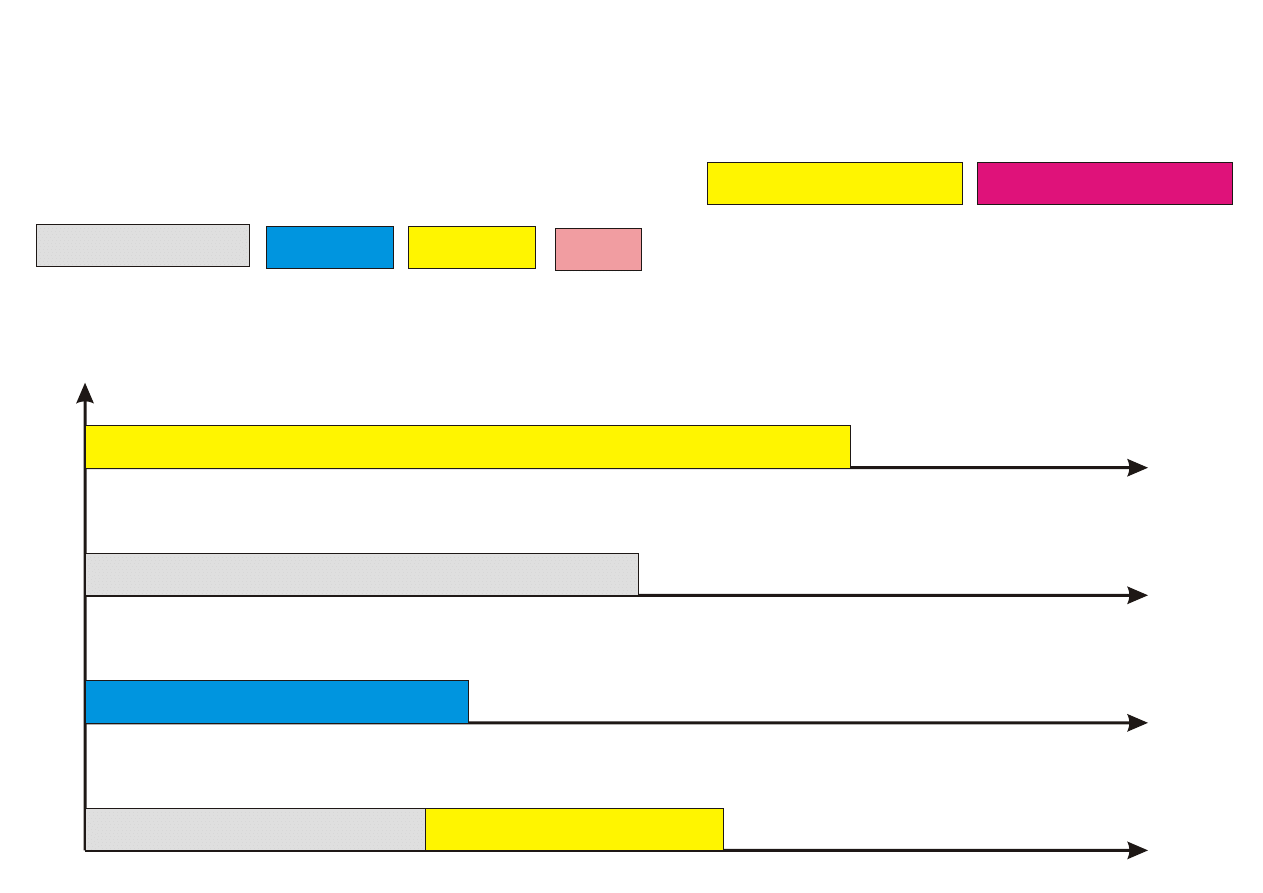
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

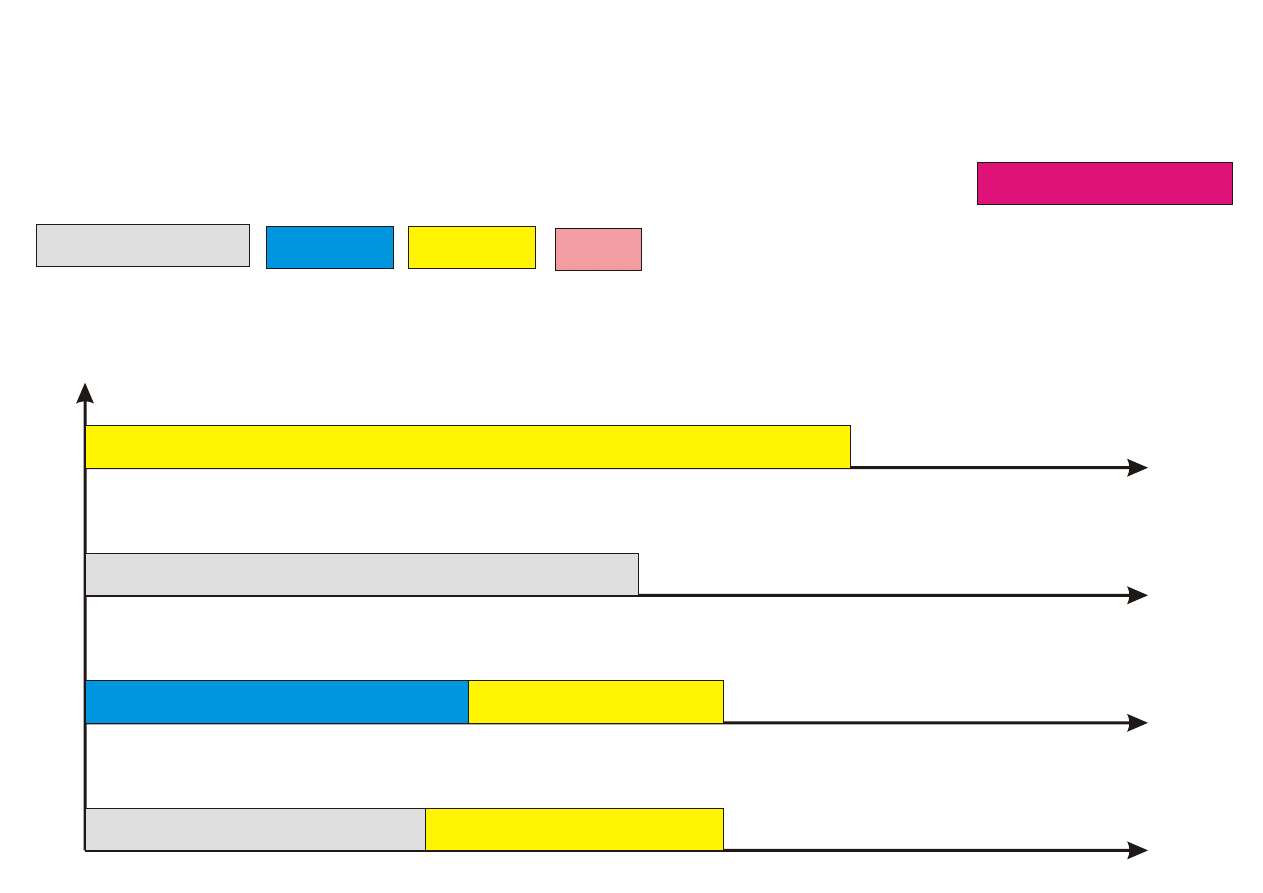
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

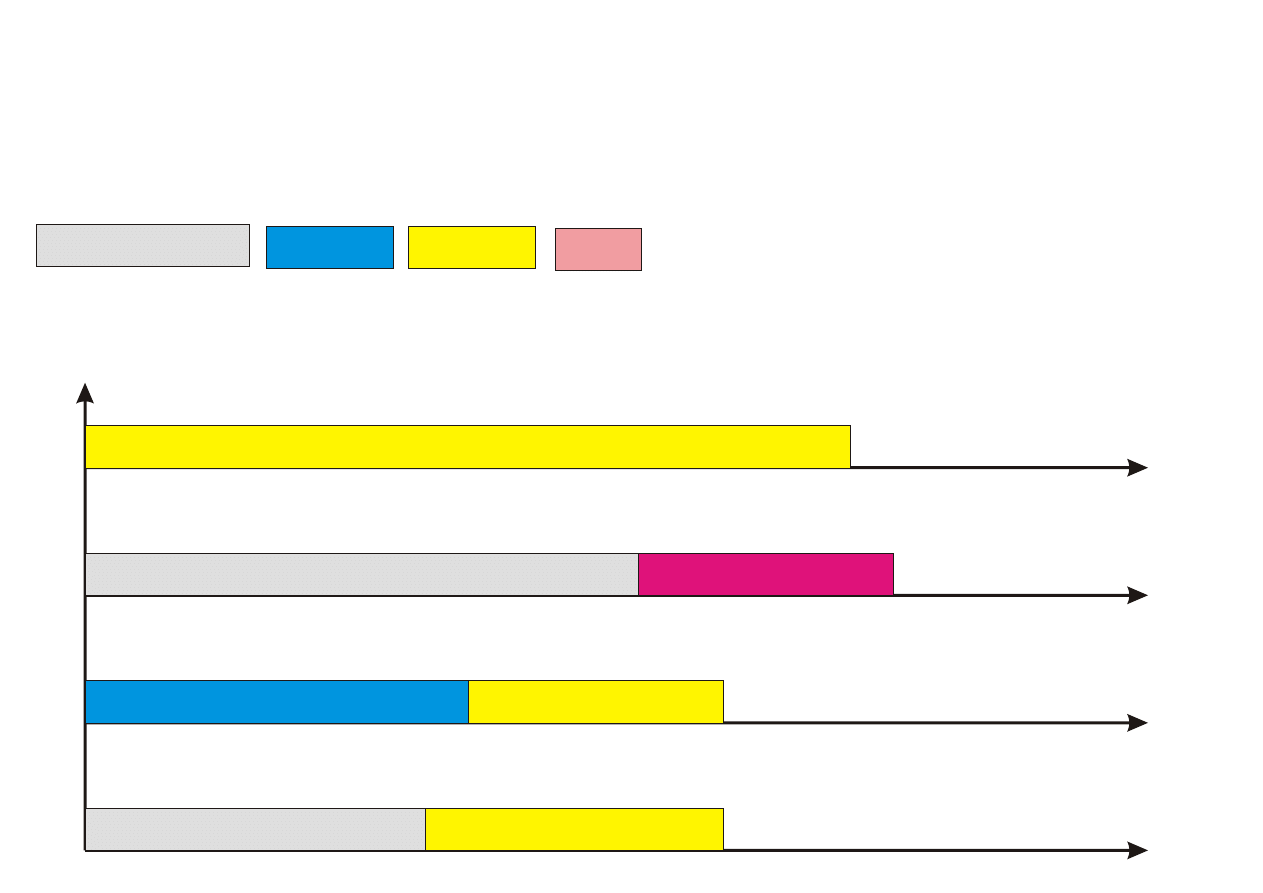
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

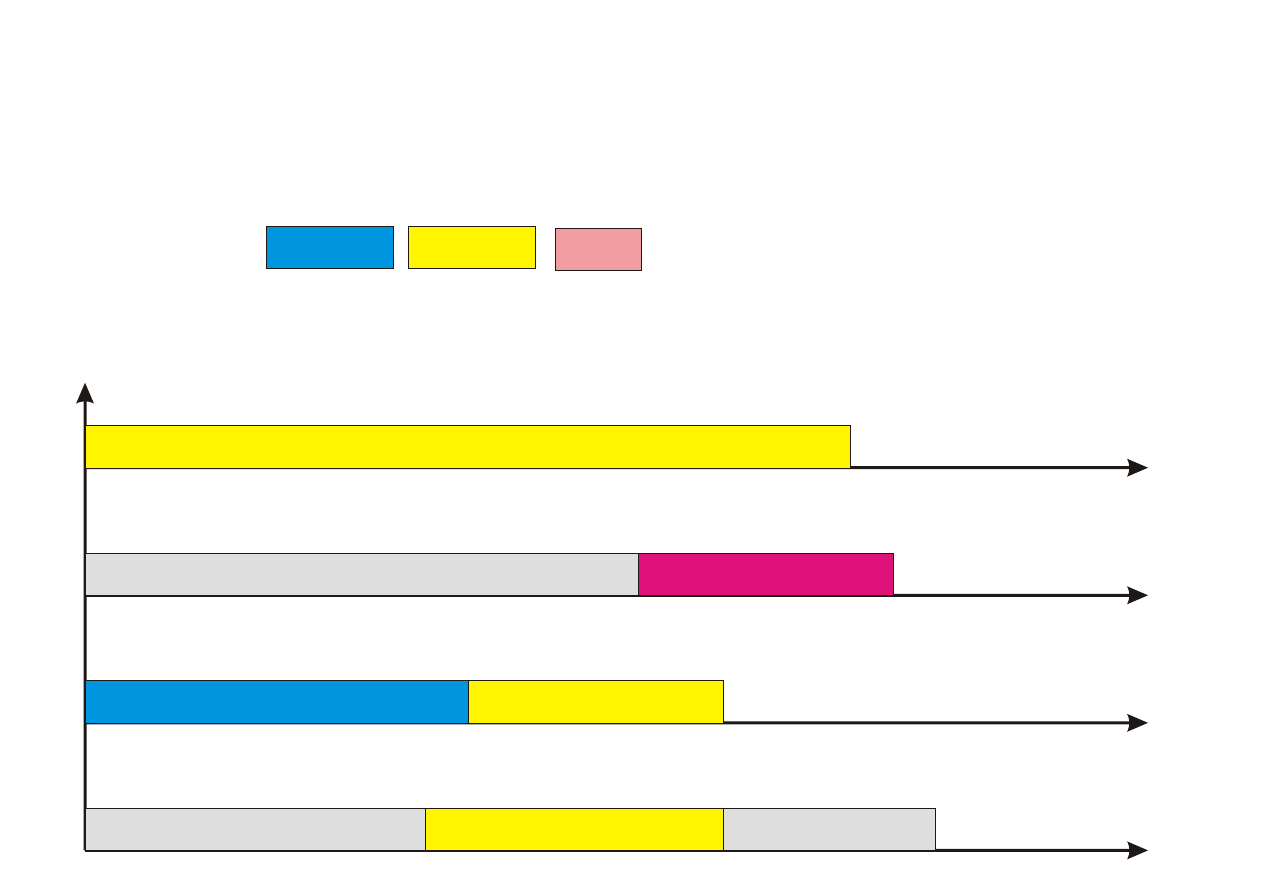
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

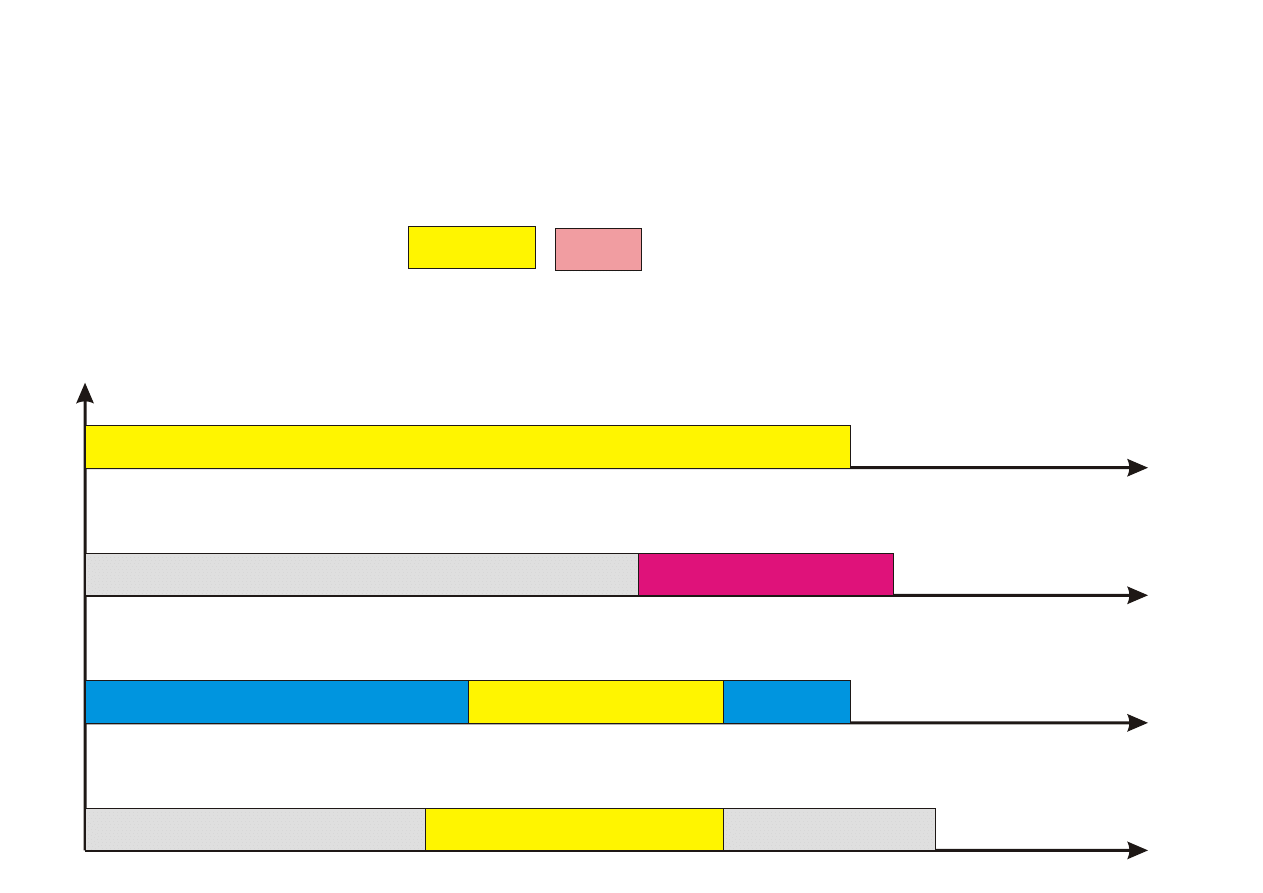
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

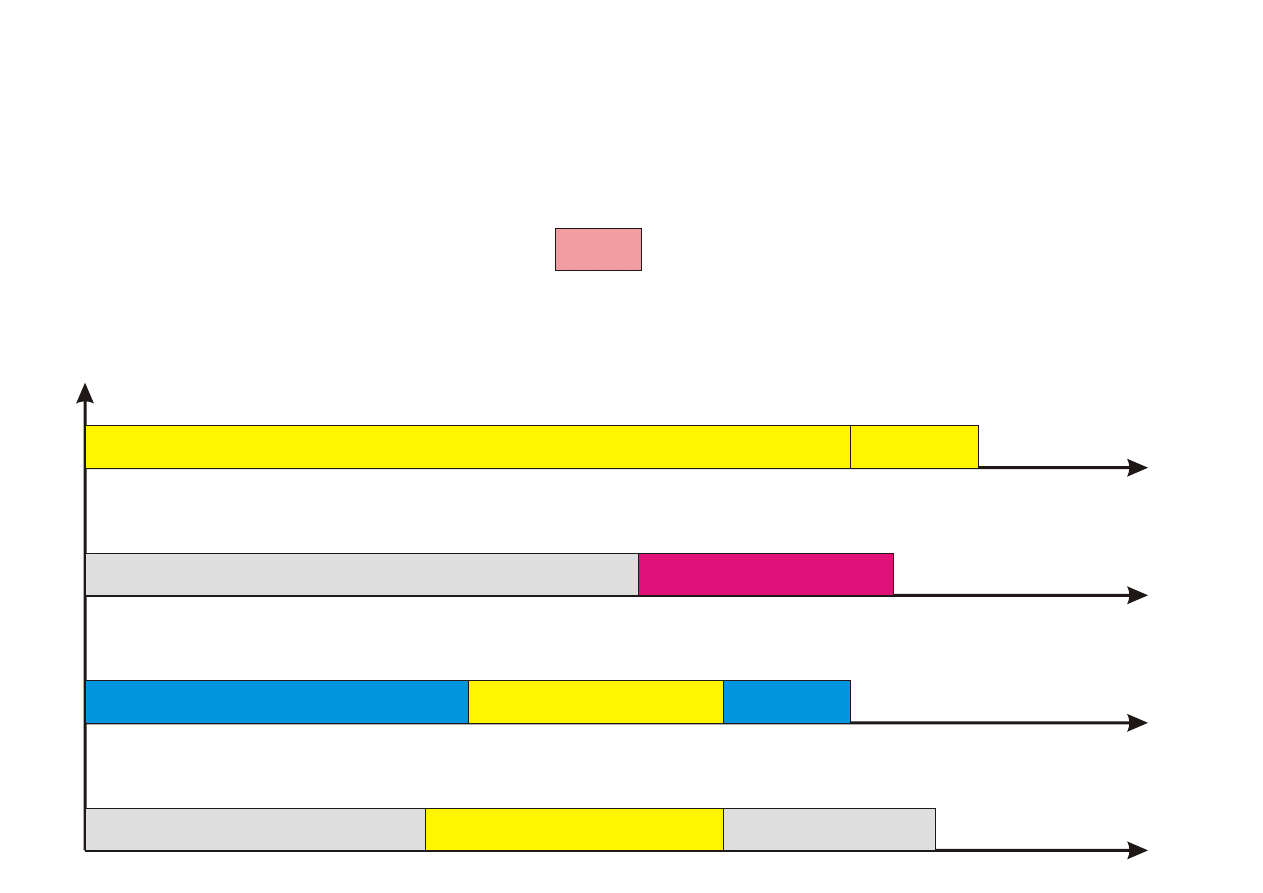
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

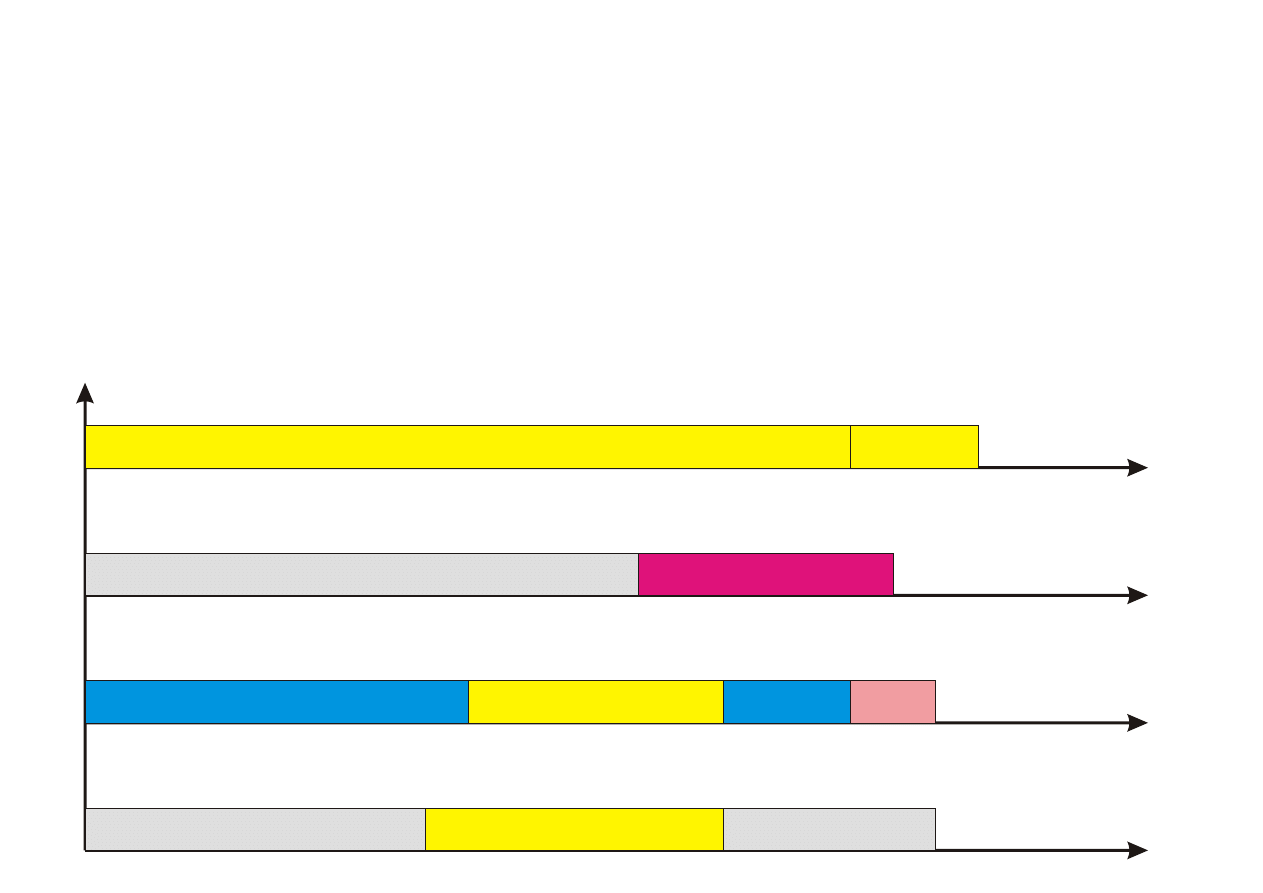
1

2

3

4

procesor

2

3

1

4

5

6

7

8

9

10

11

Lista=(11,6,2,3,9,1,5,4,10,8,7)

Schematy aproksymacyjne

Schemat aproksymacyjny rodzina algorytmów {A

ε

}

taka, »e dla ka»-

dego ε > 0 algorytm A

ε

dostarcza rozwi¡zania problemu z bª¦dem nie wi¦k-

szym ni» ε, czyli dla problemu ekstremalizacji funkcji K(x), x ∈

X

, mamy:

|K

A

ε

− K

∗

| ≤ εK

∗

,

gdzie K

∗

jest warto±ci¡ optymaln¡ funkcji K, a K

A

ε

jest warto±ci¡ funkcji

K

dla rozwi¡zania dostarczonego przez algorytm A

ε

.

Wyró»niamy dwa typy schematów aproksymacyjnych:

Wielomianowe schematy aproksymacyjne: czas dziaªania algorytmu A

ε

jest ograniczony od góry przez wielomian od rozmiaru instancji N(I) oraz
funkcj¦ wykªadnicz¡ od odwrotno±ci bª¦du 1/ε czyli:

T IM E(A

ε

) = O

p(N (I)) · e

1

ε

,

gdzie p jest wielomianem oraz e jest funkcj¡ wykªadnicz¡.

Przykªad: zªo»ono±¢ A

ε

mo»e wynosi¢ O

n

2

· 2

1

ε

.

Wielomianowy schemat aproksymacyjny skrótowo nazywamy PTAS:

Polynomial Time Approximation Scheme.

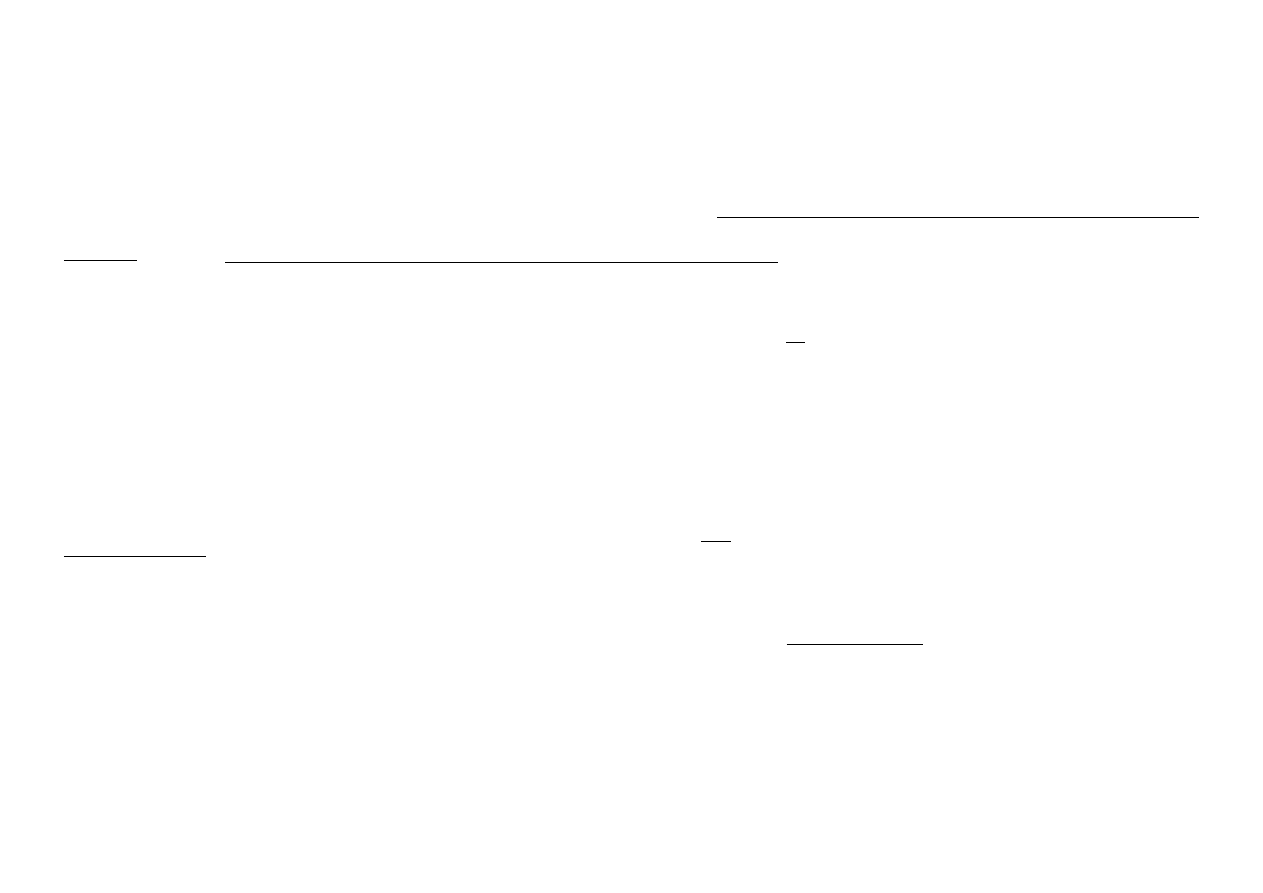
W peªni wielomianowe schematy aproksymacyjne: czas dziaªania algo-
rytmu A

ε

jest ograniczony od góry przez wielomian od rozmiaru instancji

N (I)

oraz wielomian od odwrotno±ci bª¦du 1/ε czyli:

T IM E(A

ε

) = O

p

N (I),

1

ε

,

gdzie p jest wielomianem.

Przykªad: zªo»ono±¢ A

ε

mo»e wynosi¢ O

n

3

ε

2

.

W peªni wielomianowy schemat aproksymacyjny skrótowo nazywamy FPTAS:

Fully Polynomial Time Approximation Scheme.

Przykªad:

PTAS dla problemu

P 2||C

max

Dane:
J = {J

1

, J

2

, . . . , J

n

}

zbiór n zada«, n ∈

Z

+

,

dwa procesory maj¡ce zrealizowa¢ wszystkie zadania J

1

, . . . , J

n

,

p

j

, j = 1, . . . , n

czas wykonywania (dªugo±¢) zadania J

j

, p

j

∈

R

+

.

Znale¹¢:
takie przyporz¡dkowanie zada« do procesorów x

∗

=

{x

1

, x

2

, . . . , x

n

}

(x

j

∈ {0, 1}

; x

j

= 0

oznacza, »e zadanie J

j

jest przyporz¡dkowane do pierwszego procesora,

a x

j

= 1

do drugiego, j = 1, . . . , n)

, dla którego:

C

max

= max

j∈J

{C

j

} −→ min,

gdzie C

j

jest czasem zako«czenia wykonywania zadania J

j

, j = 1, . . . , n.

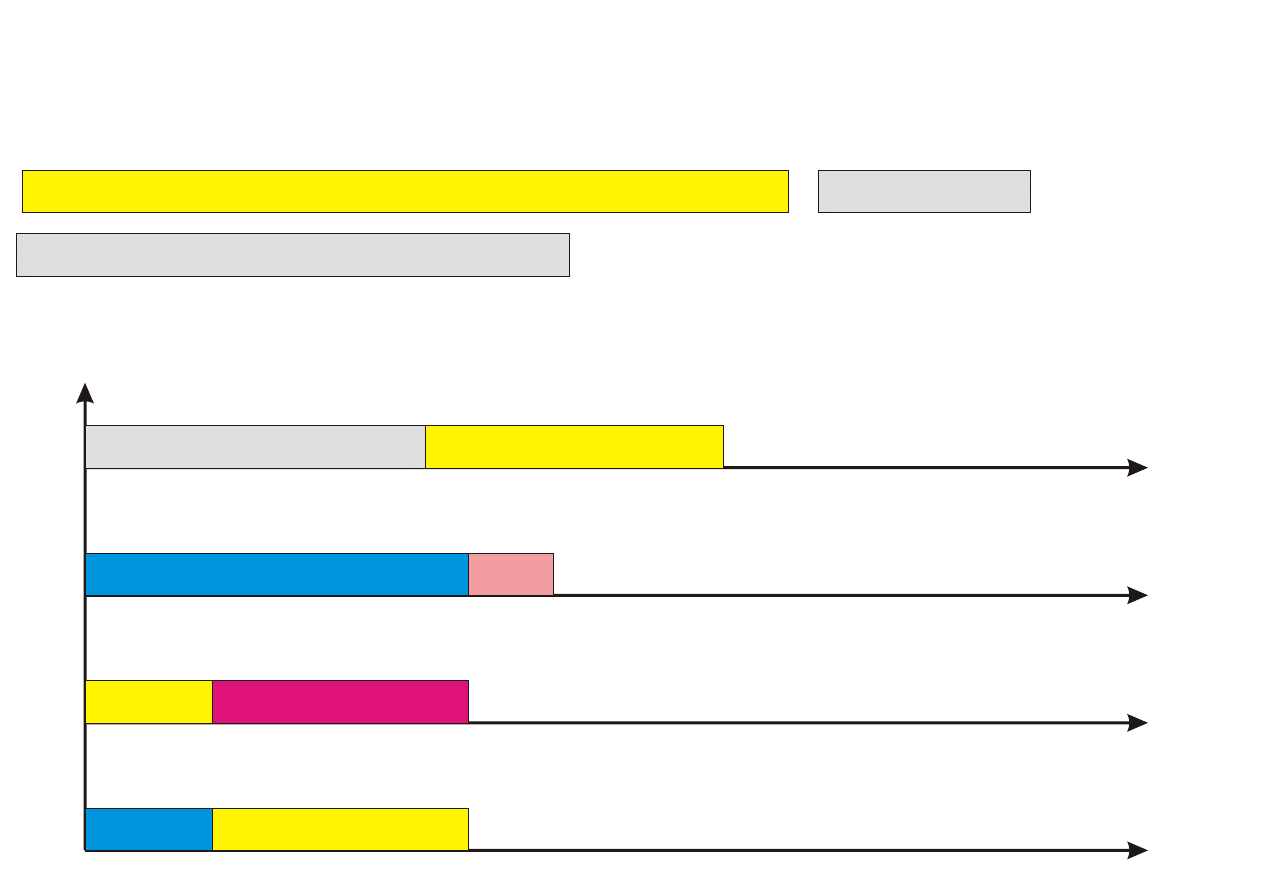
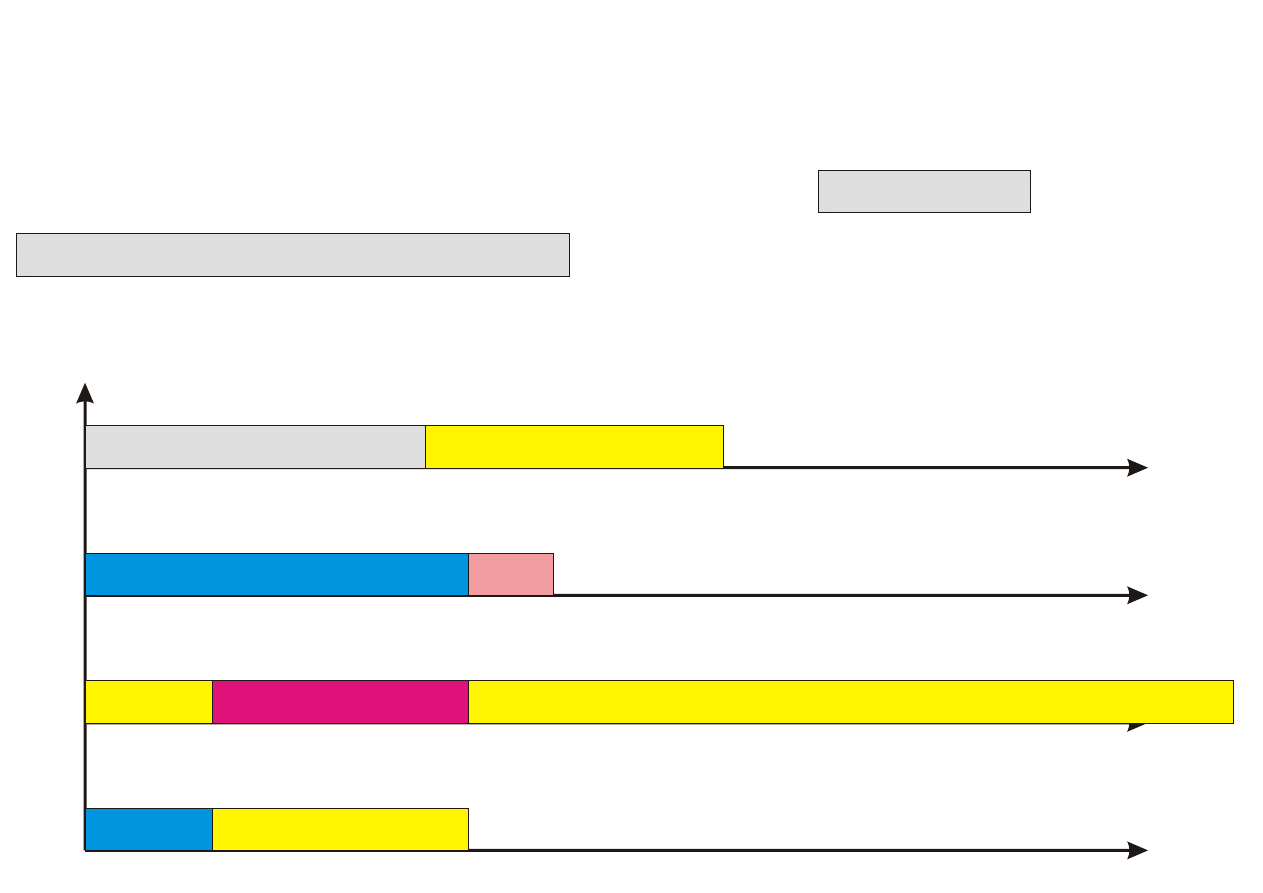
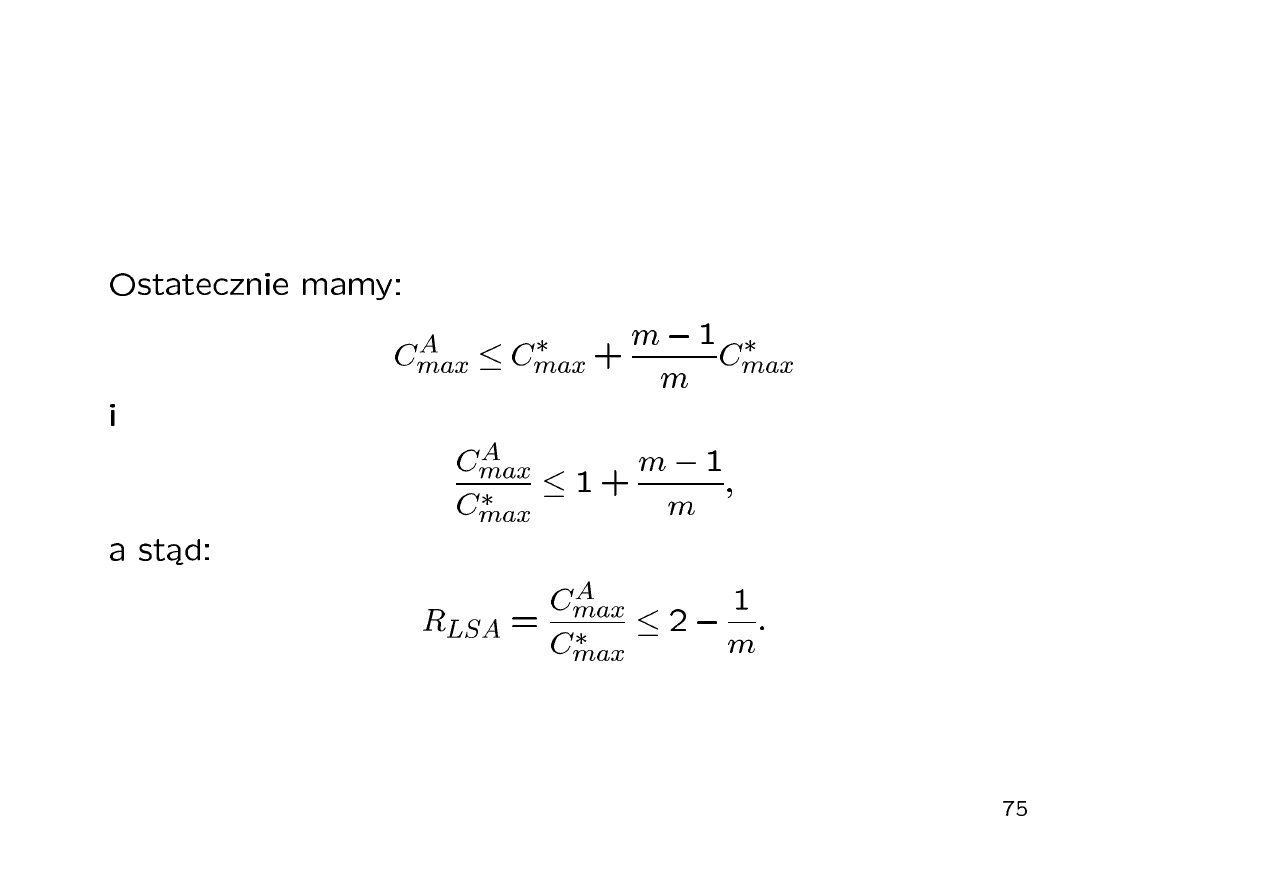
Algorytm PTAS

Procedure PTAS(n,k)

Krok 0. Posortuj zadania wg nierosn¡cego porz¡dku czasów ich wykony-

wania p

j

(p

1

≥ p

2

≥ . . . ≥ p

n

), tworz¡c list¦ zada« L.

Krok 1. Przyporz¡dkuj k pierwszych zada« (1 ≤ k ≤ n) z listy L do proce-

sorów w sposób optymalny (przegl¡d zupeªny), ignoruj¡c zadania
pozostaªe.

Krok 2. Pozostaªe (n − k) zada« przyporz¡dkowuj kolejno do najwcze±niej

dost¦pnego procesora.

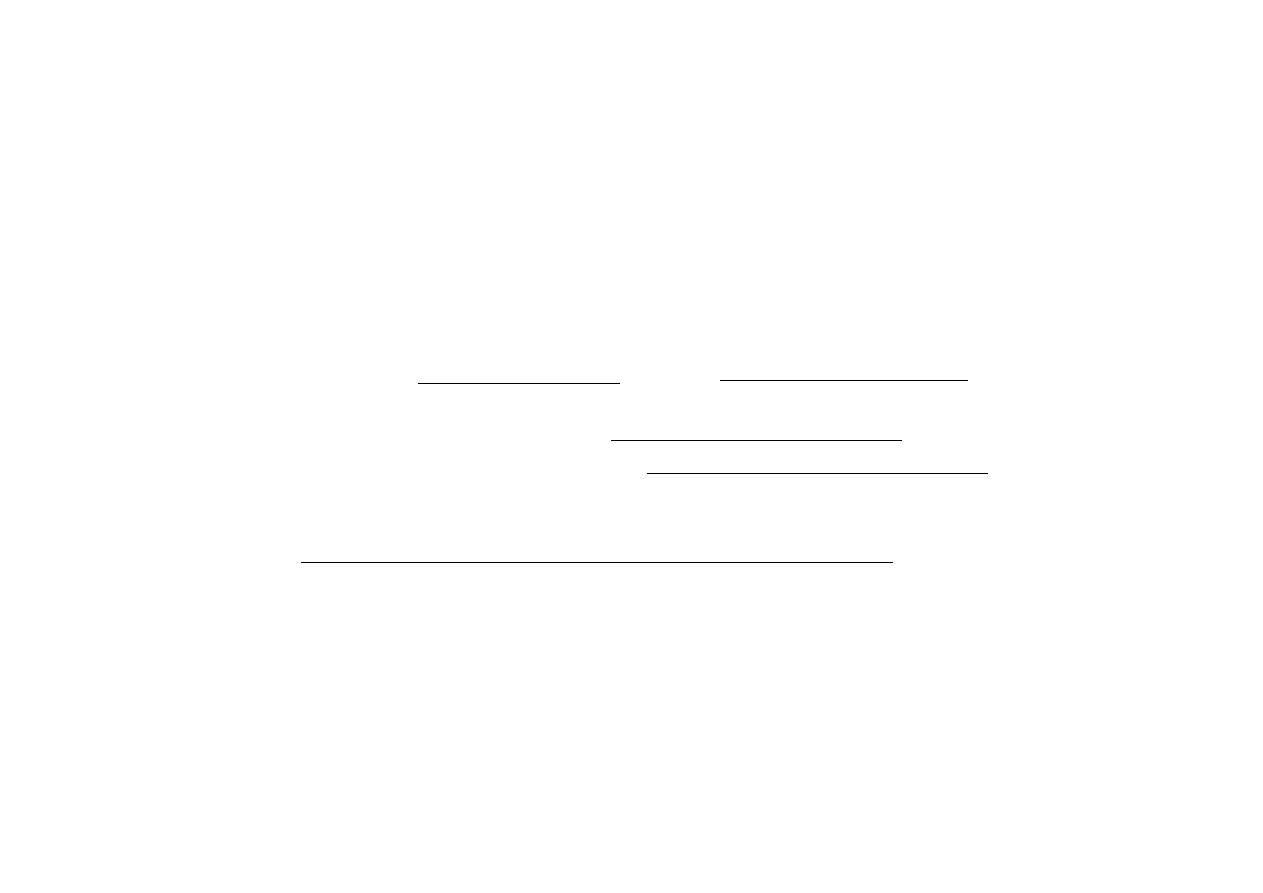
Zªo»ono±¢ obliczeniowa:

Krok 0

O(n log n)

(np. sortowanie kopcowe).

Krok 1

O(2

k

)

Przykªadowo, niech x

k

=

{x

1

, . . . , x

k

}

b¦dzie wektorem binarnym oznaczaj¡cym przy-

porz¡dkowanie k najdªu»szych zada« do procesorów. Przegl¡d zupeªny mo»emy zre-

alizowa¢, traktuj¡c wektor x

k

jako k-bitow¡ liczb¦ binarn¡. Startujemy od warto±ci

x

k

=

{0, 0, . . . , 0}

i w ka»dym kroku zwi¦kszamy warto±¢ x

k

o 1 a» do osi¡gni¦cia

warto±ci x

k

=

{1, 1, . . . , 1}

. W ten sposób w ka»dym kroku otrzymujemy nowe przy-

porz¡dkowanie. Wybieramy to, dla którego warto±¢ kryterium C

max

jest najmniejsza,

przy czym wszystkich mo»liwych przyporz¡dkowa« jest 2

k

.

Krok 2

O(n − k)

.

Ostatecznie, zªo»ono±¢ obliczeniowa alg. PTAS wynosi

O(n log n + 2

k

)

.

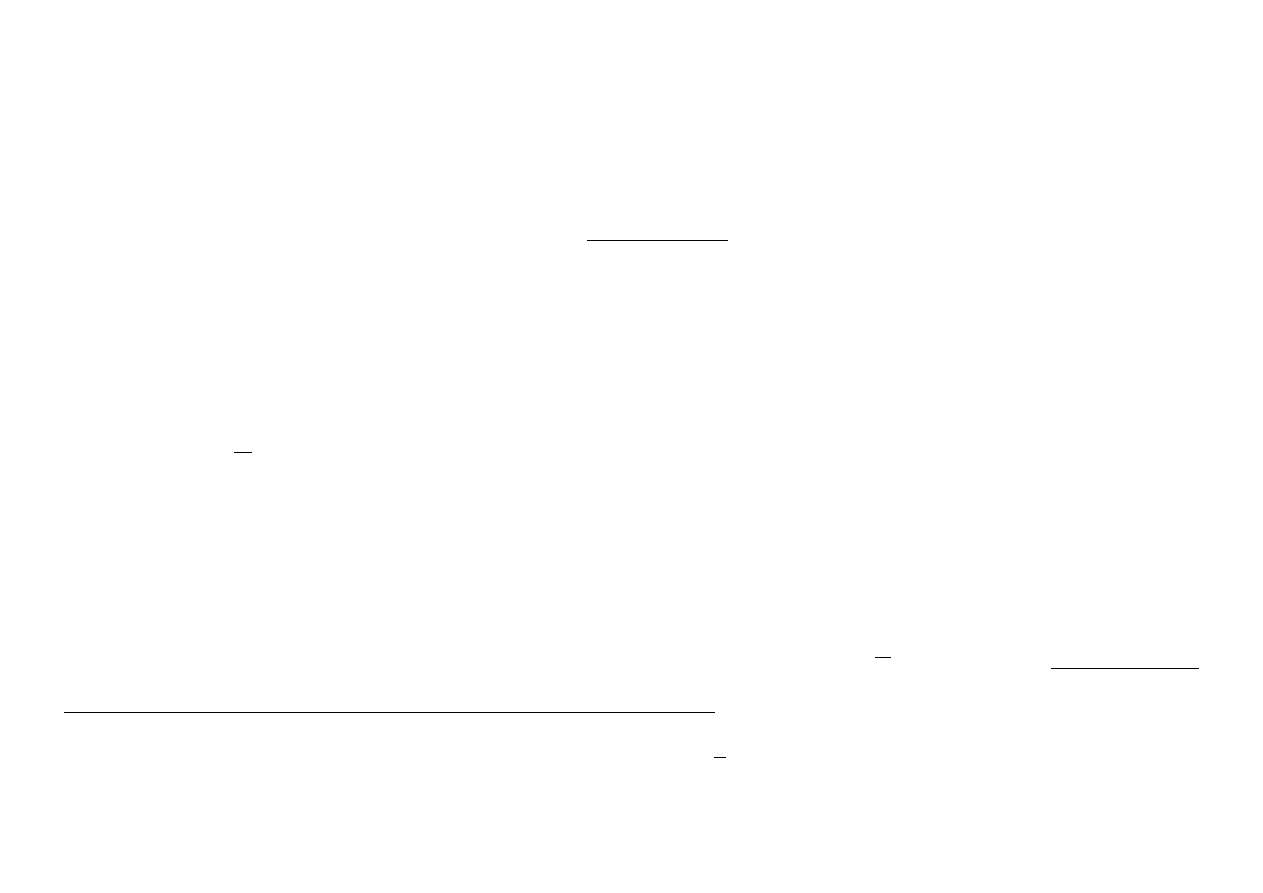
Dokªadno±¢:

ε =

1/2

1 +

bk/2c

,

(1)

gdzie bxc oznacza najwi¦ksz¡ warto±¢ caªkowit¡ nie wi¦ksz¡ ni» x (czyli zaokr¡glenie w dóª
warto±ci x).

Zatem ε ∼

1

k

.

W efekcie: wraz ze wzrostem

k

ro±nie zªo»ono±¢ (czas dziaªania)

algorytmu (wykªadniczo!), ale maleje bª¡d (proporcjonalnie).

Na podstawie wzoru (1) mo»na stwierdzi¢, »e k = O(

1

ε

)

, co daje zªo»ono±¢

obliczeniow¡ alg. PTAS zgodn¡ z denicj¡, tzn.

O






n log n + 2

1
ε






.

Algorytm FPTAS

Do skonstruowania FPTAS dla problemu P 2||C

max

wykorzystamy algorytm

programowania dynamicznego o zªo»ono±ci (pseudowielomianowej)

O(n·S)

,

gdzie S =

P

n

j=1

p

j

.

Procedure FPTAS(n,k)

Krok 0. Utwórz now¡ instancj¦ problemu P 2||C

max

, podstawiaj¡c

˜

p

j

=

p

j

k

dla

j = 1, . . . , n.

Krok 1. Rozwi¡» now¡ instancj¦ problemu metod¡ programowania dyna-

micznego (optymalnie).

Krok 2. Rozwi¡zanie uzyskane w Kroku 1 zastosuj do pierwotnej instancji

problemu (b¦dzie ono rozwi¡zaniem przybli»onym!).

Zªo»ono±¢ obliczeniowa:

Krok 0

O(n)

.

Krok 1

O(n ·

S

k

)

.

Krok 2

O(n)

(wyznaczenie warto±ci funkcji celu).

Zatem zªo»ono±¢ obliczeniowa alg. FPTAS wynosi

O(n ·

S

k

)

< O(nS)

.

Dokªadno±¢:

ε =

2nk

S

,

(2)

wi¦c ε ∼ k.

W efekcie: wraz ze wzrostem

k

maleje zªo»ono±¢ (czas dziaªania)

algorytmu (proporcjonalnie), ale ro±nie bª¡d (te» proporcjonalnie).

Wyliczaj¡c ze wzoru (2) k =

j

εS

2n

k

i podstawiaj¡c do wzoru zªo»ono±ci obli-

czeniowej O(n ·

S

k

)

, otrzymamy zªo»ono±¢ obliczeniow¡ alg. FPTAS zgodn¡

z denicj¡, tzn.

O








n

2

ε








.

•

Schematy aproksymacyjne s¡ algorytmami przybli»onymi (tzn. dostar-

czaj¡ rozwi¡za« nieoptymalnych). Ich podstawow¡ cech¡ jest mo»liwo±¢

wpªywania na maksymalny bª¡d uzyskiwanych wyników.

•

Niestety odbywa si¦ to kosztem czasu dziaªania (im mniejszy dopusz-

czalny bª¡d tym dªu»szy czas dziaªania).

•

PTAS silna zale»no±¢ bª¦dów od czasów (st¡d praktyczne ich za-

stosowanie jest ograniczone jedynie do przypadków, w których dopusz-

czamy stosunkowo du»y bª¡d rozwi¡za«).

•

FPTAS wi¦ksza skuteczno±¢ ni» PTAS (mo»liwo±¢ uzyskania re-

zultatów o mniejszym bª¦dzie w rozs¡dnym czasie).

•

Zostaªo udowodnione, »e nie dla wszystkich problemów NP-trudnych

mo»na skonstruowa¢ schemat aproksymacyjny (o ile P 6= NP ).

Ponadto, FPTAS mo»na skonstruowa¢ tylko dla problemów NP-trud-

nych w zwykªym sensie (nie silnie NP-trudnych).

Rodzaje algorytmów (metod) optymalnych:

•

Wielomianowe algorytmy dokªadne (dedykowane)

tylko dla problemów z

klasy P.

•

Programowanie dynamiczne

gªównie dla problemów NP-trudnych w zwykªym

sensie (tzn. nie silnie NP-trudnych).

•

Programowanie caªkowitoliczbowe.

•

Metoda podziaªu i ogranicze«

gªównie dla problemów (silnie) NP-trudnych.

•

Przegl¡d zupeªny.

Rodzaje algorytmów (metod) przybli»onych:

•

Algorytmy konstrukcyjne i zachªanne

gªównie dla problemów NP-trudnych.

•

Algorytmy typu popraw

gªównie dla problemów (silnie) NP-trudnych:

lokalnego poszukiwania (np. poszukiwanie zst¦puj¡ce, poszukiwanie

losowe),

metaheurystyczne (np. poszukiwanie z zabronieniami (tabu search),

symulowane wy»arzanie, poszukiwanie genetyczne (ewolucyjne), po-
szukiwanie mrówkowe).

•

Wielomianowe i w peªni wielomianowe schematy aproksymacyjne

gªównie dla problemów NP-trudnych.