Ć w i c z e n i e 36

WYZNACZANIE MOMENTU BEZWŁADNOŚCI BRYŁY

Z WYKORZYSTANIEM MASZYNY ATWOODA

36.1. Wstęp teoretyczny

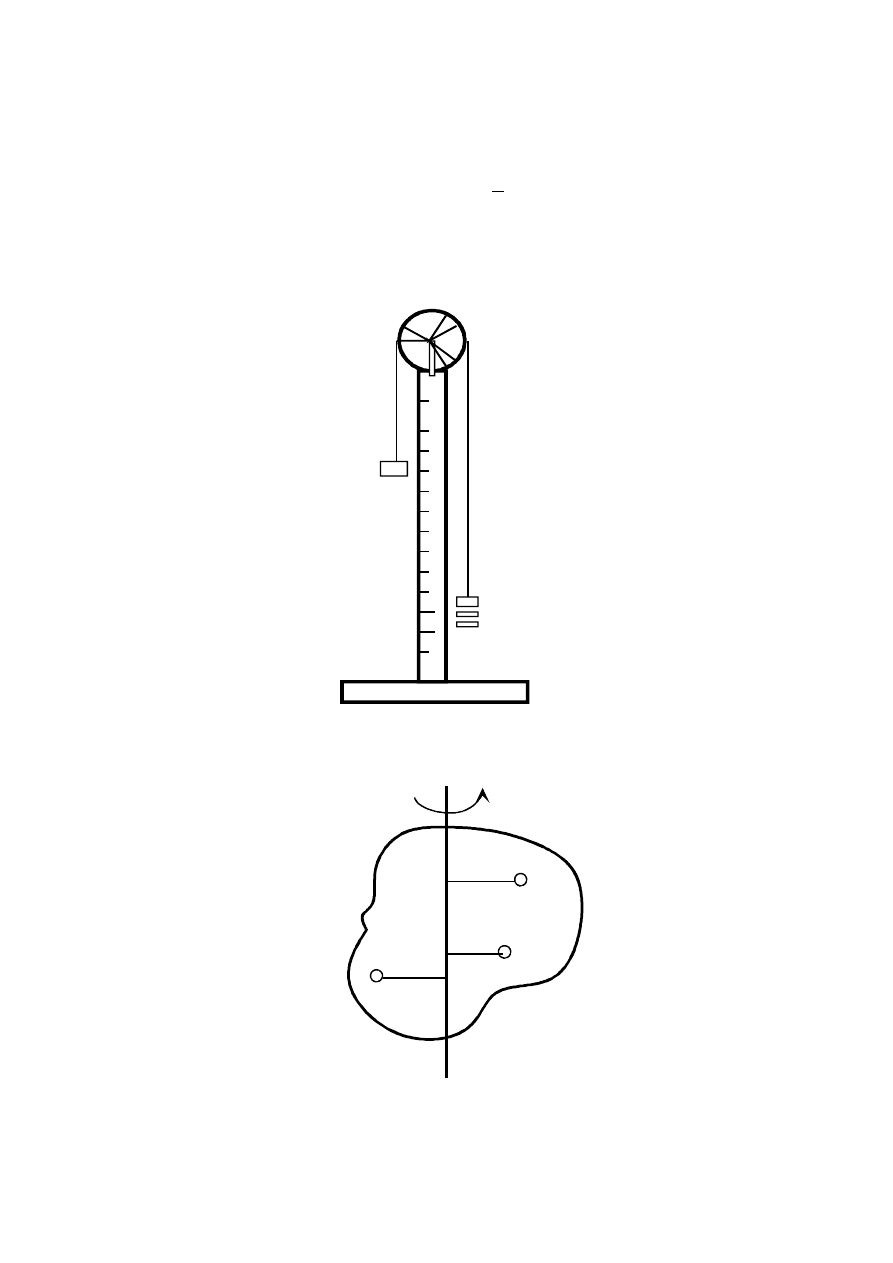
Maszyna Atwooda służy do doświadczalnego sprawdzania praw kinematyki i dynamiki. W naj-
prostszym wykonaniu składa się ona z bloczka K (rys.36.1) umieszczonego w górne części piono-
wego pręta ze skalą S. Przez bloczek przechodzi cienka i mocna nić z zawieszonymi na końcach
masami M. Dodatkowe obciążenie jednego z końców nici jest realizowane za pomocą jednakowych
blaszek o masie m każda w ilości k. Właśnie ich ciężar jest przyczyną wprowadzającą układ ciężar-
ki-nić-bloczek w ruch jednostajnie przyśpieszony.

W maszynie Atwooda mamy do czynienia z dwoma rodzajami ruchu jednostajnie przyśpieszonego:
prostoliniowym ciężarków i obrotowym bloczka.

• W ruchu prostoliniowym bezwładność ciała charakteryzowana jest przez jego masę m.
Znajduje to odzwierciedlenie w drugiej zasadzie dynamiki dla tego ruchu, zgodnie z którą siła
F nadaje ciału ruch o przyśpieszeniu a wprost proporcjonalnym do tej siły i odwrotnie pro-
porcjonalnym do masy ciała:

a

F

=

m

• W ruchu obrotowym bezwładność ciała charakteryzowana jest przez jego moment bezwład-
ności J względem osi obrotu. Znajduje to odzwierciedlenie w drugiej zasadzie dynamiki dla
tego ruchu, zgodnie z którą moment siły N nadaje ciału ruch o przyśpieszeniu kątowym

ε

wprost proporcjonalnym do momentu siły i odwrotnie proporcjonalnym do momentu bez-
władności:

ε =

N

J

Zdefiniujmy moment bezwładności bryły sztywnej. Załóżmy, że bryła obraca się wokół osi l ze sta-
łą prędkością kątową i że składa się z n mas punktowych m

ω

i

(rys. 36.2). Każda z tych mas posia-

da prędkość liniową v

i

zależną od jej odległości od osi obrotu r

i

:

v

i

r

i

= ω

oraz energię kinetyczną:

2

2

i

i

2
i

i

ki

ω

r

m

2

1

v

m

2

1

E

=

=

Energia kinetyczna całej bryły jest sumą energii kinetycznych poszczególnych mas punktowych:

∑

∑

=

=

=

=

n

1

i

2

i

i

2

n

1

i

ki

kO

r

m

ω

2

1

E

E

(36.1)

Porównajmy ten wzór z wyrażeniem na energię kinetyczną w ruchu postępowym:

E

m v

kp

=

1
2

2

Wiemy, że odpowiednikiem prędkości liniowej v jest prędkość kątowa

ω

, a masy m - moment

bezwładności J.

Wzór na energię kinetyczną w ruchu obrotowym powinien mieć postać :

E

J

kO

=

1
2

2

ω

(36.2)

Z porównania wzorów (36.1) (36.2) wynika definicyjna zależność na moment bezwładności bryły

sztywnej:

(36.3)

∑

=

=

n

1

i

2

i

i

r

m

J

S

B

A

K

Rys. 36.1. Maszyna Atwooda.

L

ω

m

m

m

i

i

i

+

-

1

1

r

r

r +

i

i

1

i

-

1

Rys. 36.2. Bryła sztywna w ruchu obrotowym wokół osi L. Należy zauważyć, że

.

m

m

i

i

n

=

=

∑

1

Widać, że zależy on od wyboru osi obrotu oraz od sposobu rozłożenia masy ciała względem niej
(czyli od kształtu ciała).

Wychodząc z definicji (36.3) można teoretycznie obliczyć momenty bezwładności dla wielu regu-
larnych brył , uzależniając je od całkowitej masy m i od ich rozmiarów geometrycznych.

Na przy-

kład:

dla walca

J

m

=

1
2

2

R

gdzie R - promień walca

dla

kuli

J

m

gdzie R - promień kuli

R

=

2

5

2

dla

pierścienia

(

J

m R

R

=

+

1
2

1

2

2

2

)

gdzie R

1

, R

2

- promienie zewnętrzny i wewnętrzny

A n a l i z a r u c h u m a s z y n y A t w o o d a

Na ciężarek A działają siły: ciężkości Mg i naprężenia nici T

1

(rys. 36.3). Pod wpływem wypadko-

wej tych sił ciężarek porusza się do góry z przyśpieszeniem a. Zgodnie z II prawem Newtona dla
ruchu postępowego możemy napisać:

(

)

T

M g

M

1

−

=

a

(36.4)

Podobnie ciężarek B będzie poruszał się (ale do dołu) pod wpływem wypadkowej siły ciężkości
równej Mg + kmg i siły naprężenia nici T

2

. Analogicznie zgodnie z II prawem Newtona dla ruchu

postępowego możemy napisać:

(

)

(

)

M k m g

T

M k m

+

−

=

+

2

a

r

, który bę

(36.5)

Przyśpieszenia obu ciężarków są jednakowe i wynoszą a, mają jednak inne zwroty, co już uwzględ-
niono w powyższych równaniach.

Siły naprężenia nici T

1

i T

2

działają prostopadle do promienia r bloczka. Wytwarzają więc wypad-

kowy moment siły równy

(

)

T

T

2

1

−

dzie obracał krążek z przyśpieszeniem kątowym

ε

.

Zgodnie z II prawem Newtona dla ruchu obrotowego możemy napisać:

(

)

T

T r

J

2

1

−

= ε

(36.6)

Ze względu na zależność a =

ε

r otrzymujemy

(

)

T

T r

J

a

r

2

1

−

=

i stąd po przekształceniu:

(

)

T

T

J

r

a

2

1

2

−

=

(36.7)

Wyliczając T

1

i T

2

ze wzorów (36.4), (36.5) i wstawiając do powyższej zależności otrzymujemy

wyrażenie na przyśpieszenie w ruchu ciężarków w maszynie Atwooda :

a

k m g

J

r

M

k m

=

+

+

2

2

(36.8)

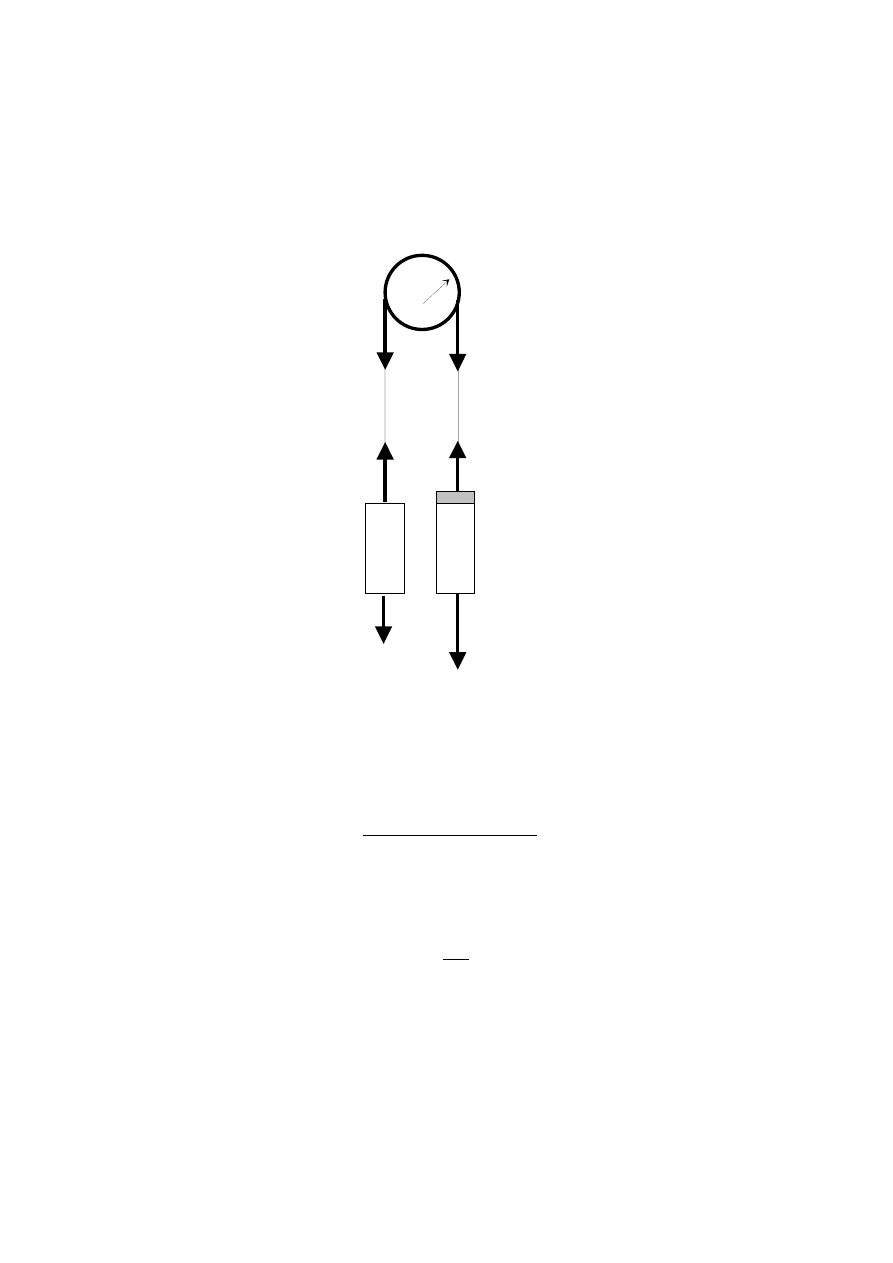
Z analizy tego wzoru wynika, że dla

k m

M

〈〈

przyśpieszenie a jest znacznie mniejsze od przy-

śpieszenia ziemskiego g. Fakt ten pozwala na łatwiejszy pomiar przyspieszenia układu przy stosun-
kowo niewielkiej wysokości przyrządu Atwooda, w odróżnieniu od pomiaru przyspieszenia przy
spadku swobodnym.

Otrzymanie dokładnych wyników jest uzależnione od możliwie mało obarczonych błędami pomia-
rów czasu. Do pomiarów czasu przy obserwacjach dokonywanych na maszynie Atwooda służą
szybkie

chronometry lub elektroniczne mierniki czasu.

B

A

Mg

T

1

T

2

T

1

T

2

r

+

Mg kmg

Rys. 36.3. Siły działające na ciężarki i bloczek w maszynie Atwooda.

W ćwiczeniu dokonuje się pomiaru przyśpieszenia a, co pozwala na wyznaczenie momentu bez-
władności bloczka K:

J

k m g

M a

k m a

a

r

=

−

−

2

2

(36.9)

Przyśpieszenie a wyznaczamy mierząc czas t , w którym ciężarki pokonują stałą drogę S. Ponieważ
ciężarki rozpoczynają ruch bez prędkości początkowej, przyśpieszenie a wyznaczamy z zależności

a

S

t

=

2

2

.

Umieszczając na osi bloczka dodatkowe ciało (w ćwiczeniu metalowy pierścień), korzystając z wy-
prowadzonych zależności, można wyznaczyć moment bezwładności J

C

, będący sumą momentu

bezwładności bloczka J

U

, i dołożonego ciała J

b

. Szukany moment bezwładności jest więc równy

różnicy:

J

J

J

b

C

U

=

−

(36.10)

36.2. Opis układu pomiarowego

Do sterowania maszyną Atwooda służy elektroniczny blok zasilająco-pomiarowy „Polydigit 1”.
Sprzężony on jest z elektromagnesem wyzwalającym ruch ciężarków oraz z dwoma fotokomórka-
mi. Dzięki temu pomiar czasu spadku ciężarków na określonej drodze odbywa się elektronicznie.
Blok „Polydigit 1” jest wyposażony w sześć dwupozycyjnych przycisków. W ćwiczeniu używane
są tylko cztery z nich (numeracja od lewej do prawej):

1)

Włącznik bloku.

2) Czerwony, opisany „Null” - służy do zerowania zegara.

3) Opisany „1000Hz” - określa dokładność zegara - podczas wykonania pomiarów musi być

stale wciśnięty.

4) Opisany „Messen” - służy do sterowania elektromagnesem. W górnej pozycji elektroma-

gnes jest włączony, a w dolnej wyłączony.

Ciężarki A i B mają jednakową masę M. Na ciężarek B mogą być nakładane blaszki o znanej ma-
sie m

o.

Przed każdym pomiarem ciężarek A utrzymywany jest przez elektromagnes (przycisk 6 nie

jest wciśnięty). Wciśnięcie przycisku 6 powoduje wyłączenie prądu płynącego przez elektromagnes
i rozpoczęcie ruchu ciężarków, jeżeli na ciężarek B nałożona jest co najmniej jedna blaszka. Przy-
cisk 6 włącza jednocześnie zegar elektroniczny, który mierzy czas pomiędzy wyłączeniem prądu
elektromagnesu a przecięciem przez ciężarek B światła padającego na fotokomórkę. Drogę ruchu
ciężarków zmieniamy poprzez położenie fotokomórki.

Do osi bloczka można przymocować metalowy pierścień, którego moment bezwładności należy
wyznaczyć.

Parametry układu:

Parametry pierścienia:

r

mm

M

m

g

=

±

=

±

=

±

98 1

2

507 1

15 3 0 1

,

,

g

m

m

m

g

R

m

R

m

p

=

±

=

±

=

±

2001 1

100 0 5

164 0 5

1

2

,

,

36.3. Przebieg pomiarów

1. Zaznajomić się z działaniem układu pomiarowego.

2. Włączyć „Polydigit 1” przez wciśnięcie przycisku (1), przycisku 1000 Hz i przycisku „Sieć” w

zasilaczu (6V, 50 Hz) żarówek fotokomórek. Obciążyć ciężarek B czterema blaszkami.

3. Ciężarek A opuścić do zetknięcia się z elektromagnesem.

4. Opuścić fotokomórkę (kręcąc korbą) na odległość S (90 cm). Zmierzyć tę odległość 10 razy.

Określić błąd pomiaru.

5. Przyciskiem „Messen” wyłączyć elektromagnes; jednocześnie włącza się pomiar czasu. W mo-

mencie przecięcia światła padającego na fotokomórkę przez ciężarek B pomiar czasu jest za-
trzymany i czas t przebycia drogi S jest wyświetlany na przyrządzie „Polydigit 1”. Czas ten za-
notować.

6. Pomiary punktów 3-5 wykonać piętnastokrotnie.

U w a g a :

Przesuwając ciężarek B do góry należy ominąć nim fotokomórkę !

7. Założyć na oś bloczka metalowy pierścień i powtórzyć pomiary wg punktów 3-6.

36.4. Opracowanie wyników pomiarów

1. Obliczyć średnią drogę spadku ciężarków

S

.

2. Dla obu serii pomiarowych ze średniego czasu

t

ruchu układu obliczyć jego przyspieszenia a .

3. Na podstawie wzoru (36.9) obliczyć wartości J

U

i J

C

.

4. Obliczyć moment bezwładności J

b

pierścienia (wzór 36.10).

5. Przy pomiarach popełniono błędy przypadkowe. Pomiary wykonywano 15 razy. Ta ilość jest

wystarczająca, żeby błędy oceniać zgodnie z rozkładem normalnym. Obliczyć odchylenia stan-
dardowe

σ

σ

S

t

i

.

6. Obliczyć średni błąd kwadratowy

σ

σ

a

i

b

J

(m, M, g przyjąć, że nie są obarczone błędami).

7. Obliczyć teoretycznie moment bezwładności pierścienia i porównać z wynikiem otrzymanym

doświadczalnie.

36.5. Pytania kontrolne

1. Sformułować II zasadę Newtona dla bryły w ruchu obrotowym.

2. Zdefiniować pojęcia: przyspieszenie kątowe, moment bezwładności, moment pędu.

3. Jak wyznaczyć przyspieszenie ziemskie oraz moment bezwładności układu za pomocą przyrządu
Atwooda?

L i t e r a t u r a

[1] Piekara A.: Mechanika ogólna. PWN, W-wa 1964.

[2] Szczeniowski S.: Fizyka doświadczalna, cz.I. Mechanika i akustyka, PWN, W-wa 1980.