
1
Jednostki podstawowe
Równania matematyczne (opisujace zjawiska fizyczne) wyrażają
ilościowe relacje między wielkościami fizycznymi
Pomiary określające liczbowo stosunek danej wielkości do
przyjętej jednostki

2
Równania matematyczne (opisujace zjawiska fizyczne) wyrażają
ilościowe relacje między wielkościami fizycznymi
Pomiary określające liczbowo stosunek danej wielkości do
przyjętej jednostki
liczba Avogadra
N
A
= 6,022137·10
23
mol
-1
Równania matematyczne (opisujace zjawiska fizyczne) wyrażają
ilościowe relacje między wielkościami fizycznymi
Pomiary określające liczbowo stosunek danej wielkości do
przyjętej jednostki

3
Równania matematyczne (opisujace zjawiska fizyczne) wyrażają
ilościowe relacje między wielkościami fizycznymi
Pomiary określające liczbowo stosunek danej wielkości do
przyjętej jednostki
Równania matematyczne (opisujace zjawiska fizyczne) wyrażają
ilościowe relacje między wielkościami fizycznymi
Pomiary określające liczbowo stosunek danej wielkości do
przyjętej jednostki
ś
wiatłość jest równa 1
kandeli dla światła
monochromatyczne o
częstości 5,4×1014 Hz i
i energetycznym
natężeniu
promieniownia 1/683
W/sr.
(wizualną jasność źródła światła)
4
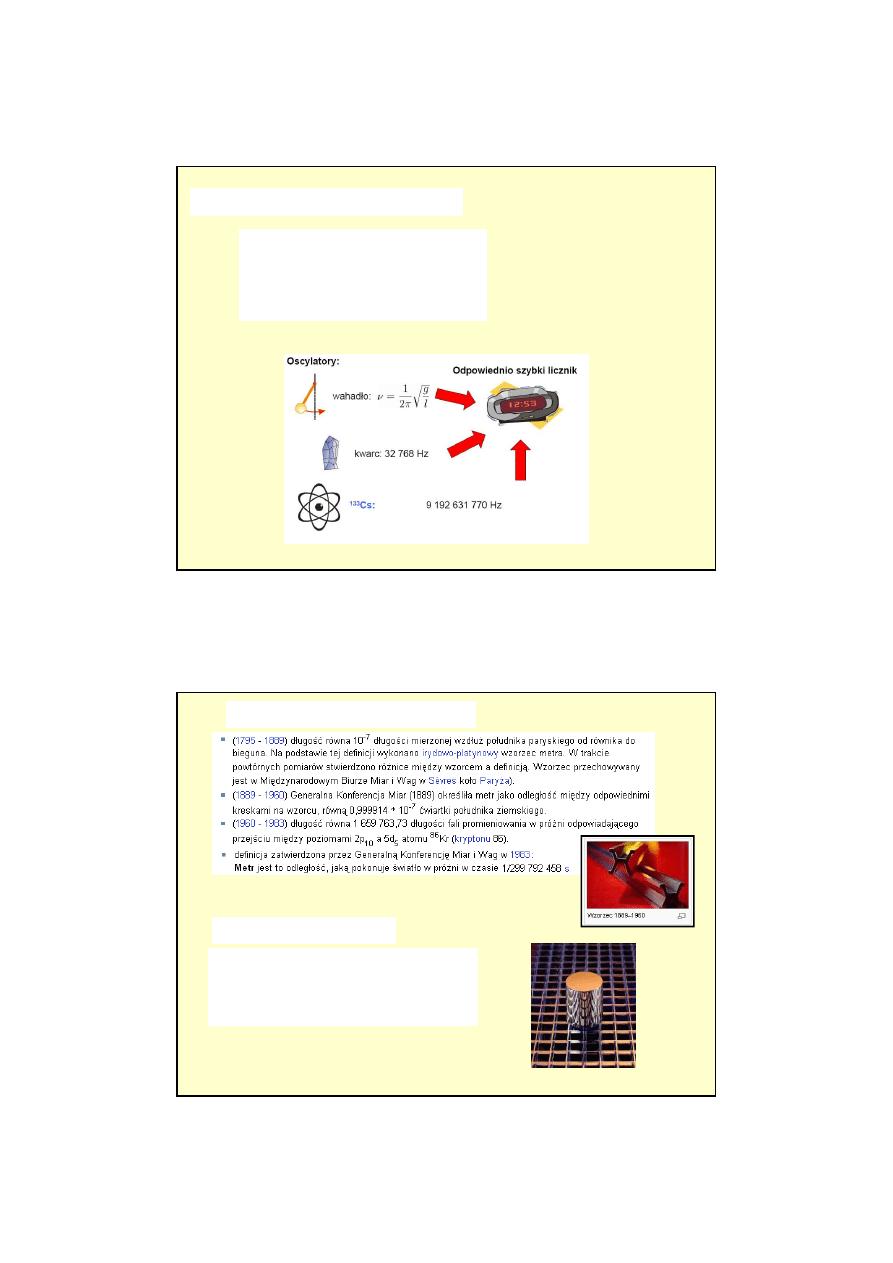
Definicja sekundy i pomiar czasu:
•Do
1967
roku: 1s = 1 / 31 556 925.9747
roku
• Od
1967
roku: sekunda to 9 192 631 770
drgań fali w przejściu HFS w
133
Cs
Dokładność 7x10
-15
Błąd 1s na 4,5 mln lat
Historia definicji metra:
• 1 kilogram - jest to masa międzynarodowego
wzorca (walca o wysokości i średnicy podstawy
39 mm wykonanego ze stopu platyny z irydem)
przechowywanego w Międzynarodowym
Biurze Miar w Sèvres koło Paryża.
Definicja kilograma:
5
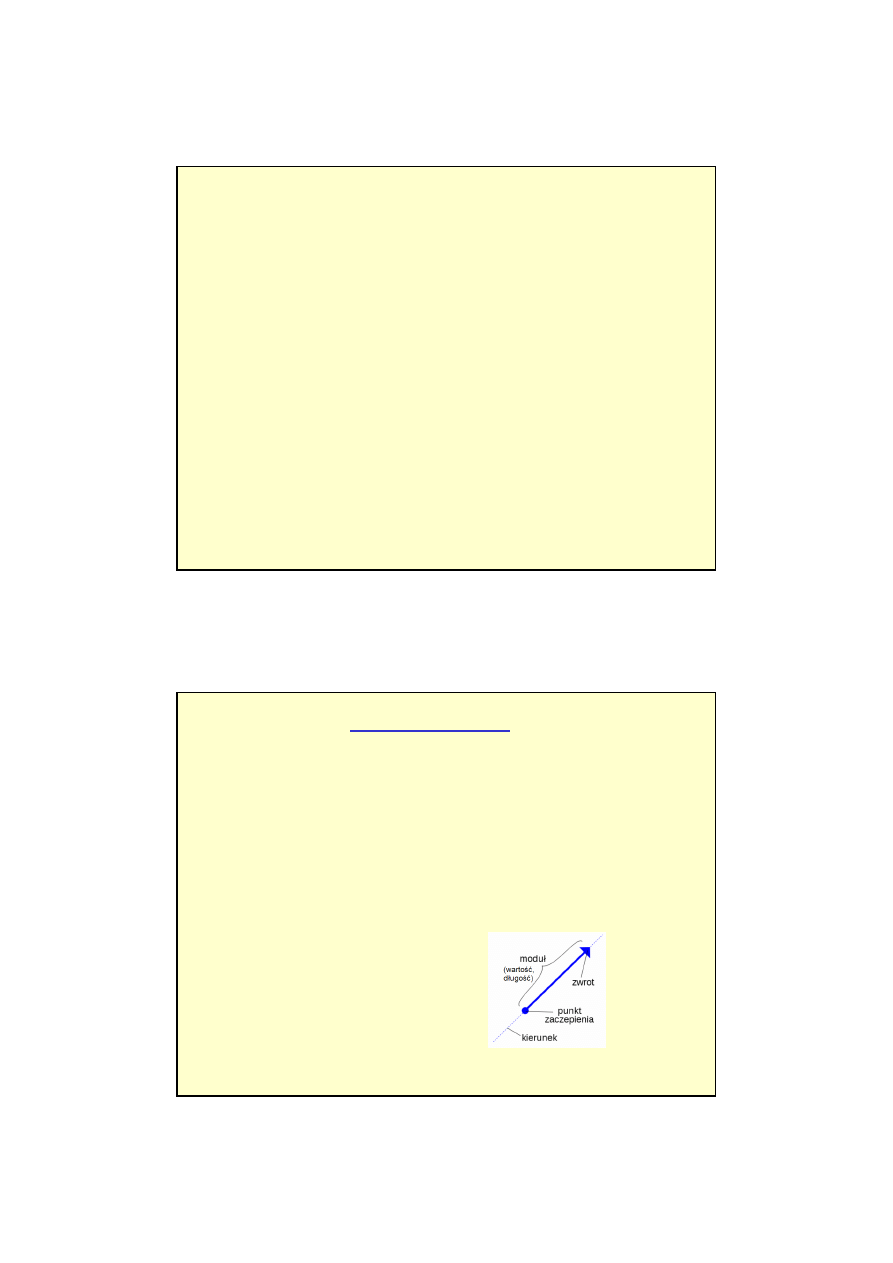
Wstawka matematyczna
1. Rachunek wektorowy
siła F
prędkość v
przyspieszenie a
pęd p
wielkości fizyczne
wielkości wektorowe
wektor – uporz
ą
dkowana
para punktów (pocz
ą
tek i koniec).
Cechy wektora:
* moduł (warto
ść
, długo
ść
)
* kierunek
* zwrot
* punkt przyło
ż
enia
masa m
czas t
energia E
temperatura T
wielkości skalarne
skalary – do okre
ś
lenia
wielko
ś
ci skalarnej wystarczy
jedna liczba
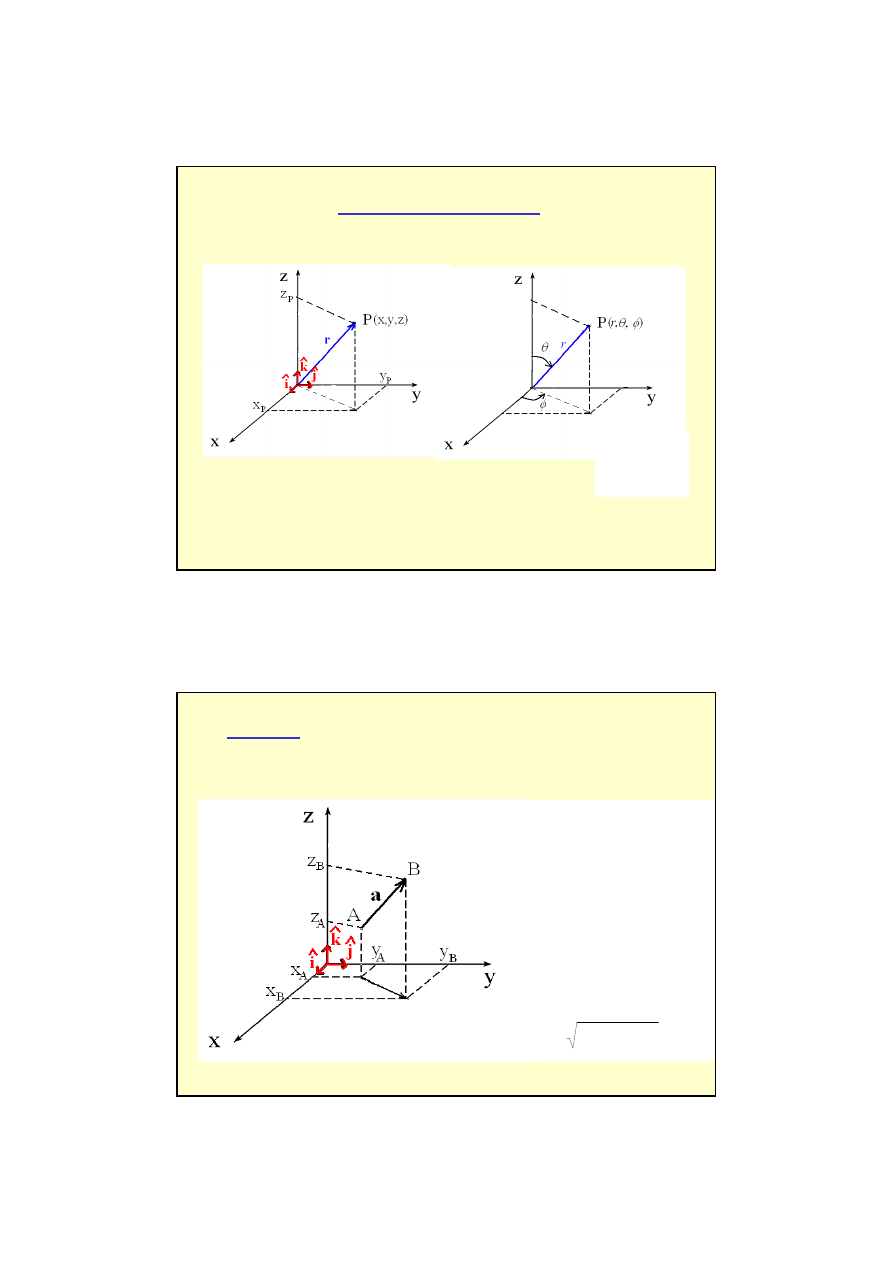
6
układ kartezjański
układ sferyczny
θ
φ
θ
φ
θ
cos
sin
sin
cos
sin
r
z
r
y
r
x
=
=
=
układy współrzędnych
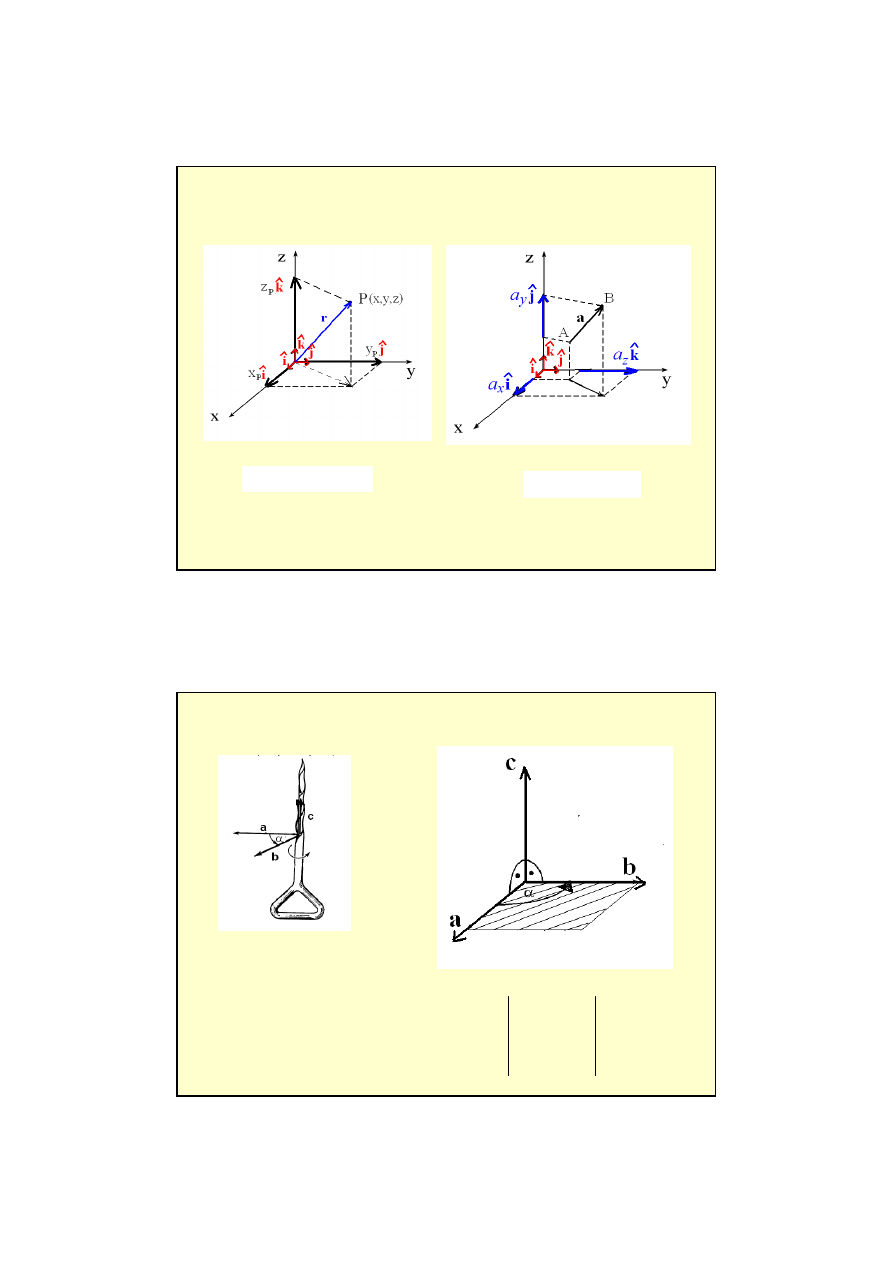
- wersor to wektor jednostkowy
iˆ
r - wektor poło
ż
enia
położenie r
prędkość v
przyspieszenie a
pęd p
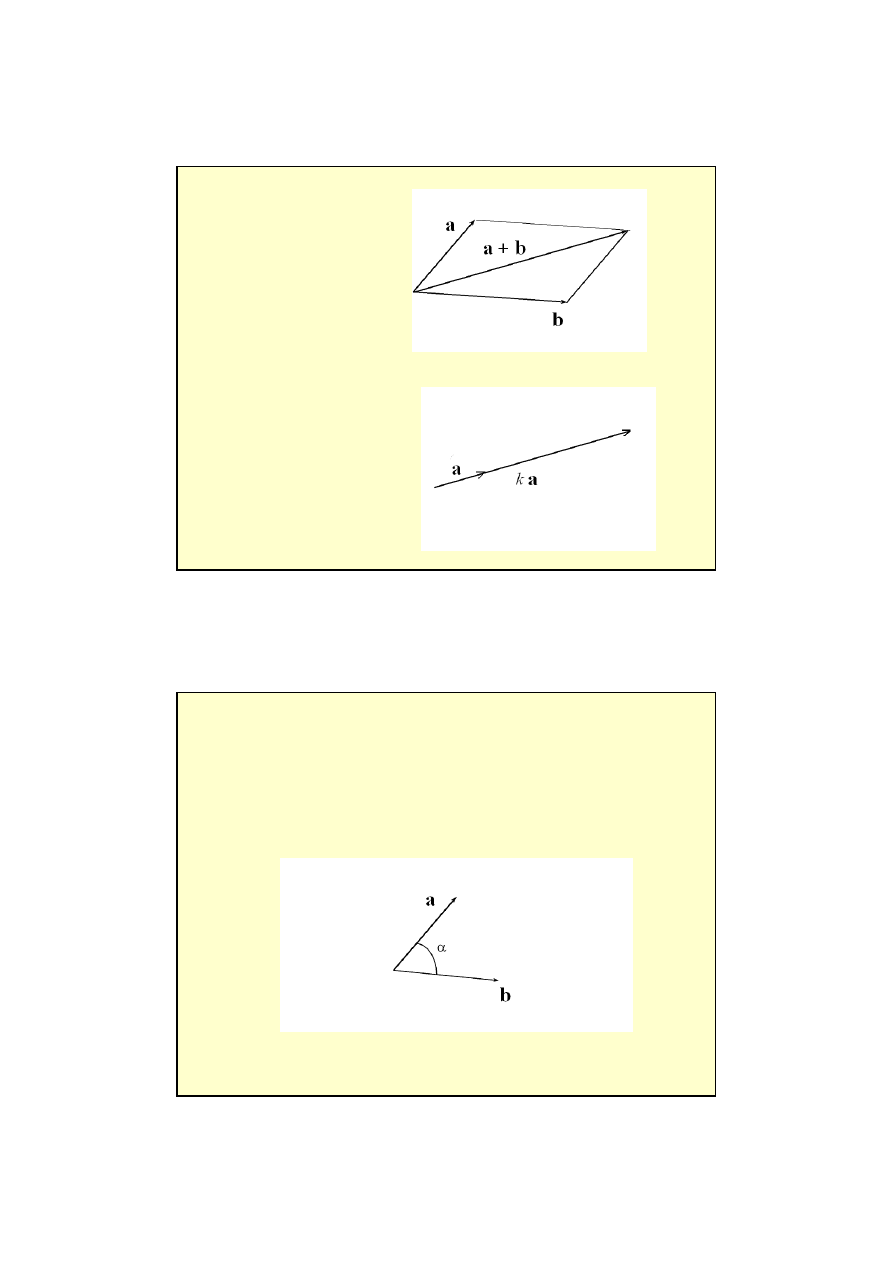
a
x
=x
B
-x
A
, a
y
=y
B
-y
A
, a
z
=z
B
-z
A
AB = a = [ a
x
, a
y
, a
z
]
wektory
długo
ść
wektora:
a
x
=b
x
, a
y
=b
y
, a
z
=b
z
.
współrz
ę
dne wektorów:
równo
ść
wektorów:
2
2
2
z
y
x
a
a
a
a
+
+
=
7
dodawanie wektorów:
mno
ż
enie wektora
przez liczb
ę
:
a + b = c
c
x
=a
x
+b
x
, c
y
=a
y
+b
y
, c
z
=a
z
+b
z
c
x
= k a
x
, c
y
= k a
y
, c
z
= k a
z
c = k a
iloczyn skalarny wektorów:
a·
·
·
·b = a b cos
α
a·
·
·
·b =a
x
b
x
+ a
y
b
y
+ a
z
b
z
8
k
j
i
a
ˆ
ˆ
ˆ
z
y
x
a
a
a
+
+
=
k
j
i
r
ˆ
ˆ
ˆ
P
P
P
z
y
x
+
+
=
......zapis za pomoca wersorów
iloczyn wektorowy :
a x
x
x
x b = c
c=a b sin
α
k
j
i
c
ˆ
ˆ
ˆ
z
y
x
c
c
c
+
+
=
z
y
x
z
y
x
b
b
b
a
a
a
k
j
i
c
ˆ
ˆ
ˆ
=
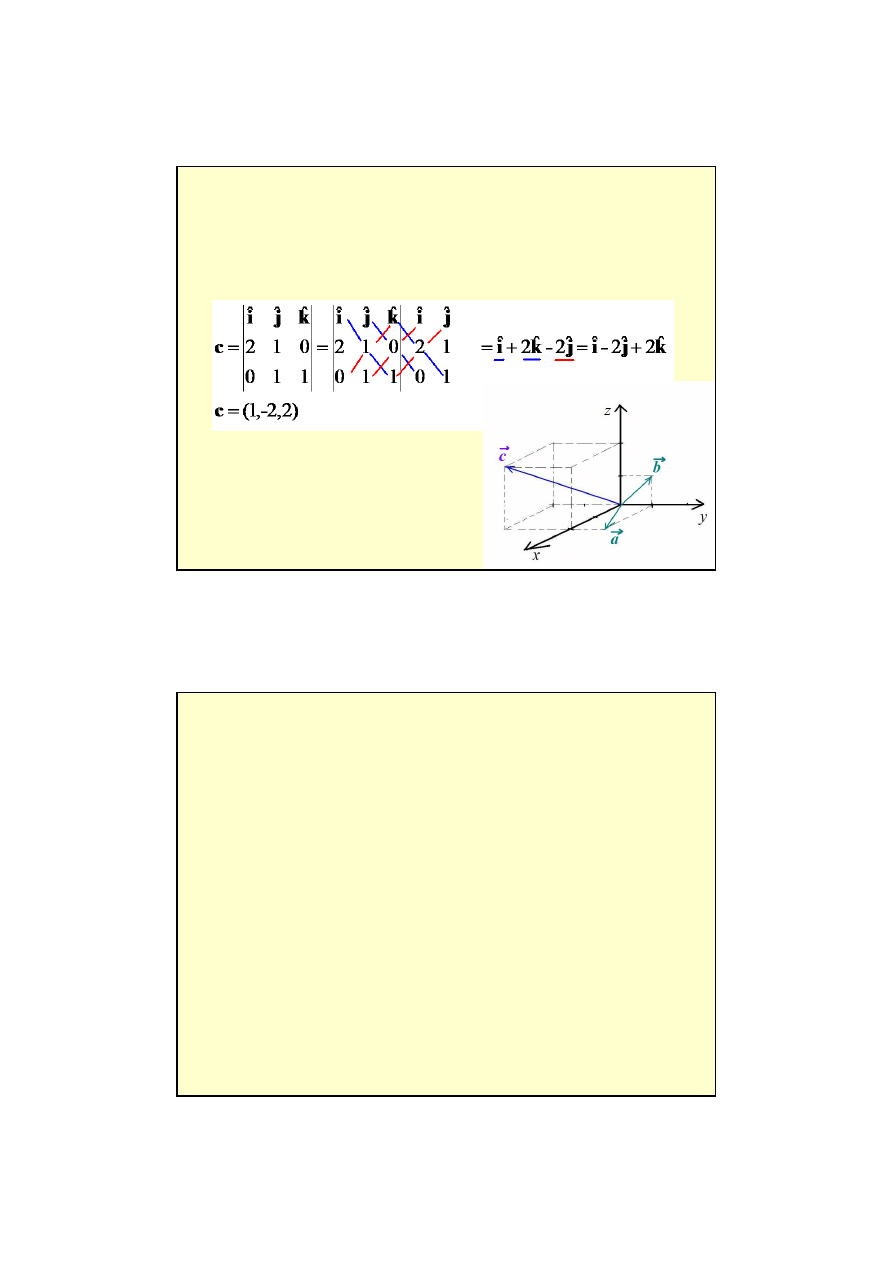
9
c = a x
x
x
x b
k
j
b
j
i
a
ˆ
ˆ
)
1
,
1
,
0
(
ˆ
ˆ
2
)
0
,
1
,
2
(
+
=
=
+
=
=
Przykład iloczynu wektorowego:
Wstawka matematyczna
2. Pochodne
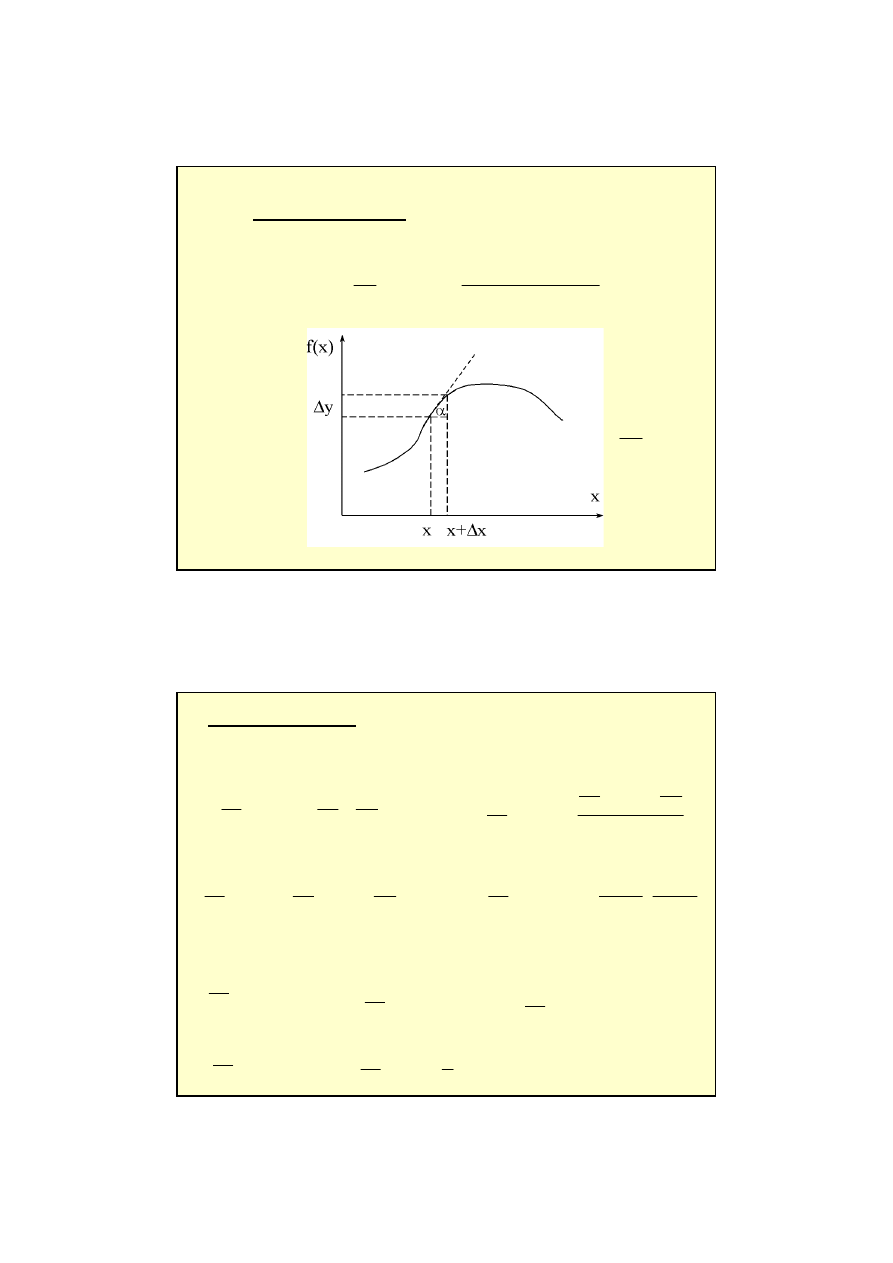
10
x
x
f
x
x
f
dx
df
x
f
x
∆
−
∆
+
=
=
→
∆
)
(
)
(
lim
)
(
'
0
Pochodna funkcji f(x)
α
tg
dx
df
=
Pochodna funkcji
Podstawowe własności pochodnej :
dx
dg
dx
df
g
f
dx
d
+
=
+
)
(
dx
dg
f
g
dx
df
g
f
dx
d
⋅
+
⋅
=
⋅
)
(
2
)
/
(
g
dx
dg
f
g
dx
df
g
f
dx
d
⋅
−
⋅
=
[
]
)
(
:
)
(
)
(
))
(
(
x
g
u
gdzie
dx
x
dg
du
u
df
x
g
f
dx
d
=
⋅
=
Przykłady:
1
)
(
−
=
n
n
nx
x
dx
d
)
0
(
1
)
(ln
>
=
x
x
x
dx
d
x
x
e
e
dx
d
=
)
(
x
x
dx
d
cos
)
(sin
=
x
x
dx
d
sin
)
(cos
−
=
11
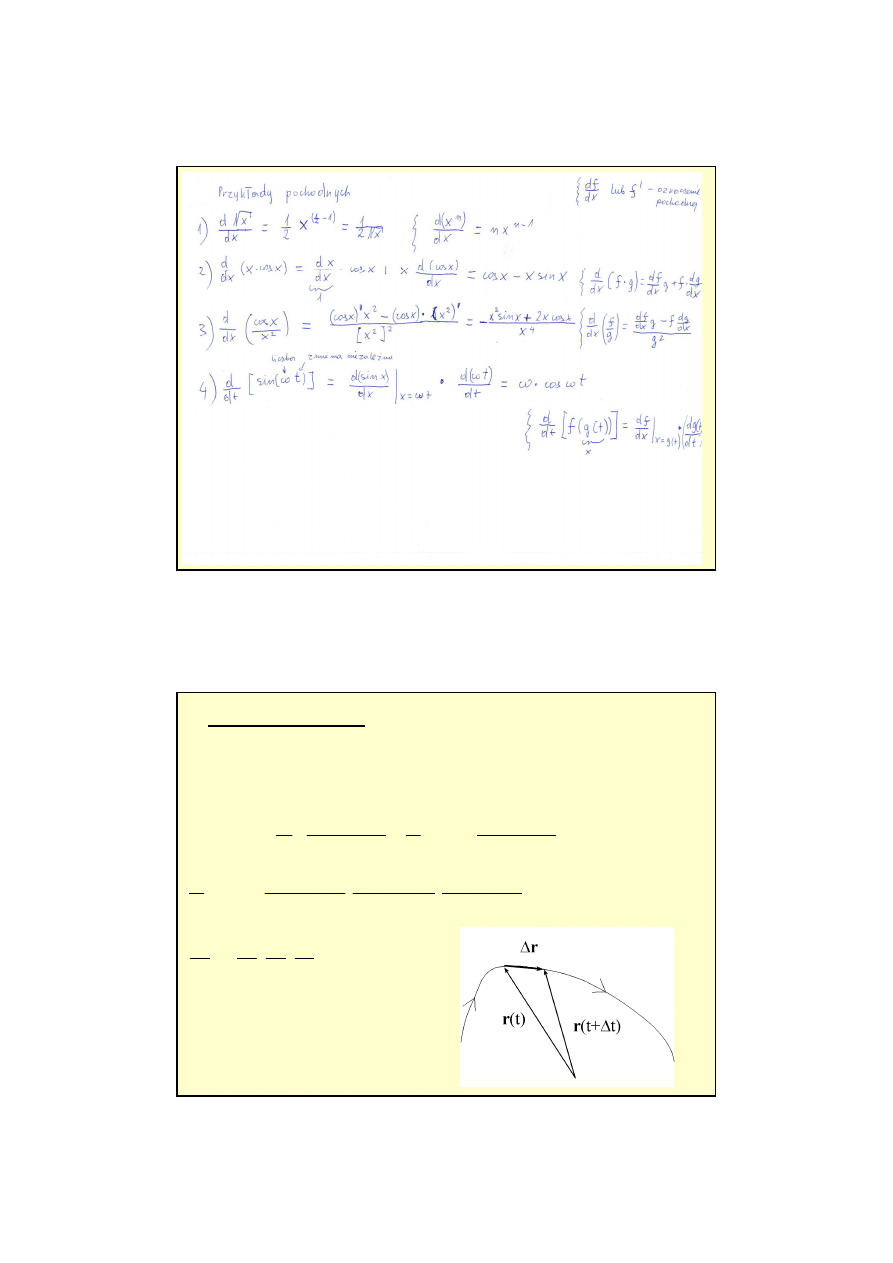
Pochodna wektora
Jeśli w przedziale czasu
∆
t przyrost wektora r(t) wynosi
∆
r:
∆
r = r(t+
∆
t) – r(t),
to stosunek:
t
t
t
t
dt
d
t
t
t
t
t
t
∆
−
∆
+
=
→
∆
−
∆
+
=
∆
∆
→
∆
)
(
)
(
lim
)
(
)
(
0
r
r
r
r
r
r
∆
−
∆
+
∆
−
∆
+
∆
−
∆
+
=
→
∆
t
t
z
t
t
z
t
t
y
t
t
y
t
t
x
t
t
x
dt
d
t
)
(
)
(
,
)
(
)
(
,
)
(
)
(
lim
0
r
=
dt
dz
,
dt
dy
,
dt
dx
dt
dr
12
Całka nieoznaczona
∫
=
)
(
)
(
x
f
dx
x
g
Wynik operacji całkowania:
znaleziona funkcja pierwotna f(x) ma taką własność, że po zróżniczkowaniu
jej otrzymujemy funkcję podcałkową g(x):
C
x
f
dx
x
g
+
=
∫
)
(
)
(
ściślej:
[f (x)+C]' = g(x)
Przykłady:
C
x
1
n
1
dx
x
1
n
n
+
+
=
+
∫
∫ e
x
dx = e
x
+ C
∫ (1/x) dx = ln x + C
∫ cos x dx = sin x + C
∫ sin x dx = - cos x + C
Całka oznaczona:
[
] [
]
∫
∫
=
=
+
−
+
=
−
b
a
b
a
dx
x
g
dx
x
g
C
a
f
C
b
f
a
f
b
f
)
(
)
(
)
(
)
(
)
(
)
(
C
x
f
dx
x
g
+
=
∫
)
(
)
(
Niech :
przyrost funkcji pierwotnej na przedziale [a,b]:
nazywamy całką oznaczoną.
)
(
)
(
)
(
a
f
b
f
dx
x
g
b
a
−
=
∫
CZYLI CAŁKA OZNACZONA TO:
C
x
f
dx
x
g
+
=
∫
)
(
)
(
gdzie:
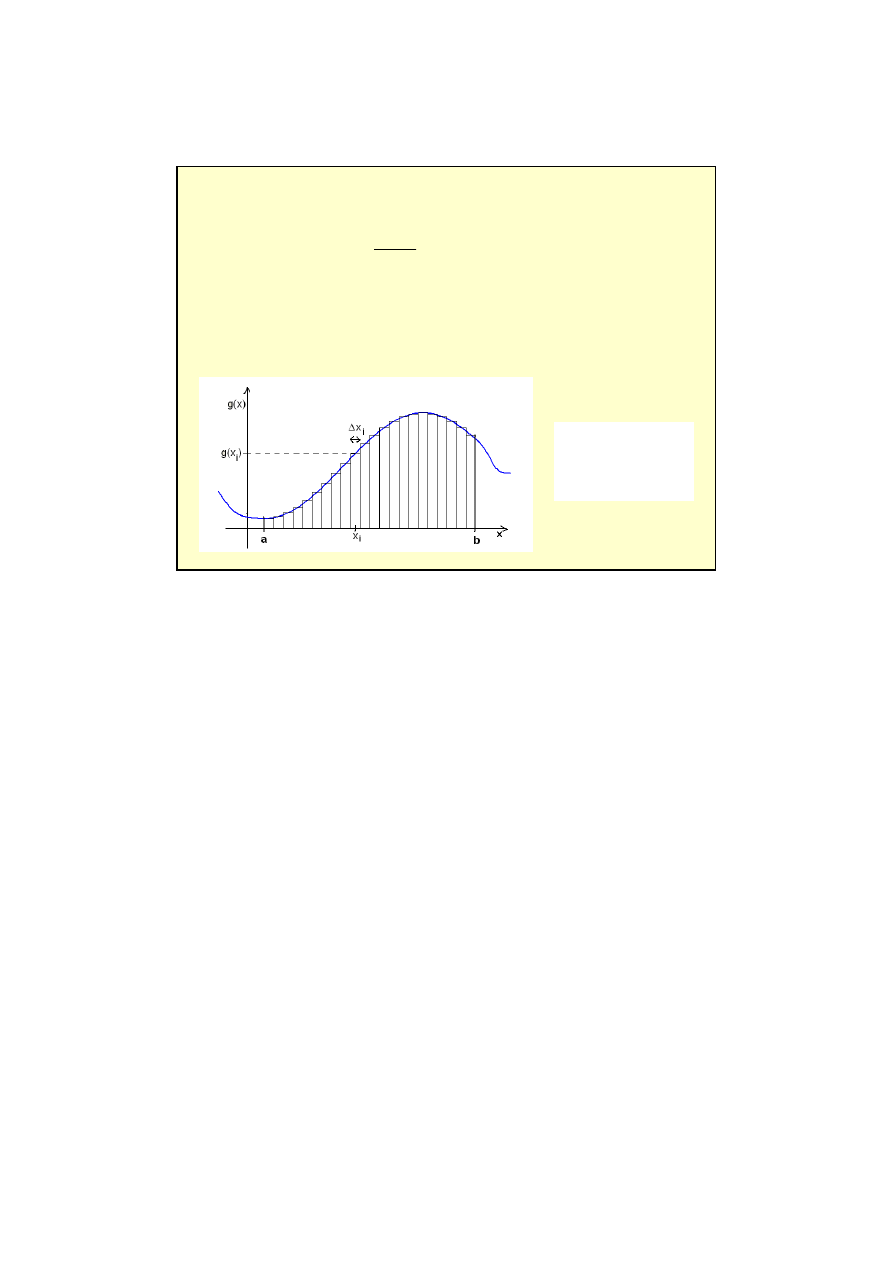
13
S
x
x
g
x
x
f
x
a
f
b
f
dx
x
g
i
N
i
i
i
N
i
i
i
b
a
=
∆
→
∆
=
∆
→
∆
=
−
=
∑
∑
∫
)
(
0
lim
)
(
0
lim
)
(
)
(
)
(
Znaczenie całki oznaczonej:
i
i
i
i
i
x
x
f
x
x
f
x
g
∆
∆
→
∆
=
=
)
(
0
lim
)
(
'
)
(
i
i
i
x
x
g
x
f
∆
=
∆
)
(
)
(
∫
=
b
a
dx
x
g
S
)
(
Wyszukiwarka
Podobne podstrony:
0 wstep jednostki matid 1877 Nieznany (2)
mat nr 2 konwers wstep do filozofii
0 Spis treści, Wykaz ważniejszych jednostek i oznaczeń, Przedmowa, Wstęp
Wstep do prawa - ściągi, itp, prawo-ze sciagami duzy i maly format, PRZEPIS PRAWA to najmniejsza jed
mat nr 3 konwers wstęp do filozofii
Wstep do Statystyki Mat zad Jokiel Rokita p9
SI wstep
Wyklad2 mat
Zajęcie1 Wstęp
Z jednostkami za pan brat
Wstęp do psychopatologii zaburzenia osobowosci materiały
Jedność budowy organizmów żywych1
układ naczyniowy wstep
ZMPST Wstep
Mat 10 Ceramika
Dekalog 0 wstęp
więcej podobnych podstron