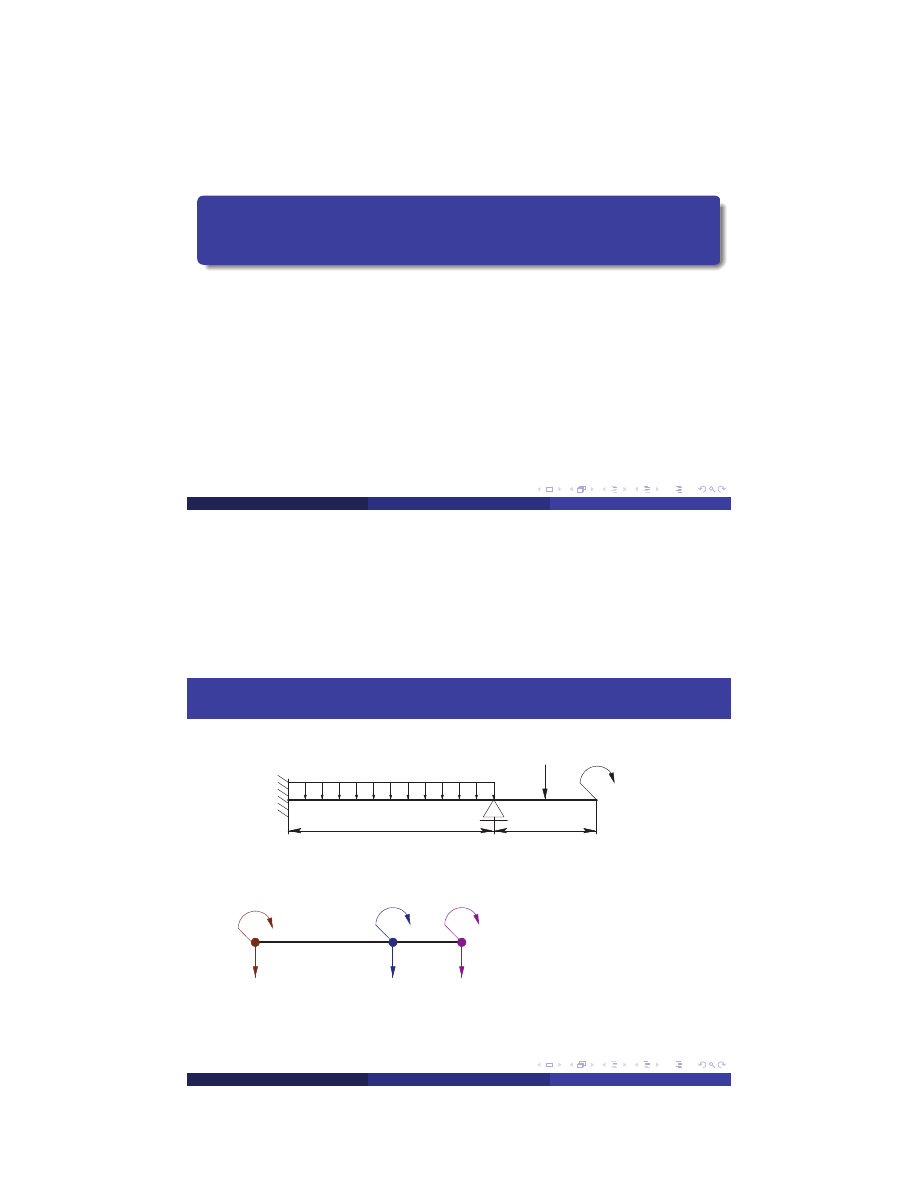
Computational Methods
1D Examples
Małgorzata Stojek
Cracow University of Technology
March 2013
MS
(L-53 CUT)
Beam & Truss
03/2013
1 / 44
Beam Example
M = qL
2
2L
L
P = qL
q
e1
e2
θ
1
w
1
θ
θ
w
w
2
2
3
3
d
1
d
2
d
3
d
4
d
5
d
6
=
w
1
θ
1
w
2
θ
2
w
3
θ
3
MS
(L-53 CUT)
Beam & Truss
03/2013
2 / 44

Beam Element Library
Prismatic Beam
Stiffness Matrix
:
K
e
=
EI
h
3
12
6h
−
12
6h
4h
2
−
6h
2h
2
12
−
6h
symm
4h
2
Load Vector due to q
(
x
)
:
constant
distributed load
concentrated
force
q
(
x
) =
q
q
(
x
) =
P
δ
x
(
x
−
h
2
)
F
e
q
=
q
h
1
2
1
12
h
1
2
−
1
12
h
F
e
q
=
P
1
2
1
8
h
1
2
−
1
8
h
MS
(L-53 CUT)
Beam & Truss
03/2013
3 / 44
First Element
Stiffness Matrix
DOFs: 1, 2, 3, 4; h
=
2L
K
e
1
4
×
4
=
EI
(
2L
)
3
12
6
(
2L
)
−
12
6
(
2L
)
6
(
2L
)
4
(
2L
)
2
−
6
(
2L
)
2
(
2L
)
2
−
12
−
6
(
2L
)
12
−
6
(
2L
)
6
(
2L
)
2
(
2L
)
2
−
6
(
2L
)
4
(
2L
)
2
=
EI
2L
3
3
3L
−
3
3L
3L
4L
2
−
3L
2L
2
−
3
−
3L
3
−
3L
3L
2L
2
−
3L
4L
2
MS
(L-53 CUT)
Beam & Truss
03/2013
4 / 44

First Element
Load Vector due to
q
(
x
)
F
e
1
q
=
q
(
2L
)
1
2
1
12
(
2L
)
1
2
−
1
12
(
2L
)
=
qL
1
1
3
L
1
−
1
3
L
y
1
3
qL
2
x
1
3
qL
2
[
element 1
]
↓
qL
↓
qL
MS
(L-53 CUT)
Beam & Truss
03/2013
5 / 44
Second Element
DOFs: 3, 4, 5, 6; h
=
L
Stiffness Matrix
K
e
2
4
×
4
=
EI
(
L
)
3
12
6
(
L
)
−
12
6L
6
(
L
)
4
(
L
)
2
−
6
(
L
)
2
(
L
)
2
−
12
−
6
(
L
)
12
−
6
(
L
)
6
(
L
)
2
(
L
)
2
−
6
(
L
)
4
(
L
)
2
Load Vector due to P
=
qL
F
e
2
q
=
P
1
2
1
8
L
1
2
−
1
8
L
y
1
8
qL
2
x
1
8
qL
2
[
element 2
]
↓
1
2
qL
↓
1
2
qL
MS
(L-53 CUT)
Beam & Truss
03/2013
6 / 44

Assembly
Global Stiffness Matrix
K
=
0
6
×
6
(+)
K
e
1
4
×
4
(+)
K
e
2
4
×
4
K
=
EI
(
L
)
3
3
2
3
2
L
−
3
2
3
2
L
0
0
3
2
L
2L
2
−
3
2
L
L
2
0
0
−
3
2
−
3
2
L
3
2
+
12
−
3
2
L
+
6L
−
12
6L
3
2
L
L
2
−
3
2
L
+
6L
2L
2
+
4L
2
−
6L
2L
2
0
0
−
12
−
6L
12
−
6L
0
0
6L
2L
2
−
6L
4L
2
K
=
EI
(
L
)
3
3
2
3
2
L
−
3
2
3
2
L
0
0
3
2
L
2L
2
−
3
2
L
L
2
0
0
−
3
2
−
3
2
L
27
2
9
2
L
−
12
6L
3
2
L
L
2
9
2
L
6L
2
−
6L
2L
2
0
0
−
12
−
6L
12
−
6L
0
0
6L
2L
2
−
6L
4L
2
MS
(L-53 CUT)
Beam & Truss
03/2013
7 / 44
Assembly
Global Load Vector
F
q
=
0
6
×
1
(+)
F
e
1
q
4
×
1
(+)
F
e
2
P
4
×
1
0
0
0
0
0
0
→
qL
1
3
qL
2
qL
−
1
3
qL
2
0
0
→
qL
1
3
qL
2
qL
+
1
2
qL
−
1
3
qL
2
+
1
8
qL
2
1
2
qL
−
1
8
qL
2
=
qL
1
3
qL
2
3
2
qL
−
5
24
qL
2
1
2
qL
−
1
8
qL
2
MS
(L-53 CUT)
Beam & Truss
03/2013
8 / 44

Assembly
Generic System of Linear Equations
Kd
=
F
q
EI
(
L
)
3
3
2
3
2
L
−
3
2
3
2
L
0
0
3
2
L
2L
2
−
3
2
L
L
2
0
0
−
3
2
−
3
2
L
27
2
9
2
L
−
12
6L
3
2
L
L
2
9
2
L
6L
2
−
6L
2L
2
0
0
−
12
−
6L
12
−
6L
0
0
6L
2L
2
−
6L
4L
2
w
1
θ
1
w
2
θ
2
w
3
θ
3
=
qL
1
3
qL
2
3
2
qL
−
5
24
qL
2
1
2
qL
−
1
8
qL
2
NOTE:
det K
=
0,
rank
(
K
) =
4
.
MS
(L-53 CUT)
Beam & Truss
03/2013
9 / 44
Boundary Conditions
kinematic constraints
natural
BCs
(essential "BCs")
(nonhomogeneous)
w
1
=
0,
θ
1
=
0,
w
2
=
0
at x
=
3L,
M
=
qL
2
w
1
θ
1
w
2
θ
2
w
3
θ
3
→
0
0
0
θ
2
w
3
θ
3
qL
1
3
qL
2
3
2
qL
−
5
24
qL
2
1
2
qL
−
1
8
qL
2
→
qL
1
3
qL
2
3
2
qL
−
5
24
qL
2
1
2
qL
−
1
8
qL
2
+
qL
2
NOTE:
rank
(
K
) =
4
&
3
support constraints
←→
beam is
statically indeterminate
.
MS
(L-53 CUT)
Beam & Truss
03/2013
10 / 44

Solution I
EI
(
L
)
3
3
2
3
2
L
−
3
2
3
2
L
0
0
3
2
L
2L
2
−
3
2
L
L
2
0
0
−
3
2
−
3
2
L
27
2
9
2
L
−
12
6L
3
2
L
L
2
9
2
L
6L
2
−
6L
2L
2
0
0
−
12
−
6L
12
−
6L
0
0
6L
2L
2
−
6L
4L
2
0
0
0
θ
2
w
3
θ
3
=
qL
1
3
qL
2
3
2
qL
−
5
24
qL
2
1
2
qL
7
8
qL
2
EI
(
L
)
3
6L
2
−
6L
2L
2
−
6L
12
−
6L
2L
2
−
6L
4L
2
θ
2
w
3
θ
3
=
−
5
24
qL
2
1
2
qL
7
8
qL
2
+
−
EI
(
L
)
3
3
2
L L
2
9
2
L
0
0
−
12
0
0
6L
0
0
0
MS
(L-53 CUT)
Beam & Truss
03/2013
11 / 44
Solution II
RECALL:
EI
(
L
)
3
6L
2
−
6L
2L
2
−
6L
12
−
6L
2L
2
−
6L
4L
2
θ
2
w
3
θ
3
=
−
5
24
qL
2
1
2
qL
7
8
qL
2
Solution is:
θ
2
w
3
θ
3
=
7
12
qL
3
EI
19
16
qL
4
EI
41
24
qL
3
EI
→
d
=
0
0
0
θ
2
w
3
θ
3
=
0
0
0
7
12
qL
3
EI
19
16
qL
4
EI
41
24
qL
3
EI
MS
(L-53 CUT)
Beam & Truss
03/2013
12 / 44

Postprocessing
Siły Przyw ˛ezłowe
RECALL:
K
e
d
e
=
F
e
=
F
e
q
+
W
e
W
e
=
Q
1
M
1
Q
2
M
2
=
K
e
d
e
−
F
e
q
y
M
1
↓
Q
1
[
beam element
]
↓
Q
2
y
M
2
MS
(L-53 CUT)
Beam & Truss
03/2013
13 / 44
Siły Przyw ˛ezłowe
Element 1
y
M
1
↓
Q
1
[
beam element
]
↓
Q
2
y
M
2
W
e
1
=
K
e
1
d
e
1
−
F
e
1
q
W
e
1
=
EI
2L
3
3
3L
−
3
3L
3L
4L
2
−
3L
2L
2
−
3
−
3L
3
−
3L
3L
2L
2
−
3L
4L
2
0
0
0
7
12
qL
3
EI
−
qL
1
1
3
L
1
−
1
3
L
Q
e
1
1
M
e
1
1
Q
e
1
2
M
e
1
2
=
−
1
8
qL
1
4
qL
2
−
15
8
qL
3
2
qL
2
→
y
1
4
qL
2
y
3
2
qL
2
[
element 1
]
↑
1
8
qL
↑
15
8
qL
MS
(L-53 CUT)
Beam & Truss
03/2013
14 / 44

Siły Przyw ˛ezłowe
Element 2
y
M
1
↓
Q
1
[
beam element
]
↓
Q
2
y
M
2
W
e
2
=
K
e
2
d
e
2
−
F
e
2
q
W
e
2
=
EI
L
3
12
6L
−
12
6L
6L
4L
2
−
6L
2L
2
−
12
−
6L
12
−
6L
6L
2L
2
−
6L
4L
2
0
7
24
qL
3
EI
43
48
qL
4
EI
17
12
qL
3
EI
−
qL
1
2
1
8
L
1
2
−
1
8
L
Q
e
2
1
M
e
2
1
Q
e
2
2
M
e
2
2
=
−
qL
−
3
2
qL
2
0
qL
2
→
x
3
2
qL
2
y
qL
2
[
element 2
]
↑
qL
↓
0
MS
(L-53 CUT)
Beam & Truss
03/2013
15 / 44
Reactions at Supports I
1
4
qL
2
y
y
3
2
qL
2
[
element 1
]
1
8
qL
↑
↑
15
8
qL
3
2
qL
2
x
y
qL
2
[
element 2
]
qL
↑
↓
0
−
15
8
qL
+
R
2
=
qL
R
2
=
qL
+
15
8
qL
=
23
8
qL
8
1
1
4
2
qL
23
8
P = qL
q
2L
L
qL
qL
M = qL
2
MS
(L-53 CUT)
Beam & Truss
03/2013
16 / 44
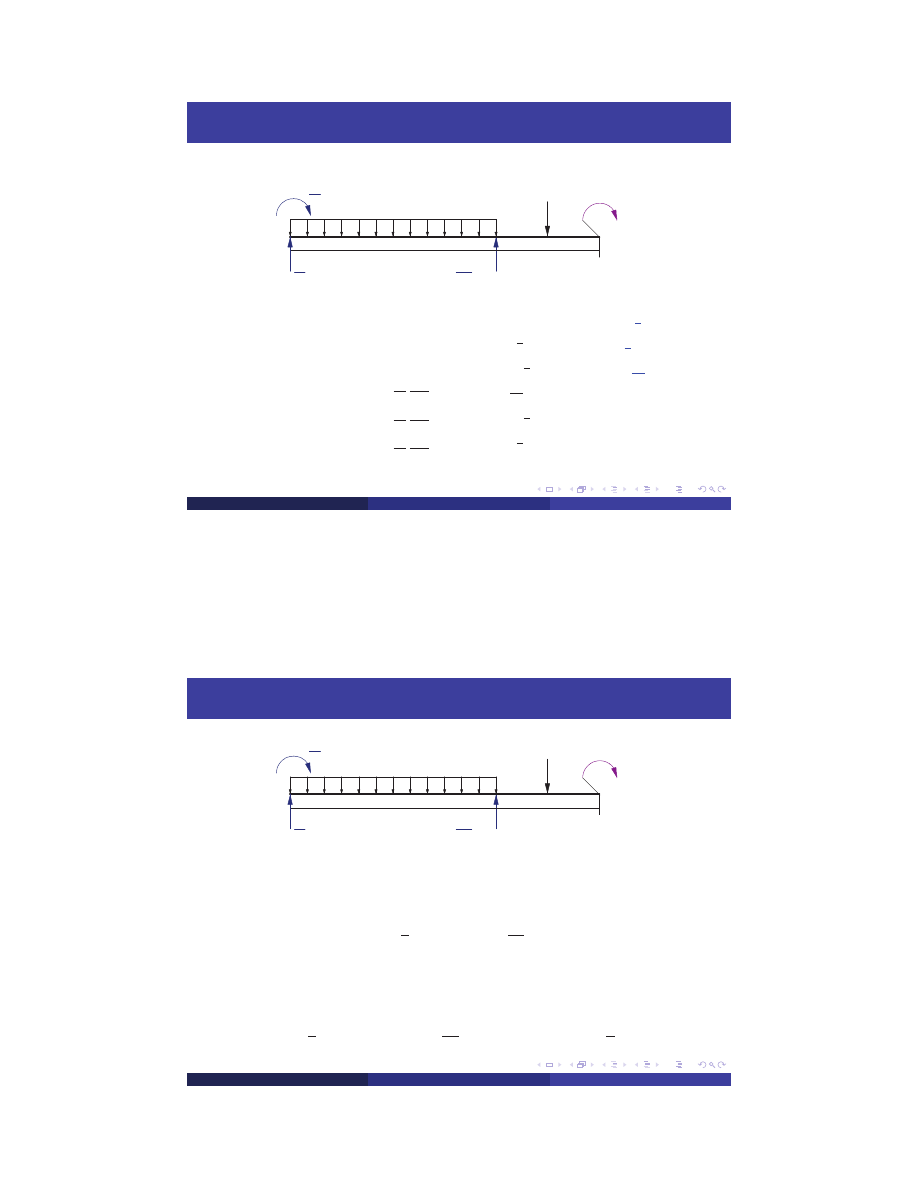
Reactions at Supports II
8
1
1
4
2
qL
23
8
P = qL
q
2L
L
qL
qL
M = qL
2
W
=
Kd
−
F
q
=
K
0
0
0
7
12
qL
3
EI
19
16
qL
4
EI
41
24
qL
3
EI
−
qL
1
3
qL
2
3
2
qL
−
5
24
qL
2
1
2
qL
−
1
8
qL
2
=
−
1
8
qL
1
4
qL
2
−
23
8
qL
0
0
qL
2
MS
(L-53 CUT)
Beam & Truss
03/2013
17 / 44
Equations of Equilibrium
8
1
1
4
2
qL
23
8
P = qL
q
2L
L
qL
qL
M = qL
2
∑
i
P
i
y
?
=
0
1
8
qL
−
q
·
2L
+
23
8
qL
−
qL
=
0
∑
i
M
i
x
=
0
?
=
0
1
4
qL
2
+
q
·
2L
·
L
−
23
8
qL
·
2L
+
qL
·
2L
+
L
2
+
qL
2
=
0
MS
(L-53 CUT)
Beam & Truss
03/2013
18 / 44
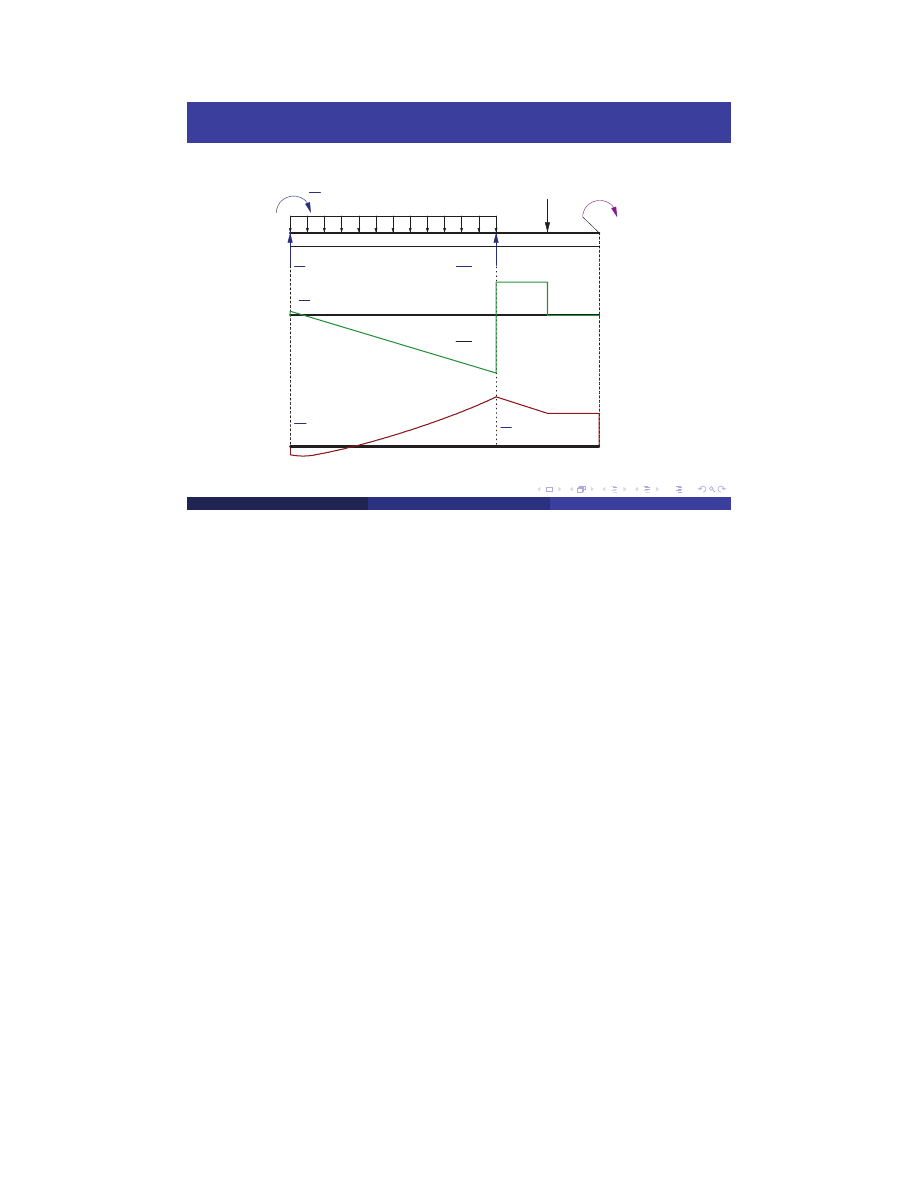
Wykresy Sił Przekrojowych
8
1
1
4
2
qL
23
8
8
1
8
15
qL
2
qL
1
4
2
3
qL
2
P = qL
q
2L
L
qL
qL
M = qL
2
Q(x)
qL
qL
M(x)
2
qL
MS
(L-53 CUT)
Beam & Truss
03/2013
19 / 44
Wyszukiwarka
Podobne podstrony:
5 lect6 beam students
6 lect6 truss students
6 lect6 truss students
Floor beam ver 1 Student id 178 Nieznany
Floor beam ver 1 Student id 178 Nieznany
2010 ZMP studenci
gruźlica dla studentów2
Prezentacja 2 analiza akcji zadania dla studentow
Szkolenie BHP Nowa studenci
Student Geneza
Kosci, kregoslup 28[1][1][1] 10 06 dla studentow
higiena dla studentów 2011 dr I Kosinska
Studenci biegunka przewlekła'
WYKŁAD STUDENCI MIKULICZ
więcej podobnych podstron