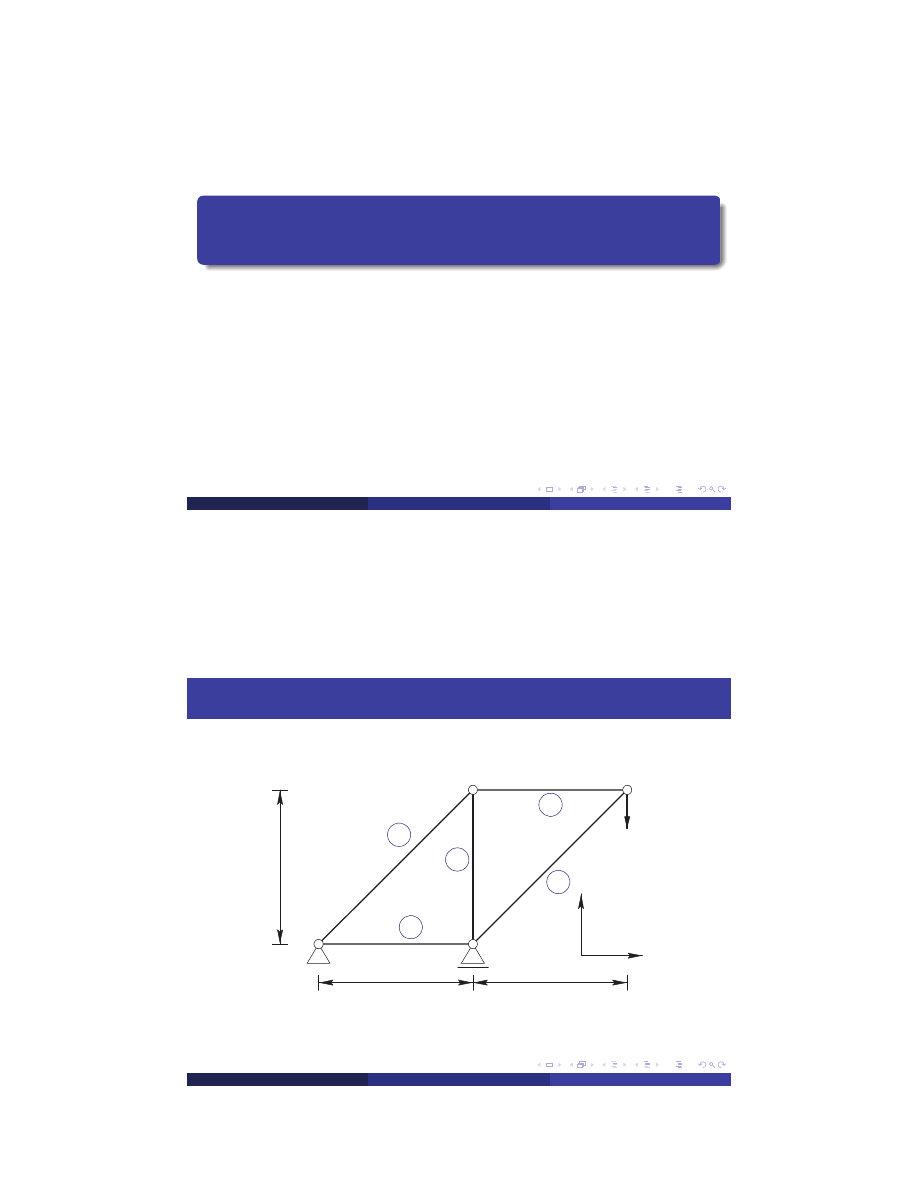
Computational Methods
1D Examples
Małgorzata Stojek
Cracow University of Technology
March 2013
MS
(L-53 CUT)
Beam & Truss
03/2013
1 / 44
Truss Example
3
2
5
1
4
EA
EA
y
x
1
1
1
2EA
2EA
EA
1
2
3
4
P
MS
(L-53 CUT)
Beam & Truss
03/2013
20 / 44

Truss Discretization
3
2
5
1
4
EA
EA
1
1
1
2 EA
2 EA
EA
x
y
1
2
4
3
u
u
u
u
u
u
u
u
1
2
3
4
5
6
7
8
no elem.
nodes
global DOFs
length
α
c
=
cos α
s
=
sin α
1
1, 3
1, 2, 5, 6
√
2
π
/
4
√
2/2
√
2/2
2
1, 2
1, 2, 3, 4
1
0
1
0
3
3, 2
5, 6, 3, 4
1
−
π
2
0
−
1
4
2, 4
3, 4, 7, 8
√
2
π
/
4
√
2/2
√
2/2
5
3, 4
5, 6, 7, 8
1
0
1
0
MS
(L-53 CUT)
Beam & Truss
03/2013
21 / 44
Truss Element Library
Prismatic Bar
Stiffness Matrix
:
K
e
=
EA
L
c
2
cs
−
c
2
−
cs
cs
s
2
−
cs
−
s
2
−
c
2
−
cs
c
2
cs
−
cs
−
s
2
cs
s
2
=
EA
L
c
2
cs
−
c
2
−
cs
s
2
−
cs
−
s
2
c
2
cs
symm
s
2
Load Vector due to q
(
x
)
:
constant
distributed load
q
(
x
) =
q
F
e
q
=
qL
2
c
s
c
s
MS
(L-53 CUT)
Beam & Truss
03/2013
22 / 44

Element Stiffness Matrix
K
e
1
4
×
4
=
K
e
4
4
×
4
=
EA
√
2
2
√
2
2
−
√
2
2
−
√
2
2
√
2
2
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
√
2
2
√
2
2
−
√
2
2
−
√
2
2
√
2
2
√
2
2
K
e
2
4
×
4
=
K
e
5
4
×
4
=
EA
1
0
−
1 0
0
0
0
0
−
1 0
1
0
0
0
0
0
K
e
3
4
×
4
=
EA
0
0
0
0
0
1
0
−
1
0
0
0
0
0
−
1 0
1
MS
(L-53 CUT)
Beam & Truss
03/2013
23 / 44
Assembly
Global Stiffness Matrix
K
=
0
8
×
8
(+)
K
e
1
4
×
4
(+)
K
e
2
4
×
4
(+)
K
e
3
4
×
4
(+)
K
e
4
4
×
4
(+)
K
e
5
4
×
4
F
q
=
0
8
×
1
(no distributed loads)
Before assembly
K
=
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
MS
(L-53 CUT)
Beam & Truss
03/2013
24 / 44

no elem.
global DOFs
1
1, 2, 5, 6
K
e
1
4
×
4
=
EA
√
2
2
√
2
2
−
√
2
2
−
√
2
2
√
2
2
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
√
2
2
√
2
2
−
√
2
2
−
√
2
2
√
2
2
√
2
2
K
=
EA
√
2
2
√
2
2
0 0
−
√
2
2
−
√
2
2
0 0
√
2
2
√
2
2
0 0
−
√
2
2
−
√
2
2
0 0
0
0
0 0
0
0
0 0
0
0
0 0
0
0
0 0
−
√
2
2
−
√
2
2
0 0
√
2
2
√
2
2
0 0
−
√
2
2
−
√
2
2
0 0
√
2
2
√
2
2
0 0
0
0
0 0
0
0
0 0
0
0
0 0
0
0
0 0
MS
(L-53 CUT)
Beam & Truss
03/2013
25 / 44
no elem.
global DOFs
2
1, 2, 3, 4
K
e
2
4
×
4
=
EA
1
0
−
1 0
0
0
0
0
−
1 0
1
0
0
0
0
0
K
=
EA
√
2
2
+
1
√
2
2
+
0
−
1 0
−
√
2
2
−
√
2
2
0 0
√
2
2
+
0
√
2
2
+
0
0 0
−
√
2
2
−
√
2
2
0 0
−
1
0
1 0
0
0 0 0
0
0
0 0
0
0 0 0
−
√
2
2
−
√
2
2
0 0
√
2
2
√
2
2
0 0
−
√
2
2
−
√
2
2
0 0
√
2
2
√
2
2
0 0
0
0
0 0
0
0 0 0
0
0
0 0
0
0 0 0
MS
(L-53 CUT)
Beam & Truss
03/2013
26 / 44
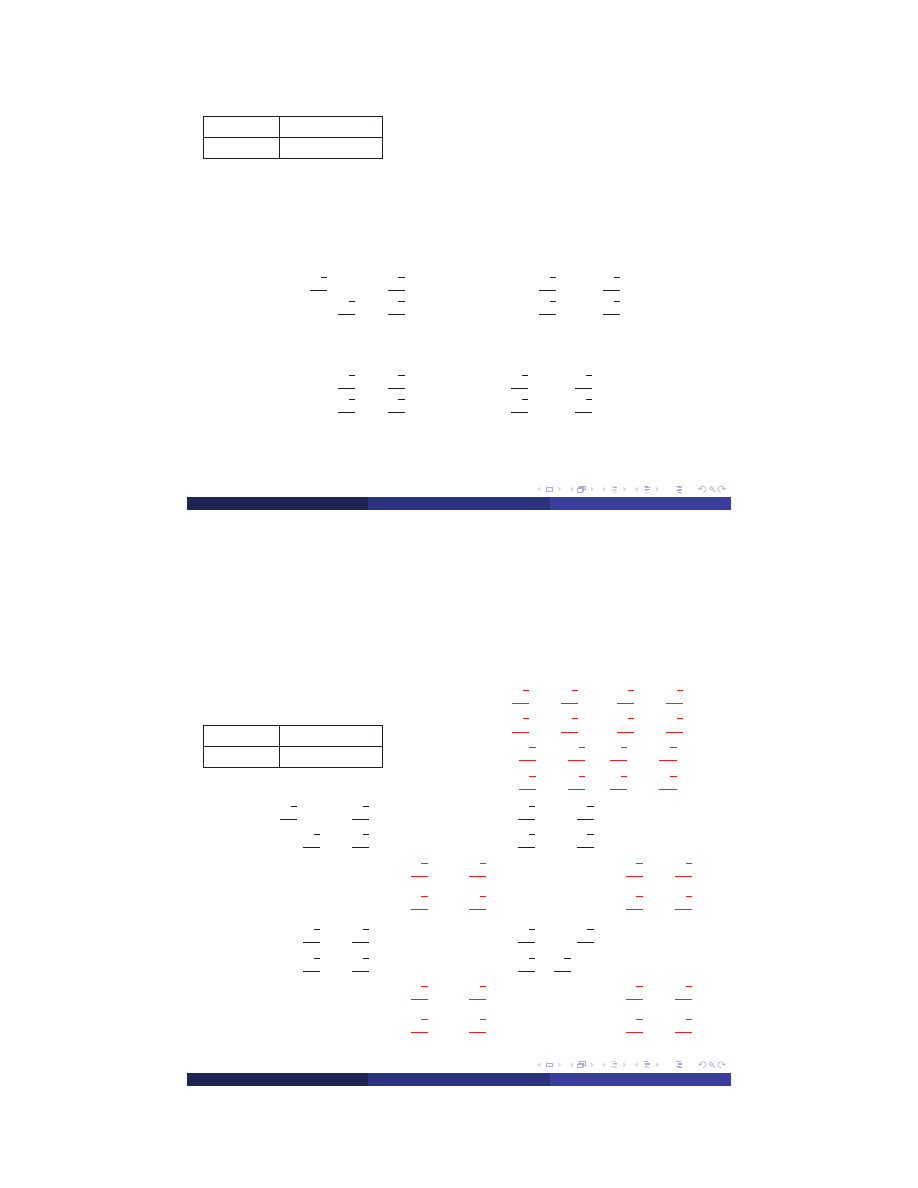
no elem.
global DOFs
3
5, 6, 3, 4
K
e
3
4
×
4
=
EA
0
0
0
0
0
1
0
−
1
0
0
0
0
0
−
1 0
1
K
=
EA
√
2
2
+
1
√
2
2
−
1
0
−
√
2
2
−
√
2
2
0 0
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0 0
−
1
0 1
+
0
0
0
0
0 0
0
0
0
1
0
−
1
0 0
−
√
2
2
−
√
2
2
0
0
√
2
2
+
0
√
2
2
+
0
0 0
−
√
2
2
−
√
2
2
0
−
1
√
2
2
+
0
√
2
2
+
1
0 0
0
0
0
0
0
0 0 0
0
0
0
0
0
0 0 0
MS
(L-53 CUT)
Beam & Truss
03/2013
27 / 44
no elem.
global DOFs
4
3, 4, 7, 8
K
e
4
4
×
4
=
EA
√
2
2
√
2
2
−
√
2
2
−
√
2
2
√
2
2
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
√
2
2
√
2
2
−
√
2
2
−
√
2
2
√
2
2
√
2
2
K
=
EA
√
2
2
+
1
√
2
2
−
1
0
−
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
−
1
0 1
+
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
√
2
2
1
+
√
2
2
0
−
1
−
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
−
1
√
2
2
√
2
2
+
1
0
0
0
0
−
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
MS
(L-53 CUT)
Beam & Truss
03/2013
28 / 44
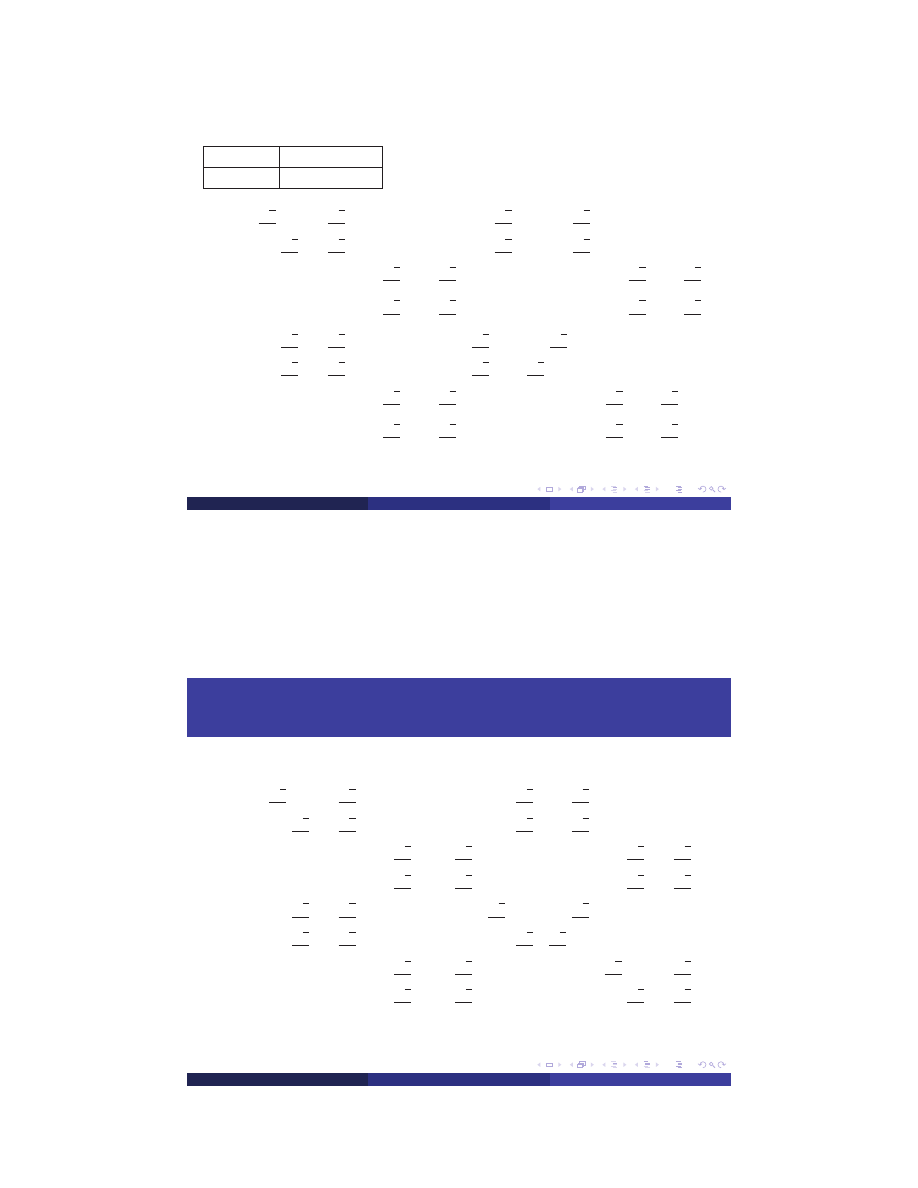
no elem.
global DOFs
5
5, 6, 7, 8
K
e
5
4
×
4
=
EA
1
0
−
1 0
0
0
0
0
−
1 0
1
0
0
0
0
0
K
=
EA
√
2
2
+
1
√
2
2
−
1
0
−
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
−
1
0 1
+
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
√
2
2
1
+
√
2
2
0
−
1
−
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
0
0
√
2
2
+
1
√
2
2
+
0
−
1
0
−
√
2
2
−
√
2
2
0
−
1
√
2
2
+
0
√
2
2
+
1
+
0
0
0
0
0
−
√
2
2
−
√
2
2
−
1
0
√
2
2
+
1
√
2
2
+
0
0
0
−
√
2
2
−
√
2
2
0
0
√
2
2
+
0
√
2
2
+
0
MS
(L-53 CUT)
Beam & Truss
03/2013
29 / 44
Assembly
Generic System of Linear Equations
Kd
=
F
q
=
0
K
=
EA
√
2
2
+
1
√
2
2
−
1
0
−
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
−
1
0 1
+
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
√
2
2
1
+
√
2
2
0
−
1
−
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
0
0
√
2
2
+
1
√
2
2
−
1
0
−
√
2
2
−
√
2
2
0
−
1
√
2
2
√
2
2
+
1
0
0
0
0
−
√
2
2
−
√
2
2
−
1
0
√
2
2
+
1
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
det K
=
0,
rank
(
K
) =
5
MS
(L-53 CUT)
Beam & Truss
03/2013
30 / 44

Boundary Conditions
kinematic constraints
external nodal forces
(essential "BCs")
(natural "BCs")
u
1
=
0,
u
2
=
0,
u
4
=
0
at node no 4,
P
=
10
u
1
u
2
u
3
u
4
u
5
u
6
u
7
u
8
→
0
0
u
3
0
u
5
u
6
u
7
u
8
0
0
0
0
0
0
0
0
→
0
0
0
0
0
0
0
−
P
MS
(L-53 CUT)
Beam & Truss
03/2013
31 / 44
Solution I
EA
√
2
2
+
1
√
2
2
−
1
0
−
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
−
1
0
1
+
√
2
2
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
√
2
2
1
+
√
2
2
0
−
1
−
√
2
2
−
√
2
2
−
√
2
2
−
√
2
2
0
0
√
2
2
+
1
√
2
2
−
1
0
−
√
2
2
−
√
2
2
0
−
1
√
2
2
√
2
2
+
1
0
0
0
0
−
√
2
2
−
√
2
2
−
1
0
√
2
2
+
1
√
2
2
0
0
−
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
0
0
u
3
0
u
5
u
6
u
7
u
8
=
0
0
0
0
0
0
0
−
P
MS
(L-53 CUT)
Beam & Truss
03/2013
32 / 44

Solution II
EA
1
+
√
2
2
0
0
−
√
2
2
−
√
2
2
0
√
2
2
+
1
√
2
2
−
1
0
0
√
2
2
√
2
2
+
1
0
0
−
√
2
2
−
1
0
√
2
2
+
1
√
2
2
−
√
2
2
0
0
√
2
2
√
2
2
u
3
u
5
u
6
u
7
u
8
=
0
0
0
0
−
P
+
−
EA
−
1
0
√
2
2
−
√
2
2
−
√
2
2
0
−
√
2
2
−
√
2
2
−
1
0
0
−
√
2
2
0
0
−
√
2
2
0
0
0
MS
(L-53 CUT)
Beam & Truss
03/2013
33 / 44
Solution III
Solution is:
u
3
u
5
u
6
u
7
u
8
=
1
EA
−
P
P
√
2
+
1
−
P
P
√
2
+
2
−
P
2
√
2
+
3
→
d
=
0
0
u
3
0
u
5
u
6
u
7
u
8
=
1
EA
0
0
−
P
0
P
√
2
+
1
−
P
P
√
2
+
2
−
P
2
√
2
+
3
MS
(L-53 CUT)
Beam & Truss
03/2013
34 / 44
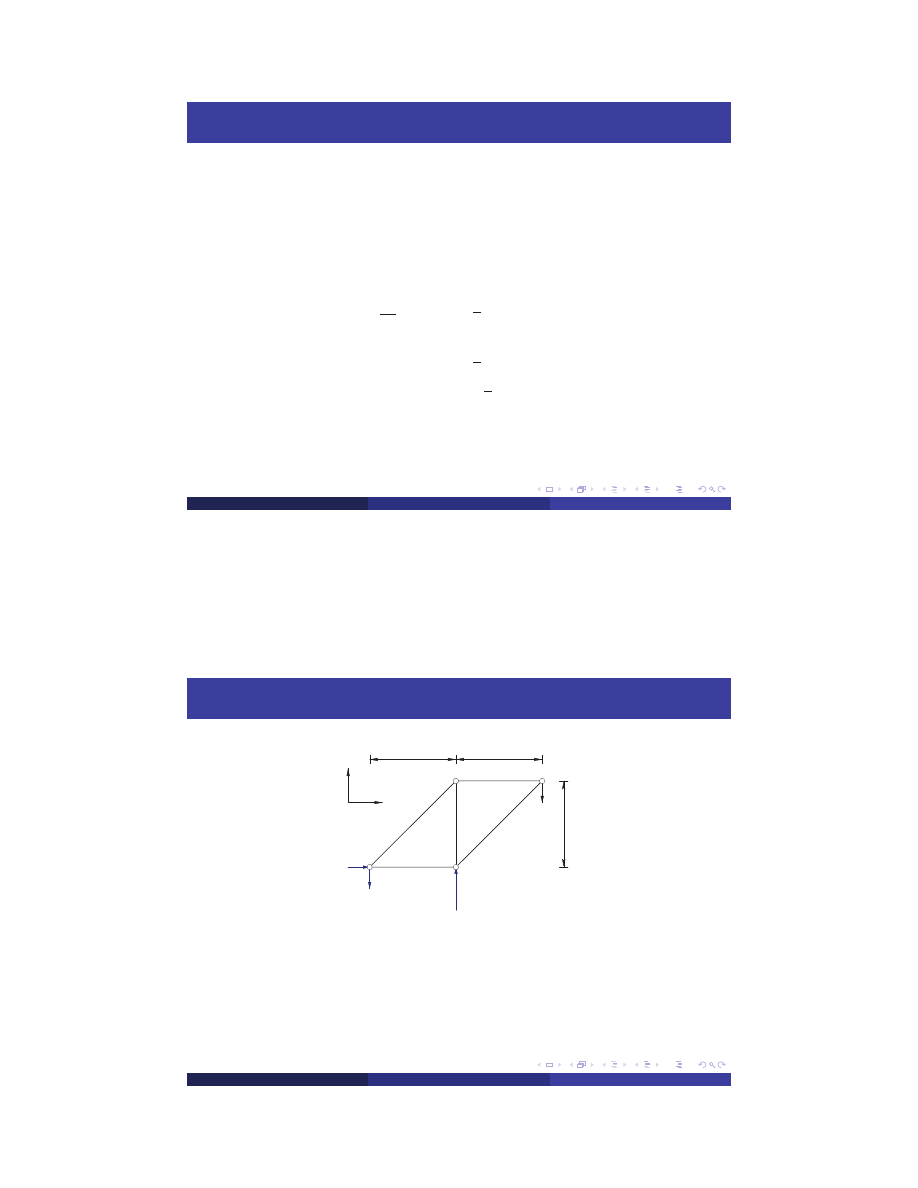
Reactions at Supports
W
=
Kd
−
F
q
=
K
1
EA
0
0
−
P
0
P
√
2
+
1
−
P
P
√
2
+
2
−
P
2
√
2
+
3
−
0
=
0
−
P
0
2P
0
0
0
−
P
MS
(L-53 CUT)
Beam & Truss
03/2013
35 / 44
Equations of Equilibrium
2
3
4
P
1
1
1
x
y
1
0
P
2P
∑
i
P
i
y
?
=
0
−
P
+
2P
−
P
=
0
∑
i
M
i
1
?
=
0
2P
·
1
−
P
·
2
=
0
∑
i
M
i
4
?
=
0
P
·
2
−
2P
·
1
=
0
MS
(L-53 CUT)
Beam & Truss
03/2013
36 / 44
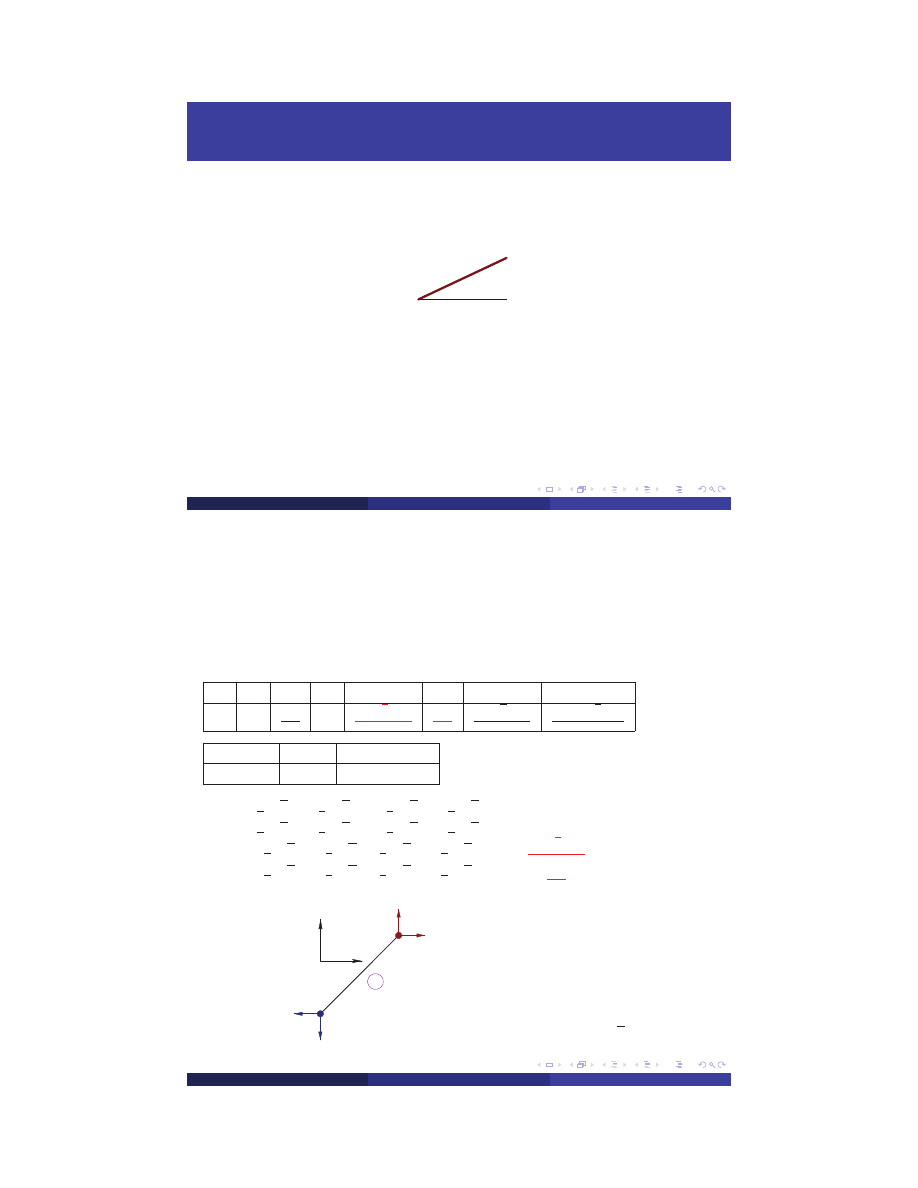
Postprocessing in Global Coordinate System
Siły przyw ˛ezłowe W
−→
W
e
x
1
,
↑
W
e
y
1
α
−→
W
e
x
2
,
↑
W
e
y
2
W
e
=
W
e
x
1
W
e
y
1
W
e
x
2
W
e
y
2
=
K
e
d
e
−
F
e
q
=
K
e
d
e
MS
(L-53 CUT)
Beam & Truss
03/2013
37 / 44
u
1
u
2
u
3
u
4
u
5
u
6
u
7
u
8
0
0
−
P
EA
0
P
(
√
2
+
1
)
EA
−
P
EA
P
(
√
2
+
2
)
EA
−
P
(
2
√
2
+
3
)
EA
no elem.
nodes
global DOFs
1
1
,
3
1, 2
,
5, 6
EA
1
2
√
2
1
2
√
2
−
1
2
√
2
−
1
2
√
2
1
2
√
2
1
2
√
2
−
1
2
√
2
−
1
2
√
2
−
1
2
√
2
−
1
2
√
2
1
2
√
2
1
2
√
2
−
1
2
√
2
−
1
2
√
2
1
2
√
2
1
2
√
2
0
0
P
(
√
2
+
1
)
EA
−
P
EA
=
−
P
−
P
P
P
x
y
1
3
1
P
P
P
P
pr ˛et rozci ˛agany
P
√
2
MS
(L-53 CUT)
Beam & Truss
03/2013
38 / 44
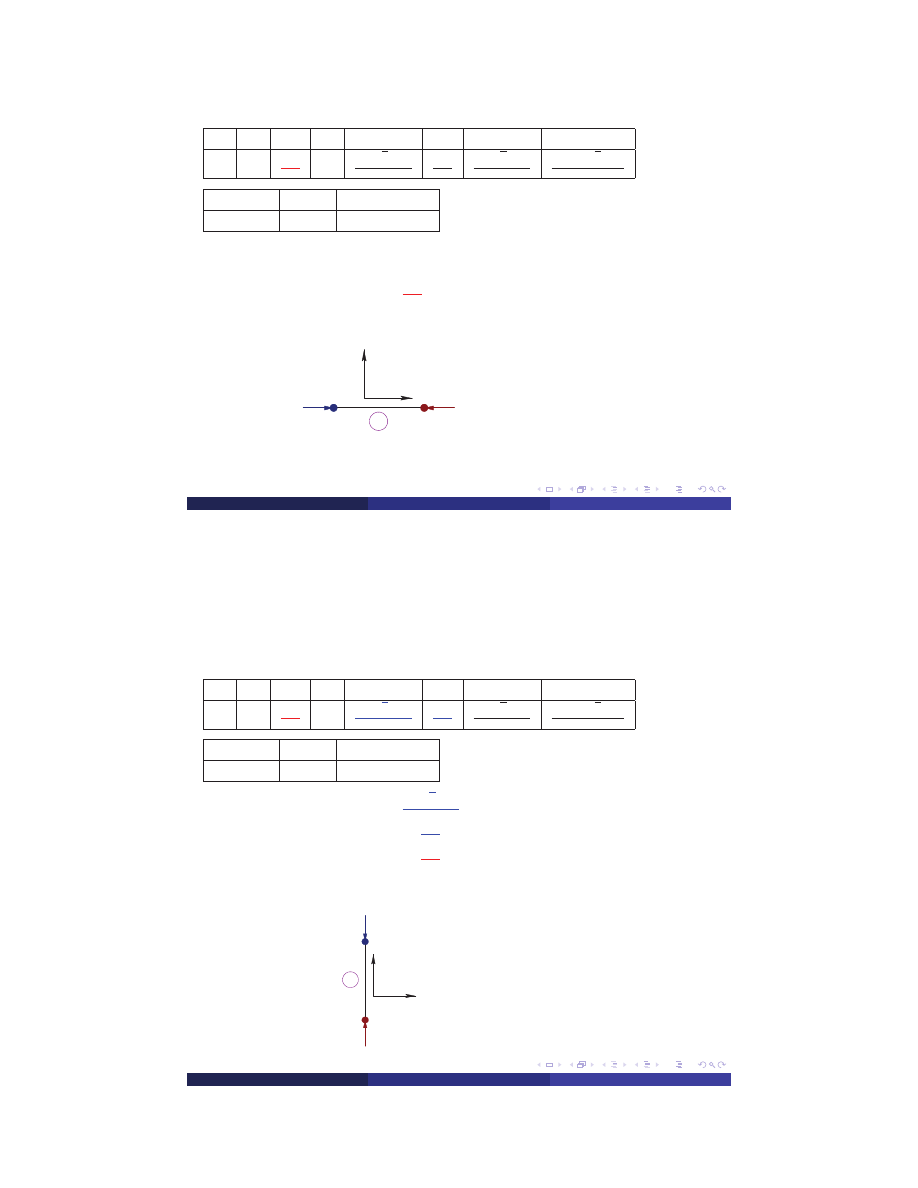
u
1
u
2
u
3
u
4
u
5
u
6
u
7
u
8
0
0
−
P
EA
0
P
(
√
2
+
1
)
EA
−
P
EA
P
(
√
2
+
2
)
EA
−
P
(
2
√
2
+
3
)
EA
no elem.
nodes
global DOFs
2
1
,
2
1, 2
,
3, 4
EA
1
0
−
1 0
0
0
0
0
−
1 0
1
0
0
0
0
0
0
0
−
P
EA
0
=
P
0
−
P
0
2
2
1
P
P
x
y
pr ˛et ´sciskany
P
MS
(L-53 CUT)
Beam & Truss
03/2013
39 / 44
u
1
u
2
u
3
u
4
u
5
u
6
u
7
u
8
0
0
−
P
EA
0
P
(
√
2
+
1
)
EA
−
P
EA
P
(
√
2
+
2
)
EA
−
P
(
2
√
2
+
3
)
EA
no elem.
nodes
global DOFs
3
3
,
2
5, 6
,
3, 4
EA
0
0
0
0
0
1
0
−
1
0
0
0
0
0
−
1 0
1
P
(
√
2
+
1
)
EA
−
P
EA
−
P
EA
0
=
0
−
P
0
P
3
3
2
P
P
x
y
pr ˛et ´sciskany
P
MS
(L-53 CUT)
Beam & Truss
03/2013
40 / 44

u
1
u
2
u
3
u
4
u
5
u
6
u
7
u
8
0
0
−
P
EA
0
P
(
√
2
+
1
)
EA
−
P
EA
P
(
√
2
+
2
)
EA
−
P
(
2
√
2
+
3
)
EA
no elem.
nodes
global DOFs
4
2
,
4
3, 4
,
7, 8
EA
1
2
√
2
1
2
√
2
−
1
2
√
2
−
1
2
√
2
1
2
√
2
1
2
√
2
−
1
2
√
2
−
1
2
√
2
−
1
2
√
2
−
1
2
√
2
1
2
√
2
1
2
√
2
−
1
2
√
2
−
1
2
√
2
1
2
√
2
1
2
√
2
−
P
EA
0
P
(
√
2
+
2
)
EA
−
P
(
2
√
2
+
3
)
EA
=
P
P
−
P
−
P
x
y
4
4
2
P
P
P
P
pr ˛et ´sciskany
P
√
2
MS
(L-53 CUT)
Beam & Truss
03/2013
41 / 44
u
1
u
2
u
3
u
4
u
5
u
6
u
7
u
8
0
0
−
P
EA
0
P
(
√
2
+
1
)
EA
−
P
EA
P
(
√
2
+
2
)
EA
−
P
(
2
√
2
+
3
)
EA
no elem.
nodes
global DOFs
5
3
,
4
5, 6
,
7, 8
EA
1
0
−
1 0
0
0
0
0
−
1 0
1
0
0
0
0
0
P
(
√
2
+
1
)
EA
−
P
EA
P
(
√
2
+
2
)
EA
−
P
(
2
√
2
+
3
)
EA
=
−
P
0
P
0
5
3
4
P
P
x
y
pr ˛et rozci ˛agany
P
MS
(L-53 CUT)
Beam & Truss
03/2013
42 / 44
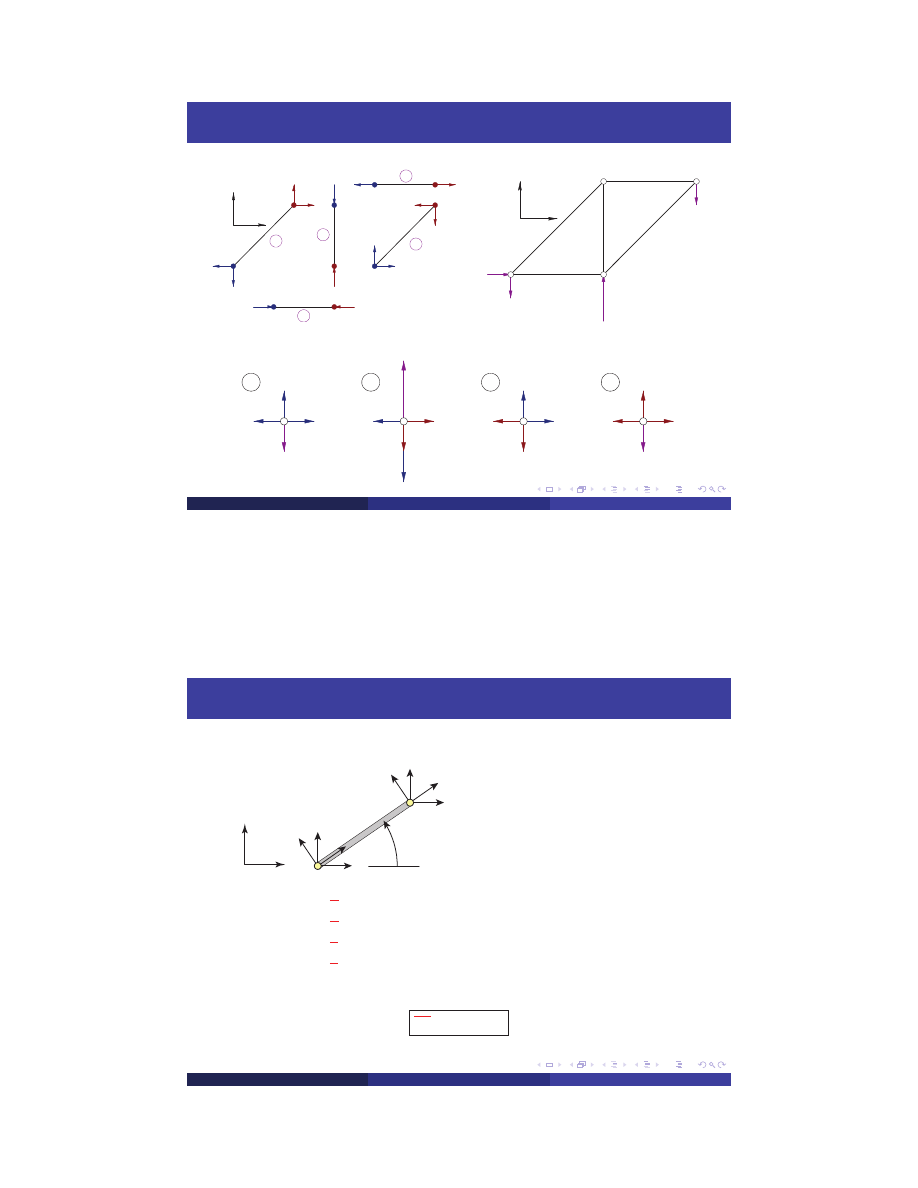
Sprawdzenie
Siły przyw ˛ezłowe w pr ˛etach.
Reakcje wi ˛ezów, obci ˛a˙zenia w ˛ezłów.
3
3
2
P
P
2
2
1
P
P
4
4
2
P
P
P
P
5
3
4
P
P
1
3
1
P
P
P
P
x
y
x
y
2
3
4
P
1
0
P
2P
Równowaga w ˛ezłów:
P
1
P
1
P
2
1
P
1
P
2
P
3
4
P
2
2P
4
P
P
1
P
1
P
3
P
5
3
P
4
P
4
P
5
4
P
MS
(L-53 CUT)
Beam & Truss
03/2013
43 / 44
Axial Forces
Gl obal i z ati on : Force Tran s form ati on
N o de f o rces tra ns f o rm a s
x
y
i
j
f
xi
f
yi
f
xj
f
yj
f
yi
f
xi
f
xj
f
yj
α
_
_
_
_
T
=
c
s
0
0
−
s
c
0
0
0
0
c
s
0
0
−
s
c
f
x
i
f
y
i
f
x
j
f
y
j
=
c
s
0
0
−
s
c
0
0
0
0
c
s
0
0
−
s
c
f
x
i
f
y
i
f
x
j
f
y
j
W
e
=
T
W
e
MS
(L-53 CUT)
Beam & Truss
03/2013
44 / 44
Wyszukiwarka
Podobne podstrony:
6 lect6 truss students
5 lect6 beam students
5 lect6 beam students
2010 ZMP studenci
gruźlica dla studentów2
Prezentacja 2 analiza akcji zadania dla studentow
Szkolenie BHP Nowa studenci
Student Geneza
Kosci, kregoslup 28[1][1][1] 10 06 dla studentow
higiena dla studentów 2011 dr I Kosinska
Studenci biegunka przewlekła'
WYKŁAD STUDENCI MIKULICZ
Wyklad FP II dla studenta
Inwolucja połogowa i opieka poporodowa studenci V rok wam 5
Materiały dla studentów ENDOKRYNOLOGIA
więcej podobnych podstron