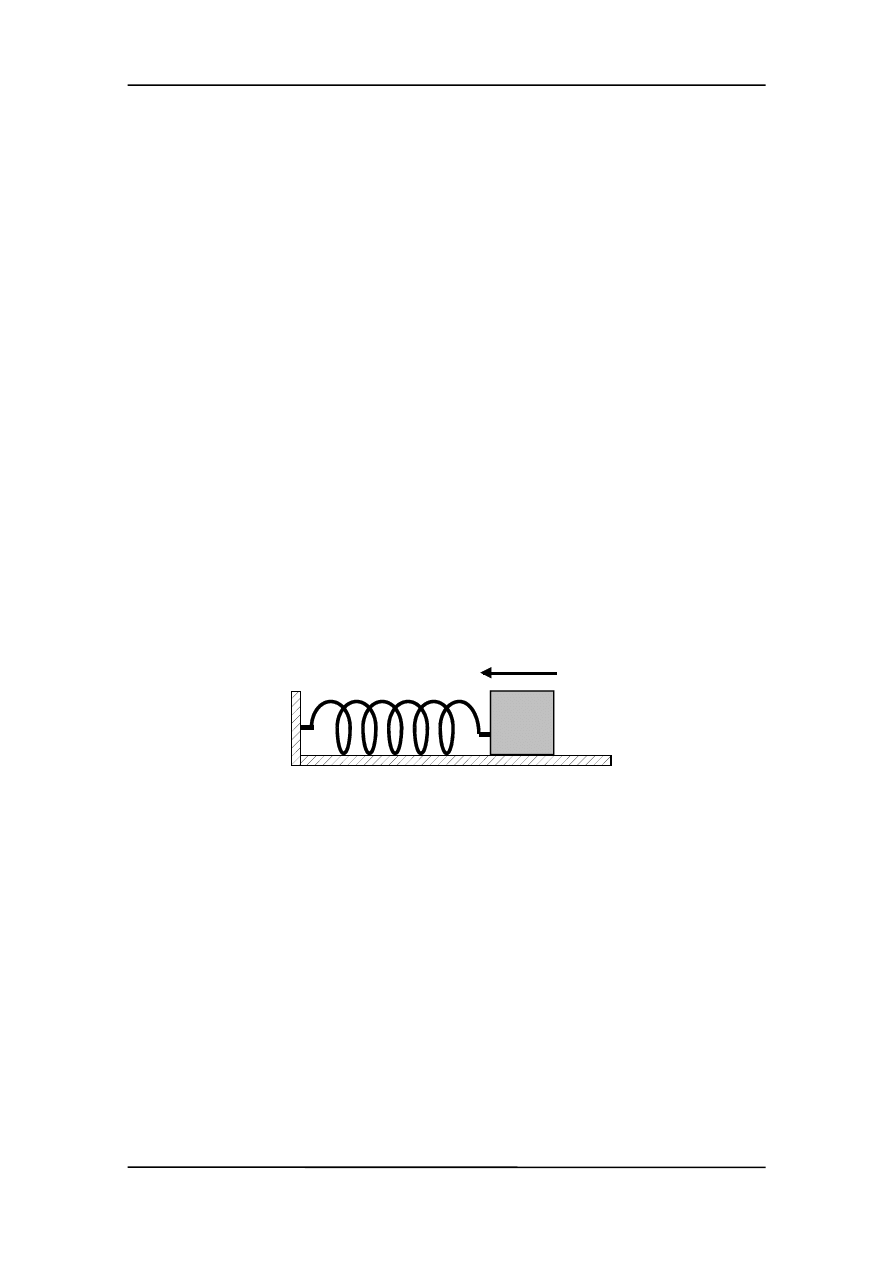
Z. Kąkol-Notatki do Wykładu z Fizyki

Wykład 8

8. Zasada zachowania energii

8.1 Wstęp

Korzystając z drugiej zasady dynamiki Newtona pokazaliśmy, że

W =

∆E

k

Często na punkt materialny działa kilka sił, których suma wektorowa jest siłą wypad-
kową: F = F

1

+ F

2

+ F

3

+.......+ F

n

. Wtedy praca jest sumą algebraiczną prac wykona-

nych przez poszczególne siły: W = W

1

+ W

2

+ W

3

+...........+ W

n

.

Twierdzenie o pracy i energii ma wtedy postać

W

1

+ W

2

+ W

3

+...........+ W

n

=

∆E

k

Będziemy właśnie rozpatrywać układy, w których działają różne siły, pozwoli to na de-
finiowanie różnych rodzajów energii.

8.2 Siły zachowawcze i niezachowawcze

Zaczynamy od rozważmy przykładów dwóch rodzajów sił:

sił zachowawczych

i

sił nie-

zachowawczych

.

V

Najpierw rozpatrzmy sprężynę jak w przykładzie z poprzedniego wykładu.
Przesuwamy ciało o masie m z prędkością

v

w kierunku sprężyny, tak jak na rysunku.

Założenia:
• ruch na płaszczyźnie odbywa się bez tarcia,
• sprężyna jest idealna tzn. spełnia ona prawo Hooke'a: F = -kx, gdzie F jest siłą wy-
wieraną przez sprężynę kiedy jej swobodny koniec jest przemieszczony na odległość x,
• masa sprężyny jest zaniedbywalnie mała w porównaniu z masą ciała, więc cała ener-

a maleje

aż

gia kinetyczna w układzie sprężyna + ciało jest zgromadzona w tym ciele.

Przy ściskaniu sprężyny, prędkość ciała, a wobec tego i energia kinetyczn
do zatrzymania ciała. Następnie ciało porusza się w przeciwnym kierunku pod

wpływem sprężyny. Prędkość i energia kinetyczna rosną aż do wartości jaką ciało miało
początkowo. Interpretowaliśmy energię kinetyczną jako zdolność ciała do wykonania
pracy kosztem jego ruchu (kosztem E

k

). Po przebyciu zamkniętej drogi (cyklu) zdolność

ciała do wykonania pracy pozostaje taka sama, jest

zachowana

. Siła sprężysta wywiera-

na przez idealną sprężynę jest

zachowawcza

. Inne siły, działają także w ten sposób, np.

8-1

Z. Kąkol-Notatki do Wykładu z Fizyki

siła grawitacji. Ciało rzucone do góry, przy zaniedbaniu oporu powietrza, wróci z tą
samą prędkością i energią kinetyczną.
Jeżeli jednak ciało, na które działa jedna lub więcej sił powraca do położenia początko-

alnie gładka,

że

ać zachowawczy charakter sił analizując pracę jaką wykonuje

ta s

z tarcia) praca wykonana przez siłę sprężystą, gdy

spr

y tarcie). Praca wykonywana przez siłę tarcia

jest

m mate-

siłami niezachowawczy-

W

AB,1

+ W

BA,2

= 0

o droga zamknięta. Możemy to zapisać inaczej

W

AB,1

= - W

BA,2

le gdyby odwrócić kierunek ruchu i przejść z A do B po drugiej drodze to, ponieważ

wego i ma inną energię kinetyczną niż na początku to oznacza, że po przebyciu drogi
zamkniętej zdolność tego ciała do wykonania pracy nie została zachowana. Oznacza to,
że przynajmniej jedną z działających sił określa się jako

niezachowawczą

.

Aby zilustrować ten przypadek, załóżmy, że powierzchnia nie jest ide

mamy do czynienia z tarciem. Ta siła tarcia przeciwstawia się ruchowi bez względu

w którym kierunku porusza się ciało (nie tak jak siła sprężystości czy grawitacji) i ciało
wraca z mniejszą energią kinetyczną. Mówimy, że siła tarcia (i inne działające podob-
nie) są

niezachowawcze

.

Możemy przeanalizow

iła nad punktem materialnym.

W pierwszym przykładzie (be

ężyna ulega ściskaniu, jest ujemna (siła jest skierowana przeciwnie do przemiesz-

czenia, cos180

° = -1). Gdy sprężyna rozprężą się praca jest dodatnia (siła i przemiesz-

czenie jednakowo skierowane). Podczas pełnego cyklu praca wykonana przez siłę sprę-
żystą (siłę wypadkową) jest równa zero.

W drugim przykładzie (uwzględniam
ujemna dla każdej części cyklu (tarcie zawsze przeciwstawia się ruchowi).

Ogólnie:

Siła jest zachowawcza, jeżeli praca wykonana przez tę siłę nad punkte

rialnym, który porusza się po dowolnej drodze zamkniętej jest równa zeru. Siła jest nie-
zachowawcza jeżeli praca wykonana przez tę siłę nad punktem materialnym, który po-
rusza się po dowolnej drodze zamkniętej nie jest równa zeru

.

Możemy jeszcze trzecim sposobem rozważyć różnicę między

A

B

1

2

A

B

1

2

mi i zachowawczymi. Rozpatrzmy ruch z punktu A do B po jednej drodze (1) a powrót z
B do A po innej (2) (patrz rysunek).
Jeżeli siła jest zachowawcza to

b

A

8-2

Z. Kąkol-Notatki do Wykładu z Fizyki

zmieniamy tylko kierunek to

W

AB,2

= -W

BA,2

Skąd otrzymujemy

W

AB,1

= W

AB,2

idać z tego, że praca wykonana przez siłę

zachowawczą

przy przemieszczaniu od A

czą jeżeli praca wykonana przez nią nad punktem mate-

ria

równoważne.

8.3 Energia potencjalna

Skupimy się teraz na odosobnionym układzie ciało + sprężyna. Zamiast mówić ciało

się

kinetyczna maleje a potem ro-

śni

∆E

k

+

∆E

p

= 0

nymi słowy, każda zmiana energii kinetycznej E

k

jest równoważona przez równą co

E

k

+ E

p.

= const.

(8.1)

W
do B jest taka sama dla obu dróg. Drogi 1 i 2 mogą mieć

dowolny kształt

byleby tylko

łączyły te same punkt A i B.

Siłę nazywamy zachowaw

lnym poruszającym się między dwoma punktami zależy tylko od tych punktów, a nie

od łączącej je drogi. Siłę nazywamy niezachowawczą jeżeli praca wykonana przez nią
nad punktem materialnym poruszającym się między dwoma punktami zależy od drogi
łączącej te punkty

.

Przedstawione definicje są

porusza będziemy mówić:

stan układu się zmienia

.

Widzieliśmy, że gdy nie występuje tarcie to energia

e tak, że wraca do początkowej wartości w cyklu zamkniętym. W tej sytuacji (gdy

działają siły zachowawcze) staje się celowe wprowadzenie pojęcia

energii stanu

lub

energii potencjalnej

E

p

. Mówimy, że jeżeli energia kinetyczna układu zmieni się o war-

tość

∆E

k

to tym samym zmienił się stan układu to energia potencjalna E

p

(stanu) tego

układu musi się zmienić o wartość równą co do wartości bezwzględnej, lecz przeciwną
co do znaku, tak że suma tych zmian jest równa zeru

In
do wartości, a przeciwną co do znaku zmianę energii potencjalnej E

p

układu, tak że ich

suma pozostaje przez cały czas stała



Energia potencjalna przedstawia formę nagromadzonej energii, która może być całko-

rcia) energia kinetyczna ciała początkowo maleje,

a zl

W =

∆E

k

ięc dla zachowawczej siły F

W =

∆E

k

= -

∆E

p

wicie odzyskana i zamieniona na energię kinetyczną. Nie można więc wiązać energii
potencjalnej z siłą niezachowawczą.

W przykładzie ze sprężyną (bez ta
okalizowana w sprężynie energia potencjalna rośnie. Z twierdzenia o pracy i energii

w

8-3

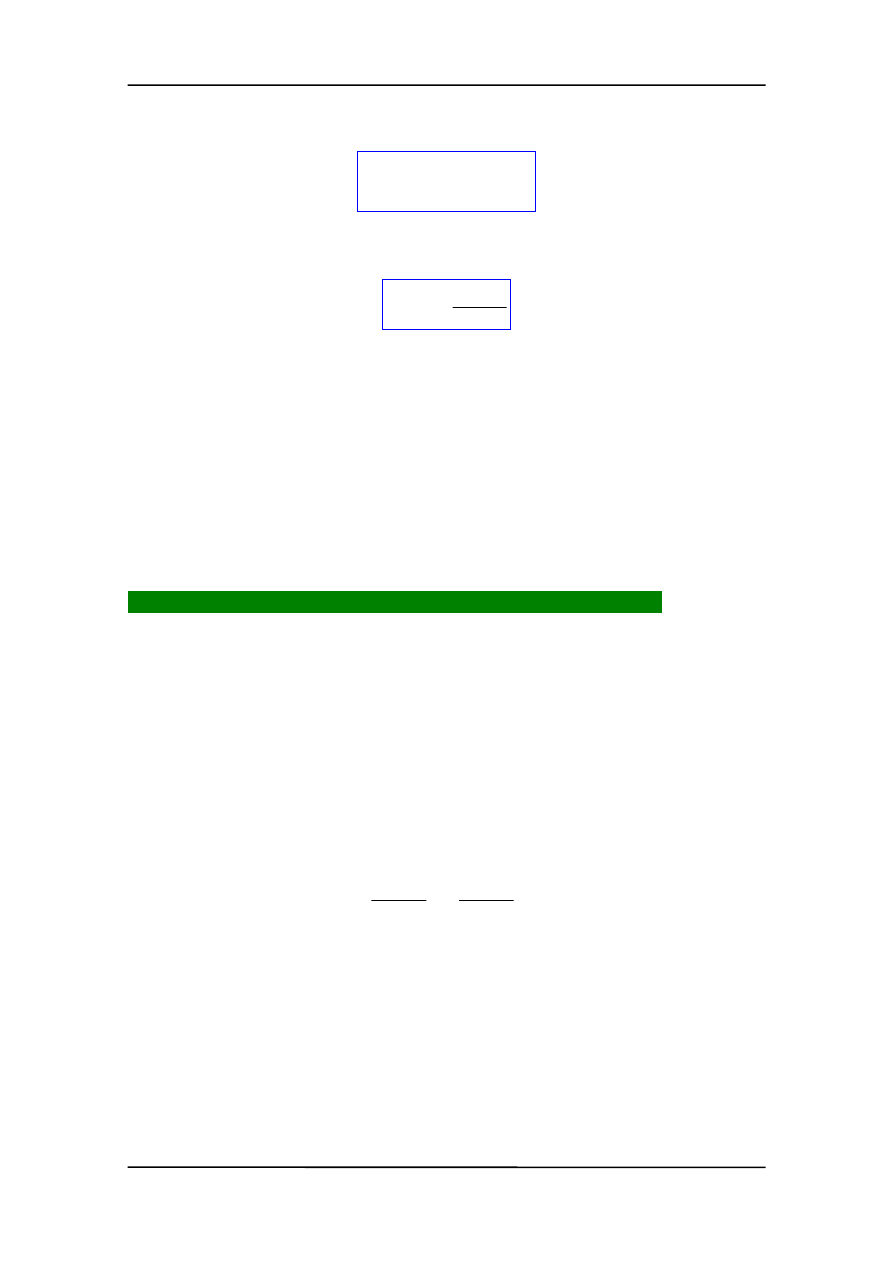
Z. Kąkol-Notatki do Wykładu z Fizyki

Stąd

x

∫

−

=

−

=

∆

x

p

x

x

F

W

E

0

d

)

(

(8.2)

ożemy więc zapisać zależność między siłą i energią potencjalną

M

x

x

F

p

d

)

(

−

=

x

E

)

(

d

(8.3)

rzeba zwrócić uwagę, że naprawdę potrafimy tylko policzyć

∆E

p

a nie E

p

samą. Po-

x

unkt A nazywamy punktem odniesienia i zazwyczaj wybieramy go tak (umowa), żeby

T
nieważ

∆E

p

= E

pB

– E

pA

. Żeby znaleźć E

pB

trzeba nie tylko znać siłę ale jeszcze wartość

E

pA

pA

x

pA

p

pB

E

x

x

F

E

E

E

+

−

=

+

∆

=

∫

0

d

)

(

P
E

p

było równe zeru w tym punkcie (porównanie z potencjałem elektrycznym).

Przykłady energii potencjalnej dla jednowymiarowych sił zachowawczych

F(y) = -mg

jest stała. Przyjmujemy, że dla y = 0, E

p

(0) = 0.

y

y

Sprawdzenie

• grawitacyjna energia potencjalna (w pobliżu powierzchni Ziemi)
Ruch wzdłuż osi y

F
Wtedy

∫

∫

=

−

−

=

+

−

=

p

p

mgy

y

mg

E

y

y

F

y

E

0

0

d

)

(

)

0

(

d

)

(

)

(

mg

y

y

F

p

−

=

−

=

−

=

d

d

mgy

y

E

)

(

d

)

(

d

energia potencjalna sprężyny

F(x) = -kx

rzyjmujemy dla x = 0, E

p

(0) = 0.

•
Ruch wzdłuż osi x

P
Wtedy

8-4

Z. Kąkol-Notatki do Wykładu z Fizyki

2

d

)

(

2

0

kx

x

kx

E

x

p

=

−

−

=

∫

Sprawdzenie:

kx

x

kx

x

x

E

F

p

−

=













−

=

−

=

d

2

d

d

)

(

d

2

8.3.1 Energia potencjalna i potencjał pola grawitacyjnego

W przykładzie powyżej obliczyliśmy energię potencjalną związaną z siłą grawita-

cyjną w pobliżu powierzchni Ziemi, gdzie przyjmowaliśmy, że siła grawitacji jest stała.
Teraz zajmiemy się zagadnieniem bardziej ogólnym i znajdziemy energię potencjalną
masy m znajdującej się w dowolnym punkcie nad powierzchnią Ziemi odległym o r od
środka Ziemi.

Dla sił zachowawczych zmianę energii potencjalnej ciała przy przejściu ze stanu A

do stanu B możemy zapisać jako

AB

pA

pB

p

W

E

E

E

−

=

−

=

∆

skąd

pB

AB

pB

E

W

E

+

−

=

Żeby policzyć energię potencjalną w punkcie B musimy znać energię potencjalną w

punkcie odniesienia A i policzyć pracę W

AB

.

Dla masy m znajdującej się w pewnym punkcie nad powierzchnią Ziemi odległym o

r od środka Ziemi stan odniesienia wybiera się tak, że Ziemia i masa m znajdują się od
siebie w nieskończonej odległości. Temu położeniu (r Æ

∞) przypisujemy zerową ener-

gię potencjalną, E

pA

= 0. Zwróćmy uwagę, że stan zerowej energii jest również stanem

zerowej siły. Siła grawitacji jest siłą zachowawczą więc dla wybranego punktu odnie-
sienia

0

)

(

+

−

=

∞r

p

W

r

E

Musimy teraz obliczyć pracę

. Ponieważ znamy siłę

r

W

∞

−

2

r

m

M

G

F

Z

−

=

to możemy obliczyć pracę i w konsekwencji energię potencjalną (znak minus wskazuje
kierunek działania siły do środka Ziemi; siła przyciągająca)

8-5

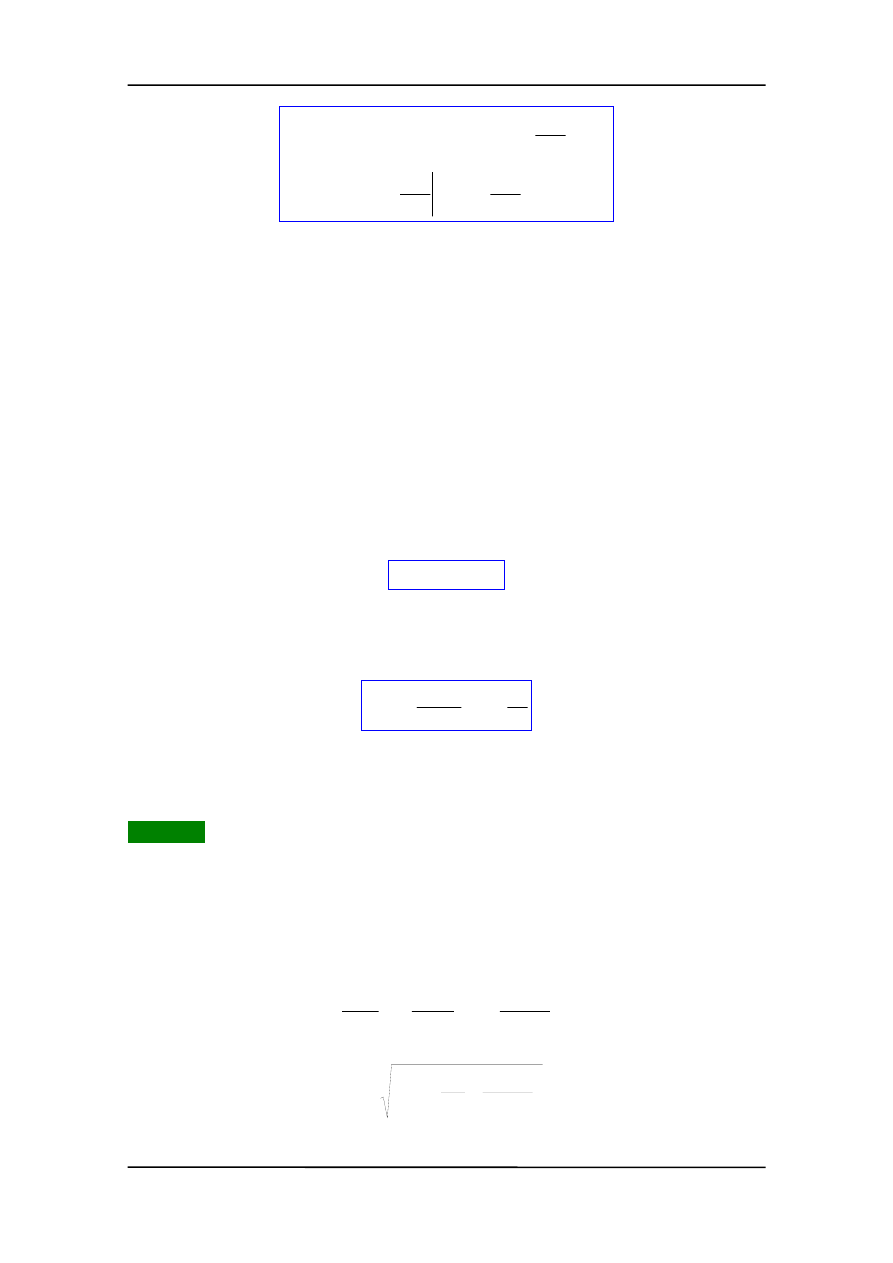
Z. Kąkol-Notatki do Wykładu z Fizyki

r

Mm

G

r

Mm

G

r

r

Mm

G

r

F

W

r

E

r

r

r

r

p

−

=

−

=











−

−

=

−

=

−

=

∞

∞

∞

∞

∫

∫

d

d

)

(

2

(8.4)

Energia potencjalna ma wartość równo zeru w nieskończoności (punkt odniesienia)
i maleje w miarę zmniejszania się r. Oznacza to, że siła jest przyciągająca. Wzór ten jest
prawdziwy bez względu na wybór drogi po jakiej punkt porusza się z nieskończoności
do r.
Widzimy,

że

z polem siły grawitacji wiąże się przestrzenny rozkład energii E(r) da-

ny równaniem (8.4)

.

Omawiając na Wykładzie 6 pole grawitacyjne przedstawialiśmy siłę działającą na

umieszczony w tym polu obiekt jako iloczyn

natężenia pola i masy

tego obiektu.

Stwierdziliśmy, że jedna masa wytwarza pole, a następnie to pole działa na drugą masę.
Inaczej mówiąc rozdzieliliśmy siłę na dwie części i w ten sposób uniezależniliśmy nasz
opis od masy obiektu wprowadzanego do pola.

Podobnie możemy postąpić z energią potencjalną. Zauważmy, że zgodnie z wyraże-

niem (8.4) możemy ją przedstawić jako iloczyn masy m i pewnej funkcji V(r)

)

(

)

(

r

mV

r

E

p

=

(8.5)

Funkcję V(r) nazywamy potencjałem pola grawitacyjnego i definiujemy jako stosunek
grawitacyjnej energii potencjalnej masy m do wartości tej masy

r

M

G

m

r

E

r

V

p

−

=

=

)

(

)

(

(8.6)

Jak już wspominaliśmy z pojęcia pola korzysta się nie tylko w związku z grawitacją.

Przy opisie zjawisk elektrycznych również będziemy się posługiwali pojęciem pola
(elektrycznego), jego natężenia i potencjału.

Przykład 1

Skorzystajmy teraz z wyrażenia na grawitacyjną energię potencjalną, żeby znaleźć

prędkość jaką należy nadać obiektowi przy powierzchni Ziemi, aby wzniósł się on na
wysokość h nad powierzchnię Ziemi Stosując zasadę zachowania energii otrzymujemy

)

(

)

(

h

R

E

R

E

E

Z

p

Z

p

k

+

=

+

czyli

h

R

m

M

G

R

m

M

G

m

Z

Z

Z

Z

+

−

=

−

2

2

v

a po przekształceniach













+

−

=

h

R

R

GM

Z

Z

1

1

2

v

8-6

Z. Kąkol-Notatki do Wykładu z Fizyki

Jeżeli na powierzchni Ziemi dostarczymy ciału dostatecznie dużej energii kinetycz-

nej wtedy ucieknie ono z Ziemi i nie powróci. Jego energia kinetyczna będzie malała w
trakcie oddalania się, a potencjalna rosła.

Przykład 2

Teraz spróbujemy obliczyć jaką prędkość należy nadać obiektowi na Ziemi aby

uciekł on z Ziemi na zawsze.
Praca potrzebna na przeniesieni ciała o masie m z powierzchni Ziemi do nieskończono-
ści wynosi

E

p

(R

Z

) = -GM

Z

m/R

Z

Jeżeli na powierzchni Ziemi dostarczymy ciału energii kinetycznej większej wtedy
ucieknie ono z Ziemi i nie powróci. Energia kinetyczna będzie malała w trakcie oddala-
nia się ciała, a potencjalna rosła. Krytyczna prędkość początkowa

v

0

(prędkość uciecz-

ki) dana jest wzorem

s

km

R

M

G

czyli

R

m

M

G

m

Z

Z

Z

Z

2

.

11

2

,

2

1

0

2

0

≅

=

=

v

v

Oczywiście pominęliśmy inne siły jak siły grawitacyjne wywierane przez Księżyc czy
Słońce itp. Ta prędkość ucieczki nosi nazwę

drugiej prędkości kosmicznej

. Natomiast

pierwszą prędkością kosmiczną

nazywamy

najmniejszą

możliwą prędkość jaką musi

mieć punkt materialny swobodnie krążący po orbicie wokół Ziemi.
Na poruszający się po orbicie obiekt działają dwie siły; siła grawitacji i siła odśrodko-
wa. Siły te mają przeciwne zwroty i dla stabilnej orbity równoważą się

2

r

m

M

G

r

m

Z

=

2

v

i stąd znajdujemy

r

GM

Z

=

v

Pierwszej prędkości kosmicznej odpowiada orbita o promieniu r równym w przybliże-
niu promieniowi Ziemi R. Dla r = R otrzymujemy wartość

v

= 7.9 km/s.

8.4 Zasada zachowania energii

Gdy działają siły zachowawcze to

W =

∆E

k

= E

kB

– E

kA

oraz

W = -

∆E

p

= - (E

pB

– E

pA

)

więc

- (E

pB

– E

pA

) = E

kB

– E

kA

czyli

E

kA

+ E

pA

= E

kB

+ E

pB

(8.7)

8-7

Z. Kąkol-Notatki do Wykładu z Fizyki

Równania (8.1, 8.4) nazywa się

zasadą zachowania energii mechanicznej

.

Mówi ona, że dla ciała podlegającego działaniu siły zachowawczej, którego energia
potencjalna jest równa E

p

, suma energii kinetycznej i potencjalnej jest stała (o ile nie

działają inne siły).

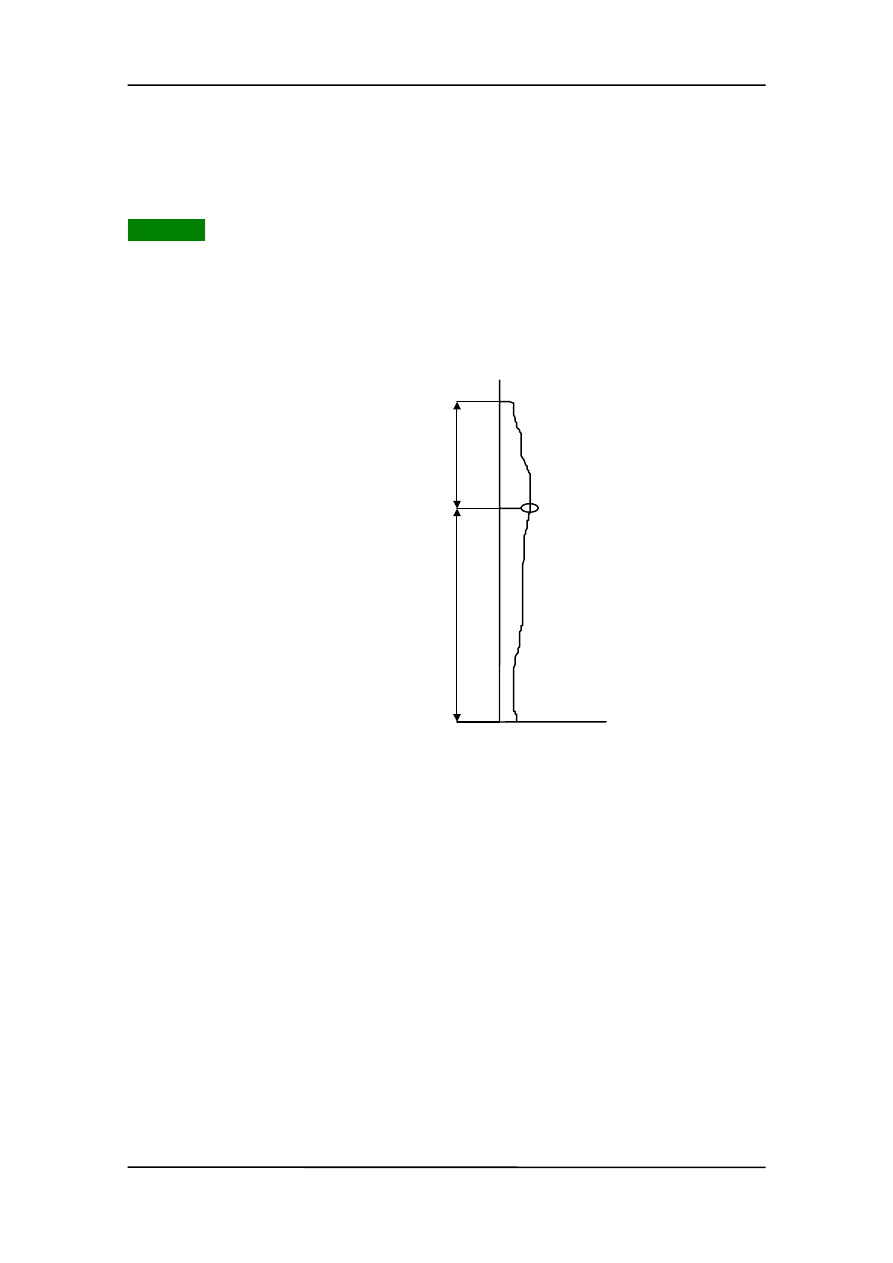
Przykład 3

Asekuracja wspinacza w górach. Wspinacz dobiera sobie linę, której wytrzymałość na
zerwanie jest 25 razy większa niż jego własny ciężar (F

liny

= 25mg). Lina (nylonowa)

podlega prawu Hooke'a aż do zerwania, które następuje gdy lina wydłuży się o 25%
w stosunku do długości początkowej. Czy wyposażony w taką linę wspinacz przeżyje
spadek (niezależnie od wysokości)?

pnkt. ubezpieczenia

ubezpieczaj¹ cy

wspinacz

l

h

W

S

Ponieważ

F

liny

= k(0.25l)

więc

25mg = k(0.25l)

skąd

k = 25mg/0.25l

czyli

k = 100mg/l

Przed spadkiem (punkt W)

E

pw

= mg(h + l)

Po spadku (punkt S)

E

ps

= mg(h - l - y) + ky

2

/2

8-8

Z. Kąkol-Notatki do Wykładu z Fizyki

Ponieważ w punktach W i S energia kinetyczna wspinacza jest równa zeru, więc

E

pw

= E

ps

czyli

mg(h + l) = mg(h - l - y) +ky

2

/2

Uwzględniając k = 100 mg/l otrzymujemy

mgl = -mgl - mgy + (1/2)(100mg/l)y

2

co daje

50y

2

– ly - 2l

2

= 0

Rozwiązanie fizyczne: y = 0.21l mieści się w granicy wytrzymałości 0.25l.
Oszacujmy teraz maksymalne przyspieszenie

F

wyp

= ky - mg

więc

ma = ky - mg

skąd

a = ky/m - g = 20g

Duże ale lina musi być sprężysta żeby "złagodzić" hamowanie.

A co z zachowaniem energii w przypadku gdy działa siła niezachowawcza?
Dla sił zachowawczych

∑

=

∆

Z

k

W

E

lub

∑

=

∆

+

∆

0

p

k

E

E

Wielkość po lewej stronie to po prostu zmiana całkowitej energii mechanicznej

∆E. Za-

tem równanie to ma postać

∆E = 0.

Jeżeli oprócz kilku sił zachowawczych działa siła niezachowawcza (np. tarcie) to wtedy

∑

∆

=

+

k

Z

NZ

E

W

W

czyli

∑

=

∆

+

∆

NZ

p

k

W

E

E

co jest równoważne

NZ

W

E

=

∆

Widać, że siła tarcia zmienia energię mechaniczną układu (zmniejsza ją bo tarcie jest
siłą rozpraszającą czyli dysypatywną).
Co stało się ze "straconą" energią mechaniczną?
Zostaje ona przekształcona na

energię wewnętrzną

U

, która objawia się wzrostem tem-

peratury. U jest równa rozproszonej energii mechanicznej. Więcej o energii wewnętrz-
nej powiemy w dalszych rozdziałach. Uogólnijmy naszą dyskusję

8-9

Z. Kąkol-Notatki do Wykładu z Fizyki

F

wyp

= F

zew

+ F

Z

+ F

NZ

Z twierdzenia o pracy i energii wynika, że praca wykonana przez siłę wypadkową jest
równa zmianie energii kinetycznej.

k

NZ

Z

zew

E

W

W

W

∆

=

+

+

co jest równoważne

W

zew

-

∆E

p

-

∆U = ∆E

k

czyli

W

zew

=

∆E

k

+

∆E

p

+

∆U

(8.8)

Z równania (8.5) wynika, że

każda praca wykonana na ciele przez czynnik zewnętrzny

równa się wzrostowi energii kinetycznej plus wzrost energii potencjalnej plus wzrost
energii wewnętrznej

.

Cała energia została zarejestrowana. Mamy obejmujące wszystko

zachowanie energii (całkowitej)

.

Wynika z niego, że

energia może być przekształcona z jednej formy w inną, ale nie mo-

że być wytwarzana ani niszczona

; energia całkowita jest wielkością stałą.

Przykład 4

Energia i biologia.
Przykładowo, na wykładzie z fizyki osoby śpiące zużywają energię w tempie około
80 J/s, a osoby uważające ok. 150W. Łagodne ćwiczenia 500 W intensywne 1000 W ale
tylko 100 W na zewnątrz ciała jako energia mechaniczna (Człowiek może wykonywać
pracę mechaniczną tylko z mocą 100 W).
Jak długo trzeba ćwiczyć (np. gimnastyka łagodna 500W) aby stracić (spalić) 500 g
tłuszczu?
Tłuszcz zawiera ok. 40000 J/g. Stąd 500 g tłuszczu zawiera 2·10

7

J. Ponieważ P = E/t

więc t = E/P = 2·10

7

J/ 500W = 11 h

Ile kalorii musi zawierać pożywienie aby utrzymać się przy życiu?
Minimalna moc 80 W (sen), 150 W gdy się nie śpi, średnio 110 W.
E = Pt = 110W·24·3600s = 9.5·10

6

J

Ponieważ 1 kilokaloria = 4180 J więc E = 2260 kcal (często mylona z cal).

Przykład 5

Energia i samochód.
Samochód jedzie z prędkością 100 km/h i zużywa 8 litrów benzyny na 100 km. Jaka
moc jest potrzebna do utrzymania tej stałej prędkości?
1 litr benzyny - 3.7·10

7

J więc P = (8·3.7·10

7

J)/(3600s) = 7·10

4

W = 70 kW.

Dla porównania w mieszkaniu zużywamy około 1 - 1.5 kW energii elektrycznej.
Samochód zużywa kilkadziesiąt razy więcej.

8-10