1
Mechanika układu korbowego- temat nr 16 (2).
a/ równanie ruchu elementów układu korbowego,
b/ siły bezwładności i zasada ich wyrównywania,
c/ przykłady wyrównywania sił i momentów bezwładności w silnikach wielocylindrowych,
d/ zasada budowy i działanie koła zamachowego,
e/ drgania skrętne wału korbowego – określenie stopnia bezpieczeństwa określonego
przypadku rezonansu drgań skrętnych,
f/ tłumiki drgań skrętnych – budowa, działanie zalecenia eksploatacyjne.
Obciążenia działające na układy i elementy silnika, rozumiane jako jedno lub wielokierunkowe stany naprężeń, wywołane są
siłami i momentami działającymi na układ tłokowo-korbowy, pochodzącymi od:
•
sił ciśnienia czynnika roboczego,
•
sił bezwładności mas poruszających się ruchem zmiennym,
•
naprężeniami termicznymi od elementów podlegających znacznym wahaniom temperaturowym ( głowice, tuleje
cylindrowe, tłoki).
Na układ tłokowo-korbowy pracującego silnika działają:
•
zmienne siły gazowe P
g,
•
zmienne siły masowe P
s
, P
o
,
•
tarcia P
µµµµ
,
•
stałe siły ciężkości P
G
.
Siły P
µµµµ
i P
G
jako relatywnie małe są z reguły w wyliczeniach są pomijane
Siły masowe P
s
zależą od przyśpieszeń ruchu poszczególnych elementów układu korbowo-tłokowego i ich wyznaczenie
wymaga znajomości równań ruchu charakterystycznych punktów układu tłokowo-korbowego.
Tłok w silnikach wodzikowych a wraz z nim trzon tłokowy i wodzik wykonują ruch zbliżony do harmonicznego zwany
ruchem posuwisto-zwrotnym lub oscylacyjnym.
Wał korbowy wykonuje ruch obrotowy wokół stałej osi, natomiast ruch korbowodu jest wypadkową ruchu posuwisto-
obrotowego i obrotowego.
2
Charakterystyczne wielkości wynikające z kinematyki układu tłokowo-korbowego:
ππππ
n
•
prędkością kątowa
ω
ω
ω
ω
=
( rad/s)
30
ππππ
n
•
prędkość liniowa c
o
=
ω
ω
ω
ω
r = r
( m/s)
30
•
przyspieszenie dośrodkowe a
d
=
ω
ω
ω
ω
2
r
( m/s
2
),
•
prędkość chwilowa tłoka c
α
αα
α
w zwrotnych położeniach c
α
αα
α
= 0,
____________________
a prędkość maksymalna
c
α
αα
α
max
= c
o
√√√√
1+
λλλλ
2
gdzie
λλλλ
= r / l i wynosi dla silników okrętowych 0,2 – 0,25
r- ramie wykorbienia;
l – długość korbowodu.
S
⋅⋅⋅⋅
n
•
ś
rednia prędkość tłoka
c
ś
r
=
( m/s)
30
gdzie:
S – skok tłoka; n – prędkość obrotowa
[obr/min]
•
przyśpieszenie chwilowe a
α
αα
α
a
α
αα
α
=
ω
ω
ω
ω
2
r (cos
α
αα
α
+
λλλλ
cos2
α
αα
α
) [m/s] gdzie kąt obrotu wału korbowego
α
αα
α
=
ω
ω
ω
ωττττ
[rad]
lub a
α
αα
α
= a
d
cos
α
αα
α
+
λλλλ
a
d
cos2
α
αα
α
[m/s] = a
I
+ a
II
3
Przyspieszenie chwilowe ruchu posuwisto-zwrotnego przedstawiamy jako sumę dwóch przyspieszeń ( rys.4.3):
•
przyspieszenie pierwszego rzędu a
I
= a
d
cos
α
αα
α
o amplitudzie a
d
i okresie 2
ππππ
;
•
przyspieszenie drugiego rzędu a
II
=
λλλλ
a
d
cos2
α
αα
α
o amplitudzie
λλλλ
a
d
i okresie
ππππ
;
Siły gazowe P
g.
Zmienne cisnienie p
g
czynnika roboczego wywierane na tłok powoduje powstanie siły gazowej, której wielkość dla
określonej średnicy tłoka wynosi:
ππππ
d
2
P
g
= p’
g
[N]
4
gdzie p’
g
– różnica ciśnień działających na tłok
p’
g
= p
g
– p
d
[Pa]
p
g
– ciśnienie w przestrzeni roboczej,
p
d
– ciśnienie w przestrzeni podtłokowej.
ππππ
d
2
wobec tego, że
= const, oraz małej wartości p
d
w stosunku do p
g
można przyjąć,
4
ż
e P
g
≈≈≈≈
p
g
i wyznaczyć P
g
na podstawie ciśnienia p
g
( wykres indykatorowy zamknięty i rozwinięty – ryz.4.4).
Siły masowe P
s
i P
o
.
Działające na układ tłokowo korbowy siły masowe, zwane też siłami bezwładności, można zastąpić dwiema siłami:
•
P
o
– siła wypadkową sił bezwładności od mas wykonujących ruch obrotowy, zwanej siła rotacyjną,
•
P
s
- siła wypadkową sił bezwładności mas wykonujących ruch posuwisto zwrotny, zwana siła oscylacyjną.
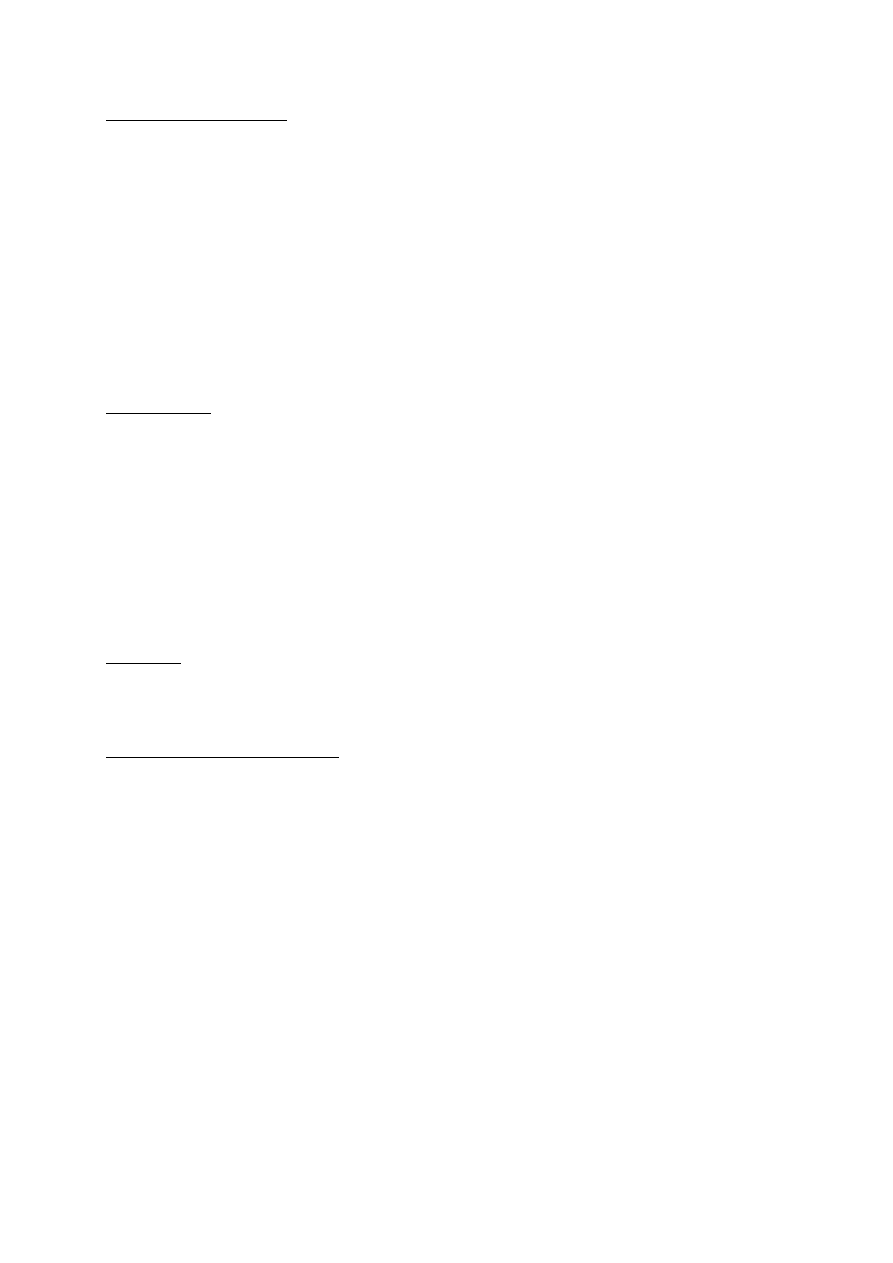
4
Siła masowa ruchu obrotowego P
o
powodowana jest przyspieszeniem
a
d
=
ω
ω
ω
ω
2
r ( m/s
2
), jakiego doznaje masa m
o
[kg] wirująca na promieniu r [m] ze stałą
ππππ
n
prędkością
ω
ω
ω
ω
[s-1] czyli P
o
=
ω
ω
ω
ω
r
2
m
o
[N] a
ω
ω
ω
ω
=
( rad/s)
30
Przyjmując r za promień wykorbienia, m
o
oznacza masę zastępczą mas obrotowych skupioną w osi czopa korbowego
(rys.4.5), zwaną masą zredukowaną na promieniu korby.
Masa zredukowana m
o
składa się z:
•
masy czopa korbowego wraz z masą zredukowaną nie wyrównoważonych ramion korby m
ow
,
•
a także z masy zredukowanej obrotowej części korbowodu m
ok
.
m
o
= m
ow
+ m
ok
[kg]
Siła rotacyjna P
o
zaczepiona w osi czopa korbowego, działając wzdłuż ramienia korby, jest stała co do wielkości oraz wiruje
w płaszczyźnie wykorbienia z prędkością wału korbowego.
Siła masowa ruchu posuwisto zwrotnego P
s
, powodowana jest zmiennym przyspieszeniem
a
α
αα
α
[m/s], jakiego doznaje podczas ruchu tłok, trzon tłokowy, wodzik i część korbowodu i wynosi:
P
s
= m
s
a
α
αα
α
= m
s
ω
ω
ω
ω
2
r (cos
α
αα
α
+
λλλλ
cos2
α
αα
α
)
[N]
α
αα
α
- kąt obrotu wału korbowego (droga kątowa)
α
αα
α
=
ω
ω
ω
ω
ττττ
[rad]
m
s
[kg] – masa zastępcza elementów poruszających się ruchem oscylacyjnym, zredukowana do osi sworznia tłokowego
(rys.4.5)
m
s
= m
st
+ m
sk
[kg]
gdzie:
m
st
– masa tłoka [kg] wraz z pierścieniami, sworzniem, itp., dla silnika wodzikowego dodatkowo masa trzona tłokowego i
wodzika,
m
sk
– masa zastępcza [kg] części korbowodu zredukowana do osi sworznia tłokowego / wodzikowego
5
Po przekształceniach ostateczny wzór na siłę masową ruchu posuwisto-zwrotnego będzie się przedstawiał:
P
s
= m
s
ω
ω
ω
ω
2
r cos
α
αα
α
+m
s
ω
ω
ω
ω
2
r
λλλλ
cos2
α
αα
α
= m
s
a
d
cos
α
αα
α
+ m
s
a
d
λλλλ
cos2
α
αα
α
[N]
Podstawiając przedstawiane wcześniej wzory na przyspieszenia chwilowe pierwszego i drugiego rzędu:
a
α
αα
α
= a
d
cos
α
αα
α
+
λλλλ
a
d
cos2
α
αα
α
[m/s] = a
I
+ a
II
otrzymamy ostateczny wzór na siłę masową ruchu posuwisto-zwrotnego:
P
s
= m
s
a
I
+ m
s
a
II
= P
I
+ P
II
wyrażenie
P
I
= m
s
a
I
nazywa się siłą masową pierwszego rzędu,
natomiast
P
II
= m
s
a
II
siłą masową drugiego rzędu.
Przebieg zmienności sił masowych w funkcji kąta obrotu
α
αα
α
jest taki sam jak dla przyspieszeń a
I
i a
II
( pierwszego i drugiego
rzędu).
Niezrównoważone siły masowe lub ich momenty mogą powodować drgania przenoszone z fundamentu silnika na kadłub
statku.
Drgania te są szczególnie niebezpieczne w warunkach rezonansu, to jest częstotliwości drgań własnych zespołu silnik-
fundament lub kadłuba statku.
Drgania te, przenosząc się na kadłub statku i elementy z nim sztywno połączone, wywołują ich dodatkowe obciążenia
mechaniczne.
Wibracja i hałas z tym związane są także uciążliwe i szkodliwe dla załogi.
Wyeliminowanie tych drgań wymaga całkowitego wyrównoważenia sił masowych i ich momentów.
6
Siła tłokowa P
t.
Sumując siłę gazową P
g
i siłę oscylacyjną P
s
oraz pomijając jako małe siły ciężkości i tarcia, otrzymuje się wypadkowa
zwaną siła tłokową
P
t
= P
g
+ P
s
Przebieg zmienności siły tłokowej P
t
w zależności od kąta obrotu wału korbowego
α
αα
α
dla silnika czterosuwowego można
przedstawić na wykresie. (rys.4.6a), dla silnika dwusuwowego rys. 4.6b.
Siła tłokowa w silniku czterosuwowym działa przemiennie w kierunku ku- i odkorbowym, w dwusuwowym silniku
wolnoobrotowym skierowana jest w zasadzie dla każdego położenia korby w kierunku kukorbowym.
Siły i momenty obciążajace kadłub silnika.
Siły w układzie korbowym.
Siła tłokowa P
t
działająca w osi cylindra przenosi się bezpośrednio na ramę fundamentową tylko w zwrotnych położeniach
tłoka, kiedy oś korbowodu i wykorbienia pokrywa się z osią cylindra.
W pozostałych położeniach korby siła P
t
rozkłada się na składowe P
N
i P
K.
Siła P
N
- wywołuje nacisk tłoka na gładź cylindrową lub nacisk wodzika na prowadnicę, wpływa na wartość siły tarcia
między tymi elementami, a tym samym na ich zużycie cierne.
Siłę P
K
- przenosi korbowód do osi czopa korbowego.
Rozkłada się ona na siłę P
R
i składową styczną P
T.
Składowa promieniowa P
R ,
przenoszona przez czop korbowy i ramiona wykorbień na czop główny jest równoważona w
łożysku głównym, a więc obciąża łożyska korbowe i główne.
Przyjmuje wartości dodatnie i ujemne i za wartość dodatnią przyjmuje się siłę ściskającą ramiona wykorbienia.
7
Siła (składowa) styczna P
T
również obciąża łożyska główne i korbowe, a działając na ramieniu r wywołuje chwilowy
moment obrotowy
M
o
= P
T
⋅⋅⋅⋅
r
którego zmienność w funkcji kąta OWK jest taka, jak siły stycznej ( wykres rys.4.9).
Zakładając równą moc każdego cylindra silnika wielocylindrowego, można przyjąć, że wykresy sił stycznych
poszczególnych cylindrów są identyczne, przesunięte względem siebie o kąt pomiędzy zapłonami.
Sumując wykresy sił stycznych wszystkich cylindrów otrzymujemy wykres siły stycznej wypadkowej dla całego silnika.
Im większa liczba cylindrów, tym mniejsze są wahania w stosunku do wartości średniej siły stycznej P
T
, a przez to i
momentu obrotowego M
o.
Dla danej liczby cylindrów, o zmienności siły P
T
( momentu obrotowego M
o
) decyduje kolejność zapłonu i równomierność
obciążenia poszczególnych cylindrów.
Silnik źle wyregulowany emituje dodatkowe drgania, co powoduje dodatkowe obciążenie kadłuba i fundamentu silnika.
Momenty działające na układ korbowy i kadłub.
Po rozłożeniu siły tłokowej P
t
na jej składowe P
N
i P
K
( rys.4.10).
Składowa P
K
działając na ramieniu a wywołuje moment obrotowy
M
o
= P
K
⋅⋅⋅⋅
a
działający na wał korbowy, który równoważy moment odbiornika mocy – śruby napędowej lub prądnicy.
Składowa P
N
działająca na ramieniu b wywołuje moment:
M’ = P
N
. b
który jest równy momentowi M
o,
lecz przeciwnie skierowany i który usiłuje obrócić silnik w płaszczyźnie poprzecznej,
czemu przeciwdziała odpowiednie mocowanie kadłuba silnika do fundamentu ( śrubami fundamentowymi).
8
Wyrównoważenie silników.
Na układ tłokow-korbowy silnika działają siły masowe P
s
i P
o
, ich momenty oraz moment M’ pochodzący od siły
normalnej P
N.
Wymienione siły i momenty określa się jako zewnętrzne – inaczej wolne – w odróżnieniu od siły gazowej, zwanej
wewnętrzną, zrównoważoną w obrębie kadłuba silnika.
Siły i momenty zewnętrzne powodują drgania silnika, a przenoszone przez kadłub silnika na fundament stanowią uciążliwe
dla otoczenia źródło hałasu i wibracji, a także powodują drgania kadłuba statku.
Wyrównoważenie silników ma na celu częściowe lub całkowite zrównoważenie zewnętrznych sił i momentów, będące
niezbędnym warunkiem ograniczenia lub eliminacji drgań silnika podczas jego pracy.
Całkowite zewnętrzne wyrównywanie silnika wymaga, aby
•
∑ sił masowych = 0
•
∑ momentów sił masowych = 0.
Powyższy cel realizuje się przez odpowiedni dobór:
•
liczby cylindrów,
•
rozstawienia wykorbień,
•
kolejności zapłonów,
•
stosowanie przeciwciężarów na ramionach wykorbień wału.
Zasady równoważenia masowych sił rotacyjnych.
Zrównoważenie siły rotacyjnej P
o
w silniku jednocylindrowym równoważy się przeciwciężarem o masie m’
o
zamontowanym
na przedłużeniu ramion wykorbienia w odległości r’ od środka obrotu.
Wartość masy oblicza się z zależności
m
o
⋅⋅⋅⋅
r = m’
o
⋅⋅⋅⋅
r’
9
r
skąd
m’
o
= m
o
⋅⋅⋅⋅
r’
Zrównoważenie siły rotacyjnej P
o
w silnikach wielocylindrowych równoważy się przeciwciężarami o masie m’
o
zamontowanym na przedłużeniu ramion każdego wykorbienia wykorbienia w odległości r’ od środka obrotu.
Warunek ten spełnia się dla wszystkich wielocylindrowych silników o równych odstępach zapłonu między cylindrami.
Zasady równoważenia masowych sił oscylacyjnych.
Siła oscylacyjna P
s
jest sumą siły masowej pierwszego rzędu i siły masowej drugiego rzędu
P
s
= P
I
+ P
II
= m
s
⋅⋅⋅⋅
ω
ω
ω
ω
2
⋅⋅⋅⋅
r
⋅⋅⋅⋅
cos
α
αα
α
+m
s
⋅⋅⋅⋅ω
ω
ω
ω
2
⋅⋅⋅⋅
r
λλλλ
cos2
α
αα
α
Zrównoważenie siły P
s
polega na zrównoważeniu jej składowych P
I
i P
II.
Równoważenie masowych sił oscylacyjnych P
s
w silniku jednocylindrowym wymaga stosowania specjalnych układów
wyrównoważających.
Praktycznie wyrównoważenie jednocylindrowego silnika sprowadza się do częściowego zrównoważenia siły P
I
przez
dodanie dodatkowej masy m’
oI
, ponieważ całkowite zrównoważenie siły oscylacyjnej pierwszego rzędu spowodowałoby
wystąpienie niezrównoważonej siły składowej, co praktycznie oznaczałoby zmianę kierunku działania siły pierwszego rzędu
P
I.
Całkowite zrównoważenie siły masowych drugiego rzędu P
II
wymagałoby stosowania złożonego układu konstrukcyjnego,
dlatego w powszechnie spotykanych rozwiązaniach siły te nie są wewnętrznie zrównoważane i przenoszą się przez kadłub na
fundament silnika.
W silnikach wielocylindrowych całkowite zrównoważenie sił masowych I i II rzędu można uzyskać, dobierając odpowiednio
kąt rozstawienia wykorbień, a zatem bez stosowania dodatkowych zabiegów konstrukcyjnych.
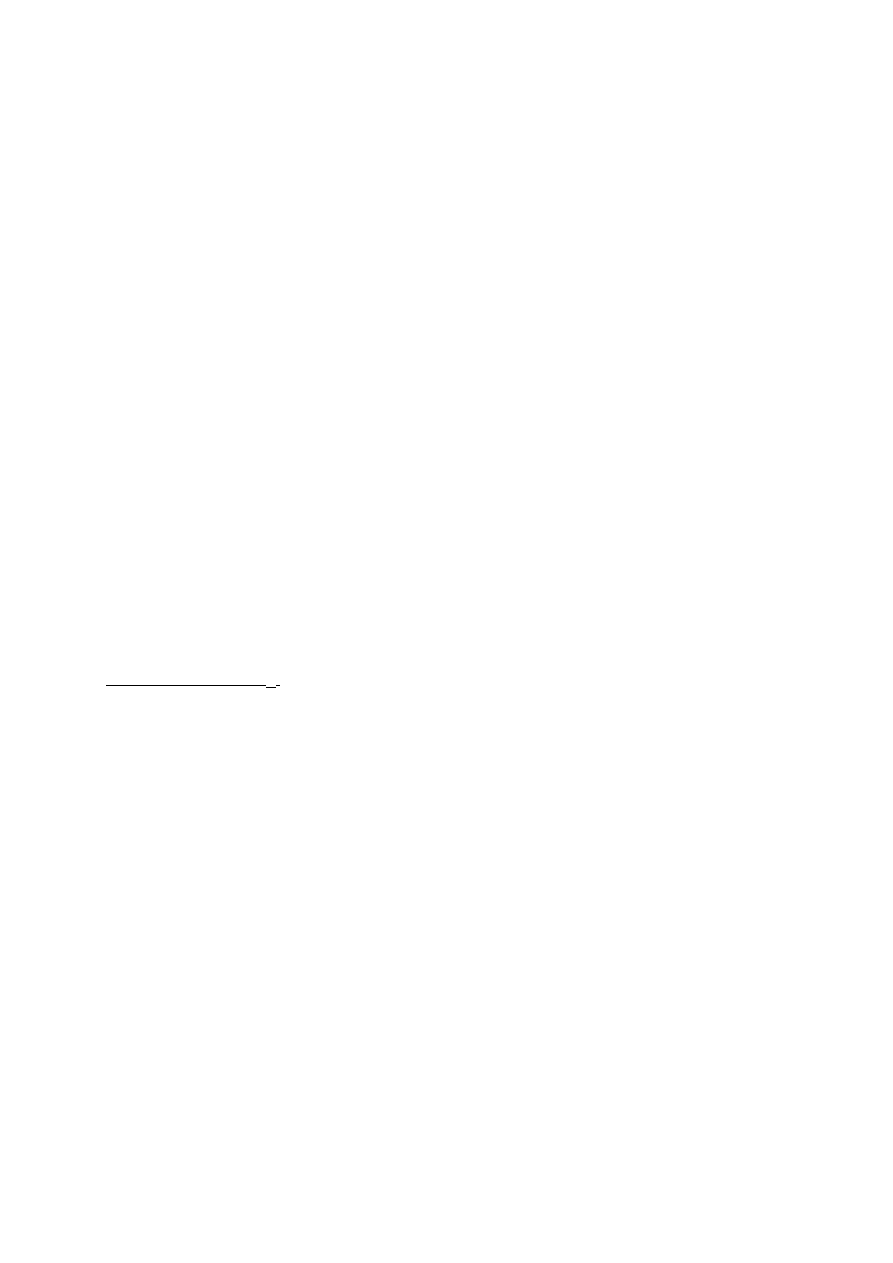
10
Zasada wyznaczania i równoważenia momentów sił masowych.
Z wyżej podanego wniosku możnaby sądzić, że w silnikach rzędowych wielocylindrowych, dla których wypadkowe sił
masowych równają się zeru ( ∑
∑
∑
∑P
o
=0; ∑
∑
∑
∑P
I
= 0; ∑
∑
∑
∑P
II
=0 ), wystepuje całkowite zewnętrzne zrównoważenie nie powodujące
zewnętrznego oddziaływania silnika na jego fundament.
Tak jednak nie jest, gdyż siły te, choć wzajemnie równoważące się, mogą powodować momenty działające na silnik w
różnych płaszczyznach.
Za przykład służy silnik dwusuwowy, dwucylindrowy (rys.4.13) z wałem korbowym o wykorbieniach przestawionych o kąt
180
o
.
Dla tego silnika
∑
∑
∑
∑P
o
= 0;
∑
∑
∑
∑P
I
= 0; ∑
∑
∑
∑P
II
≠≠≠≠
0
natomiast
∑
∑
∑
∑Mp
o
>>>>
0;
∑
∑
∑
∑M
PI
>>>>
0;
∑
∑
∑
∑M
PII
====
0
Momenty sił rotacyjnych M
Po
.
Siły rotacyjne P
o
działają stale wzdłuż ramion korb i wirują z prędkością wału korbowego.
Dla silnika dwucylindrowego, w położeniu jak na rys ( 4.13) moment tych sił, liczony względem płaszczyzny S-S
przechodzącej przez środek ciężkości silnika i prostopadłej do osi wału korbowego działa w płaszczyźnie symetrii wzdłużnej
i wynosi
l l
M
Po
= P
o1
+ P
o2
= P
o
l = m
o
ω
ω
ω
ω
2
r l
2 2
Moment ten podczas obrotu wału korbowego stara się przechylić silnik we wszystkich płaszczyznach przechodzących przez
oś wzdłużną wału korbowego.
Zrównoważenie tego momentu jest możliwe przez całkowite zrównoważenie sił rotacyjnych za pomocą czterech bądź dwóch
przeciwciężarów zamocowanych na przedłużeniu ramion wykorbienia.
11
Przy użyciu czterech przeciwciężarów masę równoważącą wylicza się według zależności
r
m’
o
= m
o
r’
przy użyciu dwóch przeciwciężarów
r
l
m’
o
= m
o
⋅⋅⋅⋅
r’ 2l’
Momenty sił oscylacyjnych M
I
i M
II
W odróżnieniu od momentu sił rotacyjnych momenty sił oscylacyjnych pierwszego i drugiego rzędu - M
I
i M
II,
działają tylko
w płaszczyźnie symetrii wzdłużnej.
Ich wartości zmieniają się w okresie 2
ππππ
( moment M
I
) i
ππππ
(moment M
II
) a więc tak jak przyspieszenia a
I
i a
II
.
Zrównoważenie tych momentów wymaga, zatem zastosowania takiego układu konstrukcyjnego, którego momenty M’
I
i M’
II
równożyłyby momenty M
I
i M
II
.
Moment I rzędu - M
I
Momenty pierwszego rzędu działają w płaszczyźnie pionowej i poziomej silnika.
Równoważone są za pomocą dodatkowych mas (przeciwciężarów) w ograniczonym stopniu zależnym od sztywności –
podatności fundamentu (kadłuba statku) na działanie składowych momentu.
Częściowe zrównoważenie przez dodanie przeciwciężarów nie likwiduje momentu M
I
a jedynie zmienia częściowo lub
całkowicie kierunek jego działania z pionowego (wertykalnego) na poziomy (horyzontalny).
Całkowita kompensacja sił masowych pierwszego rzędu M
I
możliwa jest przez zastosowanie kompensatora.
W silnikach wielocylindrowych konieczność zrównoważenia momentu M
I
zachodzi głownie dla 4- i 5-cylindrowych
silników.
Schematy konstrukcyjne kompensatorów sił masowych pierwszego rzędu stosowane w silnikach MAN – B&W - rys.4.15;
4.16 i 4.17.
12
Moment II rzędu - M
II
.
Konieczność zrównoważenia / ograniczenia momentów zewnętrznych drugiego rzędu M
II
zachodzi dla 4-,5-, i 6-
cylindrowych silników dwusuwowych oraz 3- i 5-cylindrowych silników czterosuwowych.
Niezrównoważone momenty M
II
w silnikach o liczbie
>
6 są relatywnie małe lub równe 0.
Moment M
II
= 0 dla silników 8, 10, 12-cylindrowych rzędowych silników dwusuwowych.
Z uwagi na dwukrotną, w stosunku do częstotliwości obrotów wału korbowego, częstotliwość zmian momentów M
II
,
kompensacja / ograniczenie M
II
metodą „przeciwciężarów” jest konstrukcyjnie niemożliwa.
Zrównoważenie momentu drugiego rzędu wymaga zastosowania specjalnego układu bezwładnościowego ( rys.4.18 i rys.4.19
– kompensator Lanchestera), który jest montowany po obu stronach silnika – czołowej i tylnej, – co jest rozwiązaniem
standardowym (rys.4.20).
Stosowane są również zintegrowane kompensatory zewnętrznych momentów pierwszego i drugiego rzędu – stosuje firma
SULZER dla 4-cylindrowych silników dwusuwowych dużej mocy ( np. 4RLB76; 4RLB90; 4RTA84).
Stopień kompensacji momentu M
I
zależy od podatności kadłuba statku na drgania spowodowane tym momentem w
płaszczyznach pionowej i poziomej oraz od miejsca posadowienia silnika w stosunku do węzła drgań.
Koła zamachowe.
Jak wynika z rozważań o siłach i momentach masowy, cechuje je okresowa zmienność.
Największe wahania momentu w czasie jednego cyklu występują w silniku 1-cylindrowym 4-suwowym, gdzie na jeden suw
pracy, podczas którego moment jest dodatni, występują trzy suwy pomocnicze.
Suwy pomocnicze odbywają się kosztem energii przekazanej do układu korbowego podczas suwu pracy.
Jeżeli przyjmie się stały moment odbiornika mocy, to chwilowa prędkość kątowa wału korbowego silnika nie może być stała.
13
Ruch obrotowy wału korbowego odbywa się, zatem z określona nierównomiernością, tym większą, im mniejsza jest liczba
cylindrów i masa układu korbowego.
Nierównomierność prędkości obrotowej silnika w czasie jednego cyklu roboczego, określoną stopniem nierówności biegu
silnika, można zmniejszyć przez podzielenie pracy silnika na kilka cylindrów lub przez osadzenie na wale ciężkich mas
obrotowych, zwanych kołami zamachowymi lub przez pierwsze i drugie jednocześnie.
Im większa jest liczba cylindrów silnika, tym koło zamachowe może być mniejsze, a więc i lżejsze, co jest korzystne ze
względu na obciążenie sąsiadującego z kołem zamachowym łożyska.
Koła zamachowe wraz z całym układem korbowym akumulują nadwyżki energii w okresie, gdy moment obrotowy silnika
jest większy od momentu odbiornika i oddają, kiedy jest odwrotnie.
Rodzaje wykonania – rys.6.65; 6.66. – konstrukcje tarczowe lub wieńcowe.
Wielkość koła zamachowego (zależna od żądanego stopnia nierównomierności biegu) silnika określa się momentem
bezwładności koła zamachowego I
o, którego
wartość z wystarczającą dla praktyki dokładnością określa się z zależności
mD
2
I
o
= m ( D/2)
2
=
4
gdzie:
m – masa koła zamachowego odniesiona do środka ciężkości wieńca.
D – średnica odpowiadająca środkowi ciężkości wieńca.
Charakterystycznym parametrem koła zamachowego jest iloczyn mD
2
zwany także momentem zamachowym koła
zamachowego.
Koło zamachowe osadzone na końcu wału korbowego od strony odbiornika mocy, ma na zewnętrznej powierzchni wieńca
nacięte zęby, stanowiące wraz z kołem zębatym, obracarki jednostopniową przekładnie zębatą, służącą do obrotu silnika.
Odcinek wału z kołem zamachowym jest dwustronnie łożyskowany.
14
Podsumowanie:
W rozważaniach na temat wyrównoważenia silników zakładano, że masy części powtarzających się w poszczególnych
cylindrach są jednakowe.
W rzeczywistości tak nie jest, ze względu na nieunikniony rozrzut wymiarów i mas, zwłaszcza części odlewanych ze
względu na niejednorodność struktury i surowy stan powierzchni.
Z tych względów, w razie potrzeby, przeprowadza się korektę mas wałów korbowych przez nawiercanie otworów
korekcyjnych w przeciwciężarach.
Przeciwciężary z otworami korekcyjnymi są wzajemnie niewymienialne.
Stopień wyrównoważenia silnika jest kompromisem konstrukcyjnym, uwzględniającym wiele różnych czynników – w tym:
•
przeznaczenie silnika,
•
jego ciężar,
•
rodzaj fundamentowania,
•
obciążenia łozysk.
Każde odstępstwo od tych założeń, np. praca silnika ze zdemontowanym układem tłkowo-korbowym, zwiększa stopień
niezrównoważenia silnika, co objawia się wzmożonymi drganiami.
Z tych tez względów wymontowanie uszkodzonego układu z silnika jest celowym tylko wówczas, gdy uszkodzenie
uniemożliwia kontynuowanie podróży.
Drgania skrętne układu silnik-śruba napędowa.
Każde ciało sprężyste, poddane działaniu okresowo zmiennym i odpowiedniej wartości obciążeniom ulega okresowym
wychyleniom wokół położenia spoczynkowego.
Ruch ten nazywa się drganiem.
Wał korbowy silnika wraz ze sprzęgniętym z nim wałem pośrednim i odbiornikiem mocy ( sruba napędową lub prądnicą)
stanowi układ drgający, pobudzony do drgań skrętnych, giętych i wzdłużnych, okresowo zmiennymi siłami gazowymi i
masowymi oraz momentami.
15
Drgania te są przyczyną powstawania dodatkowych sił i momentów masowych w układzie tłokowo-korbowym i
wynikających z tego dodatkowych, a trudnych do określenia obciążeń mechanicznych.
Drgania wpływają także niekorzystnie na warunki pracy łożysk układu tłokowo-korbowego.
Szczególnie niebezpieczne są rezonansowe drgania skrętne wału korbowego powstające wtedy, gdy częstotliwość okresowo
zmiennego momentu wzbudzającego drgania skrętne, zwana dalej częstotliwością wzbudzania n’
wz
jest równa częstotliwości
drgań n’
wł
własnych układu drgającego
n’
wz
= n’
wł
Układ drgający składa się z:
•
wału korbowego,
•
koła zamachowego,
•
wału pośredniego,
•
wału śrubowego,
•
ś
ruby napędowej.
Dla silnika zespołu prądotwórczego układ drgający stanowią:
•
wał korbowy,
•
koło zamachowe,
•
pradnica.
Rzeczywiste układy drgające, charakteryzujące się, między innymi, zdolnością rozpraszania energii, czyli tłumieniem drgań,
mogą pobudzić do drgań rezonansowych tylko takie siły lub momenty, których praca wzbudzenia L
wz
jest, co najmniej
równa pracy tłumienia L
tł
.
Dla obsługującego silnik ważna jest odpowiedź na pytania:
1.
dla jakich prędkosci obrotowych silnika wystepuje rezonans, czyli n’
wz
= n’
wł,
2.
dla jakich rezonansów praca momentu skręcającego, czyli praca wzbudzenia
L
wz
spełnia warunek L
wz
≥≥≥≥
L
tł
.
W aspekcie konstrukcyjnym istotnym jest również określenie dodatkowych naprężeń powstających wskutek drgań
rezonansowych.
16
Ciało sprężyste, pobudzone do drgań jednorazowym impulsem, przestaje po pewnym czasie drgać i czas ten jest zależny od
zdolności rozpraszania energii wzbudzającej drganie.
Drgania podczas których energia ulega rozproszeniu, nazywają się drganiami tłumionymi.
Każdy rzeczywisty układ drgający ma właściwości rozpraszania energii ( poprzez tarcie w łożyskach, tarcie śruby napędowej
o wodę, itp.), a zatem wszystkie drgania rzeczywiste są drganiami tłumionymi.
Jeżeli na układ drgający działają okresowo zmienne siły lub momenty, to powodowane nimi drgania nazywają się drganiami
wymuszonymi lub wzbudzanymi.
Układ rzeczywisty wzbudzony do drgań będzie drgać ze stałą amplitudą, jeśli energia wzbudzająca e
wz
– energia
doprowadzona do układu drgającego w czasie jednego okresu – będzie równa energii tłumienia e
tł
, to jest energii, jaką w tym
czasie układ jest zdolny rozproszyć.
Jeśli e
wz
>
e
tł
, to obszerność drgań będzie wzrastała, a dla e
wz
<
e
tł
drgania będą zanikać.
Drgania skrętne swobodne nie tłumione układów wielomasowych.
W celu obliczenia częstotliwości drgań własnych rzeczywistego układu drgającego sprowadza się go do układu zastępczego,
składającego się z masowych momentów bezwładności I
1
, I
2
....I
i
oraz (i-1) bezmasowych odcinków wałów o sztywności
skrętnej s
1
, s
2
......s
i
( schemat zastępczy rys.4.24)
Sztywność skrętną wału s definiuje się jako stosunek momentu skręcającego M [Nm] do statycznego kata skręcenia
ϕϕϕϕ
st
[rad]
wału spowodowanego przez moment M
M
S =
[Nm/rad]
ϕϕϕϕ
st
wobec
M
⋅⋅⋅⋅
l
ϕϕϕϕ
st
=
[rad]
G
⋅⋅⋅⋅
I
o
gdzie:
ϕϕϕϕ
st
- kat skręcenia [rad],
l – długość skręcania wału [m],
G- moduł sprężystości postaciowej materiału [N/m
2
],
17
I
o
– biegunowy moment bezwładności wału [m
4
],
ostateczny wzór na sztywność wału przyjmuje postać:
G
⋅⋅⋅⋅
I
o
s =
[Nm/rad]
l
Drgania skrętne swobodne nie tłumione układu dwumasowego – schemat ry.4.25.
Układ nie ma zdolności tłumienia drgań i składa się z:
•
dwóch mas o momentach masowych I
1
i I
2
,
•
bezmasowego odcinka wału o długosci l i sztywności skrętnej s.
Na układ działa moment skręcający M, powodujący skręcenie wału o kąty
ϕϕϕϕ
o1
i
ϕϕϕϕ
o2
.
Po ustaniu działania momentu M układ będzie drgać wokół osi wału ze stałą częstotliwością n’
wł
.
Kąty
ϕϕϕϕ
o1
i
ϕϕϕϕ
o2
to amplitudy ruchu drgającego mas 1 i 2.
Punkt W – wychylenie równe 0 (
ϕϕϕϕ
w
= 0), to węzeł drgań dla drgania pierwszego rzędu lub drgania jednowęzłowego (dla
tego przypadku).
Częstotliwość kątowa drgań własnych
ω
’wł układu drgającego dla np. układu dwumasowego wynosi
I
1
+ I
2
ω
ω
ω
ω
’
wł
=
ω
ω
ω
ω
’ =
s
[ rad / s]
√√√√
I
1
⋅⋅⋅⋅
I
2
Wyrażenia w powyższym wzorze są funkcją wielkości określających ilość, rodzaj i rozmieszczenie materiału, z którego
układ drgający jest wykonany.
Uogólniając powyższe należy stwierdzić, że częstotliwość drgań własnych drgającego układu
ω
’
wł
zależy wyłącznie od cech
własnych układu, nie zależy od wielkości częstotliwości momentu wzbudzającego drgania, ani tez od ich wielkości.
18
Drgania skrętne układów wielomasowych.
Układ trójmasowy – schemat zastępczy rys.4.26.
Układ taki można pobudzić do drgań skrętnych w dwojaki sposób:
1.
tak, aby masa środkowa i jedna z mas skrajnych wychylały się jednoczesnie w tym samym kierunku, a druga masa
skrajna w kierunku przeciwnym ( jeden węzeł drgań W
I
),
2.
tak, aby dwie skrajne masy wychylały się jednoczesnie w tym samym kierunku, natomiast masa środkowa w
przeciwnym (dwa węzły drań W
I
i W
II
– drgania dwuwęzłowe lub drgania drugiego stopnia).
Każdemu stopniowi drgań odpowiada określona częstotliwość drgań własnych:
•
drganiom pierwszego stopnia – częstotliwość pierwszego stopnia
ω
ω
ω
ω
’
I
(n’,v
I
),
•
drganiom drugiego stopnia – częstotliwość stopnia
ω
ω
ω
ω
’
II
(n”, v
II
),
Wyższym stopniom drgań odpowiada większa częstotliwość drgań własnych,
ω
ω
ω
ω
’
II
>>>>ω
ω
ω
ω
’
I
Układ wielomasowy składający się z i mas można pobudzić do drgań skrętnych na i-1 sposobów, co oznacza, ze układ taki
może drgać z częstotliwościami własnymi i-1 stopni –
ω
ω
ω
ω
’
I;
ω
ω
ω
ω
’
II
......
ω
ω
ω
ω
’
i-1
.
Przykładem ruchu drgającego wielomasowego jest układ napędowy statku.
Ilość stopni drgań takiego układu jest teoretycznie nieskończenie duża, praktycznie zależna od liczby mas zastępczych –
masowych momentów bezwładności – odwzorowujących układ rzeczywisty.
Dla układu drgającego silnik-śruba napędowa wystarczająca znajomość drgań skrętnych i nich następstw dla pierwszego i
drugiego stopnia drgań, a dla układów z silnikiem na śródokręciu – dodatkowo trzeciego.
Przykład wykresów względnych ( wartości wychyleń poszczególnych mas wyrażone w wartościach względnych przy
założeniu, że wychylenie pierwszej masy
ϕϕϕϕ
o1
= 1 ) wychyleń skrętnych I, II i III stopnia drgań dla układu statku z siłownia
na śródokręciu – rys.4.27.
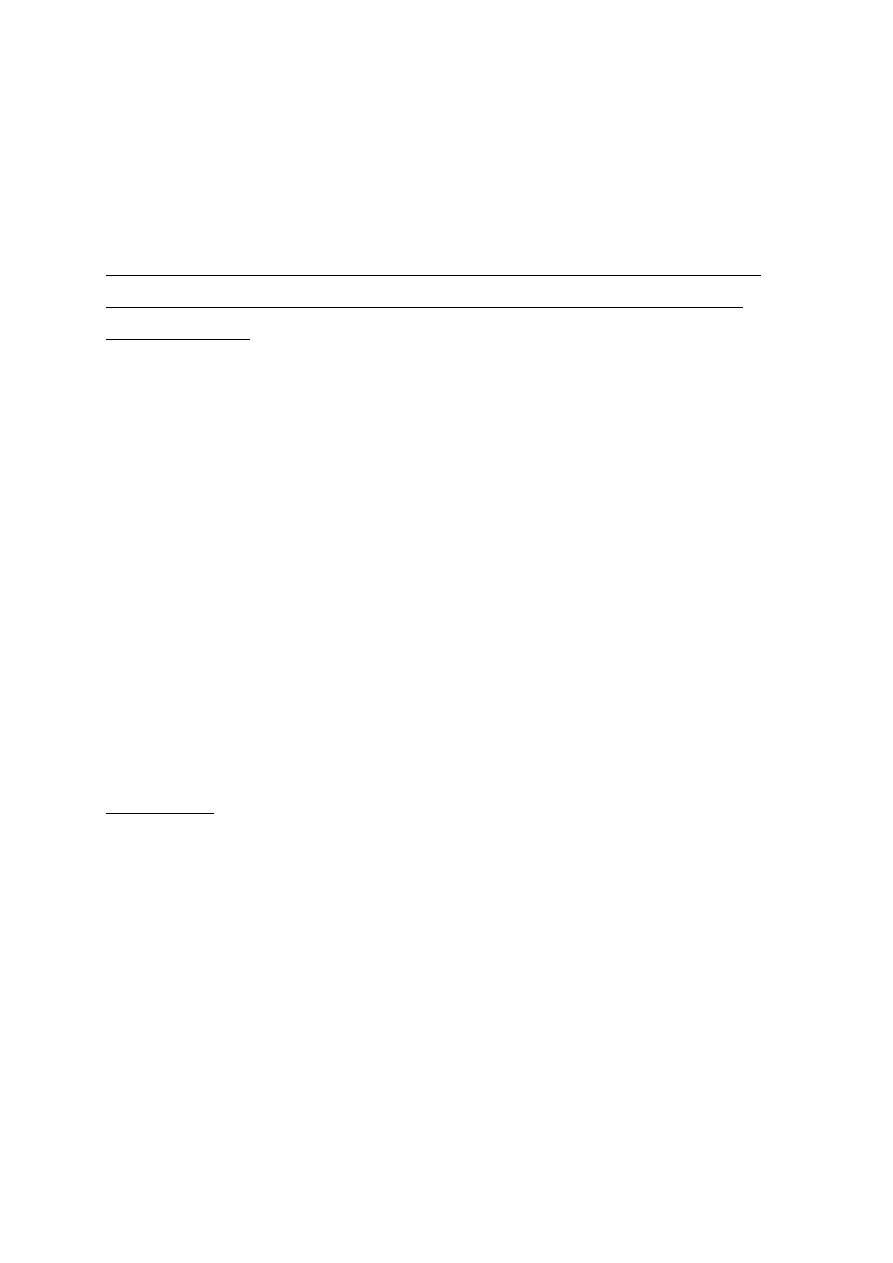
19
Momenty wzbudzające drgania skrętne.
Drgania skrętne układu rzeczywistego możliwe są tylko wtedy, gdy na układ ten działa okresowo zmienny moment, którego
praca skręcania jest równa co najmniej pracy tłumienia.
Momentem wzbudzającym drgania skrętne układu napędowego jest moment obrotowy silnika ( rys.4.28), jest on funkcja
okresowo zmienna, ciągła i określona w każdym punkcie przedziału (0,2
ππππ
) dla silników dwusuwowych lub (0,4
ππππ
) dla
silników czterosuwowych.
Rozkładając moment obrotowy silnika M na z momentów składowych, przyjmuje się w dalszych rozważaniach, że układ
korbowy działa z momentów zmiennych ( z harmonicznych) M
1
, M
2
......M
z
i każdy z nich może niezależnie wzbudzić
drgania skrętne układu silnik-śruba lub silnik prądnica.
Rezonans drgań. Krytyczna prędkość obrotowa.
Drgania skrętne układu silnik-śruba napędowa (silnik – prądnica) mogą być szczególnie niebezpieczne w warunkach
rezonansowych, to jest gdy częstotliwość zmian momentu wzbudzającego drgania
ω
ω
ω
ω
’
wz
równa się częstotliwości drgań
własnych
ω
ω
ω
ω
’
wł
układu drgającego
ω
ω
ω
ω
’
wz
=
ω
ω
ω
ω
’
wł
lub
n’
wz
= n’
wł
Częstotliwość n’
wz
harmonicznej k-tego rzędu, dla prędkości obrotowej n [obr/min] wynosi
n’
wz
= k
⋅⋅⋅⋅
n [1/min]
Prędkości obrotowe, dla których występuje równość
k
⋅⋅⋅⋅
n = n’
wł
nazywają się rezonansowymi prędkościami obrotowymi lub krytycznymi prędkościami obrotowymi n
kr
zatem
n’
wł
n
kr
=
[obr/min]
k
Dla układu silnik-śruba praktycznie należy się liczyć z trzema stopniami drgań o częstotliwościach własnych
ω
ω
ω
ω
’
I;
ω
ω
ω
ω
’
II
,
ω
ω
ω
ω
’
III
oraz z z momentami ( harmonicznymi) wzbudzającymi drgania, zatem teoretycznie możliwa liczba rezonansów wynosi 3z.
20
Pasmo rezonansowych prędkosci obrotowych dla silników wolnoobrotowych wynosi
±±±±
(0,05
÷÷÷÷
0,08) n
kr
dla rezonansów niskich stopni i rzędów oraz
±±±±
( 0,01
÷÷÷÷
0,03)n
kr
dla rezonansów wyższych stopni i
wyższych rzędów.
Szerokości pasm rezonansowych prędkosci obrotowych , niedostępnych dla pracy silników średnioobrotowych są
odpowiednio większe.
Gdyby wszystkie drgania rezonansowe były jednakowo niebezpieczne, zastosowanie silnika tłokowego jako urządzenia
napędowego statku byłoby praktycznie niemożliwe.
Krytyczna prędkość obrotowa rzędów głównych.
Niektóre z możliwych rezonansów znajdują się poza zakresem eksploatacyjnej prędkości obrotowej silnika, dla innych zaś
amplituda drgań rezonansowych jest tak mała, że drgania te nie mają żadnego praktycznego znaczenia.
Aby układ silnik-śruba pobudzić do drgań, moment wzbudzający drgania musi zmieniać się z częstotliwością rezonansową, a
praca skręcania tego momentu L
s
= L
wz
musi być co najmniej równa pracy tłumienia L
s
≥≥≥≥
L
tł
.
Praca skręcania harmonicznej k-tego rzędu silnika i-cylindrowego jest geometryczna sumą prac skręcania k-tej
harmonicznej poszczególnych cylindrów.
Prace skręcania harmonicznych k-tego rzędu poszczególnych cylindrów mogą się wzajemnie znosić lub dodawać.
Chcąc zatem określić, które harmoniczne ( którego rzędu harmoniczne) wzbudzają najbardziej niebezpieczne drgania, należy
wyznaczyć prace skręcania dla każdego stopnia i rzędu.
Aby określić rząd harmonicznej, wzbudzającej najbardziej niebezpieczne drgania, należy obliczyć dla poszczególnych stopni
drgań pracę skręcania.
Rzędy, dla których geometryczna suma pracy skręcania danego stopnia drgań jest największa, nazywają się rzędami
głównymi.
Praca skręcania dla momentu k-tego rzędu M
ok
i-tego cylindra dla s-tego stopnia drgań wynosi
21
l
kis
=
ππππ
⋅⋅⋅⋅
M
ok
⋅⋅⋅⋅
ϕϕϕϕ
ois
⋅⋅⋅⋅
sin
ββββ
ki
i jest największa, gdy przesunięcie fazowe
ββββ
ki
miedzy momentem M
ok
a kątem skręcenia
ϕϕϕϕ
ois
równa się
ππππ
/2 (90
o
).
Aby określić pracę skręcania k-tej harmonicznej silnika i-cylindrowego dla drgań s-tego stopnia, należy zsumować tak
wyliczone geometryczne prace skręcania wszystkich cylindrów.
Dla jakościowej oceny wielkości pracę skręcania harmonicznej k-tego rzędu, a przez to wyznaczenia głównych rzędów
drgań, wystarczająca jest znajomość sumy określonej wzorem (4.57b), zwanej wektorowa sumą wychyleń względnych, dla
wyznaczenia, której przyjmuje się umownie, iż wychylenie
ϕϕϕϕ
o1
= 1, stąd:
Φ
Φ
Φ
Φ
kis
= 1 +
ϕϕϕϕ
o2s
sin (90+
ββββ
k2
) + ..........+
ϕϕϕϕ
ois
sin (90 +
ββββ
ki
)
Przyjmując za wychylenie pierwszej masy dla wszystkich stopni drgań
ϕϕϕϕ
o1
= 1, wartość liczbowa tej sumy dla silnika i-
cylindrowego zawiera się w przedziale 0
<<<<
Φ
Φ
Φ
Φ
kis
<<<<
i.
Rzędy, dla których suma
Φ
Φ
Φ
Φ
kis
jest największa ( praktycznie
>>>>>>>>
0 ), przyjmuje się za rzędy główne.
Rzędy główne drugiego i wyższych stopni drgań należy określić na podstawie pracy skręcania lub wektorowej sumy
wychyleń względnych.
Spośród rezonansów rzędów głównych najniebezpieczniejsze są rezonanse dla rzędów o małej liczbie porządkowej.
Praca skręcania wału korbowego silnika ośmiocylindrowego 4-suwowego – rys.4.32.
Nie wszystkie drgania rezonansowe rzędów głównych wywołują jednakowe naprężenia skręcające na wale.
W odróżnieniu od drgań występujących podczas krytycznych prędkosci obrotowych niskich rzędów, drgania silnika w
rezonansie wyższych rzędów są słabo lub wcale nieodczuwalne w przedzialae maszynowym.
Prowadzi to często do złego zwyczaju całkowitego ich lekceważenia i ustalania eksploatacyjnej prędkości obrotowej w
paśmie krytycznej prędkosci obrotowej wyższych rzędów i stopni.
22
Mimo iż naprężenia skręcające wał, wywołane drganiami wyższych rzędów głównych są pomijalnie małe, należy unikać
pracy silnika w paśmie krytycznych prędkości obrotowych wyższych rzędów, gdyż powstałe w tych warunkach drgania
mogą mieć ujemne skutki.
Każde drgania skrętne zwiększają obciążenia dynamiczne elementów układu tłokowo-korbowego i przekładni napędowej
wału rozrzadu oraz wpływają niekorzystnie na pracę łozysk układu, a także mogą wywoływać drgania tulei cylindrowych
skutkujące zwiększoną intensywnością zużycia tulei i kawitacja powierzchni chłodzących.
Przy sztywnym połączeniu wału korbowego z odbiornikiem mocy drgania skrętne mogą wywierać niekorzystny wpływ na
prace tych ostatnich.
W wypadku napędu głównego wpływają zakłócająco na pracę śruby napędowej.
Jeśli odbiornikiem mocy jest prądnica prądu przemiennego, mogą pojawić się trudności z pracą równoległa prądnic.
Drgania te przenoszą się przez kadłub silnika na fundament oraz kadłub statku, mogą wywoływać drgania rezonansowe
innych elementów sprężystych w przedziale maszynowym lub poza nim.
Działają długotrwale powodują uszkodzenia zmęczeniowe elementów siłowni i kadłuba statku, ponadto wpływają ujemnie na
warunki bytowe załogi.
Zmiana zakresu głównej krytycznej prędkosci obrotowej.
Rezonansowe prędkosci obrotowe danego układu napędowego, wyznaczone drogą obliczeń lub doświadczalnie dla
określonych warunków pracy silnika przyjętych za normalne, mogą w warunkach eksploatacyjnych zmienić się, jeśli:
•
zmieni się częstotliwość drgań własnych układu napędowego,
•
ulegnie zmianie praca skręcania poszczególnych harmonicznych,
•
warunki wpływające na prace tłumienia.
Wymienione przyczyny mogą występować oddzielnie lub łącznie.
Masowe momenty bezwładności I oraz sztywność skręcania wału s, od których zależy częstotliwość drgań własnych układu,
są w normalnych warunkach eksploatacyjnych wielkościami stałymi.
23
Jedynie w stanach awaryjnych, którym towarzyszy ubytek masy układu napędowego, np.:
•
odpadniecie lata śruby napędowej,
•
praca silnika z wymontowanym tłokiem, itp.
Częstotliwość drgań własnych układu napędowego wzrasta.
Wyraźna zmiana warunków tłumienia drgań, np. wyraźny wzrost tarcia lub zmiana skoku śruby nastawnej, zdecydować
mogą także o zmianie częstotliwości drgań własnych, jak i o amplitudzie drgań.
W układach napędowych ze śrubą nastawną zmiana skoku śruby nastawnej powoduje zarówno zmianę częstotliwości drgań
własnych układu silnik-sruba, jak i amplitudy drgań.
Występowanie drgań skrętnych poza zakresem rezonansów głównych rzędów może być spowodowane nierównomiernym
rozkładem mocy w poszczególnych cylindrach lub w wypadku krańcowym praca silnika z wyłączonym jednym lub kilkoma
cylindrami.
Uwzględniając, że wyłączenie z pracy jednego cylindra zwiększa jednocześnie drgania giętne wału, a przez to obciążenie
mechaniczne elementów silnika, to pracę silnika z wyłączonym cylindrem lub cylindrami uznać należy za technicznie
niewłaściwą, uzasadniona tylko względami bezpieczeństwa.
Eliminacja / ograniczenie drgań skrętnych.
Ze względu na obciążenie mechaniczne wałów korbowych, niebezpieczne są drgania powodowane harmonicznymi
głównymi niskich rzędów. Niepożądane są również drgania rezonansowe pozostałych rzędów.
Eliminację drgań skrętnych lub znaczne ich zmniejszenie osiąga się w drodze konstrukcyjnej przez:
•
odpowiedni dobór kolejności zapłonów,
•
odpowiedni dobór odstępu między zapłonami,
•
ukształtowanie wału korbowego i pośredniego o możliwie największej częstotliwości drgań własnych, tak by
rezonanse rzędów głównych wypadały poza zakresem eksploatacyjnym ( sztywny wał o małej długości i dużej
ś
rednicy).
24
Jeżeli mimo określonych zabiegów konstrukcyjnych, amplitudy niektórych drgań rezonansowych w przedziale prędkosci
eksploatacyjnych są zbyt duże, to może okazać się konieczne zastosowanie specjalnych urządzeń zmniejszających lub
eliminujących drgania, takich jak:
•
tłumiki tarciowe zmniejszające amplitudy drgań rezonansowych wszystkich rzędów i stopni,
•
rezonansowe eliminatory drgań eliminujące drgania rezonansowe jednego rzędu drgań,
•
tłumiki łączące w sobie obie wyżej wymienione własności, czyli eliminatory rezonansowe z tłumieniem.
W silnikach okrętowych stosuje się głownie tarciowe tłumiki drgań.
Działanie tych urządzeń polega na tłumieniu drgań, to znaczy zmniejszeniu amplitud wychyleń skrętnych przez pochłanianie
energii ruchu drgającego.
Dodatkowym skutkiem tego działania jest zmniejszenie częstotliwosci rezonansowych.
Głownym elementem typowego tłumika tarciowego jest bezwładnik ( bezwładna masa). Połaczony podatnie ze swobodnym
końcem wału korbowego, czyli w miejscu największych wychyleń drgań skrętnych.
Tłumiki tarciowe tłumią drgania różnej częstotliwości, a ich skuteczność zależy od masy bezwładnika oraz od rodzaju złącza
tarciowego.
Powszechnie stosowany jest tłumik olejowy, składający się z pierścieniowej, całkowicie zamkniętej obudowy, wewnątrz
której znajduje się bezwładnik. Przestrzeń pomiędzy bezwładnikiem a obudową wypełnia olej silikonowy o dużej lepkości.
Różnica w rozwiązaniach konstrukcyjnych tych tłumików polega na sposobie ciernego sprzęgnięcia się bezwładnika z jego
korpusem, a przez korpus z wałem korbowym.
Tłumik w podanym wykonaniu nie wymaga bieżącej obsługi i konserwacji a jedynie w okresach określonych przez
wytwórcę pobiera się próbki oleju na podstawie, których producent tłumika określa jego stan i termin przeglądu polegający
na wymianie oleju oraz ewentualnie pierścieni dystansowych i uszczelniających.
25
Wnioski i zalecenia.
Naprężenia skręcające w wałach korbowych, powodowane rezonansowymi drganiami skrętnymi mogą przekraczać
naprężenia dopuszczalne dla ciągłej pracy silnika.
Praca silnika z rezonansową prędkością obrotową rzędów głównych jest niedopuszczalna ze względu na możliwość
zniszczenia wału.
Wzmożone drgania skrętne występują nie tylko dla rezonansowej prędkości obrotowej, ale także w określonym przedziale
wokół jej prędkosci obrotowej.
Przedział rezonansowych prędkosci obrotowych rozciąga się symetrycznie względem n
kr
.
Szerokość przedziału krytycznej prędkości obrotowej jest tym większa, im niższy jest stopień i rząd drgań.
Podczas zwiększania prędkosci obrotowej należy możliwie szybko przejść przedział krytycznej prędkości rzędów głównych.
W tym celu, po stopniowym zwiększeniu prędkosci obrotowej silnika do zakresu krytycznego, nastawę paliwowa należy
zwiększać skokowo na obciążenie poza zakres prędkosci krytycznej.
W układach automatycznego sterowania zmianę nastawy paliwowej, uwzględniającą przejście przez zakres prędkości
krytycznej, realizuje odpowiednio zaprogramowany układ sterujący.
Podczas pracy silnika z częściowym obciążeniem ( kanały, manewry, itp.) należy także unikać rezonansowych prędkosci
obrotowych wyższych rzędów i stopni, mimo iż drgania skrętne podczas tych rezonansów są praktycznie nie odczuwalne
przez obsługę.
Należy się liczyć również z tym, że przy częściowym obciążeniu silnika prawdopodobieństwo nieprawidłowego spalania, a
tym samym nierównomiernego rozkładu mocy w poszczególnych cylindrach jest większe niż podczas obciążenia
nominalnego.
W tych warunkach rzeczywiste amplitudy drgań skrętnych mogą znacznie przekraczać wartości obliczone.