Mechanika układu tłokowo–korbowego
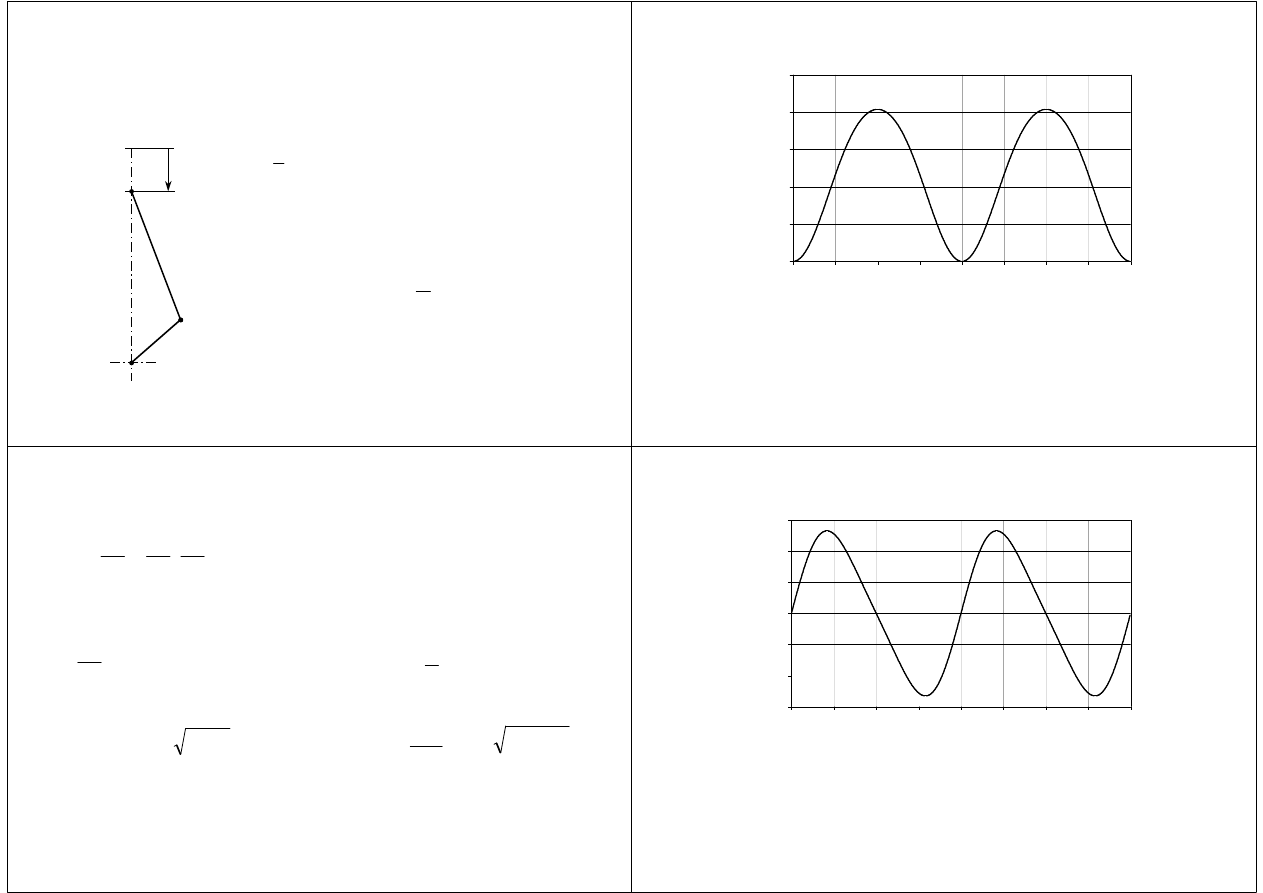
Kinematyka zbieżnoosiowego układu tłokowo–korbowego
l
r
λ
=
α
sin
r
β
sin
l
⋅
=
⋅
l
r
x
ββββ
αααα
Droga tłoka
α
⋅
−
β
⋅
−
+
=
cos
r
cos
l
r
l
x
(
)
α
−
⋅
λ
+
α
−
⋅
=
2
cos
1
4
cos
1
r
x
2
0
20
40
60
80
100
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
x
[
m
m
]
3
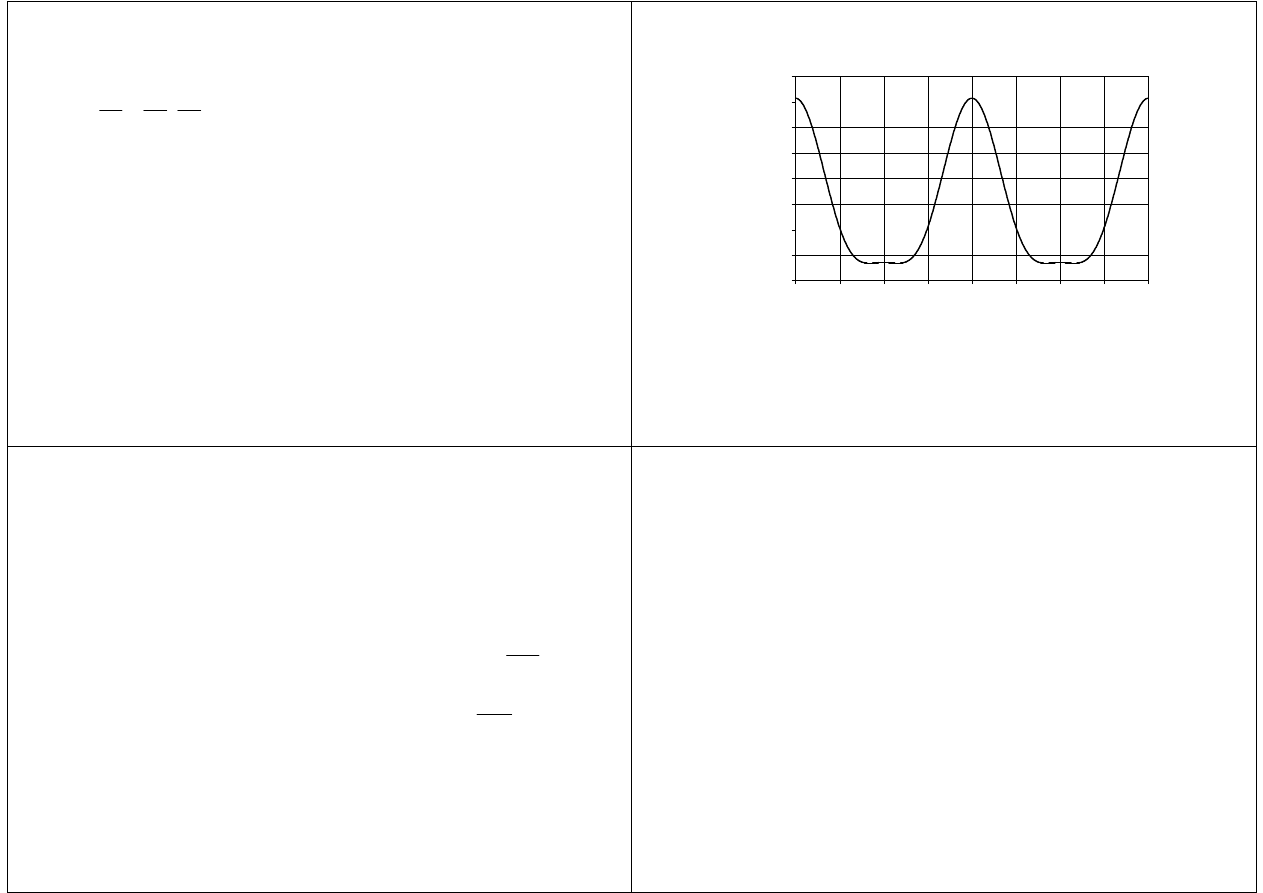
Prędkość tłoka
dt
α
d
α
d
dx
dt
dx
v
⋅
=
=
Dla n = const
const
ω
dt
α
d
=
=
⋅
+
⋅
⋅
=
α
2
sin
2
λ
α
sin
r
ω
v
2
max
λ
1
ω
r
v
+
⋅
⋅
=
dla
⋅
+
−
⋅
=
2
2
,
1
λ
8
1
1
λ
4
1
arccos
α
m
4
-30
-20
-10
0
10
20
30
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
v
[
m
/s
]
5
Przyspieszenie tłoka
dt
α
d
α
d
dv
dt
dv
a
⋅
=
=
Dla n = const
(
)
α
2
cos
λ
α
cos
r
ω
a
2
⋅
+
⋅
⋅
=
''
a
'
a
a
+
=
α
cos
r
ω
'
a
2
⋅
⋅
=
α
⋅
⋅
ω
⋅
λ
=
2
cos
r
''
a
2
6
-15000
-10000
-5000
0
5000
10000
15000
20000
25000
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
a
[
m
/s
2
]
7
(
)
λ
1
ω
r
a
2
max
+
⋅
⋅
=
dla
o
0
α
=
( )
( )
λ
1
ω
r
180
a
2
o
−
⋅
⋅
−
=
Jeżeli
25
,
0
λ
≤
to
( )
min
o
a
180
a
=
Jeżeli
25
,
0
λ
≥
to
dla
⋅
+
⋅
⋅
−
=
λ
8
1
λ
ω
r
a
2
min
λ
⋅
−
=
α
4
1
arccos
8
Dynamika układu tłokowo–korbowego
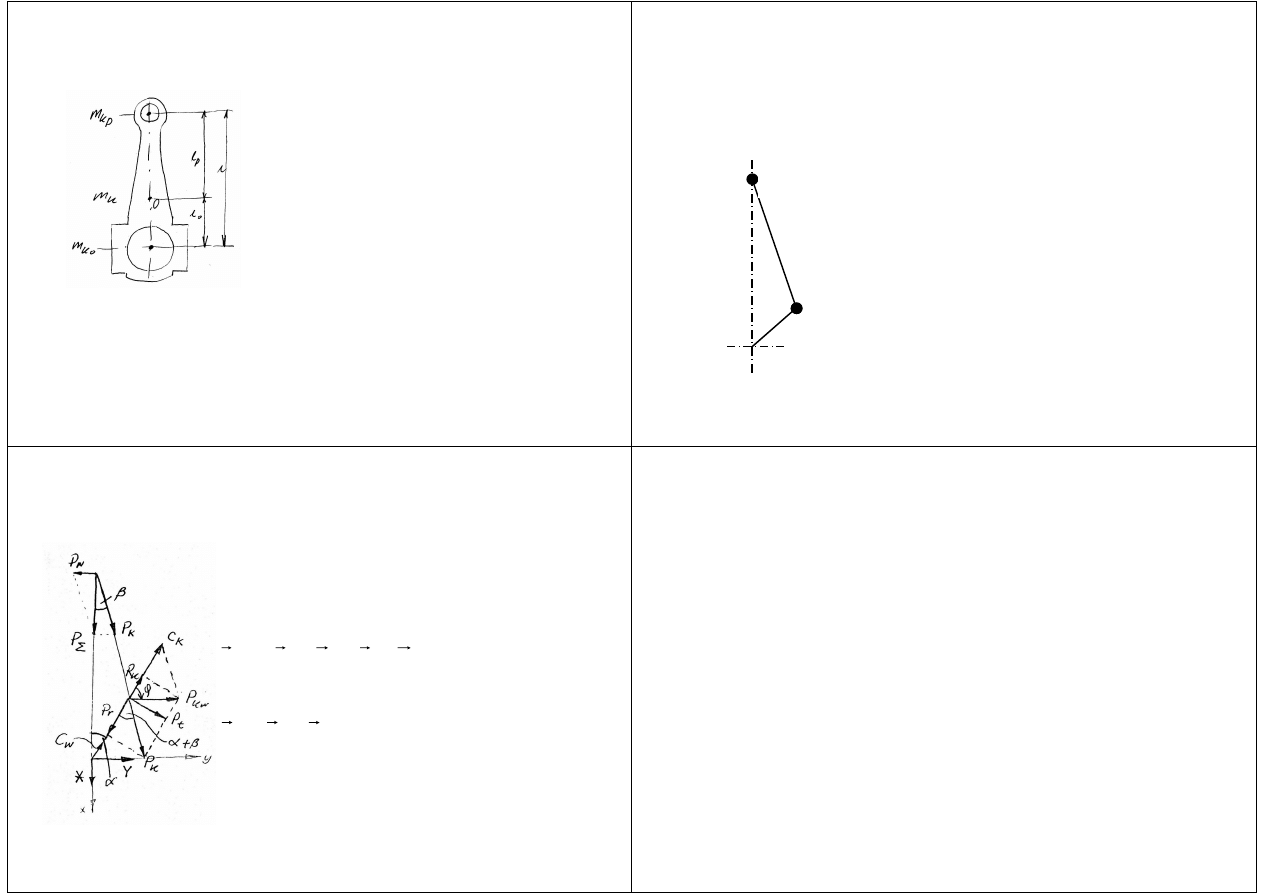
Redukcja mas w układzie tłokowo–korbowym
1.
Ciała wykonujące ruch postępowy.
Redukcja do punktu przecięcia osi sworznia tłokowego z osią
cylindra.
Masa tłoka kompletnego – m
tk
.
Masa innych części wykonujących ruch płaski, zredukowana do
masy punktu wykonującego ruch postępowy.
2.
Ciała wykonujące ruch obrotowy.
Redukcja do punktu przecięcia osi czopa korbowego
z płaszczyzną zawierającą oś cylindra i oś ramienia wału
korbowego.
Masa wykorbienia – m
w
.
9
3.
Ciała wykonujące złożony ruch płaski (zespół korbowodu).
Środek masy korbowodu kompletnego – O.
m
pk
– masa ciała wykonującego ruch
postępowy,
m
ko
– masa ciała wykonującego ruch
obrotowy.
J
o
– moment bezwładności korbowodu
względem punktu O.
Postulaty:
1.
ko
kp
k
m
m
m
+
=
2.
o
ko
p
kp
l
m
l
m
⋅
=
⋅
3.
2
o
ko
2
p
kp
o
l
m
l
m
J
⋅
+
⋅
=
10
Przyjmuje się
(
)
k
kp
m
3
,
0
25
,
0
m
⋅
÷
=
Wynik redukcji mas w układzie tłokowo–korbowym
kp
tk
p
m
m
m
+
=
ko
w
o
m
m
m
+
=
m
p
m
o
11
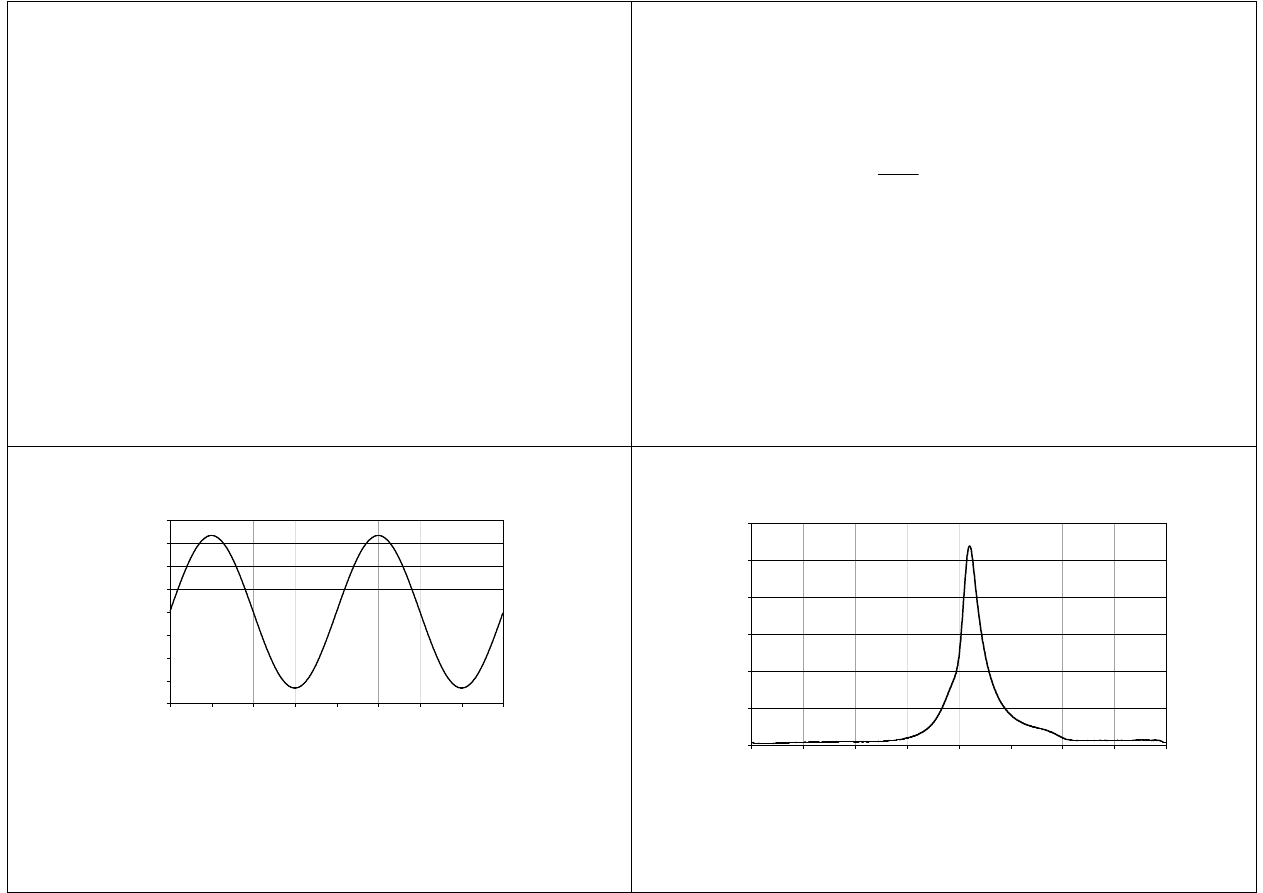
Rozkład sił w układzie tłokowo–korbowym
(
)
4
/
D
π
p
p
P
2
c
o
g
g
⋅
⋅
−
=
a
m
P
p
b
⋅
−
=
b
g
Σ
P
P
P
+
=
φ
cos
/
P
P
Σ
k
=
β
tg
P
P
Σ
N
⋅
=
k
t
k
k
kw
R
P
C
P
P
+
=
+
=
2
ko
k
r
m
C
ω
⋅
⋅
=
2
k
2
t
2
kw
R
P
P
+
=
r
t
k
P
P
P
+
=
2
r
2
t
2
k
P
P
P
+
=
(
)
β
α
sin
P
P
k
t
+
⋅
=
(
)
β
α
cos
P
P
k
r
+
⋅
=
(
)
β
α
cos
P
C
P
C
R
k
k
r
k
k
+
⋅
−
=
−
=
12
k
w
w
R
C
R
+
=
α
sin
P
α
cos
R
X
t
w
⋅
+
⋅
−
=
α
cos
P
α
sin
R
Y
t
w
⋅
+
⋅
=
13
(
)
(
)
(
)
[
]
(
)
(
)
(
)
(
)
[
]
(
)
(
)
Σ
+
α
⋅
+
−
=
β
⋅
+
α
⋅
+
−
=
=
α
⋅
β
+
α
+
α
⋅
β
+
α
⋅
+
α
⋅
+
−
=
=
α
⋅
β
+
α
⋅
+
α
⋅
β
+
α
⋅
−
+
−
=
=
α
⋅
β
+
α
⋅
+
α
⋅
+
−
=
P
cos
C
C
cos
P
cos
C
C
sin
sin
cos
cos
P
cos
C
C
sin
sin
P
cos
cos
P
C
C
sin
sin
P
cos
R
C
X
k
w
k
k
w
k
k
w
k
k
k
w
k
k
w
(
)
(
)
(
)
[
]
(
)
(
)
(
)
(
)
[
]
(
)
(
)
N
k
w
k
k
w
k
k
w
k
k
k
w
k
k
w
P
sin
C
C
sin
P
sin
C
C
cos
sin
sin
cos
P
sin
C
C
cos
sin
P
sin
cos
P
C
C
cos
sin
P
sin
R
C
Y
+
α
⋅
+
−
=
β
⋅
+
α
⋅
+
−
=
=
α
⋅
β
+
α
+
α
⋅
β
+
α
−
⋅
+
α
⋅
+
=
=
α
⋅
β
+
α
⋅
+
α
⋅
β
+
α
⋅
−
+
=
=
α
⋅
β
+
α
⋅
+
α
⋅
+
=
14
Moment indykowany dla jednego cylindra
t
i
P
r
M
⋅
=
Moment indykowany dla silnika wielocylindrowego
( )
( )
∑
=
+
⋅
−
⋅
=
c
1
i
o
t
Σ
i
α
c
720
1
i
P
r
α
M
15
-20
-15
-10
-5
0
5
10
15
20
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
ββββ
[
o
]
16
0
1
2
3
4
5
6
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
p
g
[
M
P
a
]
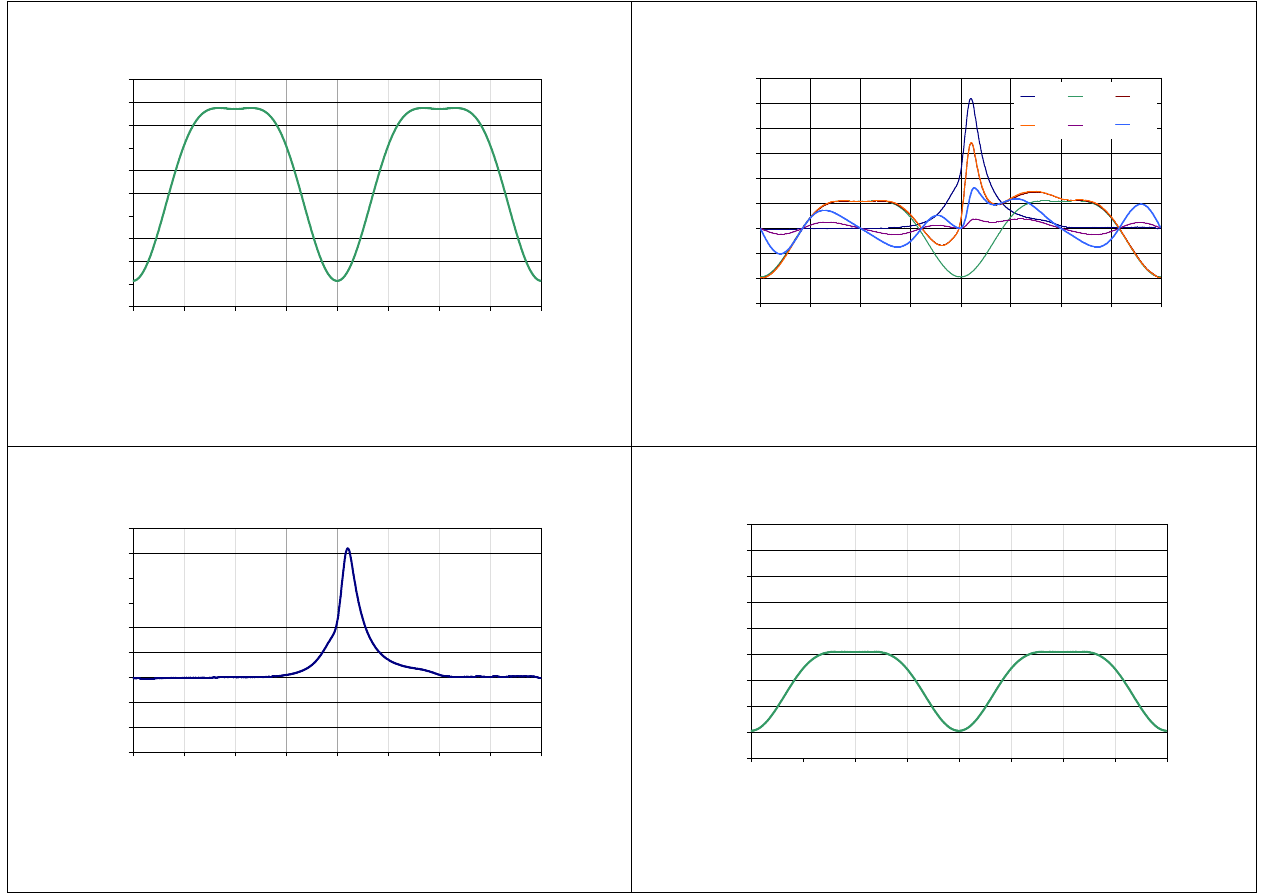
17
-12
-10
-8
-6
-4
-2
0
2
4
6
8
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
b
[
k
N
]
18
-15
-10
-5
0
5
10
15
20
25
30
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
g
,
P
b
,
P
ΣΣΣΣ
,
P
k
,
P
t
[
k
N
]
Pg
Pb
PS
Pk
PN
Pt
P
ΣΣΣΣ
P
g
P
b
P
k
P
N
P
t
19
-15
-10
-5
0
5
10
15
20
25
30
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
g
[k
N
]
20
-15
-10
-5
0
5
10
15
20
25
30
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
b
[
k
N
]
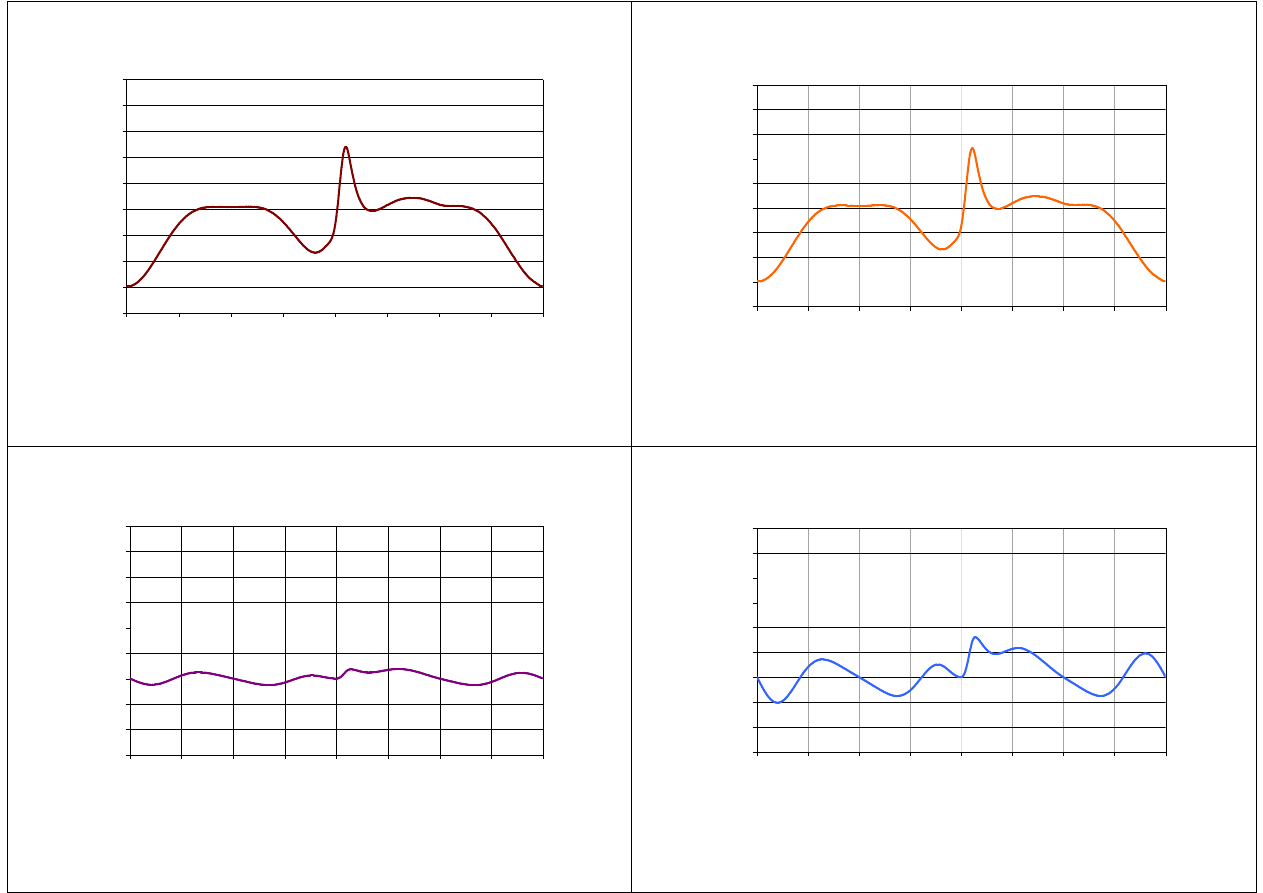
21
-15
-10
-5
0
5
10
15
20
25
30
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
ΣΣΣΣ
[
k
N
]
22
-15
-10
-5
0
5
10
15
20
25
30
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
k
[
k
N
]
23
-15
-10
-5
0
5
10
15
20
25
30
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
N
[
k
N
]
24
-15
-10
-5
0
5
10
15
20
25
30
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
t
[
k
N
]
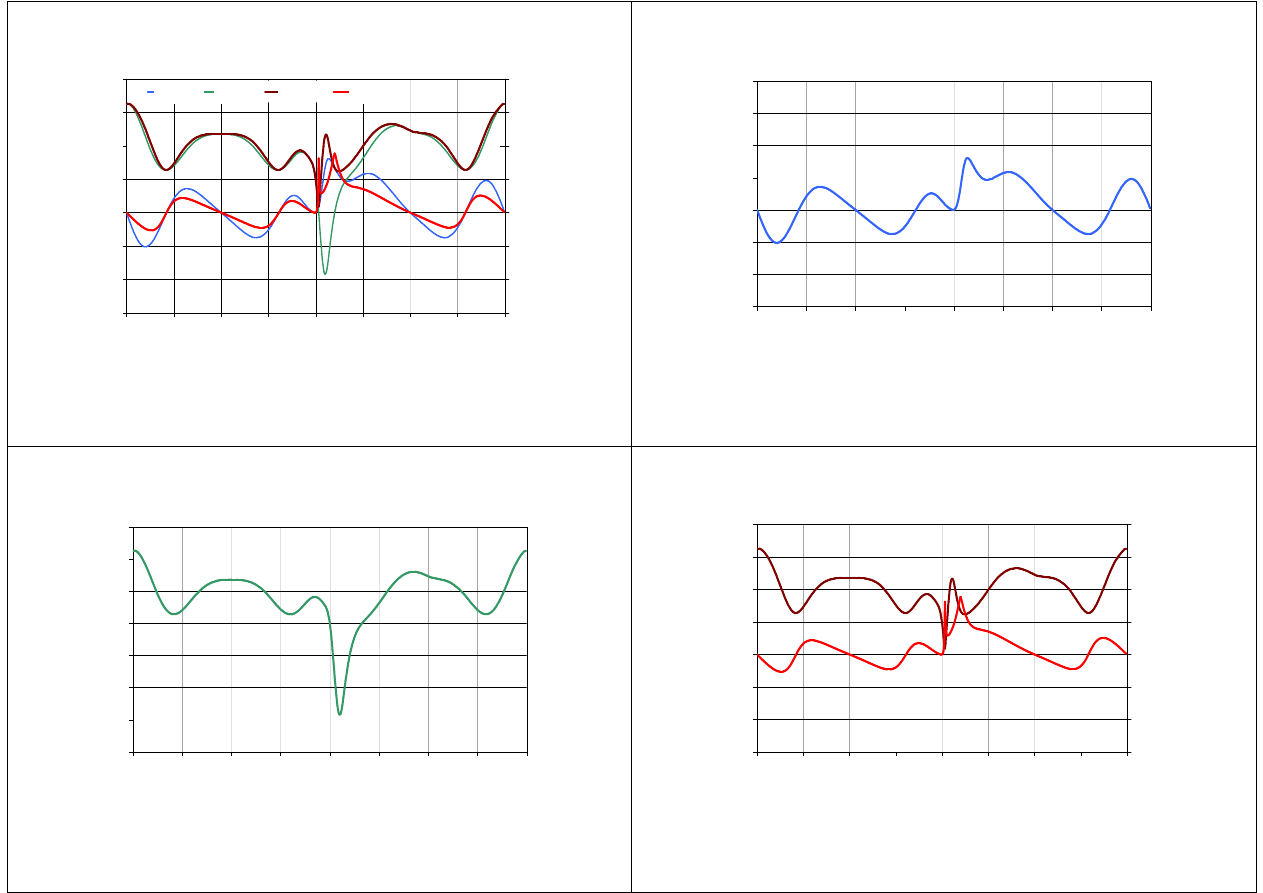
25
-15
-10
-5
0
5
10
15
20
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
t
,
R
k
,
P
k
w
[
k
N
]
-150
-100
-50
0
50
100
150
200
φφφφ
[
o
]
Pt
Rk
Pkw
f
P
t
R
k
P
kw
φφφφ
26
-15
-10
-5
0
5
10
15
20
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
t
[
k
N]
27
-15
-10
-5
0
5
10
15
20
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
R
k
[
k
N
]
28
-15
-10
-5
0
5
10
15
20
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
P
k
w
[
k
N
]
-150
-100
-50
0
50
100
150
200
φφφφ
[
o
]
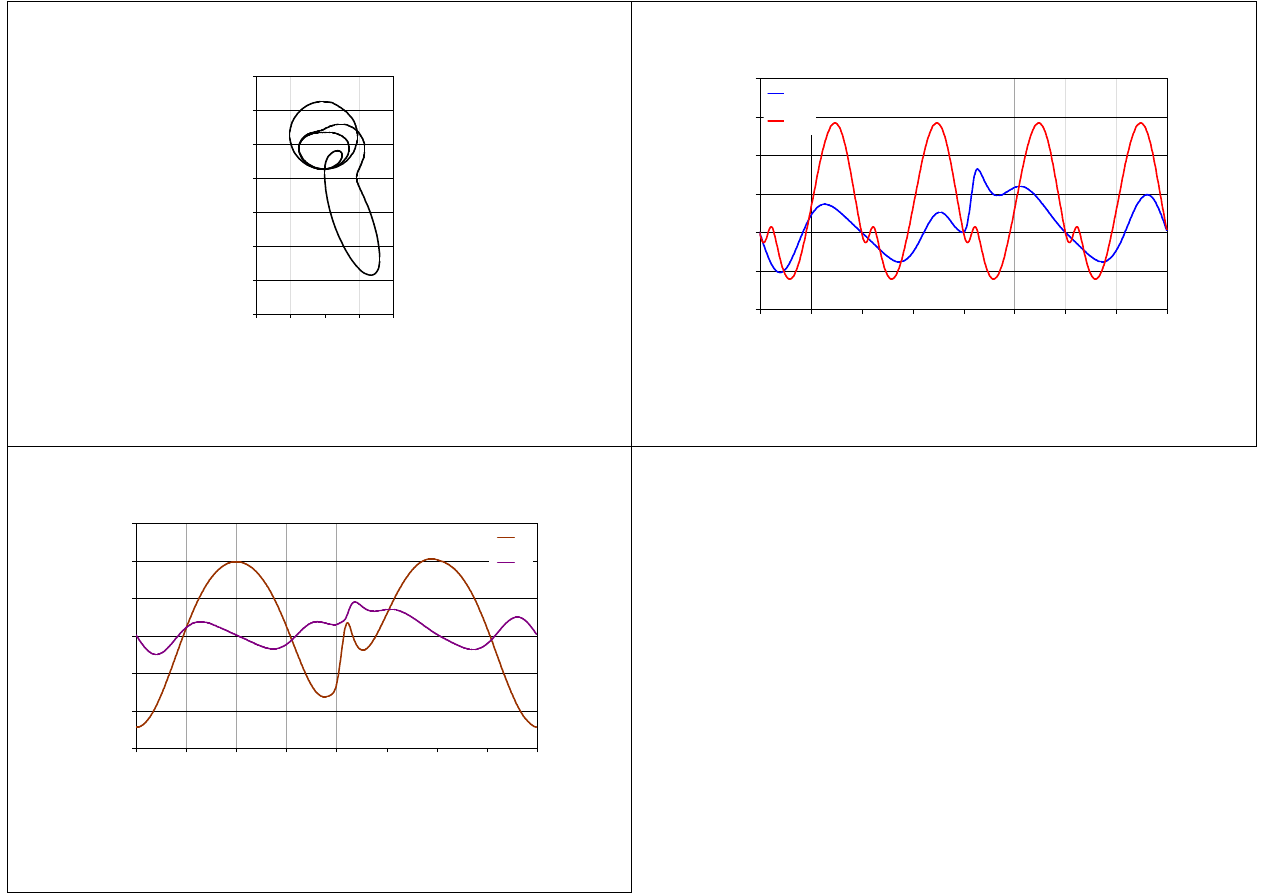
29
-15
-10
-5
0
5
10
15
20
-10
-5
0
5
10
P
t
[kN]
R
k
[
k
N
]
30
-0,4
-0,2
0
0,2
0,4
0,6
0,8
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
M
i
,
M
i
ΣΣΣΣ
[
k
N
·m
]
Mi
MiS
M
i
M
i
ΣΣΣΣ
31
-30
-20
-10
0
10
20
30
-360
-270
-180
-90
0
90
180
270
360
α [
α [
α [
α [
οοοο
OWK
]]]]
X
,
Y
[
k
N
]
X
Y
Wyszukiwarka
Podobne podstrony:
PRACA DOM. nr 2 Mech.ukł. korb. 03-04, MECHANIKA UKŁADU TŁOKOWO KORBOWEGO
MECHANIKA UKŁADU TŁOKOWO KORBOWEGO
Montaz ukladu tlokowo korbowego, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, wsm1,
DEMONTAZ UKLADU TLOKOWOkwit, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola1, I
Montaż układu tłokowo-korbowego, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola
Łożyska układu tłokowo-korbowego, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, wsm1,
Montaz ukladu tlokowego, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola1, III,
Montaż układu tłokowo-korbowego3, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkol
Montaż układu tłokowo-korbowego2, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkol
Montaz ukladu tlokowo korbowego, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, wsm1,
instrukcja bhp na stanowisku ko Nieznany
18 Mit mityzacja mitologie wsp Nieznany (2)
04 18 belki i ramy zadanie 18id Nieznany (2)
BADANIE UKLADU REGULACJI CIAGLE Nieznany (2)
Przegląd układu tłokowo – korbowego silnika MAN B&W – L 2330 H
instrukcja bhp na stanowisku ko Nieznany (3)
18 ROZ warunki tech teleko Nieznany (2)
więcej podobnych podstron