Zeszyty Problemowe – Maszyny Elektryczne Nr 77/2007

 

257

Robert Rossa 

BOBRME Komel, Katowice 

    

POPRAWA CHARAKTERYSTYK ELEKTROMECHANICZNYCH 

SILNIKÓW SynRM POPRZEZ WPROWADZENIE MAGNESÓW 

TRWAŁYCH DO WIRNIKA 

 

IMPROVEMENT OF ELECTROMECHANICAL CHARACTERISTICS  

OF SynRM BY THE USE OF PERMANENT MAGNETS IN ROTOR

 

 

Abstract: This paper deals with comparison of electromechanical characteristics of SynRM and PMSynRM of 
the same mechanical size. First the constructions of SynRM and PMSynRM are described shortly. Then the field 
circuit  method of PMSM parameters calculation,  known as   loading  method [3 ÷ 5], is described. This  method 
after same changes have been used for calculation of electromechanical characteristics presented in the paper. It 
is shown, that inserting of permanent  magnets into the rotor of SynRM results in a significant improvement of 
motor  performance.  Especially  the  maximal  value  of  synchronous  torque  T

S.max

  can  be  two  times  higher  in 

PMSynRM,  still  having  better  power  factor  and  efficiency.  It  is  shown  that  electromechanical  characteristics 
cos

ϕ

 = f(P

m

) and 

η

 = f(P

m

) of PM-SynRM are better for the all range of loads comparing to SynRM.. 

 
1. Wstęp  –  konstrukcja  silników  SynRM 
i PMSynRM 

Od  pewnego  czasu  w  Polsce  produkowane  są 
synchroniczne  silniki  reluktancyjne  (skrót  ang. 
SynRM)  o  konstrukcji  bazującej  na  blachach 
z seryjnych  silników  indukcyjnych  (Rys. 1.a). 
Rozruch  silników  SynRM  odbywa  się  poprzez 
bezpośrednie przyłączenie uzwojenia stojana do 
sieci  dzięki  obecności  klatki  rozruchowej 
w wirniku.  Silniki  SynRM  charakteryzują  się 
stosunkowo  niską  ceną  jak  na  silniki  synchro-
niczne,  co  wynika  z  prostoty  konstrukcji 
i zastosowania  podzespołów  silników  induk-
cyjnych.  Mają  one  jednakże  kilka  istotnych 
wad:  charakteryzują  się  niewielką  wartością 
maksymalną  momentu  synchronicznego  T

S.max

, 

niskim  współczynnikiem  mocy  cos 

ϕ

,  ich  moc 

znamionowa  P

N

  w typoszeregu  jest  obniżona 

o jeden stopień w stosunku do silnika indukcyj-
nego o tych samych wymiarach gabarytowych. 
W  celu  poprawy  charakterystyk  elektromecha-
nicznych  silników  SynRM  w  BOBRME  „Ko-
mel”  podjęto  prace  nad  konstrukcją  tzw.  syn-
chronicznego  silnika  reluktancyjnego  dowzbu-
dzanego  magnesami  trwałymi  (skrót  ang.  PM-
SynRM),  pokazaną  na  Rys.1.b.  Konstrukcja  ta 
jest  rozwinięciem  konstrukcji  produkowanych 
w  Polsce  silników  SynRM  bazujących  na  pod-
zespołach silników indukcyjnych [1, 2]. 
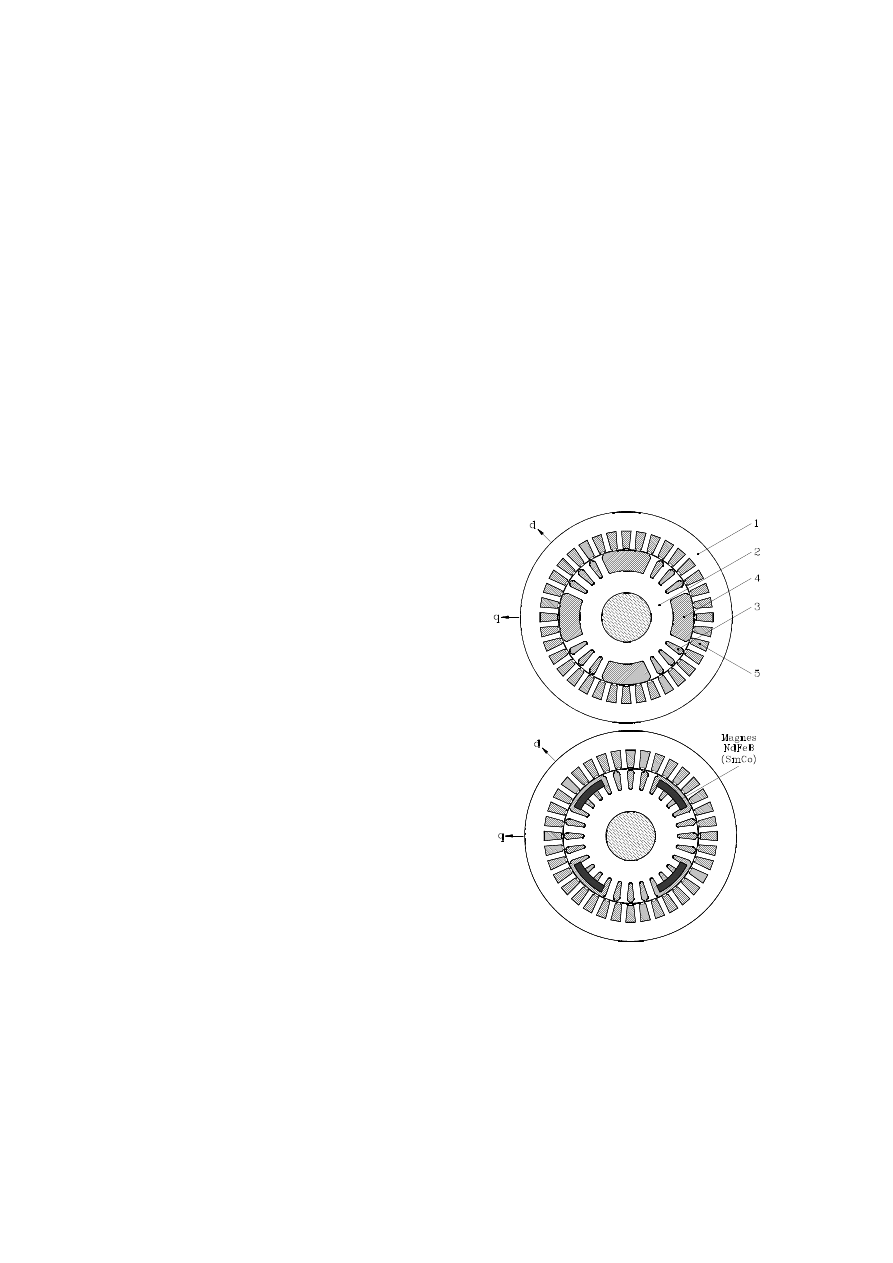
Stojan  silnika  PMSynRM  z  Rys.1.b  jest  kon-
strukcyjnie identyczny jak stojan silnika induk-
cyjnego,  zarówno  pod  względem  wykroju  bla-
chy jak i typu uzwojenia. 

 

 

Rys.1. Przekroje  poprzeczne  silników  SynRM 
(a) i PMSynRM (b) 

Blacha  wirnika  ma  wycięte  kilka  zębów  na 
każdej podziałce biegunowej, a w miejscach po 
wyciętych  zębach  wstawiono  magnesy  trwałe 
NdFeB  (lub  SmCo).  Wirnik  posiada  ponadto 
uzwojenie klatkowe odlewane z aluminium, za-
pewniające  asynchroniczny  moment  rozru-
chowy.  W  wirniku  silnika  z  Rys. 1.b  można 
wyróżnić dwie osie magnetyczne: 

a) 

b) 

Zeszyty Problemowe – Maszyny Elektryczne Nr 77/2007

 

258

•  oś „d” leżącą na kierunku wyciętych zębów 

i magnesów  trwałych,  jest  to  oś  w  której 
obwód  magnetyczny  ma  dużą  reluktancję 
1/

Λ

d

  (przenikalność  magnetyczna  względna 

aluminium  oraz  magnesów  NdFeB  lub 
SmCo jest w przybliżeniu równa jedności); 

•  oś  „q”  leżącą  na  kierunku  pozostawionych 

zębów  wirnika,  jest  to  oś  w  której  obwód 
magnetyczny ma małą reluktancję 1/

Λ

q

. 

Z  analizy  teoretycznej  parametrów  silników 
SynRM  i  PMSynRM  opartej  na  teorii  maszyn 
synchronicznych wynika, iż wprowadzenie wy-
sokoenergetycznych  magnesów  trwałych  do 
obwodu wirnika, jak pokazano na Rys. 1.b, po-
winno przyczynić się do znacznej poprawy cha-
rakterystyk  elektromechanicznych  silnika  PM-
SynRM  przy  pracy  synchronicznej  w  stosunku 
do silnika SynRM o tej samej wielkości mecha-
nicznej  i  prędkości  synchronicznej.  Powinna 
nastąpić 

m.in. 

poprawa 

charakterystyk: 

P

ei

 = f(

δ

i

),  cos

ϕ

 = f(P

m

), 

η

 = f(P

m

)).  Aby  to 

potwierdzić,  opracowano  w  BOBRME  „Ko-
mel”  algorytmy  i  programy  do  obliczania  cha-
rakterystyk 

elektromechanicznych 

silników 

SynRM i PMSynRM przy pracy synchronicznej. 
Opracowane  algorytmy  obliczeniowe  bazują  na 
zastosowaniu  tzw.  metody  polowo-obwodowej 
obciążeniowej, omówionej w punkcie 2 artykułu 
[3 ÷ 5].  W  wyniku  ich  zastosowania  możliwe 
jest bezpośrednie porównanie różnorodnych cha-
rakterystyk  elektromechanicznych  obu  typów 
silników.  Wyniki  porównania  wybranych  cha-
rakterystyk omówiono w punkcie 3 artykułu. 

2. Metoda polowo-obwodowa obciążenio-
wa 

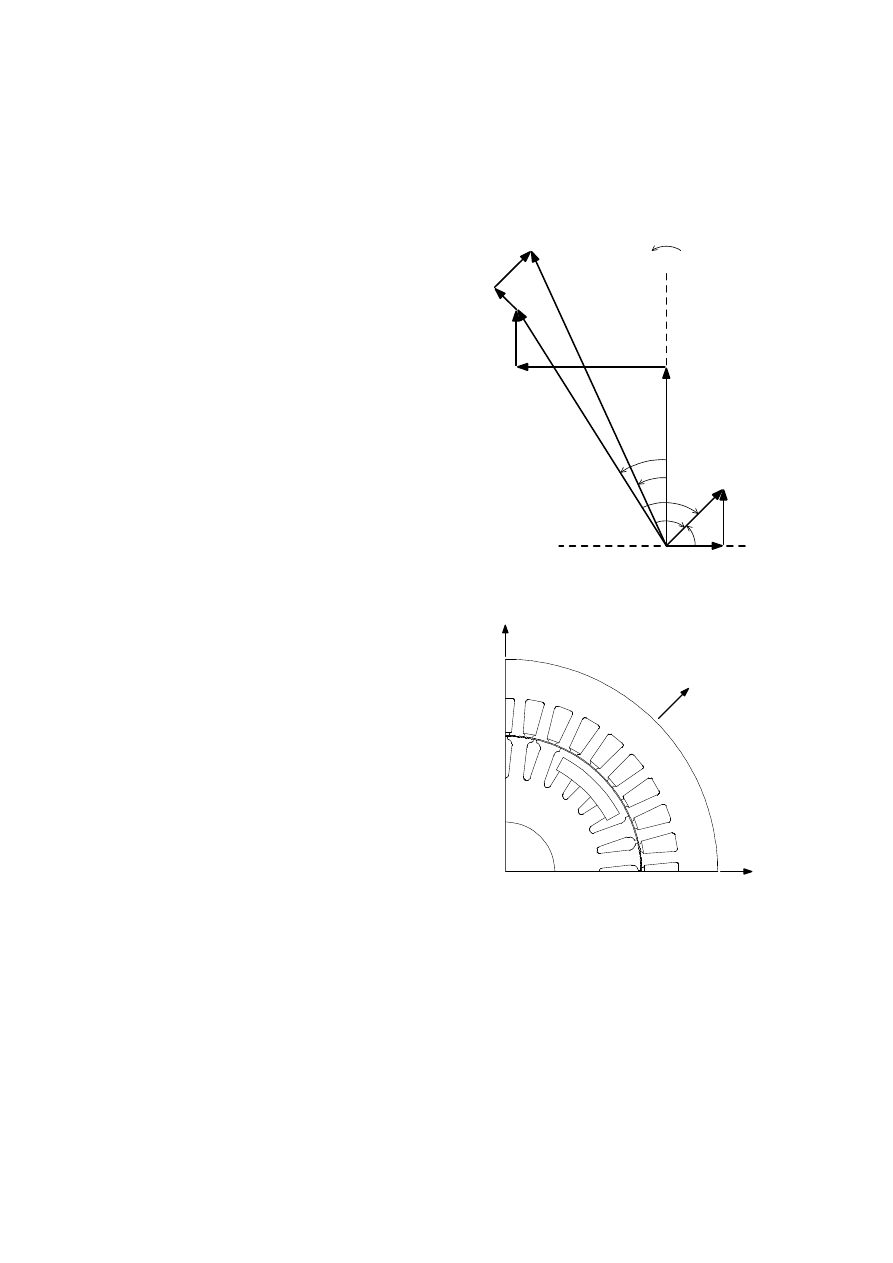
W  metodzie  polowo  –  obwodowej  obciążenio-
wej, charakterystyki elektromechaniczne silnika 
PMSynRM  (lub  ogólniej  PMSM)  dla  pracy 
synchronicznej  obliczane  są  w  oparciu  o kla-
syczne  równania  silnika  synchronicznego,  wy-
nikające z jego schematu zastępczego i wykresu 
wskazowego  dla  układu  współrzędnych dq0 
(Rys. 2).  Parametry  skupione  wykresu  wskazo-
wego  mające  zasadniczy  wpływ  na  pracę  sil-
nika  synchronicznego:  reaktancja  magnesująca 
w osi podłużnej X

md

 i poprzecznej X

mq

 oraz na-

pięcie  E

0

  indukowane  w  uzwojeniu  twornika 

przez wirujące magnesy trwałe, obliczane są dla 
poszczególnych punktów pracy silnika z wyko-
rzystaniem 

stałoprądowej, 

dwuwymiarowej 

analizy  MES  rozkładu  pola  magnetycznego  na 
przekroju poprzecznym maszyny. Przy oblicza-

niu  w/w parametrów  skupionych  uwzględniana 
jest ich zależność od aktualnego obciążenia sil-
nika,  tzn.  od  aktualnych  dla  analizowanego 
punktu pracy poziomów nasycenia w obwodzie 
magnetycznym silnika. 

I

d

I

q

I

1

E

0

V

1

E

i

jI

d 

X

md

jI

1 

X

l

I

1 

R

1

oś d

δ

ϕ

β

δ

i

ϕ

i

oś q

kierunek obr.

jI

q 

X

mq

 

Rys.2. Wykres  wskazowy  silnika  synchronicz-
nego (w tym PMSynRM) 

Oś d wirnika,

Oś fazy A

A+

N

Oś q

S

Oś q

A−

B−

C+

C+

B−

A+

B−

C+

A−

 

Rys.3.   Model  silnika  PMSynRM  w  dziedzinie 
MES.  Ze  względu  na  symetrię  obwodu  elektro-
magnetycznego  model  obejmuje  jedną  po-
działkę biegunową 

Idea  metody  polowo  –  obwodowej  obciążenio-
wej 

bazuje 

na 

możliwości 

obliczenia, 

z wykorzystaniem  modelu  silnika  w dziedzinie 
MES,  modułu  wskazu  napięcia  szczelinowego 
E

i

  oraz  kąta  fazowego 

δ

i

 + π/2  tegoż  wskazu, 

odpowiadających  aktualnemu  przy  danym  ob-
ciążeniu 

rozkładowi 

pola 

magnetycznego 

w silniku,  zakładając  że  znany  jest  moduł  I

1

 

Zeszyty Problemowe – Maszyny Elektryczne Nr 77/2007

 

259

oraz  kąt  fazowy 

β

  wskazu  prądu  stojana 

(Rys. 2). 
Model  MES  silnika  jest  tak  przygotowywany, 
że  oś  fazy  A  uzwojenia  stojana  (wybrana  jako 
faza  odniesienia)  pokrywa  się  z  osią  d  wirnika 
(Rys. 3).  Wówczas  jeśli  założy  się,  że  model 
MES będzie odpowiadać chwili czasowej t = 0, 
a  wartość  chwilowa  prądu  fazy  A  opisana  jest 
zależnością: 

 

)

cos(

2

)

(

1

A

β

ω +

⋅

⋅

=

t

I

t

i

 

(1) 

to  występujący  w  (1)  kąt  fazowy 

β

  wskazu 

prądu  I

1

  odpowiada  jednocześnie  kątowi  prze-

strzennemu  pomiędzy  wektorem  przepływu 
stojana  F

s

  a  wektorem  przepływu  wzbudzenia 

F

f

. Dzięki temu w modelu MES silnika uprasz-

cza  się  pozycjonowanie  przepływu  stojana  F

s

 

względem osi d wirnika [4]. Ze względu na sy-
metrię  obwodu  magnetycznego  model  MES 
obejmuje  tylko  jedną  podziałkę  biegunową  sil-
nika. 
Po  obliczeniu  w  MES  rozkładu  pola  magne-
tycznego na przekroju poprzecznym silnika dla 
zadanego  modułu  prądu  I

1

  i  kąta 

β

,  obliczany 

jest  następnie  rozkład  przestrzenny  wzdłuż 
szczeliny  powietrznej  wektorowego  potencjału 
magnetycznego  A

Z

(x),  gdzie  x  oznacza  pozycję 

wzdłuż obwodu szczeliny powietrznej. Rozkład 
ten  odpowiada  wypadkowemu  dla  danego 
punktu  pracy  silnika  strumieniowi  w  szczelinie 
powietrznej 

Φ

,  wynikającemu  ze  współdziała-

nia  przepływów  wzbudzenia  F

f

  i  stojana  F

s

 

(Rys. 4). 

 

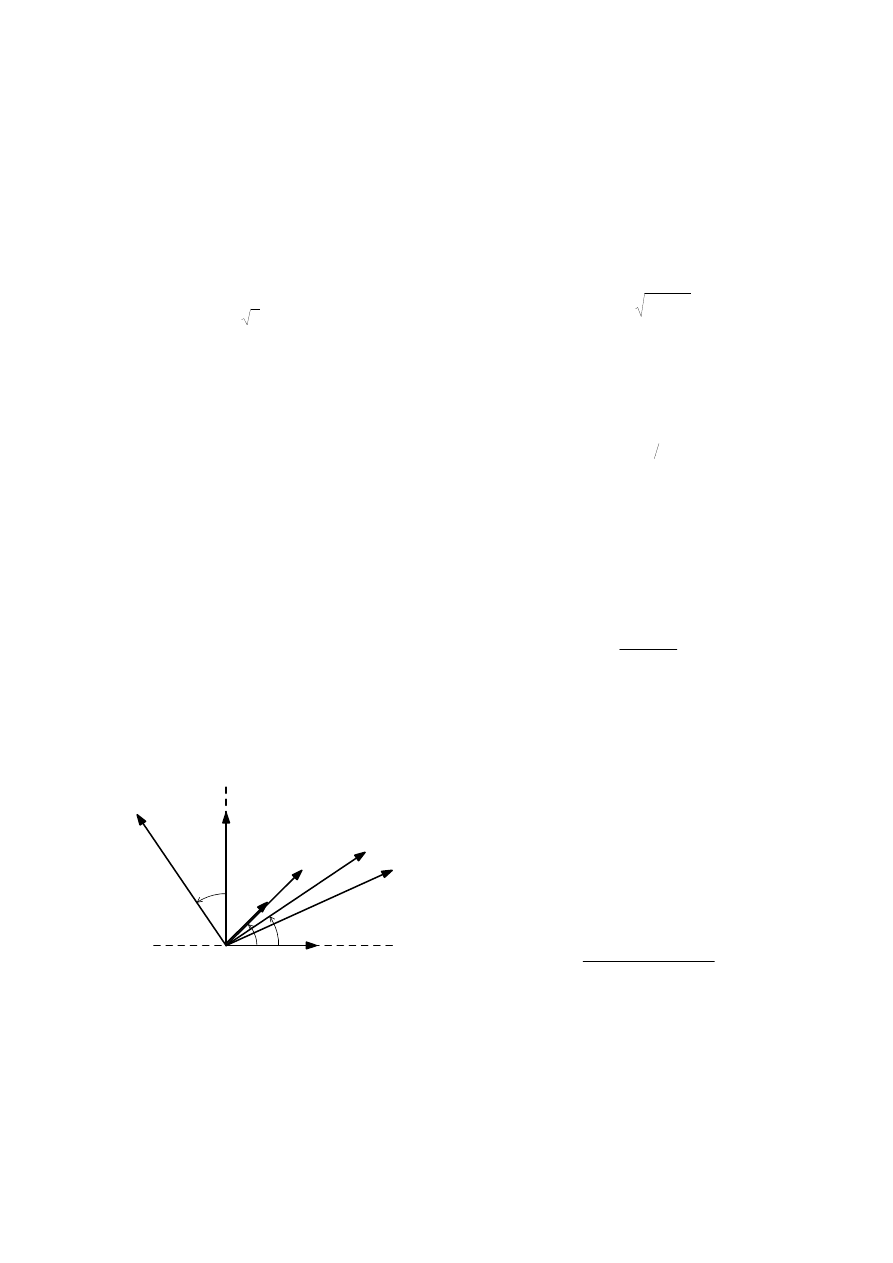
I

1

E

0

E

i

oś q

oś d

δ

i

F

s

β

δ

i

F

f

F

δ

δδ

δ

oś fazy A

Φ

Φ

Φ

Φ

 

Rys.4. Wykres 

przepływów 

i 

strumienia 

z zaznaczeniem kątów 

β

 i 

δ

i

 

Obliczony rozkład przestrzenny potencjału ma-
gnetycznego  A

Z

(x)  odpowiadający  jednej  po-

działce  biegunowej  silnika  poddawany  jest 
analizie  harmonicznej,  w  celu  obliczenia 
współczynników  szeregu  Fouriera  a

1

  i  b

1

  dla 

jego  podstawowej  harmonicznej.  Współczyn-
niki  a

1

  i  b

1

  reprezentują    odpowiednio  połowę 

strumienia  magnetycznego  w  osi  podłużnej  sil-
nika 

Φ

d

  oraz  połowę  strumienia  w  osi  po-

przecznej 

Φ

q

 [3 ÷5].

 

Znając współczynniki a

1

 i b

1

 obliczany jest wy-

padkowy strumień magnetyczny 

Φ

 w szczelinie 

powietrznej  silnika,  odpowiadający  zadanemu 
modułowi prądu I

1

 oraz zadanemu kątowi fazo-

wemu wskazu prądu 

β

: 

 

2

1

2

1

2

b

a

L

Φ

Fe

+

⋅

⋅

=

 

(2) 

gdzie L

Fe

 to długość czynna pakietu żelaza. Na-

stępnie  obliczane  jest  napięcie  szczelinowe  E

i

 

oraz  kąt  fazowy 

δ

i

  wektora  strumienia  wypad-

kowego 

Φ

 w szczelinie powietrznej: 

 

s

u

i

k

k

z

f

E

⋅

⋅

⋅

⋅

⋅

=

1

1

1

44

.

4

Φ

 

(3) 

 

(

)

1

1

a

b

arctg

i

=

δ

 

(4) 

We  wzorze  (3)  f

1

  oznacza  częstotliwość  prądu 

stojana, z

1

  liczbę  zwojów  szeregowych  w  fazie 

uzwojenia,  k

u1

  i  k

s

  odpowiednio  współczynnik 

uzwojenia i skosu. 
Znając  moduł  napięcia  szczelinowego  E

i

  oraz 

kąt  fazowy 

δ

i

,  obliczana  jest  na  podstawie  za-

leżności  (5)  reaktancja  magnesująca  w  osi  po-
przecznej X

mq

 dla danego punktu pracy silnika: 

 

β

δ

sin

sin

1

⋅

⋅

=

I

E

X

i

i

mq

 

(5) 

W celu  obliczenia  reaktancji  X

md

  i napięcia  E

0

 

zakłada  się  liniowość  równań  maszyny  wokół 
obliczanego punktu pracy. Przy takim założeniu 
można  nieznacznie  (2 ÷ 5 %)  zwiększyć  moduł 
prądu  obciążenia  I

1

  o  przyrost 

∆

I

1

  w modelu 

MES  silnika,  przyjmując  że  zmiana  ta  nie 
wpłynie  na  zmianę  stanu  nasycenia  obwodu 
magnetycznego  [3 ÷ 5].  Po  dodatkowym  obli-
czeniu  w  MES  rozkładu  pola  w  silniku  dla  I

1

’ 

oraz po obliczeniu E

i

’ i 

δ

i

’ można, na podstawie 

równań  (6)  i  (7),  obliczyć  parametry  schematu 
zastępczego  X

md

    i  E

0

,  odpowiadające  danemu 

punktowi pracy silnika: 

 

β

β

δ

δ

cos

cos

cos

cos

'

1

1

'

'

⋅

−

⋅

⋅

−

⋅

=

I

I

E

E

X

i

i

i

i

md

 

(6) 

 

md

i

i

X

I

E

E

⋅

⋅

−

⋅

=

β

δ

cos

cos

1

0

 

(7) 

W  przedstawionej  metodzie  kąt  fazowy 

β

 

wskazu prądu fazowego jest wielkością zadaną. 
Jeśli  analizowany  silnik  jest  zasilany  ze  źródła 
prądowego to znany jest również moduł wskazu 
prądu  I

1

.  Natomiast  w  przypadku  zasilania  sil-

nika  ze  źródła  napięciowego  moduł  wskazu 
prądu I

1

 musi być obliczony iteracyjnie, tak aby 

Zeszyty Problemowe – Maszyny Elektryczne Nr 77/2007

 

260

spełnione  było  równanie  napięciowe  silnika. 
Obliczenia  iteracyjne  można  wykonać  np.  me-
todą  Newtona  –  Raphsona  lub  tzw.  metodą 
siecznych [4].  
Po iteracyjnym obliczeniu modułu prądu obcią-
żenia  I

1

  oraz  odpowiadających  mu  parametrów 

E

i

, 

δ

i

, obliczane są dalej: 

•  kąt mocy 

δ

 w oparciu o zależność: 

1

1

1

1

1

cos

sin

sin

sin

R

I

X

I

E

V

i

i

⋅

⋅

−

⋅

⋅

+

⋅

=

⋅

β

β

δ

δ

  (8) 

•  współczynnik mocy cos

ϕ

 : 

 

δ

β

δ

β

ϕ

sin

cos

cos

sin

cos

⋅

−

⋅

=

 

(9) 

•  moc elektryczna P

ei

 w szczelinie powietrznej 

silnika: 

(

)

i

i

i

I

I

E

P

δ

β

δ

β

sin

cos

cos

sin

3

1

1

ei

⋅

⋅

−

⋅

⋅

⋅

⋅

=

  (10) 

•  moc elektryczna wejściowa P

1

: 

(

)

δ

β

δ

β

sin

cos

cos

sin

3

1

1

1

1

⋅

⋅

−

⋅

⋅

⋅

⋅

=

I

I

V

P

  (11) 

•  moc mechaniczna na wale P

m

: 

 

m

ei

m

P

P

P

∆

−

=

 

(12) 

•  sprawność η: 

 

1

m

P

P

=

η

 

(13) 

W  opracowanym  algorytmie  obliczeń  charak-
terystyk  elektromechanicznych  uwzględniono 
także wpływ strat w żelazie 

∆

P

Fe

. Straty 

∆

P

Fe

 są 

obliczane osobno i są uwzględnione w schema-
cie zastępczym silnika jako dodatkowy rezystor 
[6]. 

3. Porównanie  charakterystyk  elektro-
mechanicznych PMSynRM i SynRM 

W  celu  porównania  charakterystyk  elektrome-
chanicznych  silników  SynRM  i  PMSynRM  tej 
samej  wielkości  mechanicznej,  obliczono  wy-
brane  charakterystyki  silnika  SynRM  typu 
RSh80-4BM1  (wielkość  mechaniczna  80 mm, 
2p=4,  Rys. 1.a)  oraz  silnika  PMSynRM  2p=4 
o identycznym wykroju blach stojana i wirnika, 
o tej  samej  długości  pakietu  żelaza  i  o  takiej 
samej  wysokości  szczeliny  powietrznej  (patrz 
Rys. 1.b).  Silnik  typu  RSh80-4BM1  był  wcze-
śniej  zaprojektowany,  wykonany  i  przebadany 
w BOBRME  „Komel”.  Stwierdzona  w  wyniku 
obliczeń  elektromagnetycznych  i  badań  opty-
malna  liczba  zwojów  uzwojenia  stojana  wyno-
siła dla tego silnika z

1

 = 402 i taką liczbę zwo-

jów  przyjęto  do  obliczeń  charakterystyk  elek-
tromechanicznych  zamieszczonych  niżej.  W 
wirniku  silnika  SynRM  wycięte  było  syme-
trycznie  po  trzy  zęby  na  każdej  podziałce  bie-

gunowej,  jak  pokazano  na  Rys. 1.b.  W  modelu 
silnika PMSynRM w miejscu wyciętych zębów 
wirnika  umieszczono  magnesy  NdFeB  typu 
N33SH,  namagnesowane  odpowiednio  dla 
2p=4. 
Obliczenia  charakterystyk  elektromechanicz-
nych silnika SynRM, podobnie jak silnika PM-
SynRM,  wykonano  metodą  polowo-obwodową 
obciążeniową,  po  odpowiednim  zmodyfikowa-
niu  rozwiązywanych  w  niej  równań,  stosownie 
do  schematu  zastępczego  silnika  SynRM.  Na 
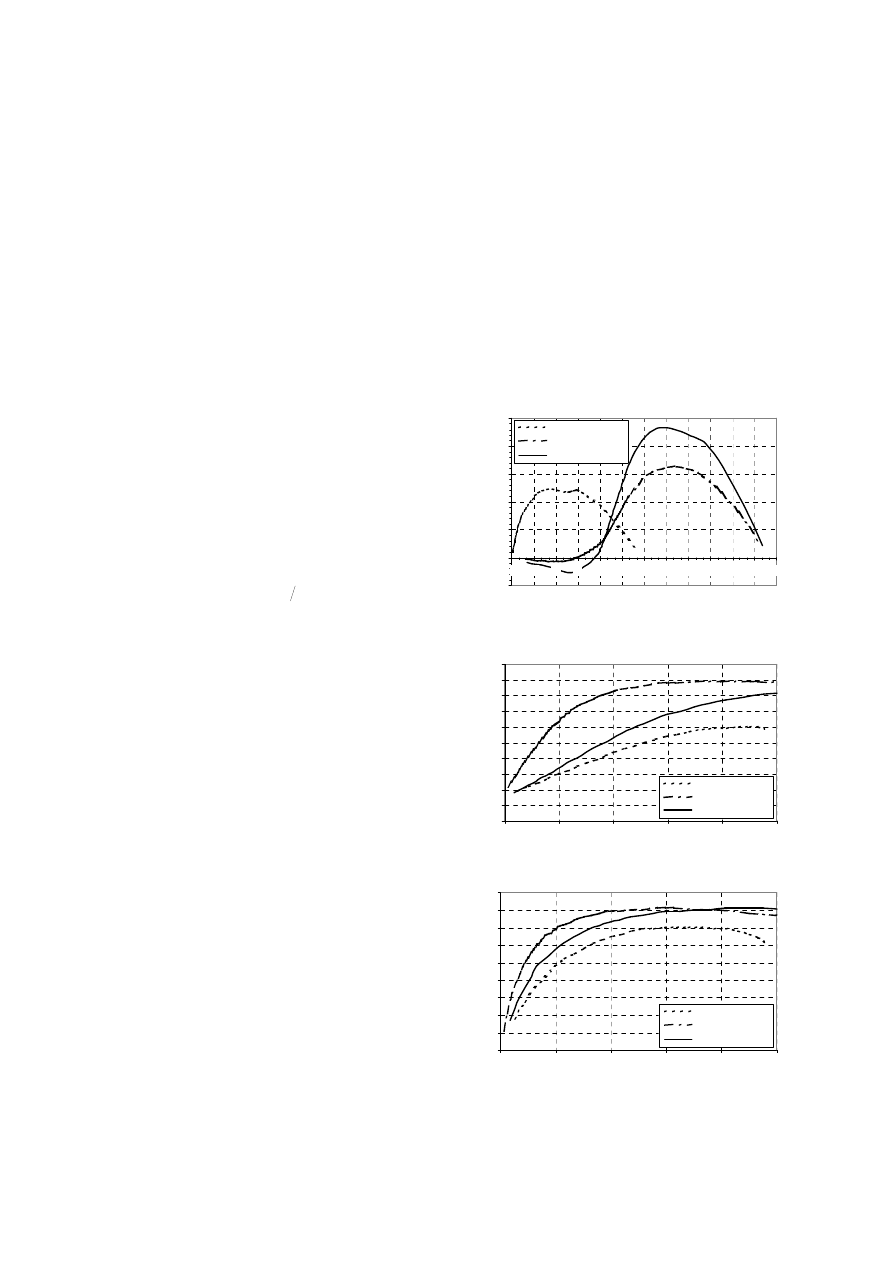
Rys. 5 ÷ 9  przedstawiono  porównanie  wybra-
nych  obliczonych  charakterystyk  elektrome-
chanicznych silników PMSynRM i SynRM. 

 

-500

0

500

1000

1500

2000

2500

0

15

30

45

60

75

90

105 120 135 150 165 180

delta_i

P

e

i

RSh80-4BM1

PMSynRM  z1=486

PMSynRM  z1=402

 

Rys.5. Porównanie  charakterystyk  P

ei

 = f(

δ

i

) 

silników SynRM i PMSynRM 

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

0

250

500

750

1000

1250

Pm

c

o

s

  ϕϕϕϕ

RSh80-4BM1

PMSynRM  z1=486

PMSynRM  z1=402

 

Rys.6. Porównanie charakterystyk cos

ϕ

 = f(P

m

) 

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0

250

500

750

1000

1250

Pm

ηηηη

RSh80-4BM1

PMSynRM  z1=486

PMSynRM  z1=402

 

Rys.7. Porównanie charakterystyk 

η

 = f(P

m

) 

Zeszyty Problemowe – Maszyny Elektryczne Nr 77/2007

 

261

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0

250

500

750

1000

1250

Pm

c

o

s

  ϕϕϕϕ

 *

  ηηηη

RSh80-4BM1

PMSynRM  z1=486

PMSynRM  z1=402

 

Rys.8. Porównanie charakterystyk 

cos

ϕ

 

⋅η

 = f(P

m

)

 

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

0

250

500

750

1000

1250

1500

1750

2000

Pm

I1

RSh80-4BM1

PMSynRM z1=486

PMSynRM z1=402

 

Rys.9. Porównanie charakterystyk I

1

 = f(P

m

) 

Tabela 1. Porównanie  obliczonych  i  zmierzo-
nych  parametrów  silnika  PMSynRM  2p = 4, 
wielkości mechanicznej 80 mm i silnika SynRM 
typu  RSh80-4BM1  dla:  z

1

 = 402,  U

LL

 = 400 V, 

n = 1500 obr/min. 

 

Obciążenie 

Bieg jałowy 

Typ sil-

nika 

P 

W 

T 

N⋅⋅⋅⋅m 

T

S.max

 

N⋅⋅⋅⋅m 

I

 (400V)

 

A 

η

η

η

η

 

--- 

cos

ϕ

ϕ

ϕ

ϕ

 

--- 

I

0 (400V)

 

A 

cos

ϕ

ϕ

ϕ

ϕ

0

 

--- 

RSh80-

4BM1 

obliczenia 

550 

3.5 

7.4 

2.6 

0.66  0.46  2.65  0.15 

RSh80-

4BM1 

pomiar 

550 

3.5 

6.6 

2.72  0.62  0.47  2.68  0.15 

PMSynRM 

obliczenia 

550 

3.5 

14.6 

1.9 

0.74  0.57  2.07  0.15 

PMSynRM 

pomiar 

550 

3.5 

12.3  2.01  0.72  0.55  2.23  0.15 

 

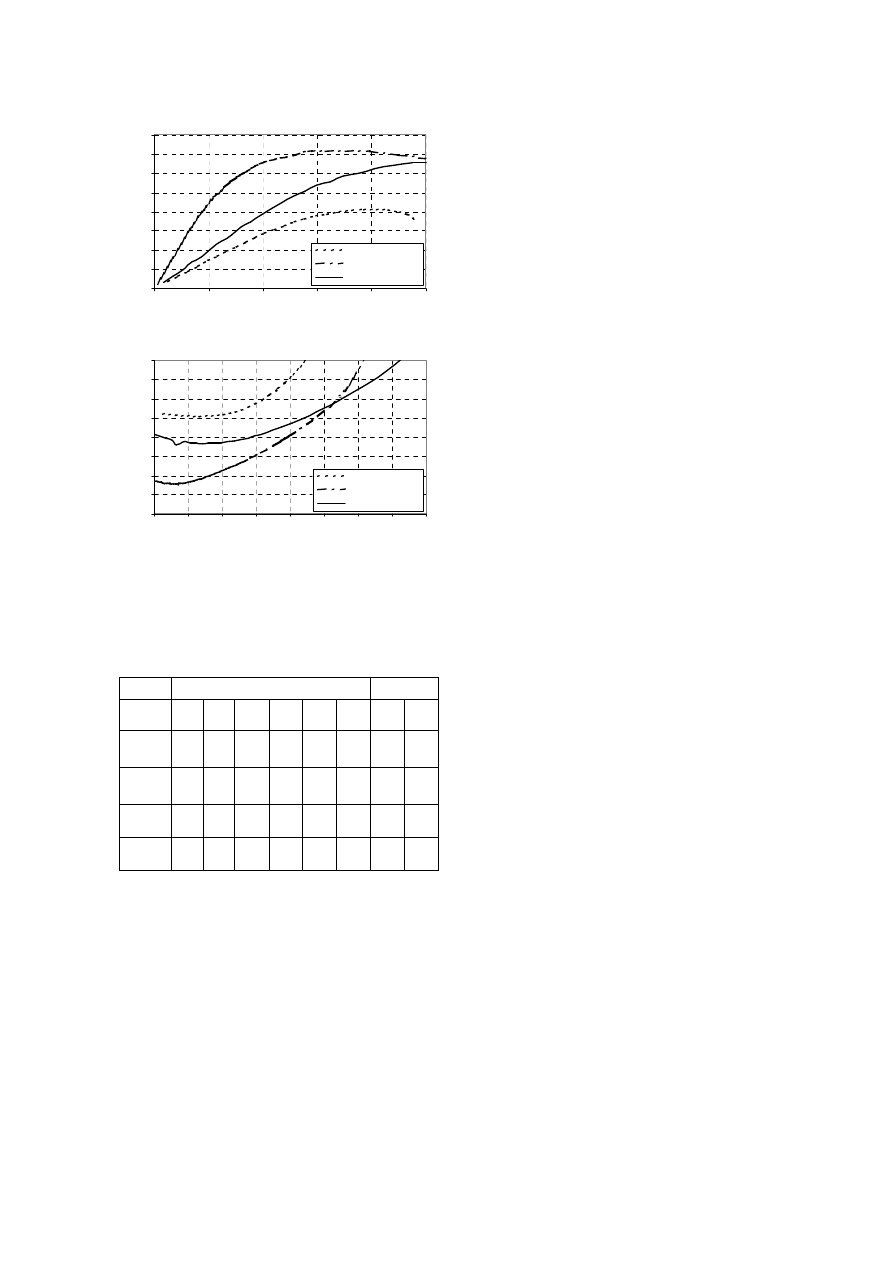
Analizując  charakterystyki  z  Rys. 5 ÷ 9  można 
stwierdzić,  że  wprowadzenie  magnesów  trwa-
łych do wirnika silnika SynRM w sposób poka-
zany na Rys. 1.b wpływa zdecydowanie na po-
prawę  parametrów  silnika.  Z  Rys. 7  widać,  iż 
przy  zachowaniu  tej  samej  liczby  zwojów  sze-
regowych z

1

 w silniku PMSynRM, maksymalna 

moc  szczelinowa  P

ei

,  a  zatem  także  moment 

synchroniczny  maksymalny  T

S.max

,  są  dla  tego 

silnika  o  około  100 %  większe  w  stosunku  do 
silnika  SynRM.  Dla  całego  zakresu  obciążeń 
mocą  P

m

,  silnik  PMSynRM  charakteryzuje  się 

lepszym  współczynnikiem  mocy  cos

ϕ

  oraz 

wyższą  sprawnością 

η

.  Korzystniejsze  charak-

terystyki  cos

ϕ

 = f(P

m

)  oraz 

η

 = f(P

m

)  silnika 

PMSynRM  przekładają  się  na  zdecydowanie 
korzystniejsze  charakterystyki  cos

ϕ

 ∗

η

 = f(P

m

) 

oraz  I

1

 = f(P

m

)  (Rys. 8 i 9).  Moc  znamionowa 

P

N

  silnika  PMSynRM  może  być  podniesiona 

w stosunku  do  mocy  znamionowej  silnika 
SynRM  (dla  PMSynRM  nie  ma  konieczności 
obniżania  mocy  P

N

  o  jeden  stopień  w  typosze-

regu w stosunku do silnika indukcyjnego, jak to 
miało  miejsce  w  przypadku  SynRM).  Zwięk-
szenie  liczby  zwojów  z

1

  w  silniku  PMSynRM, 

tak  aby  uzyskać  podobną  wartość  maksymalną 
momentu  synchronicznego  T

S.max

  jak  w  silniku 

SynRM skutkuje dalszą, znaczącą poprawą cha-
rakterystyk  elektromechanicznych  cos

ϕ

 = f(P

m

) 

i 

η

 = f(P

m

). Powyższe wnioski z wyników obli-

czeń  charakterystyk  elektromechanicznych  zo-
stały  potwierdzone  badaniami  laboratoryjnymi 
w  BOBRME  „Komel”  (patrz  Tabela 1) 
na modelu fizycznym PMSynRM. 

Literatura 

[1] T. Glinka,  M. Jakubiec,  A. Wieczorek,  Silnik 
asynchroniczny  synchronizowany  momentem  reluk-
tancyjnym,  Wiadomości  Elektrotechniczne,  Nr 
2/2001. 
[2] T. Glinka,  M. Jakubiec,  A. Wieczorek,  Wpływ 
rozwiązań  konstrukcyjnych  obwodu  elektromagne-
tycznego  na  parametry  silnika  asynchronicznego 
synchronizowanego 

momentem 

reluktancyjnym, 

Wiadomości Elektrotechniczne, Nr 6/2001. 
[3] M.A. Rahman,  P. Zhou,  Determinatiom  of  Satu-
rated  Parameters  of  PM  Motors  Using  Loading 
Magnetic  Fields,  IEEE  Trans.  on  Magnetics,  Vol. 
MAG-27, No. 5, pp. 3947-3950, Sep. 1991. 
[4] M.A. Rahman, P. Zhou, Field-Based Analysis for 
Permanent  Magnet  Motors,  IEEE  Trans.  on  Mag-
netics,  Vol.  MAG-30,  No.  5,  pp.  3664-3667,  Sep. 
1994. 
[5] P. Zhou,  M.A. Rahman,  M.A. Jabbar,  Field  Cir-
cuit  Analysis  of  Permanent  Magnet  Synchronous 
Motors,  IEEE  Trans.  on  Magnetics,  Vol. MAG-30, 
No. 4, pp. 1350-1359, July 1994. 
[6] V.B. Honsinger, Performance of Polyphase Per-
manent  Magnet  Machines,  IEEE  Trans.  on  Power 
Apparatus and Systems, Vol. PAS-99, No. 4, 1980. 

Praca  powstała  w  wyniku  realizacji  projektu 
badawczego nr 3 T10A 041 28 

Autor 

dr inż. Robert Rossa, 
info@komel.katowice.pl 
Branżowy Ośrodek Badawczo-Rozwojowy 
Maszyn Elektrycznych „KOMEL” 
40-203 Katowice, al. Roździeńskiego 188.