Konferencja Krynicka 1998

Edward MACIĄG

*)

Tadeusz TATARA

**)

Maciej WOJTASIEWICZ

***)

REAKCJA DYNAMICZNA NISKIEGO TYPOWEGO

BUDYNKU MUROWEGO NA WSTRZĄSY GÓRNICZE

1. Wstęp

Jednorodzinne, niskie budynki mieszkalne wznoszone metodą tradycyjną stanowią

liczną zabudowę na obszarach objętych wpływami dynamicznymi, do których zalicza się
m.in. wstrząsy górnicze wywołane eksploatacja górniczą węgla i rudy miedzi. Wstrząsy
górnicze są przyczyną powstawania drgań powierzchniowych oddziaływujących na obiekty
powierzchniowe.

Przybliżonej oceny szkodliwości drgań powierzchniowych dla takich budynków można

dokonać wykorzystując skale wpływów dynamicznych (SWD) zawarte w obowiązującej
normie PN-85/B-02170 [1, 2, 3]. Wykorzystanie tego sposobu nie daje jednak odpowiedzi
na pytanie, które z elementów konstrukcyjnych budynku są najbardziej wytężone, a tym
samym narażone na ewentualne uszkodzenia. Dokładniejszą ocenę wytężenia budynku
można przeprowadzić poprzez pełną analizę dynamiczną, z wykorzystaniem przebiegów
drgań. W tym celu wymagane jest przygotowanie teoretycznych modeli badanych
budynków, wykorzystanie pełnych zarejestrowanych przebiegów drgań powierzchniowych
oraz wykorzystanie odpowiedniego, “silnego" sprzętu obliczeniowego.

Referat dotyczy pełnej analizy dynamicznej niskiego, typowego dla polskich warunków

budynku jednorodzinnego, poddanego obciążeniom dynamicznym wywołanym wstrząsami
górniczymi. Rozważa się zadanie w zakresie sprężystym. Analiza objęła:

•

dobór teoretycznego modelu rzeczywistego budynku,

•

wyznaczenie cech dynamicznych budynku na podstawie jego badań w skali naturalnej
i jego teoretycznego modelu,

•

obliczenie teoretycznej odpowiedzi modelu budynku na przykładowe, rzeczywiste
pomierzone wymuszenia kinematyczne,

•

oszacowanie naprężeń w wybranych elementach konstrukcyjnych budynku na
podstawie obliczeń.

Całość obliczeń wykonana została przy użyciu programu elementów skończonych

ALGOR.

*)

Prof. Dr hab. inż. – Politechnika Krakowska

**)

Dr inż. – Politechnika Krakowska

***)

Mgr inż. – DATACOMP- Kraków

2. Badany budynek

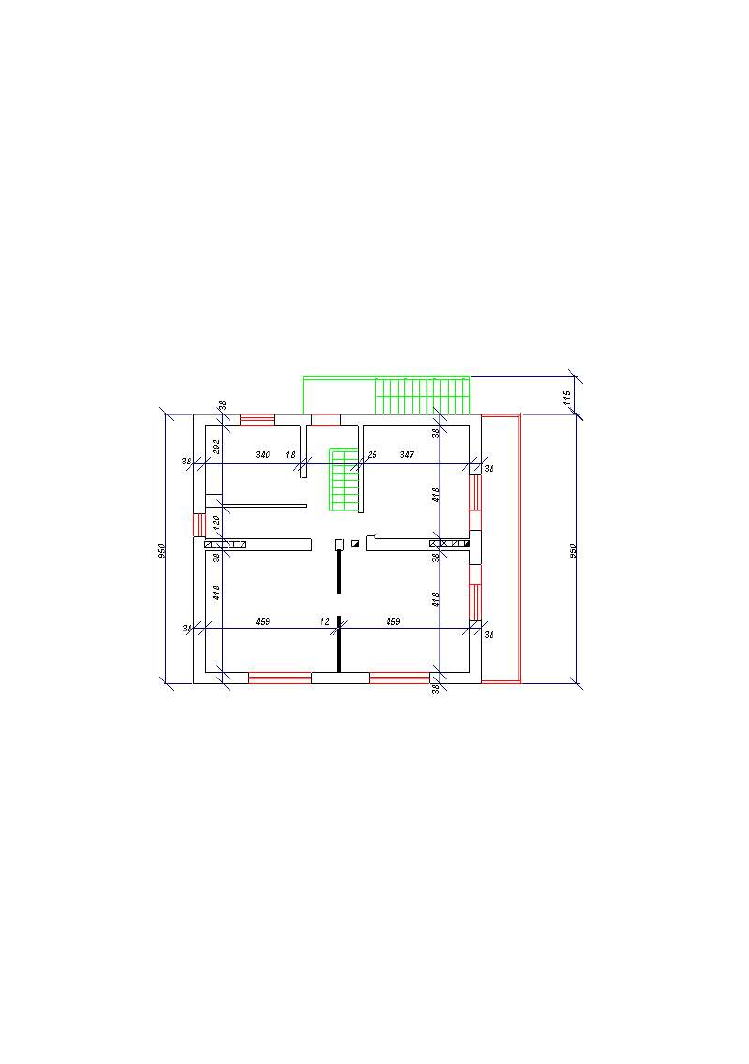
Badaniami objęto budynek murowy, dwukondygnacyjny, w całości podpiwniczony, o

poprzeczno – podłużnym układzie ścian nośnych. Podczas pierwszej serii badań budynek
był nieotynkowany, a w trakcie drugiej serii badań budynek był już otynkowany. Wymiary
rzutu poziomego budynku, jego wysokość od poziomu terenu i głębokość posadowienia
fundamentów wynoszą odpowiednio 9.50 x 10.00, 8.15 i 1.1m. Ławy fundamentowe są
betonowe, a ściany piwnic wykonano z bloczków żużlobetonowych i z cegły. Mury
zewnętrzne kondygnacji parteru i I pietra są warstwowe z bloków PGS i z cegły, a
wewnętrzne z pustaków PGS oraz z cegieł. Stropy nad piwnicami i parterem są płytowe,
żelbetowe. Przekrycie dachu stanowi stropodach wykonany z płyty żelbetowej ocieplony
żużlem. Podłoże gruntowe stanowi pospółka żwirowo - piaskowa. Rzut poziomy budynku
przedstawia rys. 1.

Rys.1

3. Opis modelu obliczeniowego

Modelowaniu fizycznemu poddano budynek opisany w p. 2, w całości otynkowany.

Elementy nośne (ściany, stropy) modelowano elementami skończonymi typu "plate/shell"
(element powłokowy, czterowęzłowy o pięciu stopniach swobody w każdym węźle),
przyjmując monolityczne połączenia żelbetowych stropów i ścian. W modelu uwzględniono
odmienne własności materiałów składowych murów, obciążenia wynikające z ciężaru
tynku, ocieplenia stropodachu oraz 40% obciążenia użytkowego zgodnie z normą [4].
Wartości współczynników charakteryzujących właściwości fizyczne materiałów przyjęto

zgodnie z normą [5]. W modelu uwzględniono wszystkie istotne z punktu widzenia
sztywności układu elementy, m.in. biegi schodów, otwory. Wpływ podłoża gruntowego
uwzględniono poprzez sprężyste zamocowanie modelu w podłożu, za pomocą elementów w
postaci sprężyn przyłożonych, w trzech kierunkach (x, y, z), w poziomie spodu
fundamentu. Charakterystyki sprężyn odpowiadały własnościom podłoża gruntowego [6].
Konstrukcję podzielono na 2400 elementów, wykorzystano 291 elementów brzegowych
modelujących podłoże gruntowe. Model posiada 2619 węzłów.

4. Cechy dynamiczne budynku

Cechy dynamiczne budynku wyznaczono na podstawie wyników wcześniejszych

pomiarów jego drgań swobodnych [7] oraz analitycznie wykorzystując jego model MES.
Kryterium przydatności modelu budynku stanowi obliczona podstawowa częstotliwość
drgań własnych (odrębnie w kierunku poprzecznym (x) i podłużnym (y)) porównywalna z
pomierzoną. Z uwagi na dużą sztywność budynku nie było możliwe uzyskanie z pomiarów
jego wyższych częstotliwości drgań własnych. W tablicy 1 zestawiono obliczone i
pomierzone częstotliwości drgań własnych. Z porównania podstawowych częstotliwości
drgań translacyjnych pomierzonych i obliczonych wynika ich dobra zgodność.

Do obliczeń przyjęto wartość ułamka tłumienia krytycznego

 = 5%; wartość ta zwykle

jest przyjmowana w budynkach murowych. Taka wartość

 jest także zgodna z zaleceniami

Eurocodu 8 [8].

Tablica 1

Częstotliwości drgań własnych [Hz]

f

1x

f

1y

f

1skr

f

2x

f

2y

z obliczeń

6.90

6.38

10.42

18.24

17.82

z pomiaru

przed
otynkowaniem

5.2

5.6 5.25.4

-

-

-

po otynkowaniu

6.4

6.3

-

-

-

5. Odpowiedzi modelu budynku na wymuszenia

kinematyczne

Jako wymuszenie kinematyczne do obliczenia odpowiedzi dynamicznej modelu

budynku wykorzystane są dwa przebiegi składowych poziomych, poprzecznej (x) i
podłużnej (y), przyspieszeń drgań zarejestrowanych w jednej ze stacji sejsmicznej w
Legnicko - Głogowskim Okręgu Miedziowym (od tego samego, reprezentatywnego
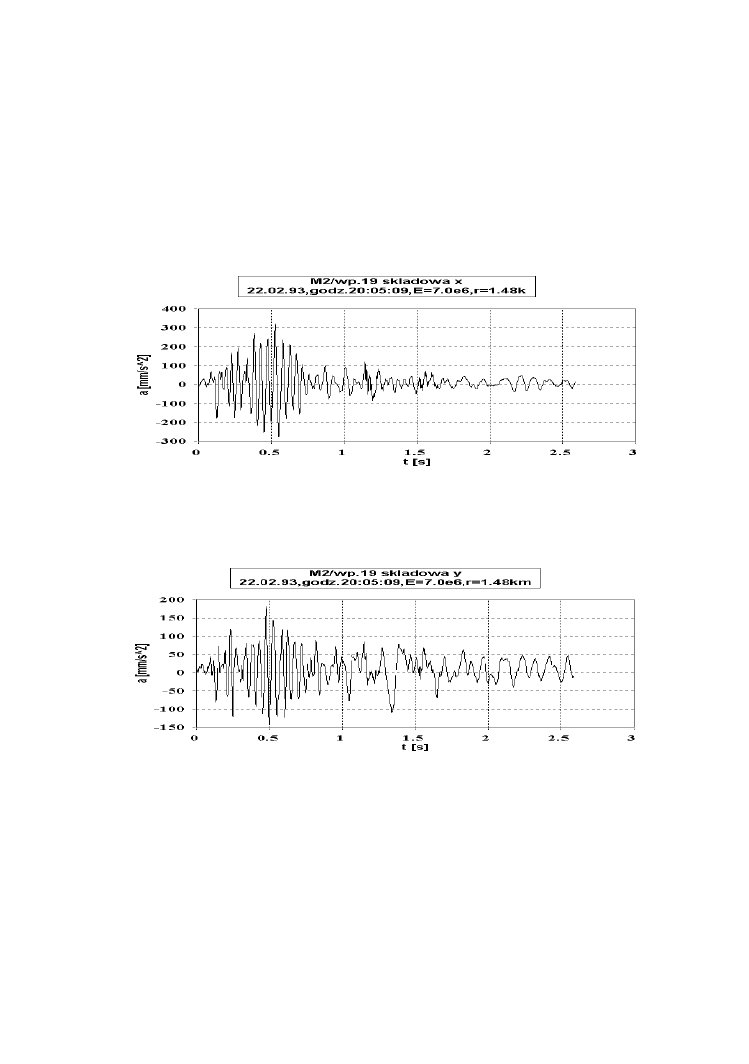
wstrząsu górniczego) - rys. 2a,b. Krok dyskretyzacji (

t) przebiegów drgań z rys. 2a i 2b

wynosi 0.002s. Maksymalne wartości przyspieszenia składowych (x) i (y) z rys. 2a i 2b
wynoszą odpowiednio 321.5 i 182 mm/s

2

i występują dla t = 0.526 oraz 0.478s, a więc z

nieznacznym przesunięciem w czasie. Najintensywniejsza faza wymuszenia, zarówno dla
składowej (x) i (y), jest krótka i wynosi ok. 0.5s – por. rys. 2a i 2b. Obie składowe drgań
charakteryzują się wysokimi dominującymi częstotliwościami w przedziale 20 – 22 Hz; dla
składowej (y) można wyróżnić również niższą dominującą częstotliwość wynoszącą ok.
6.9Hz

Obliczenia przeprowadzono zakładając:

a) działanie tylko jednej składowej wymuszenia, co jest zgodne z zaleceniami Eurocodu

8; w tym przypadku jako wymuszenie przyjęto składową (x) drgań z rys. 2a,
działającą zgodnie z kierunkiem osi poprzecznej (x) budynku – przypadek I,

b) równoczesne działanie dwóch składowych wymuszenia (x), (y) przyłożonych zgodnie z

kierunkiem odpowiednio osi poprzecznej (x) i podłużnej (y) budynku – przypadek II.
W obliczeniach wykorzystano metodę bezpośredniego całkowania równań ruchu w

a)

b)

Rys. 2

dziedzinie czasu. Celem obliczeń odpowiedzi dynamicznej modelu na przyjęte wymuszenie
kinematyczne było:

a) wyznaczenie przemieszczeń i przyspieszeń w poszczególnych węzłach modelu od I i II

przypadku wymuszenia,

b) określenie stanu wytężenia ścian budynku poprzez wyznaczenie w nich naprężeń dla I

i II przypadku wymuszenia; określano lokalizację i wartości maksymalnych naprężeń
głównych. W tym celu wyznaczano, w każdym kroku czasowym, mapy naprężeń
głównych,

c) porównanie poziomów odpowiedzi dynamicznej modelu w przypadku jedno- i

dwukierunkowego działania przyjętego wymuszenia kinematycznego.

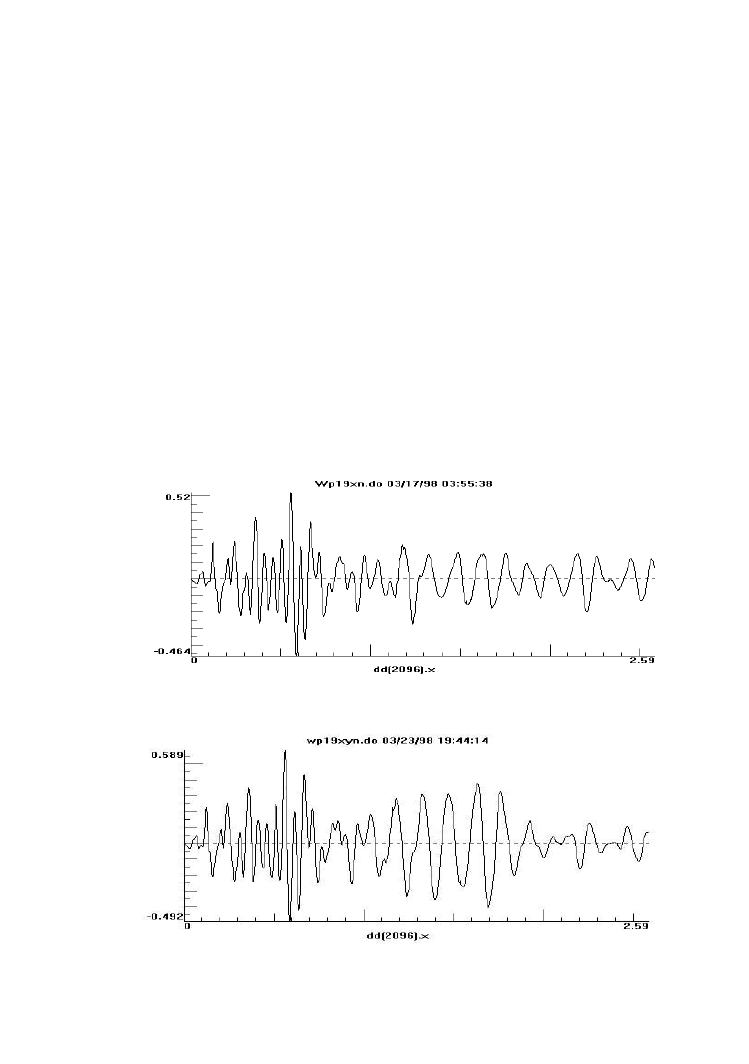
Przykładowo na rys. 3 i 4 pokazano obliczone przebiegi przyspieszenia drgań w

kierunku poprzecznym (x) jednego z naroży w poziomie dachu budynku (węzeł nr 2096),
odpowiednio od wymuszenia w przypadku I i II. Maksymalne wartości obliczonego
przyspieszenia z rys. 3 i 4 wynoszą odpowiednio 52.0 i 58.9 cm/s

2

, a więc różnią się

nieznacznie. Znacznie większe różnice w wartościach przyspieszeń od obu przypadków
wymuszenia otrzymano w kierunku (y) – odpowiednio 11.6 i 26.3 cm/s

2

. Powyższe może

być wynikiem układu poprzeczno – podłużnego ścian nośnych budynku.

Rys. 3

Rys.4

Z kolei w tablicy 2 zestawiono wartości maksymalnych naprężeń roziągających w

poszczególnych ścianach oraz czas, w którym te naprężenia wystąpiły od wymuszenia
jedno- i dwukierunkowego. Z porównania wartości tych naprężeń wynika, że w przypadku
wymuszenia dwukierunkowego, w pięciu ścianach otrzymuje się większe wartości naprężeń
niż w przypadku wymuszenia jednokierunkowego (różnice wynoszą 3.9

 90.6%). W

dwóch ścianach, wartości maksymalnych naprężeń głównych są nieco większe w
przypadku wymuszenia jednokierunkowego (różnice nie przekraczają 5%). W przypadku
wymuszenia dwukierunkowego,
maksymalne wartości naprężeń głównych w poszczególnych ścianach, pojawiają się w tym
samym lub póżniejszym czasie niż w przypadku wymuszenia jednokierunkowego (por.
Tablica 2). Najistotniejszym jest, że obliczone maksymalne naprężenia rozciągające, od
obu przypadków wymuszenia, różnią się mniej niż 4%.

Największe z maksymalnych wartości, rozciągających naprężeń głównych, w

przypadku wykorzystania wymuszenia o intensywnościach jak na rys. 2a i 2b, nie
przekraczają 75kPa, a więc są małe. Z analizy map maksymalnych naprężeń głównych dla
poszczególnych ścian (dla czasów t wykazanych w tablicy 2) wynika, że ich koncentracja
występuje przede wszystkim w poziomie piwnicy i parteru przy otworach drzwiowych i
okiennych. W tablicy 3 zestawiono miejsca lokalizacji maksymalnych naprężeń
rozciągających w poszczególnych ścianach.

Tablica 2 Wartości maksymalnych, rozciągajacych naprężeń głównych

 [kPa] w ścianach

budynku oraz czas t [s] ich pojawienia się

Nr i

oznacze-nie

ściany

Wymuszenie

Jednokierunkowe

dwukierunkowe



t



t

1

2

3

4

5

1 - (XZ 1)

24.14

0.568

29.7

1.70

2 - (XZ 2)

49.93

0.538

44.92

0.538

3 - (XZ 3)

71.67

0.62

74.45

1.44

4 - (YZ 1)

19.80

0.62

30.48

1.698

5 - (YZ 2)

59.84

0.66

57.10

0.66

6 - (YZ 3)

28.56

0.616

39.26

1.376

7 - (YZ 4)

17.07

0.538

32.53

1.458

Tablica 3 Lokalizacja maksymalnych, rozciągających naprężeń głównych w ścianach
budynku

Nr i

oznacze-nie

ściany

Wymuszenie

Jednokierunkowe

Dwukierunkowe

1

2

3

1 - (XZ 1)

w poz. Ip. przy dolnych narożach
okien

w poz. piwnicy przy narożu
okienka, w poz. stropu piwnicy na
krawędzi ściany, w poz. parteru i Ip.
przy dolnych narożach okien

2 - (XZ 2)

w poz. posadzki piwnicy przy
narożu otworu drzwiowego

w poz. posadzki piwnicy przy
dolnym narożu otworu drzwiowego
oraz w poz. piwnicy przy nadprożu
otworu drzwiowego

3 - (XZ 3)

w poz. stropu piwnicy, przy dolnej
krawedzi otworu drzwiowego

w poz. stropu piwnicy, przy dolnej
otworu drzwiowego na parterze

4 - (YZ 1)

w poz. stropu piwnicy, na krawędzi
ściany i w środku jej rozpiętości

w poz. stropu puiwnicy, na krawedzi
scian i w srodku jej rozpiętości

5 - (YZ 2)

w poz. parteru, na słupku między
otworami drzwiowymi oraz przy
otworze drzwiowym ok. Środka
wysokości

w poz. parteru, na słupku między
otworami drzwiowymi oraz przy
otworze drzwiowym ok. Środka
wysokości

6 - (YZ 3)

w poz. piwnicy, przy dolnym narożu
otworu drzwiowego

w poz. piwnicy, przy dolnym narożu
otworu drzwiowego

7 - (YZ 4)

w poz. fundamentu, przy dolnych
narożach ściany

przy wszystkich narożach otworów
okiennych w poz. piwnicy, parteru i
Ip.

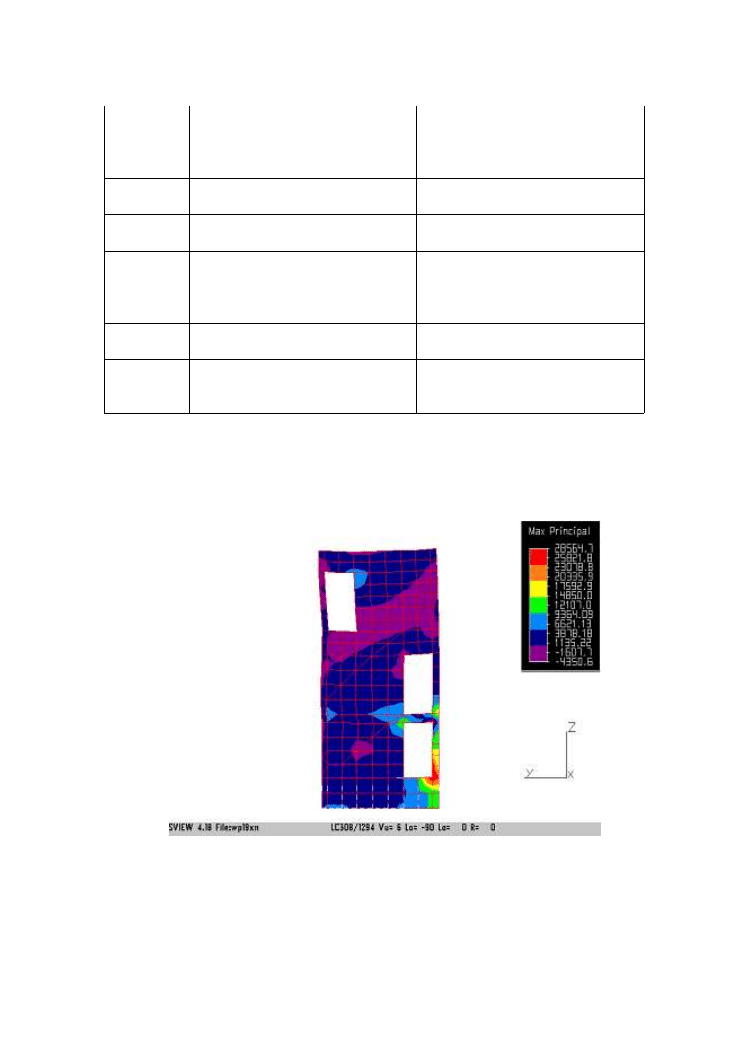
Z kolei na rys. 5 i 6 pokazano przykładowo wykonane mapy naprężeń głównych w

jednej ze ścian wewnętrznych (YZ 3) budynku od wymuszenia odpowiednio w przypadku I
i II.

Rys. 5

Rys. 6

Zamieszczony w referacie materiał ilustrujący odpowiedź dynamiczną modelu budynku jest
mało wyrazisty i wymowny i będzie, w przypadku przyjęcia referatu, w szerszej i barwnej
formie wraz z animacją zaprezentowany podczas Konferencji.

6. Wnioski i uwagi końcowe

Referat wskazuje na możliwość wykorzystania zaproponowanego modelu budynku do

obliczania dynamicznej odpowiedzi niskich budynków murowych podlegających drganiom
parasejsmicznym. Wyznaczone teoretycznie charakterystyki dynamiczne są porównywalne
z uzyskanymi z pomiarów na obiekcie rzeczywistym. Obliczone dynamiczne naprężenia w
ścianach nośnych od wymuszenia drganiami wywołanymi wstrząsami górniczymi o
intensywnościach jak na rys. 2a i 2b, są poniżej stanu granicznego. Najwieksze z
maksymalnych wartości głównych naprężeń rozciągających występują w tej samej ścianie,
obliczone od obu przypadków wymuszeń, i różnią się mniej niż 4%. Podane analizy
wskazują, że koncentracja maksymalnych, głównych naprężeń rozciągających występuje
przede wszystkim w poziomie piwnicy i parteru przy otworach drzwiowych i okiennych.
Podane wnioski dotyczą przyjętych tu przebiegów drgań i mogą się różnić od uzyskanych
od przebiegów z innymi dominującymi częstotliwościami.

Literatura

[1] Ciesielski R., Maciąg E., Tatara T.,Wpływy eksploatacji górniczej na typowy niski
budynek w LGOM, XVIII Konferencja Naukowo -Techniczna "Awarie Budowlane",
Szczecin - Międzyzdroje 1997, T.2, str. 807-814.
[2] Maciąg E., Tatara T., Szkodliwość dla niskich budynków i uciążliwość dla ludzi drgań
wzbudzanych wstrząsami górniczymi,Konferencja Naukowo-Techniczna "Ochrona powie-
rzchni i obiektów budowlanych przed szkodami górniczymi", Katowice 1997, str. 269-285.
[3] Kowalski W., Maciąg E., Tatara T., Wpływ wstrząsów górniczych na budynki i ludzi w
nich przebywających [w:] "Ochrona obiektów budowlanych na terenach górniczych",
Wydawnictwo Głównego Instytutu Górnictwa, Katowice 1997, str. 583-628.

[7]Maciag E., Tatara T., Porównanie obliczonych i pomierzonych dynamicznych
odpowiedzi budynków murowych podlegajacych drganiom parasejsmicznym, XXXIII
Konf. Nauk. KILiW PAN i KN PZITB, Krynica 1987, str. 47-52.

Normy

[4] PN-85/B-02170, Ocena szkodliwości drgań przekazywanych z podłoża na budynki.
[5] PN-87/B-03002, Konstrukcje murowe. Obliczenia statyczne i projektowanie.
[6]PN-80/B-03040, Fundamenty i konstrukcje wsporcze pod maszyny. Obliczenia i
projektowanie.
[8] Eurocode 8: Earthquake resistant design of structures – second draft 1993 CEN/TC
250/SC8/N85.

DYNAMIC RESPONSE OF LOW-RISE TYPICAL MASONRY

BUILDING DUE TO MINING TREMORS

Summary

The paper deals with dynamic analysis of a low typical dwelling masonry building

subjected to surface vibrations induced by representative mining shock. The analysis
contains the choice of dynamic model using FEM, comparison of the experimental and
theoretical determinated of the building natural frequencies. Two component of measured
surface vibrations (in x and y directions) have been respectively applied in transverse and
longitudinal direction of the building for calculations of dynamic response of the model.
According to Eurocode 8 the calculations for one component of the surface vibrations has
been also performed. The calculated principal stresses are small in both kind of excitations.