1

Wykład VI

Geometria analityczna w przestrzeni

Odległość punktów w przestrzeni

Działania na wektorach w przestrzeni

Równanie płaszczyzny

Równania prostej

2

Odległość punktów
w przestrzeni

Punkt w przestrzeni zadany jest
poprzez trzy współrzędne: x, y i z.
Niech A(x

1

,y

1

,z

1

) i B(x

2

,y

2

,z

2

)

oznaczają dwa punkty.

A(x

1

,y

1

,z

1

)

[

]

1

2

1

2

1

2

,

,

AB

z

z

y

y

x

x

−

−

−

=

→

Definicja:

Wektorem AB o początku w punkcie A i końcu w

punkcie B nazywamy wektor

→

x

z

y

k

j

i

x

1

y

1

z

1

B(x

2

,y

2

,z

2

)

y

2

x

2

z

2

Wektory i, j, k oznaczają wektory jednostkowe,

tzn. i=[1,0,0], j=[0,1,0], k=[0,0,1].

x

2

-x

1

y

2

-y

1

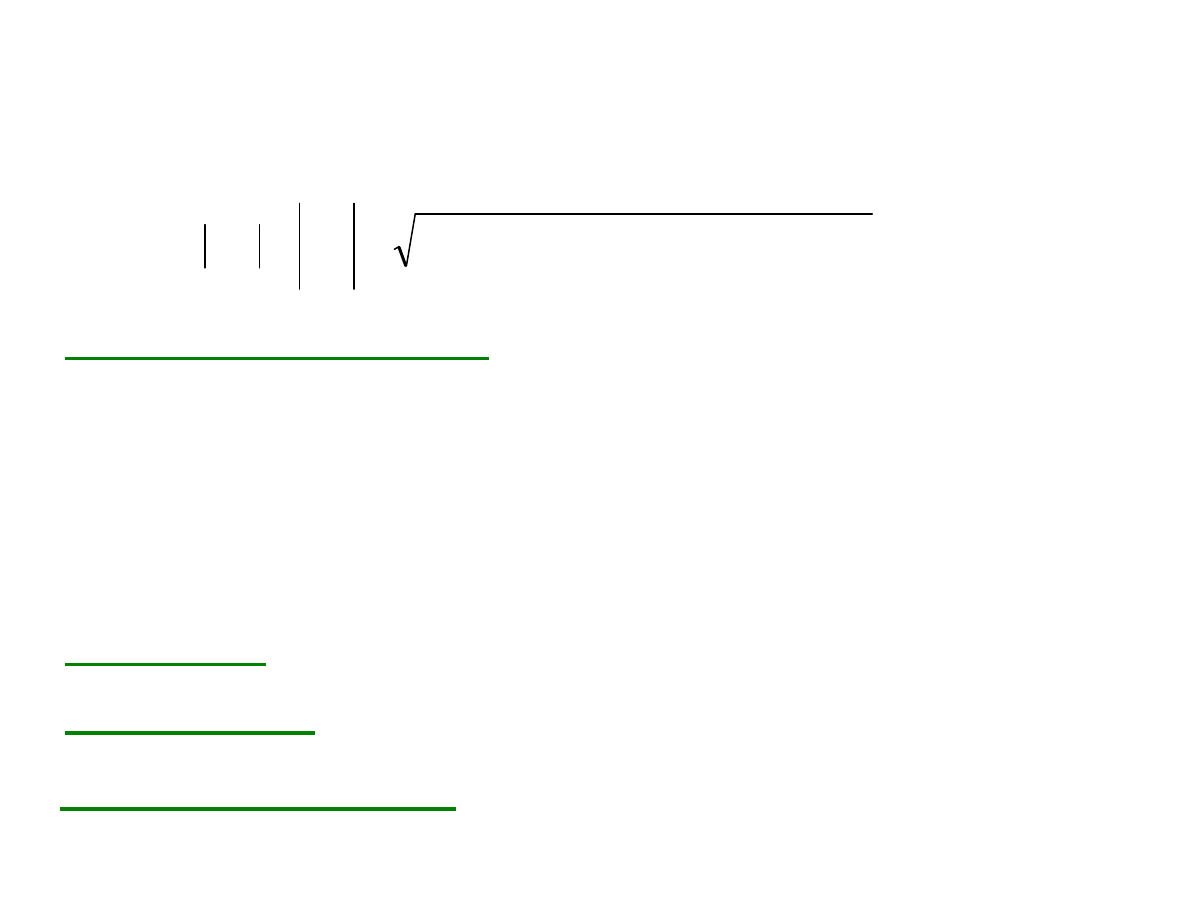
3

Działania na wektorach

Wektory możemy dodawać, odejmować, mnożyć przez liczbę.
Na wektorach określamy iloczyn skalarny, wektorowy oraz
mieszany.

Dodawanie

[

]

2

1

2

1

2

1

2

1

,

,

z

z

y

y

x

x

+

+

+

=

+

v

v

r

r

(

)

(

)

(

)

2

1

2

2

1

2

2

1

2

AB

AB

z

z

y

y

x

x

−

+

−

+

−

=

=

→

Odległość punktów AB lub długość wektora AB wyraża się
wzorem:

→

Niech

[

]

[

]

2

2

2

2

1

1

1

1

,

,

;

,

,

z

y

x

z

y

x

=

=

v

v

r

r

Odejmowanie

[

]

2

1

2

1

2

1

2

1

,

,

z

z

y

y

x

x

−

−

−

=

−

v

v

r

r

Mnożenie przez liczbę

[

]

az

ay

ax

a

,

,

=

⋅

v

r

4

Przykład 1.

Obliczyć długość wektora

[

]

[

]

1

,

2

,

1

;

1

,

5

,

3

gdzie

;

3

2

2

1

2

1

−

−

=

−

=

−

v

v

v

v

r

r

r

r

Rozwiązanie:

Niech

[

]

[

] [

]

5

,

4

,

3

1

,

2

,

1

3

1

,

5

,

3

2

3

2

2

1

−

=

−

−

−

−

=

−

=

v

v

a

r

r

r

Liczymy teraz długość:

(

)

2

5

50

5

4

3

2

2

2

=

=

+

−

+

=

a

r

Iloczyn skalarny wektorów

2

1

2

1

2

1

2

1

z

z

y

y

x

x

⋅

+

⋅

+

⋅

=

v

v

r

o

r

Iloczynem skalarnym dwóch wektorów

nazywamy liczbę postaci:

[

]

[

]

2

2

2

2

1

1

1

1

,

,

;

,

,

z

y

x

z

y

x

=

=

v

v

r

r

Iloczyny wektorów

W przestrzeni trójwymiarowej określamy następujące
iloczyny wektorów:

5

Iloczyn wektorowy

2

2

1

1

2

2

1

1

2

2

1

1

2

2

2

1

1

1

2

1

y

x

y

x

z

x

z

x

z

y

z

y

z

y

x

z

y

x

k

j

i

k

j

i

v

v

+

−

=

=

×

r

r

Iloczynem wektorowym wektorów

nazywamy wektor postaci:

[

]

[

]

2

2

2

2

1

1

1

1

,

,

;

,

,

z

y

x

z

y

x

=

=

v

v

r

r

Przykład 2.

Obliczyć iloczyn wektorowy wektorów

[

]

[

]

1

,

2

,

1

1

,

5

,

3

2

1

−

−

=

−

=

v

v

r

r

i

(

)

]

1

,

4

,

7

[

4

7

3

2

5

6

5

2

1

5

3

1

2

1

1

5

3

2

1

−

=

−

+

=

−

−

−

−

−

+

=

−

−

−

−

−

=

×

k

j

i

j

i

k

k

j

i

j

i

k

j

i

v

v

r

r

UWAGA: Iloczyn wektorowy dwóch wektorów jest
ortogonalny do obydwóch wektorów.

6

Iloczyn mieszany trzech wektorów

(

)

3

3

3

2

2

2

1

1

1

3

2

1

z

y

x

z

y

x

z

y

x

=

×

v

v

v

r

r

o

r

Iloczynem mieszanym wektorów

nazywamy iloczyn postaci:

[

]

[

]

[

]

3

3

3

3

2

2

2

2

1

1

1

1

,

,

;

,

,

;

,

,

z

y

x

z

y

x

z

y

x

=

=

=

v

v

v

r

r

r

Przykład 3.

Obliczyć iloczyn mieszany wektorów

[

]

[

]

[

]

3

,

2

,

0

;

1

,

2

,

1

;

1

,

5

,

3

3

2

1

=

−

−

=

−

=

v

v

v

r

r

r

(

)

(

)

5

15

6

0

2

0

18

2

0

2

1

5

3

3

2

0

1

2

1

1

5

3

3

2

1

=

−

−

−

+

+

−

=

−

−

−

−

−

=

×

v

v

v

r

r

o

r

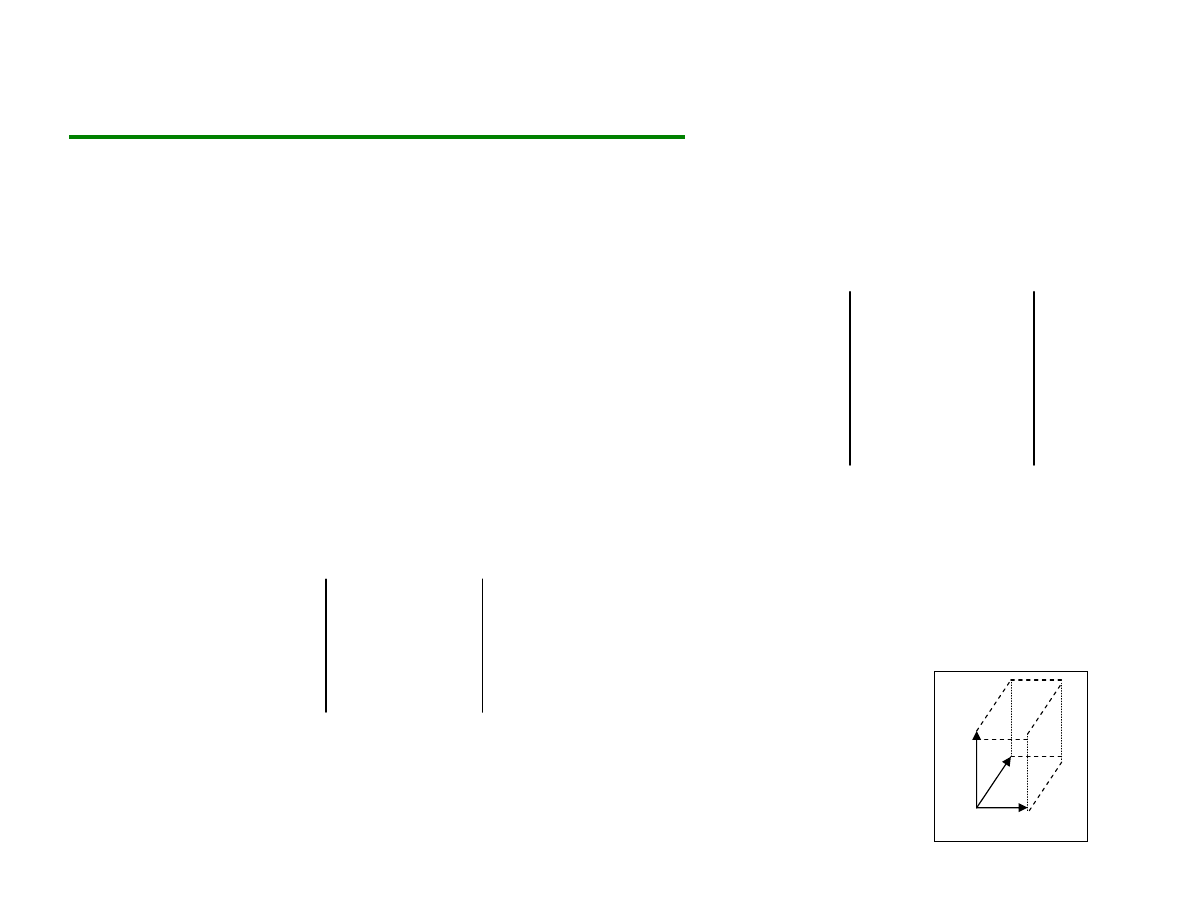
Interpretacja:

Wartość bezwzględna iloczynu

mieszanego trzech wektorów jest równa objętości
równoległościanu utworzonego przez te wektory.

6

v

1

v

3

v

2

7

Wzajemne położenie wektorów

1.Wektory

są prostopadłe

wtedy i tylko wtedy, gdy ich iloczyn skalarny jest równy 0,tzn.

[

]

[

]

2

2

2

2

1

1

1

1

,

,

i

,

,

z

y

x

z

y

x

=

=

v

v

r

r

0

0

2

1

2

1

2

1

2

1

2

1

=

+

+

⇔

=

⇔

⊥

z

z

y

y

x

x

v

v

v

v

r

o

r

r

r

(

)

0

3

2

1

=

×

v

v

v

r

r

o

r

3.Wektory

leżą w jednej płaszczyźnie (są komplementarne) wtedy i

tylko wtedy, gdy ich iloczyn mieszany jest równy 0,tzn.

[

]

[

]

[

]

3

3

3

3

2

2

2

2

1

1

1

1

,

,

;

,

,

;

,

,

z

y

x

z

y

x

z

y

x

=

=

=

v

v

v

r

r

r

2.Jeśli wektory

są

równoległe, wówczas ich iloczyn wektorowy jest wektorem
zerowym, czyli jego długość wynosi 0, tzn.

[

]

[

]

2

2

2

2

1

1

1

1

,

,

i

,

,

z

y

x

z

y

x

=

=

v

v

r

r

0

||

2

1

2

1

=

×

⇔

v

v

v

v

r

r

r

r

8

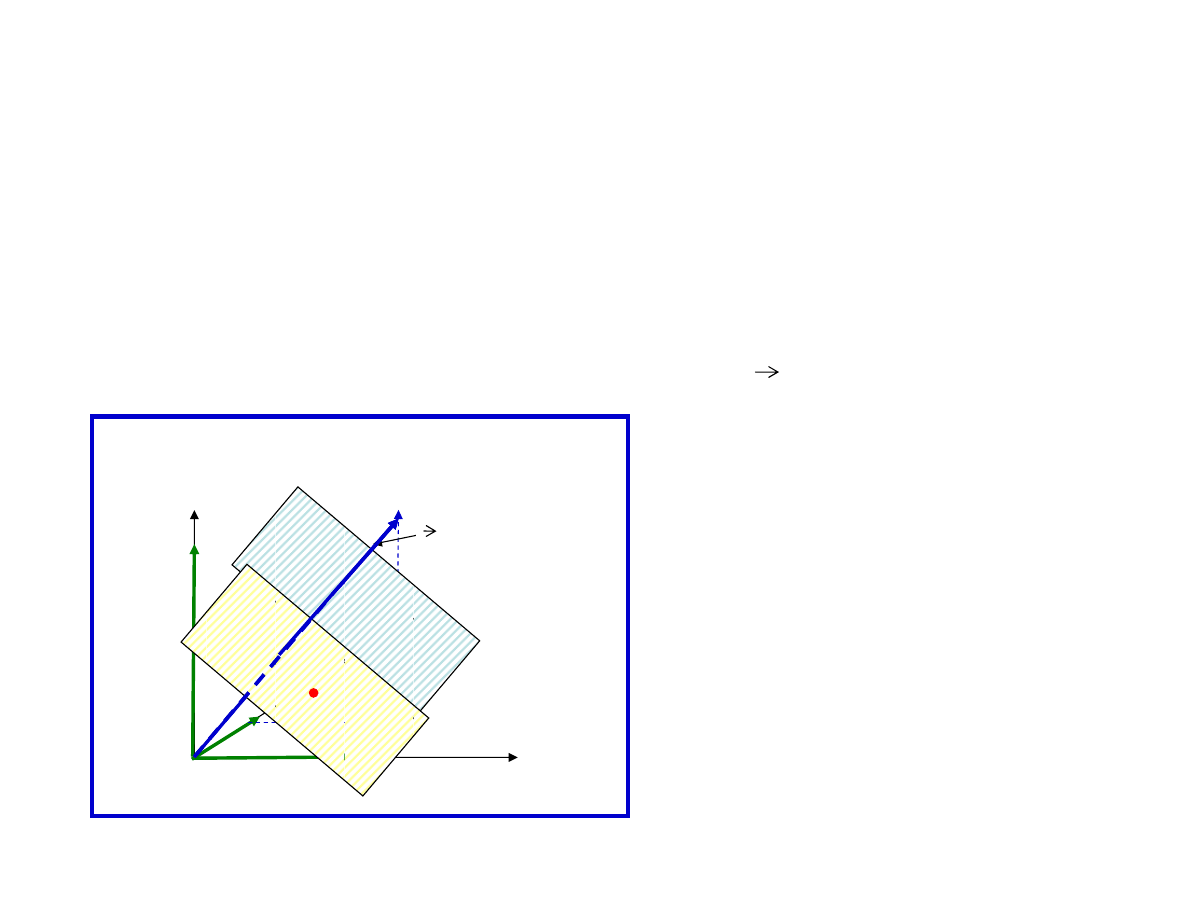
Równanie płaszczyzny

Płaszczyzna w przestrzeni trójwymiarowej opisana jest
równaniem postaci:

Ax+By+Cz+D=0

, gdzie

n=[A,B,C]

jest

wektorem normalnym płaszczyzny (prostopadłym do niej).

→

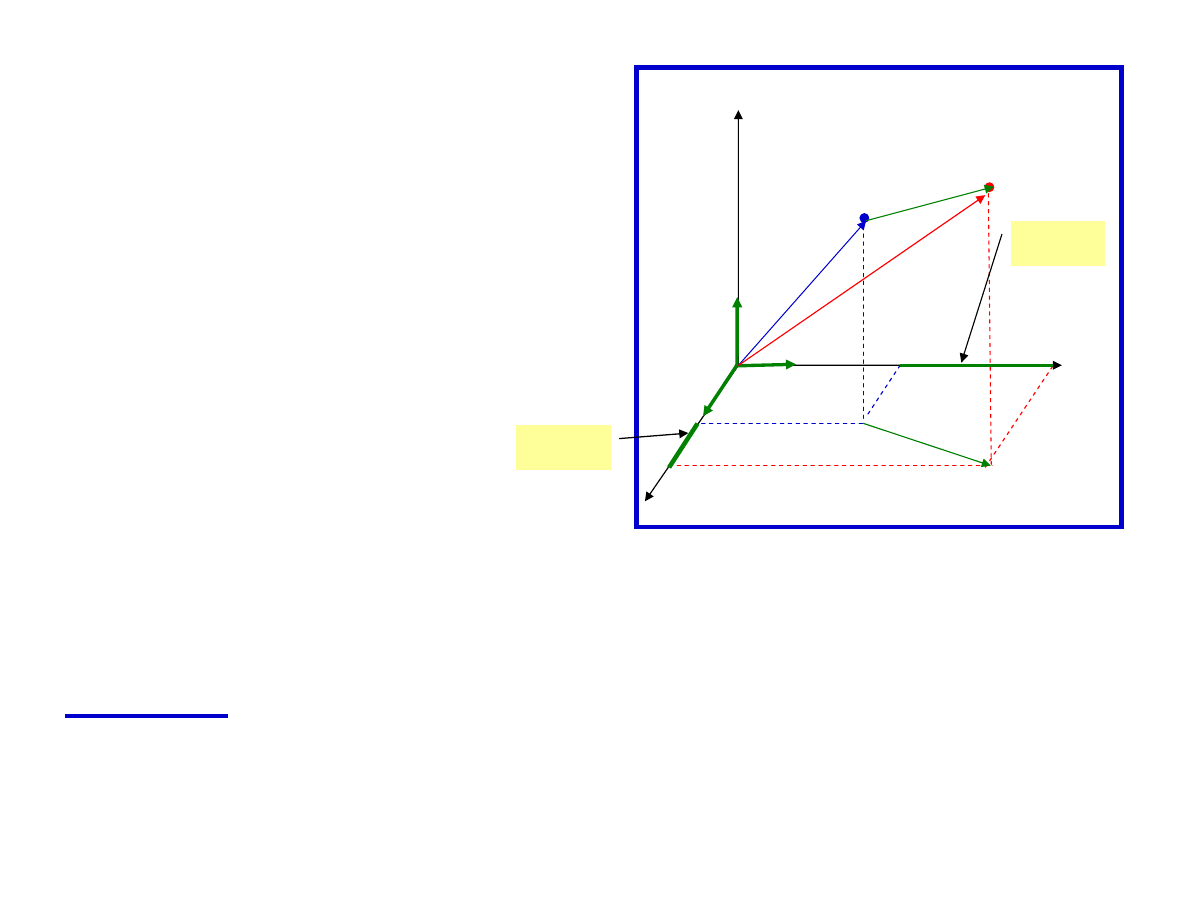
Przykład

: Rozważmy płaszczyznę π: 2x+y+3z-6=0.

n= [2, 1,3]

Wektor normalny płaszczyzny π wynosi

2

1

3

y

x

z

n= [2, 1,3]

π

Ponadto, płaszczyzna musi
przechodzić przez punkt
spełniający równanie
płaszczyzny, np. P(1,1,1).

π

P(1,1,1)

9

Prosta w przestrzeni trójwymiarowej

Prosta l w przestrzeni trójwymiarowej może być opisana
równaniami różnej postaci:

a)

Postać krawędziowa prostej

(zadana poprzez dwie

płaszczyzny nierównoległe)







=

+

+

+

=

+

+

+

0

D

C

B

A

0

D

C

B

A

:

2

2

2

2

1

1

1

1

z

y

x

z

y

x

l

b)

Postać kierunkowa prostej

przechodzącej przez punkt

P

0

(x

0

,y

0

,z

0

) i równoległej do wektora k=[a,b,c]

c

z

z

b

y

y

a

x

x

l

0

0

0

:

−

=

−

=

−

b)

Postać parametryczna prostej

przechodzącej przez

punkt P

0

(x

0

,y

0

,z

0

) i równoległej do wektora k=[a,b,c]









+

=

+

=

+

=

ct

z

z

bt

y

y

at

x

x

l

0

0

0

:

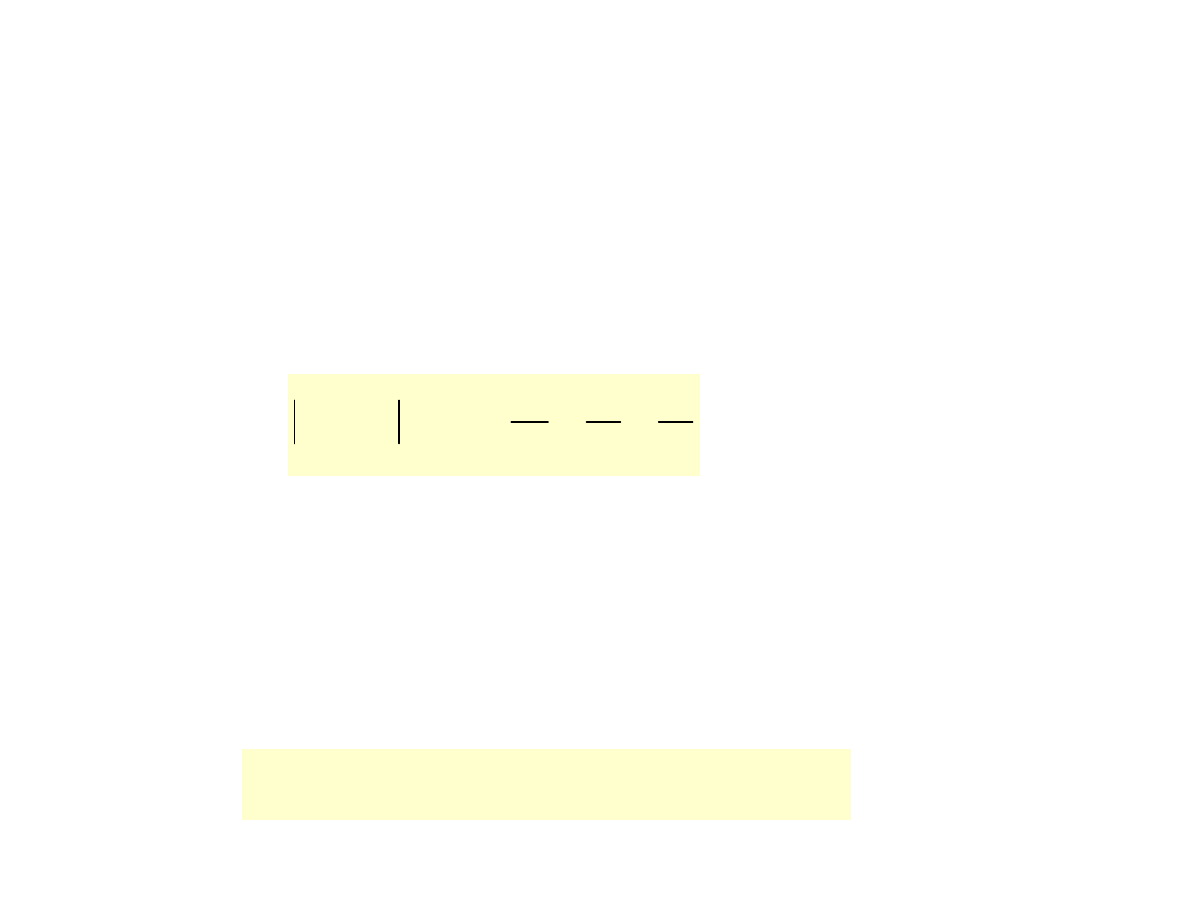
10

1

2

1

2

1

2

2

1

0

c

c

b

b

a

a

=

=

⇔

=

×

k

k

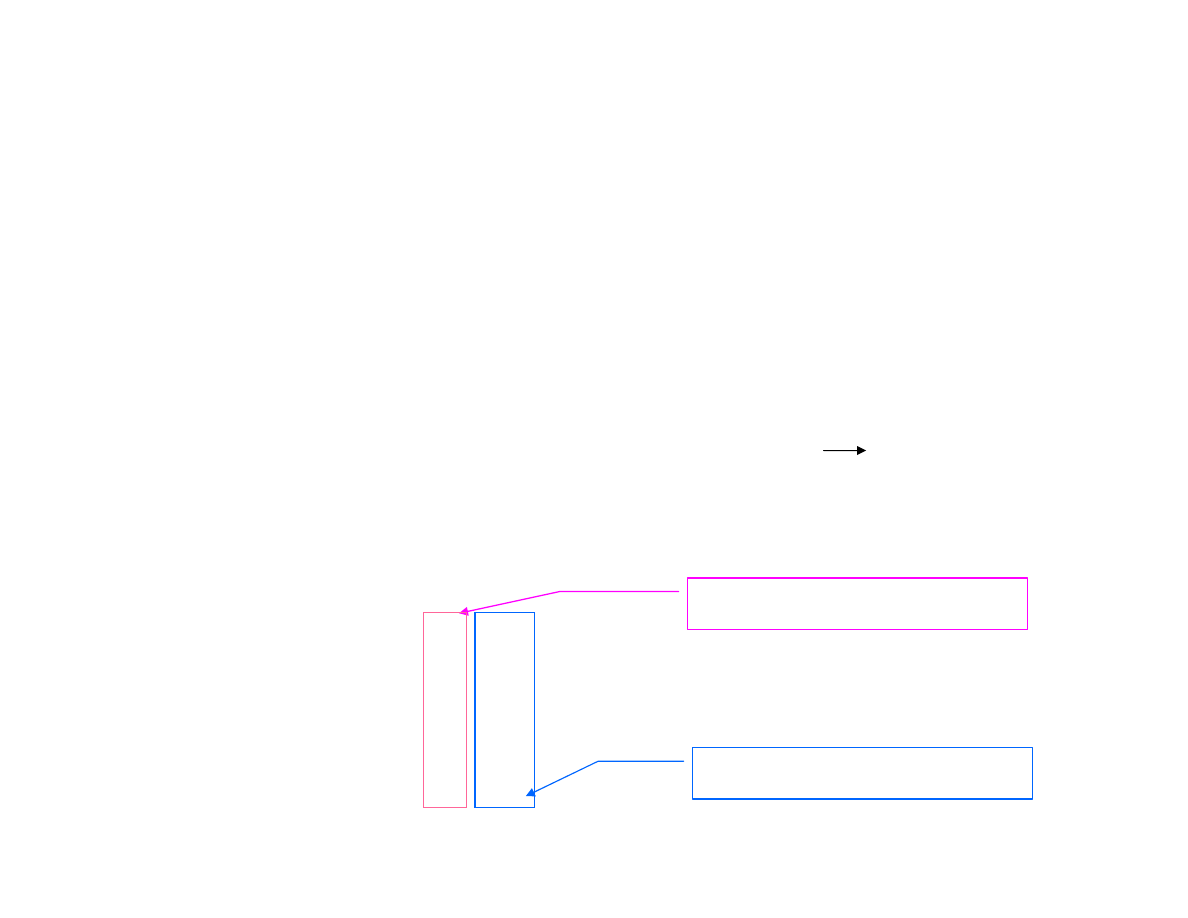
Dwie proste

l

1

oraz

l

2

są równoległe wtedy i tylko wtedy, gdy

ich wektory kierunkowe są równoległe,

tzn.

k

1

=[a

1

,b

1

,c

1

]

|| k

2

=[a

2

,b

2

,c

2

],

czyli

Wzajemne położenie prostych

0

2

1

2

1

2

1

2

1

=

⋅

+

⋅

+

⋅

=

c

c

b

b

a

a

k

k

r

o

r

Dwie proste

l

1

oraz

l

2

są prostopadłe wtedy i tylko wtedy, gdy

ich wektory kierunkowe są prostopadłe,

tzn.

k

1

=[a

1

,b

1

,c

1

]

⊥

k

2

=[a

2

,b

2

,c

2

],

czyli

11

Uwaga.

1.Dowolne dwa różne punkty w przestrzeni wyznaczają
prostą. Znajdziemy równanie prostej przechodzącej przez dwa
punkty A(1,2,3) i B(0,-1,4).









+

=

−

=

−

=

t

z

t

y

t

x

l

1

3

3

2

1

1

:

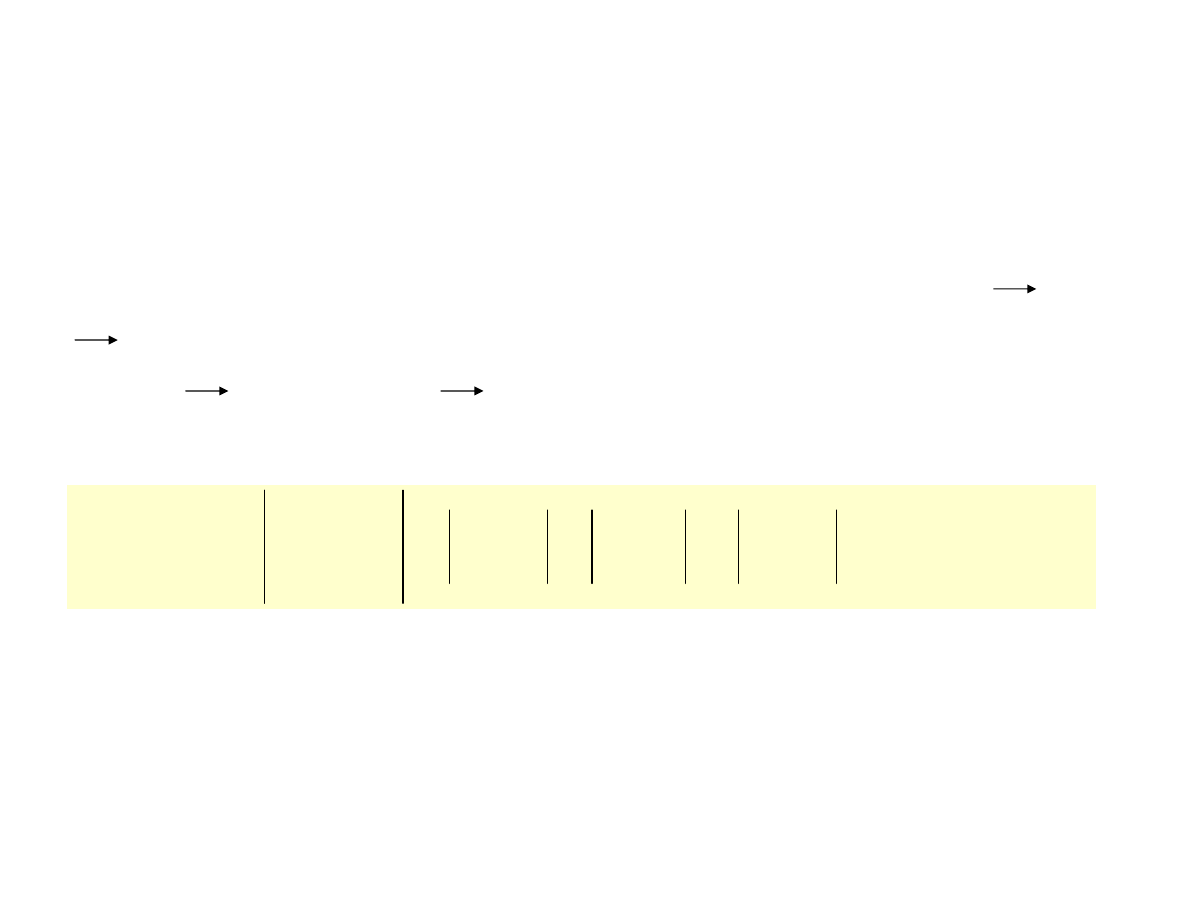
Rozwiązanie:

Wyznaczymy wektor kierunkowy prostej k=AB=[-1,-3,1].
Równanie parametryczne ma zatem postać:

Współrzędne punktu A

Współrzędne wektora k

12

3.Dowolne trzy niewspółliniowe punkty w przestrzeni
wyznaczają płaszczyznę. Znajdziemy równanie płaszczyzny
przechodzącej przez punkty A(1,2,3) i B(0,-1,4), C(3,4,2).

Rozwiązanie:

Aby znaleźć wektor normalny płaszczyzny,

należy zauważyć, że jest on ortogonalny do wektorów AB i
AC, czyli jest iloczynem wektorowym tych wektorów.
Zatem AB=[-1,-3,1] i AC=[2,2,-1], natomiast iloczyn
wektorowy tych wektorów wynosi:

]

4

,

1

,

1

[

4

2

,

2

3

,

1

1

,

2

1

,

1

1

,

2

1

,

3

1

2

2

1

3

1

AB

=

+

+

=

−

−

+

−

−

−

−

−

=

−

−

−

=

×

=

→

→

k

j

i

k

j

i

k

j

i

AC

n

r

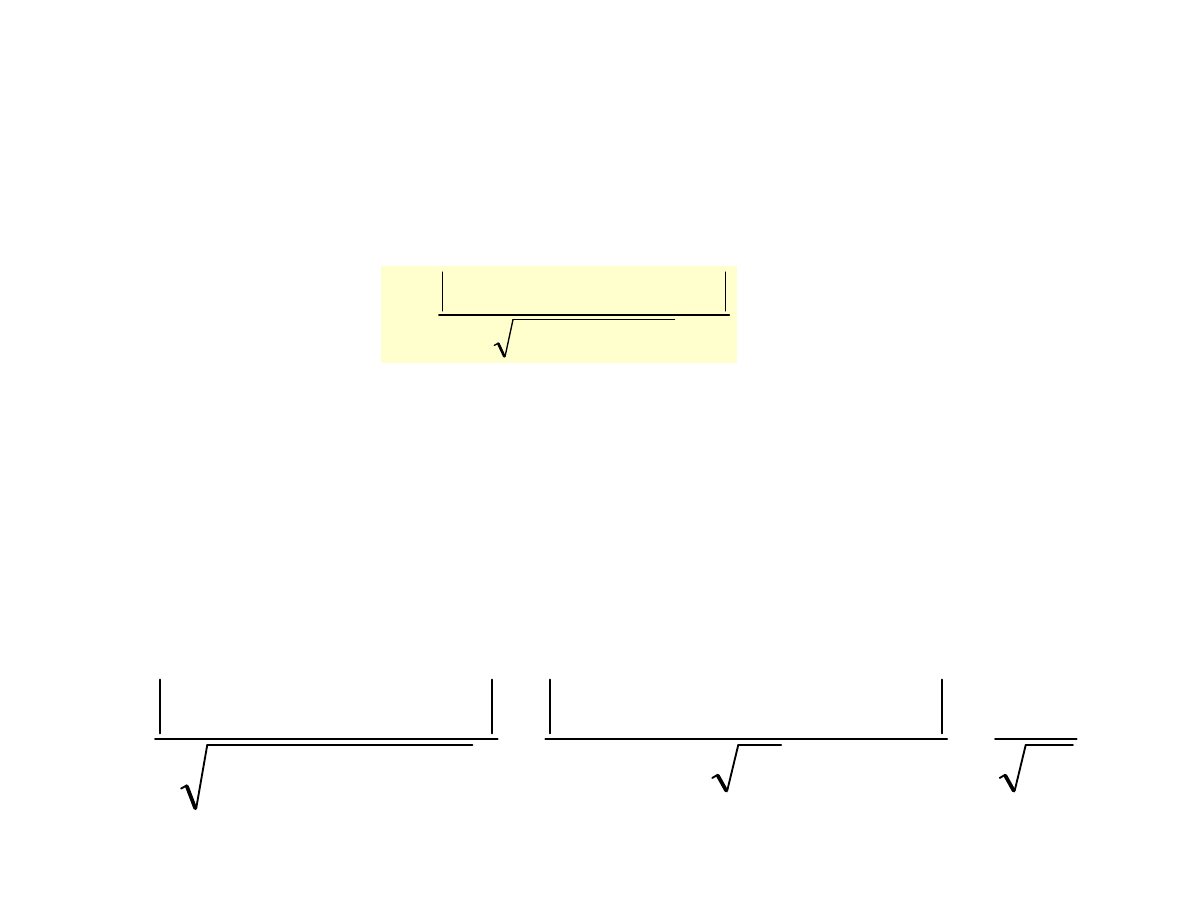
Równanie płaszczyzny ma postać: x+y+4z+D=0. Aby
wyznaczyć D wystarczy wstawić jeden z punktów.
Wstawiając A(1,2,3) dostajemy 1+2+12+D=0, czyli D=-15.

Ostatecznie równanie płaszczyzny ma postać: x+y+4z-15=0.

13

Odległość punktu od płaszczyzny

2

2

2

0

0

0

C

B

A

C

B

A

+

+

+

+

+

=

D

z

y

x

d

Odległość punktu P(x

0

,y

0

,z

0

) od płaszczyzny zadanej

równaniem Ax+By+Cz+D=0 określa wzór:

Przykład 4.

Obliczyć odległość punktu P(2,-4,1) od

płaszczyzny π:2x-3y+5z+8=0

(

)

(

)

38

29

13

8

1

5

4

3

2

2

5

3

2

8

5

3

2

2

2

2

0

0

0

=

+

⋅

+

−

⋅

−

⋅

=

+

−

+

+

+

−

=

z

y

x

d

Rozwiązanie:

Odległość punktu P(2,-4,1) od płaszczyzny π:2x-3y+5z+8=0
wynosi