TEST NORMALNOŚCI SHAPIRO - WILKA

Weryfikujemy hipotezę zerową postaci:

H

0

: F(x)

∈F

N

(gdzie F

N

jest dystrybuantą rozkładu normalnego)

wobec hipotezy alternatywnej

H

1

: ~H

0

.

Procedura testowania hipotezy zerowej jest następująca:

• Uporządkować próbę według wartości rosnących: x

(1)

, x

(2)

, ..., x

(n)

.

• Obliczyć wartość statystyki testu postaci:

(1)

∑

∑

=

=

+

−

−

















−

=

n

i

i

n

i

i

i

n

i

n

x

x

x

x

a

W

1

2

2

]

2

/

[

1

)

(

)

1

(

,

)

(

)

(

, gdzie a

n,i

są współczynnikami odczytanymi z

tablic.

• Odczytać z tablic kwantyli rozkładu W dla przyjętego poziomu istotności α wartość

W

α

.

• Obszar odrzucenia w teście jest lewostronny, zatem odrzucamy H

0

, gdy W<W

α

.

PRZYKŁAD 1.

Przeprowadzono badanie cen pewnego papieru wartościowego z 10 ostatnich tygodni i

uzyskano następujące wyniki (w zł): 285, 294, 261, 234, 320, 310, 276, 271, 294, 255. Na

poziomie istotności

α=0,05 zweryfikować przypuszczenie, że rozkład cen tego papieru

wartościowego jest rozkładem normalnym.

H

0

: F(x)=F

N

(x) – rozkład cen jest normalny

H

1

: ~H

0

.

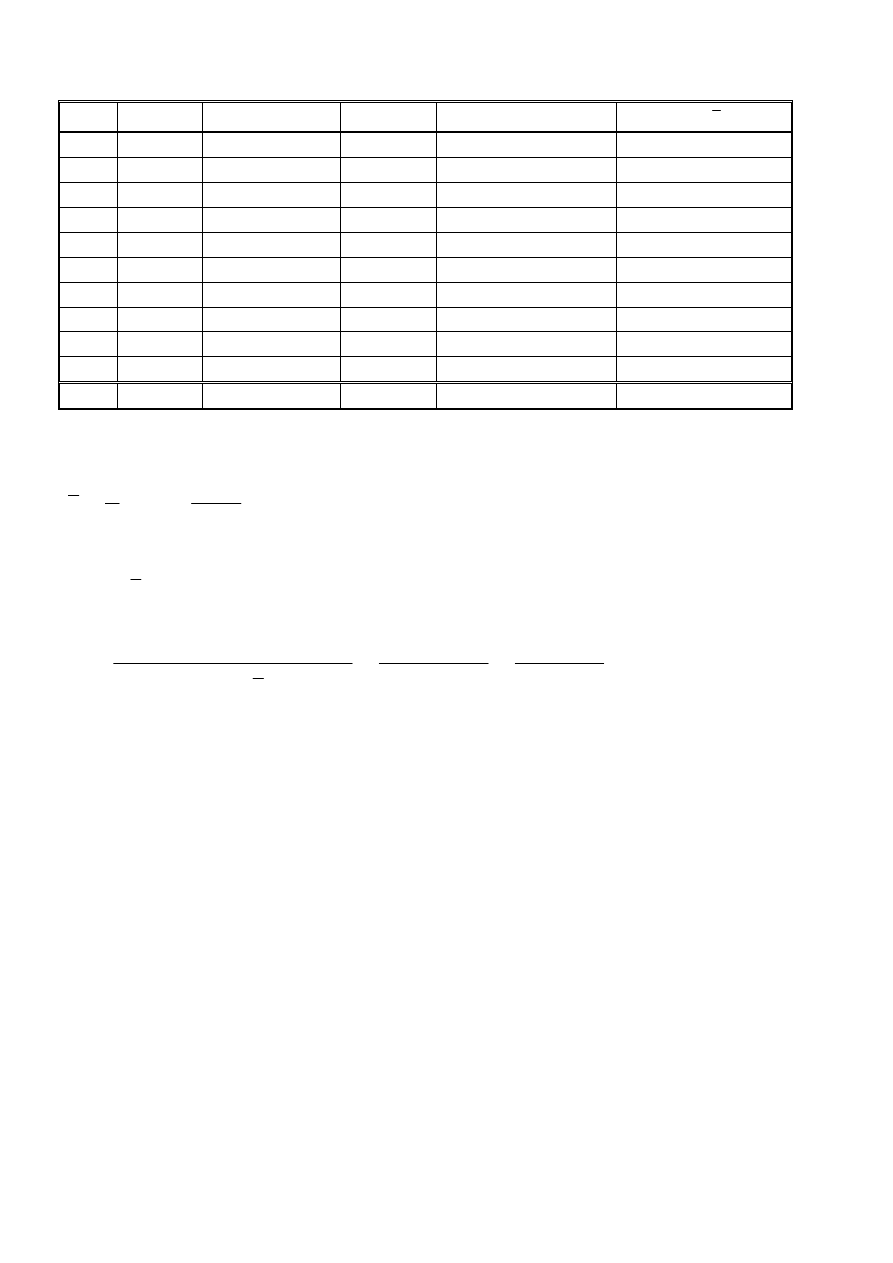
(i) x

(i)

x

(n-i+1)

– x

(i)

a

n,i

a

n,i

(x

(n-i+1)

– x

(i)

)

2

)

(

x

x

i

−

1

234 86 0,5739 49,3554

2116

2

255 55 0,3291 18,1005

625

3

261 33 0,2141 7,0653

361

4

271 23 0,1224 2,8152

81

5

276 9 0,0399 0,3591

16

6

285

25

7

294

196

8

294

196

9

310

900

10

320

1600

suma 2800

x

x

77,6955

6116

n=10

280

10

2800

1

1

=

=

=

∑

=

n

i

i

x

n

x

zł.

987

,

0

6116

591

,

6036

6116

)

6955

,

77

(

)

(

)

(

2

2

2

]

2

[

1

)

(

)

1

(

,

=

=

=

−





















−

=

∑

∑

=

+

−

i

i

n

i

i

i

n

i

n

x

x

x

x

a

W

.

Dla

α=0,05 i n=10 wartość krytyczna odczytana z tablic jest równa W

α

=0,842.

Obszar odrzucenia jest lewostronny.

Ponieważ W=0,987>0,842= W

α

,zatem na poziomie istotności 0,05 nie ma

podstaw do odrzucenia hipotezy zerowej o normalności rozkładu cen tego

papieru wartościowego.

PRZYKŁAD 2.
Przeprowadzono badanie stężenia zanieczyszczeń w półprzewodnikach używanych do
produkcji mikroprocesorów i w 15 losowo wybranych półprzewodnikach uzyskano
następujące wyniki zanieczyszczeń (w pewnych jednostkach): 45, 37, 33, 20, 26, 10, 62,
39, 35, 21, 55, 48, 46, 51, 42. Sprawdzić, czy rozkład stężenia zanieczyszczeń w
półprzewodnikach można uznać za normalny, przyjmując poziom istotności

α=0,01.

H

0

: F(x)=F

N

(x) – rozkład stężenia zanieczyszczeń jest normalny

H

1

: ~H

0

.

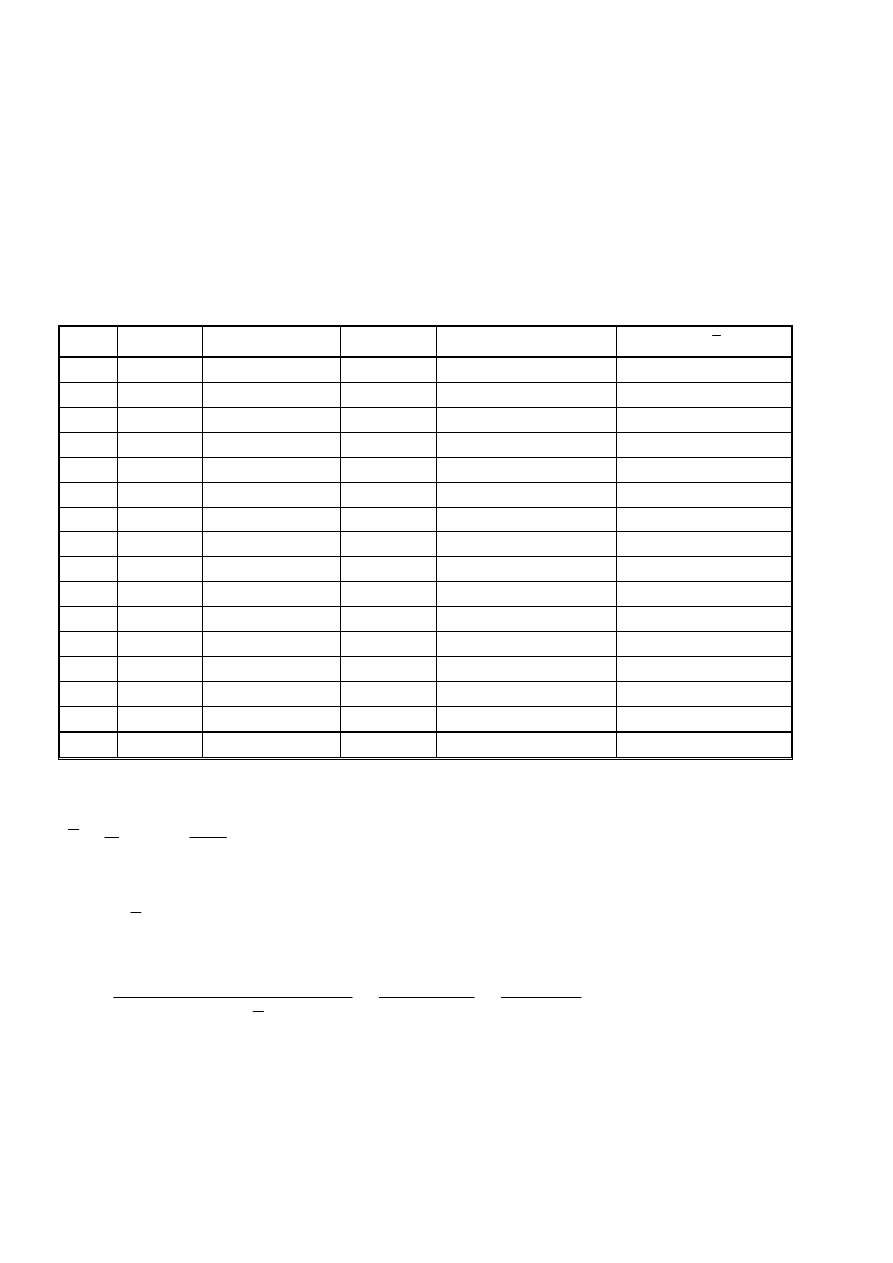
(i) x

(i)

x

(n-i+1)

– x

(i)

a

n,i

a

n,i

(x

(n-i+1)

– x

(i)

)

2

)

(

x

x

i

−

1

10 52

0,5150

26,7800

784

2

20 35

0,3306

11,5710

324

3

21 30

0,2495 7,4850

289

4

26 22

0,1878 4,1316

144

5

33 13

0,1353 1,7589

25

6

35 10

0,0880 0,8800

9

7

37 5

0,0433

0,2165

1

8

39

1

9

42

16

10

45

49

11

46

64

12

48

100

13

51

169

14

55

289

15

62

576

suma 570

x

x

52,823

2840

n=15

38

15

570

1

1

=

=

=

∑

=

n

i

i

x

n

x

jednostek

982

,

0

2840

27

,

2790

2840

)

823

,

52

(

)

(

)

(

2

2

2

]

2

[

1

)

(

)

1

(

,

=

=

=

−





















−

=

∑

∑

=

+

−

i

i

n

i

i

i

n

i

n

x

x

x

x

a

W

.

Dla

α=0,01 i n=15 wartość krytyczna odczytana z tablic jest równa W

α

=0,835.

Obszar odrzucenia jest lewostronny.

Ponieważ W=0,982>0,835=W

α

,zatem na poziomie istotności 0,01 nie ma podstaw do

odrzucenia hipotezy zerowej o normalności stężenia zanieczyszczeń.

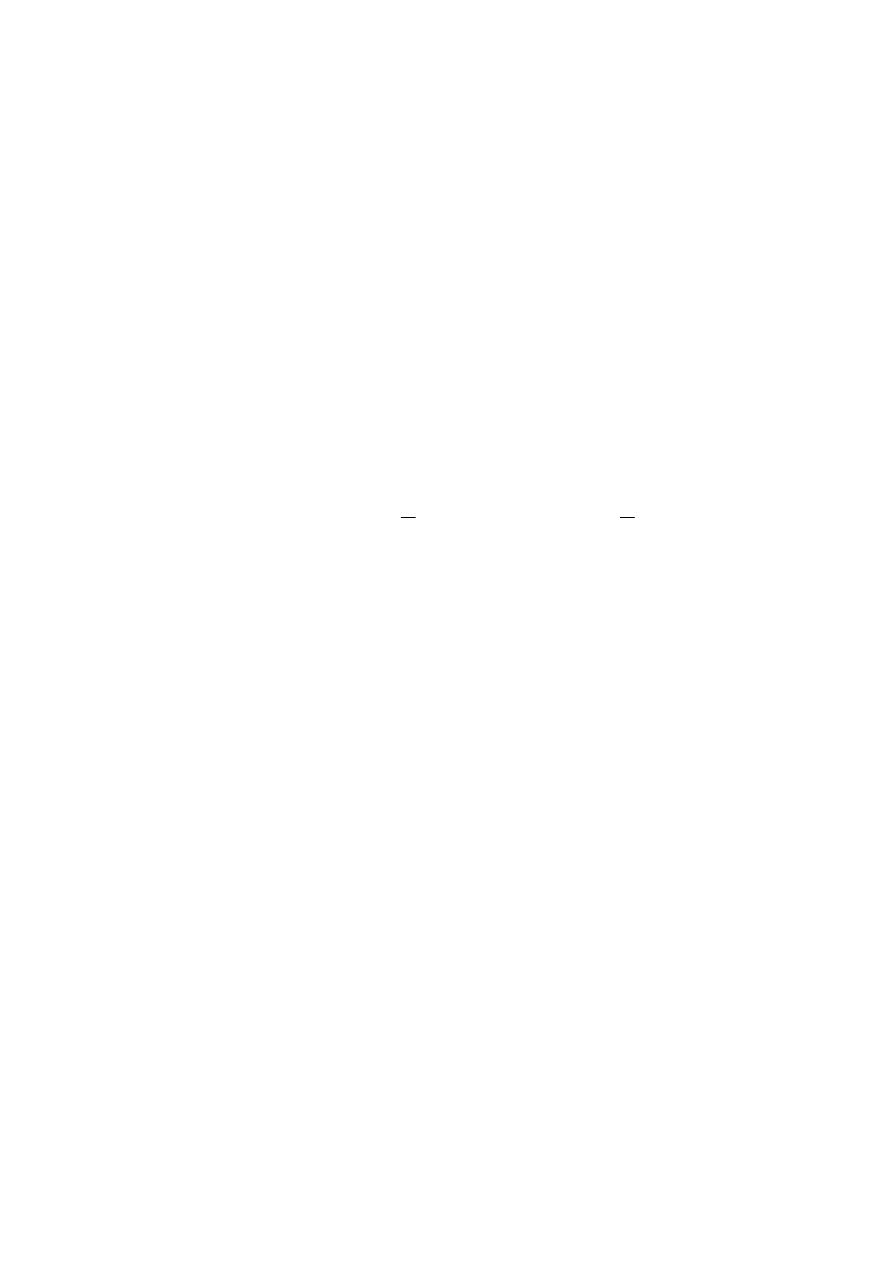
TEST SERII WERYFIKUJĄCY HIPOTEZĘ, ŻE PRÓBA MA CHARAKTER

LOSOWY (TEST MEDIANOWY)

Weryfikujemy hipotezę H

0

: próba ma charakter losowy, wobec hipotezy H

1

: ~H

0

.

Schemat postępowania jest następujący:

• Wyznaczyć medianę z próby.
• Każdemu wynikowi próby x

i

według kolejności pobierania elementów do badania

przyporządkować symbol a, gdy x

i

< Me lub symbol b, gdy x

i

> Me. Wynik x

i

= Me

można pominąć.

• Z ciągu symboli a i b wyznaczyć ogólną liczbę serii k.
• Dla ustalonego poziomu istotności α i odpowiednich n

1

i n

2

odczytujemy z tablic

rozkładu warunkowego liczby serii takie dwie wartości krytyczne k

1

i k

2

, aby

zachodziły relacje:

2

α

}

{

1

=

≤ k

k

P

oraz

2

α

1

}

{

2

−

=

≤ k

k

P

.

• Obszar odrzucenia jest dwustronny, zatem hipotezę zerową odrzucamy, kiedy

uzyskana liczba serii k z danego ciągu spełnia nierówność k

≤k

1

lub k

≥k

2

. W

przeciwnym przypadku, gdy k

1

<k<k

2

, nie ma podstaw do odrzucenia hipotezy

zerowej.

PRZYKŁAD 3.

Zbadano pracowników pewnego zakładu ze względu na ich staż pracy i otrzymano

następujące wartości analizowanej cechy (w latach) dla kolejno wybieranych

pracowników: 5, 7, 4, 9, 11, 1, 18, 18, 3, 10, 6, 22, 13, 23, 3, 2, 2, 9, 11, 4, 20, 8, 30.

Przyjmując poziom istotności

α=0,05, sprawdzić czy otrzymana próba jest próba losową.

H

0

: Próba jest losowa.

H

1

:~H

0

.

n=23

Porządkujemy niemalejąco wyniki próby:
1, 2, 2, 3, 3, 4, 4, 5, 6, 7, 8, 9, 9, 10, 11, 11, 13, 18, 18, 20, 22, 23, 30

Numer mediany –> nr

Me

=(23+1)/2=12. Mediana Me = 9.

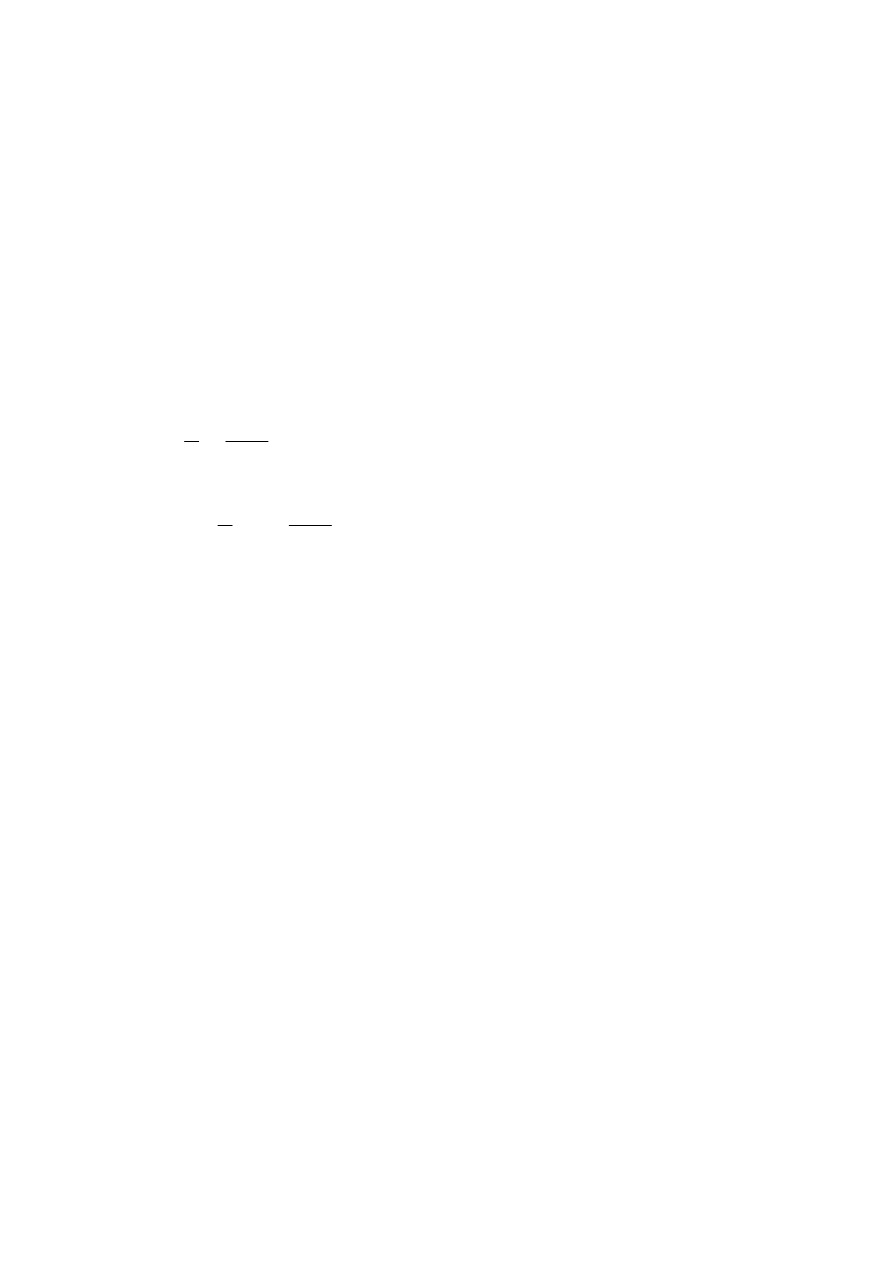
Przyporządkowujemy wartościom ciągu wyjściowego symbole: a dla x

i

<Me; b

dla x

i

>Me. x

i

=Me pomijamy:

5, 7, 4, 9, 11, 1, 18, 18, 3, 10, 6, 22, 13, 23, 3, 2, 2, 9, 11, 4, 20, 8, 30.

a a a b a b b a b a b b b a a a b a b a b

Liczba serii – k=14

Liczba symboli a – n

a

=11; liczba symboli b – n

b

=10.

α=0,05

025

,

0

2

05

,

0

2

α

)

{

1

=

=

=

≤ k

k

P

⇒ k

1

=6

975

,

0

2

05

,

0

1

2

α

1

)

{

2

=

−

=

−

=

≤ k

k

P

⇒ k

2

=16

Ponieważ k

1

=6<k=14<k

2

=16, zatem na poziomie istotności 0,05 nie ma

podstaw do odrzucenia hipotezy zerowej, że próba jest losowa.