LABORATORIUM IN

Ż

YNIERII BIOPROCESOWEJ

Kierunek: Biotechnologia

Specjalno

ść

: Agrobiotechnologia,

Biotechnologia w produkcji zwierz

ę

cej

(studia in

ż

ynierskie)

Ć

wiczenie nr 6

WYZNACZANIE PARAMETRÓW

REOLOGICZNYCH ZAWIESINY MATERIAŁU

BIOLOGICZNEGO

UNIWERSYTET TECHNOLOGICZNO – PRZYRODNICZY

WYDZIAŁ TECHNOLOGII I IN

Ż

YNIERII CHEMICZNEJ

Katedra In

ż

ynierii Chemicznej i Bioprocesowej

BYDGOSZCZ

2

1. Wprowadzenie teoretyczne

Reologia jako nauka o odkształcaniu zajmuje się także przepływem materii, będącym

odkształceniem o charakterze nieodwracalnym i ciągle wzrastającym z czasem.

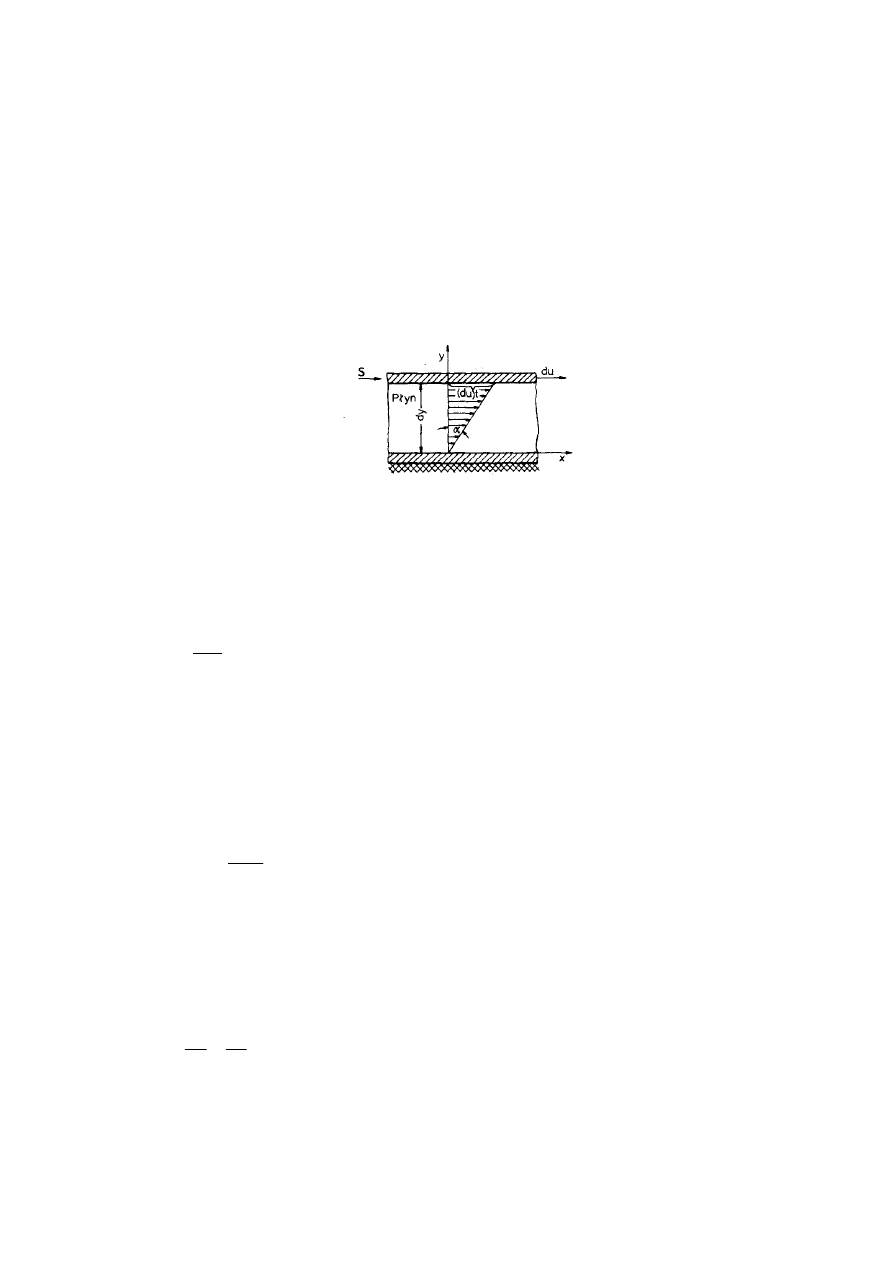
W celu zdefiniowania podstawowych wielkości rozpatrzmy sytuację pokazaną na

rys.1. Warstewka cieczy znajduje się między dwiema płaskimi równoległymi płytkami, z

których dolna jest nieruchoma, natomiast do górnej przyłożona jest styczna siła S.

Rys.1. Proste ścinanie płynu.

Stosunek siły dS, przyłożonej stycznie do powierzchni dF, na którą działa, nosi nazwę

naprężenia stycznego

τ

τ =

dS

dF

(1)

Powstały gradient prędkości wzdłuż osi y jest wynikiem istnienia sił tarcia wewnątrz

płynu, które równoważą siłę zewnętrzną S, przeciwdziałając tym samym wzajemnemu

przesuwaniu się warstewek płynu. Miarą odkształcenia płynu wywołanego występowaniem

naprężenia stycznego

τ

jest tangens kąta

α

(rys.1)

tg

t du

dy

α γ

= = ⋅

(2)

gdzie:

t-czas, [s].

Gradient prędkości płynu, noszący również nazwę szybkości odkształcania, jest równy

dy

du

dt

d

=

=

•

γ

γ

(3)

3

Płyny, dla których zależność szybkości ścinania

γ

•

od naprężenia stycznego

τ

ma

charakter liniowy

τ=η

γ

•

(4)

gdzie

η

-dynamiczny współczynnik lepkości, [Pa s]

noszą nazwę newtonowskich.

Pozostałe płyny niespełniające zależność (4) określa się jako nienewtonowskie. Płyny

nienewtonowskie można podzielić na trzy grupy:

1. Płyny reostabilne, dla których szybkość ścinania w danym punkcie zależy tylko od

naprężenia stycznego w tym miejscu.

2. Płyny reologicznie niestabilne, dla których szybkość ścinania jest funkcją naprężenia

ś

cinającego oraz czasu przykładania siły ścinającej.

3. Płyny sprężystolepkie, które wykazują powrót sprężysty po usunięciu naprężenia

stycznego.

Płyny reostabilne dzieli się ze względu na charakter zależności szybkości ścinania od

naprężenia stycznego na:

-płyny newtonowskie, charakteryzujące się liniową zależnością szybkości ścinania od

naprężenia stycznego,

-płyny rozrzedzone ścinaniem, dla których zwiększanie naprężania stycznego powoduje

nieproporcjonalnie duży wzrost szybkości ścinania; lepkość takich płynów zmniejsza się ze

wzrostem szybkości ścinania (rys.2); płyny te nazywa się często pseudoplastycznymi,

-płyny zagęszczane ścinaniem zwane zwyczajowo dilatacyjnymi.

Są to układy, dla których zwiększanie naprężenia stycznego wywołuje mniejszy przyrost

szybkości ścinania niż wynikałoby to z prostej proporcjonalności między tymi wielkościami.

Przez analogię do dynamicznego współczynnika lepkości płynów newtonowskich wprowadza

się pozorny dynamiczny współczynnik lepkości

η

a

definiowany następująco:

η

τ

γ

a

const

= ≠

•

(5)

Zależność naprężenia stycznego od prędkości ścinania podają krzywe płynięcia (rys.2).

4

Rys.2. Krzywe płynięcia płynów:

1-newtonowskiego,
2-pseudoplastycznego,
3-dilatacyjnego.

Pozorny współczynnik dynamiczny lepkości płynu nienewtonowskiego, równy tangensowi

kąta

α

na rys.2, zwiększa się lub maleje ze wzrostem szybkości ścinania.

Krzywa płynięcia płynu nienewtonowskiego ma w obszarze ruchu laminarnego trzy

charakterystyczne zakresy. W zakresie małych i dużych szybkości ścinania krzywa płynięcia

ma charakter liniowy, a więc układ zachowuje się jak płyn newtonowski o stałej lepkości

η

0

/

η

∞

.

gdzie:

η

0

-dynamiczny współczynnik lepkości ekstrapolowanej dla zerowej szybkości

ś

cinania,

η

∞

-dynamiczny współczynnik lepkości przy szybkości ścinania „dążącej do

nieskończoności”.

W zakresie pośrednich szybkości ścinania pozorny dynamiczny współczynnik lepkości płynu

pseudoplastycznego maleje, a dilatacyjnego - zwiększa się ze wzrostem

γ

•

. Najprostszym

modelem matematycznym opisującym krzywą płynięcia w tym zakresie jest model potęgowy

Ostwalda:

n

k













=

•

γ

τ

(6)

gdzie:

k,n-parametry reologiczne.

5

Na podstawie równań (5) i (6) otrzymuje się zależność:

1

−

•

•

•













⋅

=













=

n

n

a

k

k

γ

γ

γ

η

(7)

z której wynika, że dla płynów dilatacyjnych n>1, a dla płynów pseudoplastycznych n<1. W

przypadku płynów pseudoplastycznych zjawisko rozrzedzania ścinaniem tłumaczone jest

stopniowym układaniem się asymetrycznych cząstek wzdłuż linii przepływu, co powoduje

zmniejszanie tarcia wewnętrznego płynu. Według innej teorii każda cząsteczka jest otoczona

powłoką z cieczy ośrodka rozpuszczającego. Na skutek zdzierania tej powłoki występuje

spadek wartości

η

a

.

Istnieją również płyny posiadające graniczne naprężenie styczne

τ

y

(rys.3). Płyn taki

przy naprężeniach

τ

<

τ

y

zachowuje się jak ciało stałe; dopiero po przekroczeniu granicy

płynięcia trwała struktura ulega zniszczeniu, a układ wykazuje własności cieczy (rys.3). Płyny

te noszą nazwę plastycznolepkich.

Rys.3. Krzywe płynięcia płynów reostabilnych wykazujących granicę płynięcia

1 – płyn plastycznolepki Binghama, 2,3 – nieliniowe płyny plastycznolepkie.

Własności reologiczne nieliniowych płynów plastycznolepkich opisuje model

Herschela i Dulkleya:

m

p

y

/

1













⋅

+

=

•

γ

η

τ

τ

(8)

gdzie:

η

p

-dynamiczny współczynnik lepkości plastycznej, [Pa s],

m-parametr reologiczny.

6

Płyny reologicznie niestabilne wykazują lepkość pozorną

η

a

zależną od szybkości

ś

cinania, zmienną w czasie. Płyny te mogą posiadać charakter tiksotropowy lub

antytiksotropowy (reopeksyjny). Układ tiksotropowy znajdujący się przez dłuższy czas w

spoczynku, a następnie poddany stałej szybkości ścinania, wykazuje zjawisko odwracalnego

zmniejszania naprężenia stycznego z czasem. W tych samych warunkach, w przypadku

antytiksotropii naprężenie styczne zwiększa się odwracalnie z czasem. To tłumaczy

występowanie pętli histerezy (rys.4).

Rys.4. Przykłady histerezy krzywej płynięcia dla płynów

a-tiksotropowych,

b-antytiksotropowych.

Zjawisko tiksotropii jest wywołane tymi samymi przyczynami co rozrzedzanie ścinaniem

płynów reostabilnych, z tą różnicą, że w przypadku płynów reostabilnych równowaga między

naprężeniem stycznym i szybkością ścinania zachodzi natychmiast (w rzeczywistości - w

bardzo krótkim czasie), natomiast dla płynów tiksotropowych potrzebny jest pewien czas do

jej osiągnięcia.

Własności reologicznych płynów sprężystolepkich nie można opisać w prosty sposób,

ponieważ zależą one nie tylko od czasu, ale są również funkcją

τ

,

γ

•

, d

τ

/dt i d

γ

•

/dt.

Roztwory i stopy polimerów wysokocząsteczkowych, a także układy wielofazowe (np.

emulsje) wykazują cechy sprężystolepkie.

Znajomość parametrów określających własności płynów nienewtonowskich, czyli

parametrów reologicznych, w czasie przepływu tych płynów przez przewody o różnym

rodzaju przekroju poprzecznego lub warstwy porowate, jest niezbędnym warunkiem do

określenia oporów przepływu tych płynów, do obliczenia mocy i efektywności mieszania oraz

do wyznaczenia intensywności wnikania ciepła.

7

Typowe wiskozymetry (Höpplera, Englera czy wiskozymetry absolutne) nie mogą być

użyte do wyznaczania krzywych płynięcia płynów nienewtonowskich. Do pomiaru

właściwości reologicznych płynów nienewtonowskich stosuje się reometry rotacyjne. Zasada

pomiaru reometrem kapilarnym polega na ustalonym, laminarnym i izotermicznym

przetłaczaniu badanego płynu przez kapilarę o gładkiej powierzchni. Podstawą do określenia

wielkości reologicznych stanowi pomiar strumienia objętości cieczy V

1

jako funkcji spadku

ciśnienia w kapilarze o znanej długości L i średnicy d. Własności reologiczne płynu

charakteryzują w sposób jednoznaczny zależność między naprężeniem stycznym przy ścianie

d

∆

P/4L i wielkością 32V

1

/

π

d

3

postaci:

©

3

1

©

32

4

n

d

V

k

L

P

d













⋅

=

∆

π

(9)

gdzie:

n

’

-wskaźnik charakterystyczny płynięcia,

k

’

-współczynnik „konsystencji” (im większa jest wartość k

’

, tym bardziej lepki jest

dany płyn), [Pa s].

Reometry kapilarne charakteryzują się prostą konstrukcją i bardzo szerokim zakresem

pracy. Warunek ustalonego przepływu eliminuje jednak zastosowanie tego wiskozymetru do

badań płynów reologicznie niestabilnych.

W przypadku zawiesiny o dużych cząsteczkach ciała stałego stosuje się rotametry

rurowe. Zasada pomiaru jest taka sama jak w przypadku zastosowania reometrów

kapilarnych.

W

REOMETRACH ROTACYJNYCH

ścinaniu ulega płyn znajdujący się między dwoma

elementami, najczęściej cylindrami współosiowymi (jeden często nazywany jest cylindrem, a

drugi – tłokiem), z których jeden (tłok) wykonuje ruchy obrotowe.

Naprężenie styczne w rotametrze rotacyjnym oblicza się z następującej zależności:

2

2 lr

M

r

π

τ

=

(10)

Szybkość ścinania wynosi:

2

2

2

r

R

R

−

=

•

ω

γ

(11)

A dynamiczny współczynnik lepkości wyrażony jest wzorem (12):

•

=

γ

τ

η

r

(12)

8

Pomiar polega na określeniu prędkości kątowej

ω

wirującego elementu i momentu

skręcającego M

sk

. pozorny dynamiczny współczynnik lepkości płynu nienewtonowskiego

η

określa równanie (13) powstałe po podstawieniu rów.(10) i (11) do zależności (12):

(

)

ω

π

η

sk

M

R

lr

r

R

⋅

−

=

2

2

2

2

2

(13)

lub:

ω

η

sk

M

k

⋅

=

1

(14)

gdzie:

(

)

2

2

2

2

1

2

R

lr

r

R

k

π

−

=

R -promień cylindra,

r-promień tłoka

l-długość (wysokość) tłoka.

Ponieważ równanie (13) obowiązuje dla układu cylindrów nieskończenie długich,

dlatego w reometrach rzeczywistych konieczne jest uwzględnienie zakłóceń występujących

na brzegach oraz efektu wywołanego dodatkową powierzchnią pomiarową podstaw

cylindrów.

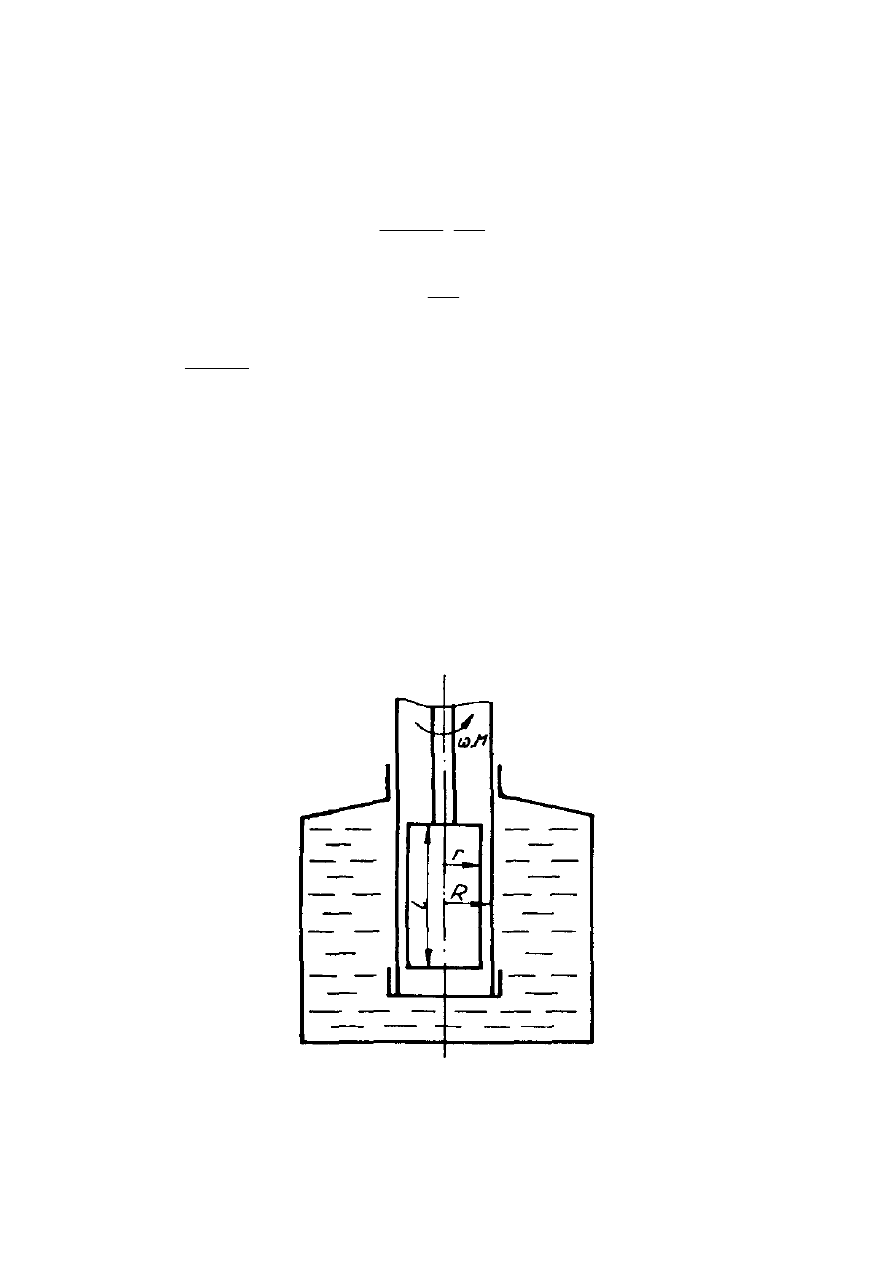
W celu zobrazowania działania reometru rotacyjnego Reotest-2 na rys.5. przedstawiono

przekrój cylindra oraz tłoka.

Rys.5. Przekrój cylindra i tłoka reometru Reotest-2.

9

2. Cel ćwiczenia

Celem ćwiczenia jest poznanie podstawowych pojęć z zakresu reologii oraz

wyznaczenie krzywej płynięcia i parametrów reologicznych płynów reometrem rotacyjnym

typ: Rheotest-2.

3. Urządzenia i odczynniki.

Do wyznaczenia parametrów reologicznych cieczy niezbędne są następujące

urządzenia i odczynniki:

•

reometr rotacyjny Rheotest-2 (schemat urządzenia przedstawiono na rysunku 5),

•

termostat U-5,

•

roztwory gliceryny, metylocelulozy lub zawiesiny drożdży.

4. Metodyka wykonania ćwiczenia

W zależności od lepkości badanej cieczy należy dobrać cylinder i tłok (patrz tabela w

załączniku 2).

W zależności od rodzaju dobranego cylindra należy użyć odpowiednią ilość badanej cieczy

(tabela 1).

Tabela 1.

Nr cylindra

N

S1

S2

S3

H

Ilość cieczy badanej [cm

3

]

±

5% 10

25

30

50

17

Po dobraniu tłoka, cylindra i wlaniu cieczy badanej do cylindra, należy:

a)

umocować tłok w uchwycie Rheotestu,

b)

umocować cylinder,

c)

umocować płaszcz grzejny,

d)

ustawić przekładnię na pozycję I i b (11),

e)

odczytać temperaturę,

f)

pokrętło regulacji obrotów R

0

(9) ustawić na pozycji 1,

g)

włączyć obroty tłoka przyciskiem O

t

(47),

h)

włączyć przycisk odczytu przyrządu na skali

α

(48),

i)

odczytać na skali wartość

α

,

10

j)

stopniowo zwiększać obroty pokrętłem R

0

. Jeżeli wskazania przyrządu pomiarowego

są poza skalą należy przerwać pomiar.

k)

Dla każdego z płynów należy wykonać po dwa pomiary. W przypadku uzyskania

rozbieżnych wyników, wykonać pomiar po raz trzeci.

5. Opracowanie wyników

1. Otrzymane wyniki pomiarów i obliczeń należy umieścić w tabeli 2.

Tabela 2. Wyniki pomiarów i obliczeń

OBROTY

(a lub b)

α

τ

r

γ

•

η

Lp.













2

cm

dyn













s

1

[cP]

1

1

2

2

3

3

4

4

5

5

6

6

7

7

8

8

9

9

10

10

11

11

12

12

2. Należy obliczyć naprężenie styczne

τ

r

[dyn/cm

2

] z równania:

τ

r

=z

⋅α

(15)

gdzie:

z-stała zależna od rodzaju tłoka i cylindra,

11

Stałą z odczytuje się z tabeli 3.

Tabela 3. Wartości stałej z

rodzaj cylindra/rodzaj tłoka

wartość stałej z

I

II

N/N

3,15

31,80

S/S1

5,56

56,10

S/S2

6,09

60,80

S/S3

8,30

82,50

H/H

29,30

293,50

3. Z tabeli 4 odczytujemy wartość szybkości ścinania

γ

•

.

Tabela 4. Wartości szybkości ścinania

γ

•

Wartość

γ

•

[1/s]

1a

2a

3a

4a

5a

6a

7a

8a

9a

10a

11a

12a

S1,N

3

5,4

9

16,2

27

48,6

81

145,8 243 437,4 729

1312

S2

1

1,8

3

5,4

9

16,2

27

48,5

81

145,8 243 437,4

S3

0,333

0,6

1

1,8

3

5,4

9

16,2

27

48,6

81

145,8

H

0,333

0,6

1

1,8

3

5,4

9

16,2

27

48,6

81

145,8

Wartość

γ

•

[1/s]

1b

2b

3b

4b

5b

6b

7b

8b

9b

10b

11b

12b

S1,N

1,5

2,7

4,5

8,1

13,5

24,3

40,5

72,9 121,5 218,7 364,5 656

S2

0,5

0,9

1,5

2,7

4,5

8,1

13,5

24,3

40,5

72,9 121,5 218,7

S3

0,1667 0,3

0,5

0,9

1,5

2,7

4,5

8,1

13,5

24,3

40,5

72,9

H

0,1667 0,3

0,5

0,9

1,5

2,7

4,5

8,1

13,5

24,3

40,5

72,9

12

4. Następnie obliczamy wartość

η

[cP] określoną następującym równaniem:

100

⋅

=

•

γ

τ

η

r

(16)

5. Należy również sporządzić wykres zależności lepkości (

η

) od szybkości ścinania (

γ

•

).

6. Na skali podwójnie logartytmicznej wykonać wykres naprężeń stycznych (

τ

r

) od szybkości

ś

cinania (

γ

•

) (krzywa płynięcia).

7. Określić rodzaj płynu.

8. Wykorzystując model Ostwalda (rów. (6)), wyznaczyć parametry reologiczne płynu (k i n).

Literatura

1. Kembłowski Z.: Reometria płynów newtonowskich. WNT Warszawa 1973.
2. Wilkinson W.: Ciecze nienewtonowskie. WNT Warszawa 1963.
3. Serwiński M.: Zasady inżynierii chemicznej. WNT Warszawa 1976, s.104-111.