Projekt z układów dynamicznych w zastosowaniach.
Alina Maląg
8.01.2016
1
Model Odella
Niech x oznacza liczebność ofiar, a y oznacza liczebność drapieżników. Zakładamy także, że
w środowisku nie występują inne populacje lub nawet jeśli występują to ich liczebność nie
ma wpływu na liczebność drapieżników i ofiar. Zakładamy także, że nie istnieją zewnętrzne
czynniki znacząco wpływające na liczebność obu populacji. Model opisujący zależność pomiędzy
liczebnościami tych dwóch populacji może być opisana następującym układem równań:
x
′
= x[x(1
− x) − y]
(1)
y
′
= y(x
− a),
(2)
gdzie a
0 oznacza parametr kontroli. Ze względu na poprawność biologiczną bierzemy pod
uwagę tylko wartości x
0 oraz y 0. Powyższy model będziemy nazywali modelem Odella.
2
Punkty stałe układu
Przyrównujemy prawe strony równań (1) i (2) do zera. Stąd otrzymujemy:
x(x
− x
2
− y) = 0
(3)
y(x
− a) = 0
(4)
Z pierwszego równania otrzymujemy, że: x=0 lub x
− x
2
− y = 0.
Przyjmując x=0 z drugiego równania uzyskujemy y=0. Stąd pierwszym punktem stałym jest
P1=(0,0).
Z drugiego równania otrzymujemy, że: y=0 lub x=a.
Przyjmując y=0 i podstawiając do piewszego równania otrzymujemy x
− x
2
= 0. Stąd drugim
punktem stałym jest P2=(1,0).
Dla x=a z pierwszego równania otrzymujemy, że a(a
−a
2
−y) = 0 skąd trzecim punktem stałym
jest P 3 = (a, a
− a
2
).
3
Stabilność punktów stałych
W celu zbadania stabilności punktów stałych układu rozważmy Jakobian dla (1) i (2).
Oznaczmy:
F (x, y) = (x(x
− x
2
− y), y(x − a)).
Aby zbadać stabilność punktów stałych, zbadamy Jakobian funkcji F:
J F (x, y) =
[
2x
− 3x
2
− y
−x
y
x
− a
]
.
1
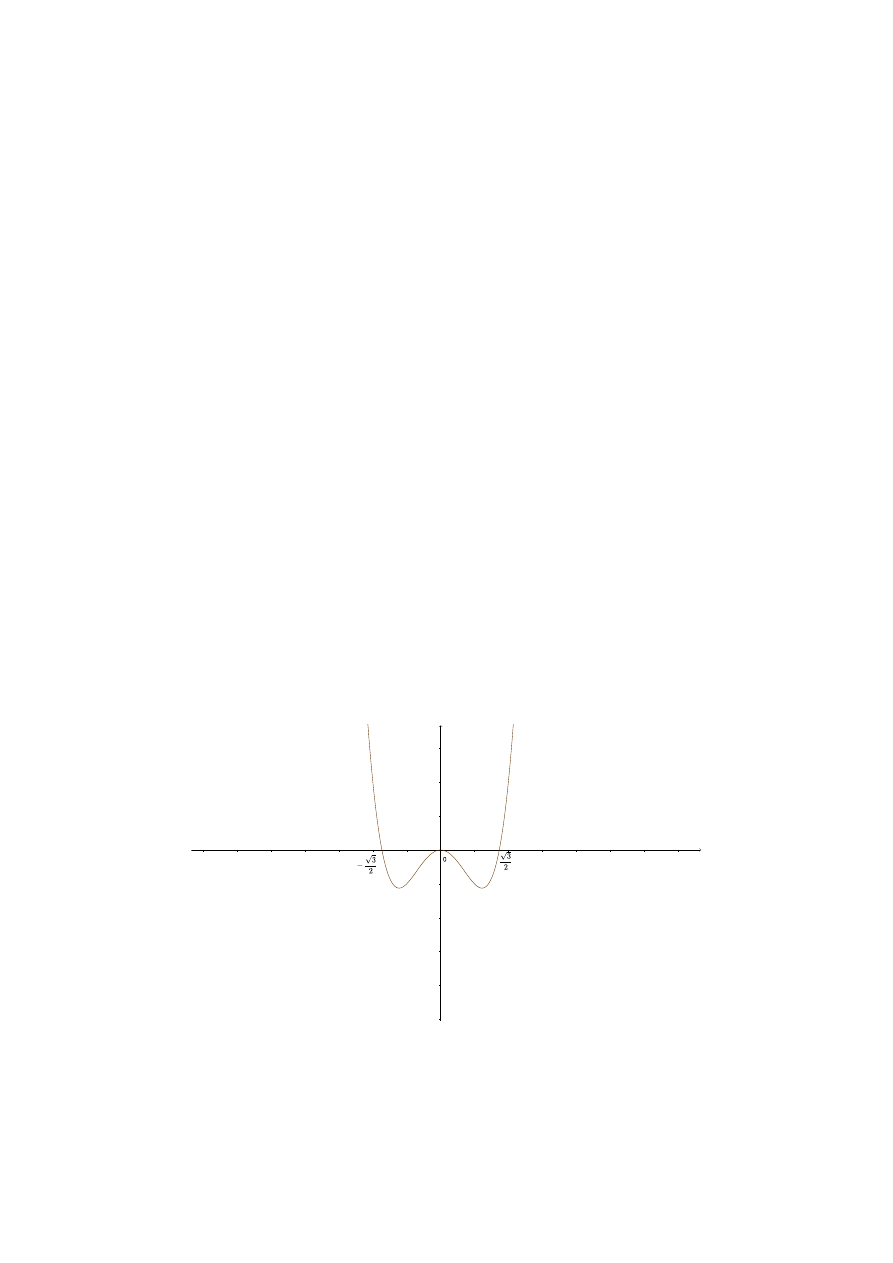
J F (P 1) = J F (0, 0) =
[
0
0
0
−a
]
.
Wartości własne macierzy JF(P1) wynoszą 0 i -a, skąd z twierdzenia Grobmanna-Hartmanna nie
możemy jednoznacznie wnioskować o jego stabilności lub niestabilności. Jednakże poszukujemy
dodatniego punktu bifurkacji skąd punkt P1=(0,0) nie spełnia kryterium poszukiwań.
J F (P 2) = J F (1, 0) =
[
−1
−1
0
1
− a
]
.
Wartości własne macierzy JF(P2) wynoszą -1 i 1-a, skąd z twierdzenia Grobmanna-Hartmanna
wnioskujemy, że dla a < 1 punkt P2 jest siodłem, a dla a
1 jest węzłem stabilnym.
J F (P 3) = J F (a, a
− a
2
) =
[
a
− 2a
2
−a
a
− a
2
0
]
.
Rozważmy wartości własne macierzy JF(P3):
det
[
a
− 2a
2
− λ −a
a
− a
2
−λ
]
=0 .
Równanie charakterystyczne wygląda następująco:
λ
2
+ λ(2a
2
− a) + a
2
− a
3
= 0
∆ = (2a
2
− a)
2
− 4(a
2
− a
3
)
∆ = 4a
4
− 3a
2
Rysunek 1: wykres funkcji a
2
(4a
2
− 3)
2
Rozważmy przypadki:
1. ∆ > 0 :
∆ = 4a
4
− 3a
2
> 0
wtedy i tylko wtedy, gdy
a
∈ (−∞, −
√
3
2
)
∪ (
√
3
2
,
∞)
Wówczas wartości własne wynoszą:
λ
1
=
−2a
2
+ a +
√
4a
4
− 3a
2
2
=
−a
2
+
1
2
a +
√
−3a
2
+ 4a
4
2
λ
2
=
−2a
2
+ a
−
√
4a
4
− 3a
2
2
=
−a
2
+
1
2
a
−
√
−3a
2
+ 4a
4
2
2. ∆ = 0 :
∆ = 4a
4
− 3a
2
= 0
wtedy i tylko wtedy, gdy
a =
{−
√
(3)
2
, 0,
√
(3)
2
}
Otrzymujemy wartość własną:
λ
0
=
−2a
2
− a
2
3. ∆ < 0 :
∆ = 4a
4
− 3a
2
< 0
wtedy i tylko wtedy, gdy
a
∈ (
−
√
3
2
, 0)
∪ (0,
√
3
2
)
Obliczmy wartości własne powyższego Jakobianu:
λ
1
=
−2a
2
+ a +
√
4a
4
− 3a
2
2
=
−a
2
+
1
2
a +
√
3a
2
− 4a
4
2
i
λ
2
=
−2a
2
+ a
−
√
4a
4
− 3a
2
2
=
−a
2
+
1
2
a
−
√
3a
2
− 4a
4
2
i
Dla parametru a
∈ (
1
2
,
√
3
2
) otrzymujemy ognisko stabilne, zaś dla parametru a
∈ (0,
1
2
)
dostajemy ognisko niestabilne. To sugeruje bifurkację Hopfa.
Aby udowodnić występowanie bifurkacji Hopfa dla układu, sprawdźmy, czy istnieje parametr a
dla którego spełnione są założenia twierdzenia o bifurkacji Hopfa:
Aby zachodziła bifurkacja Hopfa część rzeczywista wartości własnych musi być równa 0, a jej
część urojona różna od 0.
Stąd otrzymujemy:
Reλ
1,2
= 0
−a
2
+
1
2
a = 0
⇔ a = 0 lub a =
1
2
3
Ponadto:
Imλ
1,2
=
±
√
3a
2
− 4a
4
2
̸= 0
Sprawdźmy, dla jakich wartości parametru a, część urojona się zeruje:
±
√
3a
2
− 4a
4
2
= 0
a = 0 lub a =
√
3
2
lub a =
−
√
3
2
Stąd a
∈ R/
{
−
√
3
2
, 0,
√
3
2
}
.
Łącząc przypadki otrzymujemy, że bifurkacja Hopfa zachodzi dla parametru a =
1
2
4
Portrety fazowe
Rozważmy portrety fazowe modelu Odella:
1. dla parametru, w którym występuje bifurkacja a =
1
2
2. dla parametru mniejszego niż a =
1
2
, a=0.4
3. dla parametru większego niż a =
1
2
, a=0.6
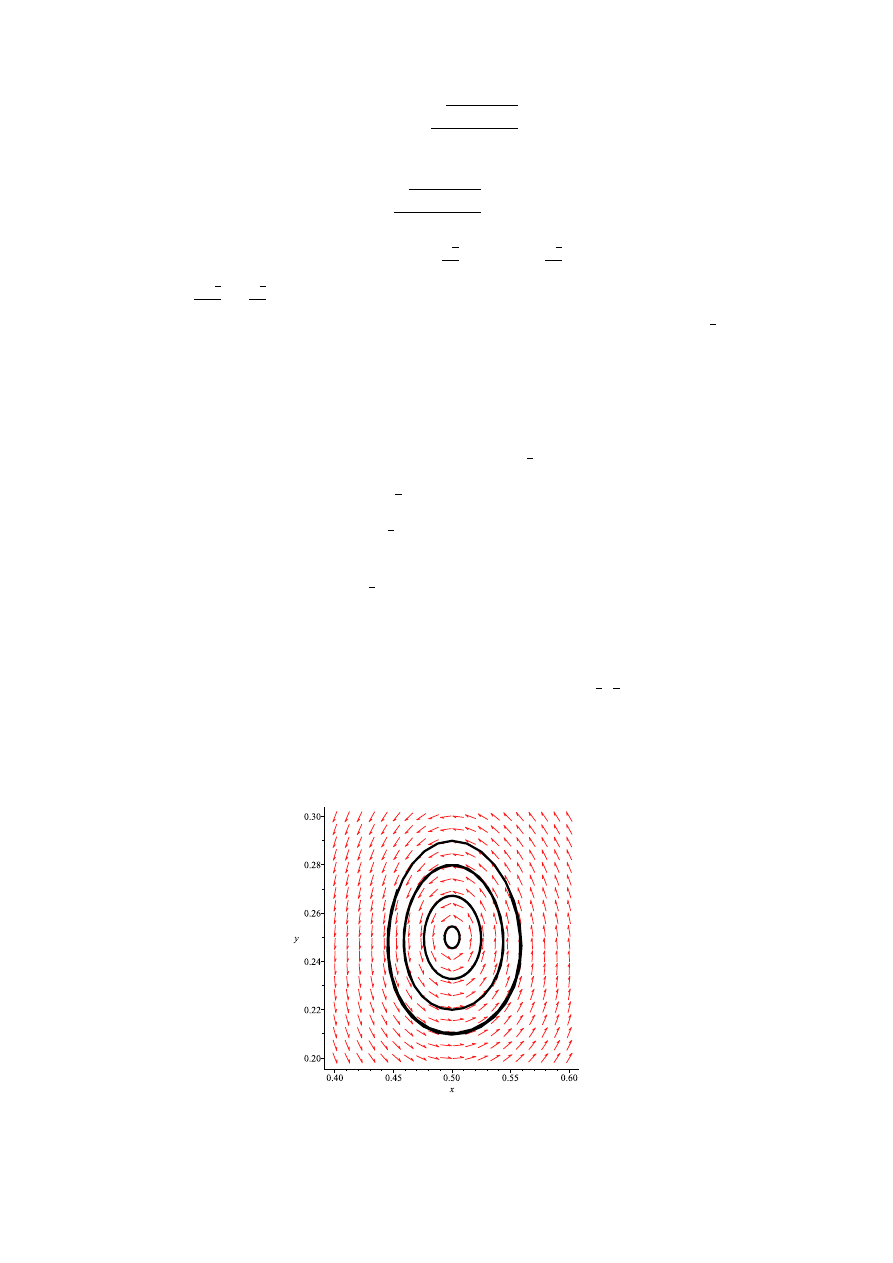
Ad.1
Rozważmy układ z parametrem a =
1
2
. Wówczas model przyjmuje postać:
x
′
= x[x(1
− x) − y]
(5)
y
′
= y(x
− 0.5),
(6)
Punkty stałe powstałego układu to: A1 = (0, 0) A2 = (1, 0) A3 = (
1
2
,
1
4
). Ze względu na badaną
bifurkację interesuje nas tylko punkt A3. Układ w otoczeniu tego punktu jest centrum.
Rysunek 2: Przypadek 1
4
Ad.2
Rozważmy układ z parametrem a = 0.4. Wówczas model przyjmuje postać:
x
′
= x[x(1
− x) − y]
(7)
y
′
= y(x
− 0.4),
(8)
Punkty stałe powstałego układu to: B1 = (0, 0) B2 = (1, 0) B3 = (0.4, 0.24). Ze względu na
badaną bifurkację interesuje nas tylko punkt A3. Układ w otoczeniu tego punktu jest ogniskiem
niestabilnym.
Rysunek 3: Przypadek 2
Ad.3
Rozważmy układ z parametrem a = 0.6. Wówczas model przyjmuje postać:
x
′
= x[x(1
− x) − y]
(9)
y
′
= y(x
− 0.6),
(10)
Punkty stałe powstałego układu to: B1 = (0, 0) B2 = (1, 0) B3 = (0.6, 0.24). Ze względu na
badaną bifurkację interesuje nas tylko punkt A3. Układ w otoczeniu tego punktu jest ogniskiem
stabilnym.
5
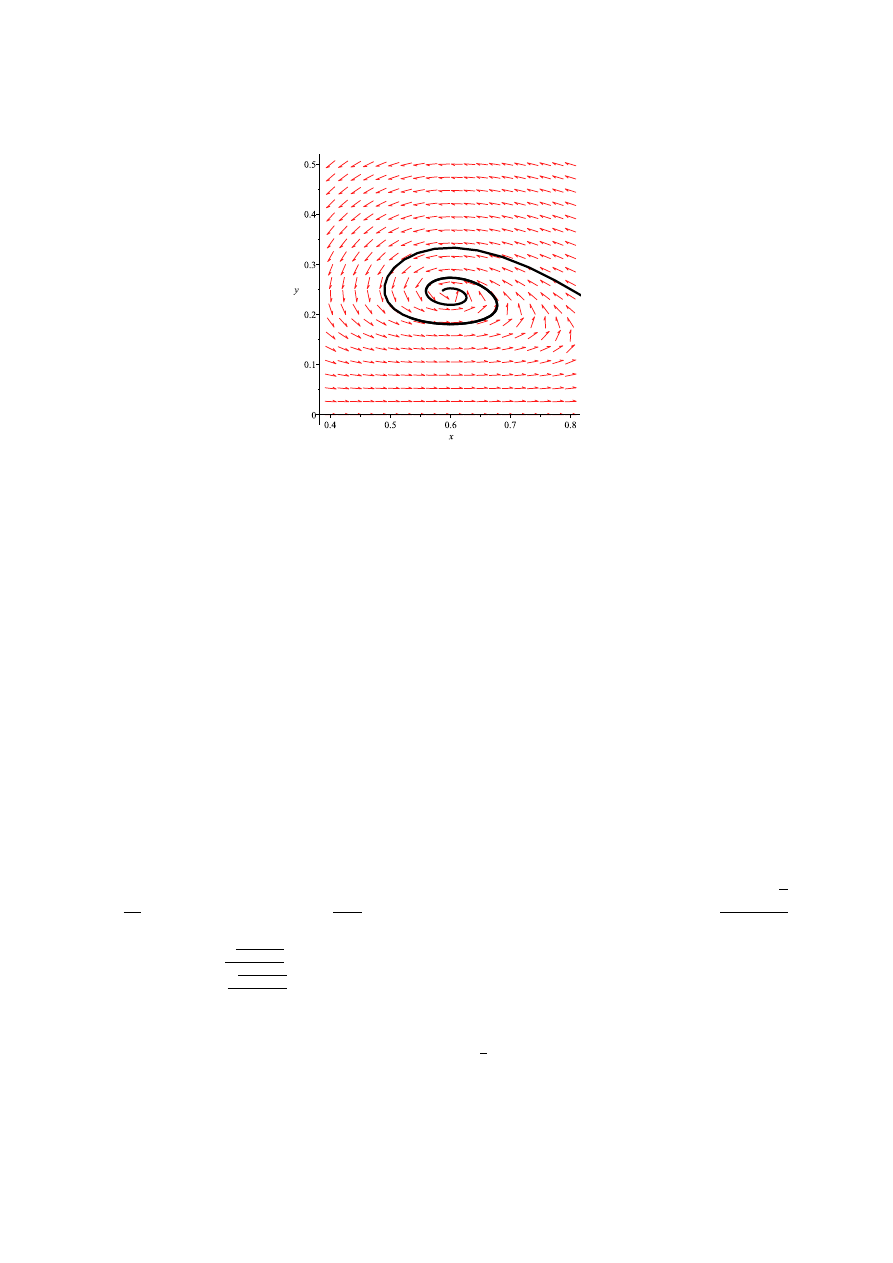
Rysunek 4: Przypadek 3
Zachowanie układu dla podanych parametrów sugeruje bifurkację superkrytyczną. Aby potwier-
dzić naszą hipotezę obliczymy współczynnik A.
Oznaczmy:
f (x, y) = x[x(1
− x) − y],
g(x, y) = y(x
− a).
Wówczas:
f
x
= 2x
− 3x
2
− y
g
x
= y
f
xx
= 2
− 6x
g
xx
= 0
f
xxx
=
−6
g
xxx
= 0
f
y
=
−x
g
y
= x
f
yy
= 0
g
yy
= 0
f
yyy
= 0
g
yyy
= 0
f
xy
=
−1
g
xy
= 1
Wówczas współczynnik A będzie miał postać:
A =
1
16
(f
xxx
+f
xyy
+g
xxy
+g
yyy
)+
1
16ω
[f
xy
(f
xx
+f
yy
)
−g
xy
(g
xx
+g
yy
−f
xx
g
xx
+g
yy
f
yy
] =
−3 +
√
2
8
< 0,
gdzie ω = Imλ =
√
3a
2
−4a
4
2
Przyjmując ω =
−
√
3a
2
−4a
4
2
wartość parametru A będzie mniejsza od otrzymanej, zatem również
ujemna.
Otrzymany współczynnik A jest mniejszy od zera, a co za tym idzie otrzymana bifurkacja jest
superkrytyczna. Oznacza to, że dla parametru a <
1
2
dostajemy następujący cykl graniczny:
6
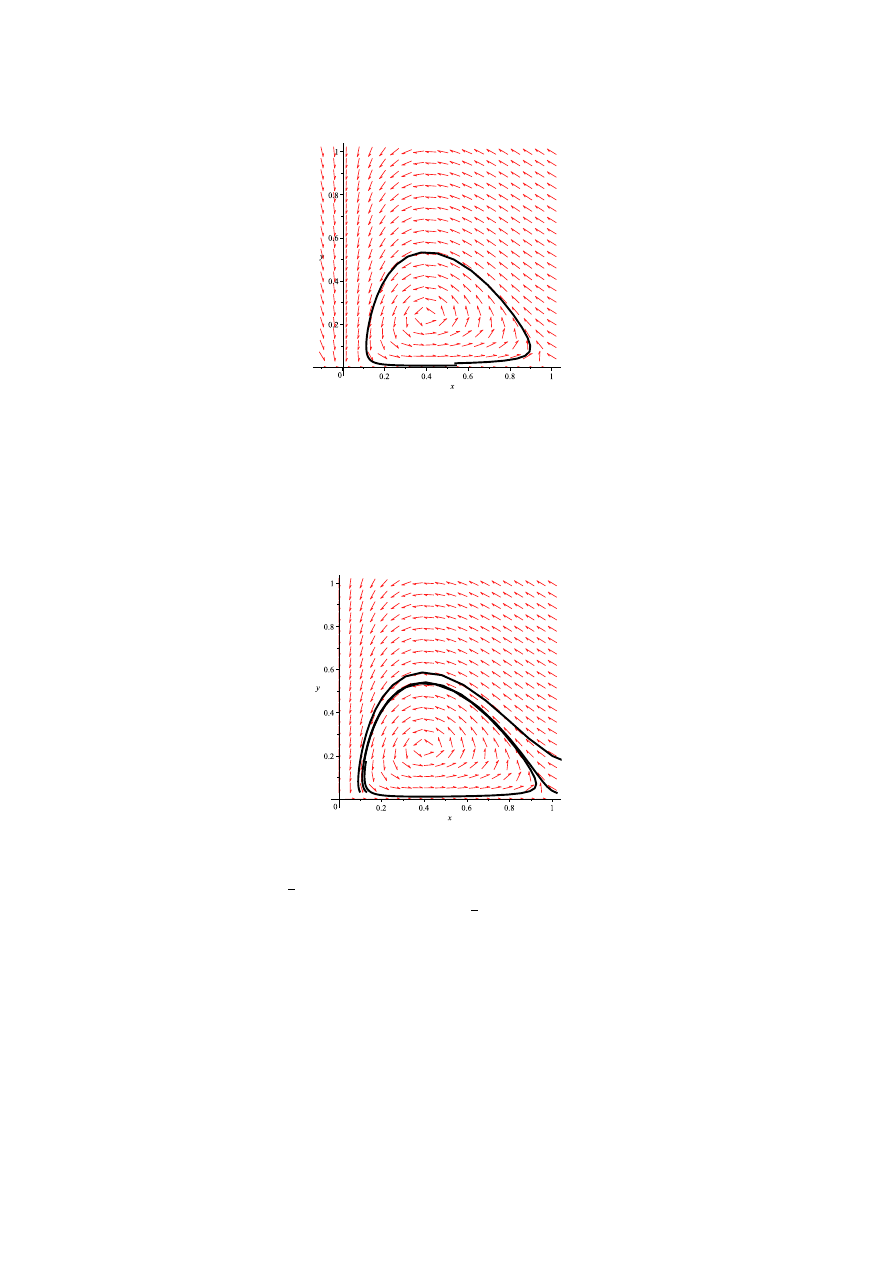
Rysunek 5: cykl graniczny
Cykl graniczny jest przyciągający, dlatego też zewnętrzna orbita nawija sie od niego od ze-
wnątrz.
Rysunek 6: Orbita nawija się z zewnątrz na cykl graniczny.
Podsumowując: dla a <
1
2
mamy punkt stacjonarny niestabilny i jednocześnie rozwiązanie
okresowe stabilne zaś po przej- ściu przez a =
1
2
dostajemy punkt stabilny, a rozwiązanie
okresowe zanika.
7