
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.1
Základy frekvenční analýzy signálů a přístrojová technika
Úvod:
Analýza signálů je základem Číslicových měřicích systémů neboť každý měřený signál se
podrobuje analýze. Analýza signálů je velmi rozsáhlý obor s určitými specialitami pro různá
odvětví.
Uveďme stručný přehled možných variant analýzy signálů.
• analýza deterministických (stacionárních) signálů
•
charakteristiky signálů v časové oblasti
•
zpracování signálů ve frekvenční oblasti, frekvenční analýza
•
číslicová filtrace
•
zpracování signálů za přítomnosti šumu
•
zpracování signálů z mechanických systémů, souběhová filtrace(order
tracking), synchronní filtrace (time enhancement), měření a hodnocení
frekvenčních charakteristik, koherenční funkce
•
modulace a demodulace signálů, amplitudová , frekvenční a fázová
charakteristika, Hilbertova transformace, analýza obálky
• zpracování stochastických signálů, z hlediska rozložení amplitud – rozdělení
pravděpodobností, časové –korelační funkce, spektrální – spektrální výkonové hustoty
• analýza nestacionárních signálů (analýza rychle se měnících signálů, spojená časově-
frekvenční analýza), moderní nástroj, který se vyvíjel zejména po r. 1985
•
lineární
• Short Time Fourier Transform (STFT)
• wavelett transformace spojité a diskrétní
• banky filtrů
• ostatní
•
nelineární
• Cohenovy třídy
• afinní
• ostatní
V rámci Číslicových měřicích systémů bude probrány Základy frekvenční analýzy a Číslicové
filtry. Další části analýzy signálů jsou probrány v předmětu Aplikace analýzy signálů.
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.2
Signál – převedená fyzikální veličina ( napětí, tlak aj.)
Základní údaje v časová oblasti
• Střední hodnota (centrální moment 1. řádu)
• Efektivní hodnota ( moment 2. řádu)
• Rozptyl, střední kvadratická odchylka ( centrální moment 2. řádu)
• Činitel výkyvu (crest factor)
• Korelační (kovarianční) funkce
• Pravděpodobnost rozložení
Frekvenční oblast
Základem pro zkoumání ve frekvenční bylo zjištění J.B.Fouriera, že jakékoliv
periodická funkce x(t) může být složena z harmonických funkcí o frekvencích, které jsou
násobkem základní frekvence dané reciprokou hodnotou periody signálu T.
( )
(
)
( )
∑
∞
=
⋅
⋅
+
⋅
⋅
+
=
+
=
1
0
2
sin
2
cos
2
k
k
k
t
k
T
b
t
k
T
a
a
t
x
nT
t
x
t
x
π
π
kde
( )
( )
dt
t
k
T
t
x
T
b
dt
t
k
T
t
x
T
a
T
k
T
k
∫
∫
⋅
⋅
=
⋅
⋅
=
0
0
2
sin
2
,
2
cos
2
π
π
x(t) je možno také rozepsat pomocí samostatných kosinových nebo sinových funkcí.
( )
(
)
( )
(
)
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
b
a
b
a
F
t
k
T
F
F
t
x
a
b
b
a
F
t
k
T
F
F
t
x
1
2
1
2
2
1
0
1
2
1
2
2
1
0
tan
,
,
2
sin
2
tan
,
,
2
cos
2
−
∞
=
−
∞
=
=
+
=
+
⋅
⋅
+
=
=
+
=
−
⋅
⋅
+
=
∑
∑
ϕ
ϕ
π
ϕ
ϕ
π
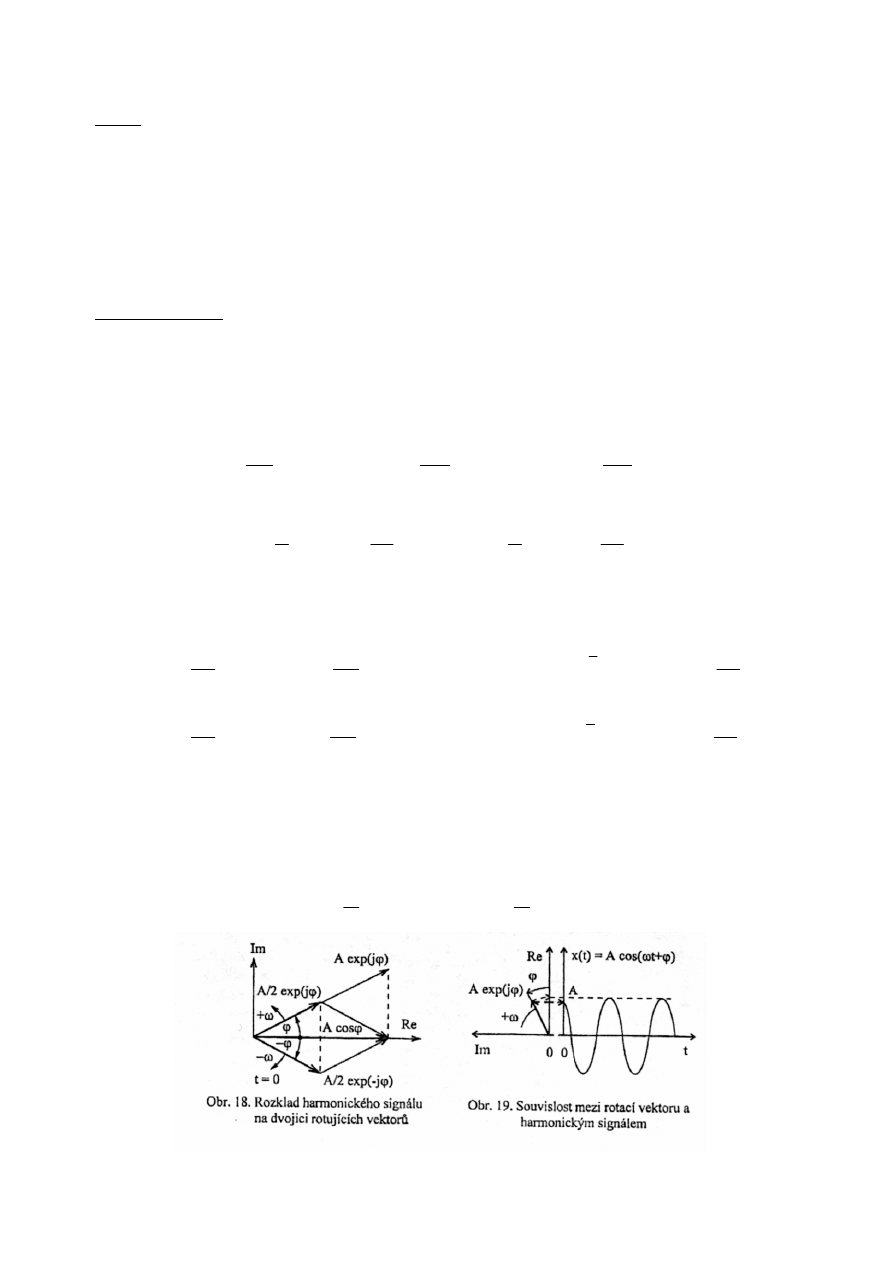
Reálný harmonický signál lze vyjádřit součtem dvou komplexně sdružených exponenciálních
funkcí:
(
)
(
)
(
)
(
)
(
)
ϕ
ω
ϕ
ω
ϕ
ω
+
−
⋅
+
+
⋅
=
+
⋅
t
j
A
t
j
A
t
A
exp
2
exp
2
cos

Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.3
Reálný harmonický signál je součet dvou rotujících vektorů (fázorů) o poloviční amplitudě
reálného signálu A/2 z nichž jeden rotuje kladným a druhý záporným směrem. V součtu se oba
promítají do reálné osy. To tvoří základ pro pochopení kladných a záporných frekvencí.
Pak lze napsat ( Fourierova řada v komplexním tvaru):
( )
( )
...
3
,
2
,
1
,
0
,
2
exp
1
,
2
exp
0
±
±
±
=
⋅
⋅
=
⋅
⋅
=
∑
∫
∞
−∞
=
k
pro
dt
t
k
T
j
t
x
T
c
t
k
T
j
c
t
x
k
t
k
k
π
π
Vzájemná souvislost reálných a komplexních definic:
(
)
(
)
(
)
k
k
k
k
k
k
k
k
k
k
k
k
c
c
j
b
c
c
a
jb
a
c
jb
a
c
−
−
−
+
=
+
=
−
=
+
=
,
2
1
,
2
1
Fourierovy řady
- určené pro periodické signály
- spektrum obsahuje pouze izolované složky s frekvencemi, které jsou násobky
základní (harmonické) frekvence
ω
0
=2
π/T.
Fourierova transformace obecného signálu
Fourierova transformace
- rozklad obecného (periodického i neperiodického) signálu na harmonické složky
- spektrum je spojitá funkce frekvence
( )
( )
{ }
( )
(
)
( )
( )
{
}
( )
( )
∫
∫
∞
∞
−
−
∞
∞
−
⋅
=
=
−
⋅
=
=
ω
ω
ω
π
ω
ω
ω
d
t
j
X
X
F
t
x
dt
t
j
t
x
t
x
F
X
exp
2
1
exp
1
Fourierova transformace vzorkovaného signálu
( )
(
) ( )
(
)
∑
∑
∞
−∞
=
∞
−∞
=
∆
−
⋅
=
∆
−
⋅
=
k
k
k
t
k
t
t
x
t
k
t
x
t
y
δ
δ
Vzorkovací signál y(t) je součin x(t) a periodické funkce obsahující Diracovy pulsy. Jde o
posloupnost Diracových pulsů posunutých o periodu vzorkování ∆t, fs=1/∆t.
( )
t
f
t
k
X
t
Y
s
s
k
∆
=
=
∆
−
∆
=
∑
∞
−∞
=
π
π
ω
π
ω
ω
2
2
,
2
1
Spektrum vzorkovaného signálu Y(
ω) je periodické s periodou ω
s
(f
s
).
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.4
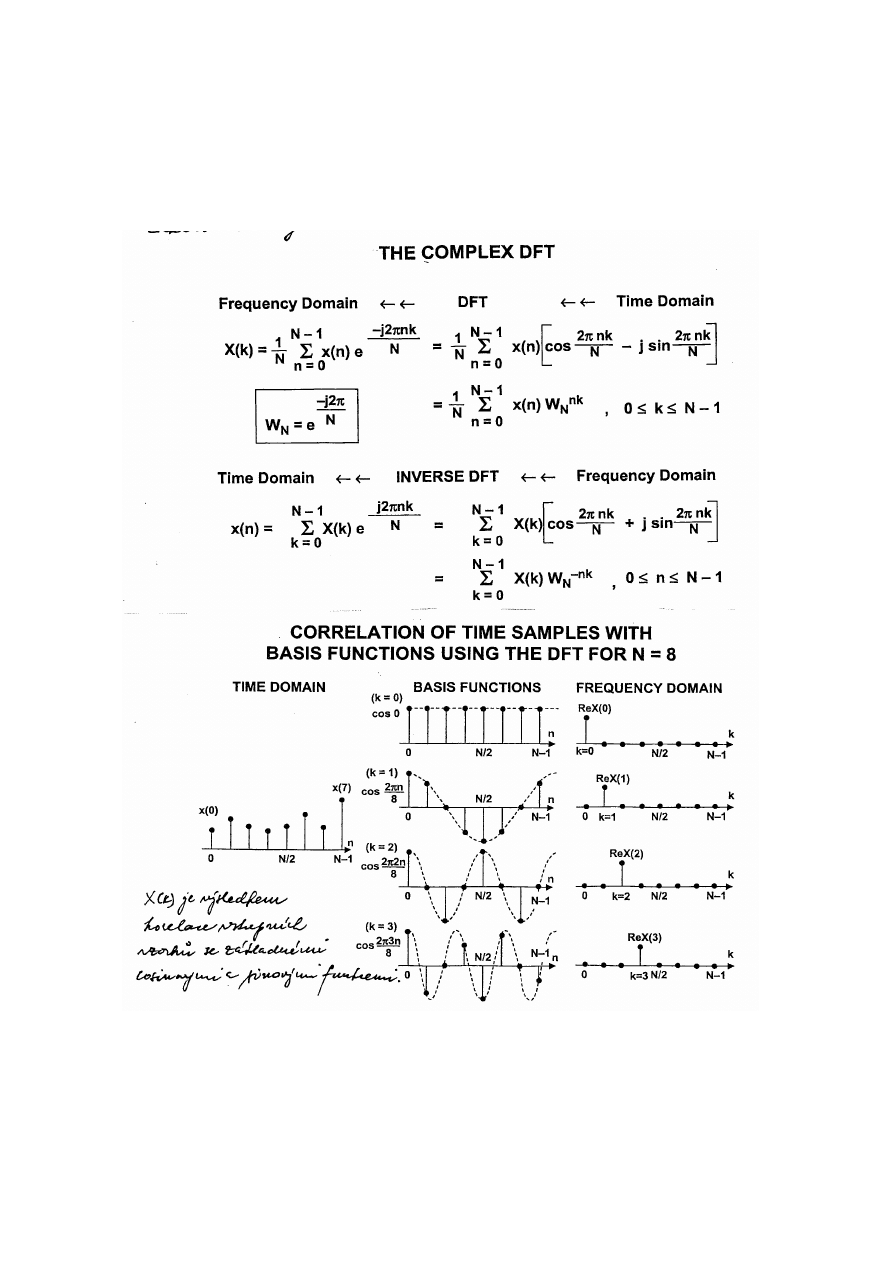
Diskrétní Fourierova transformace a algoritmy FFT
Za předpokladu, že x(t) je periodická funkce s periodou T=N*∆t – řad vzorků x(n) – je
výsledné spektrum X(k) diskrétní s odstupem frekvenčních složek ∆f=1/T a periodické
s periodou f
s
= f
vz
. Základní vztahy:
X(k) je vlastně výsledkem korelace vstupních vzorků se základními kosinovými a sinovými
funkcemi (
na obr. se jedná o cos funkce s nulovou imaginární části X(k)
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.5
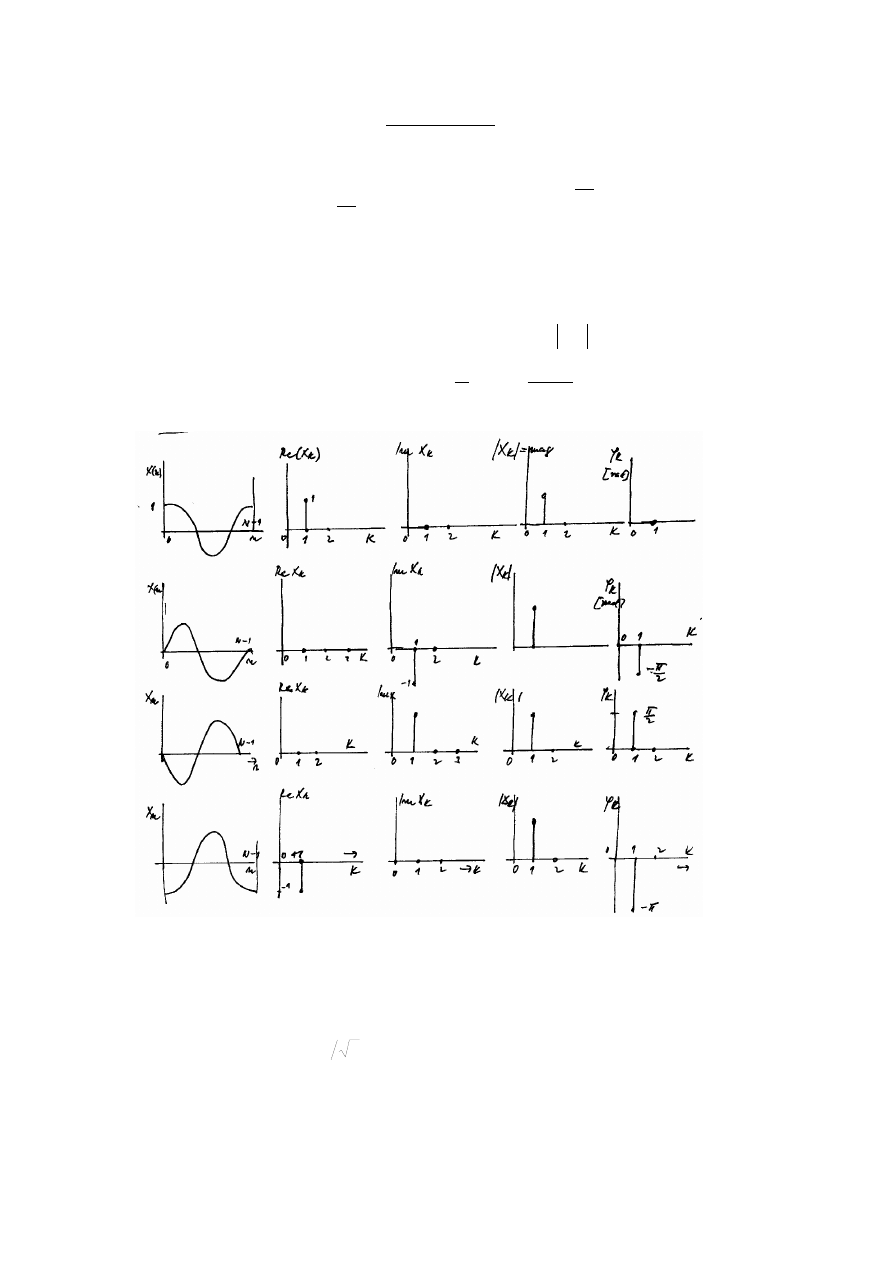
Představa DFT
Je nutno mít na zřeteli, že spektrum je komplexní, I když často, zejména v analýze náhodných
procesů není fáze komplexního spektra pro analýzu zajímavá.
[ ]
[ ]
∑
∑
−
=
−
−
−
=
⋅
=
=
⋅
=
1
0
2
1
0
,
1
N
k
nk
N
k
N
j
N
N
n
nk
N
k
w
X
n
x
e
w
w
n
x
N
X
π
spektrum je komplexní,
{ }
{ }
k
j
k
k
k
k
e
X
X
im
j
X
re
X
ϕ
−
⋅
=
⋅
+
=
s krokem ∆f
[
]
⋅
=
=
∆
⋅
=
N
f
k
X
T
k
X
f
k
X
X
s
k
Obrázky ukazují harmonický signál postupně posunutý. Magnituda spektra je ve všech
případech stejná, mění se jen reálná, imaginární část a tedy i fáze komplexního spektra. Vektor
komplexního spektra se otáčí po kružnici.
Pozn.: Hodnoty magnitudy |X[k]| bývají obvykle vyjádřeny v efektivních hodnotách namísto v amplitudách jako
odmocnina výkonového spektra, (krát
2
1
). Zvláště pokud používáme průměrování spekter.
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.6
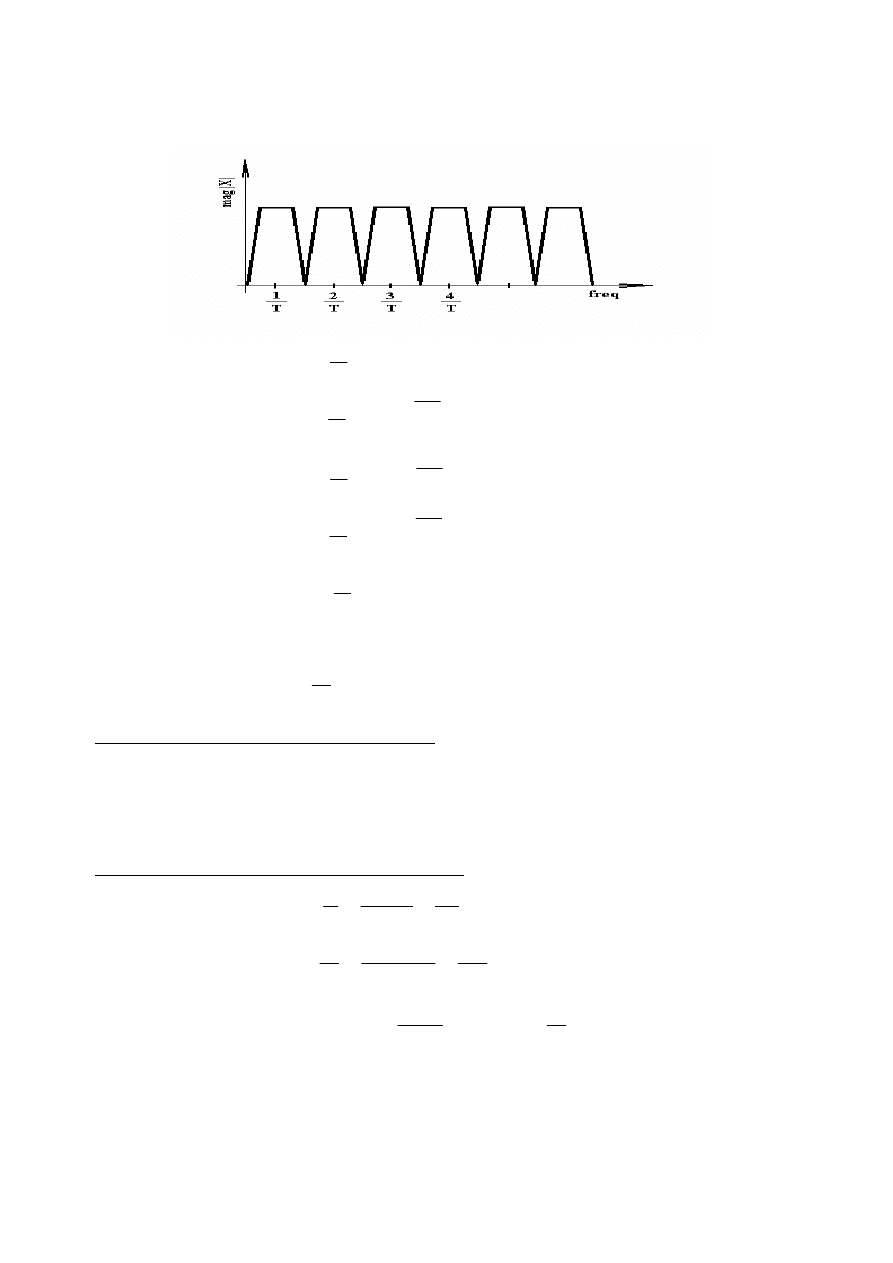
DFT si můžeme představit jako soustavu pásmových propustí se shodnou šířkou pásma danou
∆f = 1/T .
( )
[ ]
[ ]
[ ]
[ ]
[ ]
⋅
=
⋅
=
⋅
=
⋅
=
=
⇒
∑
∑
∑
∑
∑
−
=
⋅
−
−
=
⋅
−
−
=
⋅
−
−
=
⋅
−
−
=
1
0
2
1
0
3
2
3
1
0
2
2
2
1
0
2
1
1
0
0
1
1
1
1
1
N
n
n
j
N
N
n
n
N
j
N
n
n
N
j
N
n
n
N
j
N
n
e
n
x
N
X
e
n
x
N
X
e
n
x
N
X
e
n
x
N
X
n
x
N
X
t
x
π
π
π
π
Pozn.: Normalizační koeficient v definici DFT 1/N je v některých publikacích uváděn obráceně:
[ ]
{
}
{
} {
}
[ ]
{
}
n
x
N
X
X
n
x
IFT
k
k
FT
1
,
⇒
⇒
Vztah mezi DFT a koeficienty Fourierovy řady
{ }
{ }
k
k
k
k
X
im
b
X
re
a
X
a
⋅
=
⋅
=
⋅
=
2
,
2
,
2
0
0
Plyne z rozkladu reálného harmonického signálu na dvě komplexně sdružené exponenciální
funkce viz. str. 2
Základní vztahy – časová oblast / frekvenční oblast
f
N
f
t
f
f
f
f
N
T
t
N
f
t
N
T
f
s
N
MAX
N
MAX
s
∆
⋅
=
⋅
=
∆
⋅
=
=
=
⋅
=
=
∆
=
∆
⋅
=
=
∆
2
5
.
0
2
1
1
2
1
1
1
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.7
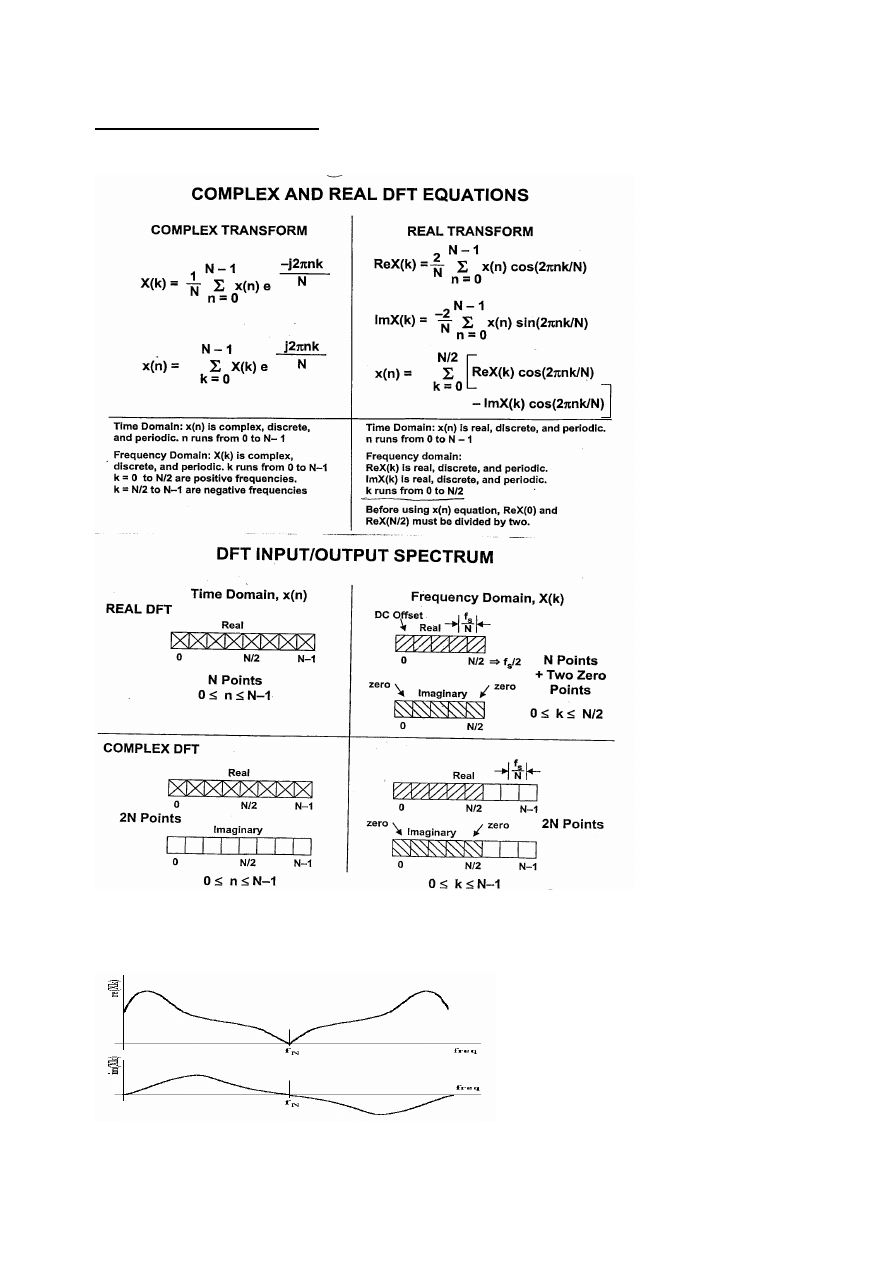
Komplexní a reálná DFT
Pro reálné signály platí sudá symetrie
ve reálných hodnotách X
k
{ }
{
}
k
N
k
X
re
X
re
−
=
,
lichá v imaginárních
{ }
{
}
k
N
k
X
im
X
im
−
−
=
.
Koeficienty
X
k
v rozsahu
<f
N
, f
s
> jsou
komplexně sdružené s koeficienty v
rozsahu
<0, f
N
>.
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.8
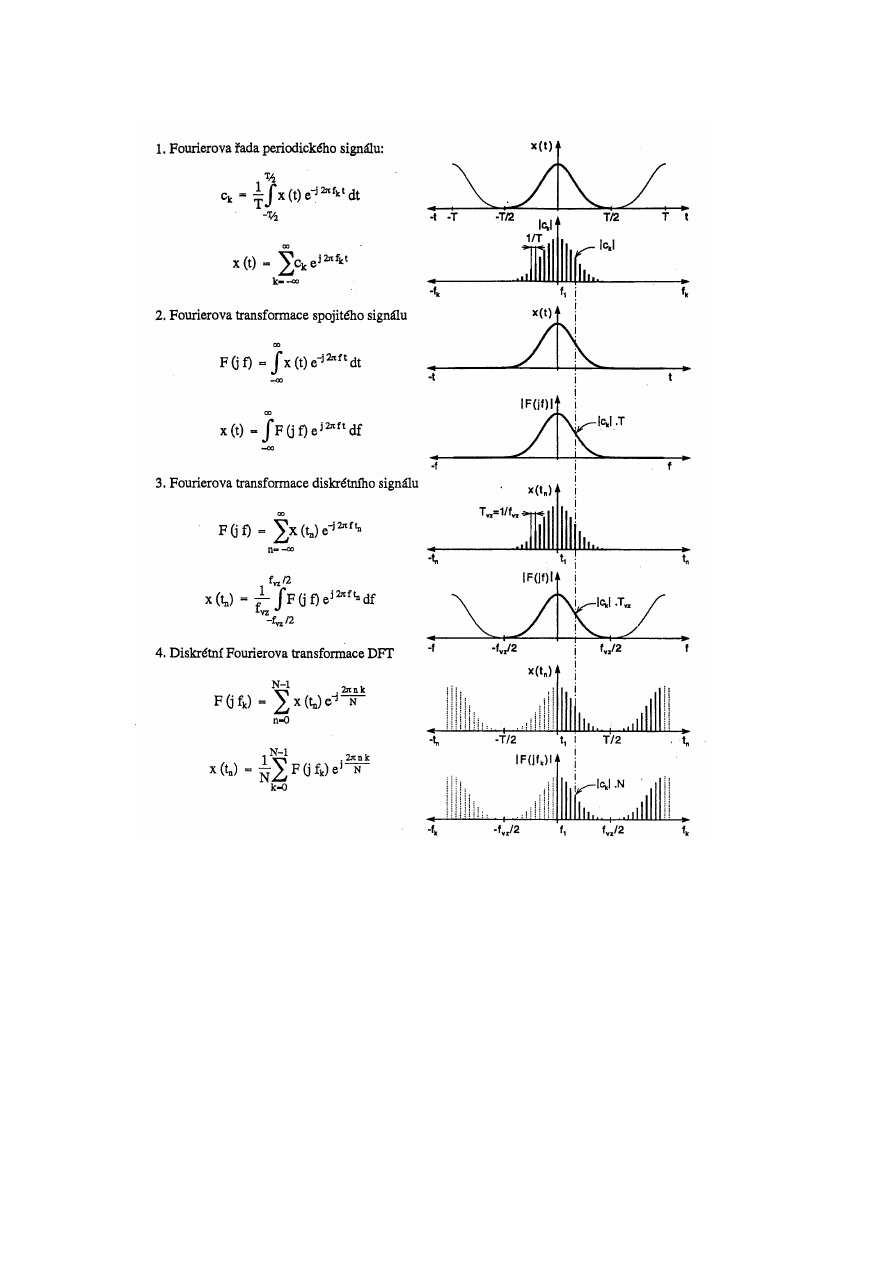
Shrnutí:
Periodický signál je dán opakováním Gausova pulzu. Spektrum Gausova pulzu je stejná funkce
jako původní časová funkce. Pozorně prohlédněte obrázky. 1.Periodický signál má diskrétní
spektrum s krokem frekvence daným převrácenou dobou periody. 2.Integrál s mezemi -∞ , ∞
dává pro neperiodický pulz spojité spektrum. 3.Diskrétní signál má periodické spektrum ( opak
bodu 1). 4.DFT je již z matematické definice periodická jak v originálech tak i obrazech.
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.9
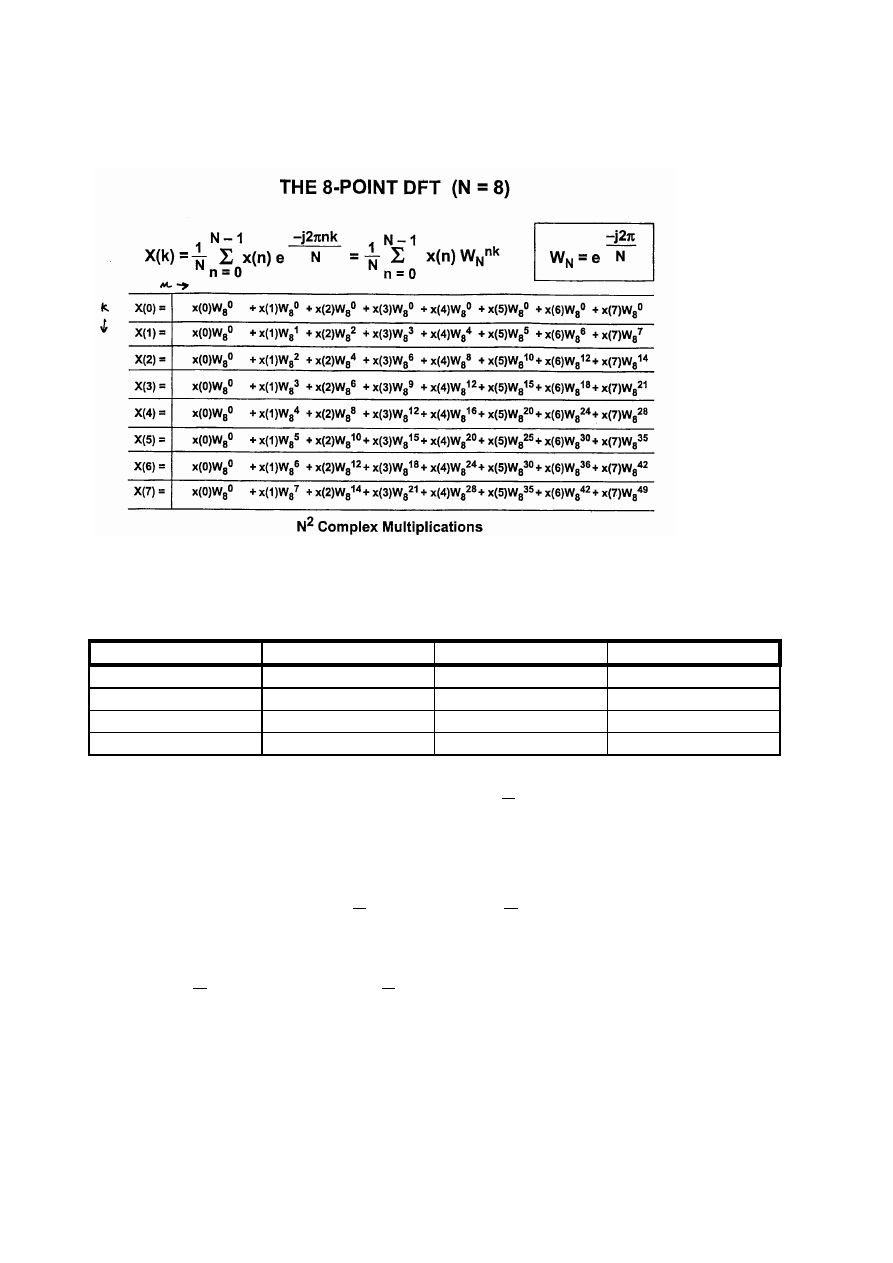
Rychlá Fourierova transformace, FFT
Klasická Fourierova transformace potřebuje
N
2
komplexních násobení a stejný počet
komplexních sčítání. FFT algoritmus redukuje počet násobení na
(N/2)log
ě
(N). FFT algoritmus
pracuje s počtem prvků v mocnině
2, N=2
m
.
N
DFT operace
FFT operace
Účinnost
256
65 534
1 024
64:1
512
262 144
2 304
144:1
1024
1 048 576
5 120
205:1
2048
4 144 304
11 264
372:1
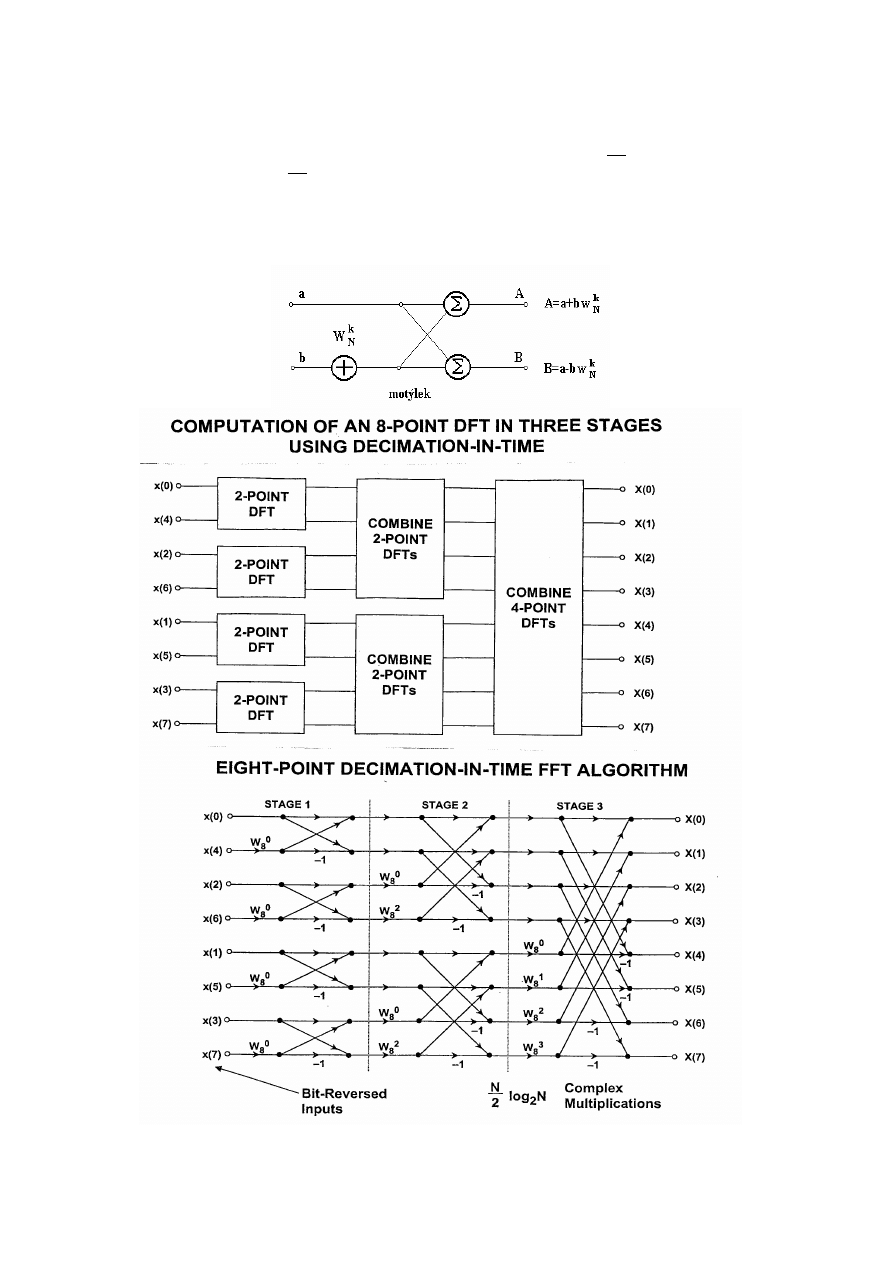
Princip FFT je založen na
1. symetrii
r
N
N
r
N
w
w
−
=
+
2
2. periodicitě
r
N
N
r
N
w
w
+
=
+
[ ]
[ ]
[
]
(
)
( )
( )
( )
( )
k
X
w
k
X
w
n
X
w
w
n
X
w
n
x
w
n
x
w
n
x
X
k
N
N
n
kn
N
k
N
N
n
kn
N
N
n
n
k
N
N
n
kn
N
N
n
kn
N
k
2
1
1
2
0
2
2
1
2
0
2
1
1
2
0
1
2
1
2
0
2
1
0
1
2
2
+
=
⋅
+
⋅
=
=
⋅
+
+
⋅
=
⋅
=
∑
∑
∑
∑
∑
−
=
−
=
−
=
+
−
=
−
=
Součet dvou N/2-bodových DFT, liché a sudé členy
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.10
( )
( )
( )
( )
( )
1
2
....
,
1
,
0
2
2
1
2
1
−
=
⋅
−
=
+
⋅
+
=
N
k
k
X
w
k
X
N
k
X
k
X
w
k
X
k
X
k
N
k
N
Potřebujeme
2(N/2)
2
= N
2
/2 operací. Postupně dělíme původní N-bodovou na čtyři (N/4)-
bodové a dále až se dostaneme k základní dvojici hodnot popisujících 2-bodovou DFT.
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.11
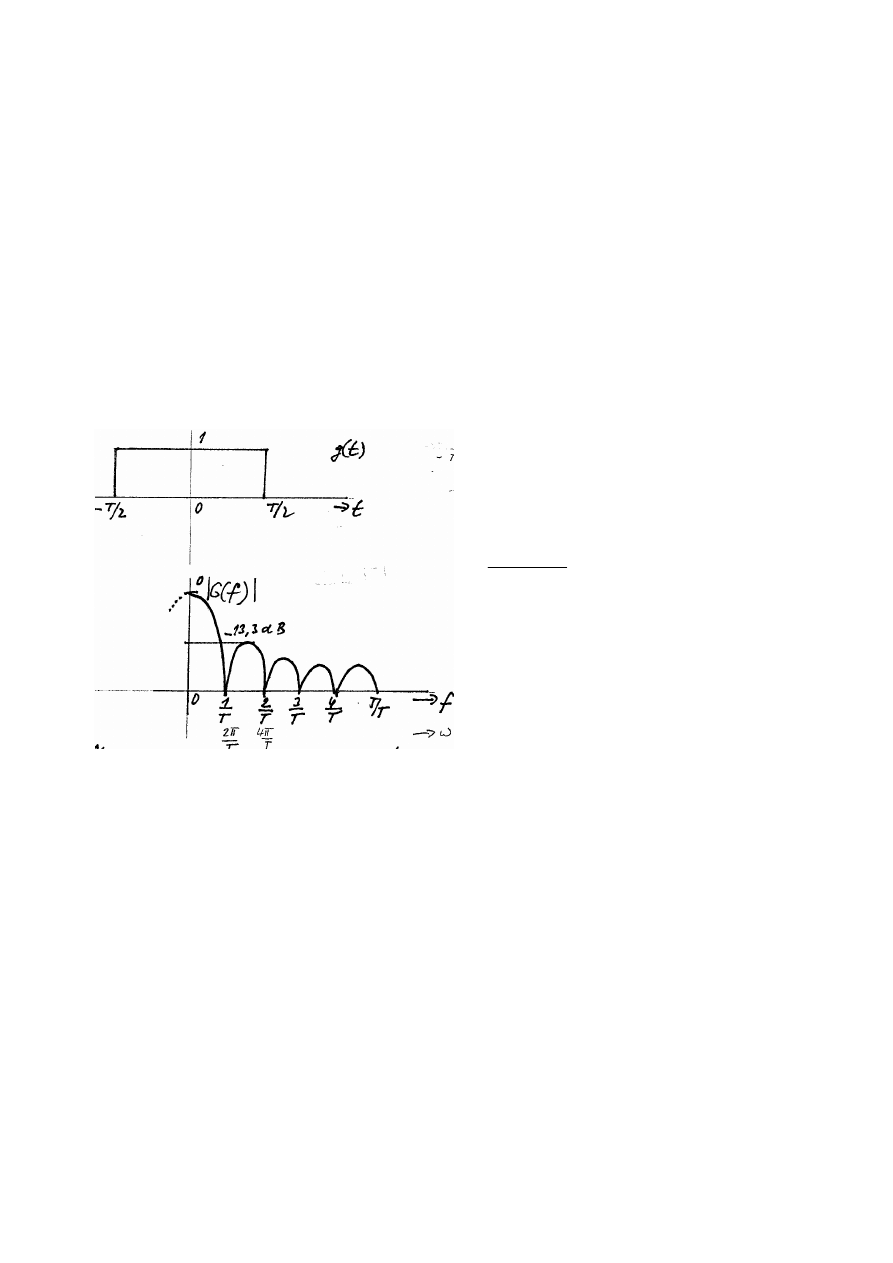
Finitní Fourierova transformace, Okénka
Finitní Fourierova transformace nese sebou dvě limitace:
• konečný čas realizace T
• konečný počet frekvencí f
k
, k=0,1,…N/2-1 s krokem ∆ f= 1/T
Diskrétní Fourierova transformace je definována za předpokladu periodické funkce jak
v originálech, tak v obrazech. Měříme-li x(t) po dobu T je signál vždy hradlován funkcí
jednotkového okénka
( )
.
0
1
T
t
pro
t
g
≤
≤
=
Mimo mezí je
( )
.
0
=
t
g
V čas. oblasti x
T
(t) = x(t) . g(t) znamená, že X
T
(f)= X(f)* G(f) a spektrum je přeměněno
konvolucí se spektrem jednotkového okénka
. Tento jev je neodstranitelný, vzhledem
k měřicímu okénku, které existuje vždy.
( )
( )
( )
( ) (
)
∫
∞
∞
−
−
⋅
=
∗
=
ϕ
ϕ
d
f
X
f
G
f
X
f
G
f
X
T
( )
( )
)
(
sin
)
sin(
))
2
sin(
)
2
((cos(
2
/
2
/
2
s
c
T
fT
fT
T
dt
ft
j
ft
dt
e
t
g
f
G
T
T
ft
j
π
π
π
π
π
π
=
=
−
=
⋅
=
∫
∫
−
∞
∞
−
−
kde s= fT
Chyba magnitudy
způsobená konvolucí změněného spektra – nejvyšší je pro frekvenci
signálu, která leží přesně v polovině diskrétních frekvencí – může být až 37 %, což je
mnohem více, než všechny chyby digitalizačního řetězce. Proto je třeba tuto chybu přesně znát
a vědět, jak ji snížit!!!
Jednotkové okénko je implicitní a nemůže být odstraněno. Spektrum okénka je funkce
sinc(x). Obdélníkovým oknem lze měřit přesně pouze spektra signálů, která obsahují jen složky
o frekvencích násobků 1/T.
Postranní laloky mají malý odstup od hlavního laloku a v případě, že spektrální
frekvence neleží na diskrétní frekvenci f
k
,
je spektrum značně roztaženo a navíc magnituda
spektra pro hlavní frekvenci je značně zkreslena. Největší pokles je tehdy leží –li frekvence
signálu přesně na polovině mezi diskrétními frekvencemi. To je ve většině případů nevýhodné,
proto bylo vymyšleno mnoho jiných okének. Spektrum těchto okének má širší hlavní složku a
větší odstup postranních laloků od hlavního. To má výhodu v menší chybě magnitudy, na druhé
straně však dochází k roztažení hlavního pásma.
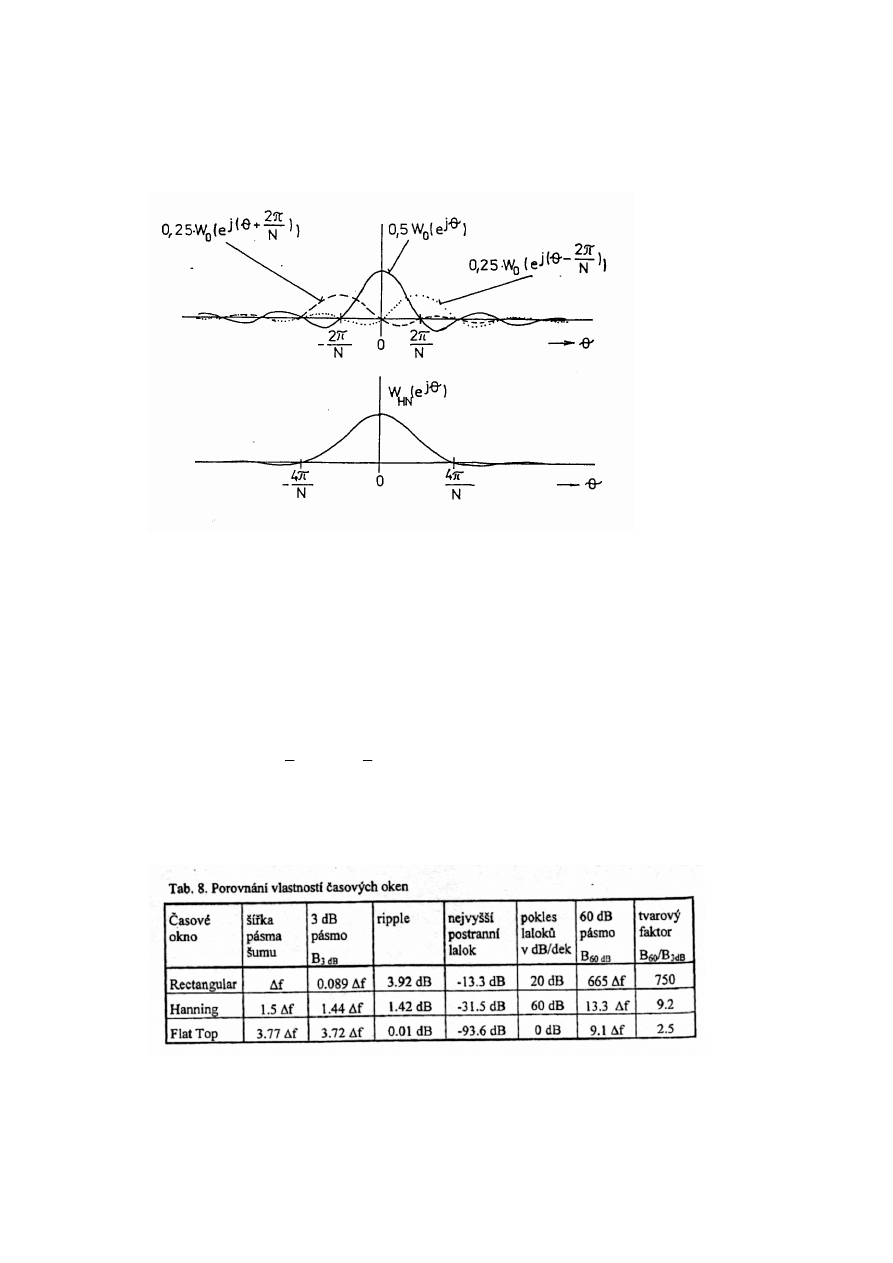
Většina okének jsou posunuté kosinusovou s různě definovanými konstantami. Všechna
mají pozvolný přechod v intervalu -1/2T +1/2T .
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.12
Konstrukce Hanningova okénka
Okénka můžeme použít v časové oblasti, kdy signál násobíme funkcí okénka
(neperiodicita signálu snížena) a poté podrobíme spektrální analýze. Je však třeba dbát na to,
aby se nesnížila celková efektivní hodnota signálu a tím i velikost spektrálních složek. Některé
programy např. MATLAB vyžadují při použití okénka korekci magnitudy spektra.
Můžeme je také použít ve frekvenční oblasti kdy provedeme dodatečnou konvoluci
spektra signálu přeměněného konvolucí se spektrem jednotkového okénka
se spektrem
použitého okénka. Spektrum okének je vzhledem ke svým definicím několik posunutých
impulsů a výpočet není složitý. Např. spektrum Hanningova okénka , viz. horní
obr.
( ) ( )
+
+
−
+
=
T
f
G
T
f
G
f
G
f
H
1
5
.
0
1
5
.
0
se skládá se tří pulzů. Konvoluce znamená, že při
použití Hanningova okénka se k příslušné spektrální čáře připočte polovina předchozí a
polovina následné. Opět musíme normalizovat.
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.13
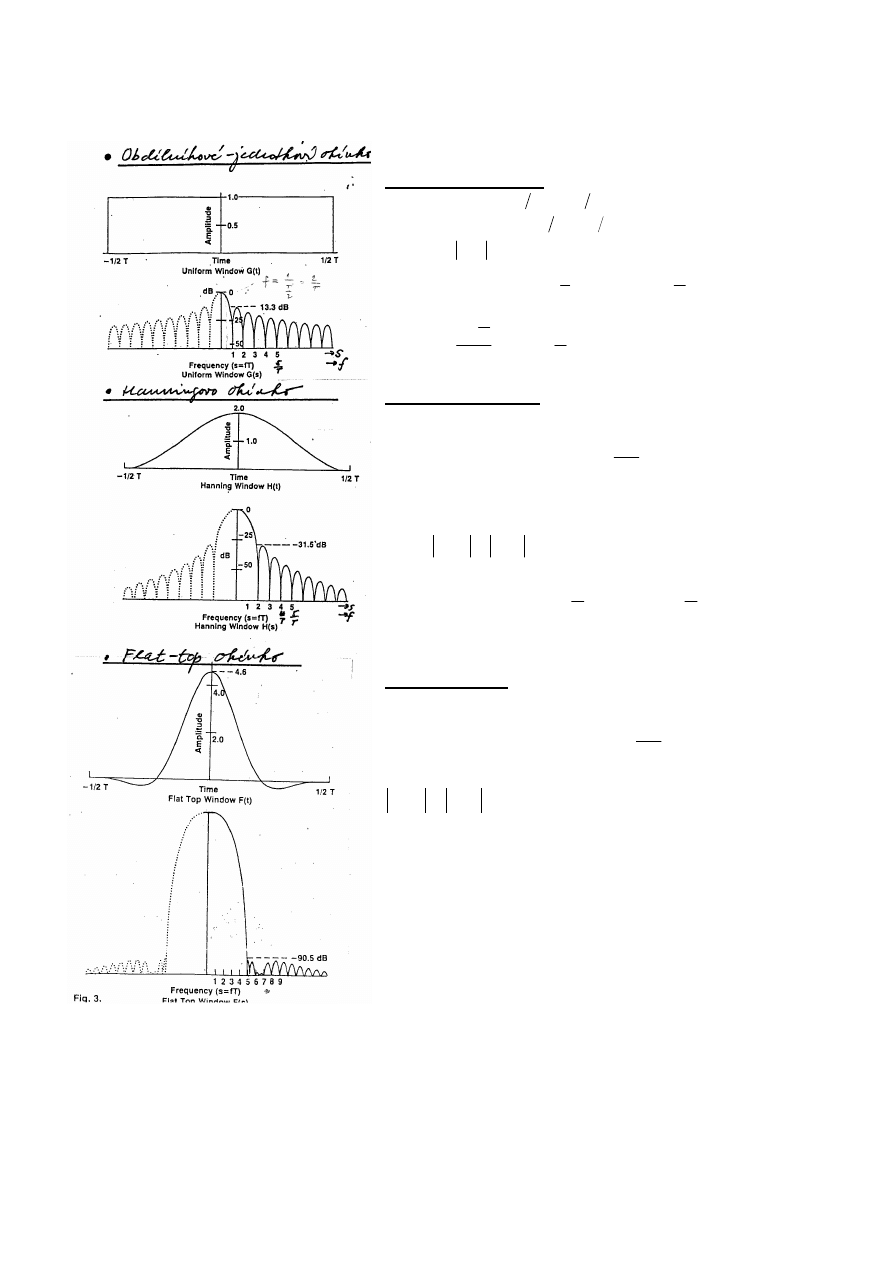
Nejčastěji používaná okénka
Obdélníkové okénko
( )
( )
( )
dB
je
T
f
pro
tedy
s
pro
je
pokles
jvetsi
ne
T
f
s
s
c
s
G
T
t
T
t
T
t
T
t
G
92
.
3
636
.
0
log
20
2
log
20
2
/
2
sin
log
20
2
,
2
1
sin
2
,
2
0
2
2
1
−
=
=
=
⋅
=
=
=
=
>
−
<
<
<
−
=
π
π
π
π
Hanningovo okénko
( )
( )
5
.
0
,
1
,
2
cos
2
1
0
1
0
=
=
+
⋅
=
A
A
t
T
A
A
t
G
t
H
π
( )
( )
(
)
( ) ( )
+
+
−
+
=
−
⋅
=
∑
−
=
T
f
G
T
f
G
f
G
f
H
k
s
A
s
G
s
H
k
k
1
5
.
0
1
5
.
0
*
1
1
δ
Pokles v
f=2/T je 1.4dB
Flattop okénko:
( )
( )
+
⋅
=
∑
=
4
1
0
2
cos
2
k
k
t
T
A
A
t
G
t
H
π
( )
( )
(
)
∑
−
=
−
⋅
=
4
4
*
k
k
k
s
A
s
G
s
H
δ
Pokles v
f=2/T je 0.1dB
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.14
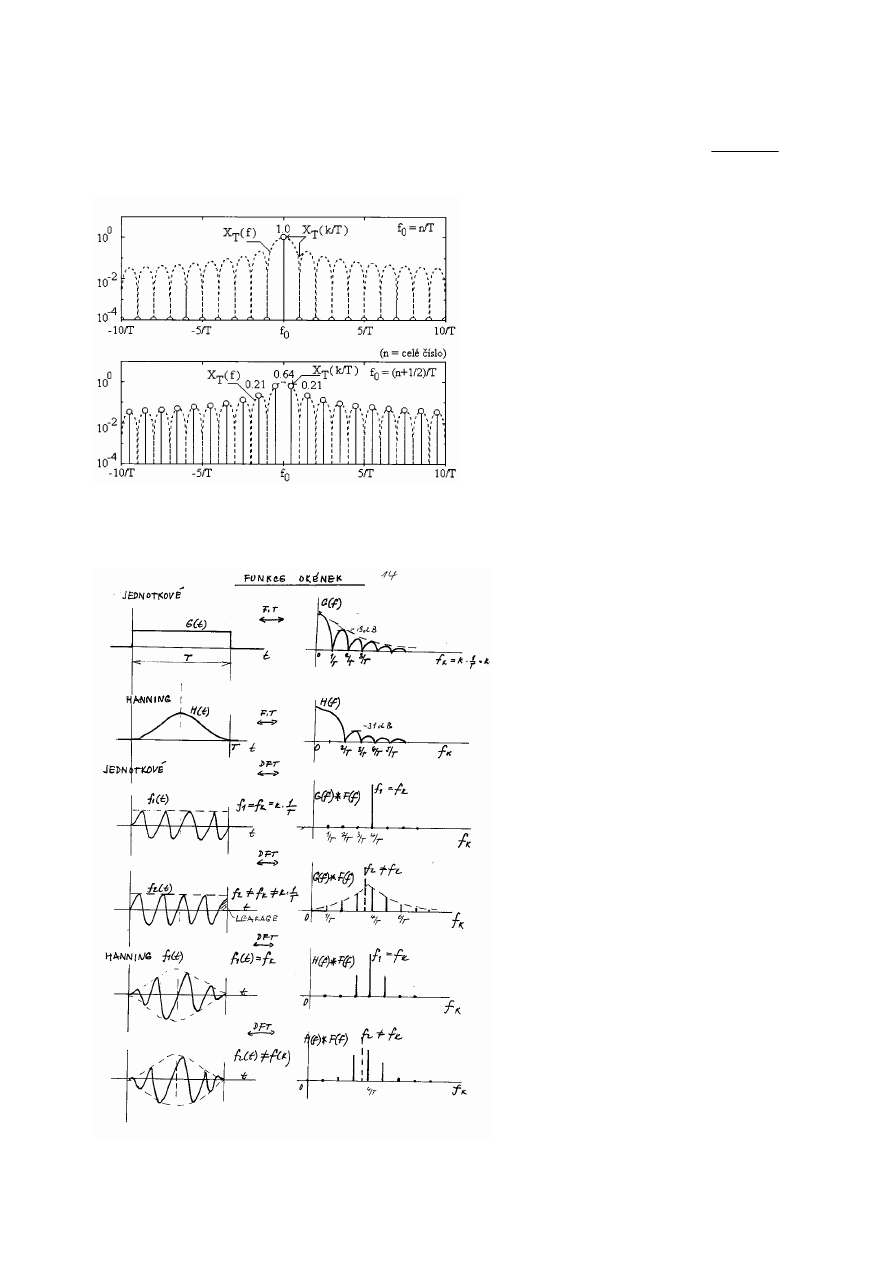
Účinek obdélníkového okénka pro signál ležící na diskrétní frekvenci f = n/T – horní obr.
a v polovině mezi diskrétními frekvencemi f = (n+1/2) /T - spodní obr.s poklesy
π
)
1
2
(
2
+
k
,
k = 0, 1, 2. tedy 0.636, 0.21 atd.
Přehledně funkce okének pro obdélníkové a Hanningovo okénko pro signál jehož frekvence
• leží na diskrétní frekvenci spektra
• je mimo diskrétní frekvenci.
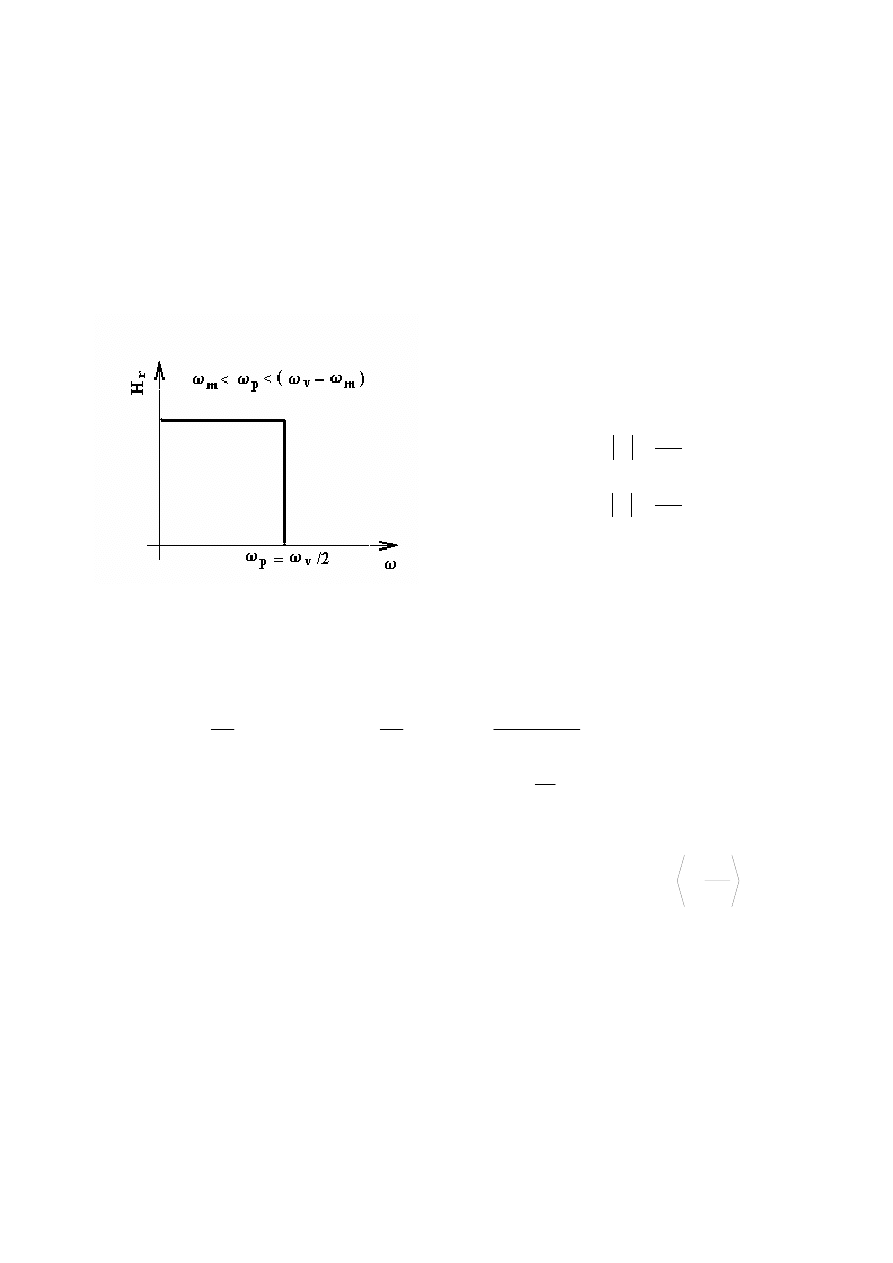
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.15
Obnovení analogového signálu z jeho vzorků ( anti-imaging filtr)
ω
m
….. maximální frekvence ve spektru
ω
v
= 2πf
s
……vzorkovací frekvence
x[n]……………posloupnost vzorků
x
a
[t]…………..rekonstruovaný analogový signál
Potřebujeme ze spektra vzorkovaného signálu odstranit všechna vyšší postraní pásma
(spektrum je periodické s f
v
) a nechat pouze základní spektrum kolem počátku do ω
v
/2. Volíme
ideální analogový filtr typu dolní propust s přenosovou funkcí H
r
(jω)
( )
>
≤
∆
=
2
0
2
v
v
r
t
j
H
ω
ω
ω
ω
ω
(Pozn. Amplituda H
r
je číselně rovno ∆t, pro matematickou správnost)
( )
(
)
( )
( )
( ) ( )
t
h
t
x
t
x
j
H
t
j
X
j
X
r
D
a
r
D
a
∗
=
⇒
⋅
∆
⋅
=
ω
ω
ω
kde X
a
je spektrum rekonstruovaného signálu z původního X
d
( )
( )
(
)
(
)
t
c
t
t
d
e
t
d
e
j
H
t
h
v
v
v
t
j
t
j
r
r
r
r
⋅
=
⋅
⋅
=
∆
=
⋅
=
∫
∫
−
∞
∞
−
2
/
sin
2
/
2
/
sin
2
2
1
2
/
2
/
ω
ω
ω
ω
π
ω
ω
π
ω
ω
ω
ω
( )
[ ]
(
)
[ ]
(
)
∑
∑
∞
−∞
=
∞
−∞
=
∆
−
⋅
=
∆
−
⋅
=
n
v
n
r
a
t
n
t
c
n
x
t
n
t
h
n
x
t
x
2
sin
ω
Obnovený signál x
a
(t) je superpozicí posunutých funkcí sinc násobených hodnotami vzorků; tím
jsou vyplněny mezery mezi vzorky a je obnoven analogový signál.
Pro rekonstrukci proto používáme ideální analogovou dolní propust s pásmem
2
,
0
v
ω
.
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.16
Číslicové zpracování signálů
Analogový signál Æ vzorkování, kvantování Æ číslicový signál
t
f
f
v
s
∆
=
=
1
• Shanon-Kotelnikův teorém
max
2 f
f
s
≥
, složky f>f
max
musí být menší jak kvantovací
úroveň převodníku.
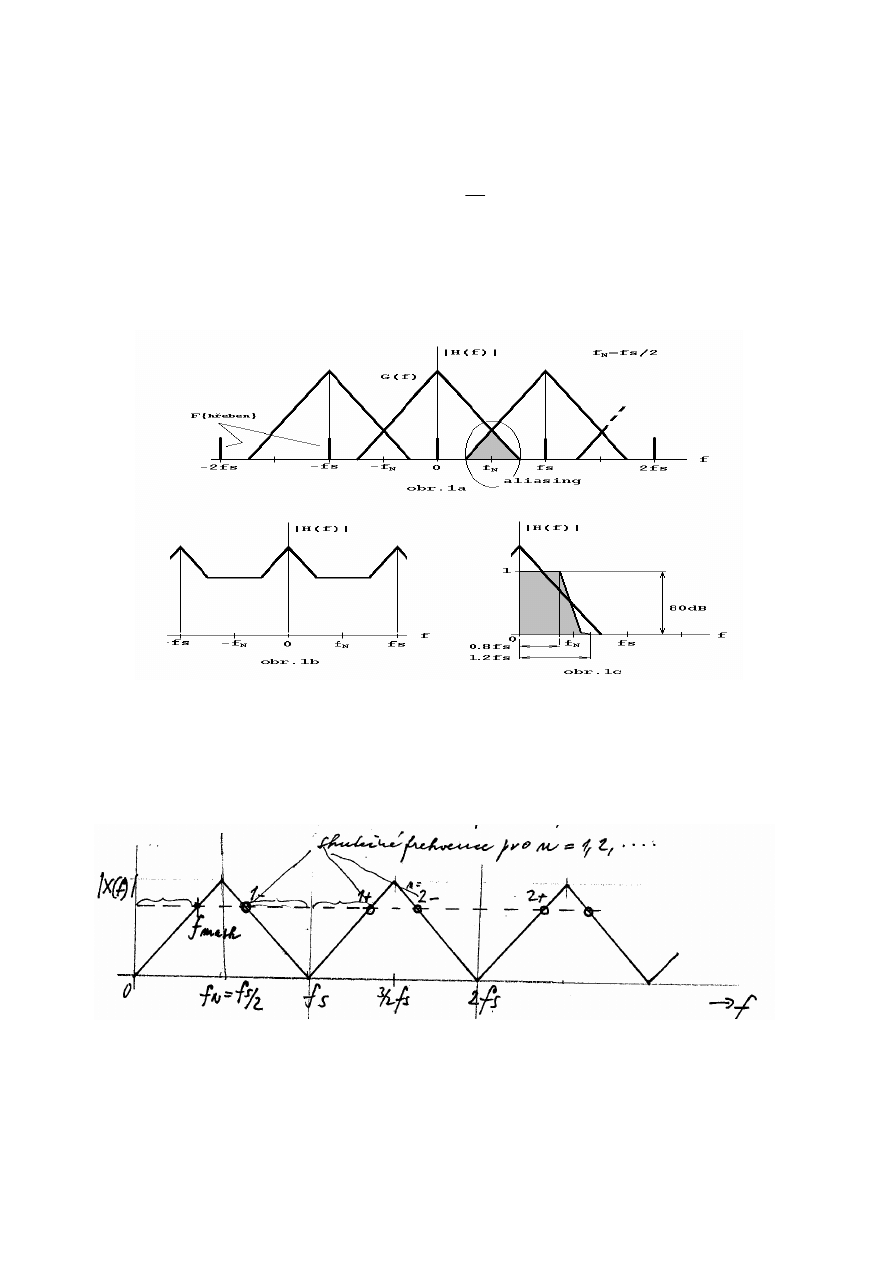
• Antialiasing, překrytí, maskování
Nastává
při nedodržení vzorkovacího teorému
Maskování:
Při nedodržení vzorkovacího teorému jsou skutečné frekvence z periodického spektra
maskovány do oblasti frekvencí 0 – f
N
. Maskování může být i přes několik (n) pásem 0 – f
s
. viz.
další obr.
Skutečná frekvence se vypočte podle vztahu
f
skut
= n f
s
± f
mask
, n= 1,2
př. Skut. frekvence označená 1- je f
skut
= f
s
- f
mask
,
Skut. frekvence označená 1+ je f
skut
= f
s
+ f
mask
,
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.17
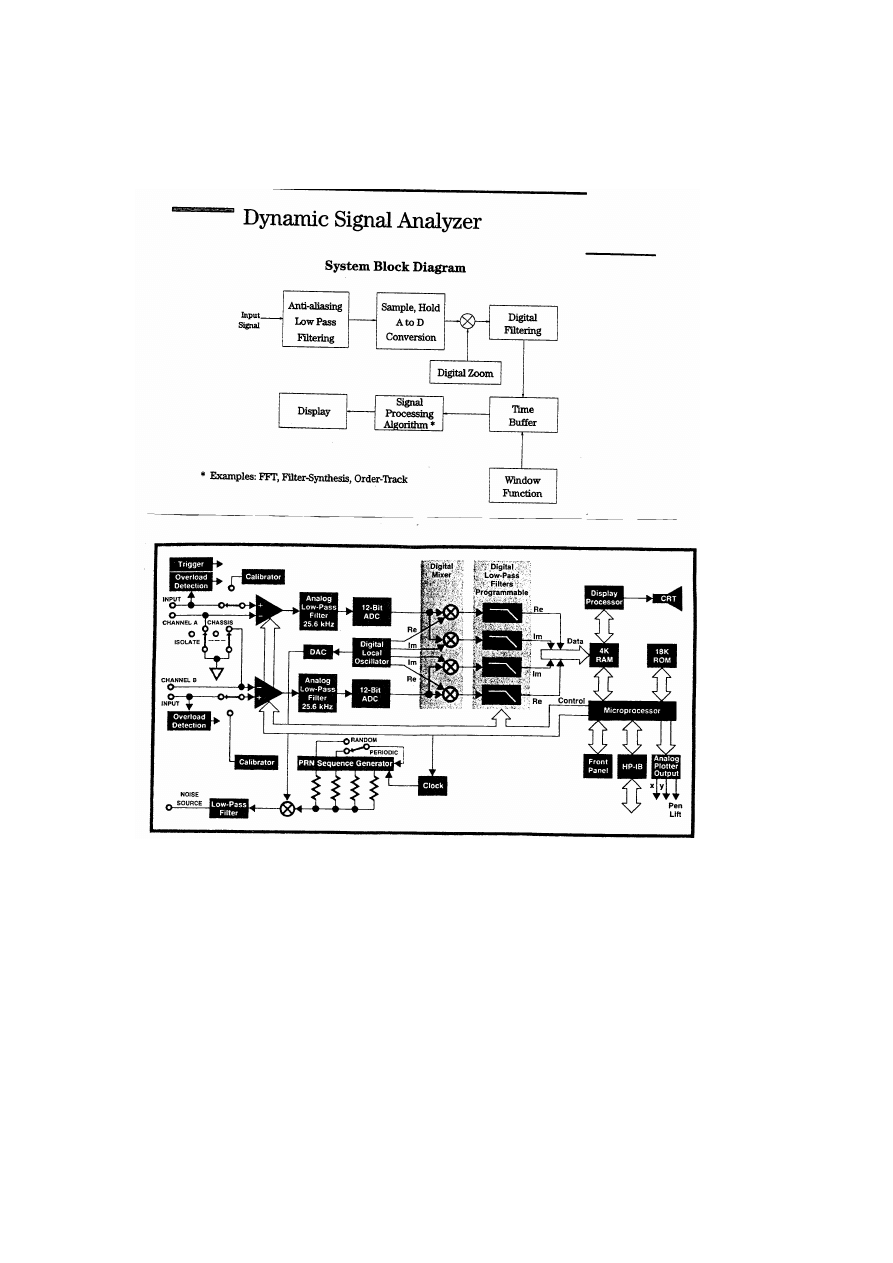
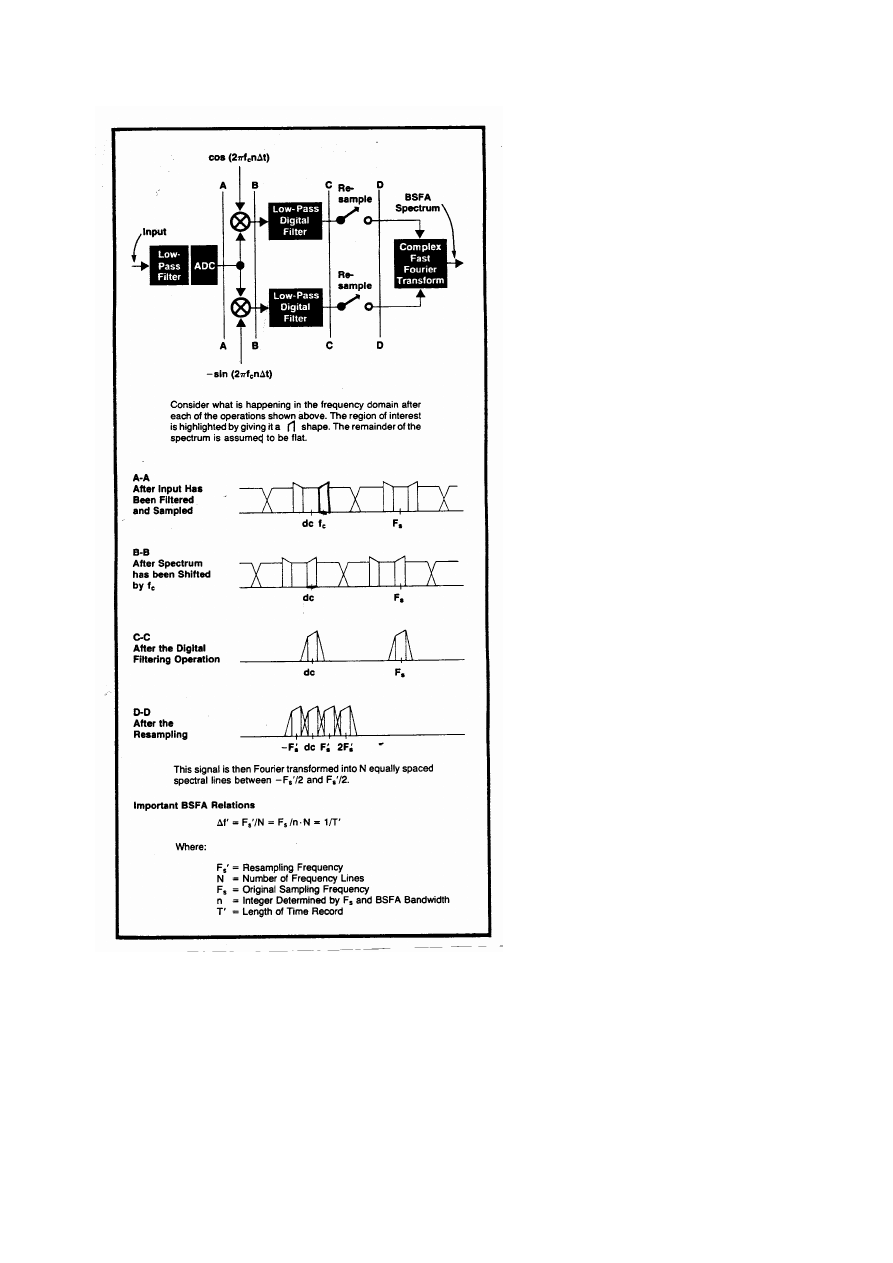
Stručný přehled přístrojové techniky:
Digitální zoom viz. horní obrázek je proveden digitálním směšováním měřeného signálu a
signálu o střední frekvenci zoomu.
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.18
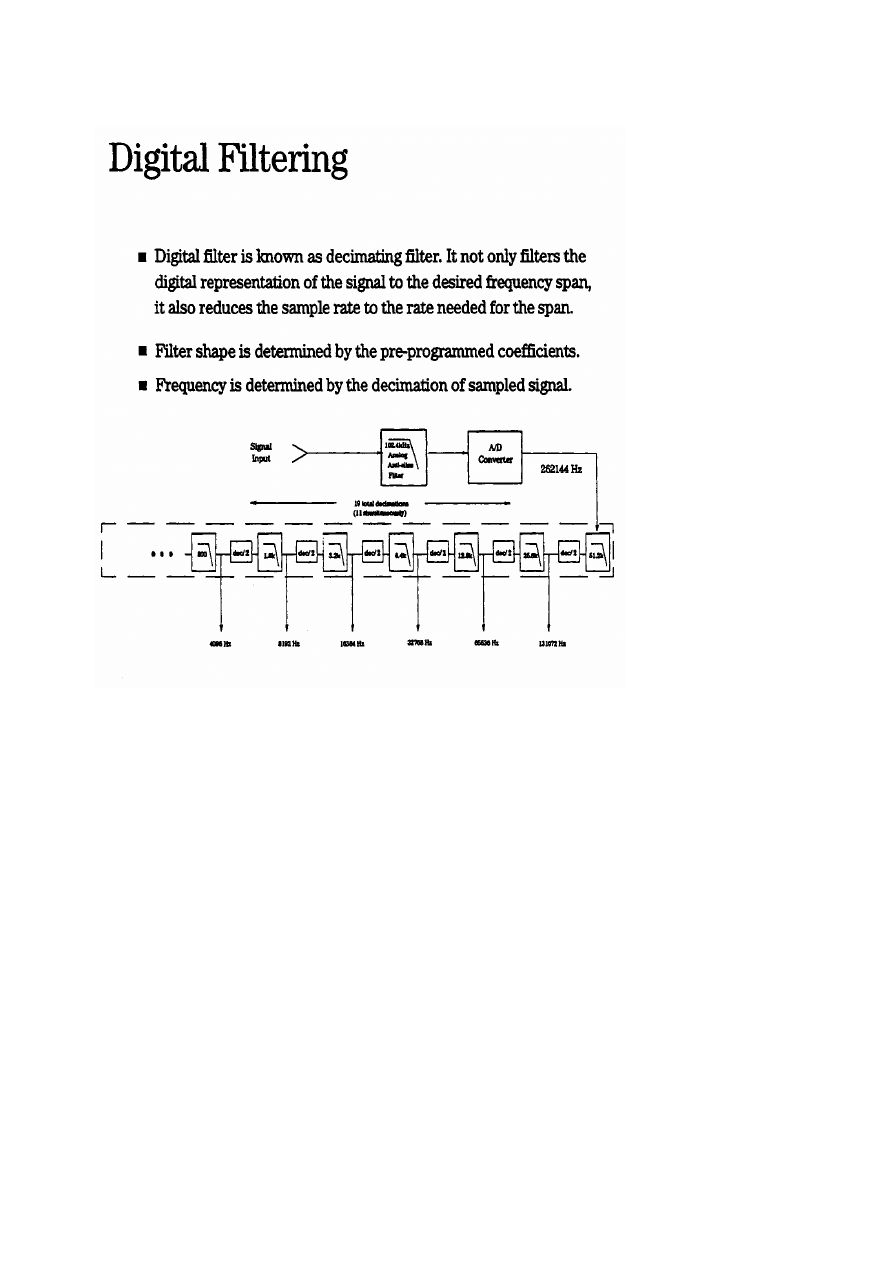
Číslicové měřicí systémy
Téma 10, Základy spektrální analýzy – str.19
[1]Literatura: M.Sedláček, Zpracování signálů v měřící technice, ČVUT FEL
[2] Analog Device, Hewlett Packard, notes, tutorials, technical articles etc.
Wyszukiwarka
Podobne podstrony:
32 piątek
32 sobota
od 24 do 32
32 pozyskujacy uczniow sluga bozy
32 Przepustka
ei 07 2002 s 32 34
PAG 32
09 1993 27 32
32 metoda pośreniego pomiaru długości
133 ROZ bhp i p poz w zakla Nieznany
32 model małżeństwa i rodziny w XVII i XVII wieku, kulturoznawstwo
Unia Europejska t1.32, Wspólna polityla rolna
32. Małopłytkowość, MEDYCYNA VI rok, Pediatria, PEDIATRIA CAŁOŚĆ, Ustny PEDIATRIA Balwierz
Nr 32 BRĄZOWA
32 Dramat w okresie pozytywizmu i Młodej Polski (na tle dramatu europejskiego)
32 Geomorfologiczna charakterystyka wybranych obszarów Polski
32 oryginał
32 Swietlinska Outsourcing procesow
więcej podobnych podstron