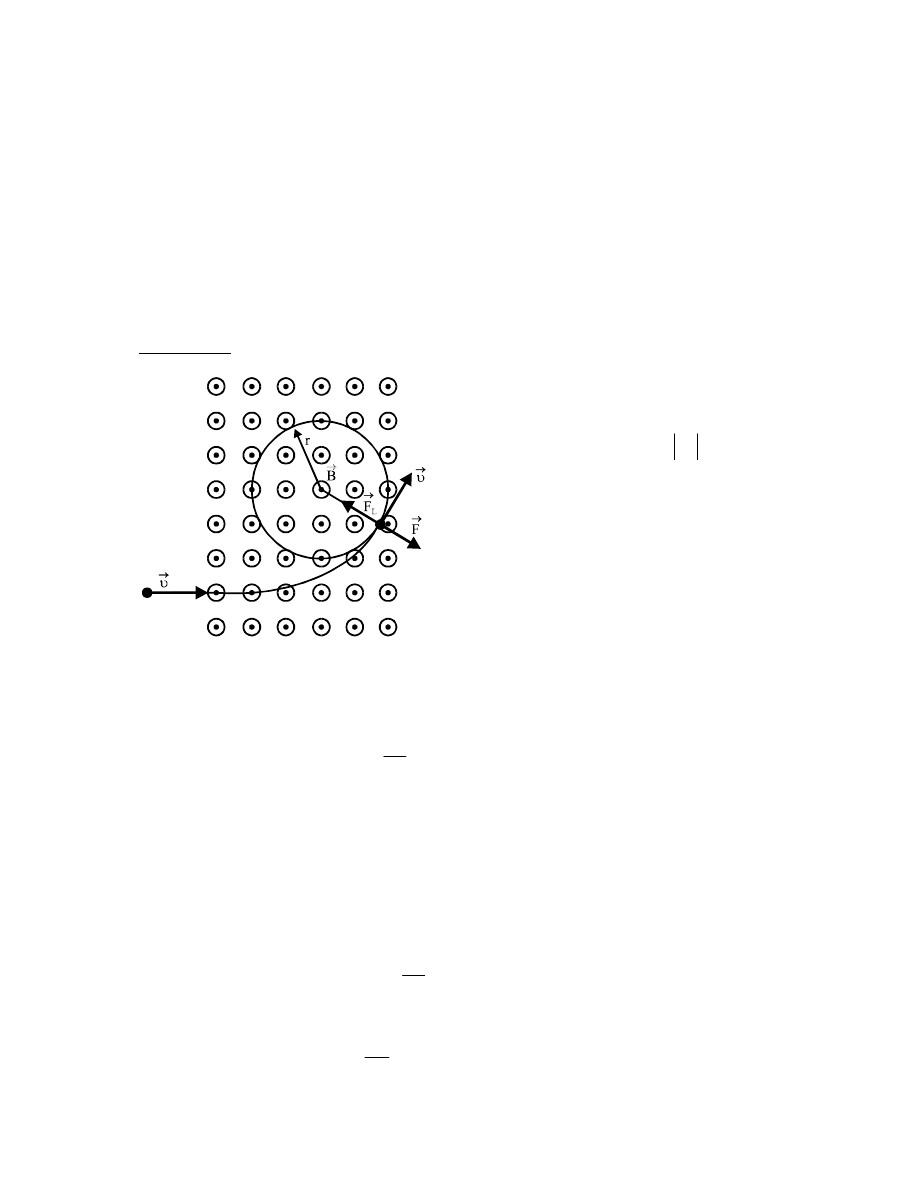
57

Zadania do rozdziału 8.

Zad.8.1.

Elektron

(o

masie

kg

10

1

,

9

m

31

−

⋅

=

i ładunku elektrycznym

C

10

6

.

1

e

19

−

⋅

=

) wpada

z prędkością

s

/

m

10

7

=

υ

w obszar jednorodnego pola magnetycznego o indukcji

T

10

B

2

−

=

prostopadle do linii sił tego pola. Znaleźć tor ruchu elektronu w polu

magnetycznym.

Rozwiązanie:

Na elektron poruszający się z prędkością

υ

G

w polu

B

G

działa siła Lorentza

L

F

G

,

( )

B

e

F

F

;

B

x

e

F

L

L

L

υ

=

=

υ

−

=

G

G

G

G

która jest skierowana prostopadle do

wektorów

B

G

i

υ

G

.

Siła

L

F

G

działa tak, jak siła dośrodkowa

(

)

υ

⊥

G

G

L

F

, a więc zakrzywia tor elektronu.

Na poruszający się elektron o masie m z prędkością

υ po torze o krzywiźnie r działa z kolei

siła odśrodkowa F

r

m

F

2

υ

=

,

która działa wzdłuż tej samej prostej co siła F

L

ale jest przeciwnie do niej skierowana.

Zatem elektron w polu magnetycznym zadania będzie poruszał się po okręgu o promieniu r w

płaszczyźnie prostopadłej do B

G

.

Promień tego okręgu wyliczymy z warunku:

F

F

L

= co

czyni:

r

m

B

e

2

υ

=

υ

Stąd

eB

m

r

υ

=

58

T

10

C

10

6

,

1

s

/

m

10

kg

10

1

,

9

r

2

19

7

31

−

−

−

⋅

⋅

⋅

⋅

=

Ale

[ ]

[ ]

[

]

2

s

/

m

kg

N

;

s

/

m

C

N

T

⋅

=









⋅

=

Zatem

2

2

3

s

/

m

kg

m

s

/

m

kg

10

7

,

5

N

C

s

/

m

C

s

/

m

kg

7

,

5

r

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

⋅

=

−

m

10

7

,

5

r

3

−

⋅

=

Zad.8.2.

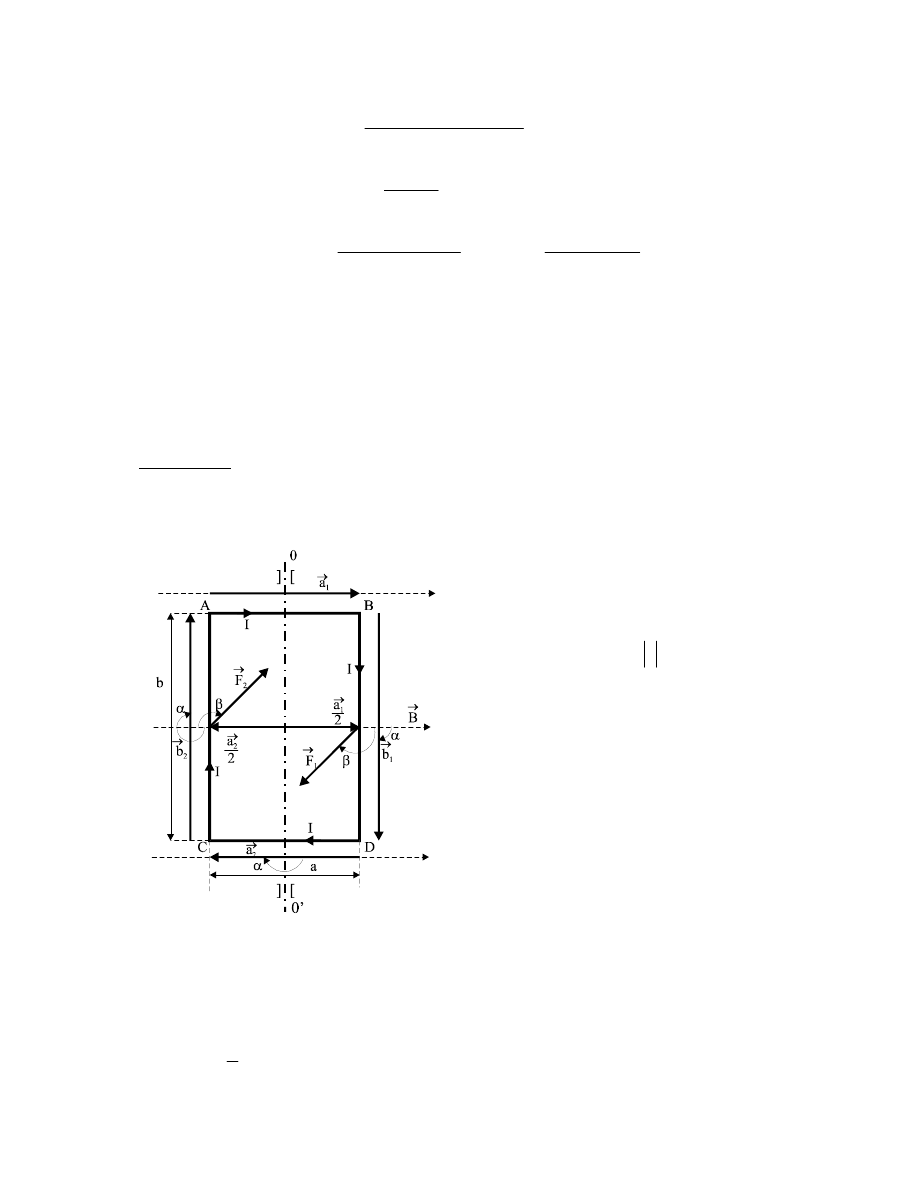
Oblicz

siły działania jednorodnego pola magnetycznego o indukcji B

G

na osadzoną na

osi 00’ prostokątną ramkę ABCD z drutu o długościach boków a i b. Oś obrotu przechodzi

przez bok a i jest symetralną ramki. Przez ramkę płynie prąd I.

Rozwiązanie:

a)

Załóżmy, że w pierwszej chwili powierzchnia ramki jest równoległa do linii siły indukcji B

G

.

Rys.a.

Korzystamy ze wzoru na siłę

F

G

działającą

na prostoliniowy przewodnik o długości l z

prądem I w polu magnetycznym B

G

.

( )

α

=

=

=

sin

BIl

F

F

;

B

x

l

I

F

G

G

G

G

gdzie

l

G

to wektor o długości l i zwrocie

wyznaczonym przez kierunek prądu I, zaś

α to kąt między wektorami

B

i

l

G

G

.

Ponieważ dla boku scharakteryzowanego

wektorem

1

a

G

α = 0 (sinα = 0), a dla boku

2

a

G

α = π (sinα=0) dlatego na boki te nie

działają żadne siły.

Na boki

2

1

b

i

b

G

G

działają odpowiednio siły

F

F

F

2

1

=

=

prostopadłe do płaszczyzny rys. a,

tworząc parę sił.

Dla

1

b

G

;

2

π

=

α

(sin

α = 1) i wtedy

BIb

F

1

=

, zaś

59

dla

2

b

G

;

π

=

α

2

3

(sin

α = -1) i wtedy

BIb

F

2

−

=

.

Ta para sił działa na ramkę momentem obrotowym M

G

2

2

1

1

F

x

2

a

F

x

2

a

M

G

G

G

G

G

+

=

β

⋅

⋅

=

=

sin

F

a

M

M

G

gdzie

β to kąt między

1

1

F

i

2

a

G

G

. Kąt ten jest również zawarty między

2

2

F

i

2

a

G

G

(patrz rys.a).

Ponieważ w rozważanym przypadku

2

π

=

β

, dlatego

BIba

F

a

M

=

⋅

=

Moment pary sił M obraca ramkę wokół osi obrotu 00’. Podczas obrotu kąt

β maleje, więc i

moment M powodujący ruch ramki maleje w myśl wzoru

β

=

sin

BIba

M

Gdy

β = 0 (wtedy płaszczyzna ramki jest prostopadła do

B

G

) to

M = 0

Zobaczmy jakie siły działają na ramkę w tym położeniu.

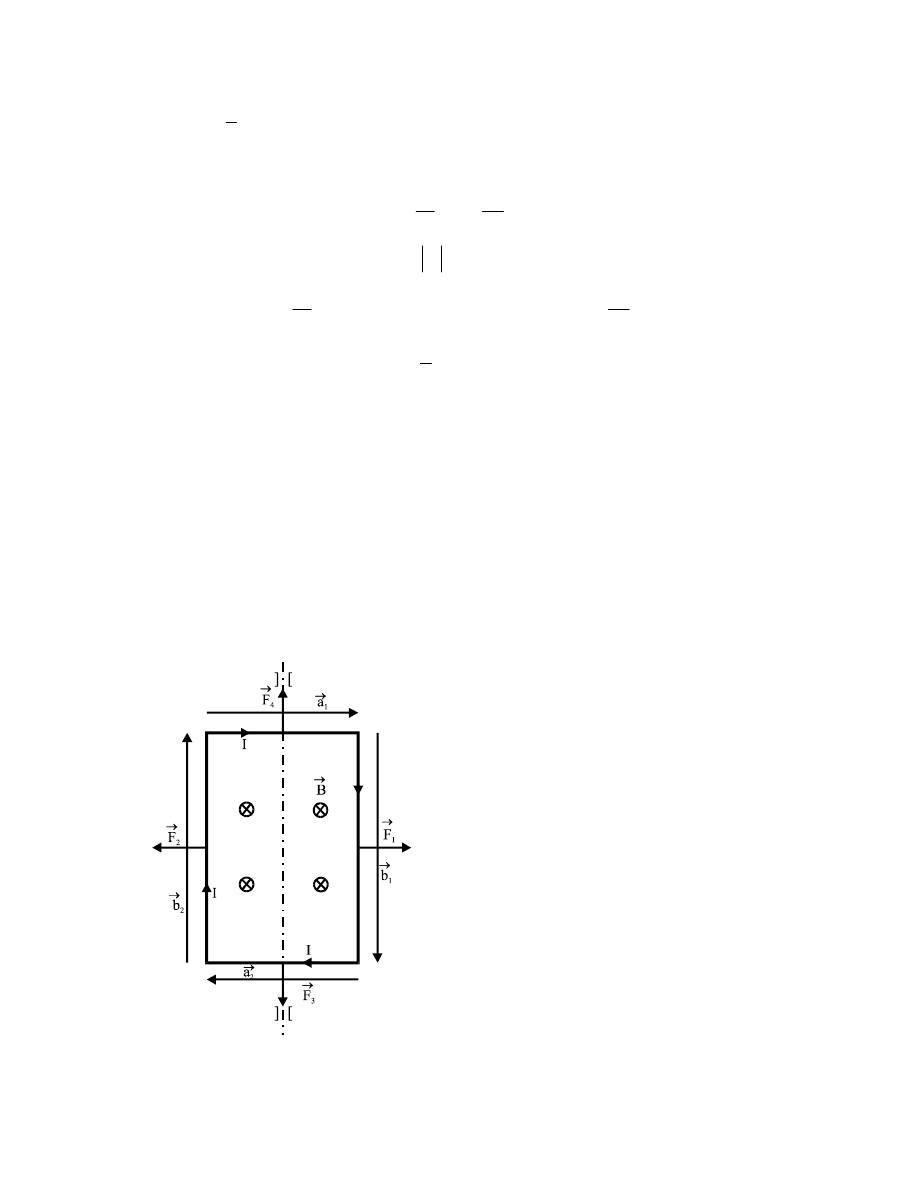
b) Ramka w położeniu prostopadłym do linii sił pola B

G

.

W tym położeniu na ramkę działają cztery

siły

4

3

2

1

F

i

F

,

F

,

F

G

G

G

G

BIb

F

F

;

F

F

2

1

2

1

=

=

−

=

G

G

oraz

BIa

F

F

;

F

F

4

3

3

4

=

=

−

=

G

G

Siły te, jak widzimy na rys.b, dążą do

rozciągnięcia ramki, lecz nie nadają jej

ruchu obrotowego bo

M = 0

Rys.b.

60

Zad. 8.3.

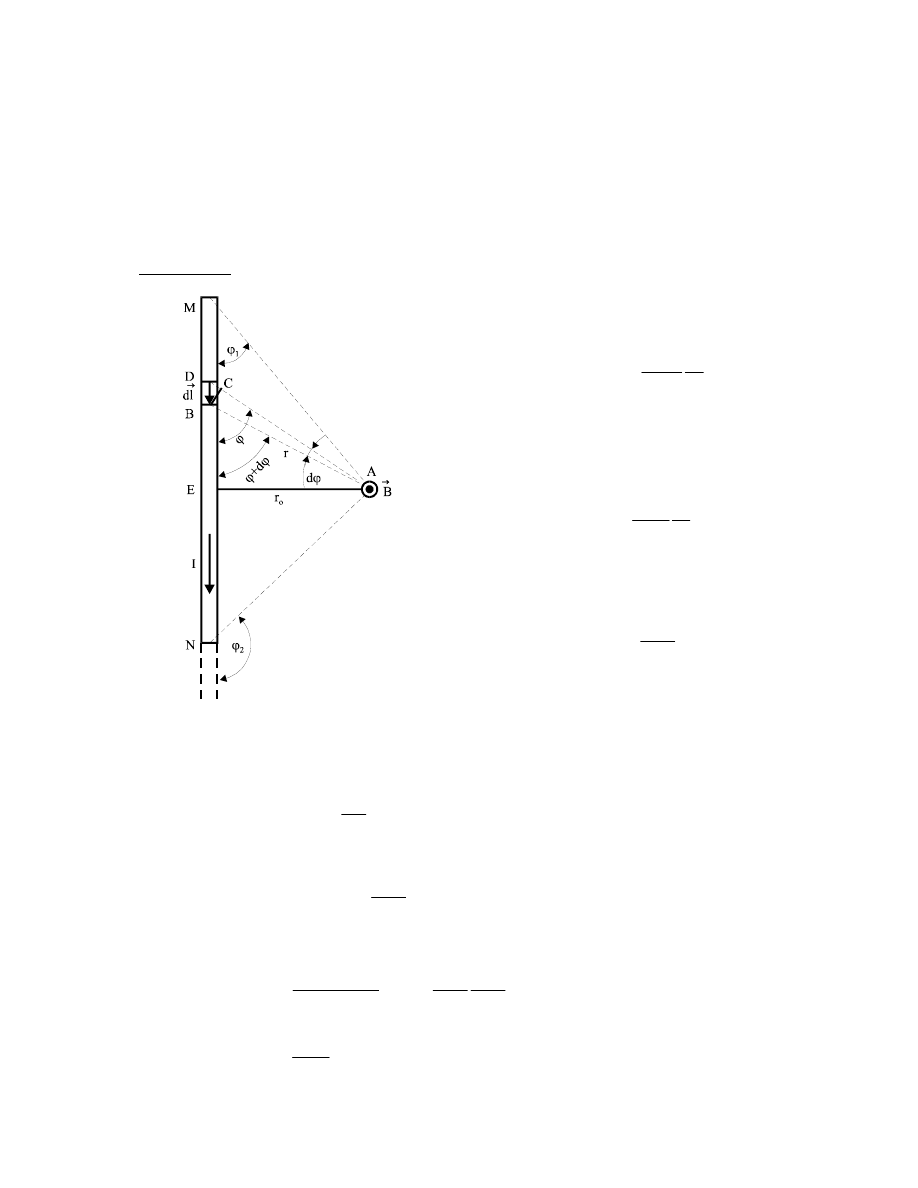
W prostoliniowym przewodniku o długości l płynie prąd o natężeniu I. Wyznaczyć

wartość indukcji magnetycznej

B

G

w punkcie A odległym o r

o

od przewodnika. Punkt A jest

tak usytuowany w przestrzeni, że z tego punktu końce M i N przewodnika widać odpowiednio

pod kątami

2

1

i

ϕ

ϕ

(patrz rysunek).

Rozwiązanie:

Indukcję magnetyczną B

G

w punkcie A

obliczamy z prawa B-S-L.

r

x

l

d

r

I

4

B

3

r

o

l

a

przewodnik

dlugości

calej

po

K

G

G

π

µ

µ

∫

=

W naszym konkretnym przypadku B

możemy przedstawić jako:

dl

r

I

4

B

2

r

o

l

a

przewodnik

dlugości

calej

po

ϕ

π

µ

µ

∫

=

(1)

Ale z trójkąta AEB wynika, że

ϕ

=

sin

r

r

o

(2)

Z trójkąta DCB otrzymujemy:

ϕ

⋅

=

sin

dl

BC

, gdzie BC możemy obliczyć z definicji kąta łukowego

ϕ

= d

r

BC

Zatem

ϕ

ϕ

=

sin

rd

dl

(3)

Podstawiając (2) i (3) do (1) otrzymujemy:

ϕ

ϕ

ϕ

ϕ

⋅

π

ϕ

µ

µ

∫

=

ϕ

ϕ

sin

d

sin

r

sin

I

r

4

sin

B

o

2

o

2

r

o

2

1

ϕ

ϕ

⋅

π

µ

µ

∫

=

ϕ

ϕ

d

sin

I

r

4

B

o

r

o

2

1

61

ϕ

ϕ

∫

π

µ

µ

=

ϕ

ϕ

d

sin

r

4

I

B

2

1

o

r

o

(

)

(

)

2

1

o

r

o

o

r

o

cos

cos

r

4

I

cos

r

4

I

B

2

1

ϕ

−

ϕ

π

µ

µ

=

ϕ

−

π

µ

µ

=

ϕ

ϕ

Gdy przewodnik jest nieskończenie długi to

π

=

ϕ

=

ϕ

2

1

a

0

Wtedy

( )

[

]

1

1

r

4

I

B

o

r

o

−

−

π

µ

µ

=

o

r

o

r

2

I

B

π

µ

µ

=

Zad. 8.4

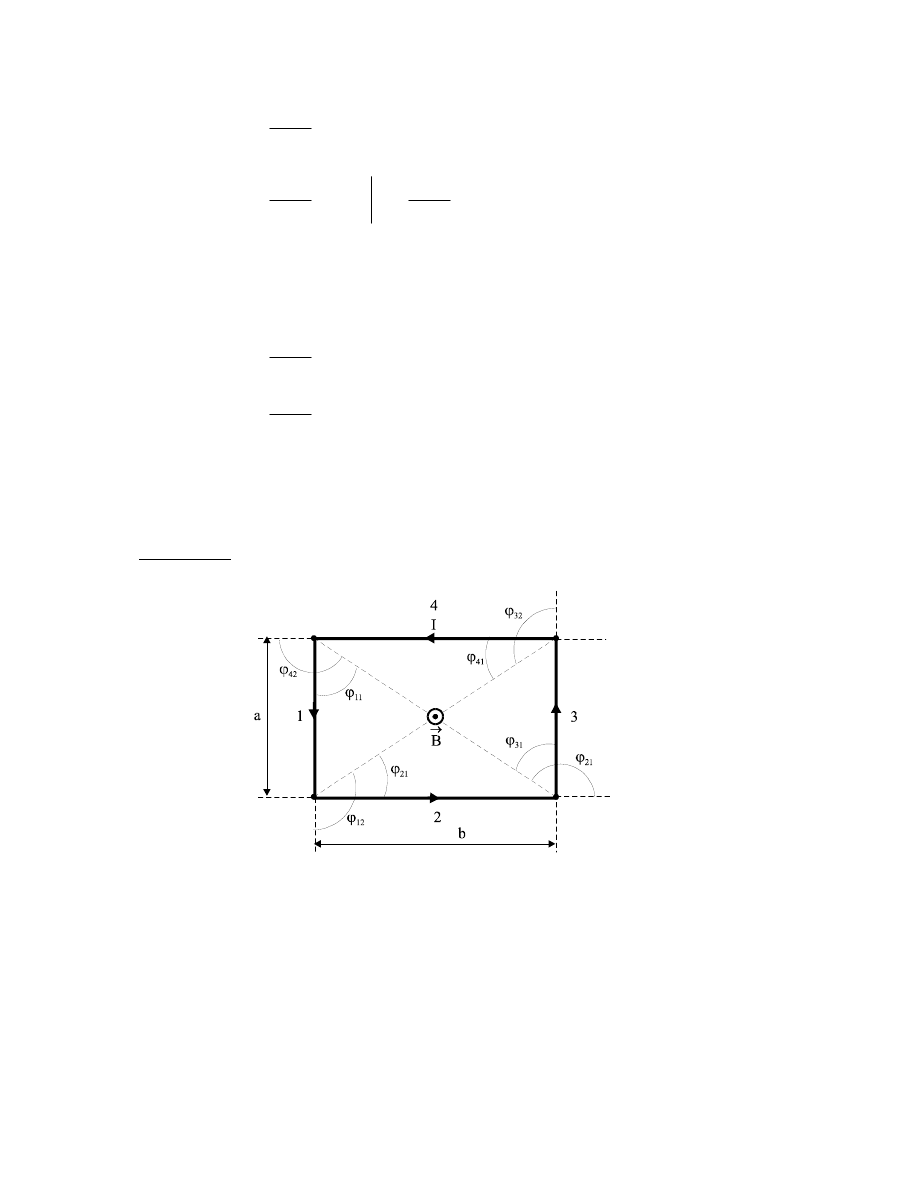
Dana jest prostokątna ramka o bokach a i b, w której płynie stały prąd elektryczny o

natężeniu I. Znaleźć kierunek i wartość wektora indukcji magnetycznej B

G

w środku ramki.

Rozwiązanie:

Z prawa B-S-L wynika, że B

G

w środku ramki jest wektorową sumą

4

3

2

1

B

i

B

,

B

,

B

G

G

G

G

wektorów indukcji pochodzących od poszczególnych boków ramki.

Wektory

4

3

2

1

B

i

B

,

B

,

B

G

G

G

G

leżą wszystkie na jednej prostej, prostopadłej do płaszczyzny ramki

i przechodzącej przez jej środek.

Zwroty tych wektorów są zgodne i są skierowane w stronę czytelnika.

Zatem

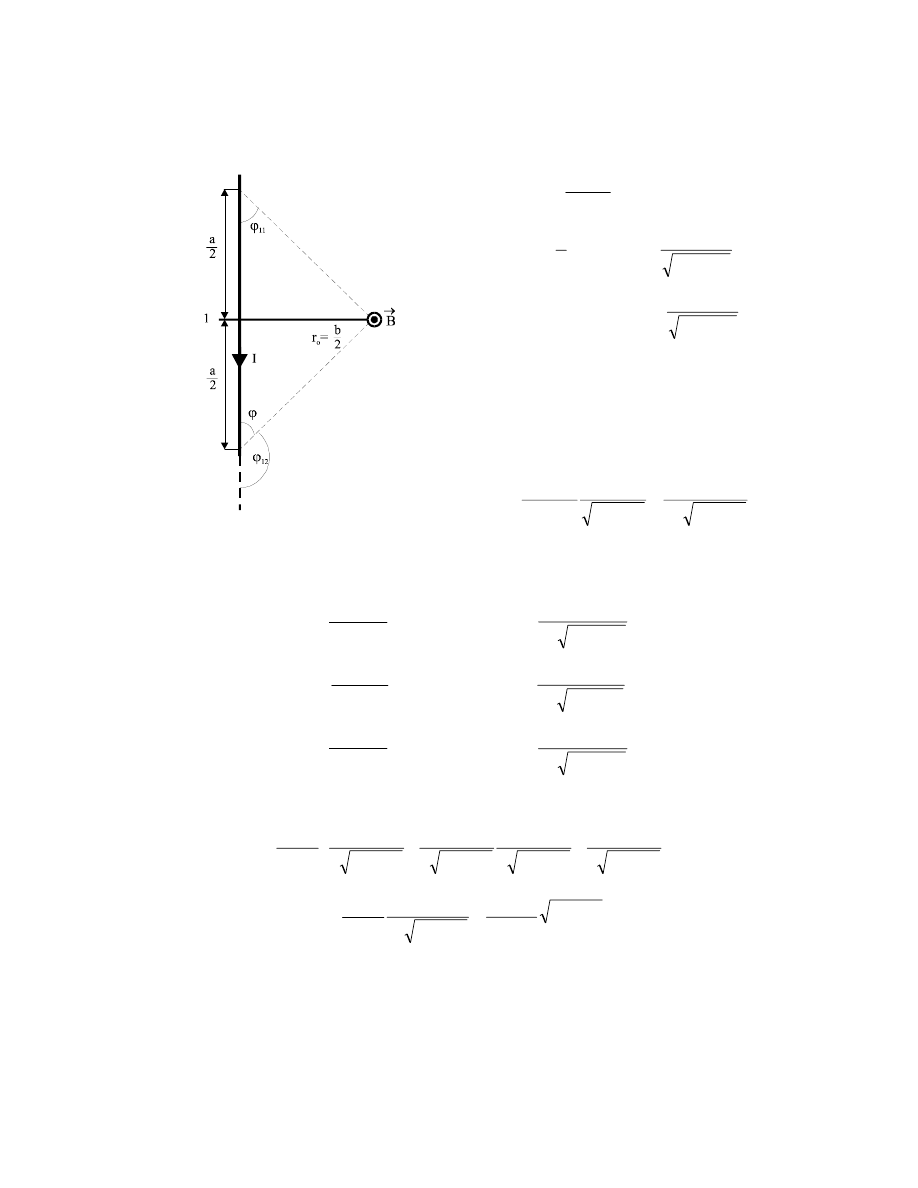
62

4

3

2

1

B

B

B

B

B

+

+

+

=

Przyczynki

4

3

2

1

B

i

B

,

B

,

B

obliczamy korzystając z wiadomości zdobytych w zad.8.2.

(

)

12

11

o

r

o

1

cos

cos

r

4

I

B

ϕ

−

ϕ

π

µ

µ

=

ale

;

b

a

a

cos

;

2

b

r

2

2

11

o

+

=

ϕ

=

;

b

a

a

cos

2

2

12

+

−

=

ϕ

bo

(

)

11

12

cos

cos

cos

cos

ϕ

−

=

ϕ

−

=

ϕ

−

π

=

ϕ

ponieważ

11

ϕ

=

ϕ

Zatem

2

2

r

o

2

2

r

o

1

b

a

b

Ia

b

a

a

2

2

/

b

4

I

B

+

π

µ

µ

=

+

⋅

π

⋅

µ

µ

=

Analogicznie

(

)

2

2

r

o

22

21

r

o

2

b

a

a

Ib

cos

cos

2

/

a

4

I

B

+

π

µ

µ

=

ϕ

−

ϕ

⋅

π

⋅

µ

µ

=

(

)

2

2

r

o

32

31

r

o

3

b

a

b

Ia

cos

cos

2

/

b

4

I

B

+

π

µ

µ

=

ϕ

−

ϕ

⋅

π

⋅

µ

µ

=

(

)

2

2

r

o

42

41

r

o

4

b

a

a

Ib

cos

cos

2

/

a

4

I

B

+

π

µ

µ

=

ϕ

−

ϕ

⋅

π

⋅

µ

µ

=

Ostatecznie















+

+

+

+

+

+

π

µ

µ

=

2

2

2

2

2

2

2

2

r

o

b

a

a

b

b

a

b

a

b

a

a

b

b

a

b

a

I

B

(

)

2

2

r

o

2

2

2

2

r

o

b

a

ab

I

2

b

a

ab

b

a

2

I

B

+

π

µ

µ

=

+

+

π

µ

µ

=

Zad. 8.5.

Wyznaczyć wartość indukcji magnetycznej

B

G

w środku obwodu kołowego o

promieniu r, w którym płynie prąd elektryczny o natężeniu I.

63

Rozwiązanie:

Zgodnie z prawem B-S-L wszystkie

elementy

l

d

G

tego obwodu z prądem I

wywołują w środku okręgu indukcję

(

)

r

x

l

d

r

I

4

B

d

3

r

o

G

G

G

π

µ

µ

=

o jednakowych kierunkach (wzdłuż prostej

prostopadłej do płaszczyzny obwodu i

przechodzącej przez środek okręgu) i

zwrotach (za płaszczyznę rysunku).

A zatem całkowanie wektorowe sprowadza się do całkowania skalarnego

dl

I

r

4

dB

B

2

r

o

r

2

0

okręgu

po

π

µ

µ

∫

∫

=

=

π

bo kąt

ϕ między wektorami

l

d

i

r

G

G

wynosi

2

π

, a więc 1

sin

=

ϕ

.

Stąd

dl

r

4

I

B

r

2

0

2

r

o

∫

π

µ

µ

=

π

[

]

0

r

2

r

4

I

l

r

4

I

B

2

r

o

r

2

0

2

r

o

−

π

π

⋅

µ

µ

=

π

µ

µ

=

π

r

2

I

B

r

o

µ

µ

=

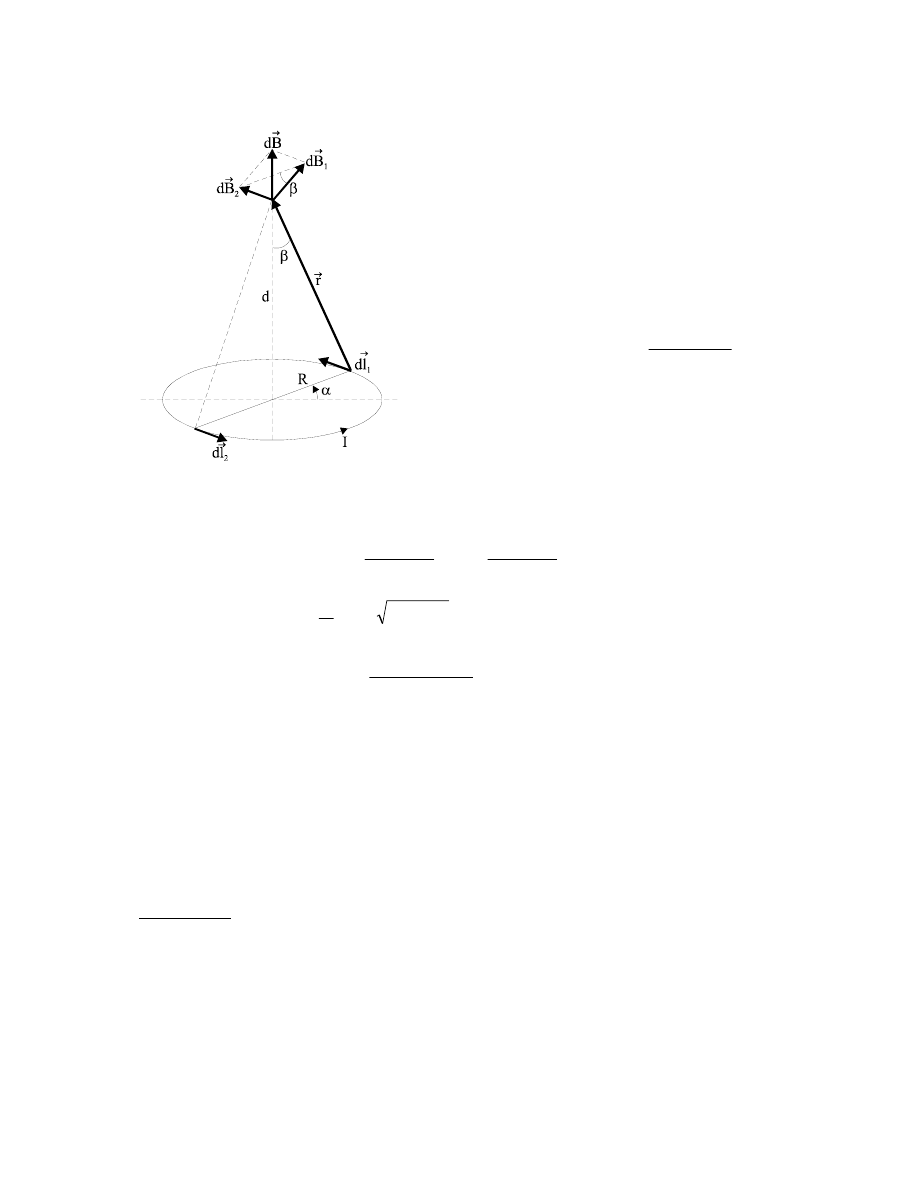
Zad. 8.6.

Obliczyć indukcję magnetyczną

B

G

na osi obwodu kołowego w odległości d od środka

obwodu. Natężenie prądu w obwodzie wynosi I, a promień obwodu R.

Rozwiązanie:

Wychodząc z prawa B-S-L

(

)

r

x

l

d

r

I

4

'

B

d

3

G

G

G

π

µ

=

; gdzie

r

o

µ

µ

=

µ

Ponieważ wektor l

d

G

oraz wektor wodzący

r

G

tworzą kąt

2

π

, więc

dl

r

I

4

'

dB

2

π

µ

=

64

Wektory indukcji

2

1

B

d

i

B

d

G

G

od

symetrycznie położonych elementów

1

l

d

G

i

2

l

d

G

przewodnika są równe co do modułu i

symetrycznie położone względem siebie,

zatem wartość indukcji wypadkowej od

oby elementów wynosi:

2

r

2

dl

sin

I

sin

'

dB

2

dB

π

β

⋅

⋅

µ

=

β

=

Wektor indukcji dB jest prostopadły do

powierzchni obwodu, i skierowany od

obwodu.

Wypadkową indukcję od całego przewodnika otrzymamy całkując powyższe równanie po

połowie okręgu czyli od 0 do

πR

R

r

2

sin

I

dl

r

4

sin

I

B

2

R

0

2

π

π

β

⋅

⋅

µ

=

∫

π

β

⋅

⋅

µ

=

π

Uwzględniając, że

r

R

sin

=

β

i

2

2

d

R

r

+

=

, otrzymamy

(

)

2

/

3

2

2

2

d

R

2

IR

B

+

µ

=

(*)

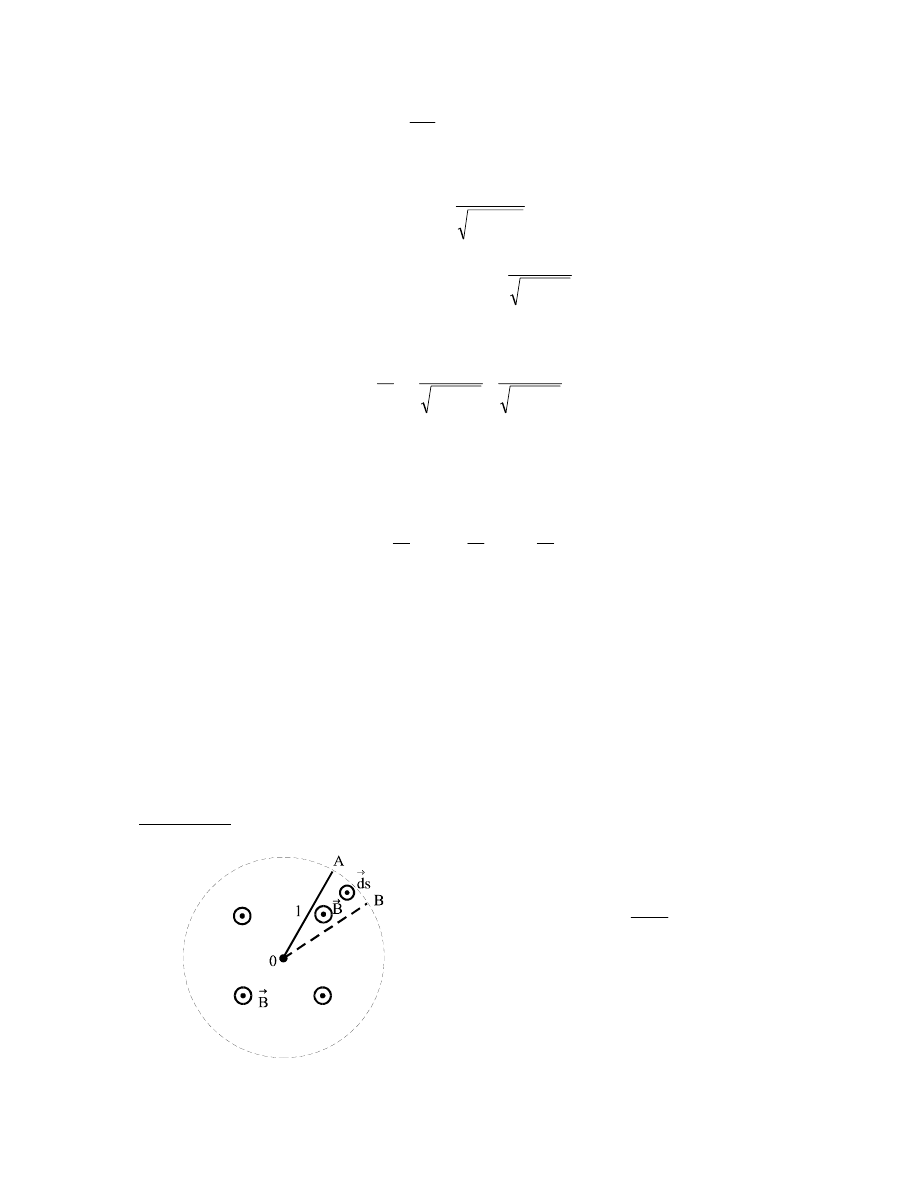
Zad. 8.7.

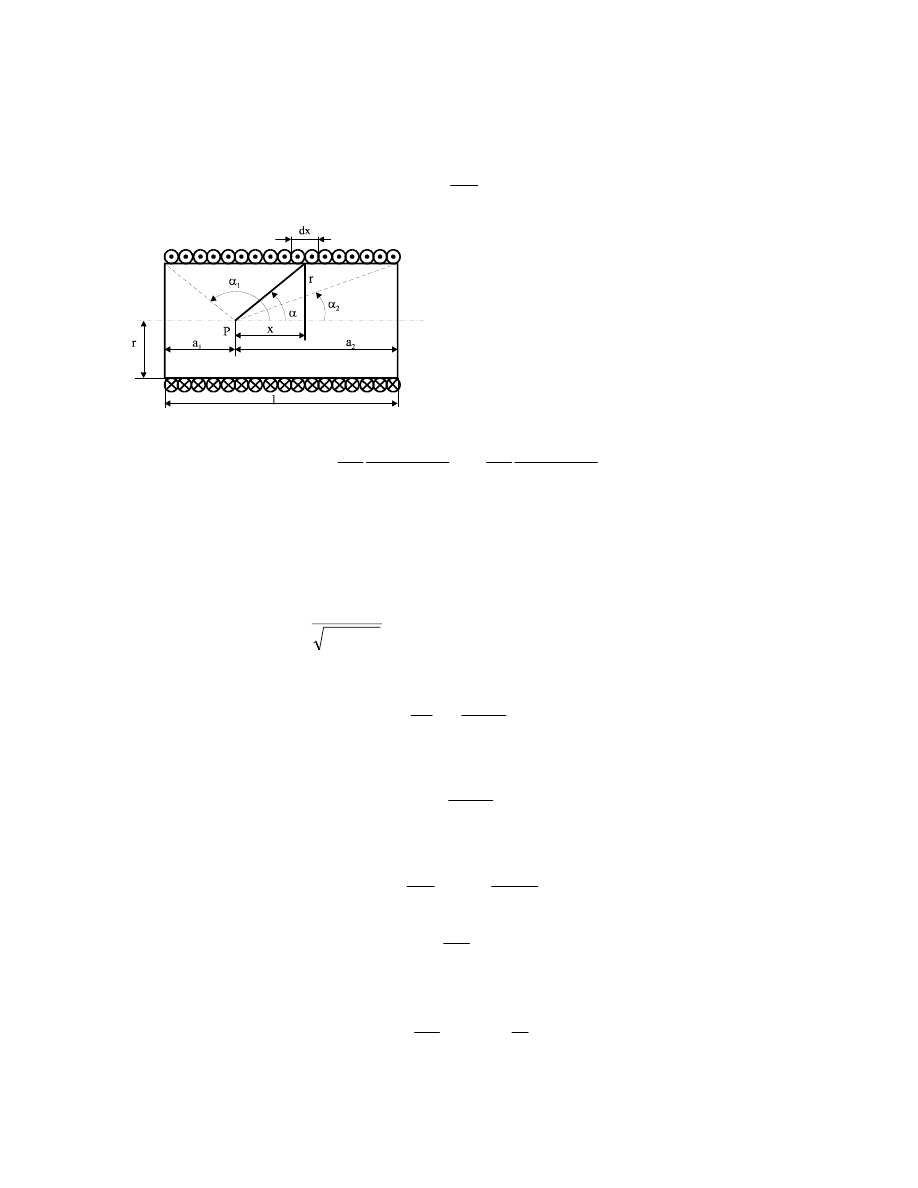
Wyznaczyć natężenie H pola magnetycznego na osi cewki cylindrycznej (solenoidu) z

równomiernie i gęsto nawiniętymi zwojami, przez które przepływa prąd o natężeniu I. Cewka

ma n zwojów, długość l i promień przekroju poprzecznego r. Położenie punktu P, dla którego

liczymy H, określają odcinki a

1

i a

2

mierzone od końca cewki. Przedyskutować otrzymany

wynik.

Rozwiązanie:

Przyjmijmy początek układu współrzędnych w rozpatrywanym punkcie P. Kierunek prądu w

uzwojeniu niech będzie taki, jak na rysunku. Jeżeli wziąć pod uwagę kołowy element cewki o

długości dx, to można go traktować jak cienki przewodnik kołowy i wykorzystać wynik z

zadania 8.6.

65

Na jednostkę długości solenoidu przypada

( )

l

/

n

I

⋅

amperozwojów czyli prąd dI płynący w

elemencie dx solenoidu wynosi:

dx

l

n

I

dI

⋅

=

Podstawiając do wyniku końcowego (*) z

zadania 8.6 za

x

d

→ , za

r

R

→ i za

dI

I

→

solenoidu oraz wiedząc, że między

wektorami B

i

H

G

G

zachodzi związek

H

B

G

G

µ

=

otrzymujemy:

(

)

(

)

dx

x

r

r

lr

2

n

I

dx

x

r

r

l

2

n

I

dH

2

/

3

2

2

3

2

/

3

2

2

2

+

⋅

=

+

⋅

=

Aby znaleźć H w punkcie P należy powyższe wyrażenie scałkować po dx w granicach od a

1

do a

2

. W tym celu zmieniamy zmienną całkowania i przechodzimy do całkowania po kącie

α

(patrz rysunek). Z rysunku wynika, że

α

⋅

=

α

=

+

ctg

r

x

oraz

sin

x

r

r

2

2

czyli

α

−

=

α

2

sin

r

d

dx

Stąd

α

α

−

=

d

sin

r

dx

2

Zatem

α

α

⋅

α

⋅

−

=

d

sin

r

sin

lr

2

n

I

dH

2

3

α

α

⋅

−

=

d

sin

ln

2

n

I

dH

i

(

)

α

α

−

∫

=

α

α

⋅

−

∫

=

∫

=

α

α

α

α

α

α

d

sin

l

2

In

d

sin

l

2

n

I

dH

H

1

2

1

2

1

2

66

(

)

1

2

cos

cos

l

2

n

I

H

α

−

α

⋅

−

=

Wyrażając kąty za pomocą odcinków określających położenie punktu P otrzymuje się:

2

2

2

2

2

a

r

a

cos

+

=

α

(

)

2

1

2

1

1

1

a

r

a

cos

cos

+

=

α

−

π

=

α

−

Wtedy:

















+

+

+

=

=

2

2

2

2

2

1

2

1

a

r

a

a

r

a

l

2

In

H

Jeżeli solenoid jest długi (l>>r), to można przyjąć, że:

r

a

i

r

a

2

1

>>

>>

to wówczas natężenie pola H jest w całym solenoidzie takie samo i wynosi:

(

)

l

In

1

1

l

2

In

H

=

+

=

,

l

In

H

=

Widzimy więc, że natężenie pola magnetycznego H wewnątrz solenoidu jest wprost

proporcjonalne do ilości zwojów n solenoidu, a odwrotnie proporcjonalne do jego długości l.

Zad. 8.8.

Wyprowadź z prawa Faradaya wzór na siłę elektromotoryczną

ε

indukowaną w pręcie

o długości l, obracającym się w jednorodnym polu magnetycznym o indukcji

B

G

ze stałą

prędkością kątową

ω wokół osi przechodzącej przez jeden z końców pręta i prostopadłej do

niego. Płaszczyzna obrotu jest prostopadła do

B

G

.

Rozwiązanie:

Wychodzimy ze znanego wzoru:

ε

dt

d

B

Φ

−

=

Elementarny strumień

B

d

Φ przecinany

przez wirujący pręt w ciągu czasu dt

wynosi:

s

d

B

d

B

G

G

⋅

=

Φ

67

gdzie s

d

G

jest to wektor powierzchni , którego moduł równa się wielkości powierzchni ds

(zakreślonej przez pręt o długości l) i jest prostopadły do powierzchni ds.

Ponieważ

s

d

||

B

G

G

(czyli kąt

α jaki tworzą te dwa wektory wynosi 0 i jest wtedy cosα = 1)

możemy zapisać:

ds

B

cos

ds

B

s

d

B

d

B

⋅

=

α

⋅

⋅

=

⋅

=

Φ

G

G

Przybliżając pole ds. zakreślone przez pręt w czasie dt polem trójkąta OAB mamy:

l

AB

2

1

ds

⋅

=

Odcinek AB trójkąta wyznaczamy z definicji miary łukowej kąta.

α

= d

l

AB

gdzie droga kątowa

dt

d

⋅

ω

=

α

Zatem

dt

l

AB

⋅

ω

⋅

=

a

dt

l

2

1

ds

2

ω

=

i wtedy

dt

Bl

2

1

d

2

B

ω

=

Φ

Ostateczny wzór na

ε zaindukowaną w pręcie ma postać:

ε

ω

=

2

Bl

2

1