A.Z.

G

RZYBOWSKI

W

YKŁADY Z

T

EORII

G

IER I

D

ECYZJI

Strona

26

normatywnej teorii decyzji.

2. Uwagi na temat użyteczności pieniędzy

W wielu sytuacjach praktycznych, zwłaszcza w działalności

gospodarczej, perspektywy można wyrazić jako sumy pieniężne. Miarami

ilości pieniędzy są pewne liczby jednostek monetarnych (złotych, euro,

dolarów itp.). W takich przypadkach często a nawet zwykle traktuje się

liczby owych jednostek monetarnych jako użyteczności lub jako liczby

proporcjonalne do użyteczności, to jest zakłada się, że u(M) = M lub u(M) =

kM.

Objawia się to tym, że często w problemach decyzyjnych (np. zadaniach

optymalizacyjnych) dążymy do maksymalizacji uzyskanych kwot pieniędzy

lub minimalizacji kwot wydawanych. Ale jeśli nawet świadomie zaniedbamy

fakt, że taka funkcja użyteczności pomija inne aspekty perspektyw (np.

etyczne i humanitarne), to i tak ta skala wartości zwykle nie jest całkowicie

odpowiednią podstawą analizy problemów decyzyjnych dotyczących

pieniędzy. Przykład tak zwanego „paradoksu petersburskiego" jest ilustracją

wynikających stąd trudności.

Przykład (Paradoks Petersburski) Proponują Wam za opłatą,

następującą perspektywę losową. Zostanie Wam wypłacona kwota 2

N

złotych, pod warunkiem, że w serii rzutów monetą pierwszego orła uzyskacie

dopiero w N-tym rzucie. Oznacza to, że jeśli orzeł wypadnie za pierwszym

razem otrzymacie 2 zł , jeśli za pierwszym razem reszka a orzeł za drugim

dostaniecie 2

2

=4zł , …., jeśli przez pierwszych 9 rzutów wypadną reszki a

orzeł wypadnie za 10 to otrzymacie 2

10

=1024 zł, itd. Jaką opłatę zgodzicie

się wnieść za udział w tej loterii

? Zastanówmy się co wasza (nieznana mi)

odpowiedź oznacza dla przypuszczenia, że użyteczność pieniędzy jest dla

was proporcjonalna do ich ilości, tzn. że jest funkcją liniową. Oznaczmy

A.Z.

G

RZYBOWSKI

W

YKŁADY Z

T

EORII

G

IER I

D

ECYZJI

Strona

27

naszą grę jako mieszankę L = [ l, 2, 3, ...]

(1/2 ,1/4,1/8,...)

. Jak wiadomo

prawdopodobieństwo uzyskania pierwszego orła dopiero w N tym rzucie jest

równe 1/2

N

.

Zatem, zakładając, że użyteczność pieniędzy jest funkcją

liniową, tzn. u(M) = k M, dla dowolnej skończonej liczby N otrzymujemy:

u

(L) ≥

kN

k

k

u

n

n

n

n

N

n

n

=

+

+

+

+

=

=

∑

∑

∞

=

=

)

1

....

1

1

1

(

2

1

2

2

1

)

2

(

1

1

Ponieważ N może być dowolnie duże, więc okazuje się, że u(L)=

• .

Okazało się więc, że jeżeli użyteczność pieniędzy mierzy się wielkością

proporcjonalną do ich kwoty, to powinniście zgodzić się na wniesienie każdej

opłaty w zamian za możliwość uczestnictwa w tej grze, ponieważ

użyteczność loterii wynosi nieskończoność, a zatem z własności A funkcji

użyteczności wynika, że loteria ta jest dla nas bardziej atrakcyjna od

dowolnej kwoty pieniędzy (np. 1 mln zł) bo użyteczność dowolnej,

określonej kwoty pieniędzy jest skończona. Jasne jest, że ludzie zdrowi na

umyśle nie wniosą dowolnie wielkiej zapłaty za udział w tej loterii - na ogół

nie chcą wnosić nawet skończonych, ale wysokich opłat za udział w tej grze.

Wynika z tego, że użyteczność pieniędzy nie jest liniową funkcją ich ilości.

W rzeczywistości badania behawioralne wykazują, że większość

ludzi ma nieliniową funkcję użyteczności pieniędzy. Na przykład całkowity

kapitał wielkości kilku groszy jest tak samo zły jak zupełny brak pieniędzy

— czyli użyteczność sum groszowych jest w istocie zerowa. Z drugiej strony

perspektywa otrzymania dwu miliardów złotych nie jest dużo atrakcyjniejsza

niż perspektywa jednego miliarda - z pewnością nie jest dwukrotnie

atrakcyjniejsza! Gdy wielkość kapitału osiąga takie wyżyny, przyrosty

użyteczności zdają się stopniowi maleć. Na rysunku 1 pokazano typowy

wykres funkcji użyteczności u(M), wykreśloną względem kapitału

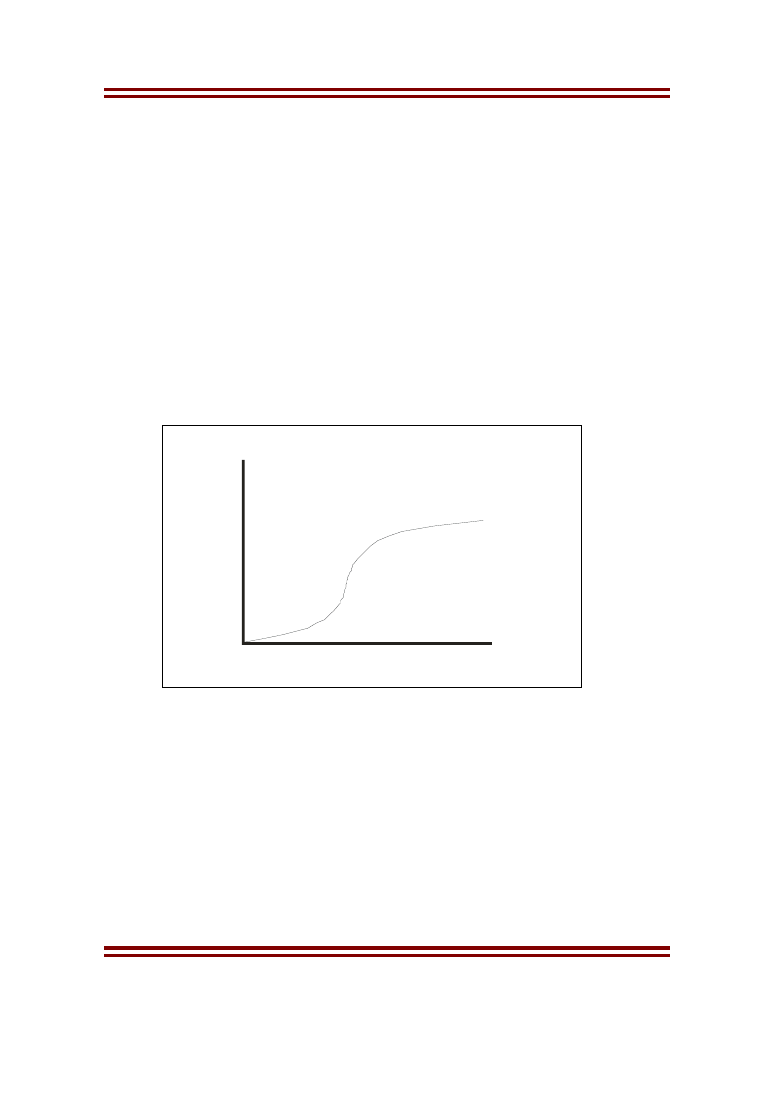
A.Z.

G

RZYBOWSKI

W

YKŁADY Z

T

EORII

G

IER I

D

ECYZJI

Strona

28

całkowitego M - krzywa ta ilustruje funkcje użyteczności pieniędzy

charakterystyczne dla większości ludzi. Jest ona zawsze funkcją rosnącą,

zgodnie z obserwacją, że im większa jest ilość pieniędzy, tym większa jest jej

atrakcyjność. W normalnych sytuacjach nie zdarza się, by większy kapitał

był mniej „użyteczny" niż mniejszy, niezależnie od osobistego stosunku

decydenta do pieniędzy. Wszak gdyby na przykład był pieniądzom zupełnie

niechętny właściciel kapitału mógłby nadmiar spalić, zakopać lub oddać

komuś (np. bardziej potrzebującym) osiągając w ten sposób wyższą

użyteczność.

Rys.1 Typowy kształt funkcji użyteczności pieniędzy

W trakcie rozwiązywania konkretnego problemu decyzyjnego

wygodnie jest czasem skupić uwagę na małym fragmencie krzywej

reprezentującej u(M), czyli naszą funkcję użyteczności pieniędzy, a

mianowicie, na tej części krzywej, która jest w danym problemie istotna.

Rzeczą naturalną jest przy tym odkładanie na osi odciętych raczej sum

pieniężnych, które można zyskać lub stracić, niż ogólnych zasobów

kapitałowych. Trzeba jednak pamiętać, że wówczas funkcja u(M), gdzie

M

u

(M)

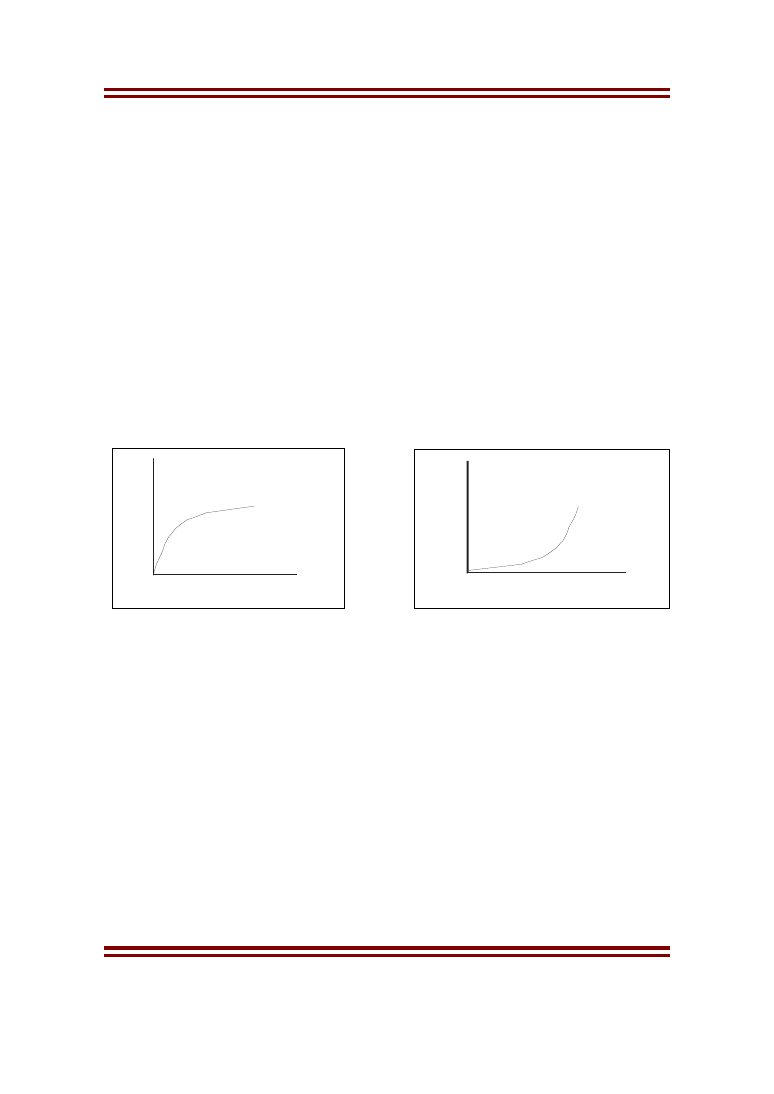
A.Z.

G

RZYBOWSKI

W

YKŁADY Z

T

EORII

G

IER I

D

ECYZJI

Strona

29

przez M oznaczono przyrost lub zmniejszenie zasobów od stanu

początkowego M

0

,

jest w rzeczywistości funkcją u

Mo

(M)=u(M+M

o

). Stąd też

przyjmowana przez daną osobę funkcja użyteczności pieniędzy może

wydawać się różną, w różnych sytuacjach, po prostu dlatego, że osoba ta

działa wokół różnych punktów na swej pełnej krzywej użyteczności. Jeżeli

przyjęta funkcja użyteczności pieniędzy jest taka, jak pokazano na rysunku 1

to jest oczywiście możliwe, że (lokalne) funkcje użyteczności dla zysków i

strat będą wypukłe w jednych, a liniowe lub wklęsłe w innych przypadkach,

czyli takie, jak pokazane na kolejnych rysunkach.

Rys. 2. Wklęsła funkcja użyteczności

Rys. 3. Wypukła funkcja użyteczności

Rysunek 2 na ogół odpowiada „dużemu” kapitałowi początkowemu

M

0

, rys 3 odpowiada sytuacjom, w których kapitał początkowy M

0

jest

„bliski” zera. Zastanówmy się co się kryje za jednym lub drugim kształtem

funkcji ryzyka.

Przykład. Przypuśćmy, że decydent staje przed następującym

wyborem: za 1600 zł może wziąć udział w loterii [10 000 zł., 0zł.]

0.16

( np. w

losowaniu na kole fortuny, lub inwestycje w pewna spółkę). Znaczy to, że

jeżeli zapłaci za udział w losowaniu (kupi akcje) to zyskuje 8 400 zł jeśli

wylosuje 10 000, jeżeli z kolei wylosuje 0 to straci posiadane 1 600zł.

u

(M)

M

u

(M)

M

A.Z.

G

RZYBOWSKI

W

YKŁADY Z

T

EORII

G

IER I

D

ECYZJI

Strona

30

Zauważmy, że wartość oczekiwana wygranej w loterii jest równa kwocie,

którą należy uiścić za wzięcie w niej udziału. Inaczej mówiąc decydent stoi

przed wyborem: pewne 1600 zł czy (w zamian) udział w loterii, której

wartość oczekiwana wynosi dokładnie tyle samo. Co wybierze? Dowiemy się

o tym jeśli poznamy jego funkcji użyteczności. Załóżmy, że jest ona dla kwot

mniejszych od 1 000 000 zł dana wzorem:

M

M

u

=

)

(

Otrzymujemy, że u(0) = 0, u(1600) = 40, i u(10 000) = 100. W takim

razie użyteczność proponowanej decydentowi loterii wyliczamy nastepująco

u

([0, 10 000]

0.16

) = 0,84 u(0) + 0,16 u(10) = 16

Użyteczność tego zakładu jest więc mniejsza niż użyteczność

zatrzymania 1 600zł przy sobie, wynosząca 40. Tak więc status quo będzie

atrakcyjniejsze dla tego decydenta niż perspektywa losowania, pomimo że

wartość oczekiwana wygranej w zakładzie jest identyczna jak kwota, która

trzeba by zainwestować. Powiemy, że nasz decydent ma awersje do ryzyka.

Rozumowanie podobne do przedstawionego w przykładzie stanowi

podstawę do umownego, ale zgodnego z intuicją podziału decydentów na

skłonnych

do ryzyka i na czujących awersje do ryzyka, no i na względem

ryzyka obojętnych.

Jeżeli decydent woli gwarantowaną kwotę M od udziału w loterii w

której oczekiwana wygrana wynosi M, to mówimy, że ma awersje do ryzyka.

Woli to znaczy, że dla niego użyteczność loterii jest mniejsza od

równoważnej jej kwoty pieniędzy uzyskiwanej na pewno. Zauważmy, że

ryzykując, mógłby zyskać więcej, ale mógłby też stracić i tego się właśnie

obawia. Ryzykując czyli biorąc udział w przedsięwzięciu, którego modelem

A.Z.

G

RZYBOWSKI

W

YKŁADY Z

T

EORII

G

IER I

D

ECYZJI

Strona

31

jest loteria, w praktyce może to być inwestycja giełdowa lub jakieś inne

przedsięwzięcie gospodarcze zamiast np. pewnej inwestycji w obligacje

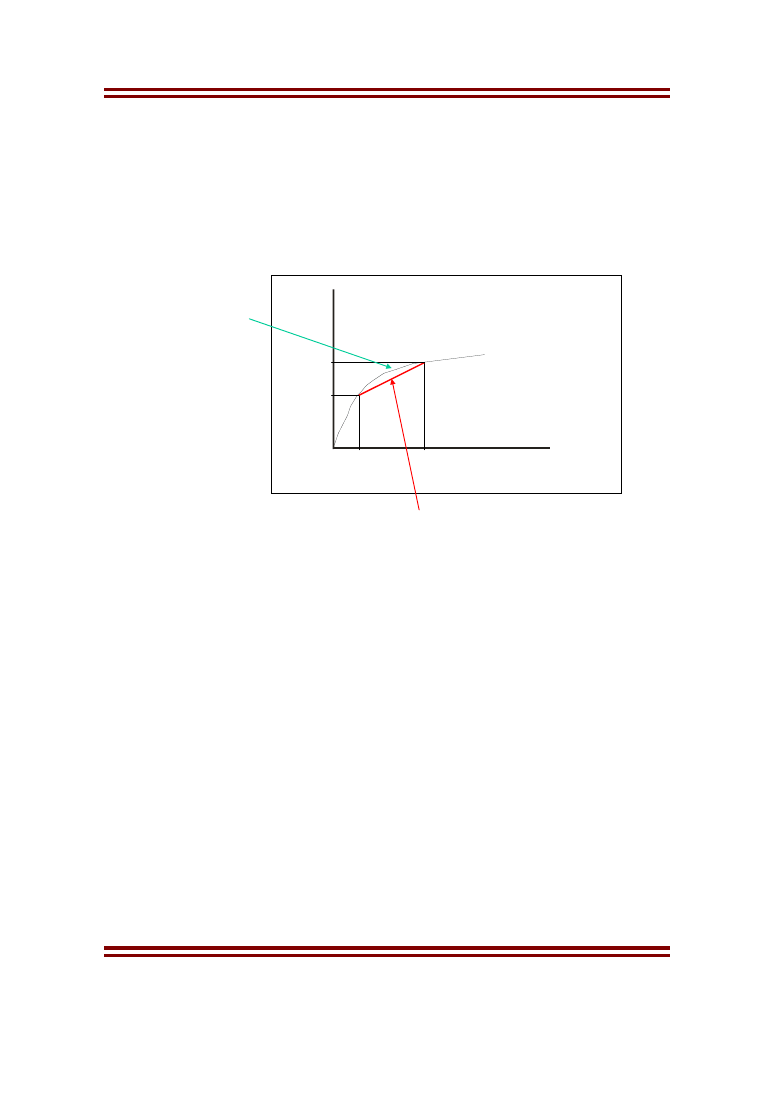
skarbu państwa. Zauważmy, że taki decydent ma wklęsłą funkcję

użyteczności, tak jak pokazano na poniższym rysunku.

u

(M)

M

M

1

M

2

u

(M

2

)

u

(M

1

)

u

([M

1

,M

2

]

r

)=r u(M

1

)+(1-r)u(M

2

)

u

(r M

1

+

(1-r)M

2

)

Na rysunku tym czerwona linia reprezentuje użyteczności różnych

loterii (różne punkty zależą od tego jakie jest prawdopodobieństwo r

wygranej M

1

). Widzimy, że użyteczności kwot równym wartościom

oczekiwanym loterii znajdują się ponad nimi tzn.

u

(E([M

1

,M

2

]

r

))=

u

(r M

1

+

(1-r)M

2

) > r u(M

1

)+(1-r)u(M

2

) = u([M

1

,M

2

]

r

)

czyli loterie są dla takiego decydenta mniej atrakcyjne.

Jest oczywiste, że analogicznie argumentując możemy wykazać, że

wypukła funkcja użyteczności obserwowana w pewnym przedziale kwot

pieniężnych sygnalizuje skłonność decydenta do ryzyka, co w naszej

interpretacji ściśle rzecz ujmując oznacza, że decydent każdą posiadaną

kwotę M uważa za mniej atrakcyjną od udziału w loterii, w której

A.Z.

G

RZYBOWSKI

W

YKŁADY Z

T

EORII

G

IER I

D

ECYZJI

Strona

32

oczekiwana wygrana wynosi M, a wygrane należą do z rozważanego zakresu

kwot. Wynika też z naszych rozważań, że decydent obojętny wobec ryzyka

to taki którego funkcja ryzyka w zakresie obejmującym rozważane w

problemie kwoty jest liniowa.

Na zakończenie wykładu poświęconego teorii użyteczności

przedstawimy jeszcze jeden interesujący przykład. Pochodzi on z pracy M.

Allais z 1953 roku. Ilustruje on dwa ważne aspekty związane z

wykorzystywaniem tej teorii. Rozważmy mianowicie sytuację, w której

decydent ma przed sobą trzy (nielosowe) perspektywy uporządkowane

następująco: P1>P2>P3. Zgodnie z poznaną teorią zawsze możemy tak

wybrać funkcję użyteczności u, że u(P1)=1 oraz u(P3)=0. Zatem wszystkie

możliwe preferencje decydenta zależą od wyboru wartości u

2

=u

(P2).

Dokładniej, preferencje te od tej wartości nie zależą – mamy na myśli jedynie

to, że różne możliwe preferencje odzwierciedlane są jednoznacznie przez

jedyny odpowiadający im wybór wartości u

2

.

Rozważmy teraz dwie różne loterie tych perspektyw. O ich postaci

decyduje

wybór

prawdopodobieństw

wylosowania

poszczególnych

perspektyw. Niech dla pierwszej loterii będzie to L1=[P1,P2,P3]

(p1,p2,p3)

a dla

drugiej: L2=[P1,P2,P3]

(q1,q2,q3)

. Zauważmy, że L1>L2 czyli u(L1)>u(L2) ma

miejsce wtedy tylko wtedy, gdy

p

1-q1+(p2-q2)u

2

> 0

(1.war)

Zatem nie znając dokładnych wartości funkcji, z samego faktu

jedynie, że funkcja użyteczności istnieje wnioskujemy ponad wszelką

wątpliwość , że np. loteria [P1,P2,P3]

(0.4,0.2,0.4)

> [P1,P2,P3]

(0.2,0.5,0.3)

wtedy i

tylko wtedy, gdy [P1,P2,P3]

(0.5,0,0.5)

> [P1,P2,P3]

(0.3,0.3,0.4)

, gdyż dla obu tych

A.Z.

G

RZYBOWSKI

W

YKŁADY Z

T

EORII

G

IER I

D

ECYZJI

Strona

33

loterii warunek (1.war) ma postać identyczną. To ciekawe spostrzeżenie,

ilustruje fakt, ze wiele można się dowiedzieć o problemie decyzyjnym

jedynie na podstawie faktu, że funkcja użyteczności istnieje.

Ale przykład ma jeszcze jeden aspekt – behawioralny. Pokazuje jak

trudno może być zidentyfikować perspektywy stojące przed decydentem.

Rozważmy dwie sytuacje praktyczne. W pierwszej z nich decydent ma do

wyboru (pierwsza perspektywa): dostać 5 milionów złotych od razu lub

(druga perspektywa) wziąć udział w losowaniu 10 milionów zł. , 5 milionów

zł lub niczego z prawdopodobieństwami odpowiednio: 0.1, 0.89, 0.01. Jaką

decyzję byś podjął?

W drugiej sytuacji możliwe są następujące nagrody (trzecia

perspektywa) 5 milionów zł lub nic z prawdopodobieństwami odpowiednio:

0.11, 0.89 lub (czwarta perspektywa) 10 milionów zł. lub nic z

prawdopodobieństwami 0.1, 0.9. Co teraz byś wybrał czytelniku?

Na czym polega istota i osobliwość tego przykładu?

Otóż zgodnie z poprzednimi rozważaniami powinno być:

[10 mln, 5 mln, nic]

(0,1,0)

> [10 mln, 5 mln, nic]

(0.1,0.89,0.01)

wtedy i tylko wtedy , gdy

[10 mln, 5 mln, nic]

(0, 0.11,0.89)

> [10 mln, 5 mln, nic]

(0.1, 0, 0.9)

Badania behawioralne pokazują, że przytłaczająca większość ludzi wskazuje

przeciwne znaki preferencji w przypadku tych loterii! Dlaczego?

Czyżby przeczyło to całej teorii, jak tą sprzeczność wyjaśnić?