Zadania z Teorii gier 1 - rozwiązania

Zad. 1

Zapisz następującą grę w postaci normalnej:

1)

Gra w orła i reszkę. Dwóch graczy jednocześnie rzuca monetą 1 zł.
Jeżeli wypadną 2 orły lub 2 reszki, to gracz nr 1 wygrywa 2 zł, zaś
gracz nr 2 przegrywa 2 zł. Jeżeli zaś wypadnie 1 orzeł i 1 reszka, to
gracz nr 2 wygrywa 2 zł, zaś gracz nr 1 przegrywa 2 zł.

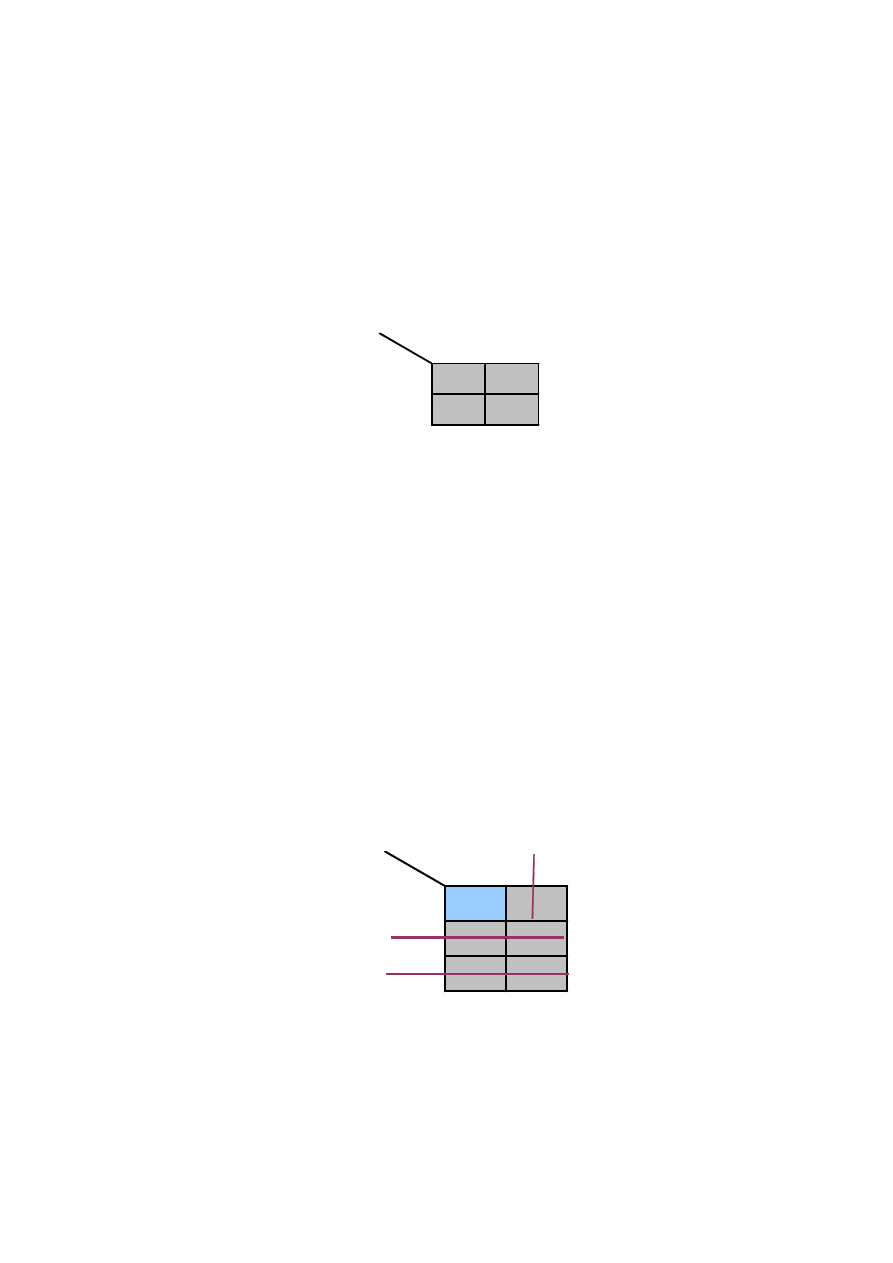
1

2

O

R

O

2;-2

-2;2

R

-2;2

2;-2

- brak strategii zdominowanych

- brak NE w strategiach czystych

2)

Firma A decyduje, czy wejść na rynek, na którym działa już firma B.
Firma B dowiaduje się o tej decyzji. Jeżeli firma A wejdzie na rynek,
to obie firmy jednocześnie decydują czy prowadzić kampanię
reklamową. W przeciwnym wypadku tylko firma B decyduje o
prowadzeniu kampanii reklamowej. Gdy obie firmy są obecne na
rynku, to każda z nich osiągnie zysk w wysokości po 3mln dolarów w
przypadku, gdy obie prowadziły kampanie reklamowe, albo zarobią
po 5mln dolarów gdyby obie zrezygnowały z kampanii. Jeżeli tylko
jedna z firm prowadzi kampanię reklamową to zarabia 6mln dolarów,
a druga firma zarabia 1mln. Gdy tylko firma B prowadzi działalność,
to zarobi 4mln dolarów jeśli reklamuje swoje wyroby, albo 3,5 mln –
jeśli nie reklamuje. Jeżeli firma A nie wejdzie na rynek to zarobi 0
dolarów.

R

A

B

R

N

WR

3;3

6;1

WR

WN

1;6

5;5

WR

NW

0;4

0;3,5

NE = {(WR;R)}

Zad. 2

Przeprowadź iteracyjną eliminację strategii ściśle zdominowanych w

następujących grach zapisanych w postaci normalnej:

1)

L

2)

C

S

3)

P

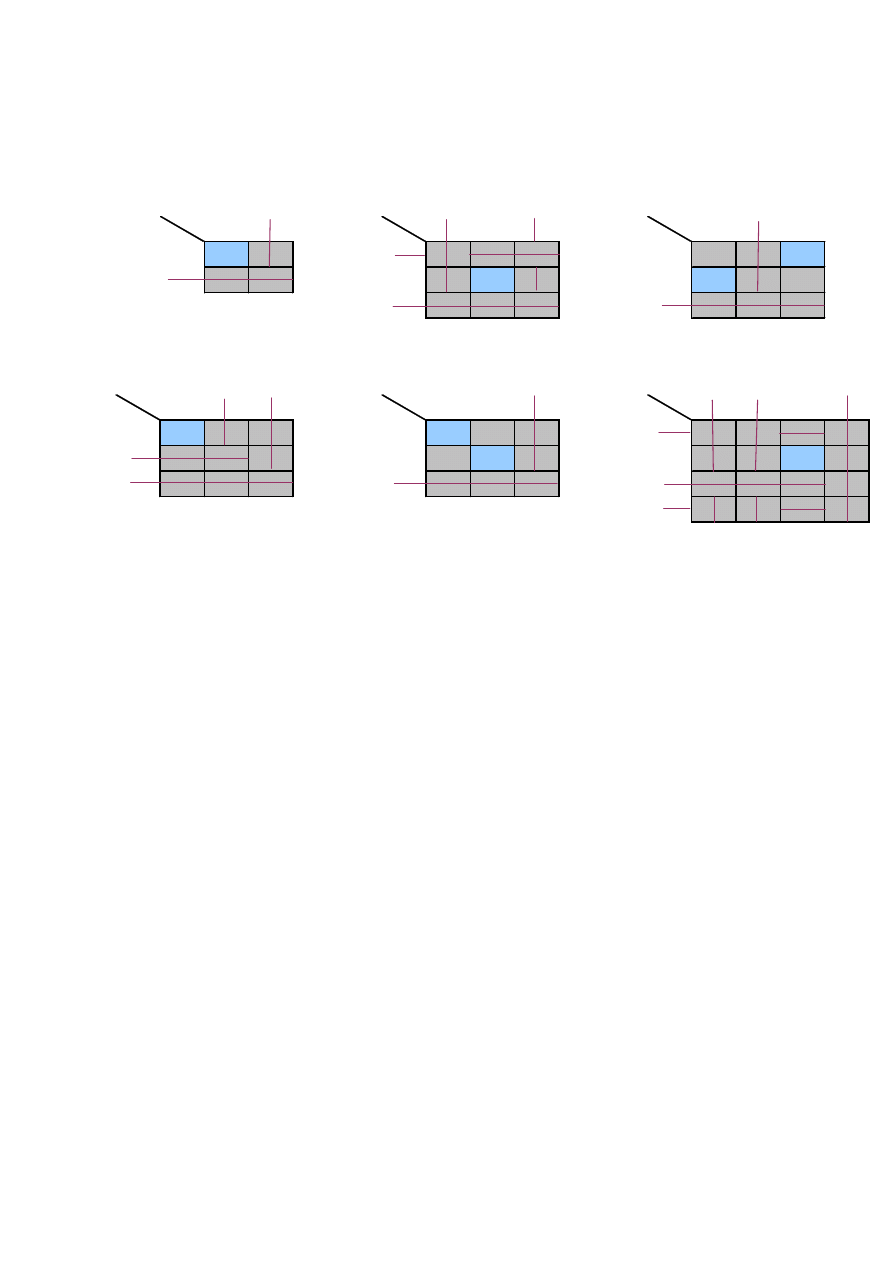
1

2

L

P

1

2

L

C

P

1

2

L

C

P

G

2;3

5;0

S

G

8;3

0;4

4;4

G

2;0

1;1

4;2

G

D

1;0

4;3

S

4;2

1;5

5;3

S

3;4

1;2

2;3

NE = {(G;L)}

S

D

3;7

0;1

2;0

G

D

1;3

0;2

3;0

NE = {(S;C)}

NE = {(S;L), (G;P)}

4)

L

L

5)

1/2L+1/2P

6)

C

C

C

1

2

L

C

P

1

2

L

C

P

1

2

A

B

C

D

G

6;3

5;1

0;2

G

8;6

0;1

8;2

X

W

5;4

4;4

4;5

12;2

G

S

0;1

4;6

6;0

S

1;0

2;6

5;1

X

3;7

8;7

5;8

10;6

1/2G+1/2S

D

2;1

3;5

2;8

S

D

0;8

1;0

4;4

X

Y

2;10

7;6

4;6

9;5

NE = {(G;L)}

NE = {(G;L), (S;C)}

X

Z

4;4

5;9

4;10

10;9

NE = {(X;C)}

Zad. 3

Wyznacz równowagi Nasha w grach z zadania 2.

Zad. 4

W teorii gier zakłada się, że wszyscy gracze są racjonalni i wszyscy

gracze wiedzą o tym. Eksperyment Beauty Contest zweryfikuje spełnienie
tego aksjomatu w Twojej grupie ćwiczeniowej.