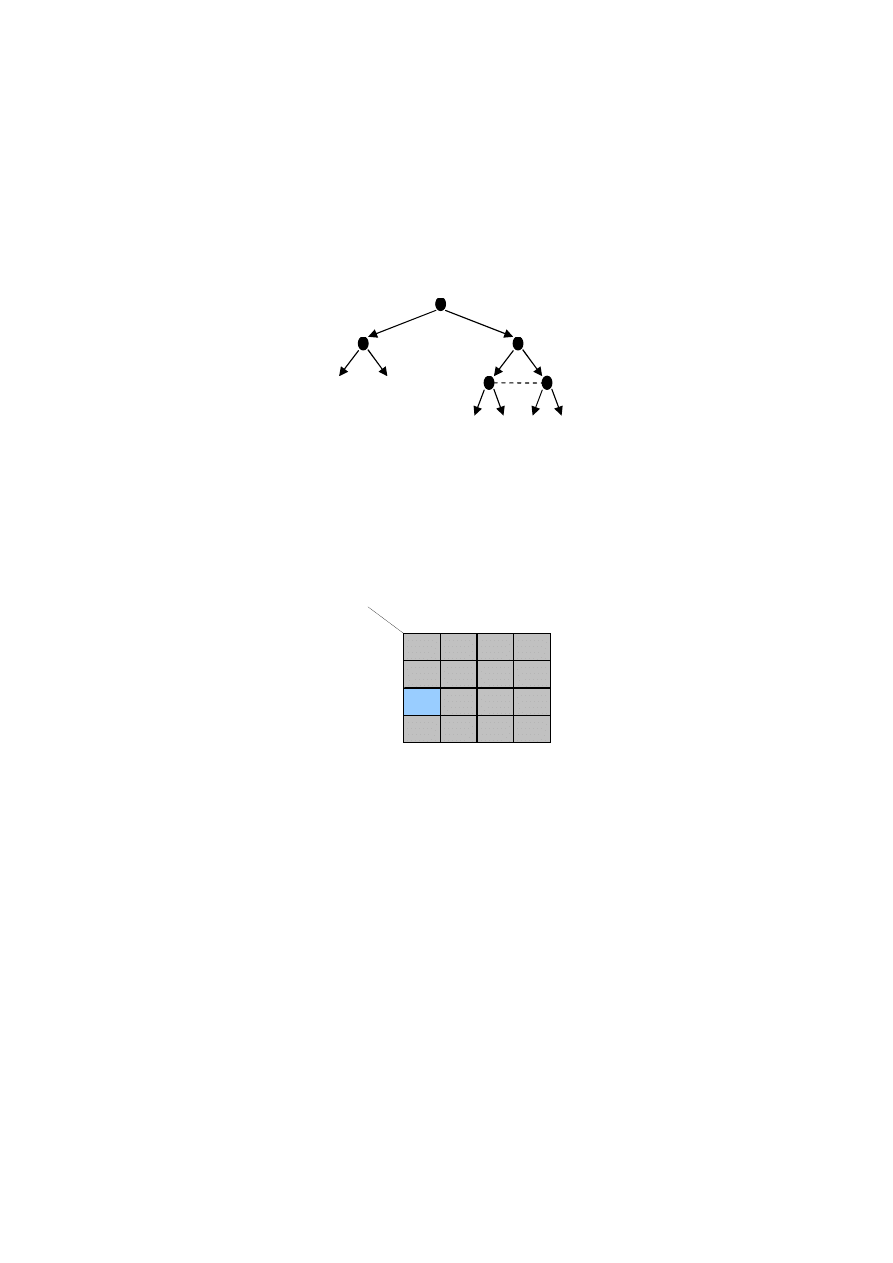
Zadania z Teorii gier 3 - rozwiązania

Zad.1

Eksperyment „Pracownik – Pracodawca” (oparty na eksperymencie:

„Gift Exchange Game”, Fehr, Kirchsteiger and Riedl, 1993)

mający na celu

sprawdzenie, jakie w rzeczywistości gracze podejmują decyzje.

Zad.2

a)

Wskaż wierzchołek początkowy oraz wierzchołki końcowe powyższej
gry.

b)

Wyznacz etapy gry.

c)

Wyznacz wszystkie możliwe strategie poszczególnych graczy:

S

1

={EA, EB, FA, FB}

S

2

={CX, CY, DX, DY}

d)

Przedstaw powyższą grę w postaci normalnej:

1

2

CX

CY

DX

DY

EA

1;4

1;4

5;2

5;2

EB

1;4

1;4

5;2

5;2

FA

3;4

1;4

3;4

1;4

FB

2;1

2;0

2;1

2;0

e)

Wyznacz równowagi Nasha tej gry (NE):

NE={(FA;CX)}
f)

Wyznacz doskonałe równowagi Nasha tej gry (SPNE):

SPNE=NE={(FA;CX)} – ponieważ jedyna

Zad.3 (Kontrakt pomiędzy dostawcą a nabywcą)

Nabywca i dostawca zastanawiają się czy podpisać umowę na

dostarczenie pewnego dobra. Jeżeli firmy nie zdecydują się na podpisanie
kontraktu, to gra kończy się, a wypłaty graczy wynoszą (0,0). Jeżeli firmy
podpiszą kontrakt, a dostawca dostarczy towar wysokiej jakości, to
wypłata nabywcy wyniesie 10, zaś dostawcy 5. Dostawca może jednak
zaoszczędzić na materiałach dostarczając towar niskiej jakości, który
będzie jednak bezużyteczny dla nabywcy. W tej sytuacji wypłata nabywcy
będzie wynosić -6, zaś dostawcy 10.

a)

Jakie jest rozwiązanie tej gry?

(1;4)

(5;2)

(3;4) (1;4)

1

2

1

2

E

F

C

D

A

B

X

Y

(2;1) (2;0)

X

Y

Nabywca nie podpisze kontraktu, gdyż wie, że dostawca dostarczyłby
mu dobro niskiej jakości.

b)

Nabywca może zabezpieczyć się przed ewentualnym oszustwem
dostawcy ustalając w kontrakcie kwotę c, którą dostawca będzie
musiał zapłacić nabywcy, jeżeli ten udowodni mu, iż dostarczony
towar jest złej jakości. Załóżmy, że z prawdopodobieństwem 0,5
oszustwo zostanie udowodnione. Oblicz wysokość kary, która:

- zrekompensuje nabywcy ewentualne straty z tytułu dostawy złej
jakości:
10

≤

-6+c/2 => c

≥

32

- skłoni dostawcę do dostarczenia dobra wysokiej jakości:
5 > 10-c/2 => c>10

- spowoduje, iż nabywca nie podpisze umowy:
(0 > -6+c/2) i (dostawca dostarczy dobro niskiej jakości) => =>
c < 12 i c < 10 => c < 10

- spowoduje, iż dostawca nie podpisze umowy:
dostawca zawsze podpisze umowę, gdyż dla kosztów większych od
10 dostarczy dobro wysokiej jakości i osiągnie zysk = 5

Zad. 4 (Zadanie z wykładu)

Przykład: Wejście na rynek [Malawski s.64]

Firma A zastanawia się nad wprowadzeniem na rynek nowego towaru.
Popyt na tego typu towar jest nieustabilizowany i może nastąpić duża albo
mała sprzedaż. Ocenia się, że prawdopodobieństwo dobrej koniunktury
wynosi 0,4, a słabej 0,6. Konkurencyjna firma B również zamierza
wprowadzić alternatywny towar na rynek. Na spodziewaną wielkość rynku
żadna z firm nie ma wpływu. Przyjmiemy, że o tym decyduje los. Firma B
może podjąć decyzję trochę później, kiedy już wie, czy rynek jest duży czy
mały, ale nie wie jaką decyzję podjęła firma A. Zyski każdej z firm będą
zależeć od tego jaka bezie koniunktura i co zrobi konkurent, a konkretnie:
- koniunktura dobra: obie firmy na rynku: (10;10); A weszła, B nie:
(100;0); A nie weszła, B weszła: (0; 120); obie nie weszły: (0;0);
- koniunktura zła: obie firmy na rynku: (-25;-39); A weszła, B nie: (2;0);
A nie weszła, B weszła: (0; -6); obie nie weszły: (0;0).

a)

Wyznacz wszystkie możliwe strategie poszczególnych graczy:

(0;0)
jakoś

(10;5)

(-6+c/2;10-c/2)

1, 2

2

brak porozumienia

porozumienie

wysoka jakość

niska jakość

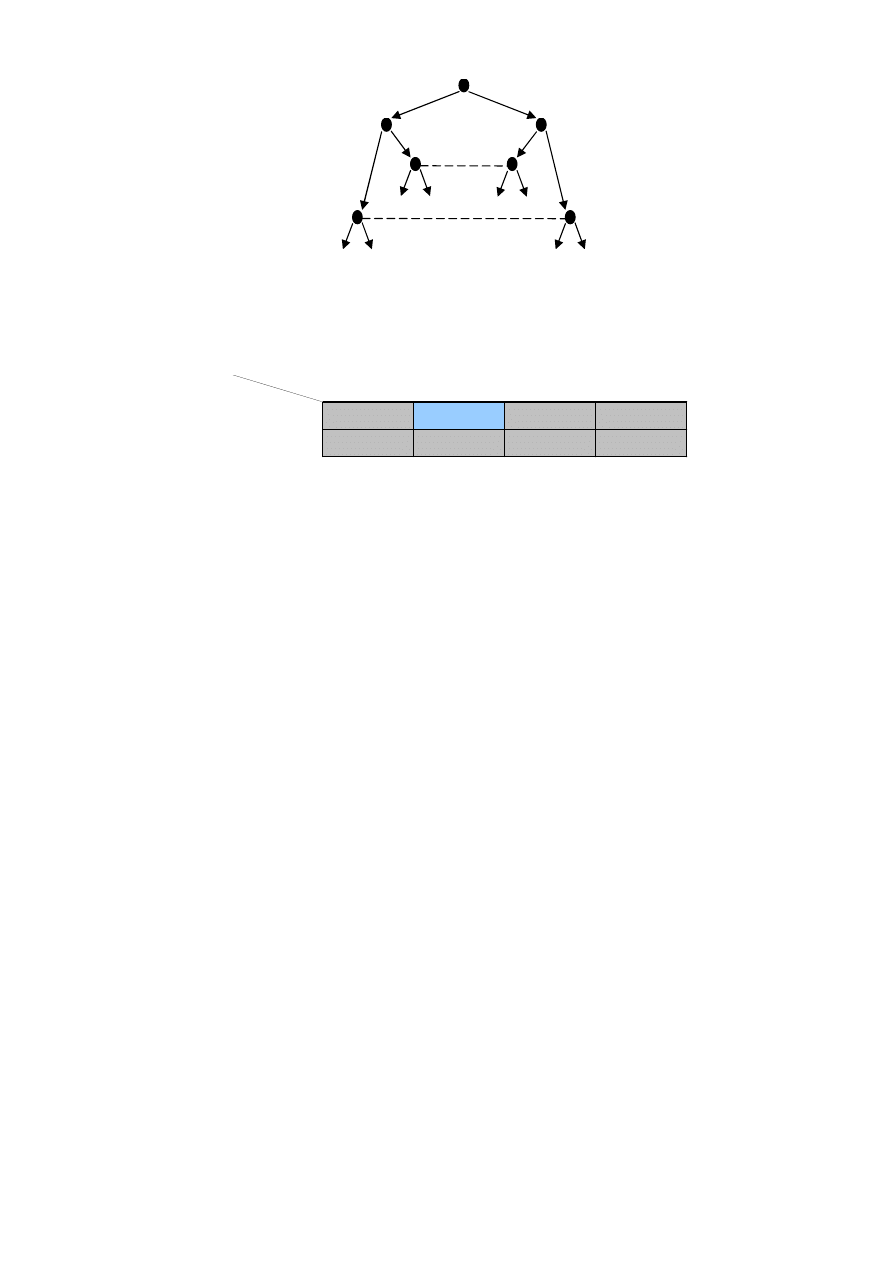
S

1

={W, NW}

S

2

={WdWm, WdNWm, NWdWm, NWdNWm}

b)

Przedstaw grę w postaci normalnej:

1

2

WdWm

WdNWm

NWdWm

NWdNWm

W

-11 ; -19,4

5,2 ; 4

25 ; -23,4

41,2 ; 0

NW

0 ; 44,4

0 ; 48

0 ; -3,6

0 ; 0

U(W;WdWz)=(0,4*10+0,6*(-25) ; 0,4*10+0,6*(-39)) = (-11 ; -19,4)
U(W;WdNWz)=(0,4*10+0,6*2 ; 0,4*10+0,6*0) = (5,2 ; 4)
U(W;NWdWz)=(0,4*100+0,6*(-25) ; 0,4*0+0,6*(-39)) = (25 ; -23,4)
U(W;NWdNWz)=(0,4*100+0,6*2 ; 0) = (41,2 ; 0)

U(NW;WdWz)=(0 ; 0,4*120+0,6*(-6)) = (0 ; -19,4)
U(NW;WdNWz)=(0 ; 0,4*120+0,6*0) = (0 ; 4)
U(NW;NWdWz)=(0 ; 0,4*0+0,6*(-6)) = (0 ; -23,4)
U(NW;NWdNWz)=(0 ; 0) = (0 ; 0)

c)

Jakie strategie wybiorą racjonalni gracze? (wyznacz NE):

NE = {(W,WdNWm)}

d)

Wyznacz SPNE:

SPNE = NE = {(W,WdNWm)}, gdyż jest to jedyna NE, a poza tym
jedyną podgrą tej gry jest cała gra.

(2;0)

(0;120) (0;0)

1

2

los

los

W

NW

M: 0,6

D: 0,4

Wd

NWd

(10;10) (100;0)

Wd

NWd

2

D: 0,4

M: 0,6

2

2

(0;-6) (0;0)

(-25;-39)

Wm

Wm

NWm

NWm