Wykład 5

Oko jako układ obrazujący

Przyosiowe modele oka

• Powierzchnie są sferyczne i scentrowane

• Współczynniki załamania są stałe w każdym ośrodku

• Obszar działania ograniczony do dołka środkowego

• Podstawa badania wielu właściwości oka

– Pozycja obrazu

– Powiększenie

– Oświetlenie siatkówki

– Odbicia od powierzchni załamujących (obrazy Purkinje’go)

– Apertury wejściowa i wyjściowa

– Wpływ wad refrakcyjnych

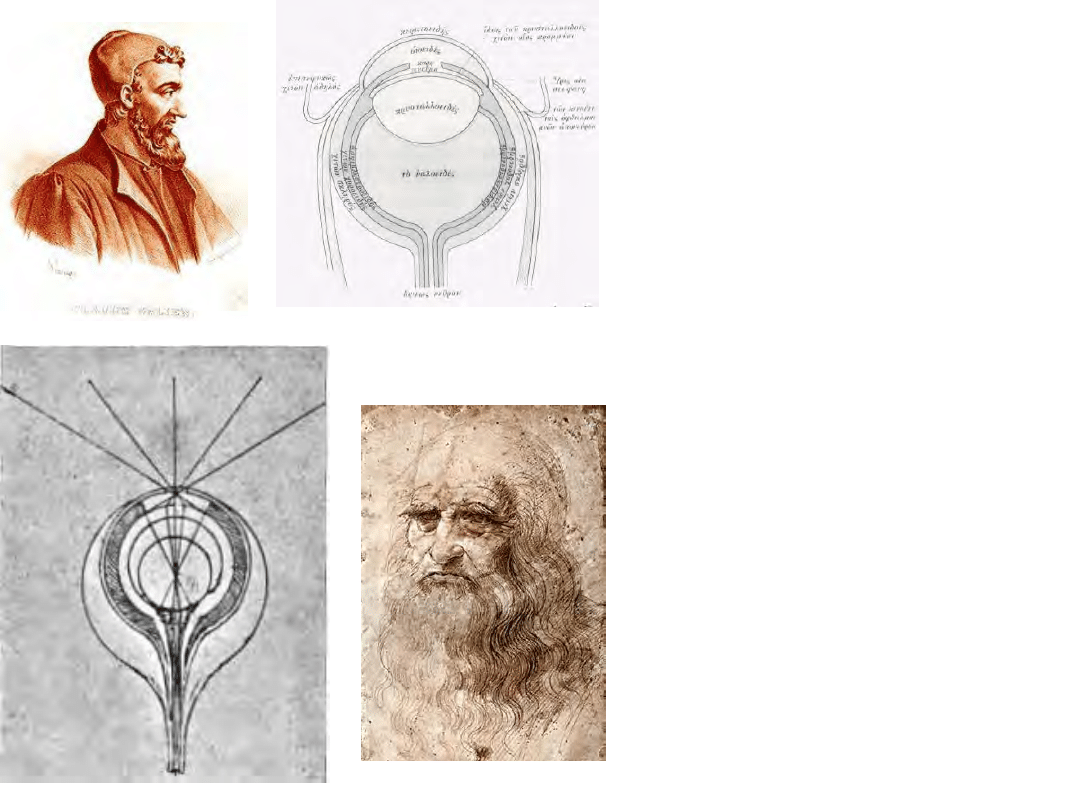
Modele oka

• Aelius Galen (II wiek AD)

– Soczewka jest

elementem czuciowym
w oku

• Leonardo da Vinci (XVI w.)

– Jest ona elementem

refrakcyjnym
formującym obraz na
siatkówce

Modele oka

• Johannes Kepler

(1604)
– Obraz jest

odwrócony

• René Descartes

(1637)
– Pierwszy

dokładny opis
układu
optycznego oka

Modele oka

• Christian Huygens

– Dwie półkule siatkówkowa i

rogówkowa wypełnione cieczą o
właściwościach wody z przesłoną

– Półkula siatkówki o 3x większym

promieniu niż rogówki

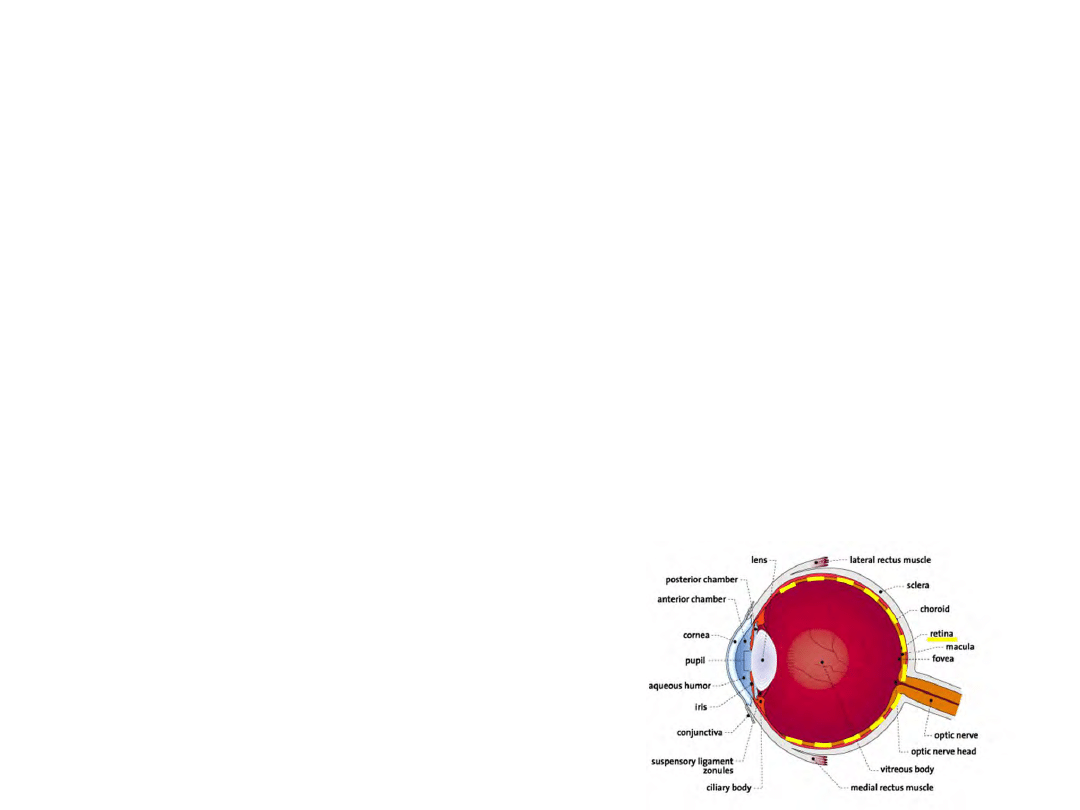
Modele oka

• Thomas Young

– Przednia powierzchnia rogówki ma promień

krzywizny 7,9 mm

– Przednia powierzchnia soczewki 7,6 mm

– Tylna powierzchnia soczewki 5,6 mm

– Szerokość komory przedniej 3,0 mm

– Współczynnik załamania

cieczy wewnątrz oka 1,333

– Współczynnik załamania

soczewek 1,44

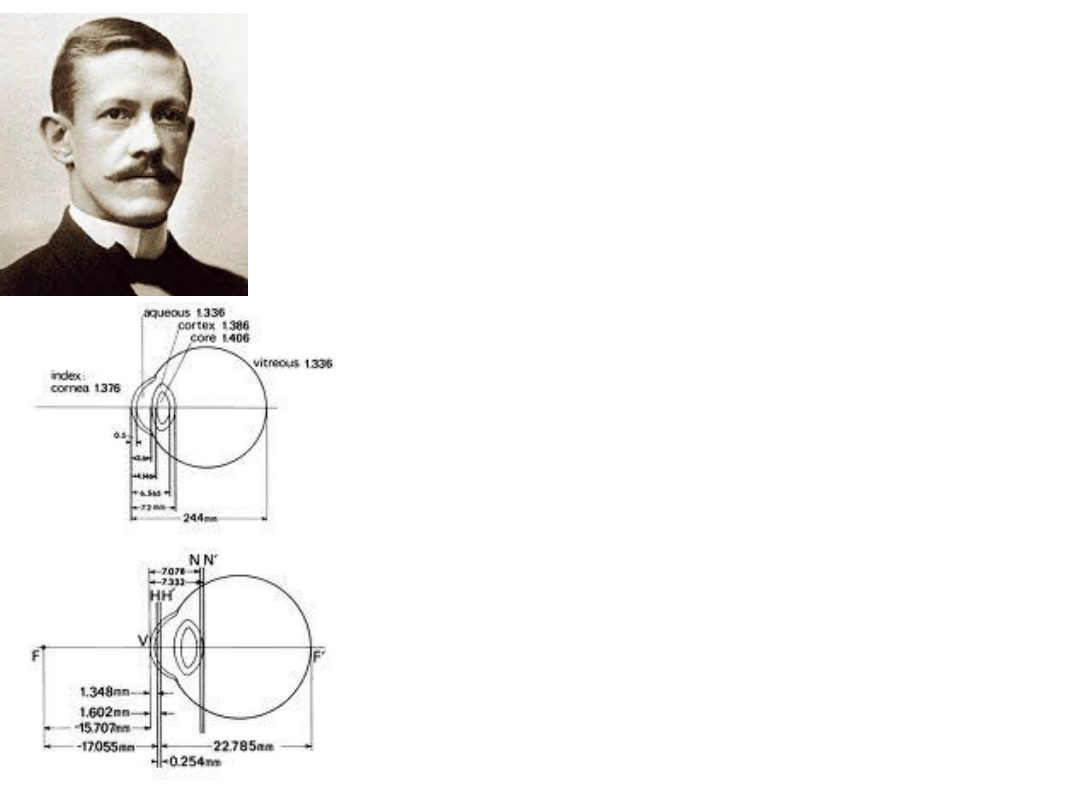
Modele oka

• Allvar Gullstrand (1909)

– tzw. Oko Gullstranda nr 1

– Rogówka składa się z dwóch

powierzchni

– Soczewka składa się z czterech

powierzchni (jądro i torebka)

– 2 stany akomodacji (0 D, 10,87 D)

– Wersja uproszczona (nr 2)

• 3 powierzchnie załamujące

• Soczewka pozbawiona grubości

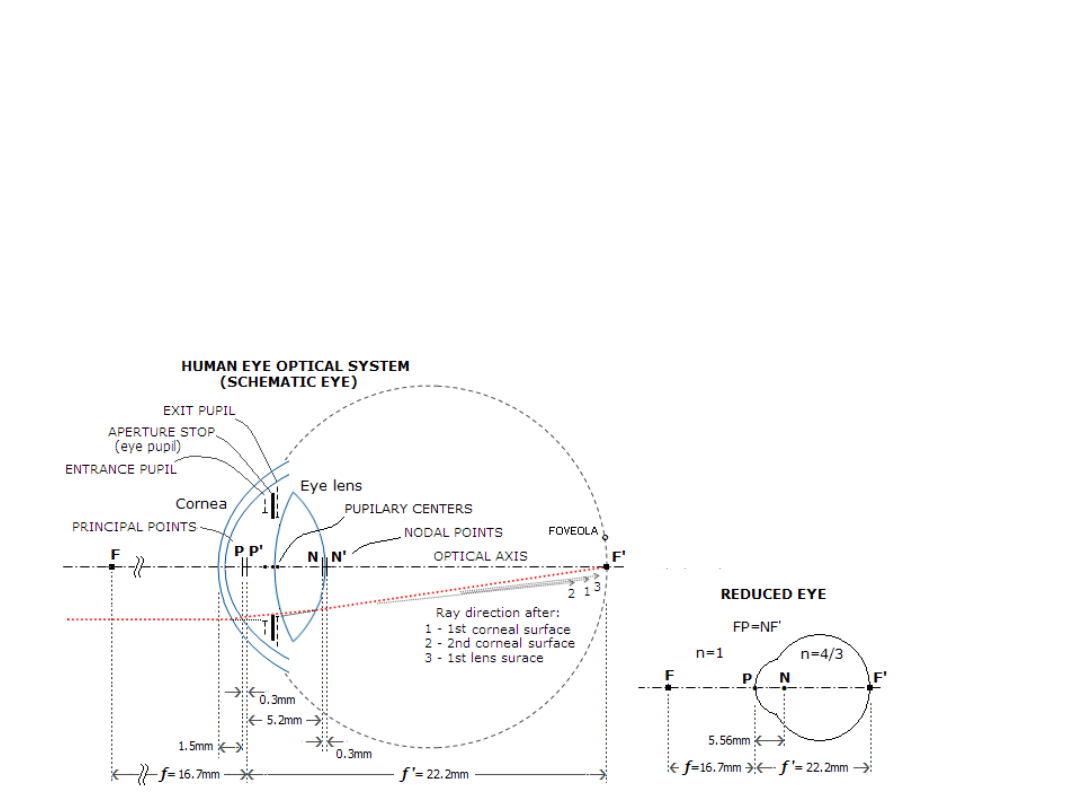
Modele oka

• Harold Heaton Emsley (1952)

– Zmodyfikowane oko nr 2 Gullstranda
– Soczewkę charakteryzuje grubość taka jak w oku nr 1
– Zmienione współczynniki załamania ośrodka wypełniającego oko (1,333)

- Zaprezentował także
zredukowane oko z jedną
powierzchnią łamiącą o
krzywiźnie 5,555mm i
współczynniku załamania 1,333

Modele oka

• Uogólnienie modelu Gullstranda nr 1 na

dowolny stopień akomodacji

– Grubość komory przedniej
– Grubość przedniej kory soczewki
– Grubość jądra soczewki
– Grubość tylnej kory soczewki
– Krzywizna przednia soczewki
– Krzywizna przednia jądra
– Krzywizna tylnia jądra
– Krzywizna tylnia soczewki

3

2

000048564

,

0

00531

,

0

052

,

1

A

A

A

x







0

)

6725

,

0

546

,

0

(

546

,

0

A

x





0

)

7

,

2

1

,

3

(

1

,

3

A

x





0

)

655

,

2

419

,

2

(

419

,

2

A

x





0

)

6725

,

0

635

,

0

(

635

,

0

A

x





0

)

333

,

5

/

1

10

/

1

(

10

/

1

A

x





0

)

655

,

2

/

1

911

,

7

/

1

(

911

,

7

/

1

A

x





0

)

655

,

2

/

1

760

,

5

/

1

(

760

,

5

/

1

A

x







0

)

333

,

5

/

1

6

/

1

(

6

/

1

A

x







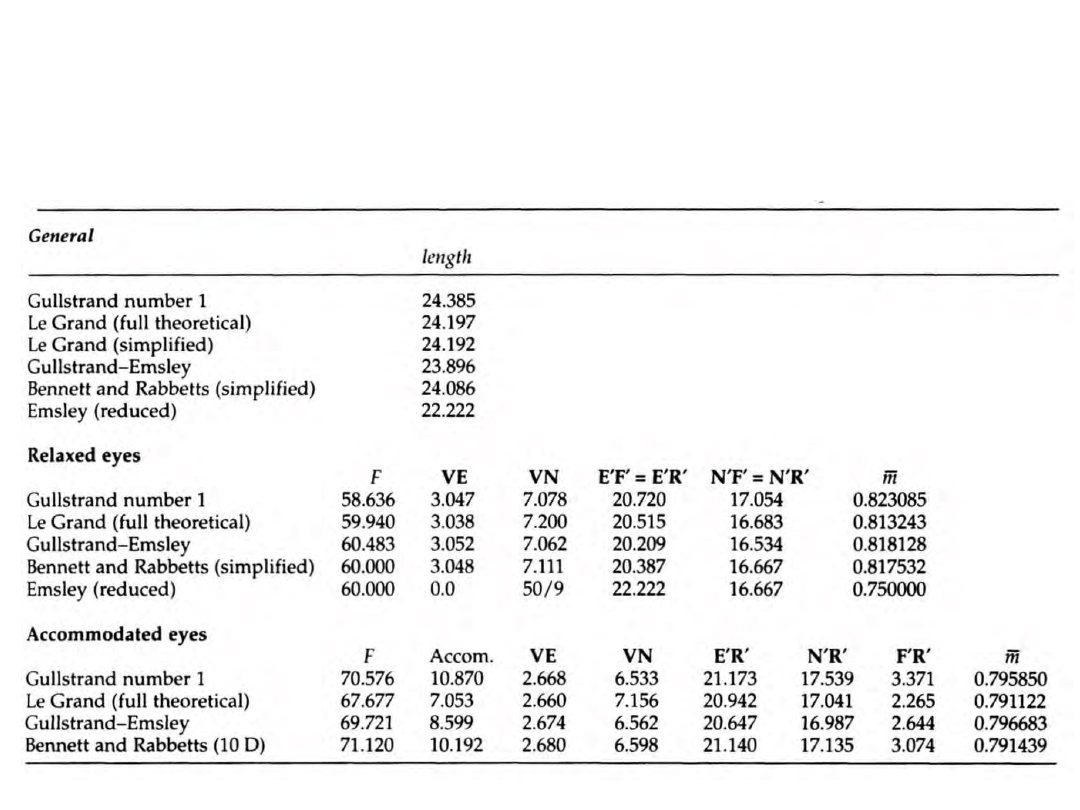
Położenie punktów kardynalnych

Modele oka

• Le Grand
• Bennett and Rabbetts
• Walker
• Kooijman
• Liu-Brennan
• Navarro
• i inne

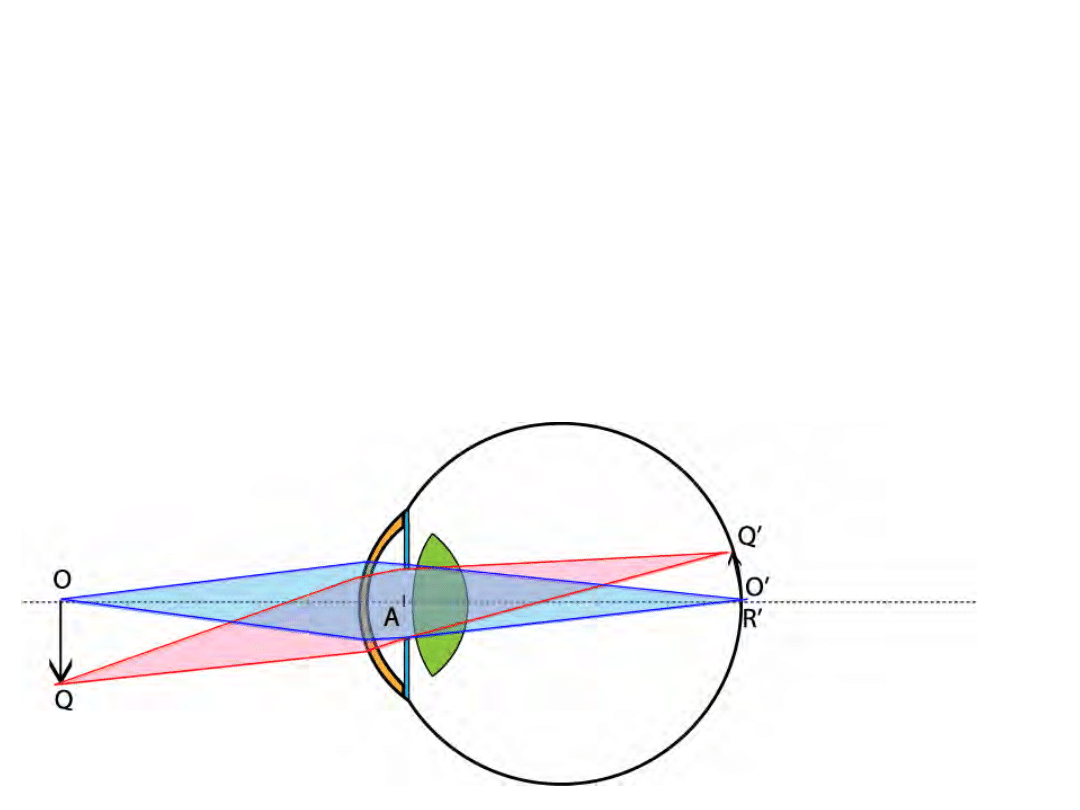
Formowanie obrazu

• Obraz odwrócony zarówno w pionie jak i w

poziomie

• Mózg na powrót odwraca obraz, przez co nie

doświadczamy odwrócenia obrazu widzianego

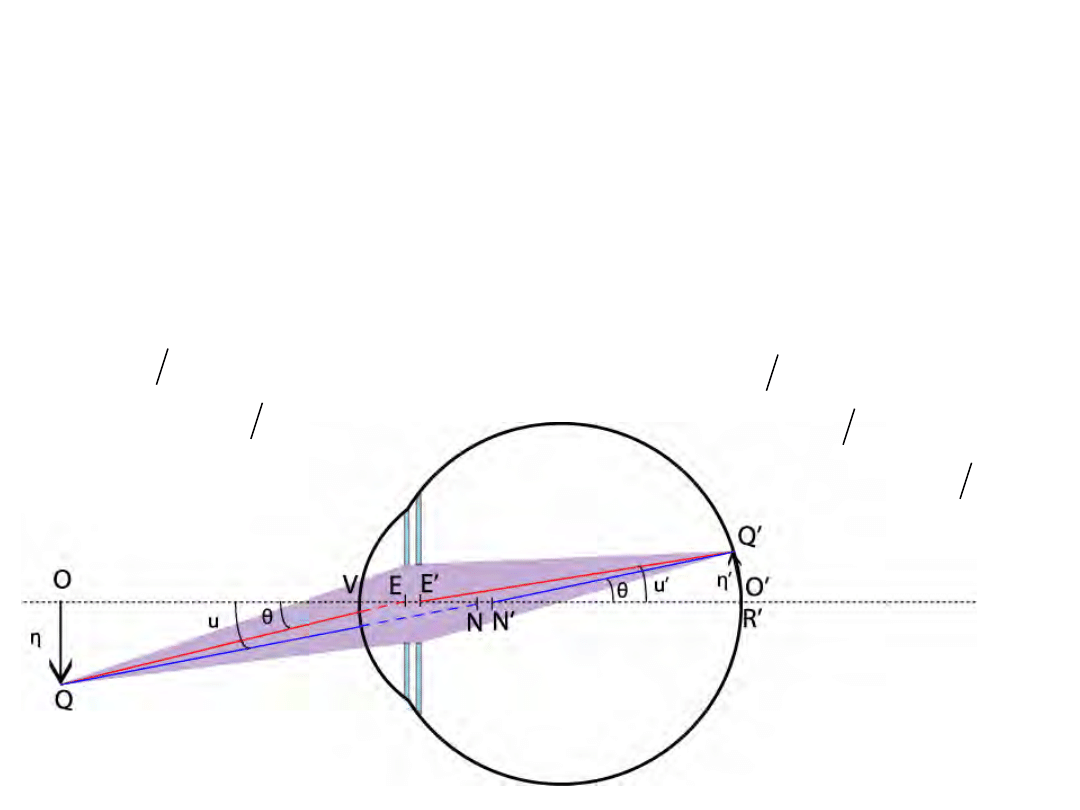
Formowanie obrazu

• Promień węzłowy Q-N-N’-Q’
• Promień aperturowy (promień główny) Q-E-E’-Q’





 



  

ON

R

N

ON

R

N







































 



  

OE

R

E

m

OE

u

m

const

u

u

R

E

u







































.

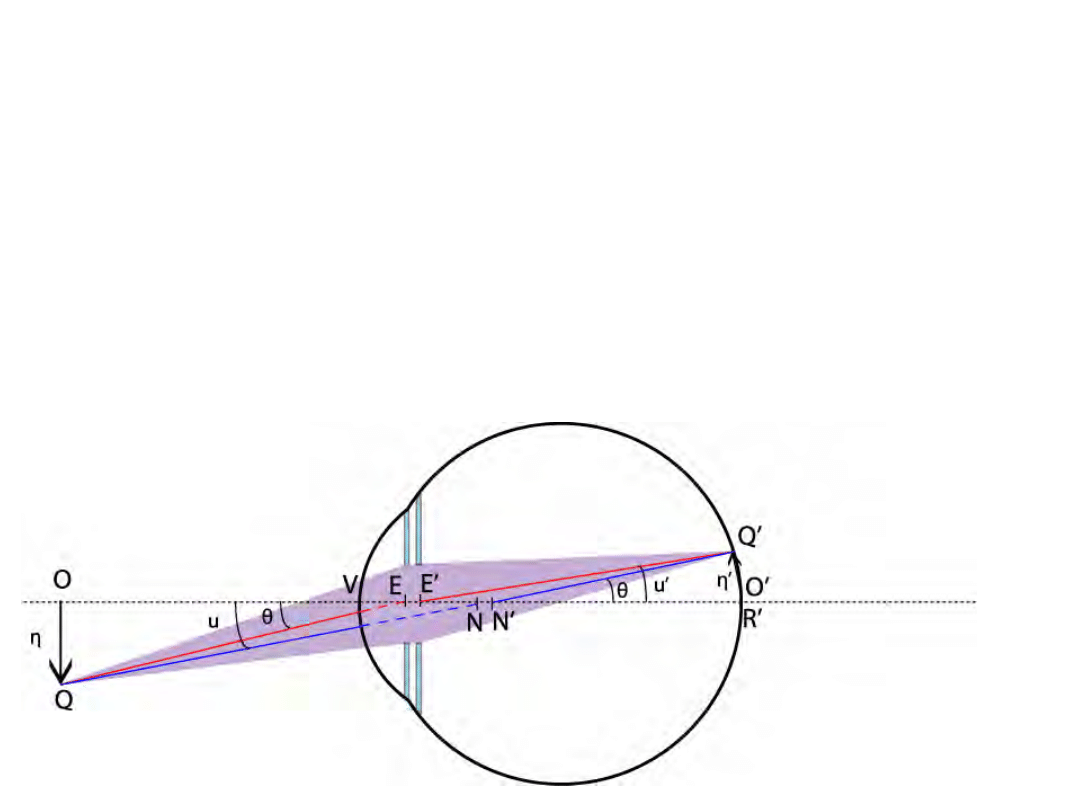
Formowanie obrazu

• Położenie punktów N i N’ oraz powiększenie m

zależą od stopnia akomodacji!

• Przykład: Gullstrand nr 1, η = 1 mm, punkt bliży

– η‘=0,178mm

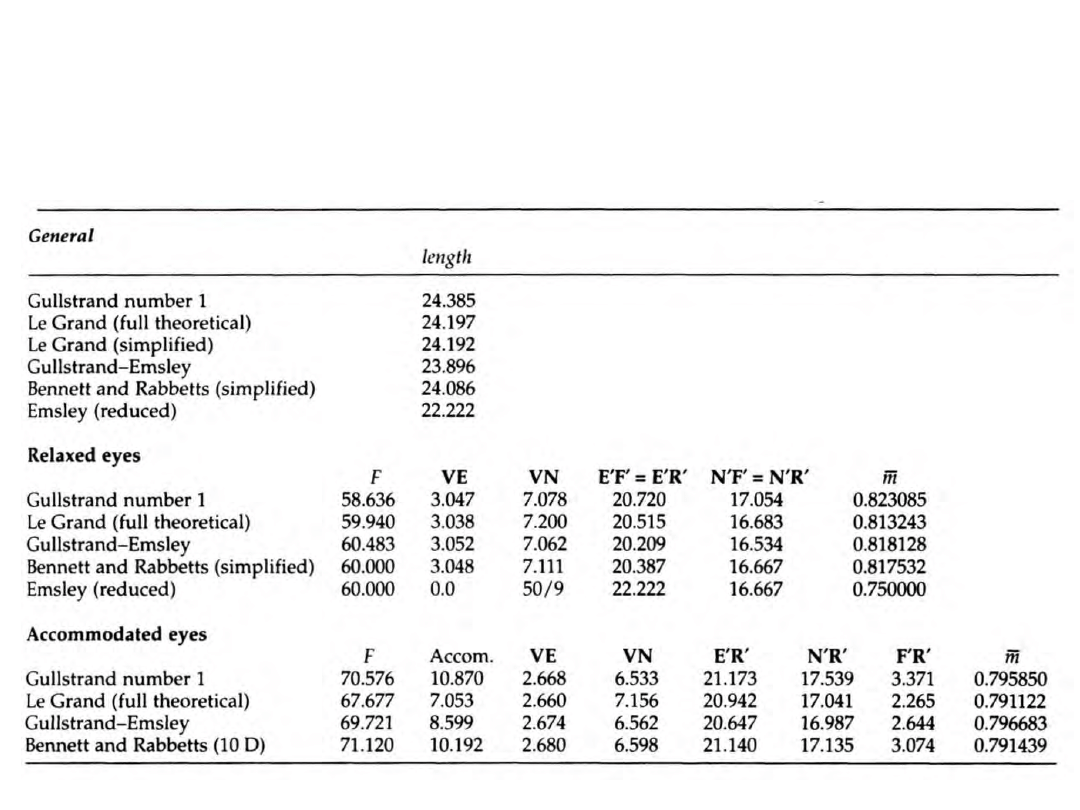
Położenie punktów kardynalnych

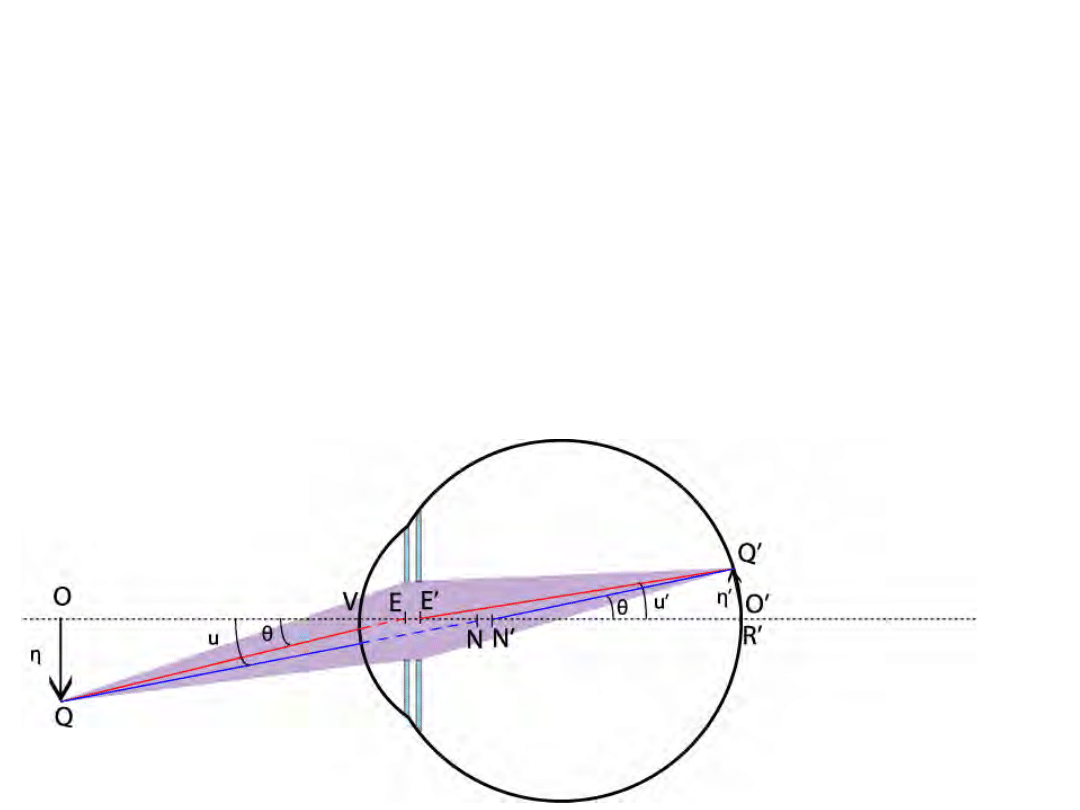
Wielkość obrazu na siatkówce a wrażenie

wielkości kątowej przedmiotów

• Analiza widzenia pozwala na określenie wielkości

obrazu na 2 sposoby

– Wielkość obrazu na siatkówce (η’)

– Wielkość kątowa w przestrzeni przedmiotowej (θ)

• Zazwyczaj ON >> VN

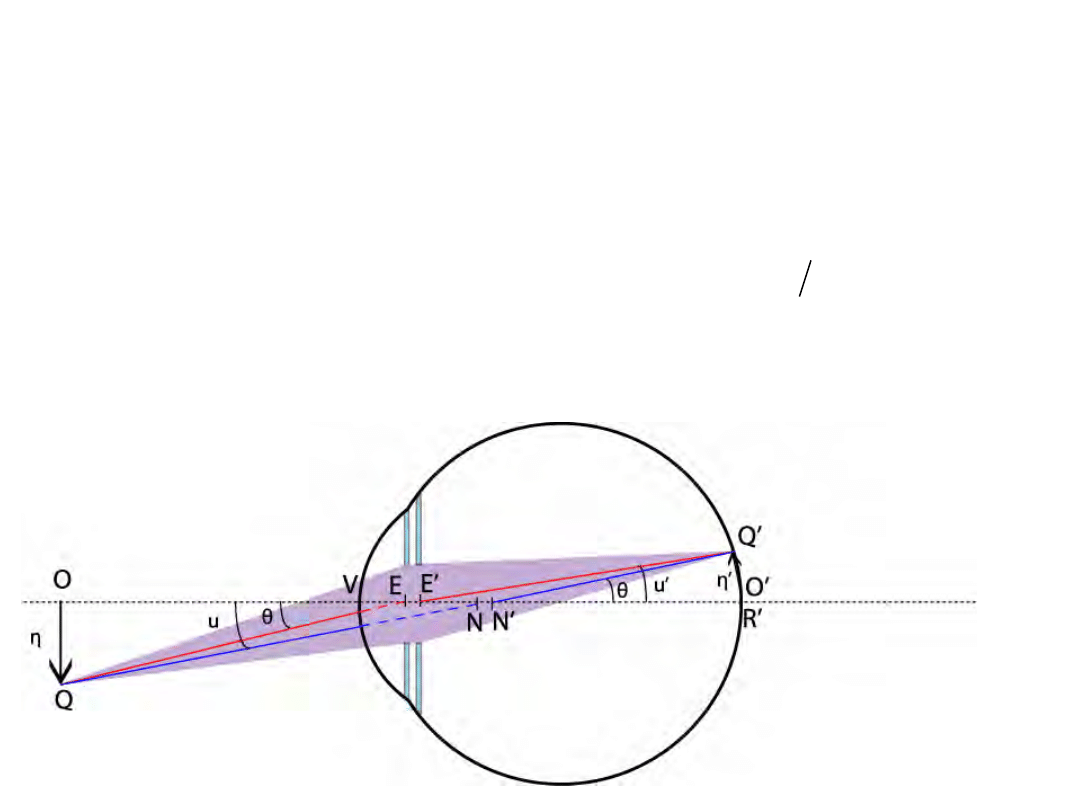
Oko skupione na nieskończoność

• Jeśli OV∞ to N’R’=N’F’=1/D (obraz tworzony

jest w punkcie ogniska obrazowego)

• Przykład: wielkość obrazu księżyca na siatkówce

– Gullstrand nr 1, θ=0,5°  η‘=0,149mm





F

E

m

D

















mm











00485

,

0

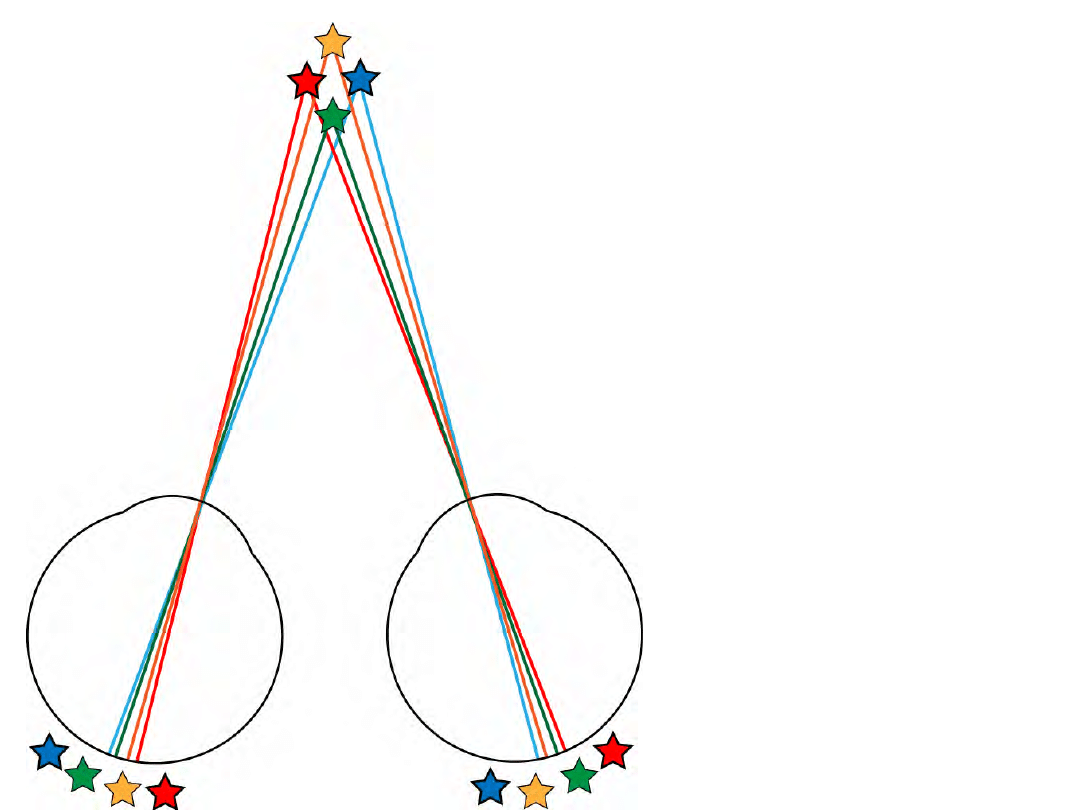
• Obiekty w jednej

linii na obu
siatkówkach są
w tej samej
kolejności

• Obiekty w

różnych
odległościach
już nie

Widzenie obuoczne

(stereoskopowe)

Aniseikonia

• Ponieważ powiększenie obrazu zależy od mocy

optycznej oka, jeśli oczy posiadają nierówne

moce optyczne wielkość obrazów na siatkówkach

także się różni

• Powoduje to problemy z integracją (fuzją) obrazu

obuocznego oraz orientacją przestrzenną

• Aniseikonia występuje często po korekcji

okularowej nierównych wad refrakcyjnych oczu

• Często ośrodek wzroku w mózgu potrafi

korygować ten problem, najczęściej problem

stanowi aniseikonia powodowana przez

wprowadzoną korekcję

Anomalie refrakcyjne

• Emetropia – punkt dali oka jest w

nieskończoności, akomodacja obejmuje cały
zakres widzenia funkcjonalnego

• Ametropia – punkt dali oka nie znajduje się w

nieskończoności

• Prezbiopia (starczowzroczność) – akomodacja ma

zbyt mały zakres dla widzenia funkcjonalnego

• Brakująca lub nadmiarową moc optyczną stanowi

miarę wady refrakcyjnej (wyrażona w dioptriach).

Ametropia

• Hyperopia (dalekozroczność)

– Punkt dali znajduje się poza nieskończonością

(za głową )

• Myopia (bliskowzroczność)

– Punkt dali znajduje się w skończonej odległości

• Astygmatyzm (niezborność)

– Wady cylindryczne układu optycznego oka, punkty dali dla

dwóch prostopadłych osi znajdują się w różnych

odległościach.

• Afakia

– Brak wystarczającej mocy optycznej wynikający z usunięcia

naturalnej soczewki oka na skutek operacji chirurgicznej

(np. usunięcia zaćmy),  bardzo silna dalekowzroczność

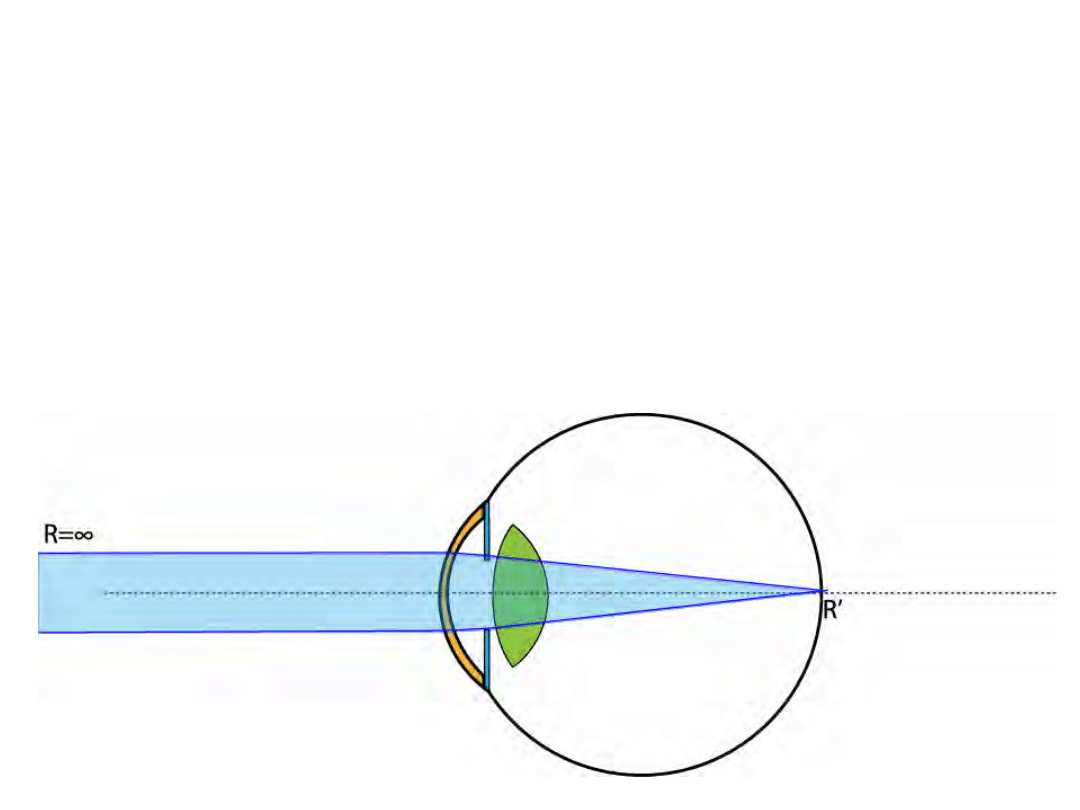
Emetropia

• Punkt dali oka w nieskończoności

• W praktyce za oko emetropowe uważa się pewien

mały zakres wad optycznych
(np. od -0,25D do +0,75D)

F’

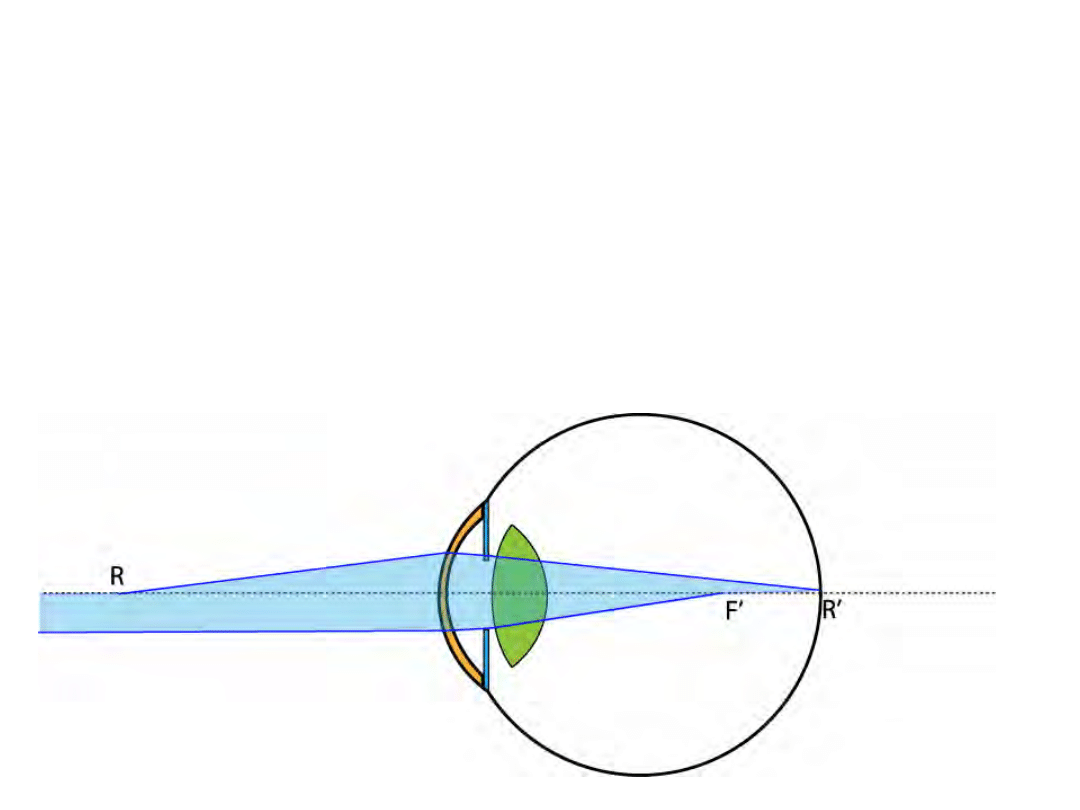
Myopia (krótkowzroczność)

• Punkt dali oka w skończonej odległości (wartości

dodatnie R)

• Moc optyczna oka zbyt duża lub oko zbyt długie

• Korekcja za pomocą soczewek o ujemnej mocy

(rozpraszających)

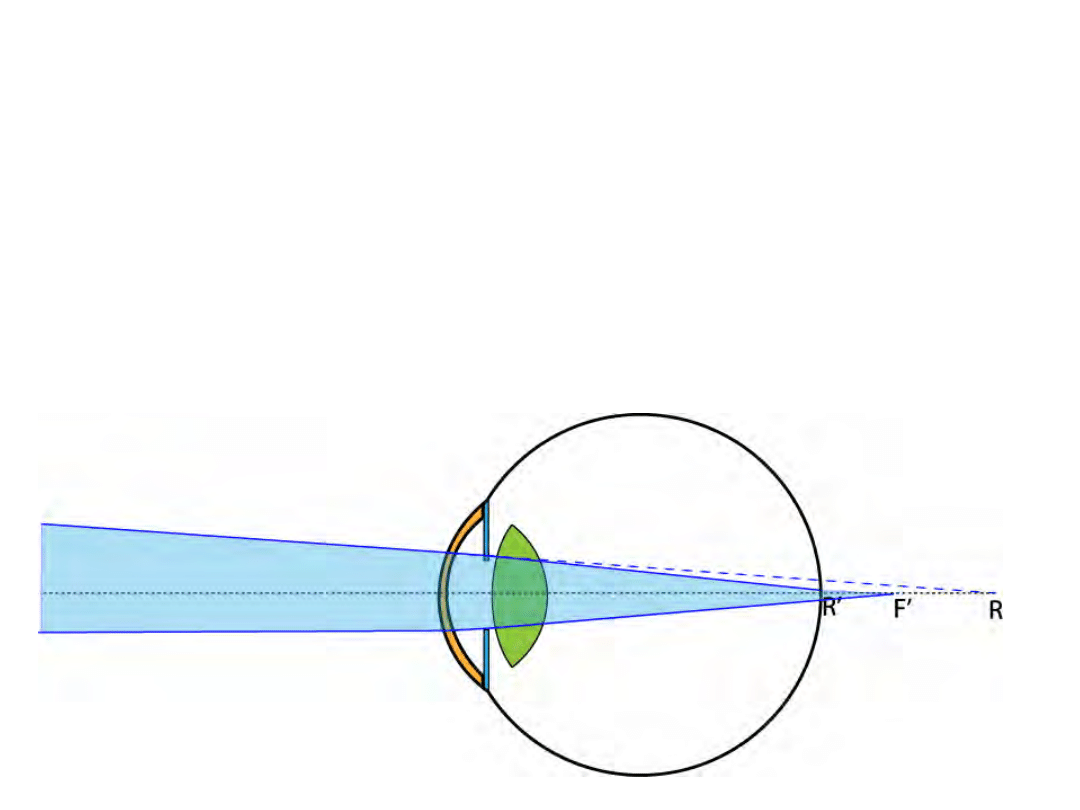
Hyperopia (dalekowzroczność)

• Punkt dali oka „poza nieskończonością”

(wartości ujemne R)

• Moc optyczna oka zbyt mała lub oko zbyt

krótkie

• Korekcja za pomocą soczewek o dodatniej

mocy (skupiających)

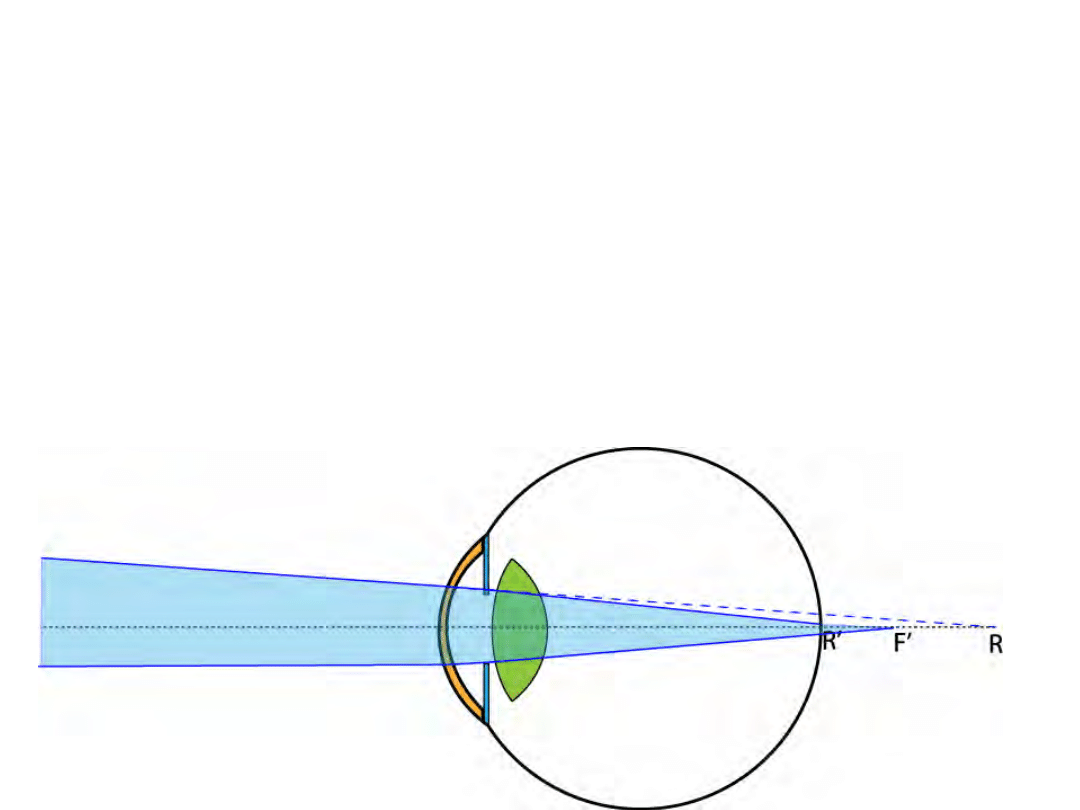
Hyperopia (dalekowzroczność)

• Nadwzroczność powoduje konieczność ciągłej

akomodacji (napięcia mięśni rzęskowych)

• Nadwzroczność utajona – kompensowana przez

akomodację

• Z wiekiem moc optyczna ośrodków optycznych

oka spada  nadwzroczność starcza

(nie należy mylić ze starczowzrocznością)

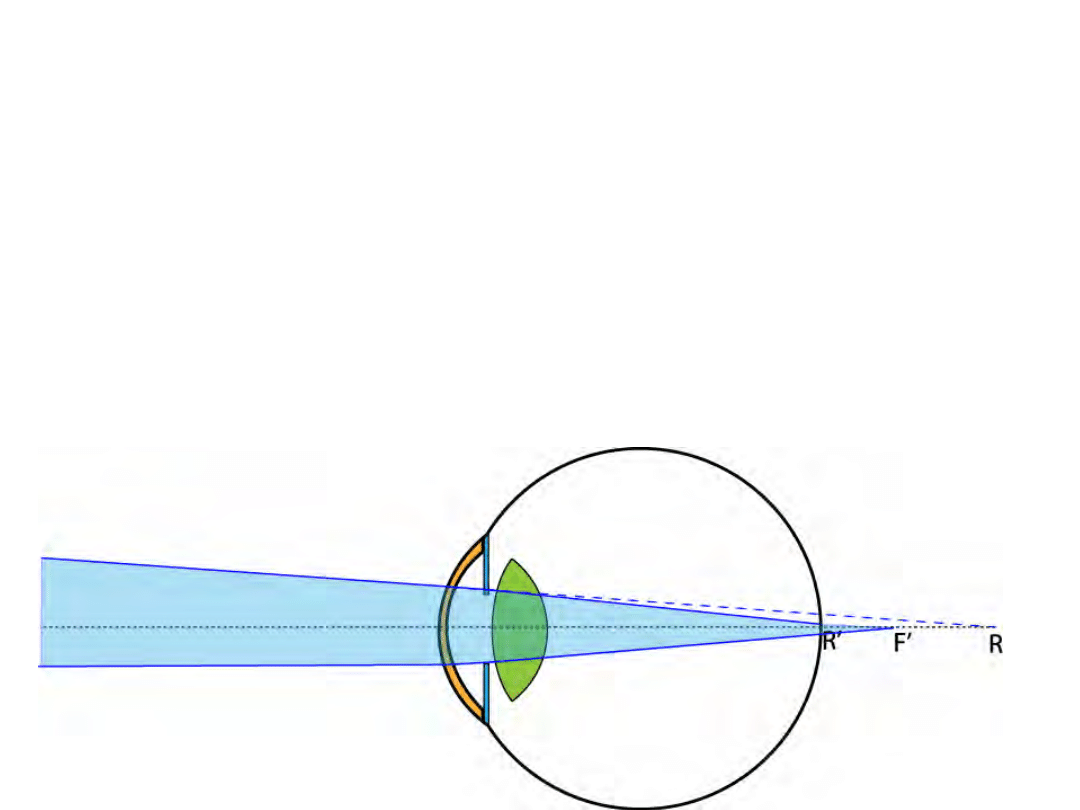
Hyperopia (dalekowzroczność)

• Może prowadzić do bólów głowy i zeza
• Stopień konwergencji (zbieżności) oczu

nieodpowiedni do stopnia akomodacji

• W zależności od wielkości wady możliwy jest

również brak możliwości widzenia dalekiego

Prezbiopia (starczowzroczność)

• Zakres możliwości akomodacyjnych oka spada

z wiekiem (średnio 0,2D/rok), co oznacza
oddalanie się punktu bliży od oka

• Po 50 roku życia zwykle spada poniżej 1 D (w oku

emetropowym punkt bliży w odległości 1m)

• Korekcja za pomocą „okularów do czytania”,

soczewek wieloogniskowych i progresywnych

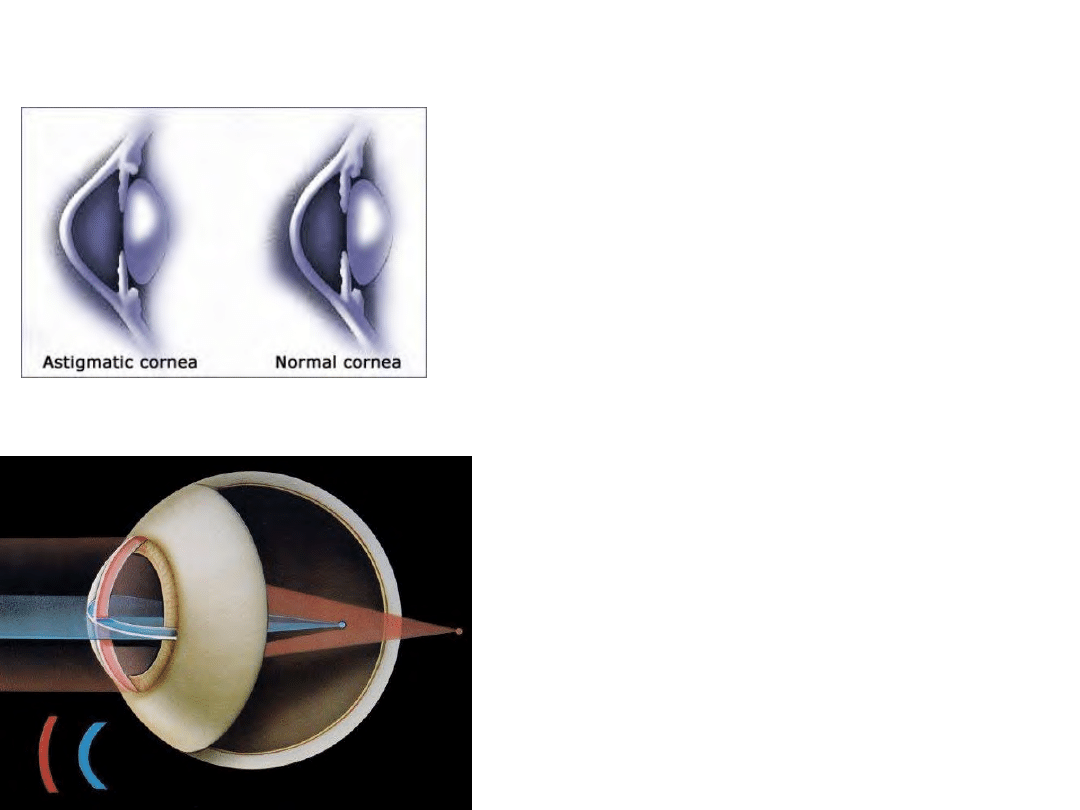
Astygmatyzm

• Wada refrakcyjna zależna od

kierunku przekroju
(południka)

• Najczęściej spowodowana

przez toryczność zewnętrznej
powierzchni rogówki, ale
może być także wynikiem
przesunięcia lub przekręcenia
powierzchni względem siebie

• Korekcja za pomocą

soczewek cylindrycznych

Astygmatyzm

• Astygmatyzm krótkowzroczny

– Oko ma zbyt dużą moc optyczną w stosunku do

swojego rozmiaru wzdłuż jednego (astygmatyzm
prosty) lub obu (astygmatyzm złożony) przekrojów
(południków)

• Astygmatyzm dalekowzroczny

– (Analogicznie)

• Astygmatyzm mieszany

– Wzdłuż jednego przekroju astygmatyzm

krótkowzroczny, a wzdłuż drugiego dalekowzroczny

Astygmatyzm

• Astymatyzm według zasady – rogówka bardziej stroma

w pionie niż w poziomie i wymaga soczewki korekcyjnej
której ujemny cylinder jest skierowany ±30° od
poziomu

– Najczęściej występuje w populacji poniżej 40 roku życia

• Astymatyzm przeciw zasadzie – rogówka bardziej

stroma w poziomie niż w pionie i wymaga soczewki
korekcyjnej której dodatni cylinder jest skierowany
±30° od poziomu

– Występuje w pierwszym roku życia (szybko zanika we

wczesnym dzieciństwie) oraz po 40 roku życia

• Astygmatyzm skośny – osie odchylone o więcej niż 30°

od poziomu i pionu

Astygmatyzm

• Astygmatyzm regularny

– Kierunki o największej i najmniejszej mocy są do

siebie prostopadłe

– Może zostać skorygowany za pomocą soczewki

sferyczno-cylindrycznej

• Astygmatyzm nieregularny

– Kierunki największej i najmniejszej mocy optycznej

nie są prostopadłe lub występują inne asymetrie
obrotowe.

– Np. keratokonus (stożek rogowki)

Anisometropia

• Różna wada refrakcyjna w obu oczach

– Anisomyopia
– Anisohyperopia
– Antimetropia

• Prowadzi do aniseikonii i efektów

pryzmatycznych

Częstość występowania wad wzroku

• Rozkład statystyczny wad wzroku jest zależny od wieku

– Noworodki mają rozkład normalny

– Od urodzenia do dojrzałości (ok. 11-13 lat) oczy rosną –

proces emetropizacji, tj. dostosowania wielkości oka i jego

mocy optycznej

– W populacji dorosłych (20-40 lat) średnia rozkładu wad jest

lekko dalekowzroczna a sam rozkład jest węższy niż

normalny i ma większy ogon w kierunku krótkowzrocznym

– Po 40 roku życia rozkład staje się mniej stromy

• Rozkład statystyczny parametrów oka (długości

osiowej, promienia krzywizny rogowki itp.) jest prawie

normalny

Przyczyny wad (Sorsby et al. 1962)

• W oczach emetropicznych występuje szeroki

zakres mocy optycznych rogówki (39-48 D),
soczewki (16-24D) i długości osiowej
(22-26 mm)

• W oczach ametropicznych z wadą od -4D do +6D

występują te same wielkości, lecz źle
dopasowane – oczy korelacyjnie ametropiczne

• W oczach ametropicznych z większymi wadami

powodem wady jest długość osiowa oka – oczy
elementowo ametropiczne

Ametropia elementowa

• Osiowa

– Wada typowo osiowa – moc optyczna w zakresie

emetropowym, zaś długość poza tym zakresem

– Wzrost oka w dzieciństwie jest głównym

mechanizmem emetropizacji

• Refrakcyjna

– Wada typowo refrakcyjna – moc optyczna oka

poza zakresem, lecz długość osiowa w zakreise
emetropowym

– Afakia, astygmatyzm

przerwa

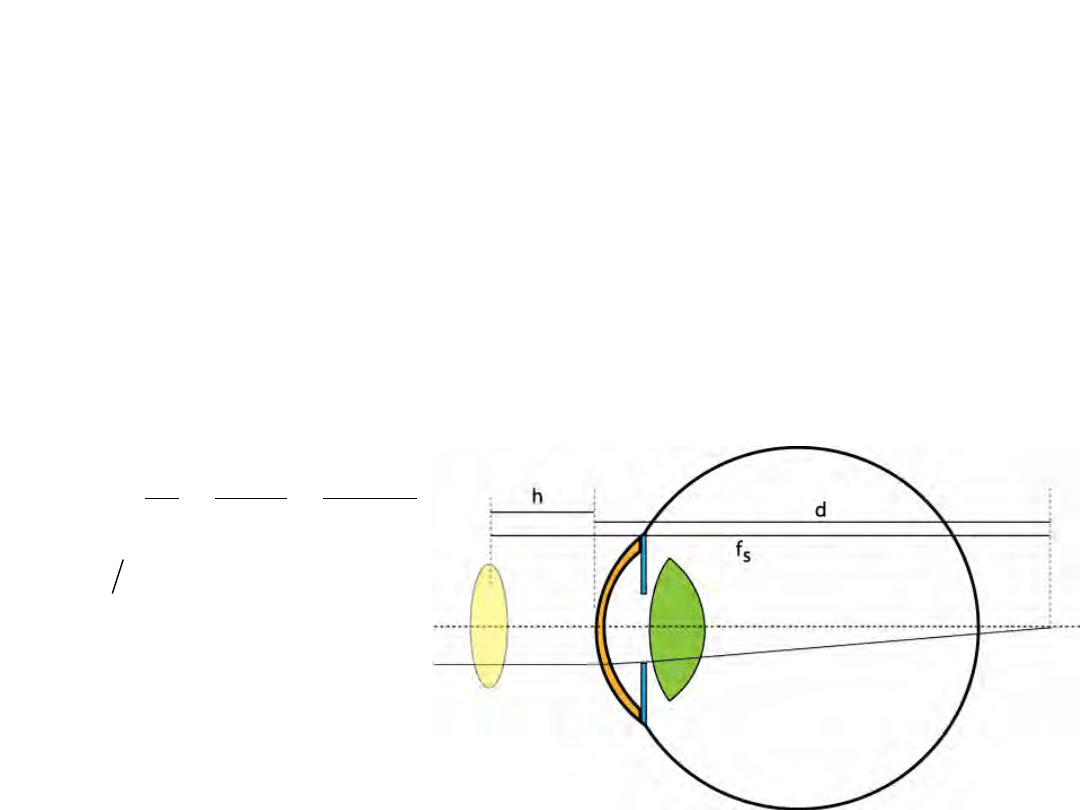
Moc soczewek korekcyjnych

• R

e

– wada refrakcyjna (brak lub nadmiar w mocy oka)

• Przykład:

– Punkt dali 45 cm przed okiem (krótkowzroczność); okulary

15 mm przed okiem, jak powinna być ich moc? (-2,30D)

 

d

R

hR

R

d

h

f

h

D

e

e

e

s

s

1

1

1

1













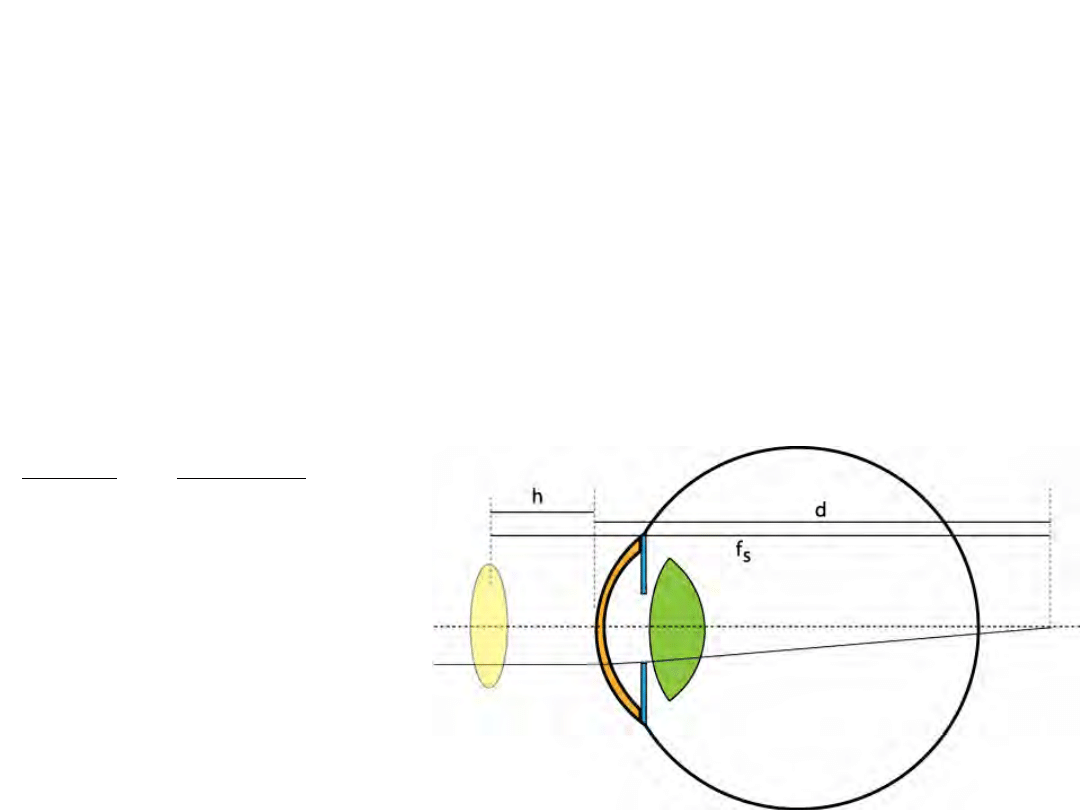
Wpływ dokładności mocy optycznej

• Przykład:

– Potrzeba okularów +12D w odległości 12 mm, jaka

będzie indukowana wada jeśli odległość wyniesie
13 mm? (-0,144D)

 





 

 

 

 

 

h

h

D

h

R

h

h

D

h

D

h

D

hR

R

h

h

D

s

e

s

s

s

e

e

s









2

2

2

2

2

1

d

d



















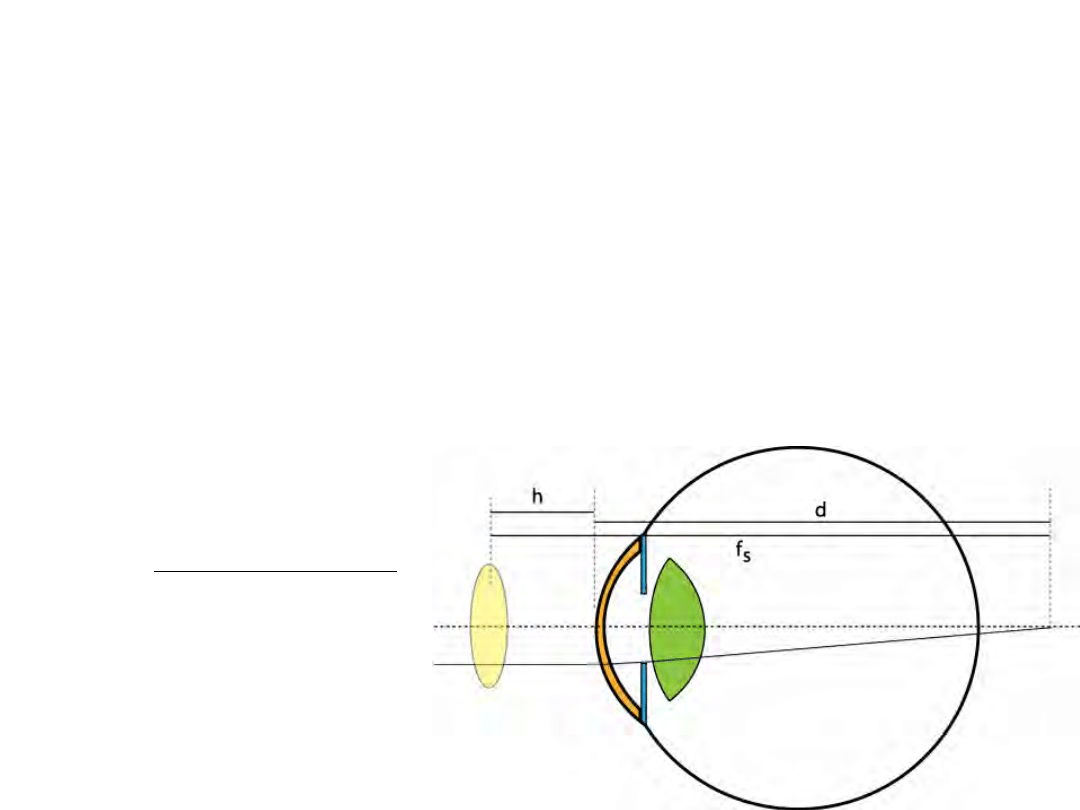
Przesuwanie soczewki korekcyjnej

• Zmiana mocy korekcyjnej związana ze zmianą

odległości szkła korekcyjnego

• Przykład:

– Jaką moc musi mieć soczewka kontaktowa korygująca tą

samą wadę co okulary o mocy +12D w odległości 12 mm?

(+14D)

 

 



  

1

1

1

2

1

2







h

D

h

h

h

D

h

D

s

s

s

Korekcja astygmatyzmu

• Moc soczewek korygujących astygmatyzm

musi zależeć od kąta azymutalnego:

• Soczewki takie z jednej (wewętrznej) strony są

sferyczne a z drugiej cylindryczne

• Kąt osi cylindrycznej α mierzony jest

przeciwnie do wskazówek zegara patrząc na
oczy z zewnątrz

• Zapis kliniczny:

 

















2

sin

cyl

sf

s

D

D

D





cyl

sf

D

D /

Wpływ grubości soczewek

• Odległość między okiem a soczewką liczona

jest od przedniego wierzchołka rogówki do
tylnego wierzchołka soczewki korekcyjnej

• Wszystkie równania zachowują ważność z tym

zastrzeżeniem

• Zmienia się jednakże wielkość obrazu na

siatkówce

Wpływ dokładności poszczególnych

parametrów

• Zmiany długości osiowej oka
• Zmiany

innych
parametrów

'

69

,

2

l

R

e







Pomiar wad refrakcyjnych oka

• Metody subiektywne

– Pacjent sam ocenia jakość ogniskowania

• Metody obiektywne

– Lekarz albo urządzenie ocenia jakość ogniskowania

• Część metod obiektywnych może zostać

zautomatyzowana

– Zautomatyzowane urządzenia używają bliskiej

podczerwieni (800-1000 nm)

– Często wyświetlają oddzielne obrazy w celu

rozluźnienia akomodacji

Metody subiektywne

• Pacjent obserwuje tablicę testową z optotypami i

ocenia czy widzi dobrze

• Przed oczy przedstawia mu się 2 delikatnie różniące się

optyczne układy korekcyjne aby mógł ocenić kiedy jest

lepiej a kiedy gorzej

• Soczewki mogą być wkładane w specjalną ramkę

okularową albo przy użyciu głowicy refraktora

• Wpływ psychofizyki na

interpretację wyników

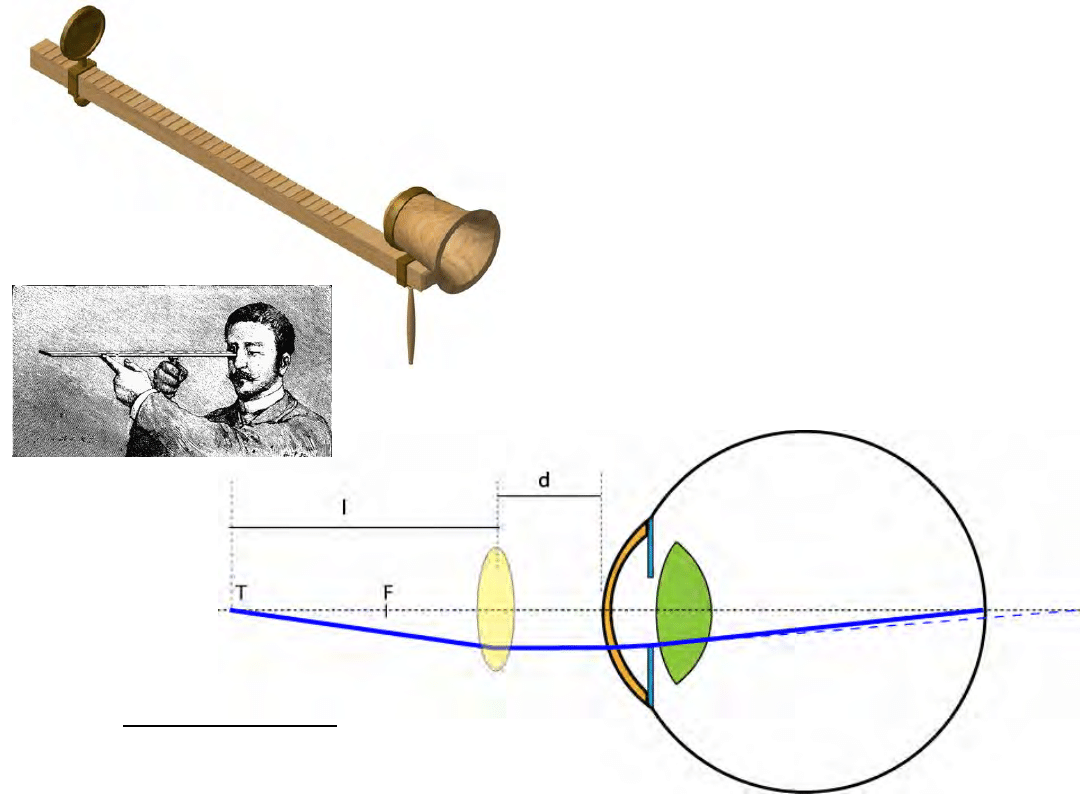
Optometr

• Optometr składa się z

celu, który zbliżamy do
oka oraz odpowiedniego
systemu optycznego który
umieszczamy blisko oka.





d

dD

l

lD

R

e









1

1

Optometr idealny

• Wada refrakcyjna powinna liniowo zależeć od

przesunięcia celu

• Widziana wielkość celu powinna być niezależna

od jego odległości aby nie pobudzać akomodacji

• Zakres pomiaru wad refrakcyjnych powinien być

pełny

• Miejsce między okiem a optometrem powinno

być na jak największe aby nie pobudzać
akomodacji

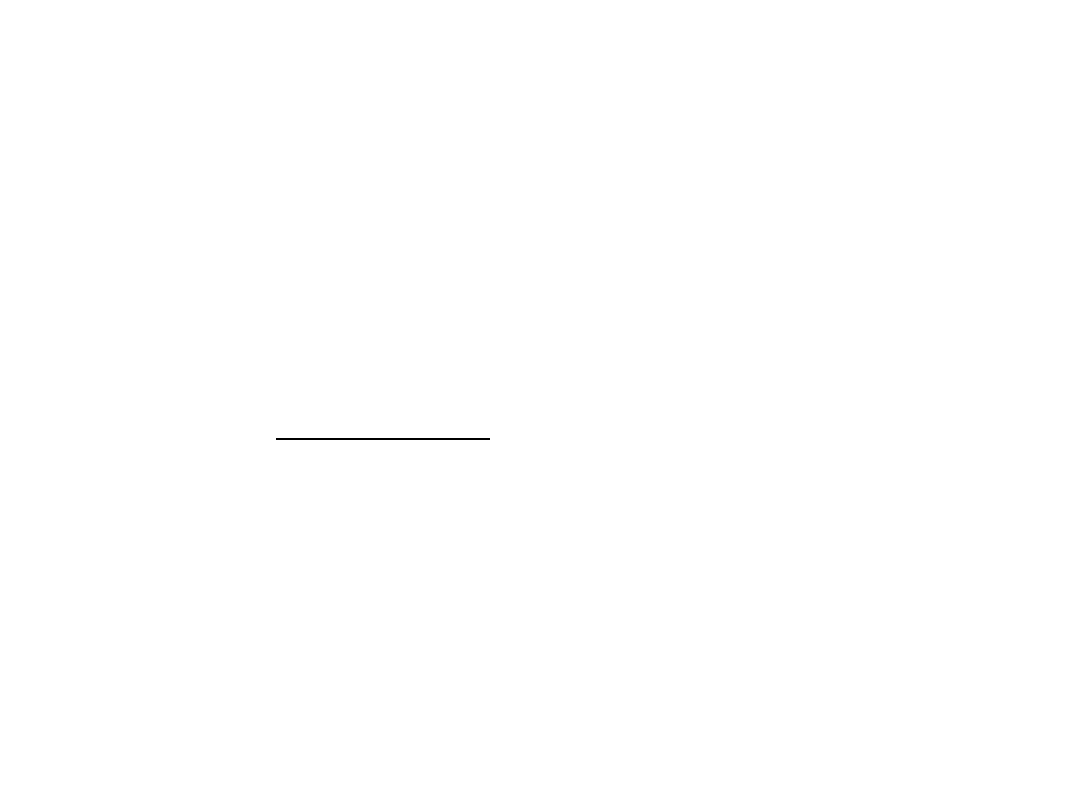
Optometr Badala

• Płaszczyzna główna oka i optometru w

odległości równej ogniskowej optometru

x jest odległością obiektu od punktu

ogniskowego (położenia dla emetropii)









D

xD

D

lD

d

dD

l

lD

R

D

d

e



























2

1

1

1

/

1

Spekle laserowe

• Jeśli koherentne światło laserowe pada na powierzchnię

rozpraszającą można zaobserwować wzór spekli, które

poruszają się gdy kręcimy głową.

• Spekle formowane są na różnych odległościach. Część z nich

znajduje się w płaszczyźnie sprzężonej do siatkówki. Każdy

ruch głowy powoduje wówczas efekt paralaksy.

• Wielkość tego ruchu zależy od pozycji owej płaszczyzny w

stosunku do odległości na której skupione jest oko, zaś

kierunek zależy od tego która z płaszczyzn jest dalej

• Krótkowidzowie widzą, że spekle przesuwają się w

przeciwną stronę niż głowa, dalekowidzowie, że w tą samą

stronę.

Podłużna aberracja chromatyczna oka

• Oko charakteryzuje ok. 2D aberracji

chromatycznej pomiędzy falami o długościach

400 nm a 700 nm.

• Jeśli w widmie światła znajdą się jedynie skrajne

wartości do światło niebieskie zostanie skupione

bliżej niż czerwone.

• Jeśli źródło świata jest daleko oko emetropowe

widzi fioletową plamkę, krótkowidz (ok. 2D)

zobaczy czerwoną kropkę otoczoną przez

niebieski pierścień, zaś dalekowidz niebieską

kropkę otoczoną przez czerwony pierścień.

Metody subiektywno-obiektywne

• Systemy zdalne i przekaźnikowe

– Soczewka korekcyjna indukowana za pomocą

systemów optycznych do oka

– Nie trzeba przykładać instrumentów bezpośrednio

do oka pacjenta

– Możliwość zajrzenia do oka (przez lekarza lub

urządzenie)

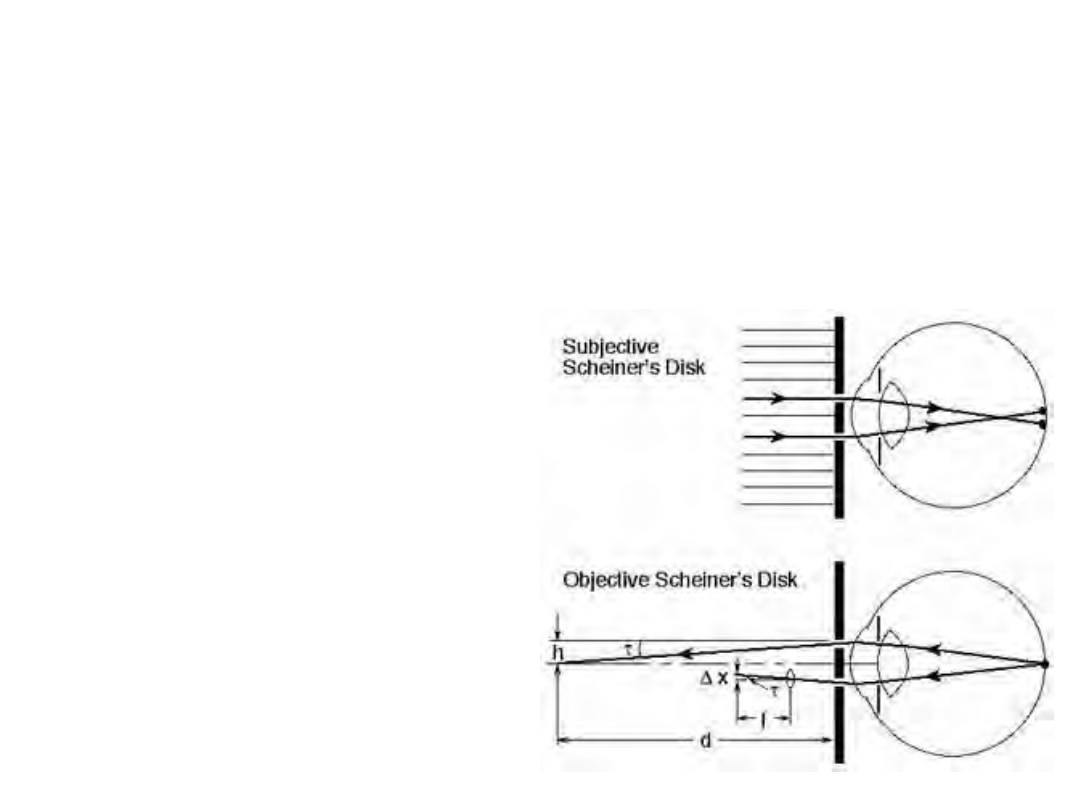
Zasada Scheinera

• Jeśli patrzymy na cel

przez 2 małe otwory,
wydaje się on podwójny
jeśli jest poza
płaszczyzną ostrości
oka.

• Którą plamkę widzimy

na dole, a która na
górze zależy od znaku
wady refrakcyjnej

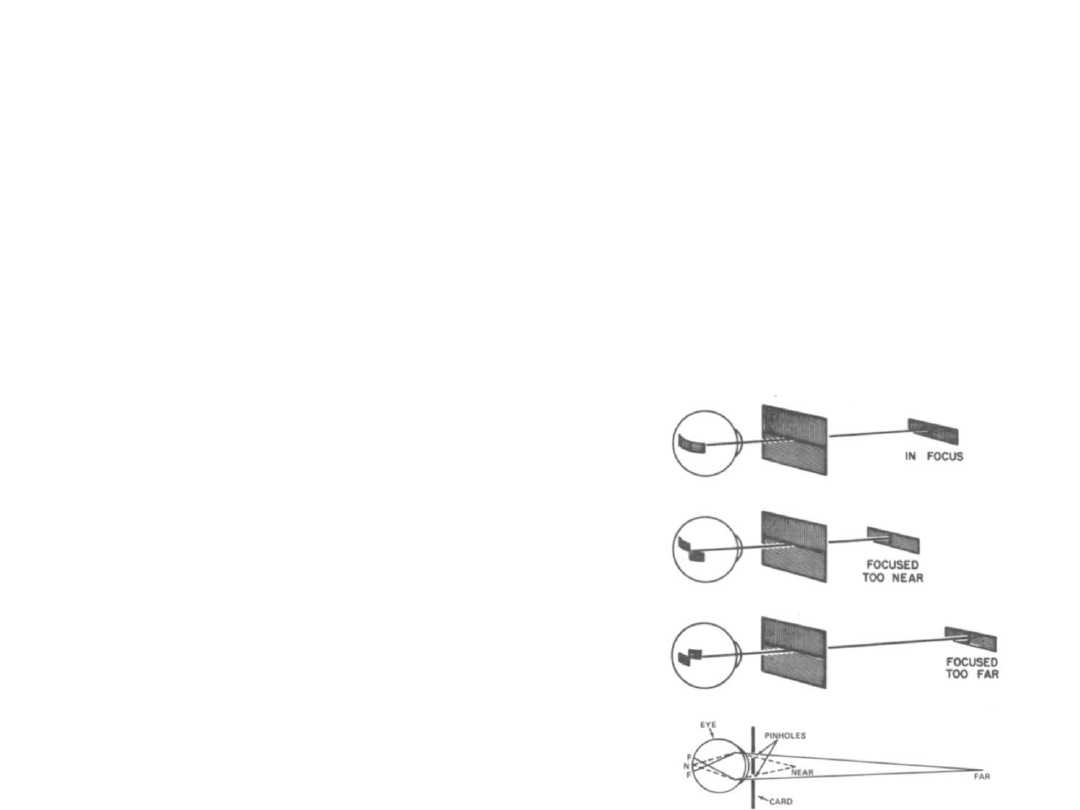
Metody koincydencji (łączenia)

• Dzielimy przedmiot testowy na dwie części w

ten sposób, aby złączyły się one tylko jeśli
jedna z nich będzie zobrazowana ostro.

• Jedną z metod jest podział

pola widzenia za pomocą
polaryzatorów

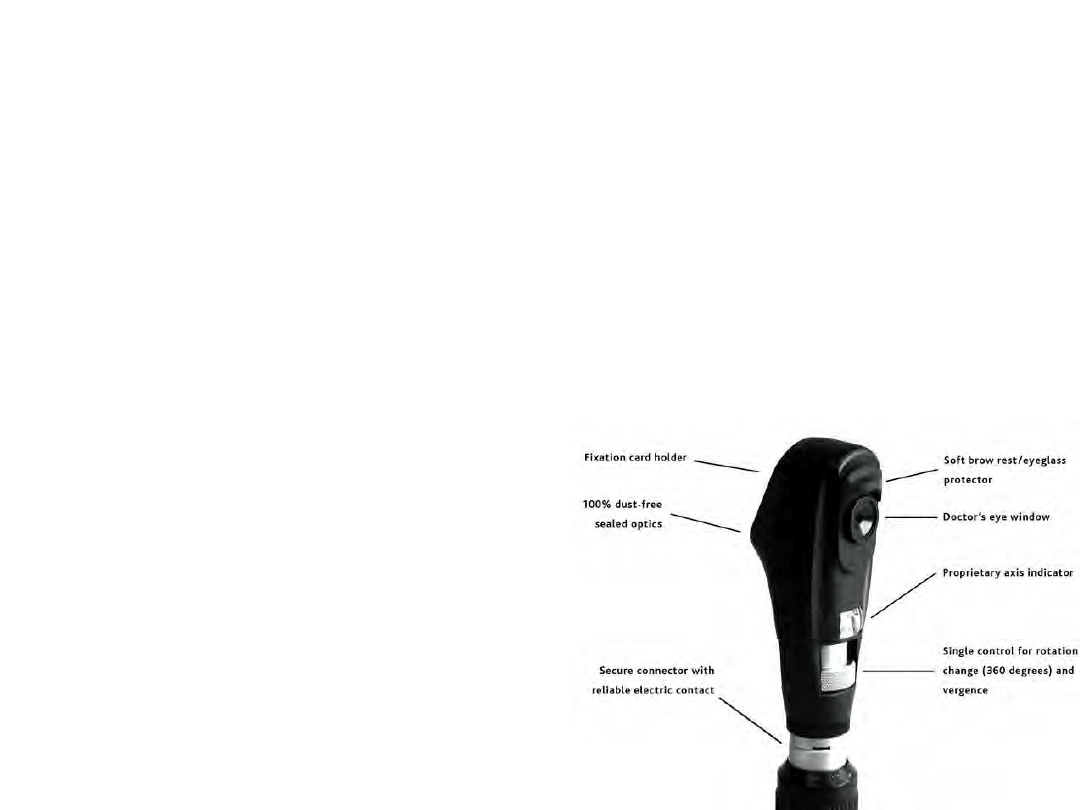
Metody obiektywne - Retinoskopia

• Wykonywana za pomocą retinoskopu

• Wprowadzamy wiązkę światła do oka i

obserwujemy jej odbicie na siatkówce

• Poruszając retinoskopem

i zmieniając jego socze-
wki znajdujemy moc
optyczną przy której
plamka się nie porusza

• Urządzenia może być

zautomatyzowane

Siatka ogniskowa

• Przedmiotem jest prostokątna siatka

podczerwieni obrazowana w oku

• Światło odbite od dna oka jest obrazowane na

fotodetektorze przez kolejną siatkę
prostokątną.

• Gdy przesuwamy siatki względem siebie

sygnał na detektorze zmienia się. Maksymalne
zmiany zachodzą jeśli siatka przedmiotowa
jest obrazowana ostro na dnie oka.

Fotografia - fotorefrakcja

• Wykonujemy zdjęcie oczu z lampą błyskową
• Wielkość i lokalizacja odbicia światła w źrenicy

determinuje stopień i kierunek wady
refrakcyjnej

• Szczególnie ważna

metoda w przy-
padku badania
dzieci

Wzrokowe potencjały wywołane

• Monitorowanie aktywności nerwowej za

pomocą elektrod

• Mało dokładna metoda używane jedynie jeśli

nie ma możliwości użycia bardziej
konwencjonalnych metod

Warunki wpływające na refrakcję

• Subiektywna dokładność oceny refrakcji

wynosi ok. 0,3D u młodych dobrze widzących
pacjentów

• Powszechnie stosuje się więc zaookrąglanie do

0,5D i taką dokładność pomiaru wad
refrakcyjnych

Zależność od celu (optotypu)

• Luminancja
• Częstości przestrzenne (rozmiar)
• Widmo spektralne
mogą oddziaływać z aberracjami oka czy

wielkością źrenicy wpływając na pomiar
wielkości wad refrakycjnych

Zależność od czynników optycznych

• Rozmiar źrenicy

– głębia widzenia, mniejsza dokładność oceny punktu

ostrości

– Możliwość przeprowadzania badań automatycznych

gdzie niezbędny jest silny sygnał zależny od obrazu

dna oka

– Jednakże duża źrenica to duże aberracje, co może

fałszować wyniki (szczególnie aberracja sferyczna)

• Aberracje chromatyczne

– Wypływają na akomodację, która przy pomiarze wad

refrakcyjnych powinna nie być aktywna

Akomodacja

• Oko podczas badania powinno być rozluźnione

– Dodatnia korekcja oka nietestowanego –

akomodacja rozmywa obraz

– Upewnienie się (w urządzeniach automatycznych)

że osie obu oczu są możliwie równoległe

– Używając celu zbieżności w kolorze niebieskim
– Używając leków rozluźniających mięsień rzęskowy