
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
1
H
PhÇn mét ThiÕt kÕ chiÕu s¸ng ph©n x−ëng
KÝch
th−íc cho tr−íc:
a =42 m ; b = 12m; H=45m
Bé ph¶n x¹ : 771
I
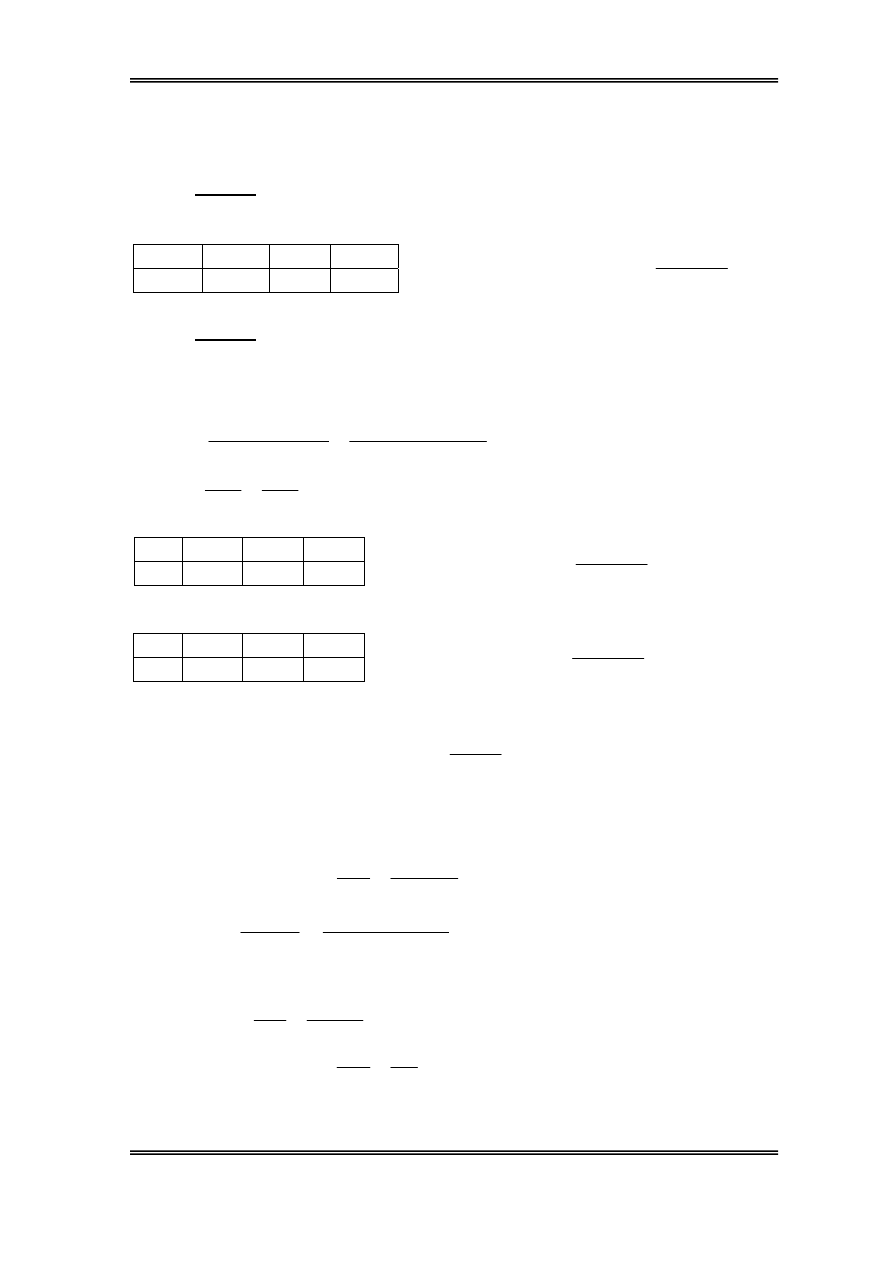
X¸c ®Þnh ®é cao treo ®Ìn
XÐt hÖ sè kÝch th−íc h×nh häc:
(
)
b
a
h
b
a
K
+
=
.
.
Trong ®ã:
a: ChiÒu dµi ph©n x−ëng
b: ChiÒu réng ph©n x−ëng
h: ChiÒu cao cña ®Ìn so víi bÒ mÆt lµm viÖc
VËy chiÒu cao treo ®Ìn lµ: h = H - 0,85 = 4,5 –0,85 = 3,65m
H: ChiÒu cao cña trÇn so víi nÒn
h’: Kho¶ng c¸ch tõ ®Ìn ®Õn trÇn
Víi chiÕu s¸ng ph©n x−ëng chän ®é räi ngang trªn bÒ mÆt lµm viÖc,
cßn gäi lµ bÒ mÆt “h÷u Ých
”
cã ®é cao trung b×nh lµ 0,85 m so víi mÆt sµn,
chän ph−¬ng ¸n chiÕu s¸ng s¸t trÇn cã h
’
= 0
ChØ sè treo ®Ìn
h'
h
h'
J
+
=
= 0
⇒ ChØ sè ®Þa ®iÓm :
(
)
56
,
2
=
+
=
+
=
12
42
3,65.
42.12
b)
h(a
a.b
k
TrÇn
II
X¸c ®Þnh c«ng suÊt ®Ìn:
-
Víi chiÕu s¸ng ph©n x−ëng ®ßi hái ®é räi E =350 lx,
-
NhiÖt ®é mÇu: T=3000
÷4200
o
K
-
ChØ sè mÇu ®èi víi ®Þa ®iÓm nµy lµ R
a
≥ 70
Dùa vµo B¶ng 6.1 trang 74 ThiÕt kÕ chiÕu s¸ng ta chän s¬ bé lo¹i ®Ìn C
mÇu tr¾ng cã nhiÖt ®é mÇu T=4000
0
K, R
a
=85, P=58W,
Φ
®Ìn
=5300 (lm)
(§Ìn èng huúnh quang thÕ hÖ thø 2, ®−êng kÝnh èng
Φ26mm)
Dïng bãng ®Ìn Primavision 240 (Phô lôc E- trang 126 ThiÕt kÕ chiÕu s¸ng)
Cã c¸c th«ng sè vÒ l−îng quang th«ng chiÕu xuèng d−íi:
F
1
F
2
F
3
F
4
F
5
168 101 66
36 29
h
BÒ mÆt lµm viÖc
Sµn
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
2
⇒
(
)
36
,
0
5
,
2
3
5
,
2
56
,
2
.
362
,
0
363
,
0
362
,
0
=
−
−
−
+
=
sd
K
⇒
(
)
916
,
0
5
,
2
3
5
,
2
56
,
2
.
91
,
0
96
,
0
91
,
0
=
−
−
−
+
=
d
u
⇒
(
)
654
,
0
5
,
2
3
5
,
2
56
,
2
.
65
,
0
68
,
0
65
,
0
=
−
−
−
+
=
i
u
a. X¸c ®Þnh hÖ sè sö dông K
sd
:
∗ C¸ch 1: Theo phô lôc E víi bé ph¶n x¹ 771
Thùc hiÖn phÐp néi suy:
K 2,5
2,56 3
K
sd
0,362 0,363
∗ C¸ch 2: K
sd
=
η
d
.u
d
+
η
i
.u
i
Trong ®ã :
η
d
: hiÖu suÊt chiÕu s¸ng trùc tiÕp cña bé ®Ìn
η
i
: hiÖu suÊt gi¸n tiÕp cña bé ®Ìn
Víi ®Ìn Prismavision 240 ta cã
029
,
0
1000
29
1000
731
,
0
1000
36
66
101
168
1000
5
4
3
2
1
=
=
=
=
+
+
+
=
+
+
+
=
F
F
F
F
F
i
d
η
η
- CÊp trùc tiÕp:
K 2,5 2,56 3
U
d
0,91
0,96
- CÊp gi¸n tiÕp:
K 2,5 2,56 3
u
i
0,65
0,68
⇒ K
sd
=0,371.u
d
+0,029.u
i
=0,371.0,916+0,029.0,654=0,36
b. Quang th«ng tæng yªu cÇu:
Φ
∑
sd
k
a.b.E.δ
=
Trong ®ã : E: ®é räi mÆt h÷u Ých
K
sd
: hÖ sè sö dông
δ: hÖ sè bï quang th«ng (hÖ sè suy gi¶m)
38
,
1
85
,
0
.
85
,
0
1
.
1
2
1
=
=
=
v
v
δ
⇒
Φ
∑
)
(
676200
36
,
0
38
.
1
.
350
.
12
.
42
δ
lm
=
=
=
sd
k
a.b.E.
⇒ Sè bãng ®Ìn cÇn thiÕt ®Ó cung cÊp ®ñ l−îng quang th«ng trªn lµ:
N
®Ìn
=
58
,
27
1
5300
676200
F
=
=
∑
φ
(§Ìn)
≈ 128 (§Ìn)
⇒ Sè bé ®Ìn:
64
2
128
2
=
=
=
den
bo
N
N
(Bé)
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
3
a=42m
b=12m
m
q
n
x
p
y
III X¸c ®Þnh l−íi ph©n bè ®Ìn
Ta dù kiÕn bè trÝ 64 bé ®Ìn thµnh 4 hµng, mâi hµng cã 16 bé
m: Sè kho¶ng c¸ch gi÷a c¸c bé ®Ìn cïng 1 cét
n: Sè kho¶ng c¸ch gi÷a c¸c bé ®Ìn cïng 1 hµng
Ta cã: 15.n+2.q=42
3.m+2.p=12
Th«ng th−êng p,q
≈0,4m ⇒
Kho¶ng c¸ch gi÷a hai ®Ìn cïng 1 hµng: x=n–1,5=1,66m
Kho¶ng c¸ch gi÷a hai ®Ìn cïng 1 cïng mét cét: y=m - 0,26 = 2,9m
⇒
m
m
p
m
n
q
26
,
1
2
16
,
3
.
3
12
2
.
3
12
05
,
1
2
66
,
2
.
15
42
2
.
15
42
=
−
=
−
=
=
−
=
−
=
0,33
)
1
3,65(42
12.1,05
42.1,26
k
gÇn
sè
Ø
0,79
)
2
3,65(3,16
6
2.3,16.2,6
n)
h.(m
2.m.n
k
l−íi
sè
ChØ
p
m
=
+
+
=
=
+
=
+
=
2
66
,
Ch
Víi bé ®Ìn Prismavision 240:
η
d
=0,371;
η
i
=0,029
- CÊp ph¸t x¹ trùc tiÕp:
903
371
,
0
66
101
168
"
"
"
725
371
,
0
101
168
"
"
453
371
,
0
168
"
3
2
1
3
2
1
2
1
2
1
1
1
=
+
+
=
+
+
=
+
+
=
+
=
+
=
+
=
=
=
d
d
d
F
F
F
F
F
F
F
F
F
F
F
F
η
η
η
Theo b¶ng 7.2- B¶ng c¸c cÊp cña bé ®Ìn (Trang 92 ThiÕt kÕ chiÕu s¸ng)
ta chän cÊp E v× 903 gÇn gi¸ trÞ trung b×nh nhÊt.
)
(
66
,
2
4
,
0
.
2
15
42
)
(
16
,
3
4
,
0
.
2
3
12
m
n
m
m
=
+
=
=
+
=
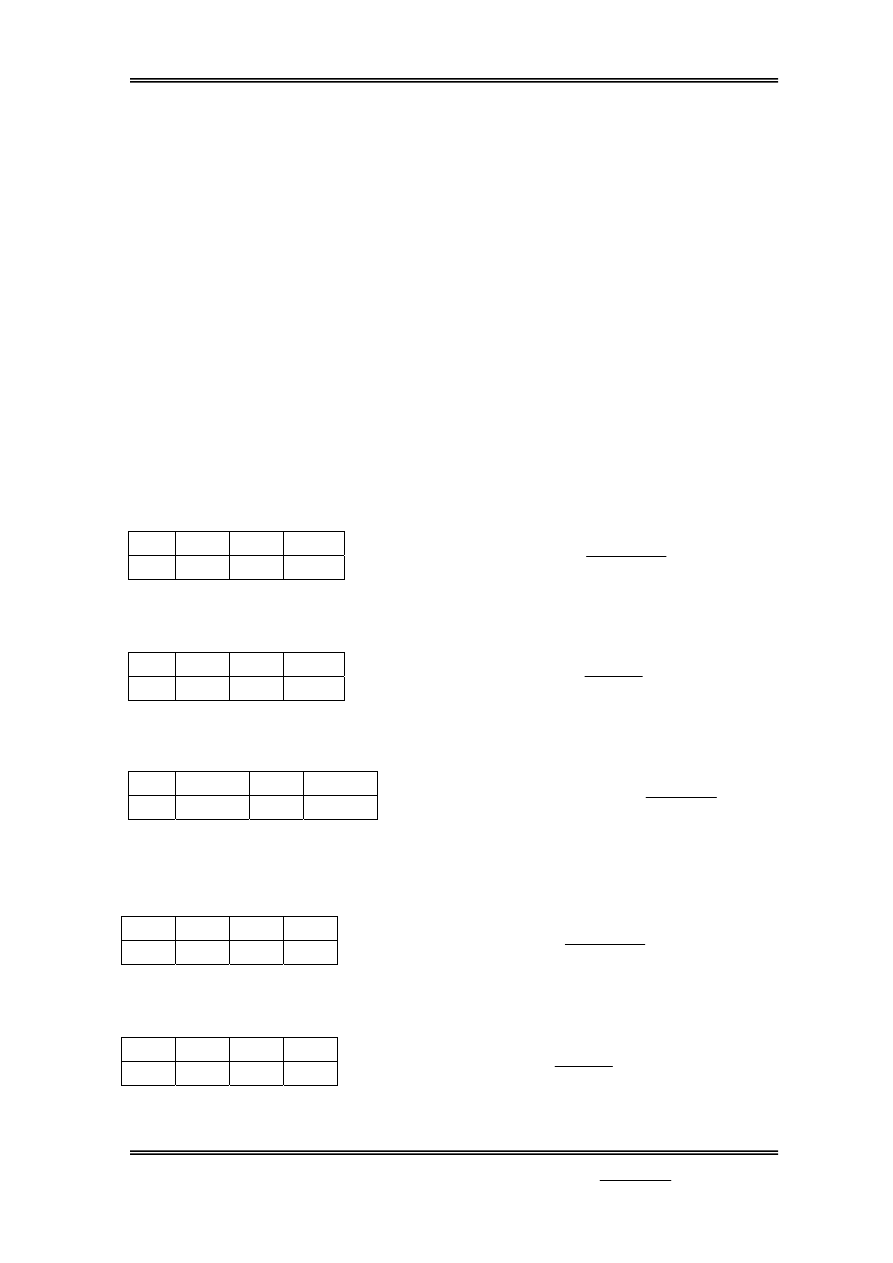
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
4
⇒
(
)
96
,
726
25
,
0
5
,
0
25
,
0
33
,
0
.
710
763
710
"
=
−
−
−
+
=
u
F
⇒
(
)
12
,
677
0
5
,
0
0
33
,
0
.
590
722
590
"
=
−
−
−
+
=
u
F
⇒
(
)
698
5
,
0
1
5
,
0
79
,
0
.
96
,
726
12
,
667
96
,
726
"
=
−
−
−
+
=
u
F
⇒
(
)
769
25
,
0
5
,
0
25
,
0
33
,
0
.
753
803
735
"
=
−
−
−
+
=
u
F
⇒
(
)
18
,
722
0
5
,
0
0
33
,
0
.
641
764
641
"
=
−
−
−
+
=
u
F
⇒
(
)
74
,
741
5
,
0
1
5
,
0
79
,
0
.
769
18
,
722
769
"
=
−
−
−
+
=
u
F
IV KiÓm tra ®é räi
∗ §Ó x¸c ®Þnh ®−îc ®é räi cña v¸ch, trÇn vµ bÒ mÆt h÷u Ých: E
1
, E
3
, E
4
ta
ph¶i x¸c ®Þnh ®−îc quang th«ng trùc tiÕp trªn bÒ mÆt h÷u Ých F
u
”
∗ Ta dïng c«ng thøc néi suy tuyÕn tÝnh:
- Dùa vµo c¸c sè liÖu cho trong b¶ng (Trang 116
÷117 ThiÕt kÕ chiÕu s¸ng)
Thùc hiÖn phÐp néi suy tuyÕn tÝnh t¹i:
K=2,56
∈[2,5÷3]
K
m
=0,79
∈[0,5÷1]
K
p
=0,33
∈[0,25÷0,5] ∈[0÷0,5]
Chó ý chç nµy ph¶i tÝnh tû sè
K
m
/K
p
®Ó sau nµy tÝnh to¸n ???
1. Néi suy F
u
” t¹i K=2,5; K
m
=0,79; K
p
=0,33
¾
Néi suy F
u
” t¹i K=2,5; K
m
=0,5; K
p
=0,33
∈[0,25÷0,5]
K
p
0,25 0,33
0,5
F
u
” 710
763
¾
Néi suy F
u
” t¹i K=2,5; K
m
=1; K
p
=0,33
∈[0÷0,5]
K
p
0 0,33
0,5
F
u
” 590
722
¾
Néi suy F
u
” t¹i K=2,5; K
m
=0,79; K
p
=0,33
K
m
0,5 0,79 1
F
u
” 726,96
677,12
2. Néi suy F
u
” t¹i K=3; K
m
=0,79; K
p
=0,33
¾
Néi suy F
u
” t¹i K=3; K
m
=0,5; K
p
=0,33
∈[0,25÷0,5]
K
p
0,25 0,33
0,5
F
u
” 753
803
¾
Néi suy F
u
” t¹i K=2,5; K
m
=1; K
p
=0,33
∈[0÷0,5]
K
p
0 0,33
0,5
F
u
” 641
764
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
5
⇒
(
)
26
,
703
5
,
2
3
5
,
2
56
,
2
.
698
84
,
741
698
"
=
−
−
−
+
=
u
F
¾
Néi suy F
u
” t¹i K=3; K
m
=0,79; K
p
=0,33
K
m
0,5 0,79
1
F
u
” 769
722,18
3. Néi suy F
u
” t¹i K=2,56; K
m
=0,79; K
p
=0,33
K
2,5 2,56
3
F
u
” 698
741,84
4. X¸c ®Þnh c¸c hÖ sè R vµ S trong quy chuÈn UTE
Theo B¶ng c¸c gi¸ trÞ hÖ sè R & S trang 128 ThiÕt kÕ chiÕu s¸ng, víi bé
ph¶n x¹ 771, ®Ìn cÊp E
K R
1
S
1
R
3
S
3
R
4
S
4
2,5
3
2,56
-0,302
-0,303
-0,30212
393
396
393,36
-1,558
-1,816
-1,58896
1636
1836
1660
0,516
0,505
0,55968
544
558
545,68
§Ó x¸c ®Þnh d−îc c¸c gi¸ trÞ R &S t¹i K=2,56 ta ph¶i dïng ph−¬ng ph¸p
néi suy tuyÕn tÝmh:
(
)
(
)
36
,
393
5
,
2
3
5
,
2
56
,
2
.
393
396
393
30212
,
0
5
,
2
3
5
,
2
56
,
2
.
302
,
0
303
,
0
302
,
0
1
1
=
−
−
−
+
=
−
=
−
−
+
−
+
−
=
S
R
(
)
(
)
1660
5
,
2
3
5
,
2
56
,
2
.
1636
1836
1636
58896
,
1
5
,
2
3
5
,
2
56
,
2
.
558
,
1
816
,
1
558
,
1
3
3
=
−
−
−
+
=
−
=
−
−
+
−
+
−
=
S
R
(
)
(
)
68
,
545
5
,
2
3
5
,
2
56
,
2
.
544
558
544
55968
,
0
5
,
2
3
5
,
2
56
,
2
.
516
,
0
505
,
0
561
,
0
4
4
=
−
−
−
+
=
−
−
−
+
=
S
R
5. TÝnh ®é räi
5.1 §é räi trùc tiÕp:
)
S
.F
(R
1000.a.b.
N.F.
E
i
''
u
i
id
+
=
δ
η
d
N: sè ®Ìn
F: quang th«ng 1 ®Ìn
η
d
: hiÖu suÊt trùc tiÕp bé ®Ìn
i=1 ⇒ E
1
: ®é räi trÇn
i=3 ⇒ E
3
: ®é räi t−êng

Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
6
i=4 ⇒ E
4
: ®é räi trªn bÒ mÆt lµm viÖc
∗ §é räi lªn trÇn:
(
)
)
(
46
,
65
36
,
393
26
,
703
.
30212
,
0
38
,
1
.
12
.
42
.
1000
δ
η
d
lux
=
+
−
=
+
=
,371
128.5300.0
)
S
.F
(R
1000.a.b.
N.F.
E
1
''
u
1
1d
∗ §é räi lªn t−êng:
(
)
)
(
33
,
196
1660
26
,
703
.
58896
,
1
38
,
1
.
12
.
42
.
1000
δ
η
d
lux
=
+
−
=
+
=
,371
128.5300.0
)
S
.F
(R
1000.a.b.
N.F.
E
3
''
u
3
3d
∗ §é räi trªn bÒ mÆt lµm viÖc:
(
)
)
(
89
,
339
68
,
545
26
,
703
.
55968
,
0
38
,
1
.
12
.
42
.
1000
δ
η
d
lux
=
+
=
+
=
,371
128.5300.0
)
S
.F
(R
1000.a.b.
N.F.
E
4
''
u
4
4d
5.2 §é räi gi¸n tiÕp:
- V× cÊp gi¸n tiÕp nªn F
u
”=0
- X¸c ®Þnh c¸c hÖ sè R & S ë cÊp gi¸n tiÕp víi bé ph¶n x¹ 771:
K 2,5 2,56 3
S
1
1129 1128,16
1122
S
3
392 392,48 396
S
4
360 632,28 649
- Dïng c«ng thøc néi suy tuyÕn tÝnh t¹i k=2,56:
(
)
(
)
(
)
28
,
632
5
,
2
3
5
,
2
56
,
2
.
630
649
630
48
,
392
5
,
2
3
5
,
2
56
,
2
.
392
396
392
16
,
1128
5
,
2
3
5
,
2
56
,
2
.
1129
1122
1129
4
3
1
=
−
−
−
+
=
=
−
−
−
+
=
=
−
−
−
+
=
S
S
S
- ¸p dông c«ng thøc tÝnh ®é räi gi¸n tiÕp ta cã:
)
(
88
,
17
28
,
632
.
38
,
1
.
12
.
42
.
1000
.
δ
η
)
(
1
,
11
48
,
392
.
38
,
1
.
12
.
42
.
1000
.
δ
η
)
(
91
,
31
16
,
1128
.
38
,
1
.
12
.
42
.
1000
.
δ
η
4
i
3
i
1
i
lux
S
lux
S
lux
S
=
=
=
=
=
=
=
=
=
,371
128.5300.0
1000.a.b.
N.F.
E
,371
128.5300.0
1000.a.b.
N.F.
E
,371
128.5300.0
1000.a.b.
N.F.
E
4i
3i
1i
5.3 §é räi tæng hîp:
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
7
∗ §é räi trªn bÒ mÆt lµm viÖc: E
4
= E
4d
+ E
4i
=369,89+17,88=357,77 (lux)
∗ §é räi lªn t−êng: E
3
= E
3d
+ E
3i
=196,33+11,1=207,43 (lux)
∗ §é räi lªn trÇn: E
1
= E
1d
+ E
1i
=65,46+31,91=9737 (lux)
5.4 KiÓm tra ®é räi :
10%
%
2
.100
350
|
350
-
357,77
|
E
chän
chän
<
=
=
−
=
22
,
|
|
Δ
4
4
4
E
E
E
tt
Tho¶ m·n
5.5 KiÓm tra tiÖn nghi chiÕu s¸ng:
Khi nh×n t−êng
)
8
,
0
5
,
0
(
5798
,
0
77
.
357
43
,
207
4
3
÷
∈
=
=
E
E
⇒ ChÊp nhËn
5.6 §é t−¬ng ph¶n bé ®Ìn – trÇn:
§−îc x¸c ®Þnh b»ng tû sè r:
∗ Khi nh×n trÇn:
TrÇn
75
L
L
r
0
=
=
γ
§èi ng−êi lµm viÖc chÊp nhËn c¸c chØ sè sau:
r
≤ 30 ®èi víi c¸c c«ng viÖc tinh x¶o (møc 2)
r
≤ 50 ®èi víi c¸c c«ng viÖc b×nh th−êng (møc 1)
∗ §é chãi khi nh×n trÇn: L
trÇn
)
(cd/m
2
3,14
0,7.97,37
.E
2
1
1
7
,
1
π
ρ
=
=
=
∗ §é chãi khi nh×n ®Ìn:
kiÕn
BiÓu
75
γ
75
γ
|
Ìn
Bé
S
I
L
o
o
=
=
=
d
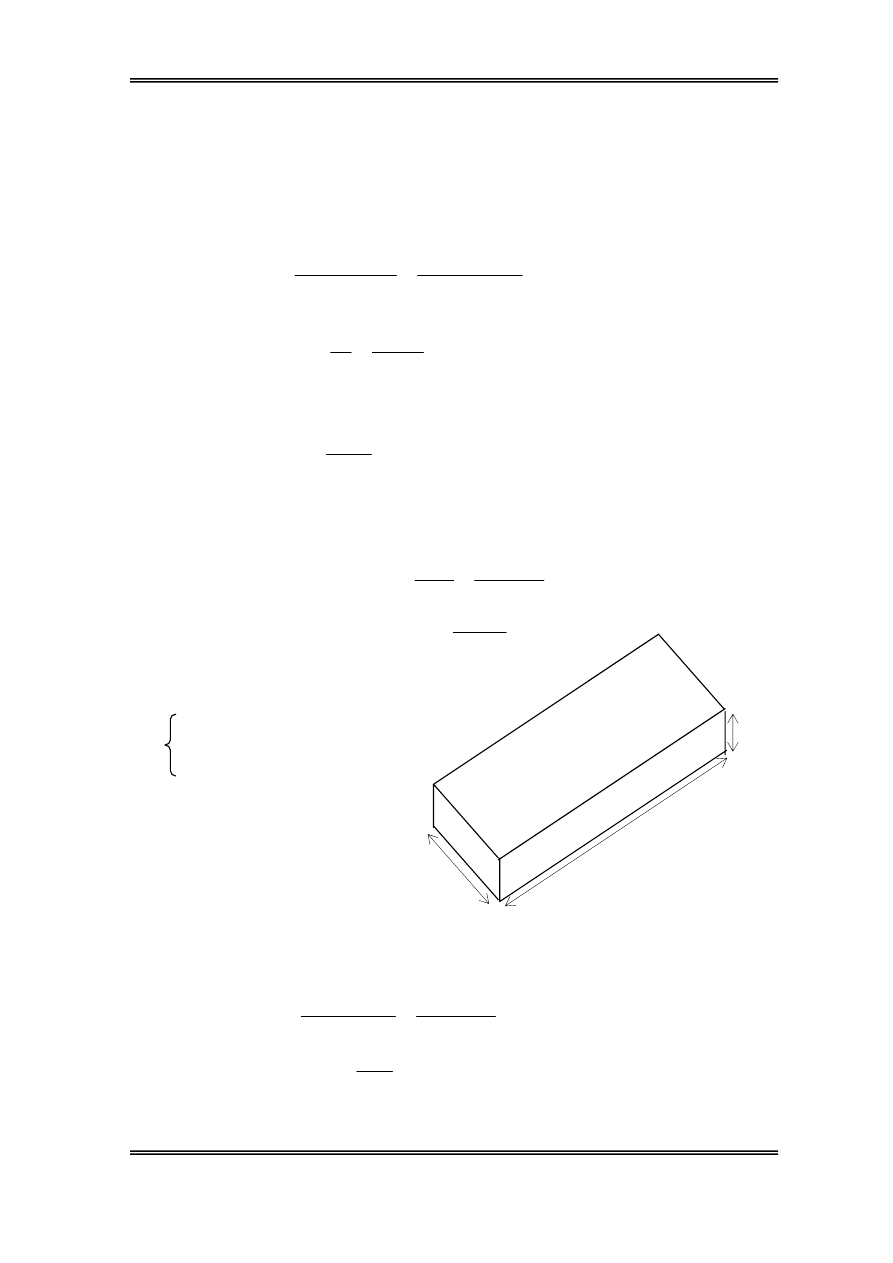
Hép ®Ìn cã:
x=0,28 m
y=1,58 m
z=0,1 m
§é chãi däc cña bé ®Ìn d−íi ®é d− vÜ 75
0
lµ :
S
biÓu kiÕn
=x.y.cos75
0
+x.z.sin75
o
=0,3.1,58.cos75
o
+0,3.0,1.sin75
o
=0,152 m
2
L
nh×n ®Ìn
γ
=75
0
=
1048
152
,
0
.
1000
5300
.
2
.
15
.
1000
5300
.
2
.
0
0
75
75
=
=
=
=
γ
γ
bk
S
I
cd/m
2
50
3
,
48
7
,
21
1048
<
=
=
⇒ r
y
x
z

Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
8
VËy víi c«ng viÖc b×nh th−êng th× r < 50 vËy tháa m·n
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
9
e
H
l
a
s
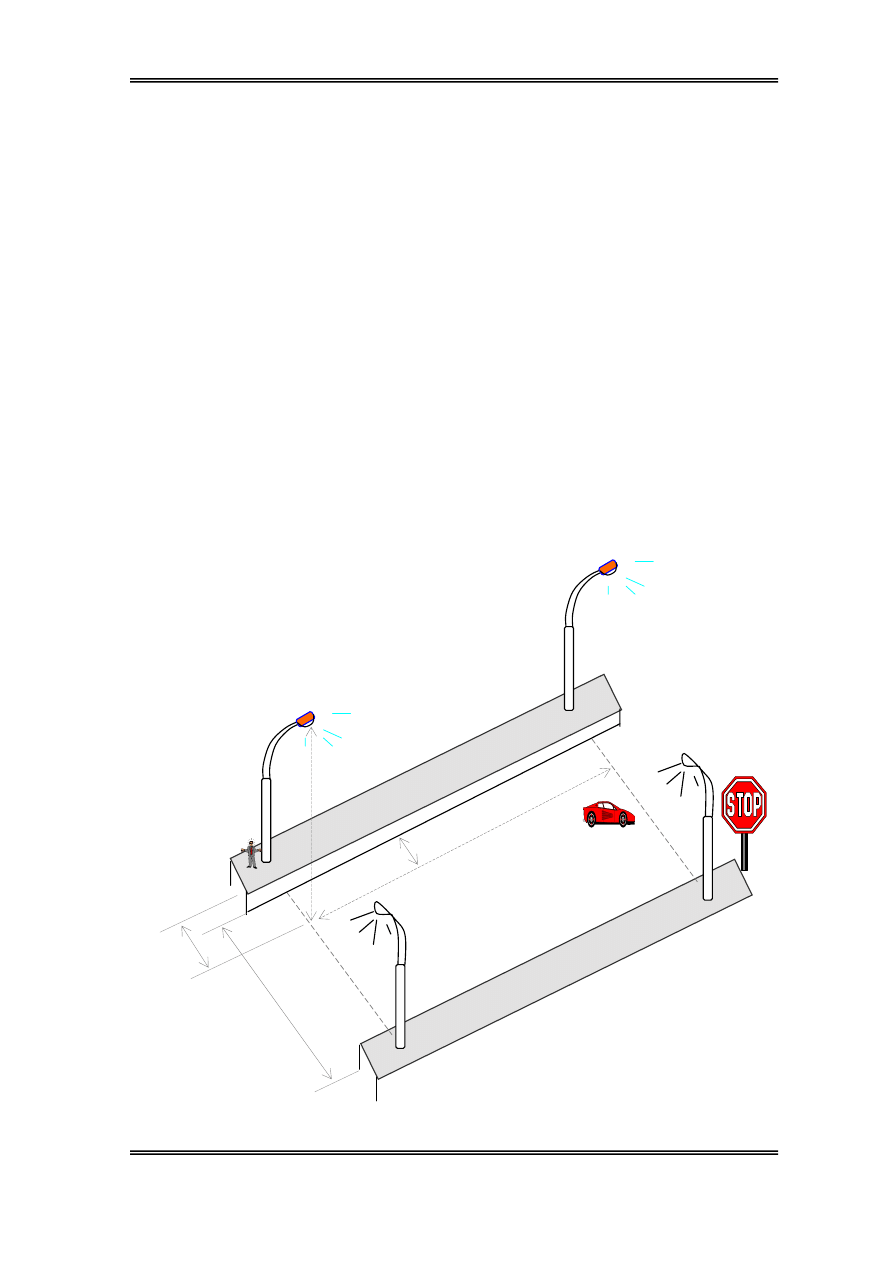
PhÇn hai: ThiÕt kÕ chiÕu s¸ng ®−êng cÊp c
BÒ réng lßng ®−êng: l=24m
Líp phñ mÆt ®−êng: S¸ng
Ö
X¸c ®Þnh ph−¬ng ¸n bè trÝ ®Ìn
Ö
X¸c ®Þnh chiÒu cao ®Ìn
Ö
X¸c ®Þnh kho¶ng c¸ch gi÷a 2 ®Ìn liªn tiÕp
Ö
X¸c ®Þnh c«ng suÊt ®Ìn
Ö
KiÓm tra ®é tiÖn nghi KiÓm tra ®é räi vµ ®é chãi cña mét ®iÓm
trªn lßng ®−êng
1 X¸c ®Þnh ph−¬ng ¸n bè trÝ ®Ìn :
∗ Theo d÷ kiÖn bµi ra lµ ®−êng cã d¶i ph©n c¸ch ë gi÷a ta bè trÝ cét
theo trôc däc ®−êng vµ sö dông mét cét cã 2 ®Çu nh« ra.
H: chiÒu cao cña ®Ìn
l: bÒ réng lßng ®−êng
e: kho¶ng c¸ch gi÷a hai ®Ìn kien tiÕp
s: kho¶ng c¸ch h×nh chiÕu cña ®Ìn ®Õn
ch©n cét
a: kho¶ng c¸ch h×nh chiªó cña ®Ìn ®Õn
mÐp ®−êng

Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
10
∗ Ph−¬ng ¸n bè trÝ ®Ìn
Do lßng ®−êng thiÕt kÕ qu¸ réng l=24m, mÆt kh¸c trªn thÞ tr−êng ViÖt Nam
chØ cã c¸c lo¹i cét ®Ìn cao: 6, 8, 10, 12, 14m.
§Ó ®¶m b¶o ®é ®ång ®Òu ta ph¶i bè trÝ c¸c cét ®Ìn ë hai bªn ®−êng ®èi
diÖn nhau ®Ó kh«ng ph¶i chän cét qu¸ cao
§Ó ®¶m b¶o sù ®ång ®Òu cña ®é räi ngang ta chän chiÒu cao ®Ìn:
H
≥0,5.l=12m
2 Kho¶ng c¸ch gi÷a hai ®Ìn liªn tiÕp
Kho¶ng c¸ch gi÷a hai ®Ìn liªn tiÕp ®−îc x¸c ®Þnh theo tÝnh ®ång ®Òu cña
®é chãi theo chiÒu däc ®−êng
Ta chän bé ®Ìn cã chôp võa, víi ®−êng bè trÝ ®Ìn hai bªn ®èi diÖn ta cã tØ
sè:
5
,
3
=
⎟
⎠
⎞
⎜
⎝
⎛
Max
H
e
(Tra b¶ng trang 169)
⇒ e
Max
=3,5.12=42m
3. X¸c ®Þnh c«ng suÊt ®Ìn
∗ §é räi trung b×nh cña ®−êng:
Tuú theo líp phñ mÆt ®−êng vµ lo¹i bé ®Ìn dïng trong thiÕt kÕ nµ ta cã thÓ
x¸c ®Þnh b»ng ph−¬ng ph¸p thùc nghiÖm tØ sè R
10
L
E
binh
trung
chãi
é
§
binh
trung
räi
é
§
R
tb
tb
=
=
=
(§−îc tra trong b¶ng trang 169 ThiÕt kÕ
chiÕu s¸ng)
a. C¸c chØ tiªu cña ®−êng
- §−êng cÊp C, mÆt ®−êng s¸ng cã c¸c sè liÖu:
§é chãi trung b×nh: L
tb
=2cd/cm
2
§é ®ång ®Òu: U
o
=
4
,
0
·
min
=
m
L
L
ChØ sè tiÖn nghi: G=5
÷ 6
b. Chän ®Ìn thÝch hîp
Chän s¬ bé lo¹i ®Ìn Natri cao ¸p, dïng bé ®Ìn chôp võa: SR201-
SOX135 (Phô lôc O trang 135 ThiÕt kÕ chiÕu s¸ng)
∗ HÖ sè giµ ho¸: v=v
1
.v
2
v
1
: sù suy gi¶m
Φ theo thêi gian
v
2
: sù suy gi¶m
Φ do m«i tr−êng bôi t¸c ®éng
v=v
1
.v
2
=0,85.0,9=0,765
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
11
∗ HÖ sè sö dông f
u
:
1
,
0
12
2
,
1
9
,
1
12
2
,
1
24
2
1
=
=
=
=
−
=
−
=
H
a
tg
H
a
l
tg
α
α
Tõ ®ã tra b¶ng ®−êng cong hÖ sè sö dông cña ®Ìn SRS 201-SOX 135 (Phô
lôc O trang 180 ThiÕt kÕ chiÕu s¸ng) ta ®−îc:
f
UAV
=0,3
f
UAR
=0,03
⇒ f
u
=f
UAV
+f
UAR
=0,3+0,03=0,33
V× bè trÝ ®Ìn 2 bªn ®èi diÖn nªn hÖ sè f
u
=2.0,33=0,66
∗ Quang th«ng ban ®Çu:
)
(
39929
66
,
0
.
765
,
0
10
.
2
.
42
.
24
.
.
.
.
lm
f
v
R
L
e
l
u
tb
=
=
=
φ
Tra b¶ng 5.1 trang 65 ThiÕt kÕ chiÕu s¸ng ta chän lo¹i ®Ìn Natri cao ¸p
bãng s¸ng cã: P=350W;
Φ=34000 (lm)
∗ §Ó ®¶m b¶o ®é ®ång ®Òu:
∗
)
(
36
42
.
39929
34000
max
m
e
e
=
=
=
to¸n
tÝnh
dÌn
φ
φ
4. KiÓm tra ®é tiÖn nghi
∗ ChØ sè tiÖn nghi cña ®Ìn:
G = ISL + 0,97.lgL
tb
+ 4,41.lgh
’
–1,46.lgP
Trong
®ã:
h
’
=h- 1,5 =12-1,5 =10,5 (m)
Sè bãng ®Ìn trªn 1 km ®−êng:
P =
58
1
36
1000
.
2
1
1000
.
2
≈
⎟
⎠
⎞
⎜
⎝
⎛
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
e
§Ìn
G = 3,3 + 0,97.lg2 + 4,41.lg10,5 – 1,46.lg58 = 5,5208
∈ [5 ÷6]
Theo tiªu chuÈn cña CIE ®−a ra ®èi víi ®−êng cÊp C th× 5< G < 6 vËy tháa
m·n
5. KiÓm tra ®é räi vµ ®é chãi cña 1 ®iÓm trªn ®−êng
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎨
⎧
=
=
=
m)
4
lµn
(mçi
6
xe
lµn
Sè
R2
phñ
Líp
m
36
dÌn
gi−a hai
c¸ch
ng
Kho¶
1
h
cao
ChiÒu
24
l
réng
ChiÒu
e
2
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
12
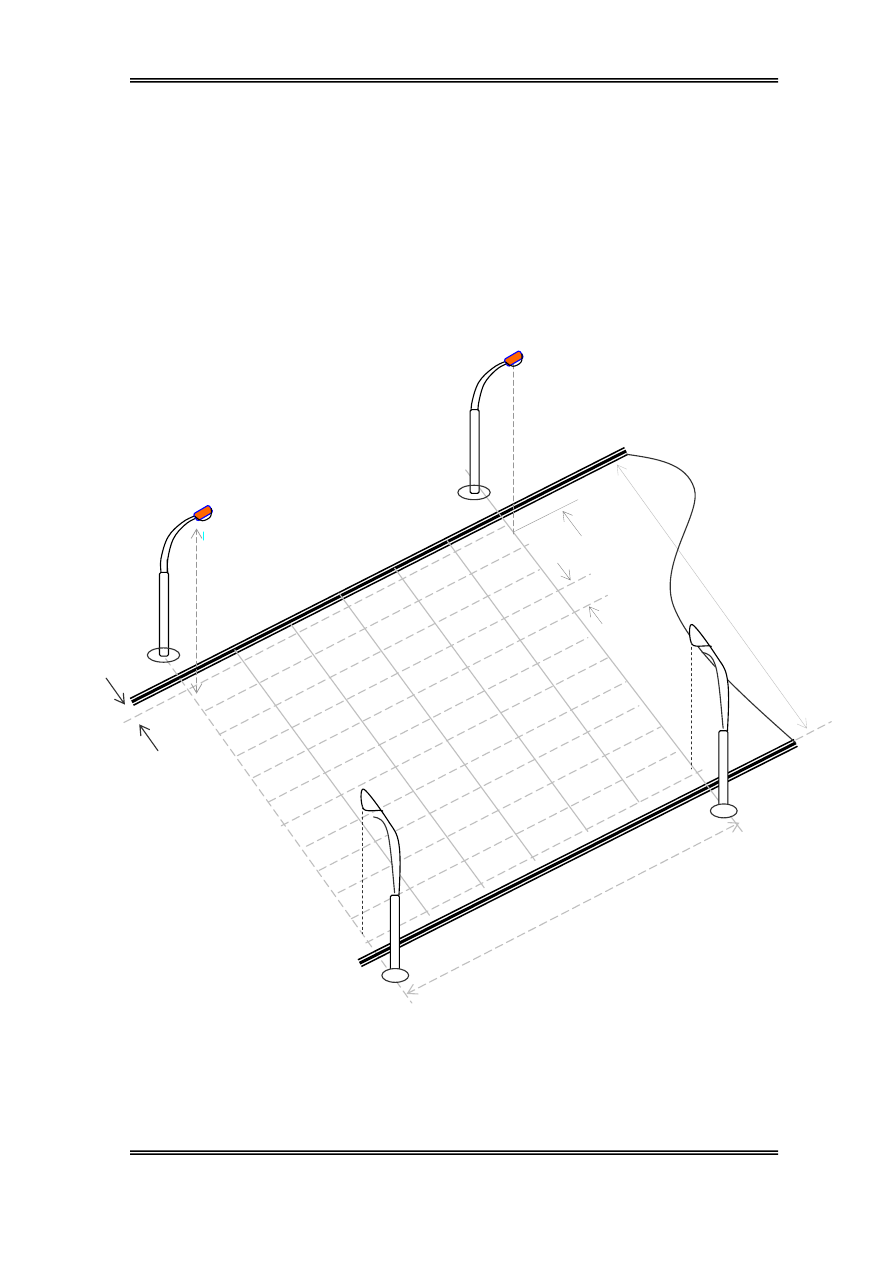
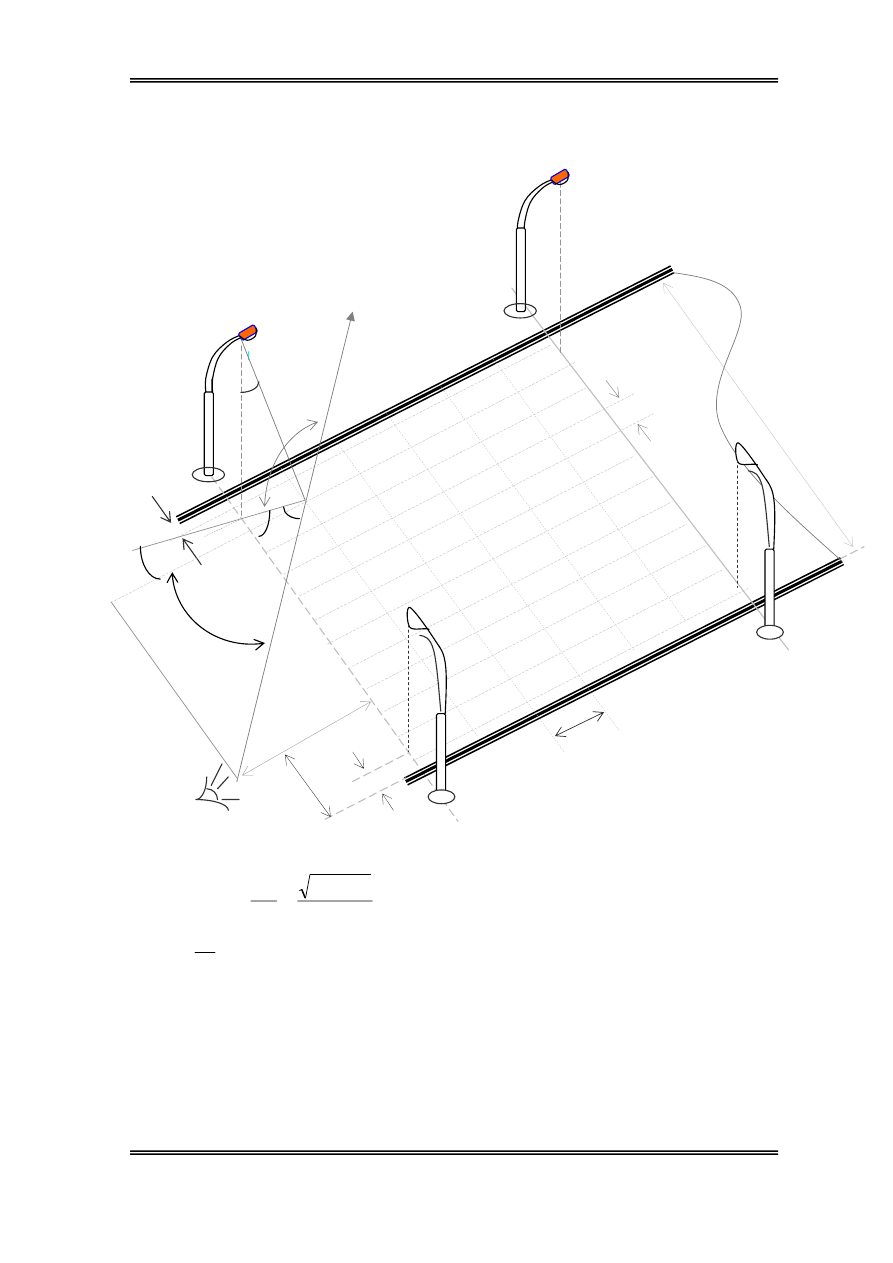
Ta sö dông ph−¬ng ph¸p ®é chãi ®iÓm ®Ó tÝnh ®é räi vµ ®é chãi t¹i mét
®iÓm trªn ®−êng
e=36 chän 6 ®iÓm theo chiÒu däc (Tõ ®Ìn 1 ®Õn ®Ìn 2 lµ 7 ®iÓm)
6 lµn xe chän 12 ®iÓm theo ph−¬ng ngang nh− h×nh vÏ
§
4
l=24m
§
1
1m
2
5
6
3
4
1
•
•
•
•
•
•
8
11
12
9
10
7
•
•
•
•
•
•
14
17
18
15
16
12
•
•
•
•
•
•
20
23
24
21
22
19
•
•
•
•
•
•
26
29
30
27
28
25
•
•
•
•
•
•
32
35
36
33
34
31
•
•
•
•
•
•
38
41
42
39
40
37
•
•
•
•
•
•
44
47
48
45
46
43
•
•
•
•
•
•
50
53
54
51
52
49
•
•
•
•
•
•
56
59
60
57
58
55
•
•
•
•
•
•
62
65
66
63
64
61
•
•
•
•
•
•
68
71
72
69
70
67
•
•
•
•
•
•
§
2
§
4
1,2m
2m
36m
H=12m
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
13
§
4
§
3
B
A
l
§
1
§
2
1
m
D
E(eye)
2
5
6
3
4
1
•
•
•
•
•
•
••
•
•
2m
6m
1,2m
•
C
6m
•
H−íng nh×n
γ
1
β
1
60m
C
P
h
0,2m
α
α
1
α
2
Q
•
15m
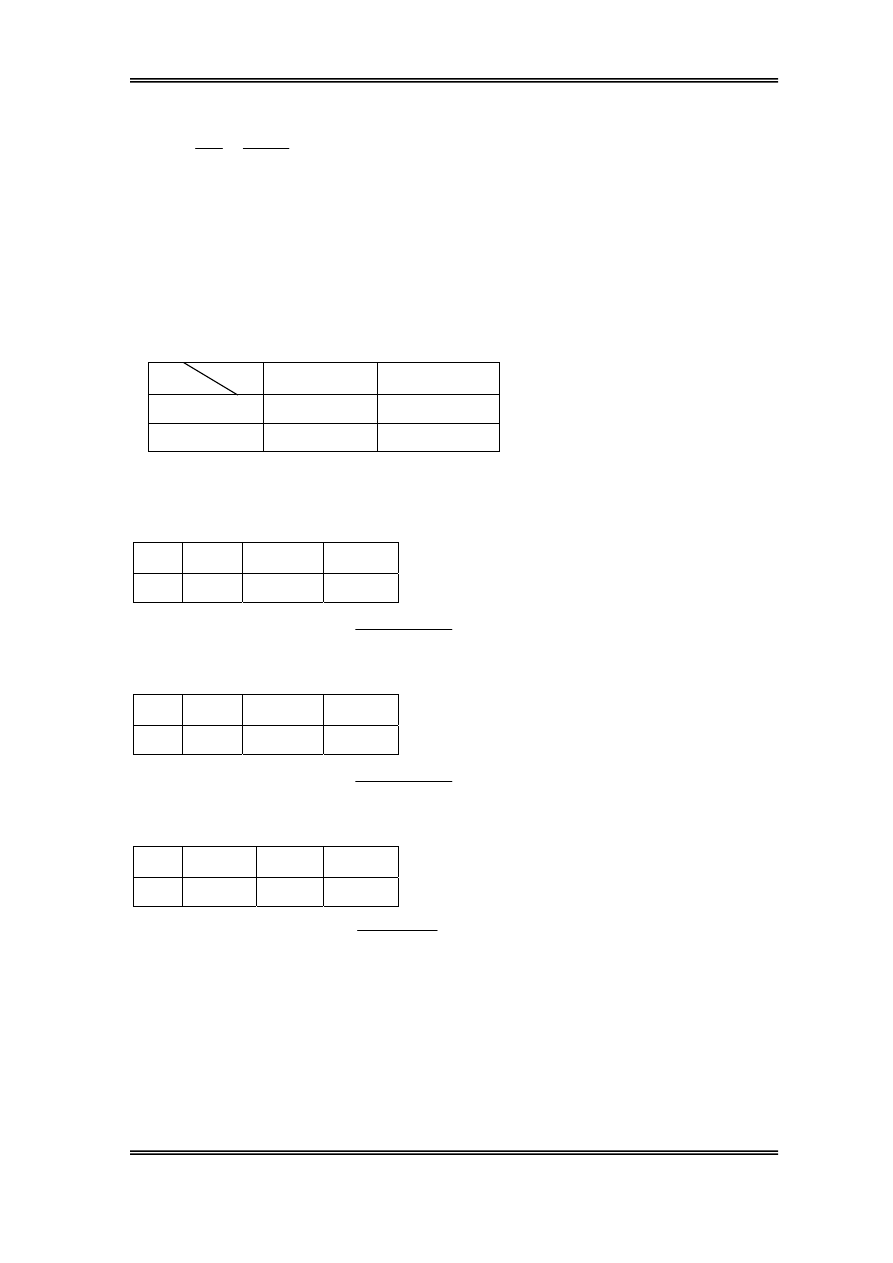
∗ TiÕn hµnh kiÓm tra ®iÓm thø 8 (theo thø tù danh s¸ch sinh viªn)
a. XÐt sù ¶nh h−ëng cña ®Ìn1:
Ta cã:
o
h
AP
tg
57
,
27
522
,
0
12
8
,
1
6
1
2
2
1
=
⇒
=
+
=
=
γ
γ
0
1
1
3
,
73
333
,
3
8
,
1
6
=
→
=
=
C
tgC
β
1
=180
0
-
α
α =α
1
+
α
2
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
14
0
0
0
2
1
0
0
0
1
0
2
0
1
1
5
,
29
7
,
16
8
,
12
7
,
16
3
,
73
90
90
8
,
12
227
,
0
6
60
15
=
+
=
+
=
=
−
=
−
=
=
→
=
+
=
=
α
α
α
α
α
α
C
QP
EQ
tg
⇒
β
1
=180
0
-
α =180
0
- 29,5
0
=150,5
0
• Tra b¶ng trang 206 ta cã: q.cos
3
γ.10
4
Víi tg
γ
1
=0,522
∈[0,5 ÷ 0,75]
β=150,5
0
[150
0
÷ 165
0
]
tg
γ β
0
150 165
0,5 260
260
0,75 206
206
Dïng c«ng thøc néi suy: Néi suy R
2
t¹i tg
γ=0,522 vµ β=150,5
0
∗ Néi suy R
2
t¹i tg
γ=0,5 vµ β=150,5
0
β
150
0
150,5
0
165
0
R
2
260
260
(
)
260
150
165
150
5
,
150
.
260
260
260
|
0
0
0
0
5
,
150
5
,
0
0
=
−
−
−
+
=
=
=
β
γ
tg
R
∗ Néi suy R
2
t¹i tg
γ=0,75 vµ β=150,5
0
β
150
0
150,5
0
165
0
R
2
206
206
(
)
206
150
165
150
5
,
150
.
206
206
206
|
0
0
0
0
5
,
150
75
,
0
0
=
−
−
−
+
=
=
=
β
γ
tg
R
∗ Néi suy R
2
t¹i tg
γ=0,522 vµ β=150,5
0
tg
γ 0,5 0,522
0,75
R
2
260
206
(
)
25
,
255
5
,
0
75
,
0
5
,
0
522
,
0
.
260
206
260
|
5
,
150
522
,
0
=
−
−
−
+
=
=
=
o
tg
R
β
γ
• Tra b¶ng ®−êng ®¼ng Candenla:
γ
1
=27,57
0
C
1
=73,3
0
I
1
=0,4.I
max
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
15
⇒
)
(
8
,
3168
1000
34000
.
233
.
4
,
0
1000
.
.
max
1
1
cd
E
I
I
I
=
=
=
γ
- §é chãi do ®Ìn 1 g©y ra t¹i P:
)
/
(
56
,
0
12
8
,
3168
.
10
.
25
,
255
.
2
2
4
2
%
1
1
m
cd
h
I
R
L
=
=
=
−
γ
- §é räi do ®Ìn 1 g©y ra t¹i P:
)
(
78
,
2
12
89
,
59
cos
.
8
,
3168
cos
.
2
0
3
2
1
3
1
1
lux
h
I
E
=
=
=
γ
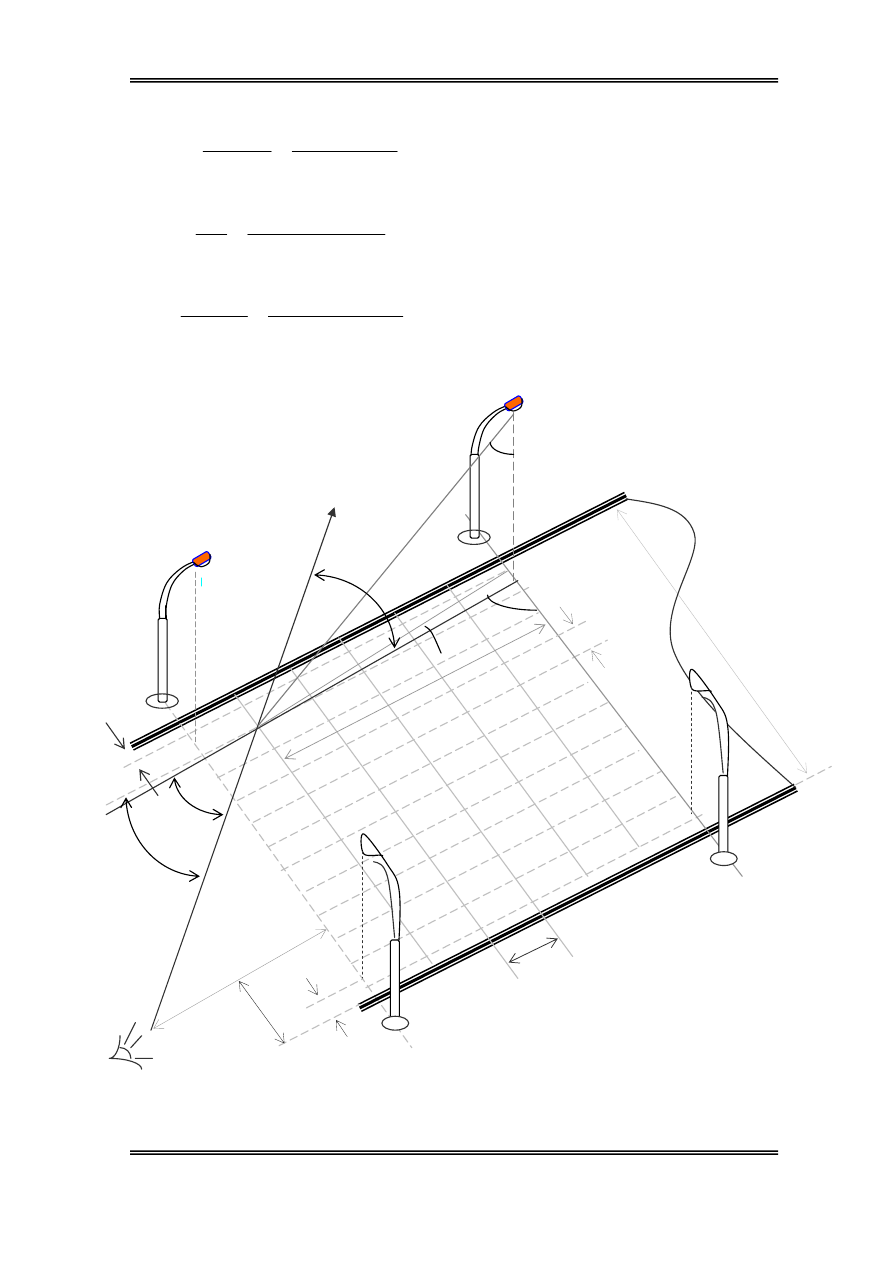
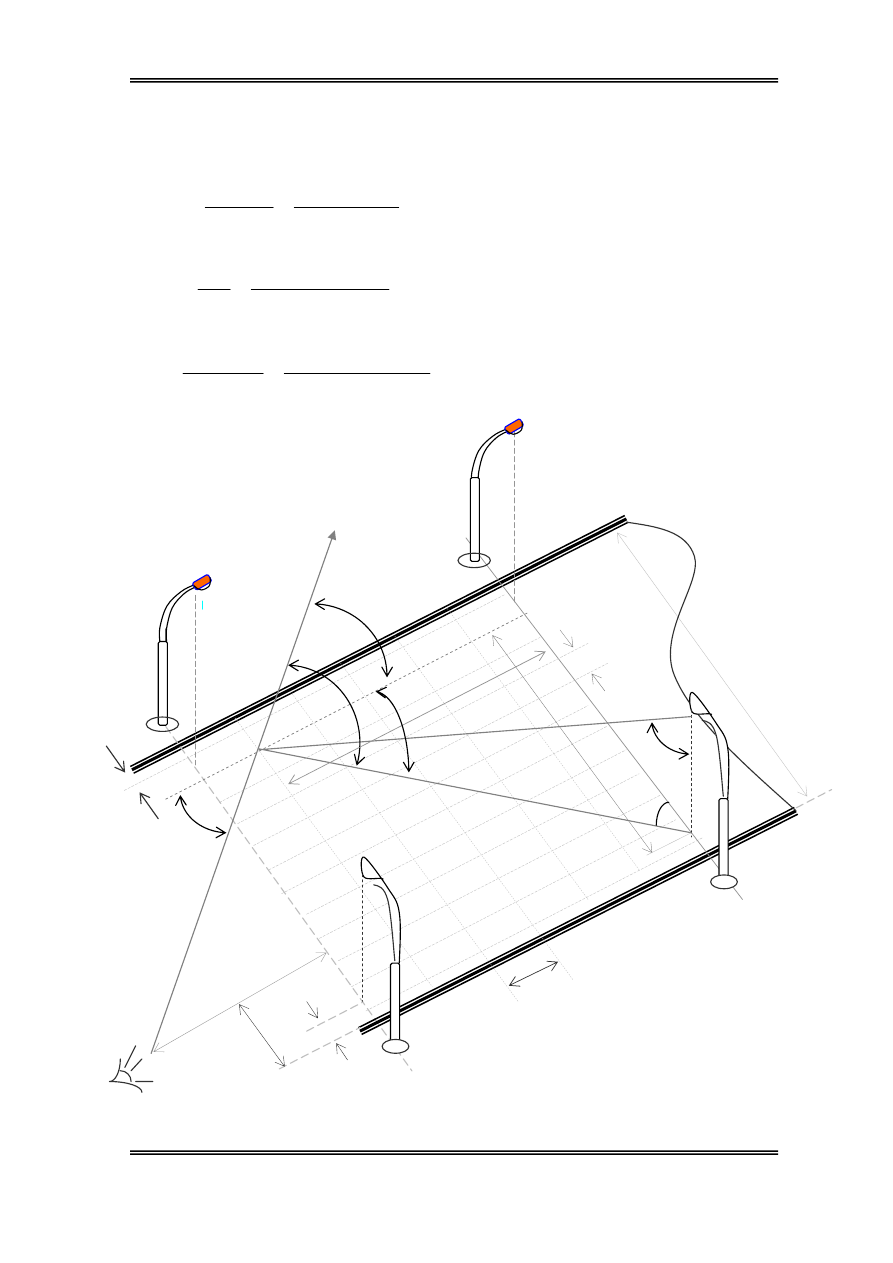
b. XÐt sù ¶nh h−ëng cña ®Ìn2:
§
4
§
3
B
A
l
§
1
§
2
1 m
D
E(eye)
2
5
6
3
4
1
•
•
•
•
•
•
••
•
•
2m
6m
1,2m
•
C
6m
•
H−íng nh×n
γ
2
β
2
60m
8
C
2
30 m
1,8 m
P
β
2
α
1
α
3
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
16
Ta cã:
0
1
2
2
2
243
,
68
5045
,
2
12
8
,
1
30
=
⇒
=
+
=
=
γ
γ
h
BP
tg
0
2
2
57
,
86
67
,
16
8
,
1
30
=
→
=
=
C
tgC
β
2
=
α
1
+
α
3
α
1
=12,8
0
0
0
0
1
2
0
3
3
42
,
12
382
,
0
8
,
12
382
,
0
006667
,
0
30
2
,
0
=
−
=
−
=
=
⇒
=
=
3
α
α
β
α
α
tg
•
Tra b¶ng trang 206 ta cã: q.cos
3
γ.10
4
Víi tg
γ
2
=2,5045
∈[2,5 ÷ 3]
vµ
β=12,42
0
∈[10
0
÷15
0
]
tg
γ β
0
10
0
15
0
2,5 110
74
3 67
43
Dïng c«ng thøc néi suy: Néi suy R
2
t¹i tg
γ=2,5045 vµ β=12,42
0
∗ Néi suy R
2
t¹i tg
γ=2,5 vµ β=12,42
0
β
10
0
12,42
0
15
0
R
2
110
74
(
)
`
484
,
74
10
15
10
42
,
12
.
110
74
110
|
0
0
0
0
42
,
12
5
,
2
=
−
−
−
+
=
=
=
o
tg
R
β
γ
∗ Néi suy R
2
t¹i tg
γ=3 vµ β=12,42
0
β
10
0
12,42
0
15
0
R
2
67
43
(
)
384
,
55
10
15
10
42
,
12
.
67
43
67
|
0
0
0
0
42
,
12
3
0
=
−
−
−
+
=
=
=
β
γ
tg
R
∗ Néi suy R
2
t¹i tg
γ=
tg
γ
2,5 2,5045 3
R
2
74,484 55,384
(
)
312
,
74
5
,
2
3
5
,
2
5045
,
2
.
484
,
74
384
,
55
484
,
74
|
0
42
,
12
5045
,
2
=
−
−
−
+
=
=
=
β
γ
tg
R
• Tra b¶ng ®−êng ®¼ng Candenla:
γ
2
=68,234
0
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
17
C
2
=86,57
0
I
2
=0,3.I
max
⇒
)
(
6
,
2376
1000
34000
.
233
.
3
,
0
1000
.
.
max
2
1
cd
E
I
I
I
=
=
=
γ
- §é chãi do ®Ìn 1 g©y ra t¹i P:
)
/
(
126
,
0
12
6
,
2376
.
10
.
312
,
74
.
2
2
4
2
%
2
2
m
cd
h
I
R
L
=
=
=
−
γ
- §é räi do ®Ìn 1 g©y ra t¹i P:
)
(
8415
,
0
12
234
,
68
cos
.
6
,
2376
cos
.
2
0
3
2
2
3
%
2
lux
h
I
E
=
=
=
γ
γ
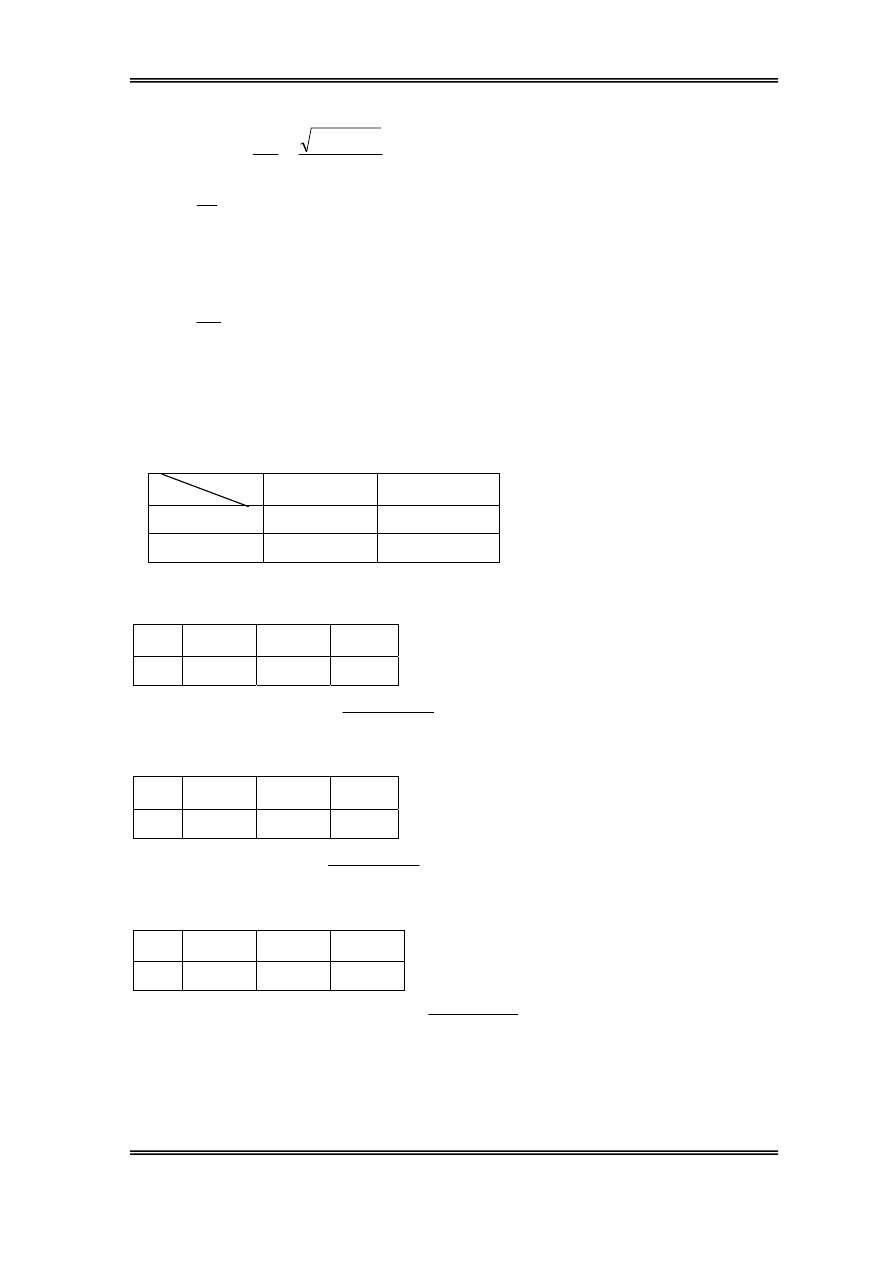
c. XÐt sù ¶nh h−ëng cña ®Ìn 3:
§
4
§
3
B
A
l
§
1
§
2
1 m
D
E(eye)
2
5
6
3
4
1
•
•
•
•
•
•
••
•
•
2m
6m
1,2m
•
C
6m
•
H−íng nh×n
γ
3
β
3
60m
8
C
3
``
P
30 m
19,8 m
α
1
α
1
α
4
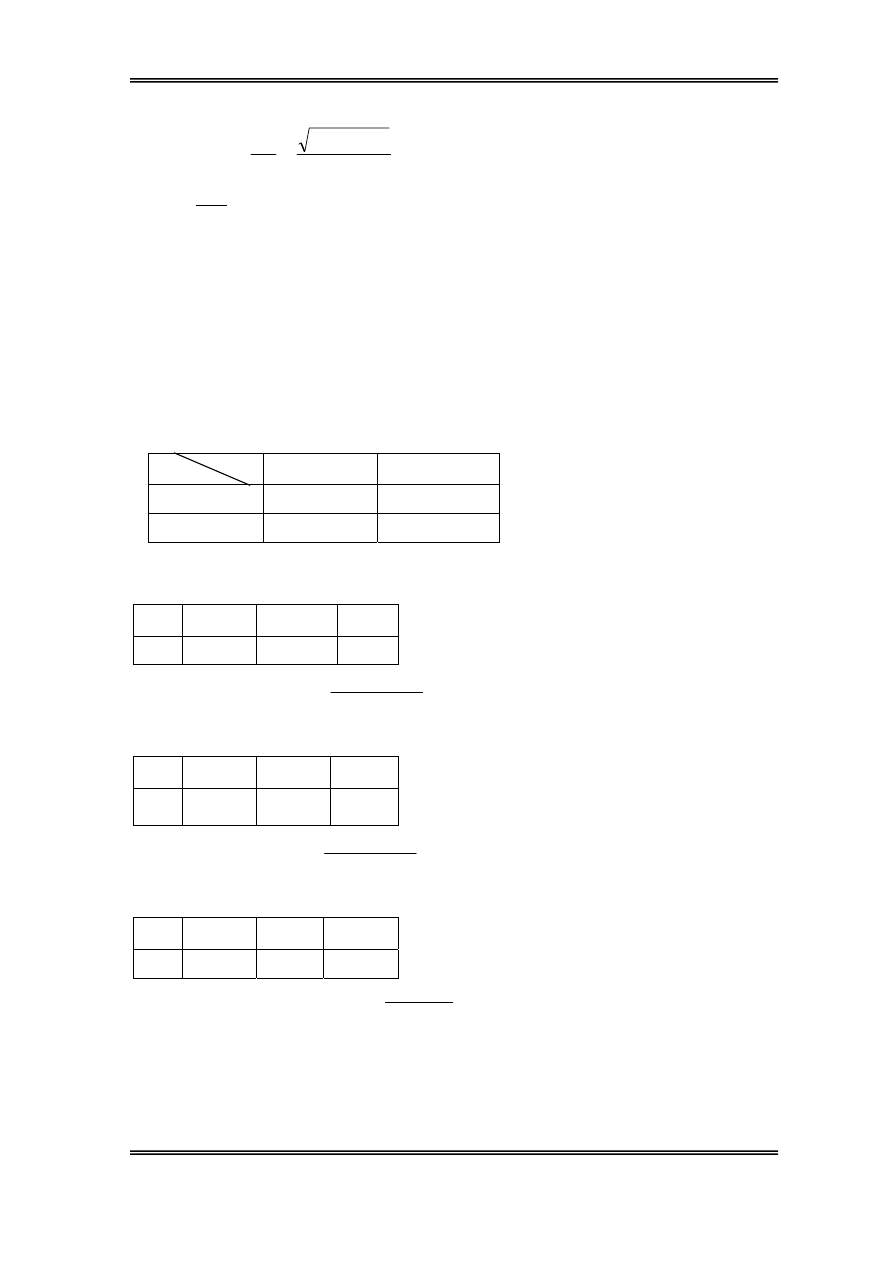
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
18
Ta cã:
54
,
71
995
,
2
12
30
8
,
19
0
1
2
2
1
=
⇒
=
+
=
=
γ
γ
h
CP
tg
0
3
3
58
,
56
52
,
1
8
,
19
30
=
→
=
=
C
tgC
β
3
=
α
1
+
α
4
α
1
=12,8
0
α
4
=90
0
- C
3
=90
0
- 56,54
0
=33,46
0
⇒
β
3
=
α
1
+
α
4
=12,8
0
+33,46
0
=46,26
0
• Tra b¶ng trang 206 ta cã: q.cos
3
γ.10
4
Víi tg
γ
3
=2,995
∈[2,5 ÷ 3]
Vµ
β
3
=46,26
0
∈[45
0
÷ 50
0
]
tg
γ 0
0
45
0
60
0
2,5 27 24
3 16 16
Dïng c«ng thøc néi suy: Néi suy R
2
t¹i tg
γ=5,995 vµ β=46,26
0
∗ Néi suy R
2
t¹i tg
γ=2,5 vµ β=46,26
0
β
45
0
46,26
0
60
0
R
2
27
24
(
)
748
,
26
45
60
45
26
,
46
.
27
24
27
|
0
0
0
0
26
,
46
5
,
2
0
=
−
−
−
+
=
=
=
β
γ
tg
R
∗ Néi suy R
2
t¹i tg
γ=3 vµ β=46,26
0
β
45
0
46,26
0
50
0
R
2
16
16
(
)
16
45
60
45
26
,
46
.
16
16
16
|
0
0
0
0
26
,
46
3
0
=
−
−
−
+
=
=
=
β
γ
tg
R
∗ Néi suy R
2
t¹i tg
γ=
tg
γ
2,5 2,995 3
R
2
26,748
16
(
)
627
,
5
5
,
2
3
2
995
,
2
.
478
,
26
16
478
,
26
|
169
06
,
3
=
−
−
−
+
=
=
=
β
γ
tg
R
• Tra b¶ng ®−êng ®¼ng Candenla:
γ
3
=71,54
0
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
19
C
3
=56,58
0
I
3
=0,5.I
max
⇒
)
(
3961
1000
34000
.
233
.
5
,
0
1000
.
.
max
%
3
1
cd
E
I
I
I
=
=
=
γ
- §é chãi do ®Ìn 1 g©y ra t¹i P:
)
/
(
0155
,
0
12
3961
.
10
.
627
,
5
.
2
2
4
2
3
3
m
cd
h
I
R
L
=
=
=
−
- §é räi do ®Ìn 1 g©y ra t¹i P:
)
(
873
,
0
12
54
,
71
cos
.
3961
cos
.
2
0
3
2
1
3
3
3
lux
h
I
E
=
=
=
γ
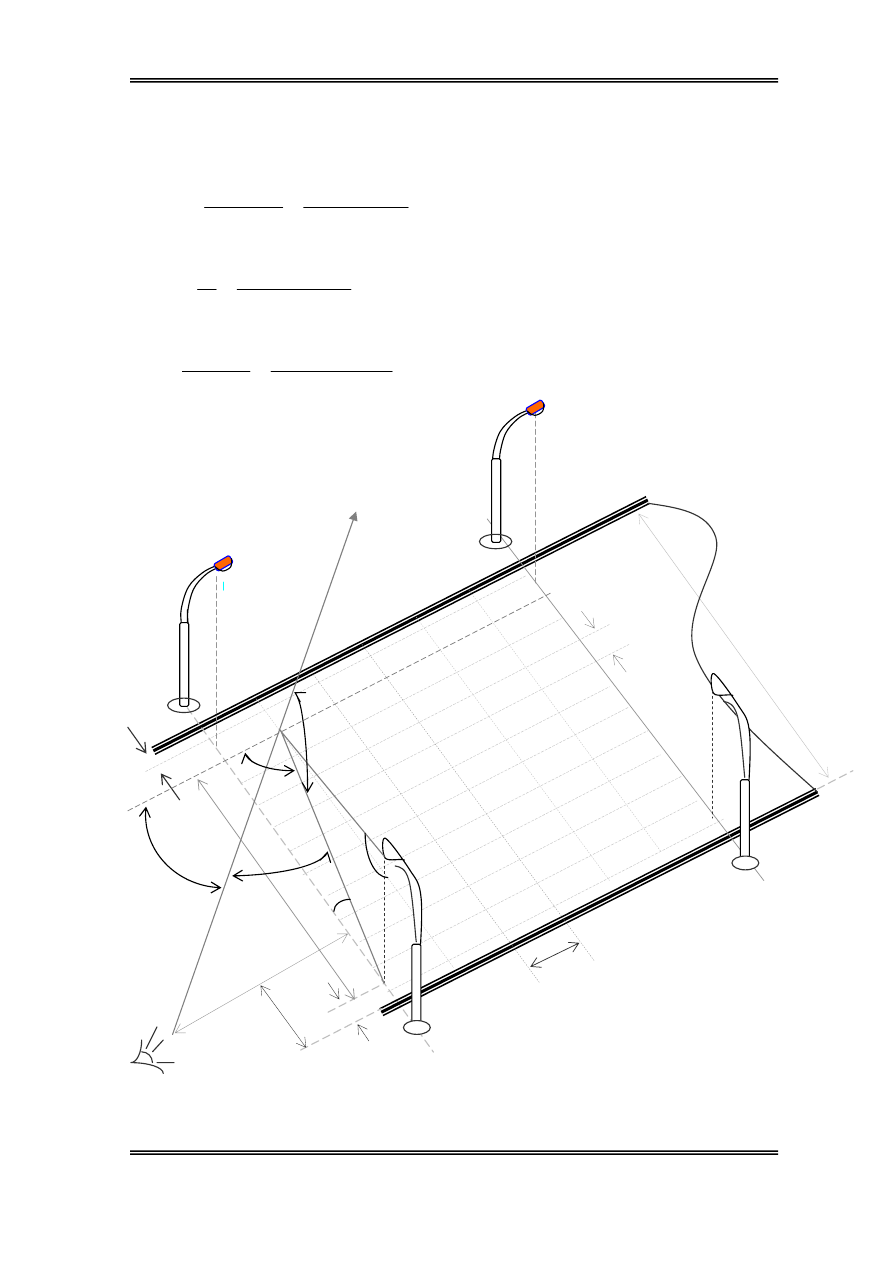
d. Sù ¶nh h−ëng cña ®Ìn 4:
§
4
§
3
B
A
l
§
1
§
2
1m
D
E(eye)
2
5
6
3
4
1
•
•
•
•
•
•
••
•
•
2m
6m
1,2m
•
C
6m
•
H−íng nh×n
γ
4
β
4
60m
8
C
4
`
P
19,8 m
α
1
α
5
α
6
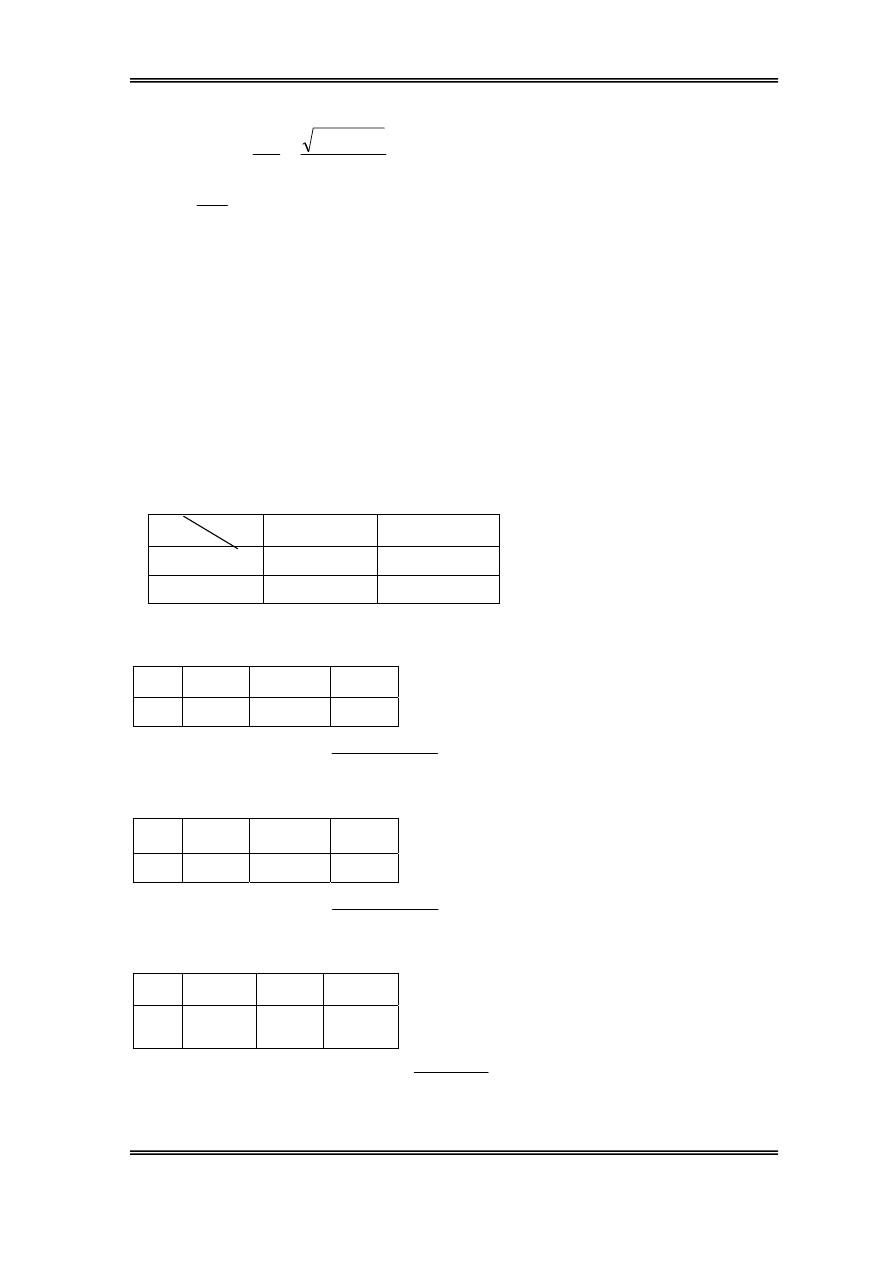
Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
20
Ta cã:
89
,
59
724
,
1
12
8
,
19
6
0
4
2
2
4
=
⇒
=
+
=
=
γ
γ
h
DP
tg
86
,
16
303
,
0
8
,
19
6
0
4
4
=
→
=
=
C
tgC
β
4
=180
0
-
α
6
α
6
=
α
5
-
α
1
α
1
= 12,8
0
α
5
=90
0
- C
4
=90
0
-16,86
0
=73,14
0
⇒
α
6
=
α
5
-
α
1
=12,8
0
+73,14
0
⇒
β
4
=180
0
-
α
6
=180
0
-73,14
0
=119,66
0
• Tra b¶ng trang 206 ta cã: q.cos
3
γ.10
4
Víi tg
γ
4
=1,724
∈[1,5 ÷ 1,75]
Vµ
β
4
=119,66
0
∈[105
0
÷ 120
0
]
tg
γ 0
0
105
0
120
0
1,5 84
87
1,75 63
67
Dïng c«ng thøc néi suy: Néi suy R
2
t¹i tg
γ=1,724 vµ β=119,66
0
∗ Néi suy R
2
t¹i tg
γ=1,5 vµ β=119,66
0
β
105
0
119,66
0
120
0
R
2
84
87
(
)
932
,
86
105
120
105
66
,
119
.
84
87
84
|
0
0
0
0
66
,
119
5
,
1
0
=
−
−
−
+
=
=
=
β
γ
tg
R
∗ Néi suy R
2
t¹i tg
γ=1,75 vµ β=119,66
0
β
105
0
119,66
0
120
0
R
2
63
67
(
)
91
,
66
105
120
105
66
,
119
.
63
67
63
|
0
0
0
0
66
,
119
75
,
1
0
=
−
−
−
+
=
=
=
β
γ
tg
R
∗ Néi suy R
2
t¹i tg
γ=1,724 vµ β= 119,66
0
tg
γ
1,5 1,724 1,75
R
2
86,932
66,91
(
)
992
,
68
5
,
1
75
,
1
5
,
1
724
,
1
.
932
,
86
91
,
66
932
,
86
|
0
66
,
119
724
,
1
=
−
−
−
+
=
=
=
β
γ
tg
R

Bμi tËp lín
ThiÕt kÕ chiÕu s¸ng
Cao ViÖt Hμ- ThiÕt BÞ §iÖn- §iÖn Tö 2, K42
Tr−êng ®¹i häc B¸ch Khoa Hμ Néi
21
Tra b¶ng ®−êng ®¼ng Candenla:
γ
4
=59,89
0
C
4
=16,86
0
I
4
=0,7.I
max
⇒
)
(
4
,
5545
1000
34000
.
233
.
7
,
0
1000
.
.
max
%
4
cd
E
I
I
I
=
=
=
γ
- §é chãi do ®Ìn 1 g©y ra t¹i P:
)
/
(
266
,
0
12
4
,
5545
.
10
.
992
,
68
.
2
2
4
2
4
4
m
cd
h
I
R
L
=
=
=
−
- §é räi do ®Ìn 1 g©y ra t¹i P:
)
(
862
,
4
12
89
,
59
cos
.
4
,
5545
cos
.
2
0
3
2
4
3
4
4
lux
h
I
E
=
=
=
γ
e. XÐt sù ¶nh h−ëng cña c¶ bèn ®Ìn ta cã:
L
∑
= ∑L
i
= 0,56+0,126+0,0155+0,873 = 1,5745 cd/m
2
E
∑
= ∑E
i
=2,78+0,8415+0,873+4,862=9,3565 lux
Víi th«ng sè trªn ta thÊy ph−¬ng ¸n thiÕt kÕ ®−îc chÊp nhËn.
Wyszukiwarka
Podobne podstrony:
ĐHBK Tài Liệu Hướng Dẫn Thiết Kế Thiết Bị Điện Tử Công Suất Trần Văn Thịnh, 122 Trang
Bài Giảng Kỹ Nghệ Phần Mềm Nguyễn Việt Hà, 75 Trang
Giáo Trình Đào Tạo Bồi Dưỡng Tư Vấn Giám Sát Khảo Sát Phạm Sanh, 20 Trang
BCVT Bài Tập Tiếng Anh Chuyên Ngành Điện Từ Viễn Thông Ths Nguyễn Quỳnh Giao, 86 Trang
Quy Phạm Trang Bị Điện 4 Bảo Vệ Và Tự Động
ĐHĐL Giáo Trình Điện Tử Căn Bản Phan Văn Nghĩa, 177 Trang
BCVT Bài Giảng Lập Trình Hướng Đối Tượng (NXB Hồ Chí Minh 2002) Nguyễn Việt Cường, 384 Trang
Bài Giảng Quang Điện Tử Và Quang Điện Ts Nguyễn Văn Cường, 56 Trang
Trường Điện Tử Nhiều Tác Giả, 105 Trang
Công Nghệ Cơ Điện Tử Trong Chế Tạo Ô Tô Pgs Ts Tạ Duy Liêm
ĐHMO Lập Dự Toán Xây Dựng Cơ Bản Ths Lương Văn Cảnh, 21 Trang
ĐHCN Giáo Trình Lý Thuyết Trường Điện Từ Võ Xuân Ân, 108 Trang
Công Nghệ Điện Thoại IP Thái Quang Tùng, 112 Trang
ĐHMO Thực Hành Điện Tử Tương Tự Ks Nguyễn Phúc Ân, 38 Trang
Suy Nghĩ, Nhận Thức Và Công Việc (Hội Ký Xây Dựng) Nguyễn Đình Cống, 160 Trang
Cấu Trúc Dữ Liệu Và Giải Thuật Phan Chí Tùng, 80 Trang
Chẩn Đoán Kỹ Thuật Ô Tô Trần Thanh Hải Tùng, 17 Trang
więcej podobnych podstron