materiał pochodzi ze strony

matematyka.pisz.pl

Figury na płaszczyźnie

Zadanie

17

(

1

pkt)

(maj 2015)

Pole rombu o obwodzie

8

jest równe

1

. Kąt ostry tego rombu ma miarę

α

. Wtedy

A. 14

◦

< α < 15

◦

B. 29

◦

< α < 30

◦

C. 60

◦

< α < 61

◦

D. 75

◦

< α < 76

◦

Zadanie

17

(

1

pkt)

(grudzień 2014)

Dany jest trójkąt równoramienny, w którym ramię o długości

20

tworzy z podstawą kąt

67,5

◦

.

Pole tego trójkąta jest równe

A. 100

√

3

B. 100

√

2

C. 200

√

3

D. 200

√

2

Zadanie

16

(

1

pkt)

(sierpień 2014)

Promień okręgu opisanego na trójkącie równobocznym jest równy

8

. Wysokość tego trójkąta

jest równa

A. 4

√

3

B. 8

√

3

C. 12

D. 6

Zadanie

21

(

1

pkt)

(czerwiec 2014)

Na planie miasta, narysowanym w skali

1 : 20 000

, park jest prostokątem o bokach

2

cm i

5

cm.

Stąd wynika, że ten park ma powierzchnię

A. 20 000

m

2

B. 40 000

m

2

C. 200 000

m

2

D. 400 000

m

2

Zadanie

18

(

1

pkt)

(czerwiec 2014)

Na trójkącie prostokątnym, którego przyprostokątne mają długości

12

i

9

, opisano okrąg. Pro-

mień tego okręgu jest równy

A.

√

108

B.

15

2

C. 15

D.

√

108

2

Zadanie

14

(

1

pkt)

(czerwiec 2014)

W trapezie

KLM N

, w którym

KL k M N

, kąt

LKN

jest prosty (zobacz rysunek) oraz

dane są:

|M N | = 3

,

|KN | = 4

√

3

,

| KLM | = 60

◦

. Pole tego trapezu jest równe

K

L

M

N

A. 4 + 2

√

3

B. 10

√

3

C. 20

√

3

D. 24 + 6

√

3

Zadanie

16

(

1

pkt)

(maj 2014)

Wysokość trapezu równoramiennego o kącie ostrym

60

◦

i ramieniu długości

2

√

3

jest równa

A. 2

B.

√

3

C. 3

D. 2

√

3

Zadanie

17

(

1

pkt)

(sierpień 2013)

Najdłuższa przekątna sześciokąta foremnego ma długość

8

. Wówczas pole koła opisanego na

tym sześciokącie jest równe

A. 4π

B. 8π

C. 16π

D. 64π

Zadanie

18

(

1

pkt)

(sierpień 2013)

Pole równoległoboku o bokach długości

4

i

12

oraz kącie ostrym

30

◦

jest równe

A. 24

B. 12

√

3

C. 12

D. 6

√

3

Zadanie

12

(

1

pkt)

(sierpień 2013)

Z prostokąta

ABCD

o obwodzie

30

wycięto trójkąt równoboczny

AOD

o obwodzie

15

(tak

jak na rysunku). Obwód zacieniowanej figury jest równy

A

B

C

D

O

A. 25

B. 30

C. 35

D. 40

—

matematyka.pisz.pl

—

1

—

matematyka.pisz.pl

—

Zadanie

14

(

1

pkt)

(czerwiec 2013)

Kosinus kąta ostrego rombu jest równy

√

3

2

, bok rombu ma długość

3

. Pole tego rombu jest

równe

A.

9
2

B.

9

√

3

4

C.

9

√

3

2

D. 6

Zadanie

13

(

1

pkt)

(czerwiec 2013)

Prostokąt

ABCD

o przekątnej długości

2

√

13

jest podobny do prostokąta o bokach długości

2

i

3

. Obwód prostokąta

ABCD

jest równy

A. 10

B. 20

C. 5

D. 24

Zadanie

16

(

1

pkt)

(marzec 2012)

Pole prostokąta jest równe

40

. Stosunek długości jego boków jest równy

2 : 5

. Dłuższy bok

tego prostokąta jest równy

A. 10

B. 8

C. 7

D. 6

Zadanie

17

(

1

pkt)

(marzec 2012)

Dany jest trójkąt prostokątny o przyprostokątnych

5

i

12

. Promień okręgu opisanego na tym

trójkącie jest równy

A. 12

B. 8,5

C. 6,5

D. 5

Zadanie

18

(

1

pkt)

Dane są dwa okręgi o promieniach

12

i

17

. Mniejszy okrąg przechodzi przez środek większego

okręgu. Odległość między środkami tych okręgów jest równa

A. 5

B. 12

C. 17

D. 29

Zadanie

21

(

1

pkt)

(sierpień 2011)

Dany jest romb o boku długości

4

i kącie ostrym

60

◦

. Pole tego rombu jest równe

A. 16

√

3

B. 16

C. 8

√

3

D. 8

Zadanie

17

(

1

pkt)

(maj 2010)

Wysokość rombu o boku długości

6

i kącie ostrym

60

◦

jest równa

A. 3

√

3

B. 3

C. 6

√

3

D. 6

Zadanie

15

(

1

pkt)

(maj 2010)

Okrąg opisany na kwadracie ma promień

4

. Długość boku tego kwadratu jest równa

A. 4

√

2

B. 2

√

2

C. 8

D. 4

Zadanie

17

(

1

pkt)

(sierpień 2010)

Okrąg opisany na trójkącie równobocznym ma promień

12

. Wysokość tego trójkąta jest równa

A. 18

B. 20

C. 22

D. 24

Zadanie

19

(

1

pkt)

(maj 2010)

30

◦

80

cm

80

cm

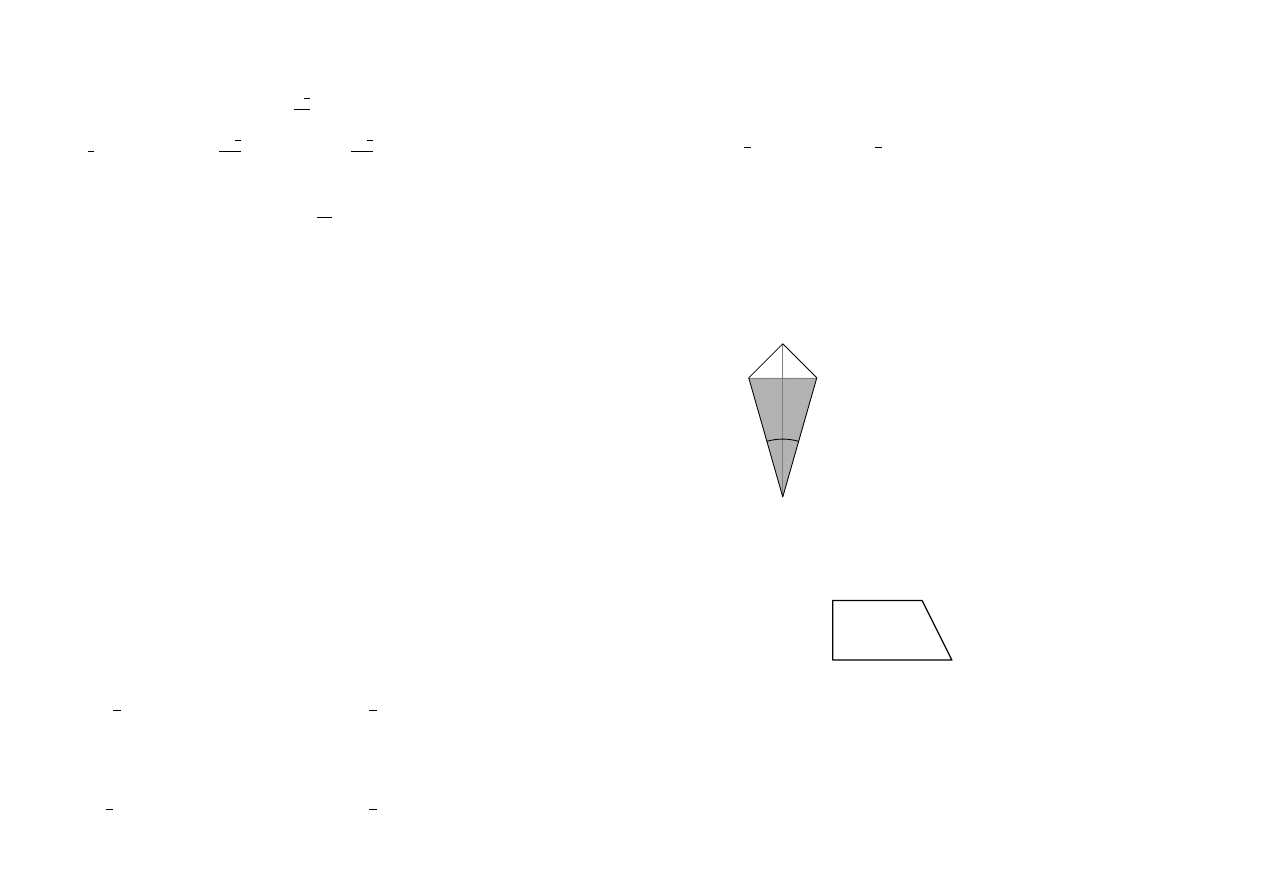
Latawiec ma wymiary podane na rysunku. Powierzchnia

zacieniowanego trójkąta jest równa

A. 3200

cm

2

B. 6400

cm

2

C. 1600

cm

2

D. 800

cm

2

Zadanie

6

(informator str. 25)

Długość ramienia

BC

trapezu prostokątnego jest dwa razy większa od różnicy długości jego

podstaw. Kąt

ABC

ma miarę

a)

30

◦

b)

45

◦

c)

60

◦

d)

75

◦

A

B

C

D

Zadanie

3

(informator str. 36)

Drut o długości

27

m pocięto na trzy części, których stosunek długości jest równy

2 : 3 : 4

.

Jaką długość ma najkrótsza z tych części?

A. 4,5

m

B. 6

m

C. 6,75

m

D. 9

m

—

matematyka.pisz.pl

—

2

—

matematyka.pisz.pl

—

Zadanie

34

(informator str. 81)

Pole kwadratu wpisanego w okrąg o promieniu

4

cm jest równe

A. 64

cm

2

B. 32

cm

2

C. 16

cm

2

D. 8

cm

2

Geometria na płaszczyźnie

Zadanie

34

(

4

pkt)

(maj 2014)

Kąt

CAB

trójkąta

ACB

ma miarę

30

◦

. Pole kwadratu

DEF G

, wpisanego w ten trójkąt

(zobacz rysunek), jest równe

4

. Oblicz pole trójkąta

ACB

.

C

A

B

D

G

F

E

30

◦

Zadanie

24

(

2

pkt)

(marzec 2012)

Podstawy trapezu prostokątnego mają długość

6

i

10

oraz tangens kąta ostrego jest równy

3

.

Oblicz pole tego trapezu.

Zadanie

31

(

2

pkt)

(maj 2010)

W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równo-

boczny. Dłuższa podstawa trapezu jest równa

6

. Oblicz obwód tego trapezu.

Zadanie

5

(informator str. 22)

W trójkącie równoramiennym

ABC

, w którym

|AC| = |BC| = 10

cm, wysokość poprowa-

dzona z wierzchołka

C

jest równa

5

cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w

stopniach.

Zadanie

6

(informator str. 25)

Długość ramienia

BC

trapezu prostokątnego jest dwa razy większa od różnicy długości jego

podstaw. Kąt

ABC

ma miarę

a)

30

◦

b)

45

◦

c)

60

◦

d)

75

◦

A

B

C

D

Zadanie

67

(

2 pkt

)

(informator str. 85)

Punkt

D

leży na boku

BC

trójkąta równoramiennego

ABC

, w którym

|AC| = |BC|

.

Odcinek

|AD|

dzieli trójkąt

ABC

na dwa trójkąty równoramienne w taki sposób, że

|AB| = |AD| = |CD|

(patrz rysunek). Oblicz miary kątów trójkąta

ABC

.

A

B

C

D

Zadanie

68

(

2 pkt

)

(informator str. 85)

Oblicz pole trójkąta równoramiennego

ABC

, w którym

|AB| = 24

i

|AC| = |BC| = 13

.

Zadanie

69

(

2 pkt

)

(informator str. 85)

Liczby

4

,

10

,

c

są długościami boków trójkąta równoramiennego. Oblicz

c

.

Zadanie

70

(

2 pkt

)

(informator str. 85)

Liczby

6

,

10

,

c

są długościami boków trójkąta równoramiennego. Oblicz

c

.

Zadanie

71

(

2 pkt

)

(informator str. 85)

Liczby

6

,

10

,

c

są długościami boków trójkąta prostokątnego. Oblicz

c

.

Zadanie

73

(

2 pkt

)

(informator str. 86)

Obwód czworokąta wypukłego

ABCD

jest równy

50

cm. Obwód trójkąta

ABD

jest równy

46

cm, a obwód trójkąta

BCD

jest równy

36

cm. Oblicz długość przekątnej

BD

.

Zadanie

103

(informator str. 91)

Dany jest trójkąt prostokątny

ABC

, w którym

|BC| = 30

,

|AC| = 40

,

|AB| = 50

. Punkt

W

jest środkiem okręgu wpisanego w ten trójkąt. Okrąg wpisany w trójkąt

ABC

jest styczny

do boku

AB

w punkcie

M

. Oblicz długość odcinka

CM

.

C

A

B

W

M

—

matematyka.pisz.pl

—

3

—

matematyka.pisz.pl

—

Zadanie

104

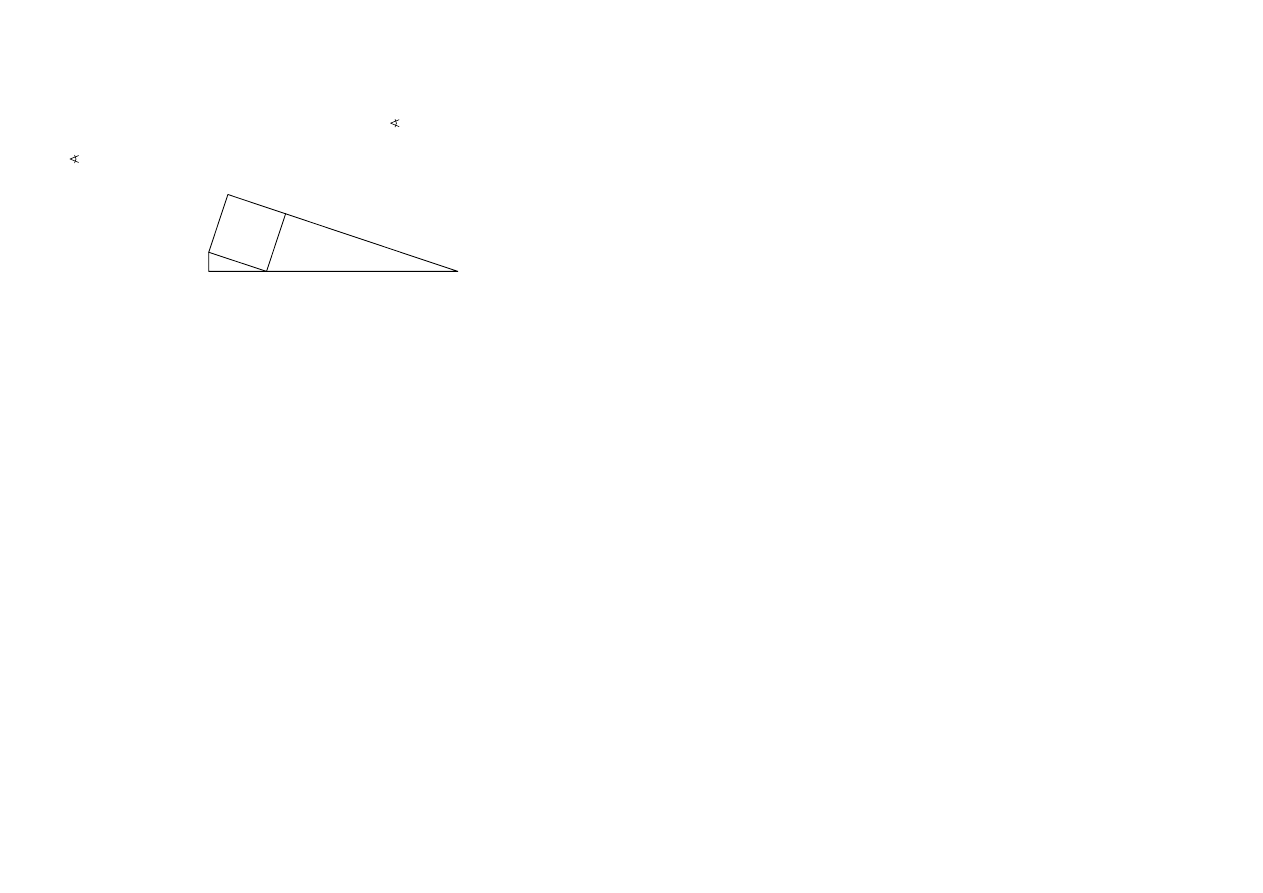
(informator str. 91)

Na zewnątrz trójkąta prostokątnego

ABC

, w którym

| ACB| = 90

◦

oraz

|AC| = 5

,

|BC| = 12

zbudowano kwadrat

ACDE

(patrz rysunek). Punkt

H

leży na prostej

AB

i kąt

| EHA| = 90

◦

. Oblicz pole trójkąta

HAE

.

H

A

B

C

D

E

—

matematyka.pisz.pl

—

4

—

matematyka.pisz.pl

—