Metoda ciasnego wiązania
W przybliżeniu elektronów prawie swobodnych zakładaliśmy że potencjał periodyczny
nieznacznie modyfikuje stany elektronu swobodnego. Innym skrajnym przybliżeniem jest
założenie że oddziaływanie pomiędzy atomami w sieci w sposób nieznaczny modyfikuje
stany izolowanych atomów.
a) Oddziaływanie między dwoma atomami
Rozważmy niezdegenerowany stan φ(r) o energii E
0
atomu będący stanem własnym
Hamiltonianu
)
(
2
2
0
r
V
m
H
+
∆
−
= h
Ograniczmy się do opisu jednowymiarowego
i załóżmy że φ(x) jest funkcją rzeczywistą,
symetryczną i szybko zanikającą z
odległością (tak jak np. funkcja 1s).
Dla dwóch atomów w odległości R mamy
Hamiltonian
)
(
)
(
2
2
R
r
V
r
V
m
H
−
+
+
∆
−
= h
.
Jeżeli atomy znajdują się w dużej odległości
to
0
)
(
)
(
≈
−
r
R
r
V
ϕ
i wzajemny wpływ atomów
można pominąć. Stan o energii E
0
jest
dwukrotnie zdegenerowany i opisany funkcjami ψ
1
=φ(r) i ψ
2
=φ(r-R). Stanem własnym
układu jest każda kombinacja liniowa stanów ψ
1
i ψ
2
.
Jeżeli zbliżamy atomy do siebie, wpływu sąsiedniego atomy nie można pominąć. Możemy
zapostulować funkcję falową postaci
2
1
ψ
ψ
ψ
b
a
+
=
.
Z równań
ψ
ψ
ψ
ψ
ψ
ψ
ψ
ψ
2
2
1
1
E
H
E
H
=
=
Otrzymujemy:
0
1
0
*
12
12
1
0
=
−
+
−
+
b
a
E
E
E
V
V
E
E
E
Gdzie
)
(
)
(
)
(
)
(
)
(
,
)
(
)
(
)
(
12
1
0
1
R
r
r
V
r
V
r
H
r
E
E
r
R
r
V
r
E
−
=
=
+
−
=
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
Zauważmy że V
12
<0
Rozwiązaniami są:
(
)
(
)
12
1
0
2
1
2
1
12
1
0
2
1
2
1
,
,
V
E
E
E
V
E
E
E
A
A
S
S
+
+
=
−
=
−
+
=
+
=
ψ
ψ
ψ
ψ
ψ
ψ
Łatwo widać że
( )
( )
0
natomiast
0
2
2
2
2
=
≠
R
A
R
S
ψ
ψ
.
Zatem energie obu stanów są teraz
różne i rozszczepienie jest zależne od
R.
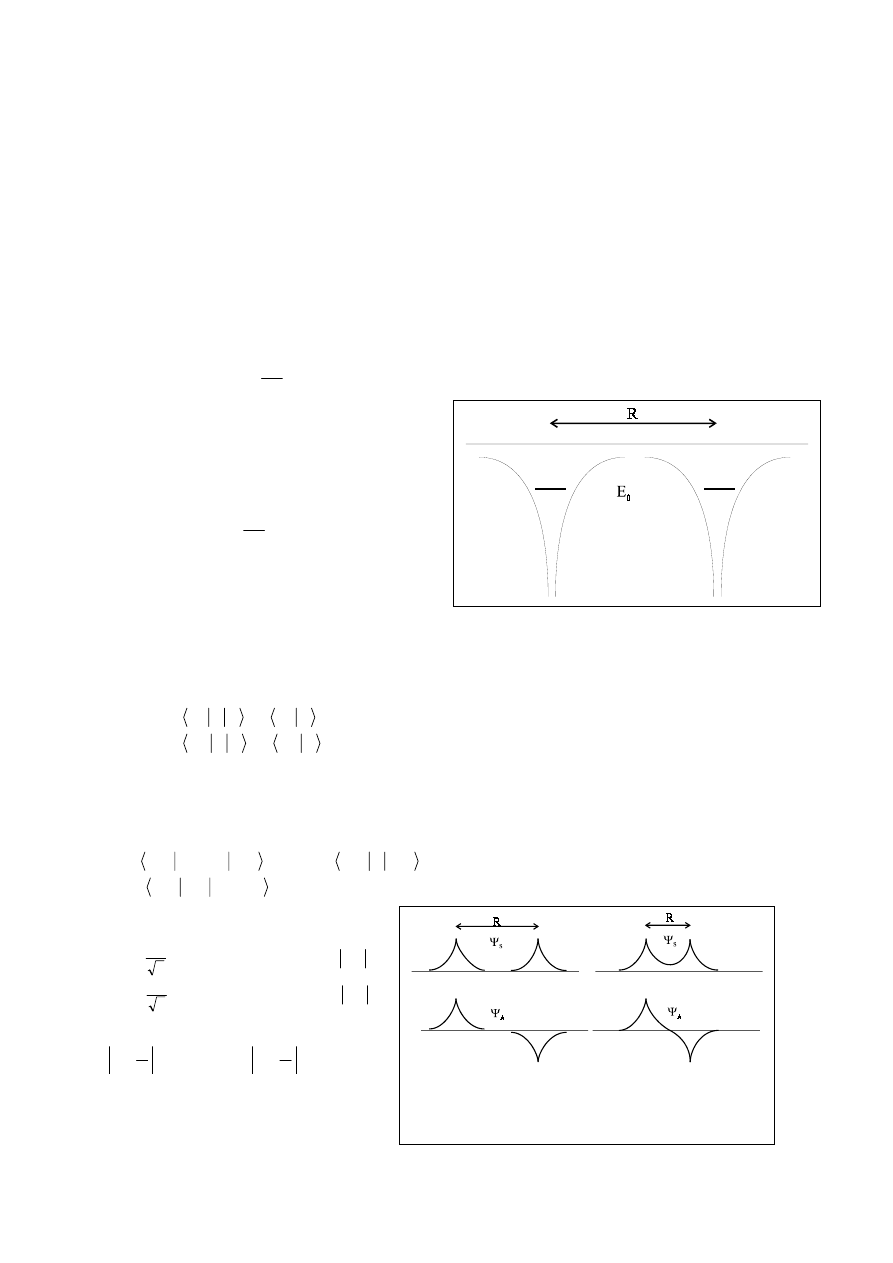
Zmiana kształtu symetrycznej i
antysymetrycznej funkcji falowej wskutek
zmniejszenia odległości pomiędzy atomami.
Przy zbliżaniu N atomów otrzymujemy rozszczepienie na N stanów. Jak zobaczymy poniżej
stany te rozciągają się w przedziale
12
2V
≈
.Stany te tworzą nieciągłe pasmo energetyczne.
Typowa szerokość pasma jest rzędu 10eV; w krysztale o objętości 1cm
3
znajduje się około
10
22
atomów. Zatem w krysztale o objętości 1cm
3
odległość pomiędzy kolejnymi stanami
pasma jest rzędu 10
-21
eV – pasmo praktycznie ciągłe.
b) Metoda ciasnego wiązania.
Rozważmy jednowymiarową sieć atomów o stałej sieci a. Postać funkcji Blocha proponujemy
w postaci:
)
(
)
(
)
(
)
(
)
(
x
u
e
na
x
e
e
na
x
e
x
ikx
n
na
x
ik
ikx
n
ikna
=
−
=
−
=
Ψ
∑
∑
−
−
ϕ
ϕ
gdzie φ(x) –funkcja falowa izolowanego atomu. Funkcja u(x) jest sumą takich samych
składników
)
( y
e
iky
ϕ
−
centrowanych na różnych punktach sieci, jest zatem funkcją
periodyczną.
Załóżmy że φ(x) jest funkcją rzeczywistą i symetryczną szybko zanikającą z odległością (tak
jak np. funkcja 1s).
Wartość energii oczekiwanej dla stanu opisanego powyżej zdefiniowaną funkcją wynosi:
.
.
.
.
)
(
)
(
)
(
)
(
)
(
el
k
el
k
x
x
x
H
x
k
E
Ψ
Ψ
Ψ
Ψ
=
gdzie ze względu na periodyczność całkowanie ograniczamy do obszaru jednej komórki
(n=0).
W obliczeniach całek ze względu na szybki zanik funkcji uwzględnimy tylko wkłady od
składników sumy odpowiadającym funkcjom centrowanym na sąsiednim komórkach.
[
] [
]
∫
−
−
−
−
+
+
+
−
+
+
+
≈
Ψ
Ψ
2
2
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
*
.
.
a
a
a
x
e
x
a
x
e
H
a
x
e
x
a
x
e
dx
x
H
x
ika
ika
ika
ika
el
k
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
Wykorzystując symetryczność funkcji φ(x) i potencjału V(x) otrzymujemy:
)
cos(
)
(
)
(
.
.
ka
B
A
x
H
x
el
k
+
=
Ψ
Ψ
gdzie:
.
.
.
.
.
.
)
(
)
(
)
(
)
(
)
(
)
(
el
k
el
k
el
k
x
H
a
x
a
x
H
x
B
x
H
x
A
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
−
+
+
=
=
Analogicznie jak poprzednio B<0.
Analogicznie
1
,
)
cos(
)
(
)
(
.
.
≈
+
=
Ψ
Ψ
C
ka
D
C
x
x
el
k
Zakładając, że B<<A i D<<C mamy
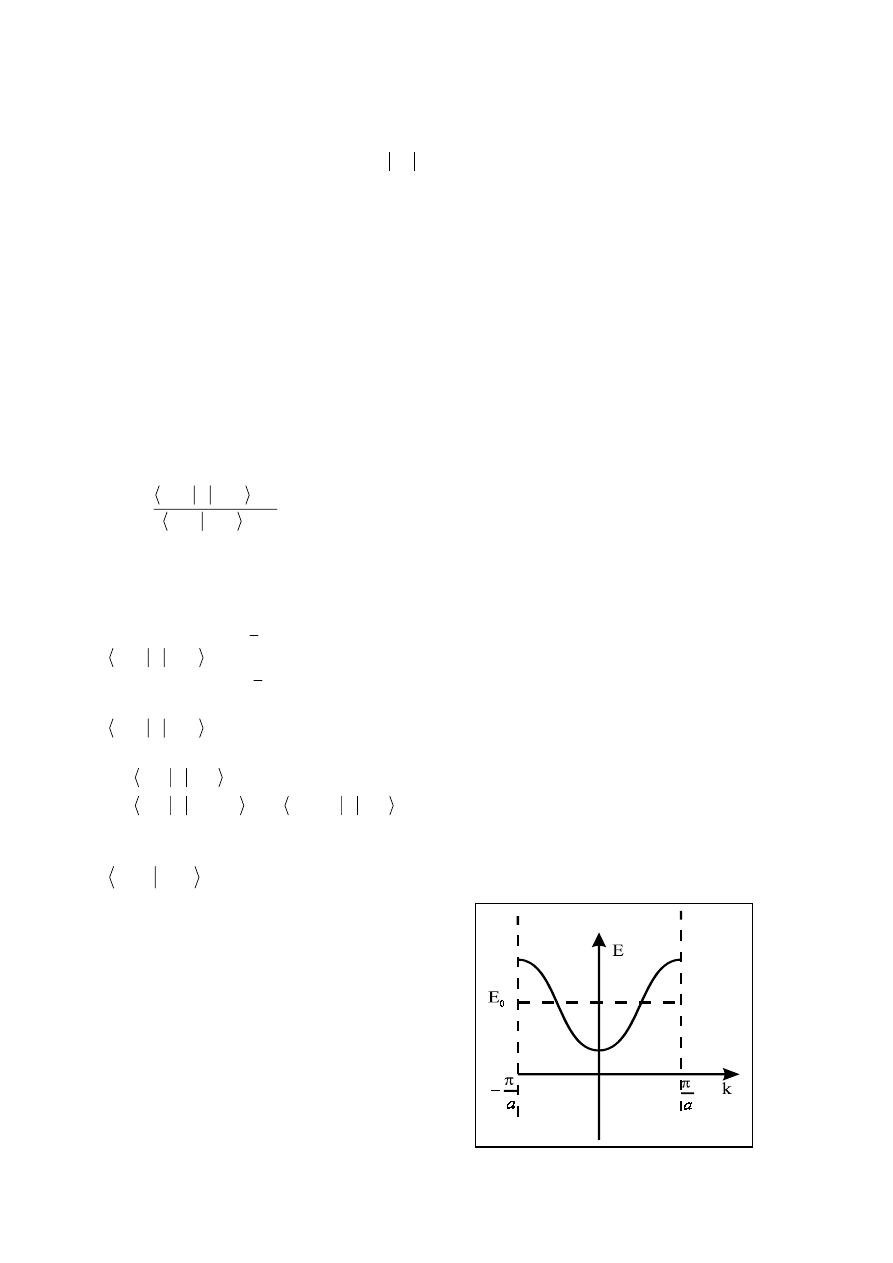
E(k)=E
0
-Mcos(ka)
Otrzymujemy pasmo energetyczne rozciągające
się w zakresie od E
0
-M dla k=0 do E
0
+M dla
k=±π/a.
Dla k=0 otrzymany stan jest analogiem stanu
symetrycznego dla rozważanego powyżej
przypadku dwóch atomów a dla k=±π/a - stanu
antysymetrycznego.
Wyszukiwarka
Podobne podstrony:
(W7a Stale do kszta t na zimno cz I [tryb zgodno ci])
ulog w7a
W7a
ekonomika w7a
w7a
(W7a Stale do kszta t na zimno cz I [tryb zgodno ci])
FPiM w3
FPiM w7b
FPiM w6
FPiM w1b
FPiM w7c
FPiM w1a
FPiM w4
FPiM w5
FPiM w2
więcej podobnych podstron