Независимый московский

университет

Московский центр непрерывного

математического образования

Высший колледж математики

А. Г. Хованский

Комплексный анализ

МЦНМО, ВКМ НМУ 2004

Аскольд Георгиевич Хованский

А. Г. Хованский

Комплексный анализ. — М: МЦНМО: ВКМ НМУ, 2004. — 48 c.

Предисловие

Этот семестровый курс читался в НМУ весной 2003 года и пред-

назначался второкурсникам. Уровень подготовки слушателей был раз-
ным. Раз в неделю была двухчасовая лекция, за которой следовал двух-
часовой семинар (имеются в виду академические часы). На лекциях, с
одной стороны, обсуждалась общая картина и связи комплексного ана-
лиза с другими областями математики. С другой стороны, основные
теоремы разбивались на короткие, понятные сами по себе утвержде-
ния, которые обяснялись шаг за шагом. После лекции эти утверждения
включались в списки задач, которые раздавались слушателям и обсу-
ждались на семинарах. Семинары вели В. А. Кисунько, И. А. Пушкарь
и С. П. Чулков. Они отдельно обсуждали с каждым студентом каждую
решенную им задачу.

Экзамен состоял из теоретического зачета и письменной домашней

контрольной. Зачет шел в течение всего семестра: студенты сдавали
решенные ими задачи на каждом семинаре и в течение нескольких до-
полнительных занятий в конце курса. Задачи для письменного экзаме-
на — рассчитанной на одну неделю домашней письменной работы — мы,
в основном, заимствовали из предыдущих письменных экзаменов по
комплексному анализу в НМУ.

Здесь приводятся в слегка отредактированном виде задачи, которые

мы обсуждали в течение семестра и которые составляли значительную
часть курса. Пункты 15, 16 и 18 написаны чуть позже и в семестре не
разбирались.

О содержании курса. Первые четыре пункта посвящены теореме

Коши и теореме Стокса. Теорема Коши опирается на теорему Стокса,
имеющую и другие многочисленные применения в теории аналитиче-
ских функций. Традиционно теорема Коши доказывается в довольно
слабых предположениях, в которых классическая теорема Стокса не-
применима. В пунктах 1–3 мы напоминаем теорему Стокса и дока-
зываем ее в довольно слабых предположениях. Теорема Коши — пря-
мое следствие этой обобщенной теоремы Стокса и простой линейной
алгебры, описывающей дифференциалы аналитических отображений
(см. п. 4).

Для доказательства интегральной формулы Коши, кроме теоремы

Коши, нужно исследовать форму

dz

z

и ее неопределенный интеграл.

Этот интеграл интересен сам по себе: он представляет собой много-
значную функцию ln z, а его обращение является однозначной функци-
ей exp z (см. п. 5).

3

В пункте 6 обсуждаются локальные свойства аналитических

функций.

Конформные отображения сферы Римана в себя являются преобра-

зованием Мбиуса. Преобразования Мбиуса определены не только на
плоскости, но и в пространстве

R

n

. Всякое преобразование Мбиу-

са — произведение инверсий. Элементарной геометрии инверсий посвя-
щен пункт 7. В пункте 8 эта геометрия применяется для определения
сферы Римана. Там же показывается, что всякая мероморфная функ-
ция на сфере Римана является рациональной функцией.

В пункте 9 обсуждаются вычеты, принцип аргумента и основная

теорема алгебры.

В пункте 10 дается представление о модели Пуанкаре пространства

Лобачевского и описываются геодезические в этой модели. Это описа-
ние использует элементарную геометрию инверсий из пункта 7. Обсу-
ждается связь геометрии Лобачевского и ТФКП, которая, в частности,
приводит к инвариантной формулировке неравенства Шварца (см. за-
дачу 10.6). Эта формулировка неравенства Шварца делает очевидным
экстремальное свойство конформного отображения, фигурирующего в
теореме Римана (см. задачу 10.8). В пункте 11 обсуждается критерий
компактности семейства аналитических функций, который нужен для
завершения доказательства теоремы Римана (см. задачу 10.17).

В пункте 12 доказывается продолжаемость отображения Римана

до границы области. Доказательство основано на принципе длин и пло-
щадей и без труда переносится на случай квазиконформных отобра-
жений.

В пункте 13 определяются римановы поверхности аналитических

функций. Показывается, что если риманова поверхность функции ком-
пактна, то функция алгебраическая.

В пункте 14 доказывается принцип симметрии Римана–Шварца и

теорема Пикара.

Дополнение 1 посвящено гармоническим функциям и их связям с

комплексным анализом. Теория гармонических функций многих пере-
менных напоминает теорию аналитических функций (см. п. 15). Ис-
пользуя обобщенную формулу Стокса, можно чуть ослабить требова-
ния гладкости в определении гармонической функции в том же духе,
как Гурса ослабил требования гладкости в определении аналитической
функции. Гармонические функции играют большую роль в математи-
ческой физике.

Аналитические функции важны для приложений, в частности, по-

тому, что их теория сильно связана с теорией гармонических функций
двух переменных. В пункте 16 обсуждается связь этих теорий и приме-

4

нения аналитических функций к теории гармонических функций двух
переменных.

В пункте 17 гармонические и субгармонические функции двух пе-

ременных применяются к теории аналитических функций. Здесь до-
казывается следующая теорема единственности.

Если аналитическая

функция в области G при стремлении к каждой точке некоторой ду-

ги, лежащей на границе области, стремится к одной и той же кон-

станте, то эта функция постоянна (см. задачи 16.10 и 16.11). Эта
теорема единственности — центральный пункт доказательства из учеб-
ника Евграфова продолжаемости конформного отображения Римана
до границы области. В процессе подготовки лекции выяснилось, что
это доказательство ошибочно (см. задачу 12.13), и продолжаемость до
границы пришлось доказывать по-другому (см. п. 12). Тем не менее,
теорема единственности интересна и сама по себе. К тому же ее до-
казательство использует замечательную формулу Йенсена и свойства
гармонических и субгармонических функций, также представляющих
самостоятельный интерес.

В дополнении 2 приводится стандартный материал о сведении гло-

бального варианта теоремы Стокса к ее локальному варианту, исполь-
зуя разбиение единицы (глобальный вариант теоремы Стокса исполь-
зовался в курсе без доказательства).

Ниже следует более подробное введение к пунктам 1–4, 15 и 18, бла-

годарности и посвящение.

Об обобщенной формуле Стокса и теореме Коши. Двумерная (плос-

кая) формула Стокса утверждает, что для ограниченной области U на
плоскости и формы ! = P (x; y) dx + Q(x; y) dy справедливо равенство

@U

! =

U

d!;

где @U — проходимая ъв направлении против часовой стрелкиё грани-

ца области U и d! =

−

@P

@y

+

@Q

@x

dx dy. Для справедливости формулы

Стокса нужно требовать некоторую гладкость формы ! и границы
@U . Можно, например, требовать, чтобы функции P и Q принадлежа-
ли классу C

1

в замыкании области U и чтобы граница @U была бы

C

1

-гладкой (или кусочно гладкой). Именно такие требования гладко-

сти накладываются в классическом варианте формулы Стокса.

Гурса придал законченную форму определению аналитической

функции: он показал, что для аналитичности комплекснозначных функ-
ций комплексного переменного достаточно требовать лишь существо-
вания первой производной в каждой точке области. Он использовал

5

найденную им форму теоремы Коши с немного меньшими требовани-
ями гладкости формы, чем обычно. С тех пор теорема Коши традици-
онно входит во все курсы комплексного анализа именно в этой форме.
Для доказательства теоремы Коши в форме Гурса классического ва-
рианта теоремы Стокса недостаточно. Мы показываем, что формула
Стокса верна, если

1) функции P и Q в каждой точке имеют дифференциалы;

2) функция

−

@P

@y

+

@Q

@x

непрерывна.

Наше доказательство, фактически, совпадает с рассуждением Гурса

(из него лишь изгоняется специфика комплексного анализа).

Формулировка и доказательство подобного обобщения теоремы

Стокса автоматически переносятся на случай k-форм на n-мерных мно-
гообразиях. Нам понадобится (при рассмотрении гармонических функ-
ций многих переменных) лишь следующий многомерный вариант этого
утверждения.

Обобщенный вариант формулы Стокса. Пусть U — компакт-

ная область с гладкой границей @U в пространстве R

n

, пусть

! = P

1

dx

2

∧ : : : ∧ dx

n

− P

2

dx

1

∧ dx

3

∧ : : : ∧ dx

n

+ : : : + (

−1)

n+1

P

n

dx

1

∧ : : :

: : :

∧ dx

n−1

— (n − 1)-форма, коэффициенты P

i

которой имеют диф-

ференциалы в замыкании области U и функция F =

@P

1

@x

1

+ : : : +

@P

n

@x

n

непрерывна в замыкании этой области. Тогда справедлива формула

Стокса

@U

! =

U

d!;

(1)

где d! = F dx

1

∧ : : : ∧ dx

n

.

В классическом варианте формулы Стокса для областей в

R

n

допол-

нительно предполагается, что функции P

1

; : : : ; P

n

принадлежат клас-

су C

1

в замыкании области U .

Обычное доказательство классического варианта формулы Стокса

не проходит для доказательства обобщенного варианта этой формулы.
Приведем хорошо известный пример аналогичной ситуации.

Пример (теорема Лагранжа). Для функции f на отрезке [a; b] суще-

ствует точка ‰ такая, что f(b) = f(a) + f

(‰)(b

− a).

Для справедливости теоремы Лагранжа нужно требовать некото-

рую гладкость функции f. Конечно, можно требовать, чтобы функ-
ция f принадлежала классу C

1

на [a; b]. Но достаточно требовать, что-

бы функция f была бы непрерывна на отрезке [a; b] и имела дифферен-
циал в каждой внутренней точке этого отрезка. Если f

непрерывна, то,

согласно формуле Ньютона–Лейбница, f(b) = f(a) +

b

a

f

(t) dt. По тео-

6

реме о среднем существует точка ‰ такая, что

b

a

f

(t) dt = f

(‰)(b

− a),

откуда и вытекает теорема Лагранжа. Если же функция f

не не-

прерывна, то она может оказаться и неинтегрируемой, и это рассу-
ждение не проходит. Здесь выручает такое соображение. Легко ви-
деть, что существует касательная к графику функции y = f(x), па-
раллельная хорде, проходящей через точки (a; f(a)) и (b; f(b)). Тогда
f(b) = f(a) + f

(‰)(b

− a), где ‰ — абсцисса точки касания.

Доказательство обобщенного варианта формулы Стокса соотносит-

ся с доказательством классического варианта этой формулы так же,
как второе из приведенных доказательств теоремы Лагранжа соотно-
сится с первым доказательством.

В курсе мы обсуждали лишь локальную формулу Стокса, т. е. фор-

мулу Стокса для стандартного квадрата на плоскости и для стандарт-
ного куба в многомерном пространстве. Формула Стокса для компакт-
ных областей с гладкой границей сводится к ее локальному варианту
при помощи разбиения единицы (см. дополнение 2).

Благодарности. Моя жена Т. В. Белокриницкая набирала и редакти-

ровала все списки задач и все варианты этой брошюры. В. А. Кисунько,
И. А. Пушкарь и С. П. Чулков весь семестр вели семинарские занятия.
Они вложили в этот курс много труда. Слушатели активно решали за-
дачи и обнаружили много неточностей и опечаток. Всем им я приношу
свою благодарность.

Посвящение. Второго ноября 2003 года исполнилось 60 лет Юлию

Сергеевичу Ильяшенко, с которым мы дружим без малого полвека. Эта
брошюра посвящается Юлию Сергеевичу.

1. Теорема Лагранжа для функций множеств

Пусть A — некоторый класс подмножеств пространства

R

n

. Мы все-

гда будем считать, что для всех множеств из класса A определено по-
нятие обема. Мы будем обозначать через V (X) обем множества X.

Для дальнейшего важен следующий пример: A состоит из кубов

пространства

R

n

, грани которых параллельны координатным гипер-

плоскостям и которые лежат внутри стандартного единичного куба
0

x

1

1; : : : ; 0 x

n

1 (особенно важен случай n = 2). Можно счи-

тать, что A — класс подмножеств из этого примера.

Разбиением множества ´ ∈ A такого, что V (´) = 0, называется его

представление в виде ´ =

m

i=1

´

i

, где

1) ´

i

∈ A, i = 1; : : :; m;

7

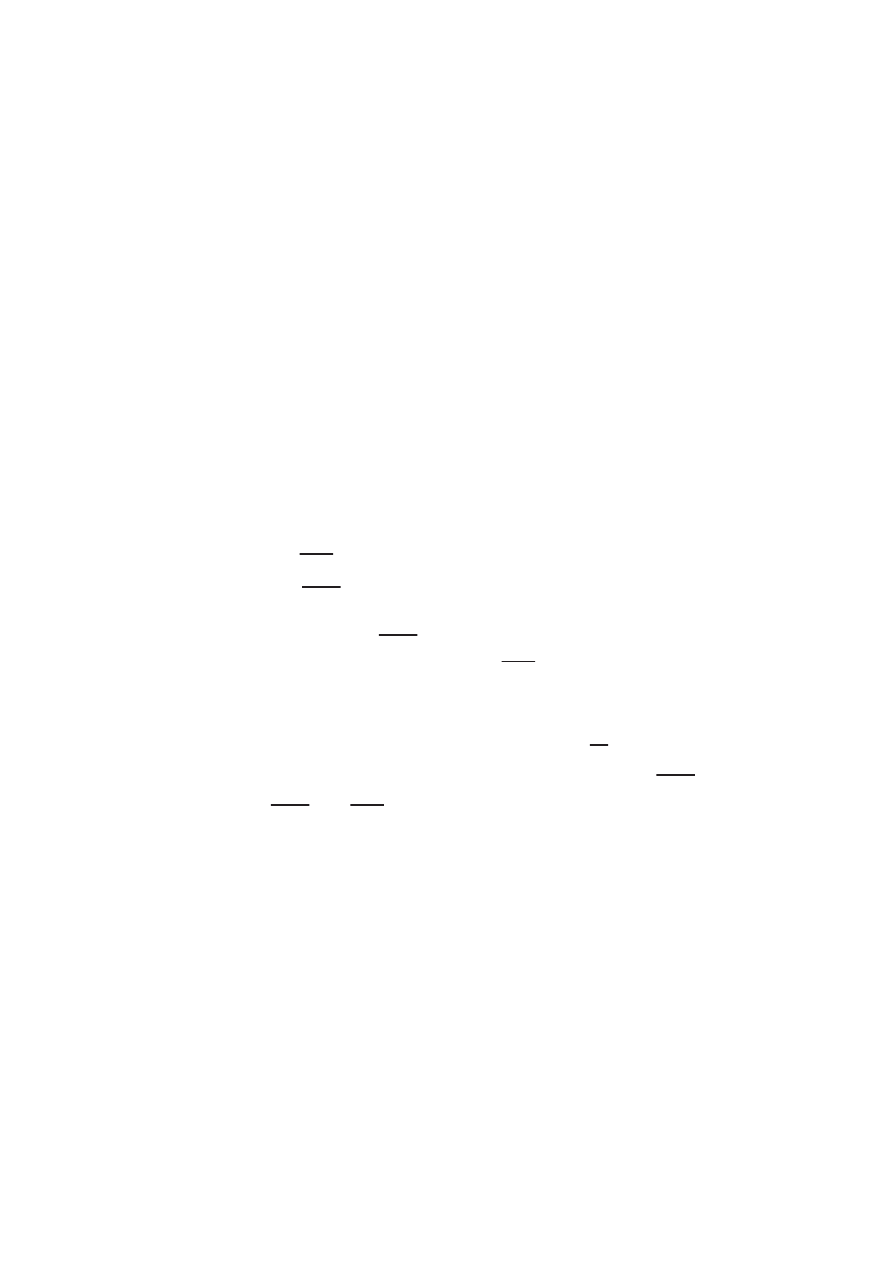
2) V (´

i

)

= 0, i = 1; : : :; m;

3) V (´

i

∩ ´

j

) = 0, 1

i < j m.

Скажем, что класс множеств A является

классом с разбиениями,

если для каждого множества ´

∈ A такого, что V (´) = 0, существует

его разбиение ´ =

´

i

, для которого диаметр каждого множества ´

i

не больше чем половина диаметра множества ´.

Класс кубов в пространстве

R

n

(см. выше) очевидно является клас-

сом множеств с разбиениями.

Рассмотрим некоторую функцию F : A

→ R

p

, сопоставляющую ка-

ждому множеству X из некоторого класса с разбиением A вектор F (X)
пространства

R

p

.

Скажем, что функция F является

функцией типа меры, если для ка-

ждого множества ´ и каждого его разбиения ´ =

´

i

, где ´; ´

i

∈ A,

справедливо равенство F (´) =

F (´

i

).

Задача 1.1. Пусть ´ =

m

i=1

´

i

— разбиение множества ´, и V (´)

= 0.

Пусть выполняется равенство F (´) =

F (´

i

). Тогда

1) точка

1

V (´)

F (´) пространства

R

p

лежит внутри выпуклой обо-

лочки точек

1

V (´

i

)

F (´

i

) этого пространства;

2) если в пространстве

R

p

есть скалярное произведение (или нор-

ма), то среди векторов

1

V (´

i

)

F (´

i

) существует хотя бы один вектор,

имеющий не меньшую длину, чем вектор

1

V (´)

F (´).

Задача 1.2. Пусть функция F : A → R

p

является функцией типа

меры. Тогда для каждого ´

∈ A такого, что V (´) = 0, существует

последовательность вложенных множеств ´

⊃ ´

1

⊃ : : : ⊃ ´

m

⊃ : : : та-

ких, что 1) ´

i

∈ A; 2) V (´

i

) > 0; 3) диаметр ´

m

1

2

m

(диаметр ´);

4)

существует

(конечный

или

бесконечный)

предел

lim

i→∞

F (´

i

)

V (´

i

)

;

5) lim

i→∞

F (´

i

)

V (´

i

)

F (´)
V (´)

. Здесь a обозначает длину вектора a в

пространстве

R

p

.

Определение 1. Скажем, что последовательность множеств ´

1

; : : :

: : : ; ´

m

; : : :

сходится к точке a (обозначение: lim

i→∞

´

i

= a), если для

любого " > 0 существует номер N такой, что все множества ´

i

при

i > N лежат в "-окрестности точки a.

Определение 2. Пусть F : A → R

p

— функция типа меры. Скажем,

что F

имеет производную F

A

(a)

∈ R

p

по A в точке a, если для лю-

бой такой последовательности множеств ´

1

⊃ : : : ⊃ ´

m

⊃ : : : из A, что

8

V (´

i

)

= 0 и lim

i→∞

´

i

= a, справедливо равенство

lim

i→∞

F (´

i

)

V (´

i

)

= F

A

(a):

Задача 1.3. Пусть A — класс множеств области U простран-

ства

R

n

, для которых определено понятие обема. Пусть f — не-

прерывная функция на A со значениями в пространстве

R

p

. Рас-

смотрим функцию F на A, сопоставляющую каждому ´

∈ A вектор

F (´) =

´

f(x) dx

1

: : : dx

n

. Тогда

1) F является функцией типа меры;
2) в каждой точке a

∈ U существует F

A

(a), причем F

A

(a) = f(a).

Задача 1.4. 1) (ъТеорема Лагранжаё.) Пусть функция F : A → R

p

является функцией типа меры и имеет производную по A в каждой
точке a, причем F

A

(a) = 0. Тогда для каждого ´

∈ A справедливо ра-

венство F (´) = 0.

2) Пусть функции типа меры F : A

→ R

p

и G : A

→ R

p

имеют про-

изводные по A в каждой точке a, причем F

A

(a)

≡ G

A

(a). Тогда функ-

ции F и G совпадают, т. е. для каждого множества ´

∈ A справедливо

равенство F (´) = G(´).

3) (ъФормула Ньютона–Лейбницаё.) Если F

A

— непрерывная функ-

ция, то

F (´) =

´

F

A

dx

1

∧ : : : ∧ dx

n

:

Задача 1.5. Пусть A — класс отрезков на прямой, лежащих вну-

три фиксированного отрезка [a; b], и пусть f : [a; b]

→ R

p

— произволь-

ная функция. Определим функцию F : A

→ R формулой F ([c; d]) =

= f(d)

− f(c). Показать, что

1) функция F является функцией типа меры;
2) существование производной F

A

(a) эквивалентно дифференциру-

емости функции f в точке a, причем F

A

(a) = f

(a);

3) если функция f дифференцируема в каждой точке отрезка [a; b],

причем f

≡ 0, то f(a) = f(b) (см. задачу 1.4, п. 1);

4) если функция f дифференцируема в каждой точке отрезка и f

непрерывна на отрезке, то f(b)

− f(a) =

b

a

f

(‰) d‰ (см. задачу 1.4, п. 3).

2. Формула Стокса для линейных форм в единичном кубе

Начнем с двумерного случая. Обозначим через ´ стандартный ква-

драт 0

x 1, 0 y 1 на плоскости.

9

Задача 2.1. Пусть функция Q: ´ → R

p

обладает следующими свой-

ствами. Во-первых, функции Q

0

и Q

1

от переменной y, определенные

при 0

y 1 соотношениями Q

0

(y) = Q(0; y), Q

1

(y) = Q(1; y), являют-

ся интегрируемыми функциями. Во-вторых, выполняется тождество
Q

1

− Q

0

≡ C, где C — постоянный вектор. Тогда

@´

Q dy = C. Ана-

логично, если функции P

0

и P

1

, определенные при 0

x 1 соотноше-

ниями P

0

(x) = P (x; 0) и P

1

(x) = P (x; 1), интегрируемы и P

1

− P

0

= C,

то

@´

P dx =

−C.

Задача 2.2. Для любых постоянных векторов A

1

, A

2

, A

3

, B

1

, B

2

, B

3

пространства

R

p

справедливо равенство

@´

(A

1

+ A

2

x + A

3

y) dx + (B

1

+ B

2

x + B

3

y) dy = (B

2

− A

3

):

Задача 2.3. Пусть P и Q — непрерывные функции в области ´ на

плоскости со значениями в

R

p

, причем

P < M и Q < M. Тогда для

всякого контура ‚ на плоскости, длина которого равна L, справедлива
оценка

‚

P (x; y) dx + Q(x; y) dy

2ML:

Перейдем к многомерной ситуации. Обозначим через ´ стандарт-

ный куб 0

x

1

1; : : : ; 0 x

n

1 в пространстве R

n

.

Задача 2.4. Пусть ! = P

1

dx

2

∧ : : :∧ dx

n

− P

2

dx

1

∧ dx

3

∧ : : :∧ dx

n

+ : : :

: : : + (

−1)

n+1

P

n

dx

2

∧ : : : ∧ dx

n

, где P

i

— линейные неоднородные функ-

ции, т. е. P

i

= A

i

+ A

i;1

x

1

+ : : : + A

i;n

x

n

, где A

i

и A

i;j

— постоянные

векторы в пространстве

R

p

. Тогда

@´

! =

´

d!, т. е.

@´

! = A

1;1

+ : : :

: : : + A

n;n

.

Следующие две задачи в дальнейшем не понадобятся.
Задача 2.5. Пусть P

1

— функция класса C

1

на ´. Тогда для куба ´

и формы ! = P

1

dx

2

∧ : : : ∧ dx

n

справедлива формула Стокса, т. е.

@´

P

1

dx

2

∧ : : : ∧ dx

n

=

´

@P

1

@x

1

dx

1

∧ : : : ∧ dx

n

:

Указание. Проинтегрировать функцию

@P

1

@x

1

по переменной x

1

и вос-

пользоваться формулой Ньютона–Лейбница.

Замечание. При доказательстве обобщенной формулы Стокса мы не

используем формулы Ньютона–Лейбница, но доказываем ее многомер-
ное обобщение (ср. задачу 1.4, п. 3).

Задача 2.6. Доказать формулу Стокса в кубе ´ для формы ! с ко-

эффициентами класса C

1

. Почему это доказательство не проходит для

доказательства обобщенной формулы Стокса в кубе ´?

10

3. Обобщенная формула Стокса в единичном кубе

Задача 3.1. Пусть A — класс квадратов на плоскости, лежащих

внутри стандартного единичного квадрата ´, стороны которых па-
раллельны координатным осям. Пусть P и Q — непрерывные функ-
ции на квадрате ´ со значениями в

R

p

. Рассмотрим функцию на A,

сопоставляющую каждому квадрату ´

0

∈ A вектор F (´

0

), равный

@´

0

P dx + Q dy. Тогда

1) функция F : A

→ R

p

является функцией типа меры;

2) если функции P и Q имеют дифференциал в точке a, то функ-

ция F дифференцируема по A в точке a, причем F

A

(a)=

−

@P

@y

(a)+

@Q

@x

(a).

Указание. См. задачи 2.2 и 2.3.

Задача 3.2 (обобщенная формула Стокса для квадрата). Пусть

1) функции P и Q, принимающие значения в

R

p

, непрерывны в ква-

драте ´, 2) в каждой точке квадрата ´ каждая из этих функ-

ций имеет дифференциал, 3) функция

−

@P

@y

+

@Q

@x

непрерывна в ´.

Тогда

@´

P dx + Q dy =

´

−

@P

@y

+

@Q

@x

dx

∧ dy. В частности, если

−

@P

@y

+

@Q

@x

≡ 0, то

@´

P dx + Q dy = 0.

Указание. См. задачу 3.1 и п. 3 в задаче 1.4.

Задача 3.3 (обобщенная формула Стокса для куба). Пусть ! =

= P

1

dx

2

∧ : : : ∧ dx

n

− P

2

dx

1

∧ dx

3

∧ : : : ∧ dx

n

+ : : : + (

−1)

n+1

P

n

dx

1

∧ : : :

: : :

∧ dx

n−1

, где P

i

— непрерывные функции в кубе ´ пространства

R

n

.

Пусть функции P

1

; : : : ; P

n

имеют дифференциалы в каждой точке ку-

ба ´, причем функция F =

@P

1

@x

1

+ : : : +

@P

n

@x

n

непрерывна в ´. Тогда

@´

! =

´

F dx

1

∧ : : : ∧ dx

n

.

Ниже мы используем обобщенную формулу Стокса не только для ку-

бов, но и для компактных областей пространства

R

n

, имеющих глад-

кую границу (в основном, нам важен случай n = 2). Переход от куба
к области с гладкой границей совершенно стандартен и делается при
помощи разбиения единицы. Для полноты картины мы приводим это
рассуждение в пункте 18 (дополнение 2).

Напомним формулу Стокса для 1-форм на гладких кривых.
Задача 3.4. Пусть ! = P

1

dx

1

+ : : : + P

n

dx

n

, где P

1

; : : : ; P

n

— непре-

рывные функции в области U пространства

R

n

со значениями в про-

странстве

R

p

. Допустим, что для любого замкнутого пути ‚ в обла-

сти U справедливо равенство

‚

! = 0. Фиксируем точку x

0

∈ U. Опре-

делим функцию F в области U следующим равенством: F (a) =

‚

!, где

11

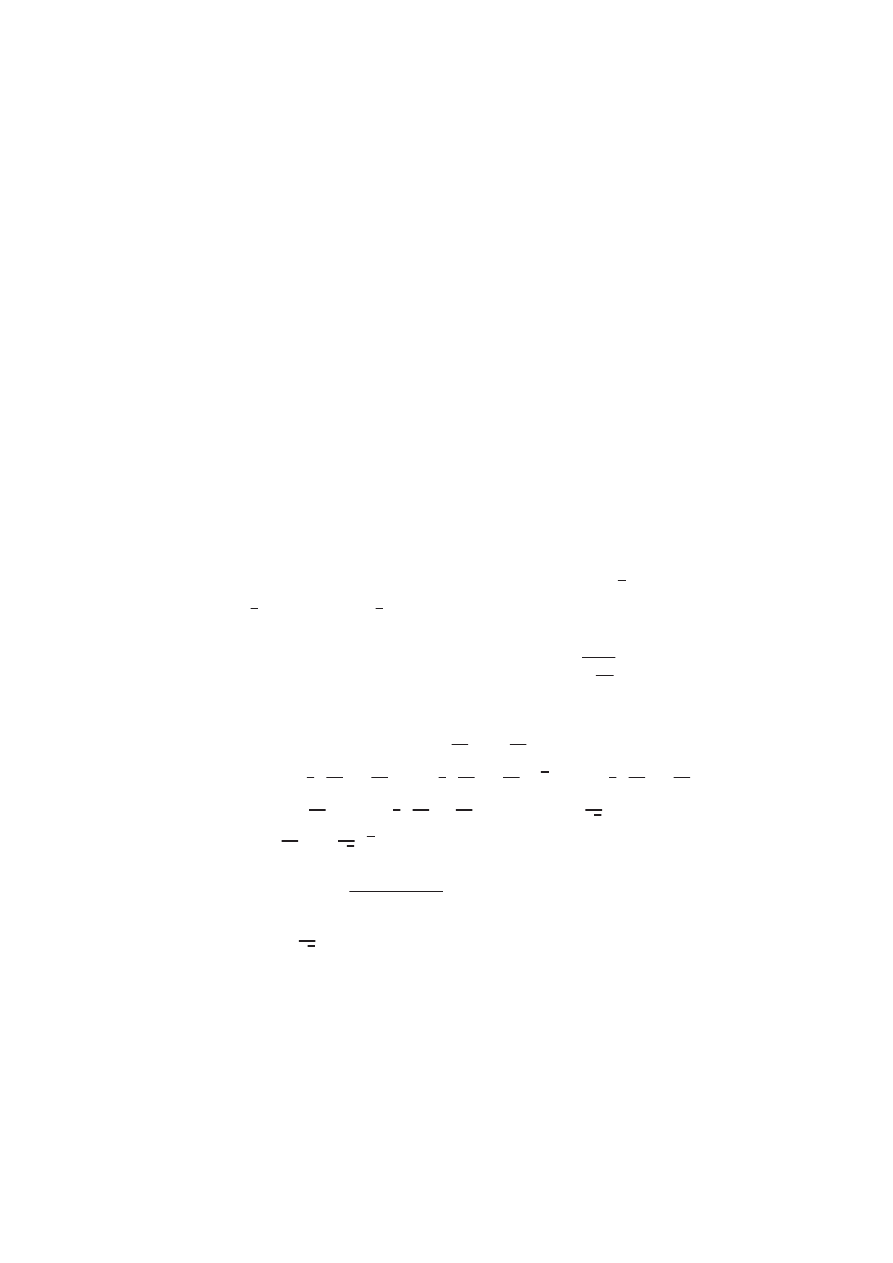
‚ — любая кривая в области U , начинающаяся в точке x

0

и заканчива-

ющаяся в точке a. Доказать, что

1) функция F определена корректно, т. е. не зависит от выбора ‚;
2) функция F в каждой точке имеет дифференциал dF и выполнено

равенство

dF = P

1

dx

1

+ : : : + P

n

dx

n

:

Задача 3.5. Пусть F — функция в области U со значениями в про-

странстве

R

p

, имеющая непрерывные частные производные P

1

; : : : ; P

n

,

и dF = P

1

dx

1

+ : : : + P

n

dx

n

. Тогда

‚

P

1

dx

1

+ : : : + P

n

dx

n

= F (b)

− F (a),

где b и a — конец и начало кривой ‚

∈ U.

4. Линейная алгебра и теорема Коши

В этом пункте мы будем отождествлять плоскость

R

2

с комплекс-

ной плоскостью (синоним: ъкомплексная прямаяё), сопоставляя точке
(x; y) комплексное число z = x + iy. Рассмотрим вещественно линейное
отображение A :

R

2

→ R

2

из вещественной плоскости в себя.

Задача 4.1. Отображение A(x; y) = P

1

x + P

2

y, где P

1

; P

2

∈ C , един-

ственным образом записывается в виде A(x; y) = Q

1

z + Q

2

z. При этом

Q

1

=

1
2

(P

1

− iP

2

), Q

2

=

1
2

(P

1

+ iP

2

). Определитель матрицы отображе-

ния A положителен, если

|Q

1

| > |Q

2

|, отрицателен, если |Q

1

| < |Q

2

|, и

равен нулю, если

|Q

1

| = |Q

2

|. Если |Q

1

| = |Q

2

| = 0, то отображение A

переводит в нуль прямую z = –z

0

, где –

∈ R, а z

0

=

−

Q

1

Q

2

.

Обозначения. Пусть U — область на плоскости и f : U → R

2

— диф-

ференцируемое отображение (т. е. у отображения f в каждой точке су-

ществует дифференциал), и df =

@f
@x

dx +

@f
@y

dy — его дифференциал.

Имеем: df =

1
2

@f
@x

− i

@f
@y

dz +

1
2

@f
@x

+ i

@f
@y

dz. Число

1
2

@f
@x

− i

@f
@y

обозначается

@f

@z

, а число

1
2

@f
@x

+ i

@f
@y

обозначается

@f

@z

. По определе-

нию df =

@f

@z

dz +

@f

@z

dz.

Производной f

(a) комплекснозначной функции f в точке a

∈ C на-

зывается число lim

z→0

f (a + z) − f (a)

z

.

Задача 4.2. 1) Если отображение f : U → R

2

имеет дифференциал

в точке a и

@f

@z

(a) = 0, то, во-первых, дифференциал является поворо-

том (на некоторый угол ¸) с растяжением (в – раз, где – — некоторое

12

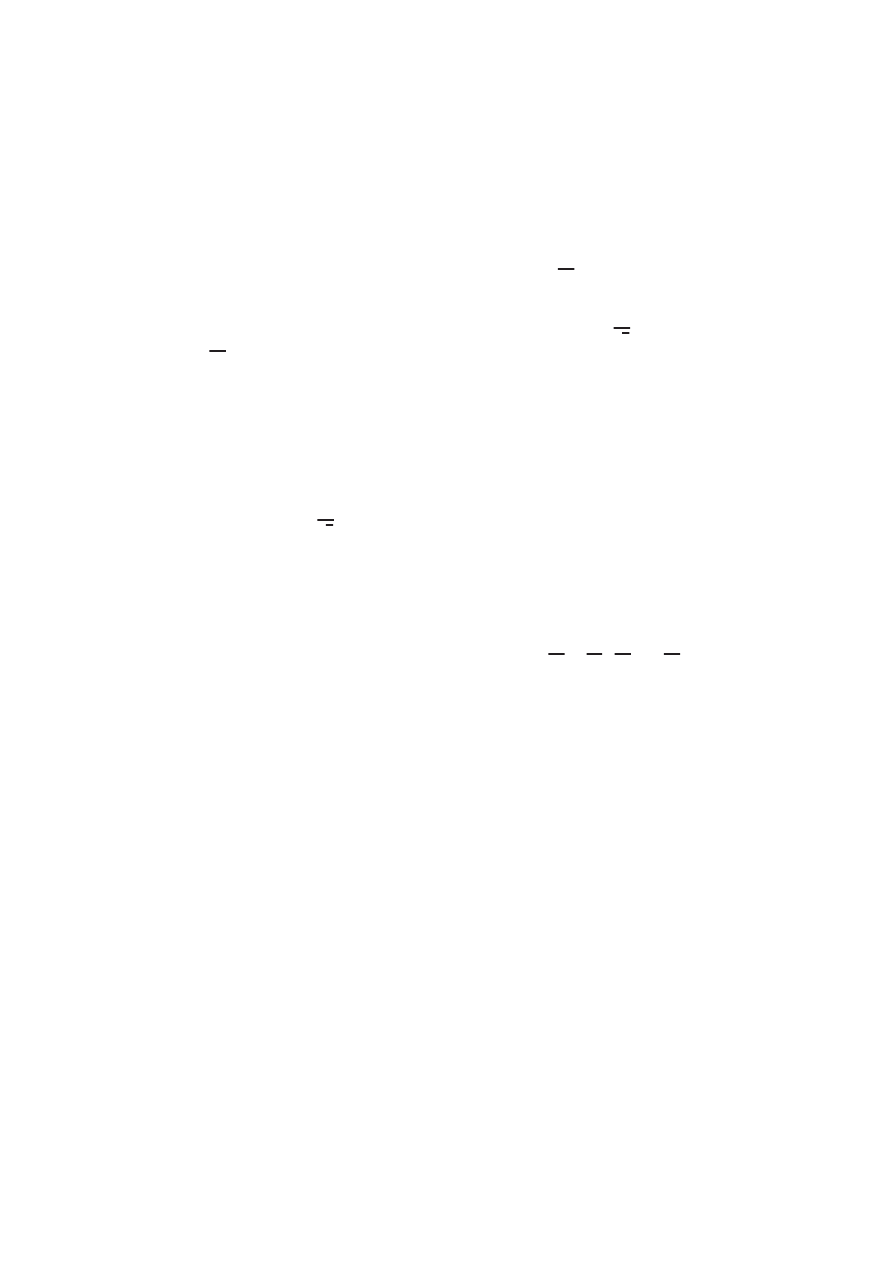
неотрицательное число), во-вторых, у комплекснозначной функции f

существует производная f

(a). При этом f

(a) =

@f

@z

(a), arg f

(a) = ¸,

|f

(a)

| = –.

2) Обратно, если производная существует, то отображение f

имеет дифференциал в точке a. При этом, во-первых,

@f

@z

(a) = 0 и

@f

@z

(a) = f

(a) и, во-вторых, дифференциал этого отображения — пово-

рот (на угол arg f

(a)) с растяжением (в

|f

(a)

| раз).

Задача 4.2 доказывает эквивалентность следующих двух опреде-

лений.

Определение 1 (аналитическая функция по Гурса). Функция f на-

зывается

аналитической в области U, если в каждой точке области U

у функции f существует комплексная производная.

Определение 2. Функция f называется аналитической в области U,

если в каждой точке области U отображение f : U

→ C дифференци-

руемо, причем

@f

@z

≡ 0 (т. е. дифференциал отображения — поворот с

растяжением).

Задача 4.3. Функция f аналитична в области U, если и только если

у формы ! = f(z) dz = f(z) dx + if(z) dy коэффициенты имеют первые
дифференциалы и d!

≡ 0.

Задача 4.4. Функция f =u+iv аналитична в области U, если и только

если функции u, v имеют первые дифференциалы в каждой точке обла-

сти и выполняются

соотношения Коши–Римана

@u
@x

≡

@v
@y

,

@u
@y

≡ −

@v
@x

.

Определение 3. Функция f называется аналитической вплоть до

границы области U, если функция f определена и аналитична в неко-
торой большей области V , содержащей замыкание области U .

Задача 4.5 (Теорема Коши). Для всякой функции f, аналитической

вплоть до границы ограниченной области U с гладкой границей @U ,
справедливо тождество

@U

f dz = 0:

Указание. Воспользоваться задачей 4.3 и обобщенной формулой

Стокса для областей с гладкой границей.

Задача 4.6. Пусть f(z) — аналитическая функция в односвязной

области U . Проверить, что функция F (z) =

z

z

0

f(z) dz определена кор-

ректно и аналитична. Здесь

z

z

0

f(z) dz — это интеграл функции f по

любой лежащей в области U гладкой кривой, начинающейся в точке z

0

и заканчивающейся в точке z. Доказать, что F

(z) = f(z).

Указание. Воспользоваться теоремой Коши и задачей 3.4.

13

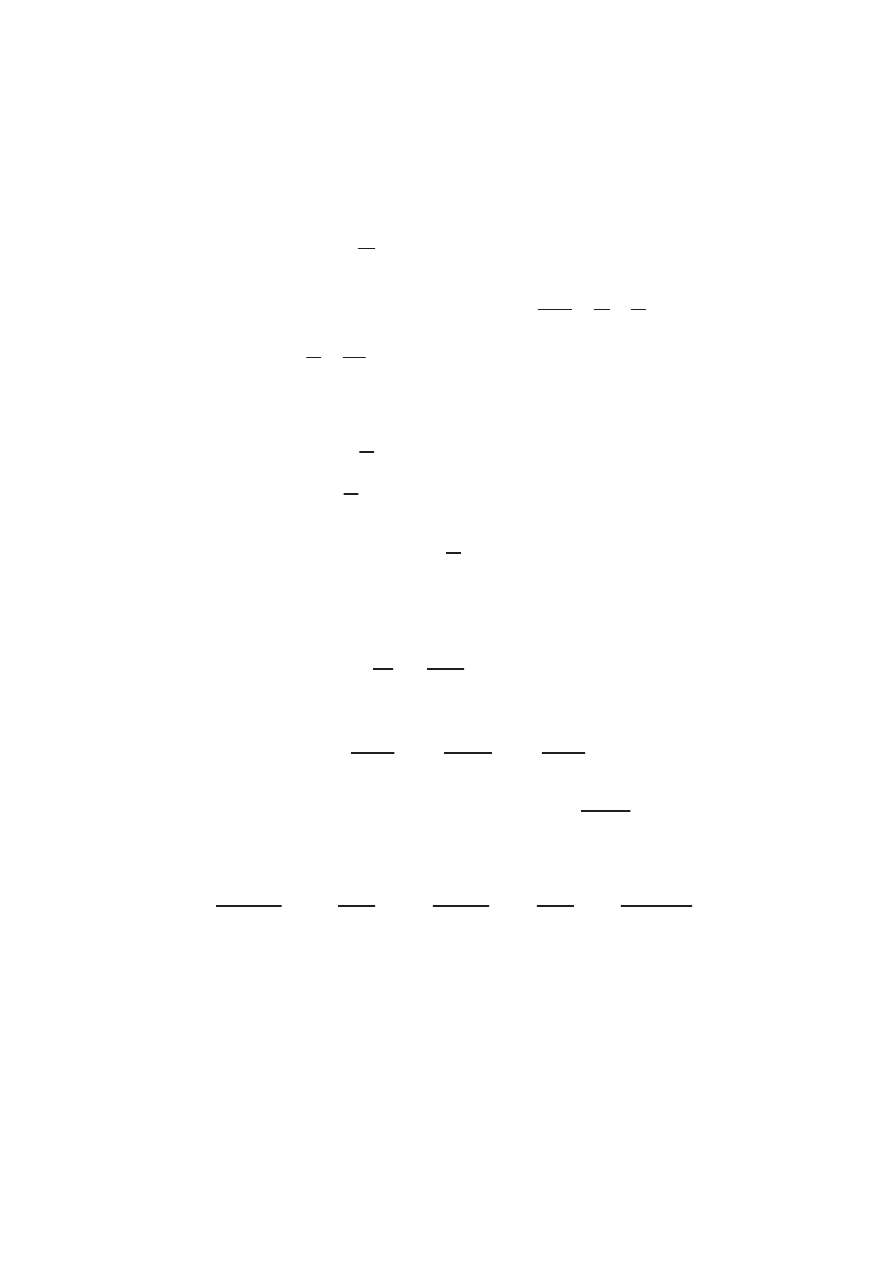
5. Форма

dz

z

и интегральная формула Коши

Задача 5.1. 1) Пусть f : U → C , g : U → C — любые гладкие комплекс-

нозначные функции на области U

⊂ R

n

. Тогда

d(f g)

f g

=

df

f

+

dg

g

.

2) Применить 1) к функциям f =

|z| и g = cos ’ + i sin ’ и доказать

соотношение

dz

z

=

d|z|

|z|

+ i d’, где ’ = arg z.

Задача 5.2. 1) Пусть область U на плоскости не охватывает точку 0

и содержит точку 1, и пусть arg : U

→ R—однозначная ветвь аргумента

на области U (для которой arg 1 = 0). Тогда

z

1

dz

z

= ln

|z| + i arg z (при z ∈ U):

2) Интеграл

‚

dz

z

по контуру ‚, один раз обходящему точку нуль

(например, по границе ‚ = @U выпуклой области U , содержащей точку
нуль), равен 2ıi.

Мы вернемся к интегралу

z

1

dz

z

в задачах 5.12–5.14. А сейчас пе-

рейдем к интегральной формуле Коши.

Задача 5.3 (интегральная формула Коши). Пусть f — функция, ана-

литическая вплоть до границы ограниченной области U , имеющей глад-
кую границу @U . Тогда справедлива следующая интегральная формула
Коши:

1

2ıi

@U

f (z)

z

− z

0

dz = f(z

0

):

Указание. Представить область U в виде обединения малого за-

мкнутого круга B с центром в точке z

0

и области V = U

\ B. Тогда

@U

f (z) dz

z

− z

0

=

@V

f (z) dz

(z − z

0

)

+

@B

f (z) dz

z

− z

0

:

Первый из этих интегралов вычисляется при помощи теоремы Коши.

Второй интеграл мало отличается от интеграла

@B

f (z

0

) dz

z

− z

0

, который

вычислен в задаче 5.2.

Задача 5.4. Пусть ´ — комплексное число, причем |´| < |z − z

0

|. Тог-

да справедливо равенство

1

z

− z

0

− ´

=

1 +

´

z

− z

0

+ : : : +

´

n

(z − z

0

)

n

+ : : :

1

z

− z

0

=

∞

n=0

´

n

(z − z

0

)

n+1

;

причем ряд, стоящий в правой части равенства, сходится равномерно
в каждой области

|z − z

0

| > |´| + " при " > 0.

14

Задача 5.5. В условиях задачи 5.3 доказать равенство

f

(n)

(z

0

) =

n!

2ıi

@U

f (z) dz

(z − z

0

)

n+1

:

Указание. См. задачу 5.3.

Задача 5.6. Пусть, в условиях задачи 5.3, R — расстояние от точки z

0

до границы области. Доказать, что при

|´| < R справедливо равенство

f(z

0

+ ´) = f(z

0

) + f

(z

0

)´ + : : : +

1

n!

f

(n)

(z

0

)´

n

+ : : : :

Показать, что ряд сходится равномерно в области

|´| < R − ", где

" — любое положительное число.

Указание. См. задачи 5.3 и 5.4.

Задача 5.7. Показать, что производная аналитической функции

является аналитической функцией.

Указание. См. задачу 5.5.

Задача 5.8 (теорема Морера). Пусть f(z) — непрерывная комплекс-

нозначная функция в области U , причем интеграл формы f(z) dz по
любому замкнутому контуру, лежащему в области U , равен нулю. То-
гда функция f аналитична в области U .

Указание. См. задачи 3.4 и 5.7.

Задача 5.9. Пусть f — равномерный предел аналитических функций

в области U . Тогда f — аналитическая функция в области U .

Указание. Воспользоваться теоремой Морера.

Задача 5.10 (оценки производных с потерей области). Пусть функ-

ция f аналитична в области U , L — длина границы области U ,
и M — максимум модуля функции f в U . Тогда справедлива оценка

f

(k)

(z)

k! ML

2ır(z)

k+1

, где r(z) — расстояние от точки z до границы

области.

Указание. См. задачу 5.5.

Задача 5.11 (теорема Лиувилля). Функция, аналитическая на

всм

C , модуль которой ограничен, является константой.

Указание. См. задачу 5.10 для k = 1.
Задача 5.12. Многозначная аналитическая функция ln z =

z

1

dz

z

=

= ln

|z| + i arg z (функция arg z определена с точностью до слагаемого

2kı) имеет однозначную обратную функцию: если ln z = u = u

1

+ iu

2

,

то z = e

u

1

(cos u

2

+ i sin u

2

). Эта функция называется

экспонентой.

Задача 5.13. Из задачи 6.1 будет следовать, что функция y = exp z

аналитична (во всей комплексной плоскости). Проверить, что y

= y и

что y

(n)

= y для всех n. Ряд Тейлора exp z сходится к exp z во всей

15

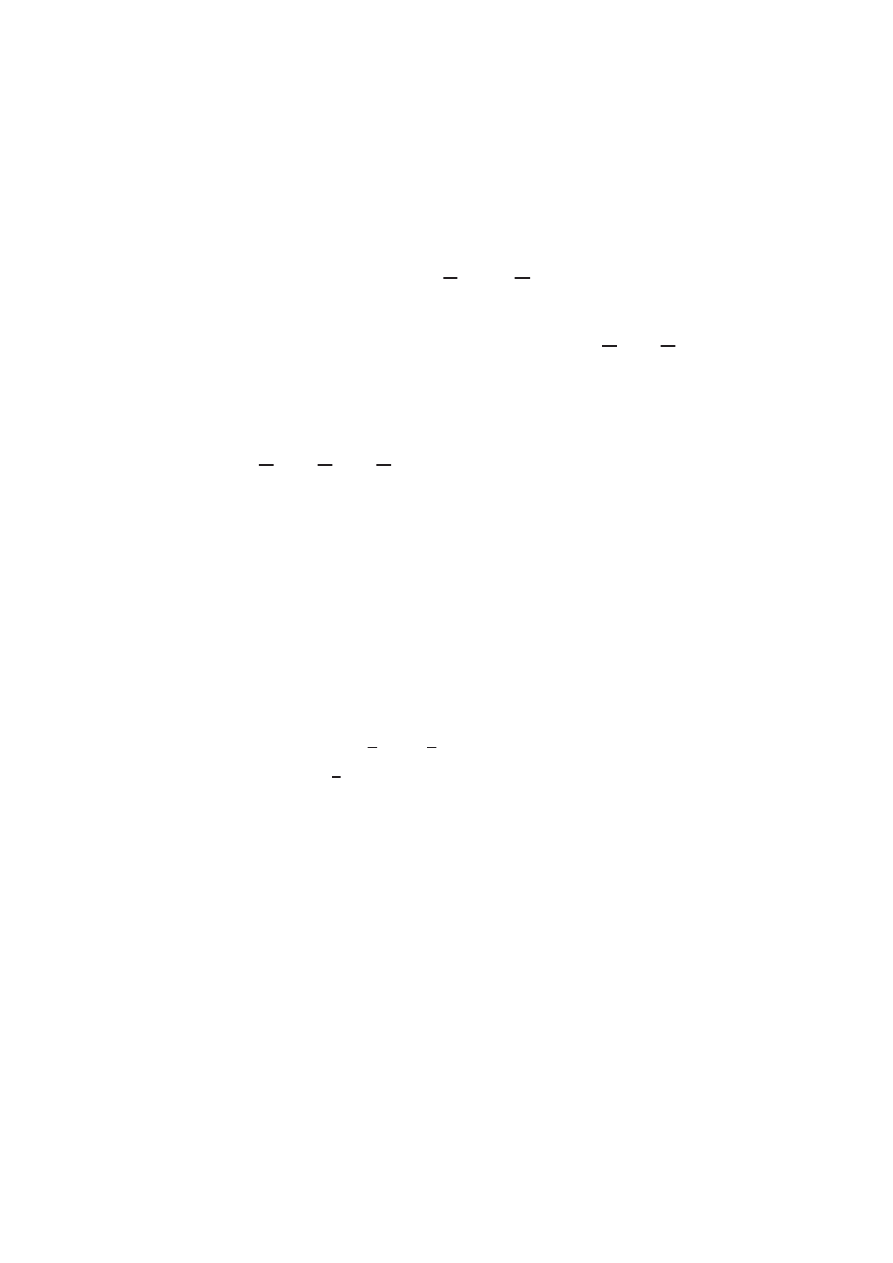
комплексной области (см. задачу 5.6). Поэтому

exp z = 1 + z +

z

2

2

+ : : : +

z

n

n!

+ : : : :

Задача 5.14. Пусть ‚ : [0; 1] → (C \ 0) — кривая на комплексной

плоскости, не проходящая через нуль. Рассмотрим новую кривую

‚

1

: [0; 1]

→ C , где ‚

1

= a‚, a

∈ C , a = 0. Доказать, что

‚

dz

z

=

‚

1

dz

z

.

Задача 5.15. Пусть ‚

1

: [0; 1]

→ (C \ 0) и ‚

2

: [0; 1]

→ (C \ 0) — пути на

проколотой комплексной прямой, начинающиеся в точке 1 и кончающи-
еся в точках a и b соответственно, @‚

1

= a

− 1, @‚

2

= b

− 1. Рассмотрим

кривую ‚, являющуюся обединением кривых ‚

1

и a‚

2

. Кривая ‚ связ-

на. Она начинается в точке 1 и заканчивается в точке ab. Проверить,

что

‚

dz

z

=

‚

1

dz

z

+

‚

2

dz

z

, т. е. что для некоторых ветвей функции ln z

справедливы равенства ln(ab) = ln a + ln b. Вывести отсюда равенство
exp(a + b) = exp a exp b.

6. Локальные свойства аналитических отображений

Задача 6.1 (теорема об обратной функции). Пусть f — аналитиче-

ская функция в окрестности точки a, причем f

(a)

= 0. Тогда f взаим-

но однозначно отображает окрестность точки a на окрестность точки
f(a), причем обратное отображение является аналитической функцией.

Указание. Воспользоваться теоремой об обратной функции для ото-

бражения f, рассматриваемого как гладкое отображение плоскости в
плоскость.

Задача 6.2. Многозначная функция f(z) = z

1=n

(определенная равен-

ством (f(z))

n

= z) удовлетворяет следующим соотношениям:

1) z

1=n

=

|z|

1=n

cos

’
n

+ i sin

’
n

, где ’ = arg z + 2kı;

2) z

1=n

= exp

1

n

ln z

Задача 6.3. 1) Пусть f

(z

0

) = : : : = f

(k−1)

(z

0

) = 0, но f

(k)

(z

0

)

= 0. Если

´ достаточно мало, то f(z

0

+ ´) = f(z

0

) + ´

k

’(z

0

+ ´), где ’ — ана-

литическая функция, причем ’(z

0

)

= 0.

2) Существует аналитическая функция g такая, что f(z

0

) + (g(z))

k

=

= f(z), причем g

(z

0

)

= 0 (область определения функции g может быть

меньше, чем область определения функции f).

3) Доказать, что если в условиях п. 1) аналитическая функция f

непостоянна, то в окрестности точки z

0

существует такая голоморф-

ная замена переменной u = u(z), z = z(u), что выполняется равенство
f(z(u)) = u

k

+ f(z

0

). (Вопрос п. 3 — переформулировка вопроса п. 2.)

16

Задача 6.4. Пусть U — связная область на плоскости, и f : U → C —

непостоянная аналитическая функция. Тогда

1) f сохраняет области (т. е. образ f(U

1

) каждого открытого мно-

жества U

1

⊂ U является открытым множеством);

2) прообраз f

−1

(a) каждого значения a состоит из изолированных

точек.

Задача 6.5. Если непостоянная аналитическая в связной ограничен-

ной области U функция f непрерывна вплоть до границы @U , то функ-
ция

|f| достигает максимума на границе @U области U. Если f не обра-

щается в нуль ни в какой точке z

0

∈ U, то функция |f| достигает ми-

нимума на границе области.

Указание. См. задачу 6.4.

Задача 6.6. Используя задачу 6.5, доказать основную теорему алге-

бры: всякий полином положительной степени имеет корень.

7. Инверсия

Инверсией в пространстве R

n

относительно сферы радиуса R с цен-

тром в точке A называется преобразование, переводящее точку

x в

точку

y такую, что

1) луч из точки A, проходящий через точку

x, содержит точку y;

2) произведение (A;

x) · (A; y), где (·; ·) — расстояние между дву-

мя точками, равно R

2

.

Преобразование инверсии определено в любой точке

x ∈ R

n

, отлич-

ной от A.

Задача 7.1. 1) Для всякой инверсии fi справедливо равенство

fi

◦ fi = id, где id — тождественное преобразование.

2) Пусть fi

1

и fi

2

— инверсии относительно сфер радиусов R

1

и R

2

с

центром в точке нуль. Доказать, что fi

2

= `

◦ fi

1

, где ` — гомотетия с

коэффициентом (R

2

=R

1

)

2

.

3) Инверсия относительно сферы оставляет эту сферу на месте.

В каждой точке a сферы дифференциал инверсии — отражение отно-
сительно гиперплоскости, касательной к сфере в точке a.

4) Дифференциал инверсии в произвольной точке — композиция

отражения относительно гиперплоскости (какой?) и растяжения (во
сколько раз?). В частности, инверсия сохраняет углы между любыми
кривыми.

Задача 7.2 (ъквадратный трехчленё в евклидовом пространстве R

n

).

Рассмотрим евклидово пространство

R

n

и уравнение

a

x; x + b; x + c = 0;

(1)

17

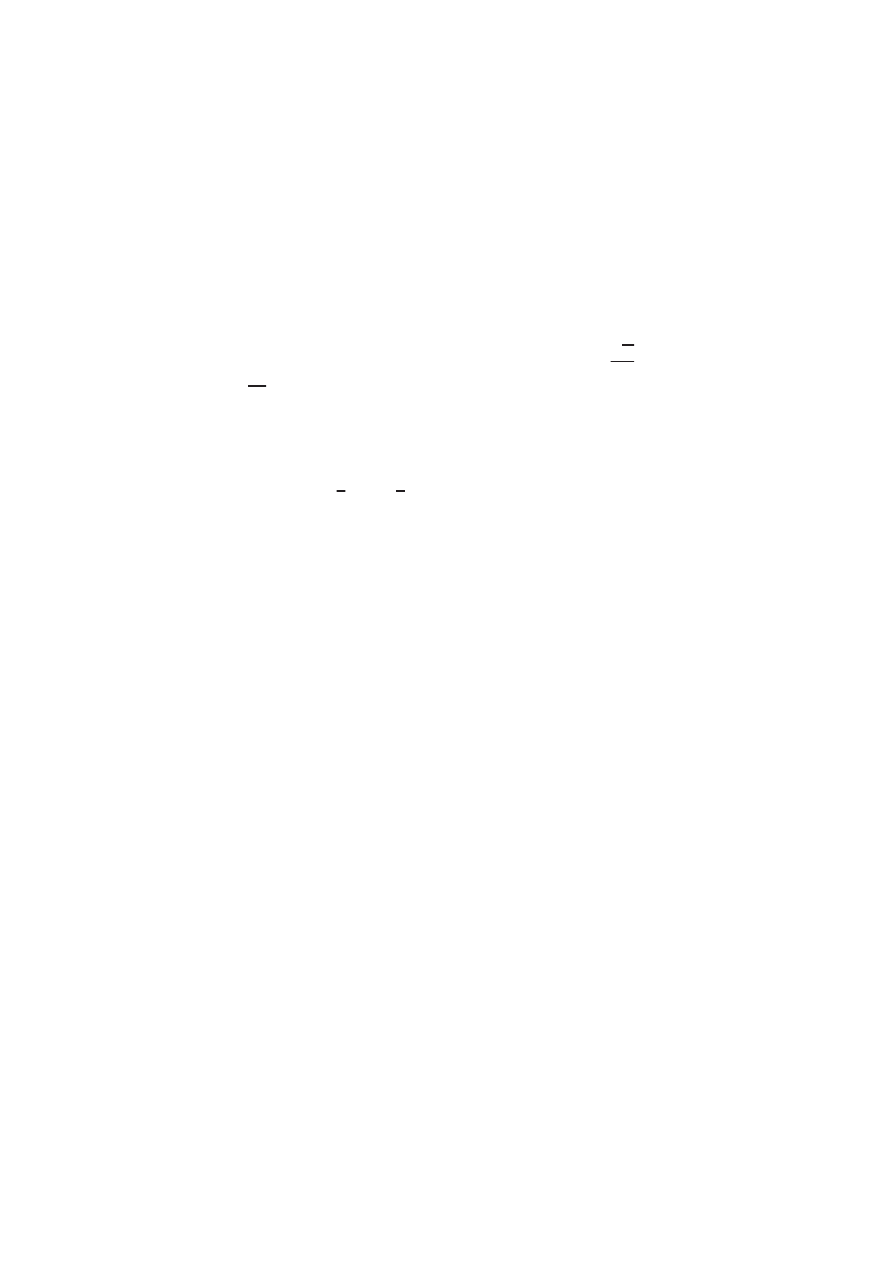
где a; c — данные числа,

b — данный вектор в R

n

,

x — неизвестный век-

тор в

R

n

и

; — скалярное произведение.

1) Если a = 0, но

b = 0, то уравнение (1) определяет гиперплоскость.

2) Если c = 0, то множество решений содержит нулевой вектор.
3) Пусть a

= 0. Если ъдискриминантё D = b; b − 4ac отрицателен,

то уравнение (1) несовместно. Если D

0, то решением x уравнения (1)

является любая точка

x ∈ R

n

, находящаяся на расстоянии

√

D

2a

от точки

x

0

=

−b

2a

. В частности, общее решение уравнения (1) — это сфера.

Задача 7.3. Рассмотрим инверсию относительно сферы радиуса 1 с

центром в нуле.

1) Эта инверсия задается формулой

u(x) = x=x; x. Обратное пре-

образование задается формулой

x(u) = u=u; u. На комплексной плос-

кости в комплексных обозначениях эти преобразования описываются
формулами u = 1=x, x = 1=u.

2) Эта инверсия переводит решение уравнения a

x; x + b; x +

+ c = 0 в решение уравнения c

u; u + b; u + a = 0.

3) При этой инверсии: сферы, не проходящие через нуль, переходят

в сферы, не проходящие через нуль; сферы, проходящие через нуль,
переходят в гиперплоскости, не проходящие через нуль, и наоборот.

4) Прямые и окружности в

R

3

переходят в прямые и окружности.

(Когда окружность переходит в прямую?)

Задача 7.4 (задача Кокстера). Пусть сферы S

1

, S

2

, S

3

и S

4

в трех-

мерном пространстве лежат вне друг друга и касаются друг друга.
Построим сферу S

5

, касающуюся сфер S

1

, S

2

, S

3

и S

4

. Затем построим

сферу S

6

, касающуюся сфер S

1

, S

2

, S

3

и S

5

такую, что S

6

= S

4

. За-

тем построим сферу S

7

, касающуюся сфер S

1

, S

2

, S

3

и S

6

такую, что

S

7

= S

5

, и т. д. Доказать, что всегда S

10

= S

4

.

Задача 7.5. Стереографическая проекция сферы на плоскость —

ограничение на сферу некоторой инверсии пространства

R

3

(какой?).

Поэтому стереографическая проекция переводит окружности на сфере
в окружности и прямые на плоскости и сохраняет углы между кривыми.

Задача 7.6. Фиксируем на сфере S в R

3

ориентацию, противопо-

ложную обычной, т. е. такую, что вектор внутренней нормали и пара
правильно ориентированных на сфере касательных векторов в точке
a

∈ S образуют тройку положительно ориентированных векторов в R

3

.

1) Стереографическая проекция из ъсеверного полюсаё на сфере на

горизонтальную плоскость (предполагается, что сфера лежит на гори-
зонтальной плоскости и что горизонтальная плоскость ориентирована
стандартным способом) сохраняет ориентацию.

2) Стереографическая проекция из ъюжного полюсаё на сфере на

18

горизонтальную плоскость (предполагается, что горизонтальная плос-
кость сферы лежит на сфере и что горизонтальная плоскость ориенти-
рована стандартным способом) меняет ориентацию.

3) Отождествим верхнюю и нижнюю касательные плоскости к сфе-

ре при помощи параллельного переноса на вертикальный вектор (по
длине равный диаметру сферы). Доказать, что после этого отожде-
ствления стереографическая проекция x(a) точки a, описанная в п. 1),
и стереографическая проекция y(a) той же точки a, описанная в п. 2),
связаны между собой преобразованием инверсии. Относительно какой
окружности?

4) В комплексных обозначениях точки x(a) и y(a) из п. 3) связаны

соотношением y(a) = 1=x(a). (При условии, что диаметр сферы равен
единице.)

Преобразование Мбиуса — это отображение плоскости, пополнен-

ной бесконечно удаленной точкой, в себя, переводящее прямые и окруж-
ности в прямые и окружности и сохраняющее углы между кривыми (но
не обязательно сохраняющее ориентацию).

Аналогично определяется преобразование Мбиуса сферы в

R

3

в себя.

Задача 7.7. 1) На плоскости R

2

всякий поворот и всякий параллель-

ный перенос можно представить в виде произведения двух симметрий
относительно прямых. Каких?

2) В пространстве

R

n

гомотетию с положительным коэффициентом

можно представить в виде произведения двух инверсий. Каких?

Задача 7.8. Будем говорить, что две точки симметричны относи-

тельно окружности, если они переставляются при инверсии относитель-
но окружности. Показать, что точки x и y симметричны относительно
окружности S, если и только если всякая окружность L, проходящая че-
рез x и y, пересекает S под прямым углом. Вывести отсюда, что симме-
трия точек относительно окружности сохраняется при преобразовани-
ях Мбиуса (т. е. если F — преобразование Мбиуса и x; y симметричны
относительно S, то F (x), F (y) симметричны относительно F (S)).

Задача 7.9. Пару окружностей S

1

и S

2

можно перевести преобразо-

ванием Мбиуса

1) в пару прямых, проходящих через точку нуль, если S

1

и S

2

пере-

секаются;

2) в пару параллельных прямых, если S

1

и S

2

касаются;

3) в пару концентрических окружностей, если S

1

и S

2

не пересека-

ются.

Указание к п. 3. Построить прямую и окружность, ортогонально

пересекающие S

1

и S

2

. Эту прямую и окружность перевести в пару

прямых, проходящих через точку нуль.

19

8. Сфера Римана

Задача 8.1 (теорема об устранимой особенности). 1) Пусть f анали-

тична и ограничена в проколотой окрестности точки a. Тогда f анали-
тически продолжается в точку a.

2) Если в условиях п. 1) вместо ограниченности f имеем неравенство

|f(z)| < C|z − a|

−N

для некоторой константы C и некоторого целого N ,

то f(z)(z

− a)

N

является аналитической функцией. Такая функция f(z)

в окрестности точки a представима в виде ряда

f(z) =

∞

m−N

c

m

(z

− a)

m

:

Если при этом c

−N

= 0 и −N < 0, то говорят, что функция f имеет

полюс порядка N в точке a.

Задача 8.2. Рассмотрим такое гладкое отображение f области U ⊂

⊂ R

2

в

R

2

, что:

1) дифференциал f обращается в нуль лишь на дискретном множе-

стве точек;

2) во всех остальных точках дифференциал сохраняет ориентацию

и углы между любыми двумя кривыми, проходящими через эту точку.

Тогда f — аналитическая функция (мы отождествляем

R

2

с

C ).

Указание. Воспользоваться теоремой Коши и теоремой об устрани-

мой особенности.

Определение. Фиксируем на сфере S в R

3

некоторую ориентацию.

Отображение f области U

⊂ S на ориентированной сфере в комплекс-

ную плоскость называется

аналитическим, если df обращается в нуль

лишь в дискретном множестве точек и в остальных точках df сохра-
няет ориентацию и углы между любыми двумя кривыми.

Задача 8.3. Фиксируем на сфере диаметра 1, лежащей на горизон-

тальной плоскости, ориентацию, противоположную стандартной.

1) Стереографическая проекция ı

1

из ъсеверного полюсаё сферы на

горизонтальную плоскость, касающуюся сферы в ъюжном полюсеё сфе-
ры, является аналитическим отображением. Если область U

⊂ S

2

не

содержит верхней точки сферы, то отображение f : U

→ C является

аналитическим, если и только если функция комплексного переменно-
го f(ı

−1

1

(z)) в области ı

1

(U ) является аналитической.

2) Стереографическая проекция ı

2

из ъюжного полюсаё сферы на

горизонтальную плоскость, касающуюся сферы в ъсеверном полюсеё
сферы, является антианалитическим отображением, т. е. отображе-
ние ı

2

является аналитическим (мы отождествляем верхнюю и ниж-

нюю касательные плоскости при помощи параллельного переноса на

20

единичный вертикальный вектор и отождествляем обе плоскости с ком-
плексной прямой). Если область U не содержит нижней точки сферы,
то отображение f : U

→ C является аналитическим, если и только если

функция f(ı

−1

2

(u)) комплексного переменного u в области ı

2

(U ) явля-

ется аналитической.

3) ъКомплексные координатыё z(a) = ı

1

(a) и u(a) = ı

2

(a) точки a на

сфере связаны соотношениями u = 1=z, z = 1=u.

Так называемую сферу Римана можно воспринимать как комплекс-

ную плоскость, дополненную одной точкой, обозначаемой

∞. Около

этой точки есть координата u = 1=z, причем u(

∞) = 0.

Говорят, что функция f переменной z аналитична в окрестности

бесконечности, если и только если функция переменной u, опреде-
ленная формулой (u) = f(1=z), аналитична в окрестности нуля. Если
функция имеет полюс порядка N в нуле, то говорят, что функция f
имеет полюс порядка N в бесконечности.

Определение. Функция f мероморфна в области U на сфере Римана,

если все ее особые точки в этой области являются полюсами.

Задача 8.4. Доказать, что
1) функция f, мероморфная на сфере Римана, представима в виде

f(z) = P (z) +

1ik

1jm(i)

c

i

j

(z − a

i

)

j

;

Поэтому всякая функция, мероморфная на сфере Римана, рациональна.

2) всякая рациональная функция раскладывается на простейшие

дроби;

Задача 8.5. 1) Всякое аналитическое взаимно однозначное преобра-

зование сферы Римана в себя — это дробно-линейное преобразование

z

→

az + b
cz + d

, где ad

− bc = 0.

2) Всякое дробно-линейное преобразование, для которого c

= 0,

представимо в виде z =

A

z

− z

0

+ B.

3) Всякое дробно-линейное преобразование представимо в виде про-

изведения не более чем четырех инверсий.

4) Дробно-линейное преобразование имеет либо две неподвижных

точки, либо одну (кратную) неподвижную точку, либо тождественно.

5) Для любых трех различных точек a; b; c и для любых трех различ-

ных точек A; B; C существует единственное дробно-линейное преобра-
зование z

→ F (z) такое, что F (a) = A, F (b) = B и F (c) = C.

6) Всякая композиция четного числа инверсий является дробно-ли-

нейным преобразованием.

21

Задача 8.6. 1) Сохраняющее ориентацию преобразование Мбиу-

са — это дробно-линейное преобразование.

2) Меняющее ориентацию преобразование Мбиуса имеет вид

F (z) =

az + b
cz + d

, где ad

− bc = 0.

3) Любое преобразование Мбиуса — произведение инверсий.
Задача 8.7. Всякое взаимно однозначное преобразование сферы в R

3

в себя, сохраняющее углы между любыми двумя кривыми, является
преобразованием Мбиуса. Оно всегда представимо в виде композиции
инверсий относительно сфер, ортогональных данной сфере.

9. Вычеты

Рассмотрим форму f(z) dz, где f(z) — аналитическая функция в

проколотой окрестности U точки a.

Задача 9.1. Интеграл

‚

f(z) dz по любому контуру ‚, лежащему в

области U и ъобегающему один раз вокруг точки a в направлении про-
тив часовой стрелкиё, не зависит от выбора контура ‚.

Определение. 1) Число

1

2ıi

‚

f(z) dz, где ‚ — контур из задачи 9.1,

называется

вычетом формы ! = f(z) dz в точке a и обозначается Res

a

!;

2) если a =

∞, то вычет формы f(z) dz по определению равен вычету

формы f(1=z) d(1=z) в точке 0.

Задача 9.2. 1) Пусть в окрестности точки a = ∞ функция f(z) пред-

ствима сходящимся рядом f(z) =

−∞<k<∞

C

k

(z

− a)

k

. Вычислить Res

a

!,

где ! = f(z) dz.

2) Пусть при достаточно больших z ряд

−∞<k<∞

C

k

z

k

сходится.

Найти Res

∞

!, где ! = f(z) dz.

Задача 9.3 (теорема о сумме вычетов). Пусть U — область на сфере

Римана с кусочно гладкой границей ‚ = @U . Пусть f(z) — функция,
аналитическая вплоть до границы области U всюду, за исключением
конечного числа внутренних точек. Тогда

‚

f(z) dz = 2ıi

a∈U

Res

a

f(z) dz:

В частности, если U — сфера Римана, то

Res

a

f(z) dz = 0:

Задача 9.4. Пусть функция f(z) мероморфна в окрестности точки a,

т. е. представима в виде f(z) =

mk<∞

C

k

(z

− a)

k

, и коэффициент C

m

не

22

равен нулю. Тогда вычет формы ! =

df

f

в точке a равен m, т. е. этот

вычет отрицателен в полюсе, положителен в нуле и по модулю равен
кратности соответствующего полюса или нуля.

Задача 9.5 (принцип аргумента). 1) Пусть функция f мероморфна

в области U , P — число полюсов функции f в области U , посчитанных
с учетом кратности, N — число нулей функции f в области U , посчи-
танных с учетом кратности. Тогда

1

2ıi

@U

df

f

= P

− N:

2) Число

1

2ıi

@U

df

f

равно приросту аргумента функции f при пол-

ном обходе границы области U .

Задача 9.6. Для рациональной функции на сфере число нулей (по-

считанных с учетом кратности) равно числу ее полюсов (посчитанных
с учетом кратности). В частности, число нулей полинома степени n
равно n.

Указание. См. задачи 9.4 и 9.5.

10. Геометрия Лобачевского и ТФКП

Задача 10.1. Рассмотрим в R

n

верхнее полупространство

R

n

+

, опре-

деленное неравенством x

n

> 0, где x

n

— последняя координата точки

x = (x

1

; : : : ; x

n

). Зададим риманову метрику Пуанкаре в

R

n

+

(ds)

2

=

(dx

1

)

2

+ : : : + (dx

n

)

2

x

2

n

:

Доказать, что эта метрика инвариантна относительно инверсий, цен-
тры которых лежат в гиперплоскости x

n

= 0, а радиусы произвольны.

Указание. См. п. 4 задачи 7.1.

Задача 10.2. Пусть у точек x

1

и

x

2

в

R

n

+

все координаты, кроме по-

следней, равны. Тогда среди всех кривых, соединяющих

x

1

и

x

2

, самая

короткая кривая в смысле метрики Пуанкаре — вертикальный отрезок.

Указание. Аналогичный факт верен для любой метрики

(ds)

2

= f(x

n

)((dx

1

)

2

+ : : : + (dx

n

)

2

);

где f — любая неотрицательная функция, зависящая лишь от одной пе-
ременной x

n

.

Задача 10.3. Пусть x

1

и

x

2

— две точки в

R

n

+

. Тогда самая корот-

кая в смысле метрики Пуанкаре кривая, соединяющая

x

1

и

x

2

, — дуга

окружности, ортогональной гиперплоскости x

n

= 0.

Указание. См. задачи 10.2 и 10.1.

23

Полупространство

R

n

+

с метрикой Пуанкаре называется моделью

Пуанкаре пространства Лобачевского L

n

.

Задача 10.4 (неравенство Шварца). Пусть B

1

— открытый единич-

ный круг на комплексной плоскости (т. е. B

1

определено неравенством

|z| < 1), и пусть f : B

1

→ B

1

— такое аналитическое отображение, что

f(0) = 0. Тогда

1) справедливо неравенство

|f(z)| |z|;

2) если хотя бы в одной точке z

0

∈ B

1

, z

0

= 0, достигается равенство

|f(z

0

)

| = |z

0

|, то f(z) ≡ c · z, где c — комплексное число, |c| = 1.

Указание. Для всякого замкнутого круга |z| (1 − ") воспользо-

ваться принципом максимума для функции ’(z) =

f (z)

z

.

Задача 10.5. Переведем открытый круг B

1

в верхнюю полуплоскость

R

2

+

любым преобразованием Мбиуса (т. е. произведением инверсий) и

индуцируем в B

1

риманову метрику из метрики Пуанкаре в

R

2

+

. То-

гда индуцированная метрика не зависит от выбора преобразования
Мбиуса (почему?) и тоже называется метрикой Пуанкаре. Открытый
круг B

1

вместе с метрикой Пуанкаре называется моделью Пуанкаре

плоскости Лобачевского в единичном круге. Чему равна эта римано-
ва метрика? Как выглядит кратчайшая в смысле этой метрики линия,
соединяющая две точки в B

1

?

Задача 10.6. Пусть точка a лежит в открытом единичном круге B

1

.

Рассмотрим функцию h, определенную формулой h(z) =

z

− a

az

− 1

. Пока-

зать, что

1) h задает взаимно однозначное отображение B

1

в себя, сохраняет

метрику Пуанкаре в круге и переводит точку a в точку нуль;

2) всякая другая функция g, обладающая этими свойствами, име-

ет вид g = ch, где c — комплексное число, по модулю равное единице
(функция h выделяется среди функций, обладающих этими свойства-
ми, тем, что она переводит прямую, соединяющую точки нуль и a, в
себя).

Задача 10.7. Пусть f : B

1

→ B

1

— аналитическое отображение от-

крытого единичного круга в себя (не обязательно оставляющее точку
нуль на месте). Тогда для любых двух точек z

1

; z

2

∈ B

1

справедливо

неравенство

(f(z

1

); f(z

2

))

(z

1

; z

2

);

где — расстояние в метрике Пуанкаре. Если для некоторой пары
точек z

0

1

; z

0

2

∈ B, где z

0

1

= z

0

2

, выполняется равенство (f(z

0

1

); f(z

0

2

)) =

= (z

0

1

; z

0

2

), то для любой пары точек z

1

; z

2

∈ B (f(z

1

); f(z

2

)) = (z

1

; z

2

).

24

Указание. Рассмотреть отображение F = h

2

◦ f ◦ h

1

, где h

1

и h

2

—

функции из задачи 10.6, переводящие, соответственно, точку нуль в
точку z

1

и точку f(z

1

) в точку нуль. Для отображения F воспользо-

ваться неравенством Шварца.

Задача 10.8. 1) Пусть f : B

1

→ B

1

— взаимно однозначное анали-

тическое отображение. Тогда отображение f сохраняет метрику Пу-
анкаре и является преобразованием Мбиуса, сохраняющим ориен-
тацию.

2) Всякое взаимно однозначное отображение плоскости Лобачевско-

го в себя, сохраняющее углы между любыми двумя кривыми, является
движением плоскости Лобачевского.

Указание. См. задачу 10.7.

Задача 10.9. Для любой пары различных точек z

1

и z

2

в единичном

круге B

1

=

{z ∈ C : |z| < 1} и для любого выбора корней b

1

=

√

z

1

и

b

2

=

√

z

2

справедливо неравенство (z

1

; z

2

) < (b

1

; b

2

), где — расстоя-

ние в метрике Пуанкаре.

Указание. См. задачу 10.7.

Задача 10.10. Пусть f : D → B

1

— однолистное отображение (т. е. ес-

ли f(z

1

) = f(z

2

), то z

1

= z

2

) односвязной области D в единичный

круг B

1

. Пусть точка a

∈ B

1

не принадлежит образу отображения f.

Пусть ’ : B

1

→ B

1

взаимно однозначное аналитическое отображение

круга B

1

в себя, переводящее точку a в точку 0. Обозначим через g

одну из однозначных ветвей функции g =

’(f) на области D (поче-

му такая ветвь существует?). Тогда для любых двух различных точек
a; b

∈ D справедливо неравенство

(g(a); g(b)) > (f(a); f(b))

(здесь — метрика Пуанкаре), причем функция g : D

→ B

1

однолист-

на в D.

Указание. См. задачу 10.9.

Задача 10.11. Фиксируем две различные точки a; b в односвязной

ограниченной области D. Пусть f : D

→ B

1

— однолистное отображе-

ние, для которого (f(a); f(b)) принимает самое большое возможное
значение. Тогда f — взаимно однозначное отображение.

Указание. См. задачу 10.10.
Теорема Римана утверждает, что для всякой ограниченной одно-

связной области D существует взаимно однозначное аналитическое
отображение в единичный круг.

Для завершения доказательства теоремы Римана нам нужен крите-

рий компактности семейства аналитических функций.

25

11. Компактность функциональных множеств

и теорема Римана

Метрические пространства и компактность. В задачах 11.1–11.3 мы

напомним теорему Арцел«

а. Метрическое пространство называется

пол-

ным, если в нем каждая фундаментальная последовательность сходит-
ся. Топологическое пространство называется

компактом, если из лю-

бого его покрытия открытыми множествами можно выбрать конечное
подпокрытие. Множество X в метрическом пространстве называется
вполне ограниченным, если для любого " > 0 в нем существует конеч-

ная "-сеть, т. е. такое конечное подмножество A, что для любой точки
x

∈ X существует точка a ∈ A, расстояние которой до точки X меньше

или равно ".

Задача 11.1. Метрическое пространство является компактом, если

и только если оно полно и вполне ограничено.

Задача 11.2. Непрерывное отображение метрического компакта в

метрическое пространство равномерно непрерывно.

Задача 11.3 (теорема Арцел«а). Рассмотрим пространство C(X; R

n

)

непрерывных отображений метрического компакта X в евклидово про-
странство

R

n

. Это пространство наделено равномерной метрикой. Под-

множество A

⊂ C(X; R

n

) имеет компактное замыкание в C(X;

R

n

), если

и только если

1) функции из A равномерно ограничены, т. е. существует констан-

та C такая, что если f

∈ A, то f < C (f — это максимальная длина

вектора f(x), x

∈ X);

2) функции из A равностепенно непрерывны, т. е. для любого

" > 0 существует ‹ > 0, такое, что если (x

1

; x

2

) < ‹ и f

∈ A, то

(f(x

1

); f(x

2

)) < ".

Компактные семейства аналитических функций. Пусть D — любая

область и K — компакт, содержащийся в D.

Задача 11.4. Если множество A аналитических функций в области D

равномерно ограничено, то ограничения этих функций на K

⊂ D рав-

ностепенно непрерывны.

Указание. Производная функции оценивается в меньшей области

при помощи интегральной формулы Коши (см. задачу 5.10).

Задача 11.5 (компактность ограниченного семейства аналитиче-

ских функций). Если множество A аналитических функций в обла-
сти D равномерно ограничено, то из всякой последовательности функ-
ций из A можно выбрать подпоследовательность, ограничение кото-
рой на каждый компакт K

⊂ D сходится равномерно на этом ком-

пакте.

26

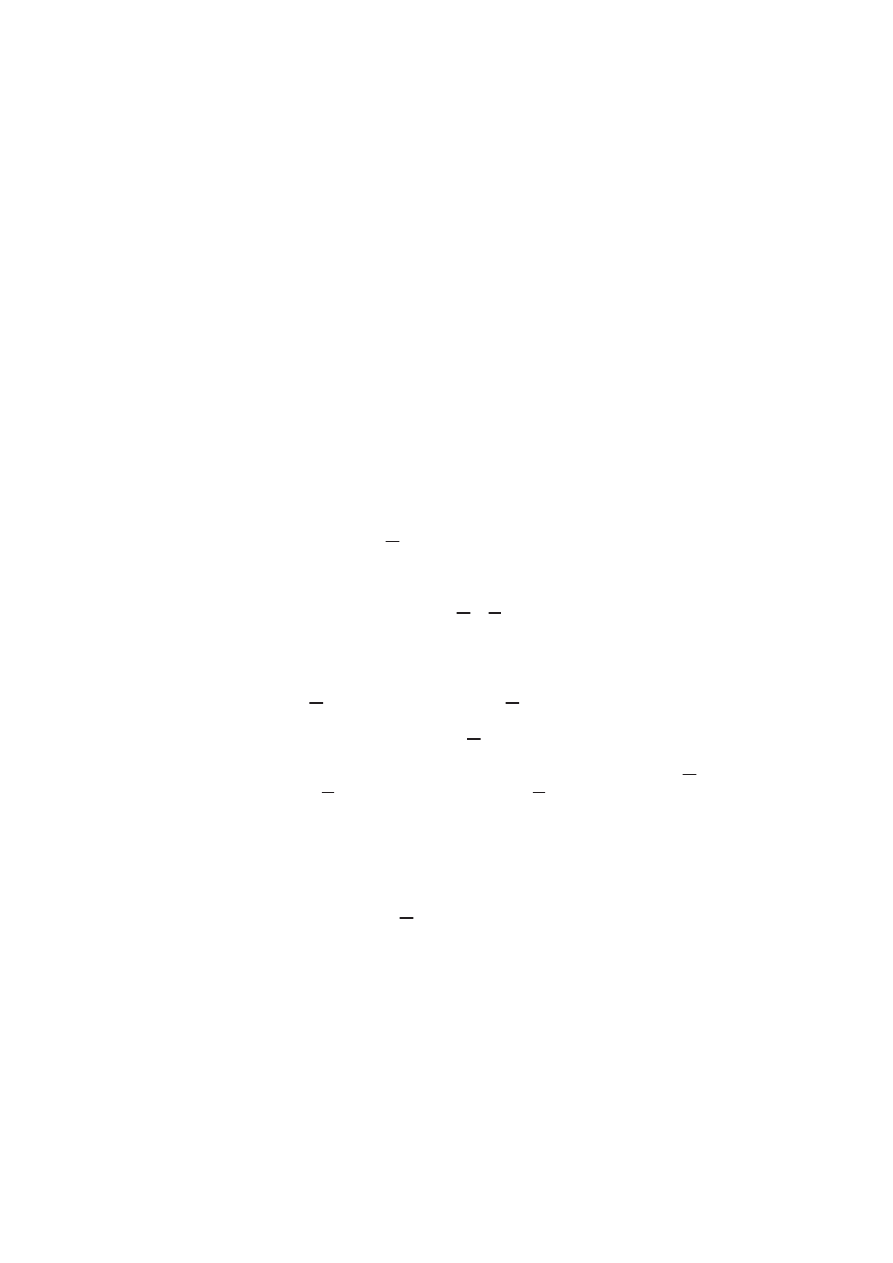
Указание. Воспользоваться задачей 11.4 для такой счетной последо-

вательности компактов K

1

⊆ K

2

⊆ : : : ; что

K

i

= D, и ъдиагональным

процессом Кантораё.

Задача 11.6. Пусть каждая из функций f

1

; : : : ; f

n

; : : : аналитична в

области D и однолистна в ней. Пусть функция f есть предел функ-
ций f

1

; : : : ; f

n

; : : : ; причем для каждого компакта K

⊂ D ограничения f

i

на K равномерно сходятся к ограничению f на K. Тогда f либо посто-
янна, либо однолистна в D.

Задача 11.7 (теорема Римана). Пусть D — односвязная ограничен-

ная область. Тогда существует взаимно однозначное аналитическое
отображение f : D

→ B

1

области D в единичный круг.

Указание. Воспользоваться задачами 10.11, 11.5 и 11.6.

12. Продолжаемость до границы

Задача 12.1. Пусть X ⊂ R

n

— ограниченное множество, и f : X

→

→ R

m

— непрерывное отображение. Отображение f непрерывно про-

должается на замыкание X множества X, если и только если отобра-
жение f равномерно непрерывно.

Задача 12.2. Пусть X ⊂ R

n

и Y

⊂ R

m

— ограниченные множества, и

f : X

→ Y — гомеоморфизм. Показать, что гомеоморфизм f продолжа-

ется до гомеоморфизма замыканий X и Y , если и только если отобра-
жения f : X

→ Y и f

−1

: Y

→ X равномерно непрерывны.

Задача 12.3. Доказать, что непрерывная вещественнозначная функ-

ция на связном множестве принимает все промежуточные значения.

Задача 12.4. Скажем, что множество X ⊂ R

n

локально связно в сво-

ем замыкании X, если у каждой точки a ∈ X существует сколь угодно
малая окрестность U

⊂ R

n

такая, что U

∩ X непусто и связно. Пока-

зать, что если X локально связно в X, то каждая сфера достаточно
малого радиуса с центром в точке a пересекает множество X.

Задача 12.5. Пусть f : X → Y — гомеоморфизм, a

i

∈ X, lima

i

= a

∈ X

и lim f(a

i

) = b

∈ Y . Если Y локально связно в Y , то для любого " > 0

найдется такое ‹ > 0, что на всякой сфере радиуса ‹

0

, 0 < ‹

0

< ‹, с

центром в точке a существует точка c

∈ X, для которой расстояние от

f(c) до b меньше ".

Задача 12.6. Пусть X и Y — ограниченные области на плоскости, и

f : X

→ Y — диффеоморфизм. Допустим, что

1) X и Y локально связны в своих замыканиях;
2) для каждой точки a

∈ X пересечение существует такое R

0

(a) > 0,

что для любого R < R

0

(a) пересечение окружности S

R

радиуса R с

центром a и области X связно;

27

3) для каждой точки b

∈ Y пересечение существует такое R

0

(b) > 0,

что для любого R < R

0

(b) пересечение окружности радиуса R с цен-

тром b и области Y связно.

Тогда если отображение f : X

→ Y не равномерно непрерывно, то

существует точка a

∈ X и число > 0 такие, что каждая кривая f(‚

R

),

где ‚

R

= S

R

∩ X, 0 < R < R

0

, имеет длину больше .

Принцип длины и площади. Пусть G ⊂ C

1

— область на комплексной

плоскости, и f : G

→ C

1

— аналитическая функция, однолистная в обла-

сти G. Фиксируем систему полярных координат ; „. Введем следующие
обозначения:

‚() — кривая

|z| = , z ∈ G,

l() — длина кривой ‚(),
L() — длина образа f(‚()) кривой ‚() при отображении f,
S(f(G)) — площадь области f(G).
Задача 12.7. Обяснить формулы:
1) L() =

|z|=; z∈G

|f

(z)

| ds, где ds = d„.

2) S(f(G)) =

∞

0

|z|=; z∈G

|f

(z)

|

2

d„ d.

Задача 12.8. Доказать неравенство

|z|=; z∈G

|f

(z)

|

2

d„

L()

2

l()

:

Используя задачу 12.7, показать, что

S(f(G))

∞

0

L()

2

l()

d

(последнее неравенство называется принципом длины и площади).

Задача 12.9. Используя принцип длины и площади, показать, что

конформное отображение f : X

→ Y ограниченных областей на плоско-

сти, удовлетворяющих условиям задачи 12.6, равномерно непрерывно.

Указание.

R

0

0

2

d

2ı

=

∞:

Задача 12.10. Используя предыдущие задачи, доказать, что кон-

формное отображение f : X

→ Y ограниченных областей на плоскости,

удовлетворяющих условиям задачи 12.6, продолжается до их границ.

Квазиконформные отображения. Диффеоморфизм f области на

плоскости в другую область называется

квазиконформным с коэффи-

циентом квазиконформности k, если якобиан df отображения f удо-
влетворяет следующему условию:

max

x=1

df(x) k min

x=1

df(x):

28

Будем использовать обозначения, введенные перед задачей 12.7, для
квазиконформного отображения f.

Задача 12.11. Пусть f — квазиконформное отображение с коэффи-

циентом квазиконформности k. Введем следующие обозначения:

c(z) = min

x=1

df(x); C(z) = max

x=1

df(x);

C(z)

kc(z). Обяснить следующие соотношения:

1) L()

z=;z∈G

c(z) ds, где ds = d„;

2) S(f(G)) =

∞

0

z=;z∈G

c(z)C(z) d„ d;

3) S(f(G))

k

∞

0

L

2

()

l()

d.

Задача 12.12. Доказать продолжаемость квазиконформного диф-

феоморфизма до границы области.

Указание. См. задачи 12.9 и 12.11.

Ошибка в учебнике Евграфова.

1

Скажем, что гладкое отображение

f : U

→ V обладает свойством единственности, если выполнено следу-

ющее условие: не существует связной дуги ` на границе @U области U
для которой lim

z→x

f(z) существует при всех x

∈ `, причем все эти преде-

лы равны.

В учебнике М. А. Евграфова ъАналитические функцииё (М.: Наука,

1968) доказана продолжаемость конформного отображения исходя из
того, что аналитические функции f и f

−1

обладают свойством един-

ственности.

Задача 12.13. 1) Привести пример диффеоморфизма f : U → V тако-

го, что f и f

−1

обладают свойством единственности, но отображение f

не продолжается до границы области.

2) Указать конкретную ошибку на с. 378 этого учебника.

13. Римановы поверхности аналитических функций

Росток f

a

аналитической функции в точке a сферы Римана ~

C — это

ряд Тейлора f

a

=

∞

k=1

c

k

(z

− a

k

)

k

с центром в точке a, сходящийся

в некотором открытом круге с центром в точке a (если a =

∞, то

f

a

=

∞

k=0

c

k

u

k

, где u =

1
z

, и ряд сходится при

|u| < R).

1

Книга Евграфова, по-моему, — один из самых лучших учебников по комплекс-

ному анализу. Ошибка, о которой пойдет речь в задаче 12.13, — дело житейское;

собственно говоря, я наткнулся на нее потому, что использовал книгу Евграфова

при подготовке курса лекций.

29

Пусть I = [0; 1], ‚ : I

→ ~C — непрерывная кривая на сфере Римана с

началом в точке a, т. е. ‚(0) = a.

Аналитическим продолжением рост-

ка f

a

вдоль кривой ‚ называется отображение, сопоставляющее каждой

точке t

0

∈ [0; 1] аналитический росток f

b

в точке b = ‚(t

0

) таким обра-

зом, что для всякого t

∈ [0; 1] существуют такие окрестность U ⊂ ~C

точки ‚(t), окрестность V

⊂ [0; 1] точки t и аналитическая функция

f : U

→ C в области U, что для всякой точки b ∈ V аналитический рос-

ток f

‚(b)

— это росток в точке ‚(b)

∈ U функции f.

Задача 13.1. Для кривой ‚ : I → ~C , ‚(0) = a, и ростка f

a

существует

не более одного аналитического продолжения.

Задача 13.2. Пусть росток f

a

аналитически продолжается вдоль

кривой ‚ : I

→ ~C , ‚(0) = a, ‚(1) = b, и f

b

— росток, полученный

при этом продолжении. Тогда существует конечная цепочка точек
0 = t

0

< t

1

< : : : < t

n

= 1, для которой ряд f

‚(t

i

)

сходится в точке ‚(t

i+1

),

причем ряд f

‚(t

i

)

— это ряд Тейлора в точке ‚(t

i

) полученной аналити-

ческой функции.

Задача 13.3 (теорема о монодромии). Рассмотрим непрерывное ото-

бражение F единичного квадрата I

2

с координатами u; v, 0

u 1,

0

v 1, в ~C такое, что каждая кривая F

v

: I

→ ~C , где F

v

(u) = F (u; v),

начинается в точке a и кончается в точке b, т. е. F (v; 0)

≡ a и F (v; 1) ≡ b.

Пусть для каждой кривой F

v

росток f

a

аналитически продолжается

вдоль этой кривой. Тогда результат аналитического продолжения до
точки u = 1 не зависит от выбора кривой F

v

, где 0

v 1.

Указание. Если немного изменить кривую в малой окрестности лю-

бой из ее точек, то результат аналитического продолжения не изме-
нится.

Определение. Два аналитических ростка f

a

и g

b

, заданные в точ-

ках a и b сферы Римана, называются

эквивалентными, если существу-

ет такая кривая ‚ : I

→ ~C , ‚(0) = a, ‚(1) = b, что росток g

b

— результат

продолжения ростка f

a

вдоль кривой ‚.

Задача 13.4. Описанные выше соотношение действительно являются

соотношением эквивалентности, т. е.

1) f

a

∼ f

a

;

2) если f

a

∼ g

b

, то g

b

∼ f

a

;

3) если f

a

∼ g

b

и g

b

∼ ’

c

, то f

a

∼ ’

c

.

Определение. Как множество точек риманова поверхность рост-

ка f

a

— это совокупность всех ростков g

b

, эквивалентных ростку f

a

.

На римановой поверхности R ряда f определены два естественных

отображения:

1)

проекция ı : R → ~C , сопоставляющая каждому ростку точку, в

окрестности которой этот росток определен;

30

2)

функция f : R → C , сопоставляющая каждому ростку его значение

в точке, в окрестности которой он определен.

Топология на R определяется как наименее тонкая топология, в ко-

торой проекция ı : R

→ ~C непрерывна.

Задача 13.5. Отображение ı : R → ~C является локальным гомеомор-

физмом, т. е. у каждой точки p

∈ R существует такая окрестность U,

что ограничение ı на U — гомеоморфизм на свой образ.

Задача 13.6. Каждая точка a ∈ ~C имеет не более чем счетное число

прообразов при отображении ı : R

→ ~C .

Определение. Функция g : R → C называется аналитической, если

для каждой области U

⊂ R, для которой проекция ı : U → ~C является

гомеоморфизмом, функция ’ в области V = ı(U ), определенная равен-
ством ’ = g

◦ ı

−1

, является аналитической.

Аналогично определяется мероморфная функция на R.
Алгеброидные ростки. Скажем, что росток f

p

аналитической функ-

ции в связной окрестности U точки a, p

∈ U \ a, алгеброиден, если

1) росток f

p

аналитически продолжается вдоль любой кривой

‚ : I

→ U \ a, ‚(0) = p;

2) существует лишь конечное число k ростков g

p

в точке p, полу-

чающихся аналитическим продолжением ростка f

p

вдоль замкнутой

кривой ‚ : I

→ U \ a, ‚(0) = p, ‚(1) = p;

3) существуют такие натуральное число N и вещественная констан-

та C, что для всякого ростка g

q

, полученного из f

p

при продолжении

вдоль некоторой кривой ‚ : I

→ U \ a, ‚(0) = p, ‚(1) = q, справедливо

одно из неравенств

|g

q

(q)

| C|q − a|

−N

;

если a

= ∞,

|g

q

(q)

| C|q|

N

;

если a =

∞.

Задача 13.7. Росток f

p

функции переменной z алгеброиден в U

\ a

если и только если f

p

= g

p

(u), где g — мероморфная функция перемен-

ной u в окрестности 0 и z

− a = u

k

при a

= ∞ или 1=z = u

k

при a =

∞

(переменная u определена этими равенствами однозначно с точностью
до умножения на любой из корней k-й степени из 1). Так как меро-
морфная функция g раскладывается в ряд Лорана g(u) =

m−M

c

m

u

m

,

алгеброидная функция f раскладывается в

ряд Пюиз:

f(z) =

m−M

c

m

(z

− a)

m=k

;

если a

= ∞, или

f(z) =

mM

c

m

z

m=k

;

если a =

∞.

31

Докажите сформулированные утверждения. Если в рядах Пюиз, напи-
санных выше, каждый из коэффициентов c

m

заменить на коэффициент

~

c

m

= c

m

‰

m

, где ‰ — фиксированный корень k-й степени из единицы,

то получаются новые ряды Пюиз, которые считаются

эквивалентны-

ми исходным. Как связаны между собой многозначные аналитические
функции в U

\ a, определяемые эквивалентными рядами Пюиз?

Определение. Полная риманова поверхность ростка f

a

(как мно-

жество точек) — это совокупность всех рядов Тейлора и рядов Пюиз,
которые получаются аналитическим продолжением из исходного рост-
ка f

a

(при этом считается, что эквивалентные ряды Пюиз задают од-

ну и ту же точку полной римановой поверхности ростка f

a

). На полной

аналитической поверхности R определены два отображения: ı : R

→ ~C

и f : R

→ C (они определяются так же, как это делалось для римано-

вой поверхности ростка f

a

.

Топология в R определяется как наименее

тонкая топология (т. е. топология, содержащая наименьший класс от-
крытых множеств), в которой проекция ı непрерывна.

Аналитическая

функция в окрестности точки, соответствующей ряду Пюиз, — это
аналитическая функция от параметра u (см. задачу 13.7).

Скажем, что аналитический росток f

a

в точке a сферы Римана ~

C

является

ростком алгебраической функции (или алгебраическим рост-

ком), если

1) существует конечное подмножество A

⊂ ~C , a =∈ A такое, что ро-

сток f

a

аналитически продолжается вдоль любой кривой ‚ : I

→ ~C \ A,

‚(0) = a, не пересекающей множества A;

2) существует лишь конечное множество ростков f

a

1

; : : : ; f

a

k

, кото-

рые могут быть получены аналитическим продолжением вдоль замкну-
тых кривых ‚ : I

→ ~C \ A, ‚(0) = ‚(1) = a;

3) для каждой точки b

∈ A существуют такие окрестность U

b

, нату-

ральное число N и вещественная константа C, что каждый росток g

q

,

q

∈ U

b

, эквивалентный ростку f

a

, удовлетворяет одному из неравенств

|g

q

(q)

| C|q − b|

−N

;

если b

= ∞, или

|g

q

(q)

| C|q|

N

;

если b =

∞.

Задача 13.8. Показать, что всякий алгебраический росток f

a

удо-

влетворяет некоторому алгебраическому уравнению

f

k

a

+ R

1

(z)f

k−1

a

+ : : : + R

k

(z) = 0;

в котором R

i

(z) — рациональные функции.

Указание. Рассмотреть симметрические функции

1

; : : : ;

k

от рост-

ков f

a

1

; : : : ; f

a

k

, эквивалентных ростку f

a

в точке a (

1

=

f

a

i

,

32

2

=

i>j

f

a

i

f

a

j

и т. д.). Проверить, что функции

1

; : : : ;

k

рациональ-

ны, используя задачу 8.4.

Задача 13.9. Полная риманова поверхность алгебраического рост-

ка f

a

компактна.

Указание. Чтобы из последовательности точек b

1

; : : : ; b

n

; : : : на R

выбрать сходящуюся подпоследовательность, нужно выбрать сходящу-
юся подпоследовательность из точек ı(b

i

)

∈ ~C и воспользоваться тем,

что каждая точка a

∈ ~C имеет одно и то же конечное число прообразов

при отображении ı : R

→ ~C (если учитывать кратности).

Определение. 1-форма, определенная в области на римановой по-

верхности R, называется

аналитической, если около каждой точки

области она локально представима в виде f(z) dz, где z — локальный
параметр на R и f(z) — аналитическая функция.

Задача 13.10. Пусть U — компактная область на R с гладкой грани-

цей @U и ! — аналитическая форма в области U . Тогда

@U

! = 0.

Определение. Пусть форма ! аналитична в малой проколотой

окрестности точки a на римановой поверхности R и @U — граница

малой односвязной области U , содержащей точку a. Число

1

2ıi

@U

!

называется

вычетом формы ! в точке a.

Задача 13.11. Вычет определен корректно, т. е. не зависит от выбора

окрестности точки a.

Задача 13.12. Пусть ! — мероморфная форма (т. е. локально пред-

ставимая в виде f(z) dz, где f — мероморфная функция). Тогда сумма
вычетов формы ! по всем ее особым точкам равна 0.

Задача 13.13. 1) Для всякой мероморфной функции f : R → C на

компактной римановой поверхности ее число полюсов P , посчитанных
с учетом кратности, равно числу N ее нулей, посчитанных с учетом
кратности, т. е. P = N .

2) Пусть N (a) — посчитанное с учетом кратности количество точек,

в которых мероморфная функция равна a. Тогда N (a) = P и не зависит
от выбора точки a.

Указание. См. задачу 9.5.

Задача 13.14. Пусть ı : R → ~C — мероморфное отображение ком-

пактной римановой поверхности в сферу Римана. Тогда множество
точек a

∈ ~C , среди прообразов которых есть кратные, является

конечным.

Задача 13.15. Пусть полная риманова поверхность ı : R → fi функ-

ции f компактна. Тогда функция f алгебраична.

Указание. См. задачи 3.8 и 3.14.

33

14. Принцип симметрии Римана–Шварца. Теорема Пикара

Задача 14.1 (теорема об устранимости особенностей вдоль линии).

Пусть U — область на плоскости, и l

⊂ U — гладкая кривая в этой обла-

сти, которая разбивает ее на две области U

1

и U

2

, граничащие друг с

другом по кривой l. Пусть f : U

→ C — непрерывная функция в обла-

сти U , ограничения которой на подобласти U

1

и U

2

аналитичны в этих

областях. Тогда f аналитична в U .

Указание. Воспользоваться интегральной формулой Коши для обла-

стей U

1

и U

2

. Показать, что сумма двух полученных интегралов задает

интегральное представление функции f в области U

\ l. Убедиться, что

это интегральное представление продолжается на всю область U и со-
впадает с интегральной формулой Коши для функции f в области U .

Задача 14.2 (принцип симметрии Римана–Шварца). Пусть U и G —

области на плоскости. Пусть граница области U содержит дугу l

1

окружности S

1

, а граница области G содержит дугу l

2

окружности S

2

.

Обозначим через fi

1

и fi

2

отображения инверсии относительно окружно-

стей S

1

и S

2

. Пусть образ fi

1

(U ) области U при инверсии fi

1

не пересека-

ется с областью U . Допустим, что существует аналитическое отобра-
жение f : U

→ G, которое непрерывно продолжается на дугу l

1

, причем

f(l

1

)

⊆ l

2

. Тогда аналитическое отображение f : U

→ G аналитически

продолжается до отображения F : ~

U

→ ~

G, где ~

U = U

∪ fi

1

(U )

∪ l

1

и ~

G =

= G

∪ fi

2

(G)

∪ l

2

, определенного на области fi

1

(U ) следующей формулой:

F (z) = fi

2

◦ f ◦ fi

1

(z):

Указание. Воспользоваться предыдущей задачей и конформностью

инверсии.

Замечание. Если области U и fi

1

(U ) пересекаются, то функция f

аналитически продолжается в fi

1

(U ), но функция F на области ~

U будет,

вообще говоря, многозначной.

Задача 14.3. Пусть G — многоугольник на плоскости, стороны кото-

рого — дуги окружностей. Тогда по теореме Римана существует вза-
имно однозначное аналитическое отображение f :

→ G, где — верх-

няя полуплоскость Im z > 0. По теореме о продолжаемости до границы
отображение f непрерывно продолжается на ось вещественных чисел,
пополненную точкой

∞, причем полученное отображение вещественной

проективной прямой на границу @G многоугольника G является гомео-
морфизмом. Обозначим через A

1

; : : : ; A

n

прообразы последовательных

вершин A

1

; : : : ; A

n

многоугольника G.

1) Доказать, что отображение f непрерывно продолжается в ниж-

нюю полуплоскость вдоль любого интервала A

i

; A

i+1

вещественной оси

34

(один из этих интервалов содержит

∞). Это означает, что существует

функция F : ~

U

→ C , где ~

U — это обединение верхней полуплоскости ,

нижней полуплоскости (z

∈ , если Im z < 0) и интервала A

i

; A

i+1

.

2) Что собой представляет образ нижней полуплоскости при ото-

бражении F ?

3) Доказать, что росток f

a

отображения f в точке a

∈ аналити-

чески продолжается вдоль любой кривой ‚ : I

→ C , ‚(0) = a, не прохо-

дящей через точки A

1

; : : : ; A

n

.

Задача 14.4. Пусть в условиях предыдущей задачи G — треугольник

с нулевыми углами, вписанный в единичную окружность и имеющий
вершины A

1

; A

2

; A

3

. Сделав, если нужно, вещественное дробно-линей-

ное преобразование u =

az + b
cz + d

, где a; b; c; d;

∈ R, можно считать, что

A

1

= 0, A

2

= 1, A

3

=

∞. Рассмотрим многозначную аналитическую

функцию ъ :

C \ {0; 1} → C , полученную аналитическим продолжени-

ем функции f :

→ G. Доказать, что функция ъ

−1

определена и голо-

морфна в открытом единичном круге (и, стало быть, что все значения
многозначной функции ъ по модулю не превосходят единицы).

Указание. Пусть G

— треугольник, полученный инверсией тре-

угольника G относительно одной из его сторон. Тогда G

тоже впи-

сан в единичную окружность. Треугольник G

снова можно инверсион-

но отразить в одной из его сторон. Получится треугольник G

, тоже

вписанный в единичную окружность. Повторяя эту процедуру, мож-
но получить ъпаркетё, замощающий внутренность единичного круга и
состоящий из треугольников, полученных из G последовательными ин-
версиями.

Задача 14.5. Аналитическая функция, определенная на всей ком-

плексной плоскости, называется

целой функцией. Показать, что вся-

кая целая функция g :

C → C , не принимающая значение a, имеет вид

g = e

f

+ a, где f — целая функция.

Указание. Рассмотреть однозначную ветвь функции ln(g(z) − a) на

комплексной плоскости. (Почему такая однозначная ветвь существует?)

Задача 14.6 (теорема Пикара). Всякая целая функция g : C → C , не

принимающая двух значений a и b, является константой.

Указание. Пусть ъ — функция из задачи 14.4. Тогда многозначная

функция ъ

z

− a

b

− a

продолжается вдоль любой кривой, не проходящей

через a и b, и все ее значения не превосходят по модулю единицы.
Рассмотреть однозначную ветвь на комплексной плоскости функции

ъ

g(z) − a

b

− a

. (Почему такая однозначная ветвь существует?) Восполь-

зоваться теоремой Лиувилля.

35

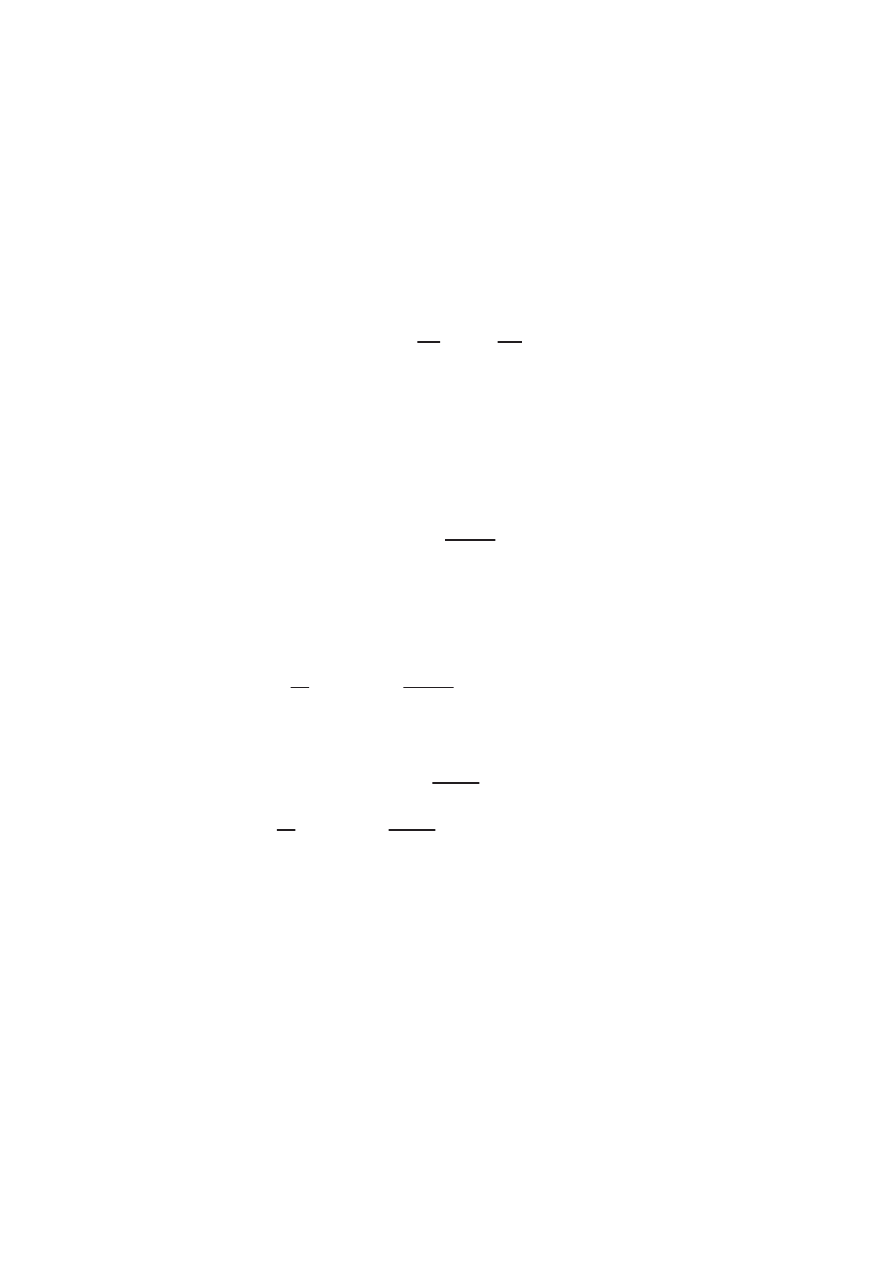
ДОПОЛНЕНИЕ 1

15. Гармонические функции многих переменных

Оператор Лапласа ´ в

R

n

— это дифференциальный оператор

´ =

@

2

@x

2

1

+ : : : +

@

2

@x

2

n

:

Задача 15.1. Для всякой функции f класса C

2

в области U

⊂ R

n

спра-

ведливо тождество

´f = div grad F:

Определим оператор усреднения Mid(R; a). Пусть S

R;a

и B

R;a

— сфе-

ра и шар радиуса R с центром в точке a

∈ R

n

. Для всякой непрерыв-

ной функции f в области, содержащей сферу S

R;a

, определим число

Mid(R; a)f как среднее значение функции f по сфере S

R;a

, т. е.

Mid(R; a)f =

1

V (S

R;a

)

S

R;a

f;

где — форма (n

− 1)-мерного обема на сфере S

R;a

, V (S

R;a

) —

(n

− 1)-мерный обем сферы S

R;a

.

Задача 15.2. Для всякой функции f класса C

2

в области U , содержа-

щей шар B

R

0

;a

радиуса R

0

с центром в точке a, при R < R

0

справедливо

тождество

d

dR

Mid(R; a)f

≡

1

V (S

R;a

)

B

R;a

´f dx

1

∧ : : : ∧ dx

n

:

Указание. Пусть a = 0. Растяжением в R

−1

раз интеграл по сфере

S

R;0

сводится к интегралу по фиксированной сфере S

1;0

:

Mid(R; 0)f =

1

V (S

1;0

)

S

1;0

f(Rx):

Поэтому

d

dR

Mid(R; 0)f =

1

V (S

1;0

)

S

1;0

~n; gradf(R; x), где ~n — единич-

ная нормаль к единичной сфере в точке x. Преобразовать последний
интеграл, используя формулу Стокса.

Задача 15.3. Пусть f — функция класса C

2

в области U . Тогда:

1) если в области U выполнено неравенство ´f > 0, то Mid(R; a)f

f(a);

2) если в области U выполнено неравенство ´f < 0, то Mid(R; a)f

f(a);

36

3) если в области U выполнено тождество ´f

≡ 0, то Mid(R; a)f =

= f(a).

(В задаче предполагается, что область U содержит шар B

R;a

ради-

уса R с центром в точке a.)

Определение 1 (классическое определение гармонической функции).

Функция f класса C

2

в области U называется

гармонической в этой

области, если справедливо тождество

´f

≡ 0:

Задача 15.4. Обозначим через r(x) расстояние от точки x ∈ R

3

до

точки 0. Проверить, что функция f(x) =

1

r(x)

является гармонической

функцией в

R

3

\ 0 и что градиент этой функции по длине равен

1

r

2

(x)

и направлен от точки 0.

Замечание. Согласно закону всемирного тяготения сила гравитаци-

онного притяжения к массе, расположенной в точке 0, пропорциональ-

на градиенту функции

1

r(x)

(коэффициент пропорциональности зави-

сит от массы). По задаче 15.4 потенциал силы притяжения к массив-
ной точке, а значит, и к любой системе точек, является гармонической
функцией вне области, содержащей эти точки. Аналогичное верно и
для сил электрического притяжения. Это одна из причин, по которым
гармонические функции играют столь фундаментальную роль в мате-
матической физике.

Определение 2 (интегральное определение гармонической функции).

Непрерывная функция f в области U называется

гармонической в обла-

сти U , если для всякой точки a и шара B

R;a

таких, что B

R;a

⊂ U, вы-

полняется равенство

Mid(R; a)f = f(a):

Приведем еще одно близкое определение.
Непрерывная функция f в области U называется

субгармонической

в области U , если для всякой точки a и шара B

R;a

таких, что B

R;a

⊂ U,

выполняется неравенство

Mid(R; a)f

f(a):

Задача 15.5. 1) Если к определению 2 добавить требование гладко-

сти f, f

∈ C

2

, то определения 1 и 2 станут эквивалентными.

2) Функция f класса C

2

является субгармонической, если и только

если выполняется неравенство ´f

0.

Указание. См. задачу 15.3.

37

Для следующей задачи нам понадобится обобщенная формула Сток-

са в векторной форме. Рассмотрим в пространстве

R

n

стандартное

скалярное произведение. В этом случае обобщенный вариант (так же
как и классический вариант) формулы Стокса допускает векторную
трактовку. Приведем ее.

Обобщенная формула Стокса в векторном виде. Пусть U — ком-

пактная область с гладкой границей @U в пространстве R

n

, пусть

V = (P

1

; : : : ; P

n

)

— векторное поле, коэффициенты P

i

которого име-

ют дифференциалы в замыкании области U и дивергенция которо-
го div V =

@P

1

@x

1

+ : : : +

@P

n

@x

n

непрерывна в замыкании этой области.

Тогда поток

@U

~V ;

−→

dS

векторного поля через границу области (здесь

−→

dS

— вектор, ортогональный границе @U области U, направленный

наружу и равный по длине (n − 1)-мерному обему рассматриваемо-

го малого элемента dS границы этой области) равен интегралу ее
дивергенции

U

div V dx

1

∧ : : : ∧ dx

n

.

Обобщенная формула Стокса в векторном виде не нуждается в от-

дельном доказательстве, поскольку она является переформулировкой
обобщенной формулы Стокса (см. раздел ъОб обобщенной формуле
Стокса. . . ё предисловия).

Определение 3 (определение гармонической функции в духе Гурса).

Функция f класса C

1

в области U

⊂ R

n

называется

гармонической в

области U , если

1) функция f в каждой точке имеет второй дифференциал (другими

словами, отображение grad f : U

→ R

n

в каждой точке имеет первый

дифференциал);

2) справедливо тождество ´f

≡ 0.

Задача 15.6. Всякая функция, являющаяся гармонической в смысле

определения 3, является гармонической в интегральном смысле.

Указание. Можно действовать, как в задаче 15.5, но вместо класси-

ческой формулы Стокса нужно использовать ее обобщенный вариант.

Гармоническая функция в смысле классического определения, ра-

зумеется, является гармонической в смысле определения 3. В зада-
чах 15.7, 15.8 мы проверим, что функция, удовлетворяющая интеграль-
ному определению гармонической функции, автоматически является
гладкой. Поэтому определения 1, 2 и 3 эквивалентны.

Задача 15.7. Пусть ’: R

n

→ R— такая непрерывная функция, что

1) ’ зависит лишь от расстояния точки до нуля, т. е. ’(x) = g(

x);

2) ’ обращается в нуль во всех достаточно удаленных от нуля точ-

ках;

38

3)

R

n

’(x) dx

1

∧ : : : ∧ dx

n

≡ 1.

Проверить,

что

если

для

функции

f

выполнено

тождество

Mid(R; a)f

≡ f(a), то

R

n

f(x)’(x

− a) dx ≡ f(a). (Здесь предполага-

ется, что область U содержит шары B

R;a

, о которых идет речь в

первом тождестве, и носители функций ’(x

− a), о которых идет речь

во втором тождестве.)

Задача 15.8. Если для функции f справедливо тождество Mid(R; a) ≡

≡ f(a), то функция f гладкая.

Указание. Воспользоваться тождеством из задачи 15.7 для гладкой

функции ’(x

− a).

Задача 15.9. 1) Для гармонических функций справедлив принцип

максимума: если гармоническая функция достигает максимума во вну-
тренней точке связной области U , то эта функция постоянна.

Указание. Воспользоваться интегральным определением гармониче-

ской функции.

2) Для субгармонических функций также справедлив принцип мак-

симума: если субгармоническая функция достигает максимума во вну-
тренней точке связной области U , то эта функция постоянна.

Задача 15.10. Пусть функции f

1

; : : : ; f

n

; : : : в области U равномерно

сходятся к функции f. Тогда

1) если функции f

i

гармонические, то функция f тоже гармониче-

ская в U ;

2) если функции f

i

субгармонические, то функция f тоже субгар-

моническая в U .

Указание. Воспользоваться интегральным определением гармониче-

ской функции.

Пусть на границе @U ограниченной области U задана вещественная

непрерывная функция h : @U

→ R. Задача Дирихле состоит в нахожде-

нии непрерывной в замыкании U и гармонической в U функции f такой,
что f совпадает с h на @U .

Задача 15.11. Задача Дирихле имеет не более одного решения.
Отметим, что задача Дирихле разрешима для широкого класса обла-

стей (не обязательно односвязных).

16. Гармонические функции на плоскости и

аналитические функции

Вещественная и мнимая части аналитической функции являются

гармоническими функциями. (Это несложно проверить, используя как
классическое, так и интегральное определение гармонических функ-

39

ций.) Этот факт обясняет роль аналитических функций в математиче-
ской физике — во многих физических задачах гармонические функции
зависят лишь от двух переменных, и теория таких функций сводится
к ТФКП.

Задача 16.1. Вещественная и мнимая части аналитической функции

в области U являются C

2

-гладкими функциями и удовлетворяют урав-

нению Лапласа ´f

≡ 0.

Указание. Воспользоваться гладкостью аналитических функций и

уравнениями Коши–Римана.

Задача 16.2. Вещественная и мнимая части аналитической в обла-

сти U функции удовлетворяют тождеству

Mid(R; a)f

≡ f(a):

Указание. Воспользоваться интегральной формулой Коши.

Задача 16.3. Если u— гармоническая в односвязной области U функ-

ция, то существует такая функция v (определенная с точностью до про-
извольной постоянной), что функция f = u + iv является аналитической
в области U .

Указание. Из уравнений Коши–Римана можно вычислить частные

производные

@v
@x

и

@v
@y

функции v, используя частные производные

функции u. Система

@v
@x

= p,

@v
@y

= q разрешима в односвязной обла-

сти U , если и только если

@p
@y

=

@q

@x

. Проверить, что в нашей ситуации

условие разрешимости эквивалентно тождеству ´u

≡ 0.

Задача 16.4. Пусть g — гармоническая функция в области V ⊂ C , и

пусть f : U

→ V — аналитическая функция. Тогда функция g(f) явля-

ется гармонической в области U .

Указание. См. задачи 16.1–16.3

Задача 16.5. Показать, что для всякого тригонометрического мно-

гочлена h(¸) = c

0

+

n

k=0

(a

k

sin k¸ + b

k

cos k¸) задача Дирихле разрешима.

Указание. Если |z| = 1, ¸ = arg z, то Re z

k

= cos k¸, Im z

k

= sin k¸.

Задача 16.6. Используя плотность тригонометрических многочле-

нов в множестве непрерывных функций на окружности, доказать раз-
решимость задачи Дирихле для круга.

Указание. Воспользоваться тем, что предел равномерно сходящихся

гармонических функций является гармонической функцией (см. зада-
чу 15.10) и принципом максимума.

Зная априори, что задача Дирихле для круга разрешима, несложно

написать ее решение в явном виде. Пусть мы ищем значение в точ-

40

ке a,

|a| < 1, решения задачи Дирихле ´u ≡ 0, u|

|z|=1

= h в круге

|z| 1.

Переведем точку a в точку 0 преобразованием ’

a

(z) =

z

− a

az

− 1

. Функ-

ция v(z) = u(’

−1

a

(z)) гармонична в круге

|z| < 1, и ее значение в нуле

совпадает с искомым числом u(a). Имеем

u(a) = v(0) =

1

2ı

|z|=1

h(’

−1

a

(z))

|dz| =

1

2ı

|‰|=1

h(‰)

d

d‰

’

a

(‰)

|d‰|:

Задача 16.7 (формула Пуассона). 1) Явно вычислить ядро Пуассона

d

d‰

’

a

(‰)

|d‰|;

зависящее от точки ‰ на единичной окружности

|‰| = 1 и точки a внутри

единичного круга.

2) Проверить, что ядро Пуассона является вещественно-аналитиче-

ской функцией (т. е. ряд Тейлора этой функции является сходящимся)
от координат x(a); y(a) в точке a.

3) Из вещественной аналитичности ядра Пуассона как функции от a

вытекает вещественная аналитичность гармонической функции двух
переменных (не обязательно в круге, а в любой области плоскости).
Почему?

Отметим, что задача Дирихле в многомерном шаре так же явно ре-

шается при помощи явно выписываемого ядра Дирихле, являющегося
вещественно-аналитической функцией. Отсюда вытекает, что гармони-
ческие функции многих переменных являются вещественно-аналитиче-
скими функциями.

Задача 16.8. Для всякой односвязной области U ⊂ C

2

, для которой

выполнены условия непрерывной продолжаемости до границы отобра-
жения Римана (см. п. 12), задача Дирихле разрешима. Более того, если
явно написано отображение Римана области U в единичный круг, то
для всякой задачи Дирихле в области U можно написать явное решение.
Почему?

Задача 16.9. На комплексной плоскости оператор Лапласа ´ =

@

2

@x

2

+

+

@

2

@y

2

представим в виде ´ = 4

@

@z

@

@z

, где z = x + iy, а операторы

@

@z

,

@

@z

определены в п. 4.

17. Субгармонические функции и теорема единственности

Задача 17.1 (формула Йенсена). Пусть функция f голоморфна в за-

мыкании круга радиуса R с центром в точке 0. Доказать следующую

41

формулу:

1

2ıR

|z|=R

ln

|f| ds = ln |f(0)| +

f(z

i

)=0; |z

i

|<R

ln

R

|z

i

|

;

где нули функции f входят в последнюю сумму с учетом кратности.

Указание. Провести доказательство в три этапа:
1) доказать, что если формула Йенсена верна для функций f и g, то

она верна и для произведения fg;

2) доказать формулу Йенсена для функций, не имеющих нулей в

рассматриваемом круге;

3) для каждой точки a круга построить явно такую функцию f

(голоморфную в замыкании данного круга), что f обращается в нуль
только в точке a, а модуль f тождественно равен 1 на граничной окруж-
ности. Проверить формулу для таких функций.

Обединяя все три пункта, доказать утверждение задачи.
Нам понадобится немного расширить определение субгармониче-

ской функции на плоскости, разрешив функции принимать значе-
ние

−∞. Ниже под словами ъсубгармоническая функцияё мы имеем в

виду следующее чуть более общее понятие.

Определение. Пусть U — область в комплексной плоскости, и

A

⊂ U — дискретное подмножество. Рассмотрим вещественнозначную

функцию f на U

\ A, которая в точках множества A ъравна −∞ё. Такая

функция считается непрерывной, если функция e

f

: U

→ R, доопреде-

ленная в точках множества A числом 0, непрерывна. Функция такого
вида называется

субгармонической, если для всякого круга |z − a| R,

целиком лежащего в области U , выполнено неравенство

1

2ıR

|z−a|=R

f(z) ds

f(a):

Если окружность

|z − a| = R содержит точки множества A, то предпо-

лагается, что интеграл, стоящий в левой части неравенства, существует
как несобственный интеграл.

Задача 17.2. Обобщить формулу Йенсена на случай, когда окруж-

ность

|z| = R содержит нули функции f(z). Доказать, что функ-

ция ln

|f(z)| субгармонична в области U, в которой функция f ана-

литична.

Задача 17.3. Обобщить формулу Йенсена на случай мероморфных

функций.

Задача 17.4 (принцип максимума для субгармонических функций).

Рассмотрим функцию f, субгармоническую в связной области G. Пред-

42

положим, что существует такая точка a

∈ G, что для любой точки z ∈ G

выполнено неравенство f(a)

f(z). Доказать, что f — константа.

Задачи 17.5–17.7 представляют собой варианты принципа макси-

мума.

Задача 17.5. Рассмотрим ограниченную сверху субгармоническую

функцию u в области G. Обозначим через ` границу области G. Для
каждой точки a границы положим

—

u(a) =

lim

z→a; z∈G

u(z):

Доказать, что для произвольной точки x области G выполнено нера-
венство u(x)

sup

a∈`

—

u(a).

Задача 17.6. В условиях предыдущей задачи предположим, что

область G ограничена и ее диаметр равен D. На границе ` области G
отметим произвольные точки a

1

; : : : ; a

k

. Пусть ~

` = `

\ {a

1

; : : : ; a

k

}. До-

казать, что для любой точки x области G выполнено неравенство
u(x)

sup

a∈~`

—

u(a).

Указание. Воспользоваться принципом максимума для функции

u

"

= u + "

ln

|x − a

i

|

D

:

В качестве " здесь нужно рассматривать произвольное положительное
число.

Задача 17.7. Перенести утверждение предыдущей задачи на неогра-

ниченную область G, дополнение которой до сферы Римана имеет хотя
бы одну внутреннюю точку.

Задача 17.8. Если отбросить требования ограниченности сверху суб-

гармонической функции, то утверждение задачи 17.6 станет неверным.
Привести пример ненулевой гармонической в верхней полуплоскости
функции, которая непрерывно продолжается на вещественную ось и
тождественно равна нулю на этой оси.

Задача 17.9. Рассмотрим замкнутый круг B на комплексной прямой.
1) Отметим на граничной окружности различные точки A

1

и A

2

.

Предявить такую ограниченную гармоническую во внутренности
круга B функцию, что она непрерывна вплоть до граничной окруж-
ности за исключением точек A и B, равна 1 на дуге AB и равна 0 на
дополнительной дуге. Доказать, что функция, удовлетворяющая усло-
виям задачи, единственна. Нарисовать картину ее линий уровня.

Указание. Функция

1

2ı

arg z гармонична и ограничена в верхней по-

луплоскости. На вещественной прямой она равна нулю для положитель-
ных z и единице для отрицательных z.

43

2) Предположим теперь, что граничная окружность разбита на

n дуг l

1

; : : : ; l

n

. Сформулировать и решить задачу, аналогичную п. 1).

Задача 17.10. Пусть B — замкнутый круг на комплексной прямой.

Отметим на граничной окружности дугу между различными точка-
ми A

1

и A

2

. Для каждого действительного числа A рассмотрим такую

ограниченную гармоническую во внутренности круга B функцию f

A

,

что f

A

тождественно равна A на дуге A

1

A

2

и тождественно равна не-

которой константе C (фиксированной для всех функций) на дополни-
тельной дуге. Доказать, что для любой внутренней точки круга B вы-
полнено равенство

lim

A→−∞

f

A

(x) =

−∞:

Определение. Точку a, принадлежащую границе области G, назовем

простой граничной точкой этой области, если каждая достаточно ма-
лая окружность с центром в точке a содержит дугу, целиком лежащую
в дополнении к G.

Задача 17.11 (граничная теорема единственности). Пусть f : G →

→ C — ограниченная аналитическая функция в области G, и
пусть a — простая граничная точка этой области. Если для некото-
рого " > 0 выполнено равенство lim

z→b

f(z) = 0 для всякой точки b

∈ @G

такой, что

|a − b| < ", то f(z) ≡ 0.

Указание. На достаточно малом круге B с центром в точке a рас-

смотреть гармоническую функцию u

A

, равную

−A на некоторой ду-

ге `

1

окружности @B, лежащей вне области G, и равную ln

|c| на до-

полнительной дуге окружности @B. Здесь A — большое отрицательное
число и c = sup

z∈G

|f(z)|. Доказать, что при z ∈ B ∩ G справедливо нера-

венство u

A

(z)

ln |f(z)|. Воспользовавшись задачей 17.9, показать, что

f(z)

≡ 0.

Задача 17.12. Обобщить граничную теорему единственности на лю-

бую (не обязательно простую) граничную точку a, предполагая, что
область G односвязна.

Указание. Воспользоваться (локально) отображением

√

z

− a. Про-

верить, что образ точки a будет простой граничной точкой для образа
области G.

ДОПОЛНЕНИЕ 2

18. Формула Стокса для областей с гладкой границей

После того как классическая или обобщенная формула Стокса до-

казана для кубов, ее легко доказать для областей в

R

n

(и для ори-

44

ентированных гладких многообразий) с гладкой границей. Для этого
достаточно воспользоваться разбиением единицы. Напомним, как это
делается.

Определение. Пусть X ⊆ R

n

— компакт, и U

¸

— любое покрытие

этого компакта открытыми множествами.

Разбиением единицы, со-

гласованным с покрытием U

¸

, называется конечное множество глад-

ких функций ’

i

, i = 1; : : : ; N , определенных в некоторой окрестности

компакта X, таких, что

1) ограничение функции ’

1

+ : : : + ’

N

на X тождественно равно

единице;

2) для каждой функции ’

i

существует открытое множество U

¸

i

из

покрытия такое, что функция ’

i

тождественно равна нулю на допол-

нении к множеству U

¸

i

Задача 18.1. Для всякого компакта X ⊂ R

n

и всякого его покры-

тия U

¸

существует согласованное с этим покрытием разбиение едини-

цы ’

1

; : : : ; ’

N

, в котором ’

i

— бесконечно гладкие функции.

Указание. 1) Существует неотрицательная бесконечно гладкая

функция в

R

n

, равная единице в круге радиуса R

0

и равная нулю

вне круга радиуса R

1

с тем же центром, где R

1

> R

0

;

2) используя функцию из 1) и компактность X, построить конечный

набор функций g

1

; : : : ; g

N

, каждая из которых равна нулю вне некото-

рого множества U

¸

i

, но сумма F =g

1

+: : :+g

N

строго больше нуля на X;

3) функции ’

i

= g

i

=F дают искомое разбиение единицы.

Локальной картой около точки a ∈ R

n

называется окрестность U

a

точки a вместе с диффеоморфизмом

x: U

a

→ V на область V в R

n

таким, что

x(a) = 0. Компоненты x

1

; : : : ; x

n

вектор-функции

x называ-

ются

локальными координатами в карте U

a

.

Определение. Граница @U области U в R

n

называется

гладкой в

окрестности точки a

∈ @U, если существует локальная карта в окрест-

ности этой точки такая, что в локальных координатах x

1

; : : : ; x

n

замы-

кание области задается неравенством x

n

0.

Задача 18.2. Пусть замыкание области U в R

n

задано неравенством

f

0, где f — гладкая функция, дифференциал df которой не обра-

щается в нуль ни в одной точке поверхности f = 0. Доказать, что
область U имеет гладкую границу.

Пусть U — ограниченная область в

R

n

с гладкой границей. Фикси-

руем локальные координаты U

a

около каждой точки a замыкания обла-

сти U . Для граничных точек a

∈ @U мы предполагаем, что локальная

система координат около точки a удовлетворяет условиям предыдуще-
го определения. Рассмотрим стандартные кубы ´

"

и ~

´

"

в простран-

стве

R

n

, определенные неравенствами

−" x

1

"; : : : ; −" x

n

" и

45

−" x

1

"; : : : ; −" x

n−1

"; 0 x

n

2". Подходящим кубом ´

"

a

для

точки a в локальной карте U

a

с координатами

x: U

a

→ R

n

будем на-

зывать множества

x

−1

(´

"

a

), если a — внутренняя точка области U

a

, и

x

−1

( ~

´

"

a

), если a — граничная точка области U

a

. При этом предполага-

ется, что образ

x(U

a

) карты U

a

целиком содержит соответствующий

куб ´

"

a

или ~

´

"

a

.

Задача 18.3. Пусть U — ограниченная область в R

n

, a

∈ U — точ-

ка в этой области и ´

"

a

— подходящий куб около точки a. Пусть

! — (n

− 1)-форма в R

n

, равная нулю вне куба ´

"

a

и удовлетво-

ряющая условиям обобщенной формулы Стокса (т. е. коэффициенты
формы ! имеют дифференциалы, а форма d! непрерывна). Тогда

U

d! =

@U

! = 0.

Задача 18.4. Пусть U — ограниченная область в R

n

, a

∈ @U — точка

границы этой области и ~

´

"

a

— подходящий куб около точки a. Пусть

! — (n

− 1)-форма в R

n

, равная нулю вне куба ~

´

"

a

и удовлетворяющая

условиям обобщенной формулы Стокса. Тогда

@U

! =

U

d!.

Задача 18.5. Пусть ! — форма, удовлетворяющая условиям обобщен-

ной формулы Стокса в замыкании ограниченной области U с гладкой
границей @U , и пусть ’

1

; : : : ; ’

N

— некоторое разбиение единицы на

большом шаре B, содержащем замыкание области U в своей внутрен-
ности, такое, что для каждой формы !

i

= ’

i

! справедлива формула

Стокса

@U

!

i

=

U

d!

i

. Тогда

@U

! =

U

d!.

Задача 18.6. Доказать обобщенную формулу Стокса для произволь-

ной компактной области с гладкой границей.

Указание. Достаточно подобрать разбиение единицы на большом

шаре B, для которого выполняются условия задачи 18.5. Для этого
достаточно взять разбиение единицы, согласованное с покрытием ша-
ра B следующими открытыми множествами V

p

. Для всякой точки p

∈ B

определим V

p

следующим образом:

1) если p не лежит в замыкании области U , то в качестве V

p

можно

взять любое открытое множество, для которого p

∈ V

p

, V

p

∩ U = ∅;

2) если p принадлежит замыканию области U , сначала фиксируем

локальную карту x

1

; : : : ; x

n

около точки p и подходящий куб ´

"

p

для точ-

ки p и этой карты. После этого в качестве V

p

достаточно взять любое

открытое множество, для которого: 1) p

∈ V

p

, 2) V

p

⊂ B, 3) V

p

∩ U ⊂ ´

"

p

.

Проверить, что выполнимость условий задачи 18.5 для разбиения

единицы, согласованного с покрытием V

p

, вытекает из задач 18.3 и 18.4.

46

Оглавление

Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3

1.

Теорема Лагранжа для функций множеств . . . . . . . . . . .

7

2.

Формула Стокса для линейных форм в единичном кубе . . . .

9

3.

Обобщенная формула Стокса в единичном кубе . . . . . . . . 11

4.

Линейная алгебра и теорема Коши . . . . . . . . . . . . . . . . 12

5.

Форма

dz

z

и интегральная формула Коши . . . . . . . . . . . . 14

6.

Локальные свойства аналитических отображений . . . . . . . 16

7.

Инверсия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

8.

Сфера Римана . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

9.

Вычеты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

10.

Геометрия Лобачевского и ТФКП . . . . . . . . . . . . . . . . 23

11.

Компактность функциональных множеств
и теорема Римана . . . . . . . . . . . . . . . . . . . . . . . . . . 26

12.

Продолжаемость до границы . . . . . . . . . . . . . . . . . . . 27

13.

Римановы поверхности аналитических функций . . . . . . . . 29

14.

Принцип симметрии Римана–Шварца. Теорема Пикара . . . . 34

15.

Гармонические функции многих переменных . . . . . . . . . . 36

16.

Гармонические функции на плоскости и аналитические
функции

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

17.

Субгармонические функции и теорема единственности . . . . 41

18.

Формула Стокса для областей с гладкой границей . . . . . . . 44

О НЕЗАВИСИМОМ МОСКОВСКОМ

УНИВЕРСИТЕТЕ

НМУ — негосударственное высшее учебное заведение для подготовки
профессиональных математиков.

Занятия в НМУ проводятся в вечернее время (обычно с 17.30). Это
связано с тем, что многие наши студенты совмещают обучение в НМУ
с занятиями в другом вузе (как правило — но не исключительно! — на
мехмате МГУ). Наши занятия по физике и математике может посещать
любой желающий (не обязательно студент или аспирант НМУ).

Обучение в НМУ бесплатное. Студентам выплачивается стипендия.

Наш адрес:
119002, Москва, Б. Власьевский пер., д. 11.
Телефон:
[phone].
Факс:
[phone].
E-mail:
[e-mail]

Подробности см. на сайте

http://ium.mccme.ru/