MODELOWANIE INśYNIERSKIE

ISSN 1896-771X

36, s. 11-18, Gliwice 2008

MODELOWANIE KINETYKI SŁONECZNEGO SUSZENIA OSADÓW

ŚCIEKOWYCH W WARUNKACH DOBY WZORCOWEJ

K

RZYSZTOF

B

ADYDA

,

P

IOTR

K

RAWCZYK

Zakład Maszyn i Urządzeń Energetycznych, Instytut Techniki Cieplnej, Politechnika Warszawska
e-mail: [e-mail], [e-mail]

Streszczenie. W niniejszym artykule omówiono podstawowe założenia modelu

matematycznego słonecznego suszenia osadów ściekowych. Przedstawiono
również wyniki uzyskane z omawianego modelu w warunkach letniej doby
wzorcowej.

1. WSTĘP

Specyficzna struktura fizyko – chemiczna osadów ściekowych sprawia, że nawet po

mechanicznym odwodnieniu wciąż zawierają w swojej masie ponad 70% wody. Ich
ostateczne zagospodarowanie na tym etapie przetworzenia nastręcza wielu problemów
(transport, składowanie).

Suszenie słoneczne wydaje się być najprostszą i najtańszą w eksploatacji technologią

redukcji masy osadów ściekowych, mogącą zracjonalizować gospodarkę osadową małych i
średnich oczyszczalni ścieków.

W 2005 r. w Instytucie Techniki Cieplnej Politechniki Warszawskiej został opracowany

projekt suszarni słonecznej osadów ściekowych, na podstawie którego w oczyszczalni
ścieków w Skarżysku Kamiennej zrealizowano pilotażową instalację suszarniczą.

Projekt zakładał umieszczenie na nieprzepuszczalnej płycie betonowej, lekkiej konstrukcji

stalowej pokrytej płytami poliwęglanowymi. Wewnątrz obiektu zlokalizowano instalację
wentylacyjną oraz przegarniania osadów. Instalacja wentylacyjna została skonfigurowana w
sposób zapewniający równomierne rozprowadzanie powietrza po powierzchni suszonych
osadów poprzez system nawiewników.

Projektowanie procesów suszenia, w których powierzchnia ciała suszonego poddawana jest

działaniu gazu suszącego wypływającego z dyszy, napotyka poważne trudności wynikające z
faktu, że wraz ze wzrostem odległości od osi dyszy zmieniają się warunki transportu ciepła i
masy między wilgotną powierzchnią a fazą gazową. Zmiany dotyczą zarówno warunków
hydrodynamicznych decydujących o lokalnych wartościach współczynników wnikania, jak i
siły napędowej procesu, określanej przez temperaturę wilgotnej powierzchni w danym
miejscu oraz parametry fazy gazowej. Dodatkową trudnością jest uwzględnienie zmiennego w
czasie strumienia ciepła wynikającego z promieniowania słonecznego.

Okoliczności te sprawiają, że zawodzą tu tradycyjne metody opisu procesu suszenia i w

celu pełnego scharakteryzowania należy podejmować próby opisu procesu z wykorzystaniem
równań transportu pędu, masy i ciepła.

12

K. B

ADYDA

,

P.

K

RAWCZYK

Autorzy referatu nie odnaleźli w dostępnej literaturze informacji na temat istniejących

modeli opisujących kinetykę słonecznego suszenia osadów ściekowych w warunkach
pierwszego i drugiego okresu suszenia.

Autorzy wyrażają jednocześnie nadzieję, że dzięki stworzonemu modelowi możliwa będzie

optymalizacja układu technologicznego oraz harmonogramu pracy słonecznych suszarni
osadów ściekowych.

2. PODSTAWOWE ZAŁOśENIA MODELU SŁONECZNEGO SUSZENIA OSADÓW

Zakresem zaproponowanego modelu objęto transport ciepła i masy:

• w materiale suszonym (osadach ściekowych);
• w otaczającym materiał suszony powietrzu;
• na granicy tych dwóch ośrodków.

Ze względu na zmieniające się w czasie właściwości termodynamiczne osadów oraz

warunki suszenia, (natężenie promieniowania słonecznego, wilgotność i temperaturę
powietrza wentylacyjnego), zachodzące wewnątrz suszarni procesy cieplno – przepływowe
należy traktować jako nieustalone.

2.1. Transport ciepła i masy w powietrzu

Modelowanie procesu transportu ciepła i masy w otaczającym materiał suszonym

powietrzu wymaga rozwiązania równań mechaniki płynów, tzn. równania ciągłości,
zachowania pędu, zachowania energii oraz transportu składnika.

W równaniach tych występują właściwości fizykochemiczne płynu, którego stan jest

opisywany. W omawianym problemie jest to wilgotne powietrze traktowane jako mieszanina:
tlenu, azotu i pary wodnej.

Równanie transportu pary wodnej w powietrzu można zapisać w postaci:

(

)

(

)

)

(

2

2

2

O

H

i

O

H

i

i

O

H

J

x

Y

u

x

Y

t

∂

∂

−

=

∂

∂

+

∂

∂

ρ

ρ

(1)

gdzie:
ρ – gęstość powietrza;
Y

H2O

– ułamek masowy pary wodnej w powietrzu;

J

H2O

– dyfuzyjny strumień pary wodnej w powietrzu;

u

i

– składowa prędkości powietrza (dla i=1 na kierunek x, dla i =2 na kierunek y, dla i =3 na

kierunek z)
x

i

– zmienna (dla i =1, x; dla i=2, y; dla i=3, z).

Dla obliczenia dyfuzyjnego strumienia masy pary wodnej w powietrzu posłużono się

równaniem:

(

)

i

O

H

O

H

O

H

x

Y

T

D

J

∂

∂

=

2

2

2

)

(

ρ

(2)

W którym D

H2O

(T) - współczynnik dyfuzji pary wodnej w powietrzu [1]:

8

1

273

28

,

2

)

(

2













⋅

=

T

P

T

D

O

H

(3)

P – ciśnienie powietrza [bar]; T – temperatura powietrza [K];

M

ODELOWANIE KINETYKI SŁONECZNEGO SUSZENIA OSADÓW ŚCIEKOWYCH W

…

13

Prezentowane powyżej równanie (2) opisuje również strumień masy odprowadzanej z

wilgotnej powierzchni suszonego materiału. Dla sprecyzowania tegoż strumienia wymagane
jest określenie warunku brzegowego, tzn. ułamka masowego pary wodnej w powietrzu
znajdującym się w kontakcie z powierzchnią suszonych osadów.

Zależność na ułamek masowy pary wodnej w powietrzu pozostającym w kontakcie z

powierzchnią suszonego materiału w zależności od temperatury tejże powierzchni oraz okresu
suszenia można wyrazić jako:

w

w

a

T

f

T

Y

⋅

=

)

(

)

(

(4)

gdzie:
Y

w

(T) – ułamek masowy pary wodnej w powietrzu nad powierzchnią suszonych osadów;

f(T) – funkcja określająca ułamek masowy pary wodnej w powietrzu pozostającym w stanie
nasycenia, w zależności od temperatury powietrza;
a

w

– aktywność wody wyrażona dla osadów ściekowych w zależności od ich temperatury i

zawartości wody [2]:

A

A

w

e

e

a

+

=

1

(5)

)

(

)

(

ln

4

3

2

1

T

K

K

T

K

K

X

A

⋅

+













⋅

+

=

(6)

gdzie:

X – zawartość wody w osadach [kg H

2

O/kg s.m.o.]

K

1

, K

2

, K

3

, K

4

- stałe

T – temperatura osadów [K]

Wartość aktywności wody przyjmuje wartość a

w

=1 w I okresie suszenia oraz wartości a

w

< 1

w drugim okresie suszenia.

2.2 Transport masy w materiale suszonym

Do obliczenia szybkości ruchu wilgoci w suszonym materiale wykorzystano równanie

dyfuzji nieustalonej w postaci:













∂

∂

⋅

⋅

∂

∂

=

∂

∂

i

w

i

x

X

T

X

D

x

t

X

)

,

(

(7)

gdzie:
X – zawartość wody w osadach [kg H

2

O/kg s.m.o.];

D

w

– współczynnik dyfuzji wilgoci w osadach ściekowych [m

2

/s];

Warunek graniczny dla powyższego równania (7) stanowi strumień masy wody

odprowadzanej z powierzchni materiału suszonego do powietrza, wyznaczony na podstawie
zależności (2).
Dla wyznaczenia współczynnika dyfuzji wilgoci w osadach ściekowych posłużono się
natomiast równaniem [5]:











 −

⋅

=

T

b

X

D

T

X

D

a

exp

)

,

(

0

(8)

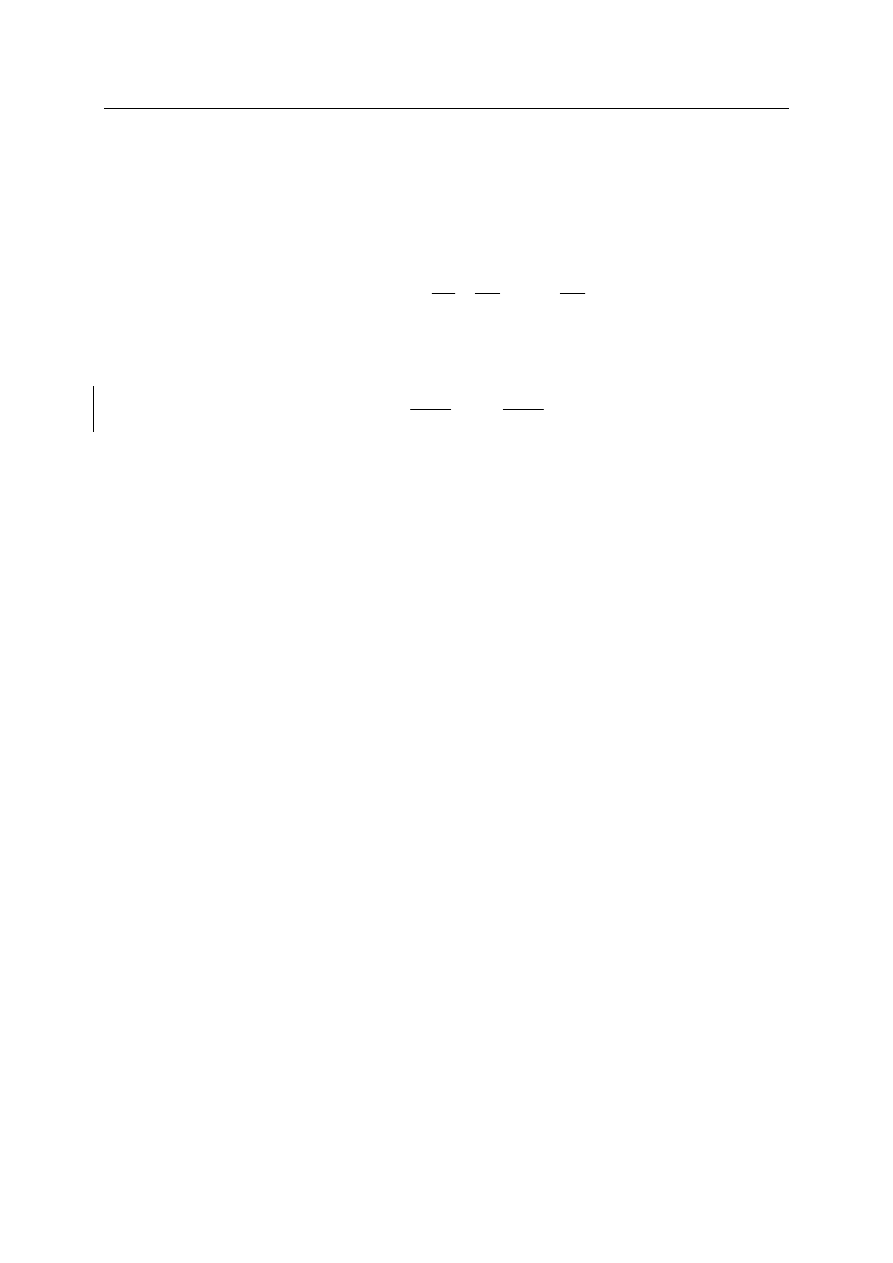
14

K. B

ADYDA

,

P.

K

RAWCZYK

gdzie:
D

0

, a, b – stałe;

T – temperatura osadów [K]

X – zawartość wody w osadach [kg H

2

O/kg s.m.o.]

2.3 Transport ciepła w materiale suszonym

Transport ciepła w suszonym materiale opisuje prawo Fouriera.













∂

∂

⋅

∂

∂

=

∂

∂

⋅

⋅

i

i

p

x

T

X

x

t

T

T

X

c

)

(

)

,

(

λ

ρ

(9)

Na podstawie badań [3] ciepło właściwe suszonych osadów w zależności od ich

temperatury i zawartości wody można obliczyć, korzystając z równań:

.

.

.

1

1

1

)

,

(

o

m

s

pw

p

c

X

c

X

X

T

X

c

⋅

+

+

⋅

+

=

(10)

t

c

o

m

s

⋅

+

=

29

,

3

1434

.

.

.

(11)

gdzie:

c

p

– ciepło właściwe osadów [J/kgK];

X – zawartość wody w osadach [kg H

2

O/kg s.m.o.]

t – temperatura osadów [

o

C]

c

s.m.o.

- ciepło właściwe suchej masy osadów [J/kgK];

c

pw

– ciepło właściwe wody (przyjęto 4187 J/kgK)

Przewodność cieplną osadów w zależności od zawartości wody można natomiast opisać

równaniem [4]:

X

e

X

⋅

−

=

0051

,

0

5148

,

0

)

(

λ

(12)

gdzie:
X – zawartość wody w osadach [kg H

2

O/kg s.m.o.]

2.4 Bilans ciepła na powierzchni suszonego materiału

W procesie suszenia jednym z kluczowych zagadnień jest sposób dostarczania ciepła

do powierzchni suszonego materiału kontaktującej się z powietrzem. Oprócz wymiany ciepła
przez przejmowanie, przewodzenie, promieniowanie, suszona powierzchnia wymienia ciepło
z otoczeniem poprzez wymianę masy.

(

)

)

,

(

)

(

T

X

h

T

r

m

q

sorp

evap

+

⋅

=

•

(13)

gdzie:

•

m

- strumień masy wody odparowywanej z powierzchni materiału suszonego [kg H

2

O/s];

r(T) – ciepło parowania wody [J/kg];
h

sorp

(X,T) – entalpia wiązania wody związanej sorpcyjnie.

Jak wykazują badania, podczas dosuszania osadów ściekowych (w II okresie suszenia)

w strumieniu ciepła wynikającego z ilości odprowadzanej wody należy uwzględnić, oprócz
ciepła parowania, ciepło wymagane do uwolnienia wody związanej sorpcyjnie z osadem.
Entalpię wiązania wody związanej sorpcyjnie dla osadów ściekowych w zależności od
temperatury i zawartości wody można, według [6], określić, posługując się zależnością:

M

ODELOWANIE KINETYKI SŁONECZNEGO SUSZENIA OSADÓW ŚCIEKOWYCH W

…

15

O

H

w

sorp

M

T

B

a

h

2

)

ln(

⋅

⋅

−

=

(14)

gdzie:
a

w

– aktywność wody

T – temperatura osadów [K]

B – uniwersalna stała gazowa [J/molK];

M

H2O

– masa molowa wody [g/mol]

3. REALIZACJA CYFROWA MODELU

W celu uzyskania rozwiązania modelu słonecznego suszenia osadów posłużono się

komercyjnym oprogramowaniem bazującym na metodzie objętości kontrolnych – programem
Fluent 6.2.16. z zaimplementowanym autorskim kodem UDF.

Rozpatrzono oddziaływanie pojedynczej kratki wentylacyjnej, w modelu dwuwymiarowym

osiowosymetrycznym o geometrii skonfigurowanej jak poniżej (rys.1).

Rys.1. Geometria modelowanego układu (po prawej) i rozkład prędkości powietrza

Prędkość powietrza opuszczającego kratkę wentylacyjną (v=8,8 m/s) oraz parametry

geometryczne modelowanego obszaru przyjęto za obiektem badawczym.
W suszarni w Skarżysku Kamiennej wyloty powietrza wentylacyjnego umieszczone są na
wysokości 3,2 m ponad posadzką, w podziałce liniowej co 6 m [7]. Siatka obliczeniowa
zbudowana w układzie cylindrycznym ma promień 3 m. Pole powierzchni wylotu powietrza
wynosi 0,05m

2

(promień 0,126m).

4. WYNIKI MODELOWANIA KINETYKI SŁONECZNEGO SUSZENIA OSADÓW
ŚCIEKOWYCH W WARUNKACH DOBY WZORCOWEJ

W celu sprawdzenia poprawności przyjętych założeń omawianego modelu postanowiono

przeprowadzić obliczenia dla jednej doby suszenia. Jako dane wejściowe dla tego zadania
posłużyły rzeczywiste dane pogodowe dla wybranej doby czerwcowej, których rozkłady
godzinowe przedstawiono poniżej.

16

K. B

ADYDA

,

P.

K

RAWCZYK

0

100

200

300

400

500

600

700

800

1

3

5

7

9

11

13

15

17

19

21

23

Godzina

N

a

tę

ż

e

n

ie

p

ro

m

ie

n

io

w

a

n

ia

s

ło

n

e

c

z

n

e

g

o

[

W

/m

2

]

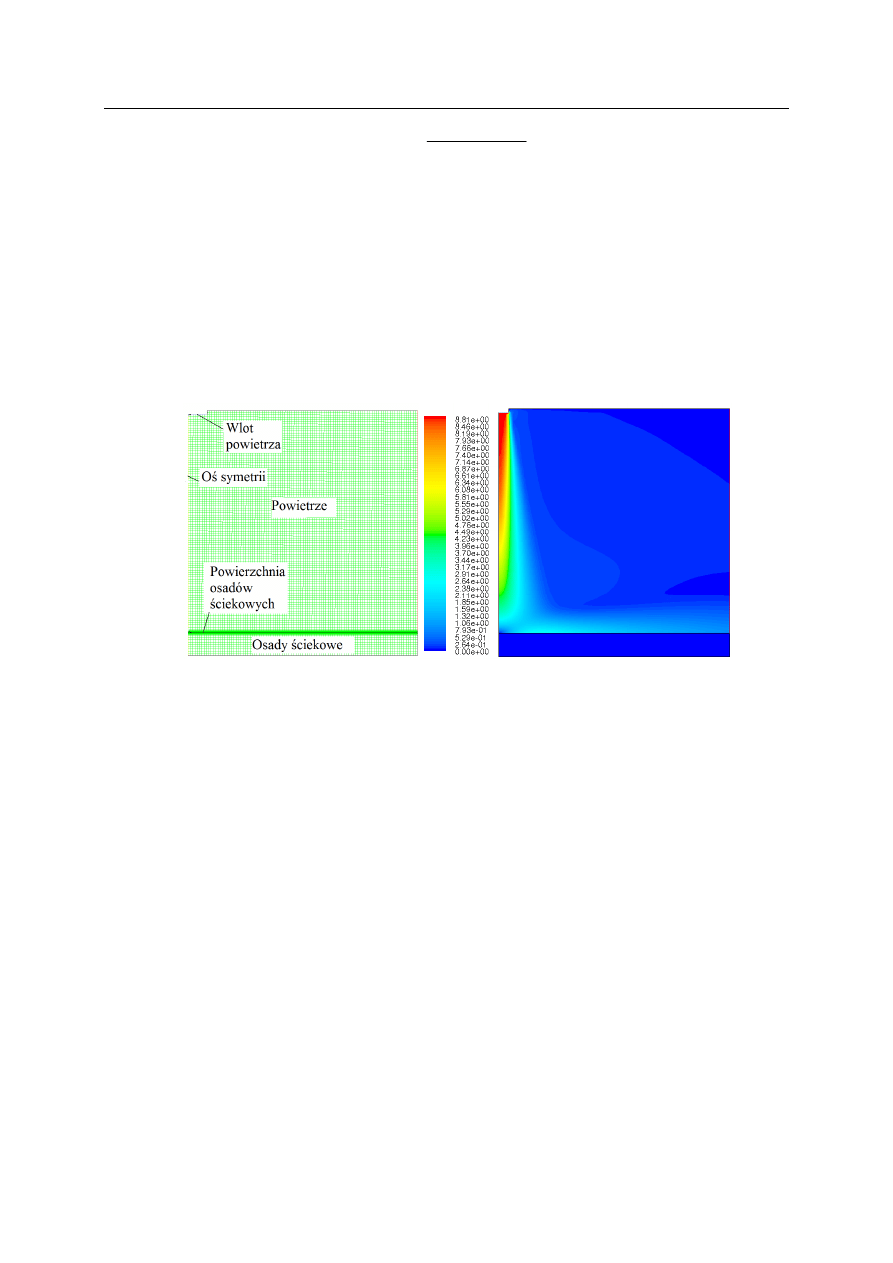
Rys.2. Dobowy rozkład natężenia promieniowania słonecznego dla modelowanej doby.

0

10

20

30

40

50

60

70

80

90

1

3

5

7

9

11

13

15

17

19

21

23

Godzina

Wilgotność względna [%]

Temperatura [C]

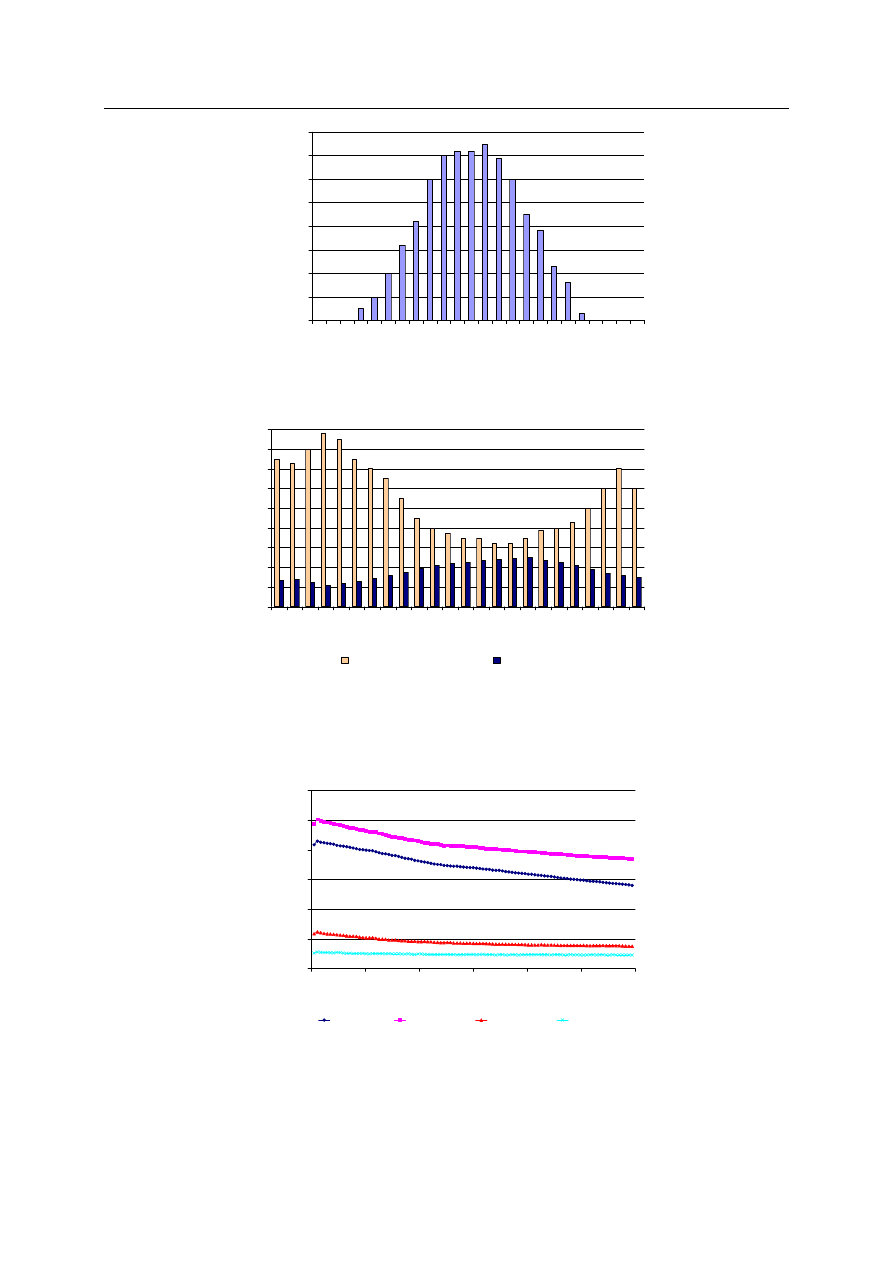
Rys.3. Dobowy rozkład wilgotności względnej i temperatury powietrza wentylacyjnego dla

modelowanej doby.

W czasie modelowanej doby suszenia założono, iż osady pozostają w pierwszym okresie

suszenia, a co za tym - idzie aktywność wody a

w

=1.

0,00000

0,00005

0,00010

0,00015

0,00020

0,00025

0,00030

0

0,5

1

1,5

2

2,5

3

Odległość od osi dyszy [m]

S

tr

u

m

ie

ń

w

o

d

y

[

k

g

/m

2

s

]

godzina 9:00

godzina 14:00

godzina 22:00

godzina 4:00

Rys.4. Strumień wody wynoszonej ze złoża suszonych osadów w funkcji odległości od osi

dyszy, dla różnych pór modelowanej doby.

M

ODELOWANIE KINETYKI SŁONECZNEGO SUSZENIA OSADÓW ŚCIEKOWYCH W

…

17

280

285

290

295

300

305

310

0

0,5

1

1,5

2

2,5

3

Odległość od osi dyszy [m]

T

e

m

p

e

ra

tu

ra

p

o

w

ie

rz

c

h

n

i

o

s

a

d

ó

w

[

K

]

godzina 09:00

godzina 14:00

godzina 22:00

godzina 04:00

Rys.5. Temperatura powierzchni suszonych osadów w funkcji odległości od osi dyszy, dla

różnych pór modelowanej doby.

Powyżej przedstawiono otrzymane w wyniku modelowania przykładowe krzywe,

obrazujące strumień wody wynoszonej ze złoża suszonych osadów (rys.4) oraz temperaturę
powierzchni złoża suszonych osadów (rys. 5) w funkcji odległości od osi dyszy wdmuchującej
powietrze wentylacyjne, dla różnych pór modelowanej doby.

W celu uzyskania dobowego rozkładu tempa odprowadzania wody z osadów uśredniono

charakterystyki (których przykłady zostały pokazane na rys. 4) według następującej zależności

∫

⋅

⋅

−

⋅

=

i

Z

i

W

i

i

R

R

W

Z

i

dr

r

W

R

R

W

π

π

2

)

(

)

(

1

2

2

(15)

gdzie:
R

zi

– promień zewnętrzny modelowanego obszaru;

R

wi

– promień wewnętrzny modelowanego obszaru;

W(r) – funkcja rozkładu strumienia wody wynoszonej z suszonych osadów (rys.4).

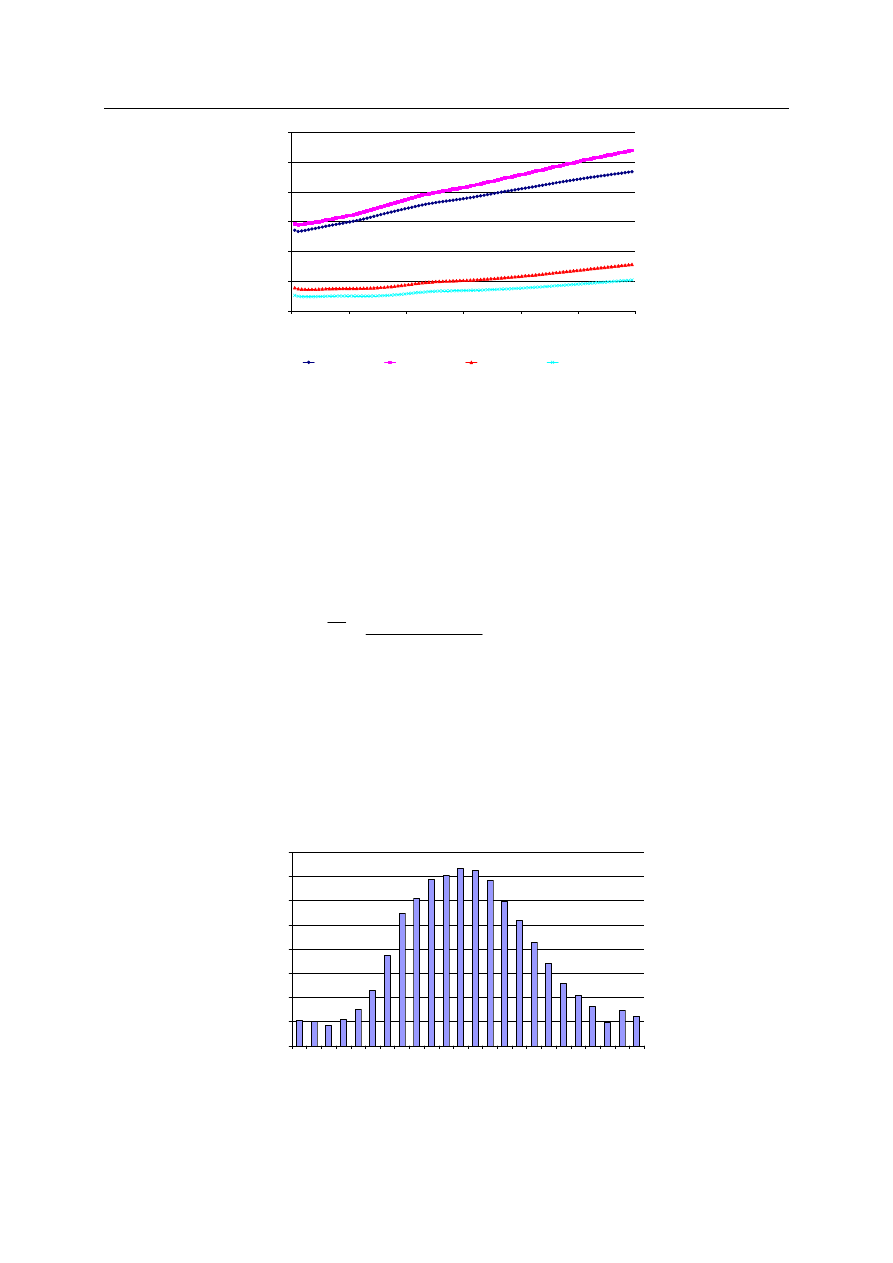
a następnie zsumowano uśrednione wartości chwilowe do okresów godzinowych, uzyskując
poniższy rozkład:

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Godzina

S

tr

u

m

ie

ń

w

o

d

y

[

k

g

H

2

O

/m

2

*h

]

Rys.6. Policzony rozkład strumienia wody odprowadzanej z osadów w ciągu doby.

18

K. B

ADYDA

,

P.

K

RAWCZYK

Wyznaczony w wyniku modelowania jednostkowy, dobowy strumień odprowadzanej
z osadów wody wyniósł:

d

m

O

kgH

W

i

⋅

=

2

2

73

,

8

Pomierzony w rzeczywistości, w suszarni w Skarżysku Kamiennej, średni dobowy strumień
odprowadzanej z osadów wody dla okresu suszenia czerwcowego wyniósł 8,3 kgH

2

O/m

2

d.

5. PODSUMOWANIE I WNIOSKI

Wydaje się, że uzyskana zgodność wyników modelowania z rzeczywistymi wynikami

pomiarowymi pozwala stwierdzić, iż podstawowe założenia modelu słonecznego suszenia
osadów zostały przyjęte w sposób prawidłowy.

Tym samym opracowany model może być wykorzystany w następnym kroku do

optymalizacji konfiguracji słonecznych suszarni osadów ściekowych oraz harmonogramu ich
pracy, również z instalacjami wykorzystania ciepła zewnętrznego.

LITERATURA

1. Strumiłło Cz.: Podstawy teorii i techniki suszenia. Warszawa: WNT, 1983.,
2. Katsiris N., Koszeli-Katsiris A.: Bound water content of biological sludges in relation to

filtration and dewatering. “Water Res.” 1987, 21, p. 1319-1327.

3. Arlabosse P., Chavez S., Prevot C.: Drying of municipal sewage sludge: from a laboratory

scale batch indirect dryer to the paddle dryer. “Brazilian Journal of Chemical
Engineering” 2005, Vol. 22, No. 02, p. 227 – 232..

4. Dewil R., Baeyens J., Neyens

E.:

Fenton peroxidation improves the drying performance

of waste activated sludge. “Journal of Hazardous Materials” 2005, B117, p. 161–170.

5. Stolarek P., Ledakowicz S., Pakowski Z., Grębowski M.: Wyznaczanie dyfuzyjności

wody w osadzie ściekowym za pomocą termograwimetrii. „Przegląd Papierniczy” 2003,
nr 12, s. 745 – 748.

6. Brus J.H., Christensen J.R, Rasmusen H.: Anaerobic storage of activated sludge: effect on

conditioning and dewatering performance. “Water Sci Tech.” 1993, 28, p. 109-116.

7.

Krawczyk P., Szczygieł J., Szwarc W.: Technologia słonecznego suszenia osadów
ściekowych – realizacja projektu i wstępne doświadczenia eksploatacyjne. W: Materiały
konferencji „Zintegrowane, inteligentne systemy wykorzystania energii odnawialnej”.
Częstochowa – Podlesice 2005.

MODELING OF SOLAR DRY KINETICS OF SLUDGE IN

STANDARD DAY CONDITIONS

Summary. In article have been presented basic assumptions and equations of

mathematical model which describe sludge solar drying processes. Paper presents
also results obtained from discussed model in summer standard day conditions.