Ćwiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjności.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
1
Ćwiczenie
MC_12
Temat ćwiczenia:
Bezstykowy pomiar temperatury,
wyznaczanie współczynnika
emisyjności
Załącznik 1
Teoria
V_1.0
12.1.Teoria
Zjawiska fizyczne związane z działaniem kamery termograficznej
Każde ciało o temperaturze wyższej od zera bezwzględnego emituje promieniowanie
elektromagnetyczne (EM) przy czym zdolność emisji promieniowania zależy od jego temperatury oraz
właściwości fizycznych i chemicznych (głównie powierzchni).
Ponieważ promieniowanie cieplne jest rodzajem drgań elektromagnetycznych, podlega ono tym
samym co i one prawom ogólnym, tj. prawu odbicia, załamania, polaryzacji, pochłaniania itd.
Z całkowitej ilości energii promieniowania padającej na ciało, część ulega absorpcji (zostaje
pochłonięta), część zostaje odbita, część zaś przenika przez ciało.
Na podstawie bilansu energii zachodzi związek:
1
=
+
+
D
R
A
(1)
gdzie: A - absorpcyjność, R - refleksyjność, D - przepuszczalność (transmisyjność).
Wielkości te są bezwymiarowe, są one liczbami zawartymi w granicach 0
÷
1. Ściśle biorąc, powyższy
bilans wielkości A, R, D może zależeć od długości fali λ.
Ze względu na wymienione współczynniki rozróżnia się następujące przypadki rzeczywistych ciał:
• A
λ
= A = 1 - ciało doskonale czarne,
• A
λ
= A < 1 - ciało szare,
• R
λ
= R = 1 - ciało białe ( zwierciadlane),
• D
λ
= D = 1 - ciało diatermiczne (przezroczyste),
• D
λ
= D = 0 - ciało adiatermiczne (nieprzezroczyste),
(dolny indeks λ oznacza zależność danej wielkości od długości fali).
Jeżeli wymienione właściwości zależą od λ mówimy o wielkościach selektywnych lub spektralnych, to
znaczy istotnych dla pewnych długości lub przedziałów długości fal. Ważną grupę stanowią ciała
szare
(np. materiały przegród budowlanych), dla których:
1
=
+ R
A
(2)
Wystarczy dla nich znać jedną wielkość, najczęściej A lub , A
λ
aby wyznaczyć drugą wielkość (tutaj -
refleksyjność R).
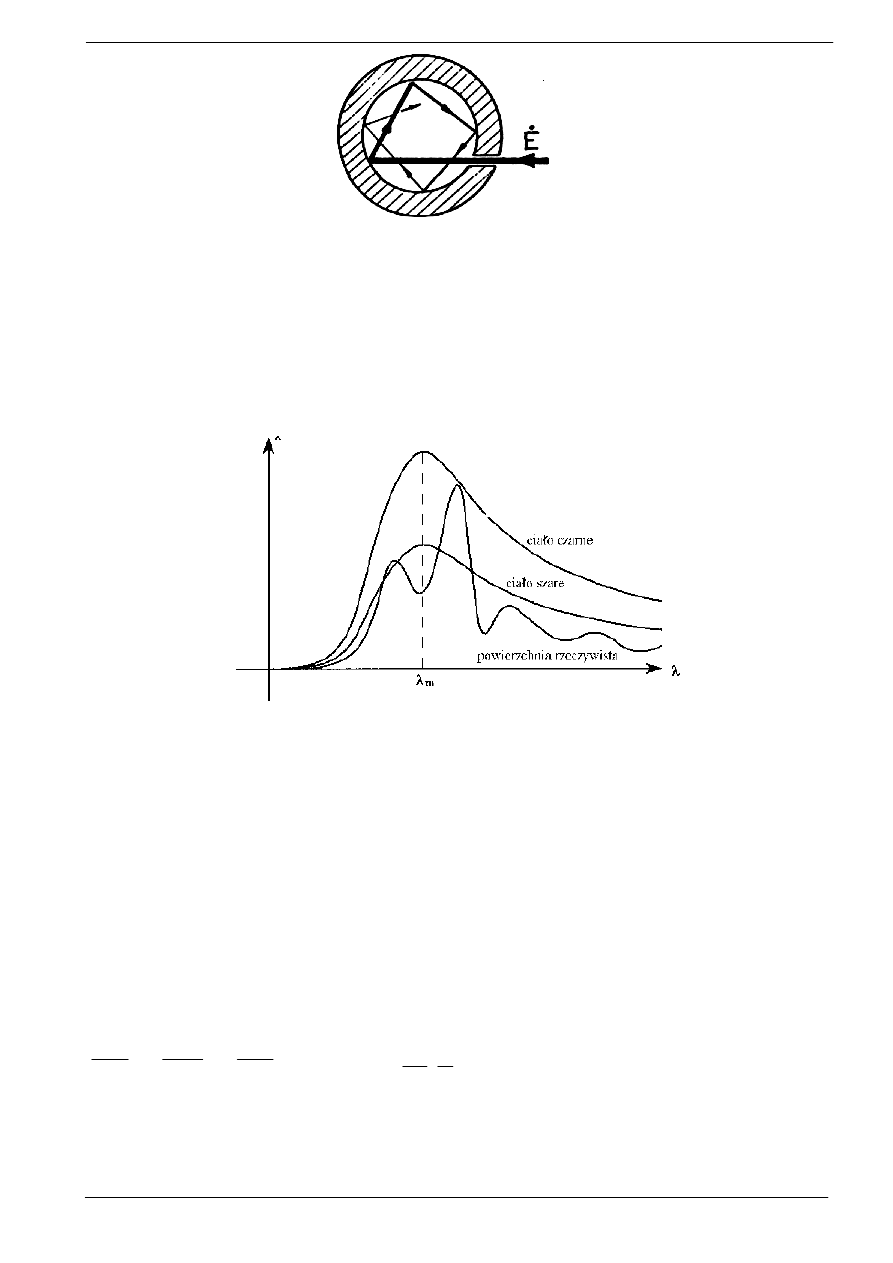
Pojęcie ciała doskonale czarnego wprowadził Kirchhoff. Modelem jest otwór znajdujący się w ściance
pustego wewnątrz ciała (rys.12.1). Ciało doskonale czarnych, białych i przezroczystych nie ma w
przyrodzie.
Ćwiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjności.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
2
Rys. 12.1. Model ciała doskonale czarnego
W odniesieniu do ciał rzeczywistych pojęcia te stanowią jednak bardzo wygodne punkty odniesienia,
jak pokazano na rysunku.12.2, gdzie widać, że ciało szare ma podobny przebieg egzytancji jak ciało
doskonale czarne. W przypadku ciała rzeczywistego przebieg ten może znacznie się różnić.
.
Rys.12.2. Przebieg egzytancji widmowej w funkcji długości fali promieniowania ciała doskonale
czarnego, szarego i rzeczywistego.
Polerowane powierzchnie metaliczne mają dużą zdolność odbijania promieniowania cieplnego, w
odróżnieniu od powierzchni szorstkich, dla których zdolność ta jest dużo mniejsza.
• Prawo Kirchhoffa:
Równowaga termiczna dla promieniowania znajdującego się w jakiejś przestrzeni o jednakowej
temperaturze ma charakter dynamiczny, to znaczy polega na równowadze pomiędzy emisją
(zdolnością promieniowania ciała E) a
absorpcją (zdolnością absorpcji A) promieniowania dla każdego
zakresu długości fali.
Dla układu kilku ciał o różnych absorpcyjnościach można to zapisać następująco:
)
(
T
E
A
E
A
E
A
E
c
i
i
=
=
=
2
2
1
1
,
⋅
m
1
m
W
2
(3)
gdzie ogólnie A
i
= A
i
( λ ,T)
oraz E
i
= E
i
( λ,T).
Słownie pierwsze sformułowanie prawa Kirchhoffa brzmi:
Ćwiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjności.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
3
"Stosunek emisji ciała do jego absorpcyjności jest zależny tylko od temperatury i dla danej
temperatury stały, niezależnie od innych właściwości ciała". Ze wzoru (3) wynika jednoznacznie, że
dla T = const stosunek zdolności promieniowania E do zdolności pochłaniania energii promieniowania
A
jest jednakowy dla wszystkich ciał i równa się zdolności promieniowania ciała doskonale czarnego
E
c
(dla którego A = 1). Ponieważ absorbowana energia jest największa dla ciała czarnego, to i jego
zdolność emisji jest największa.
W warunkach równowagi promieniowania cieplnego emisyjność ciała jest równa jego absorpcyjności
(dla tej samej temperatury, dla identycznej długości fali) stąd:
)
,
(
)
,
(
T
A
T
E
λ
λ
λ
λ
=
(4)
• Prawo Plancka:
Prawo to wyraża zależność między intensywnością promieniowania monochromatycznego, E
λ
emitowanego przez ciało doskonale czarne, jego temperaturą T i długością fali
λ
emitowanego
promieniowania:
1
2
5
1
−
=
−
T
C
e
C
E
λ
λ
λ
,
⋅
m
1
m
W
2
(5)
gdzie:C
1
= 2πh
2
0
c
= 3,7418·10
-16
[W·m
2
]oraz C
2
= hc
0
/k = 1,4388·10
-2
[m·K],
gdzie: h- stała Plancka; h= 6,6256·10
-34
[J· s ];c
0
= prędkość światła w próżni; c = 2,997925 ·10
8
s
m
są
wielkościami stałymi, zaś k oznacza stałą Boltzmanna (k = 1,3806·10
-23
K
J
).
Wielkość E
λ
jest nazywana również monochromatyczną gęstością emisji (promieniowania). Wzór (5)
przedstawia zależność E
λ
od λ i T, a więc widmo promieniowania ciała czarnego.
• Prawo Stefana – Boltzmanna:
Prawo to jest konsekwencją prawa Plancka i mówi o tym, że całkowita ilość energii
wypromieniowanej w ciągu sekundy przez jednostkę powierzchni ciała doskonale czarnego w
temperaturze T wynosi:
4
T
E
c
⋅
=
σ
2
m
W
, (6)
Wielkość
σ
nosi nazwę stałej promieniowania ciała czarnego i w obliczeniach technicznych
przyjmuje się
σ
= 5,67·10
-8
(
)
⋅
4
2
K
m
W
.
Prawo Stefana - Boltzmanna stosuje się do wyznaczania całkowitej energii promieniowania,
obejmującej wszystkie długości fal, emitowanych we wszystkich kierunkach. Prawo to zostało
opracowane dla ciała doskonale czarnego. Okazuje się jednak, że prawo to może także być
stosowanego dla ciał szarych. Intensywność ich promieniowania, dla T = const, jest dla wszystkich
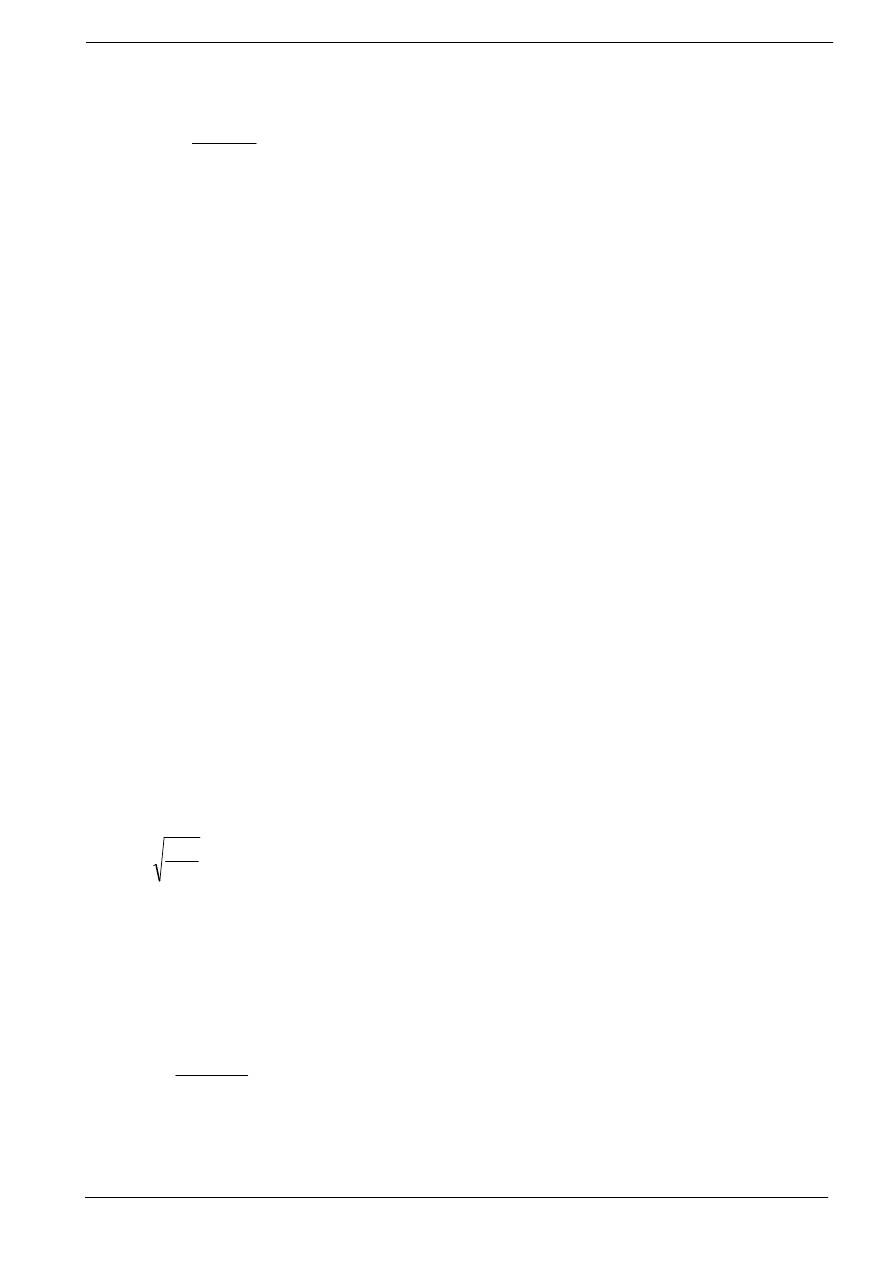
Ćwiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjności.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
4
długości fal jednakowo proporcjonalna do intensywności promieniowania ciała doskonale czarnego.
Wtedy:
4
T
E
c
⋅
=
σ
ε
(
)
⋅
4
2
K
m
W
, (7)
Współczynnik ε nosi nazwę względnej zdolności emisyjnej, stopnia czarności powierzchni ciała
szarego lub względnej emisyjności.
Zmienia się w granicach 0 ≤ ε ≤ 1. Dla wielu, ważnych technicznie
materiałów, wartości tego współczynnika można znaleźć w literaturze. Mając ε można łatwo obliczyć
energię promieniowania emitowaną przez ciało szare. Względna zdolność emisyjna dla ciał szarych
jest mniejsza od jedności, ε < 1, natomiast dla ciała doskonale czarnego ε = 1. Oznacza to, że ciało
czarne charakteryzuje się tym, że potrafi wysłać przy danej temperaturze maksymalną ilość energii.
Wszystkie pozostałe ciała tzw. ciała szare będą emitować ze swojej powierzchni zawsze mniejszą ilość
energii.
Emisyjność ciał zależy od wielu czynników, wśród których najważniejszymi są temperatura, długość
fali, kierunek emisji fali, rodzaj ciała (ze względu na własności elektryczne - dielektryk lub
przewodnik) i stan jego powierzchni. Największą emisyjność posiadają różne chropowate i matowe
powierzchnie, najmniejszą zaś polerowane srebro i złoto. Emisyjność powierzchni utlenionych jest
znacznie większa niż czystych metali. Bardzo interesującym materiałem jest szkło, które w pewnym
zakresie λ jest przeźroczyste. Szkło kwarcowe przepuszcza także promieniowanie nadfioletowe,
natomiast szkło zawierające siarczek arsenu przepuszcza również promieniowanie podczerwone.
W obliczeniach technicznych najczęściej przyjmuje się model ciała doskonale szarego, gdyż upraszcza
to znacznie obliczenia, a w szczególnych przypadkach trzeba jednak uwzględnić zależność
emisyjności od wymienionych czynników.
Emisyjność może być wyznaczona jeżeli dokonamy jednoczesnego pomiaru temperatury danego
obiektu metodą radiometryczną (np. kamera termograficzna) i stykową (np. termopara). Korzystamy
wtedy z następującego związku (bezpośrednia konsekwencja prawa Stefana Boltzmana):
4
95
.
0
ε
⋅
=
k
p
T
T
, [K] (8)
gdzie: T
p
i T
k
– temperatury tego samego punktu na badanej płaszczy
ź
nie wskazywane odpowiednio
przez termopar
ę
(T
p
) i kamer
ę
termograficzn
ą
(T
k
),
ε
- emisyjno
ść
badanej powierzchni (czynnik 0.95
wynika z ustawienia kamery na tak
ą
emisyjno
ść
).
• Prawo Wiena:
Pozwala na wyznaczenie długo
ś
ci fali dla której rozkład promieniowania osi
ą
ga maksimum.
3
2
965
,
4
C
C
T
m
=
=
λ
, [m·K] (9)
gdzie C
3
= 2,898·10
-3
[m·K ].
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
5
Równanie (9) nosi nazw
ę
prawa Wiena. Prawo Wiena pozwala mi
ę
dzy innymi na pomiar temperatury
odległych ciał. Mierzy si
ę
spektralny rozkład emisji i wyznacza maksimum, temperatura wynika z
równania (9).
Działanie i budowa kamery termograficznej
Z prawa Stefana – Boltzmanna wynika,
ż
e mierz
ą
c nat
ęż
enie emitowanych przez dane ciało fal EM
mierzymy po
ś
rednio jego temperatur
ę
. Pomiar temperatury powierzchni ciała polega na pomiarze
mocy tego promieniowania, a nast
ę
pnie przetworzeniu jego energii na impulsy elektryczne
wyskalowane w jednostkach temperatury.
Prekursorem pomiarów termograficznych był angielski astronom William Herschel, który w 1800
roku odkrył promieniowanie podczerwone. Przesuwaj
ą
c termometr w rozszczepionym za pomoc
ą
pryzmatu
ś
wietle słonecznym zaobserwował stały wzrost temperatury id
ą
c w kierunku barwy
czerwonej. Zaobserwował jednocze
ś
nie wzrost temperatury nawet wtedy, gdy termometr znajdował
si
ę
poza obszarem
ś
wiatła widzialnego.
Pierwsze detektory w kamerach termowizyjnych wymagały schłodzenia ich podczas pracy do
temperatury około -200°C. Ci
ą
głe doskonalenie technik termograficznego pomiaru temperatury
doprowadziły do skonstruowania nowych typów detektorów pracuj
ą
cych zadowalaj
ą
co ju
ż
w
temperaturze -70°C. Do chłodzenia tego typu detektora wystarczaj
ą
ce było zastosowanie chłodziarek
termoelektrycznych wykorzystuj
ą
cych efekt Peltiera. Dalsze prace doprowadziły do opracowania
konstrukcji współczesnych detektorów działaj
ą
cych zadowalaj
ą
co w temperaturze 30°C.
Rozwój detektorów promieniowania IR poci
ą
gn
ą
ł za sob
ą
rozwój metod generacji obrazu
termograficznego.
Współczesny detektor promieniowania IR ma posta
ć
dwuwymiarowej stałej matrycy składaj
ą
cej si
ę
z
240 x 320 pojedynczych mikro-detektorów. Obraz badanego obiektu padaj
ą
c przez obiektyw na
matryc
ę
powoduje wygenerowanie w ka
ż
dym pojedynczym mikrodetektorze sygnału elektrycznego
stosownego do nat
ęż
enia padaj
ą
cego promieniowania. Sygnały te zbierane s
ą
z du
żą
cz
ę
stotliwo
ś
ci
ą
przez układ odczytu i po obróbce elektronicznej słu
żą
do utworzenia obrazu termograficznego badanej
powierzchni. Obecnie w urz
ą
dzeniach termowizyjnych stosowane s
ą
fotodetektory.
Ci
ą
głe doskonalenie detektorów umo
ż
liwiło równie
ż
prowadzenie pomiarów za pomoc
ą
jednego
urz
ą
dzenia w zakresie temperatury od
–
40 °C do 2000 °C. Równocze
ś
nie z rozszerzaniem zakresu
pomiarowego temperatury poprawiana była czuło
ść
termiczna urz
ą
dze
ń
termograficznych.
Przy temperaturze 30 °C czuło
ść
termiczna współczesnych kamer o ogólnym przeznaczeniu jest na
poziomie 0,08 do 0,1 K. Parametr ten informuje o tym, jak
ą
minimaln
ą
ró
ż
nic
ę
, temperatury jest w
stanie wykry
ć
detektor kamery.
Zasada działania kamery termowizyjnej
Termograficzne metody bada
ń
, w przeciwie
ń
stwie do metod konwencjonalnych, pozwalaj
ą
na
uzyskanie dwuwymiarowego rozkładu temperatur powierzchni badanego obiektu. Badania
termograficzne cechuje, bezinwazyjno
ść
, co oznacza,
ż
e układ detekcyjny urz
ą
dzenia nie
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
6
oddziaływuje na badany obiekt, termografy mog
ą
znajdowa
ć
si
ę
w znacznej odległo
ś
ci od badanego
ciała. Do zalet tej metody nale
ż
y zaliczy
ć
,
ż
e pomiary dokonywane s
ą
w czasie rzeczywistym.
Podstawowymi elementami składowymi kamery termowizyjnej s
ą
:
• cz
ęść
optyczna,
• detektor,
• blok elektroniczny.
Cze
ść
optyczna składa si
ę
z układu soczewek, maj
ą
cych za zadanie skupienie promieniowania emi-
towanego z powierzchni badanego obiektu na detektorze. Materiał soczewek musi spełnia
ć
okre
ś
lone
wymagania, a mianowicie musi si
ę
charakteryzowa
ć
maksymaln
ą
transmisyjno
ś
ci
ą
przy minimalnych
warto
ś
ciach absorpcyjno
ś
ci i refleksyjno
ś
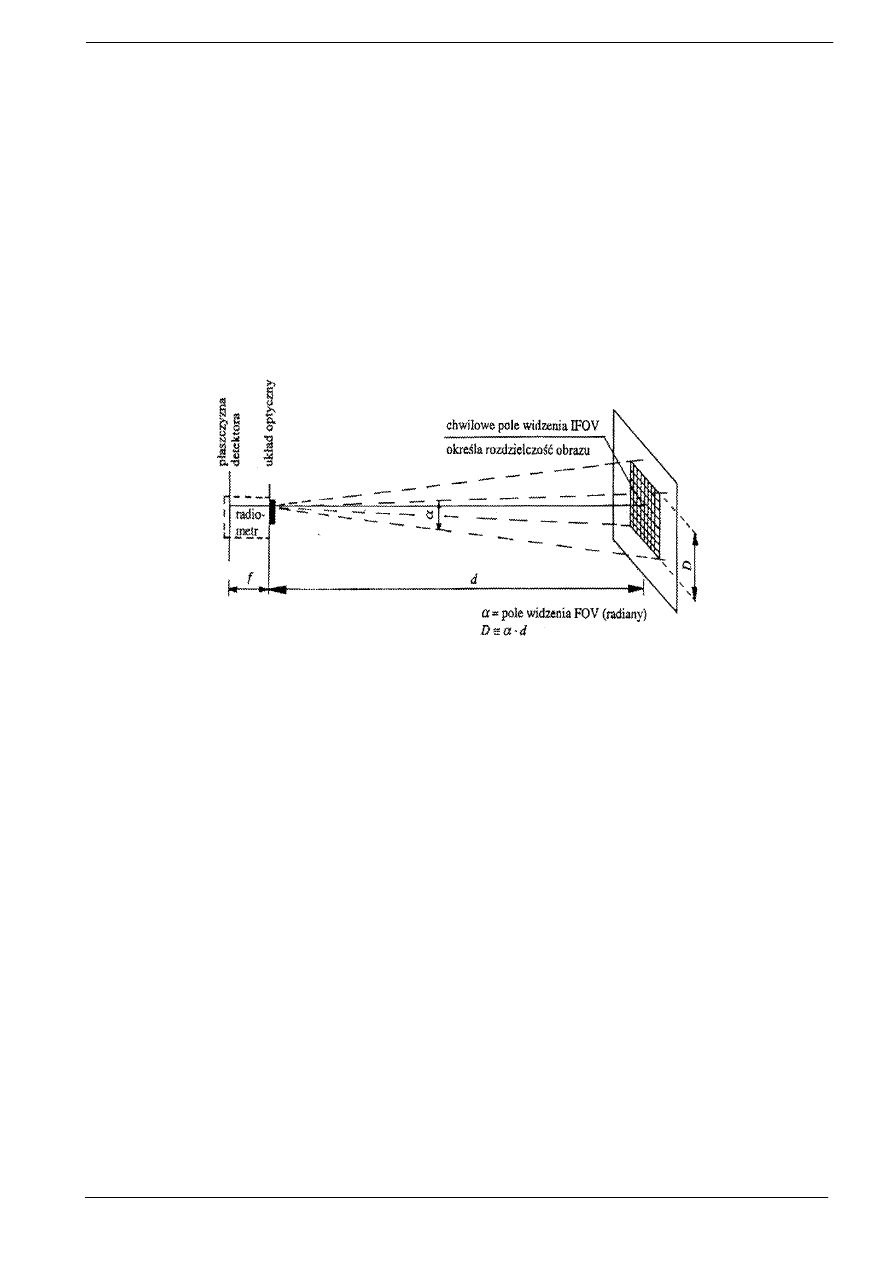
ci. Idea pomiaru przedstawiona jest na Rys12.3.
Rys.12.3
. Pole widzenia oraz chwilowe pole widzenia
Pole widzenia FOV (Field of View) jest definiowane jako zbiór tych punktów, znajduj
ą
cych si
ę
na
powierzchni badanego obiektu, z których emitowane fale elektromagnetyczne skupiane s
ą
przez układ
optyczny kamery. Z kolei chwilowe pole widzenia IFOV (Interim Field of View) jest to element
powierzchni obiektu, którego promieniowanie zostaje skupione na detektorze, dzi
ę
ki czemu istnieje
mo
ż
liwo
ść
utworzenia podstawowego elementu obrazu termalnego – piksela tego obrazu. Zmiana
IFOV odbywa si
ę
dzi
ę
ki układowi skanuj
ą
cemu (układ ruchomych zwierciadeł) powoduj
ą
cemu,
ż
e w
danej chwili jest badane kolejne chwilowe pole widzenia
Detektory skanuj
ą
ce ukazuj
ą
ró
ż
nice mocy promieniowania odbieranego z poszczególnych punktów
powierzchni obiektu bada
ń
, w wyniku, czego obraz termalny jest dwuwymiarowym rozkładem
temperatury powierzchni tego obiektu. Rozmiar chwilowego pola widzenia IFOV radiometru
skanuj
ą
cego nazywany jest czasem rozdzielczo
ś
ci
ą
jego obrazu.
Istniej
ą
równie
ż
przyrz
ą
dy w których układ skanuj
ą
cy jest zast
ą
piony przez matryc
ę
detektorów, z
której ka
ż
dy detektor odbiera promieniowanie z przypisanego sobie elementu chwilowego pola
widzenia.
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
7
Detektory mo
ż
emy podzieli
ć
na dwie zasadnicze grupy, mianowicie detektory termiczne i fotonowe.
O detektorach termicznych mówimy, gdy odbierane promieniowanie wywołuje zmiany termiczne
wraz, z którymi nast
ę
puje mierzalna zmiana jakiej
ś
charakterystycznej własno
ś
ci tych detektorów np.
oporno
ś
ci. Detektory fotonowe reaguj
ą
bezpo
ś
rednio na fotony promieniowania, które wzbudzaj
ą
elektrony detektora podczas wewn
ę
trznego procesu fotoelektrycznego.
Mianem czuło
ś
ci temperaturowej okre
ś
la si
ę
najmniejsz
ą
ró
ż
nic
ę
temperatur, obiektu powoduj
ą
c
ą
emisj
ę
promieniowania wywołuj
ą
c
ą
sygnał wyj
ś
ciowy detektora równy jego szumowi.
Przepływ ciepła przez przegrod
ę
Przepływ ciepła, zwany równie
ż
wymian
ą
ciepła jest zjawiskiem wyst
ę
puj
ą
cym powszechnie w
przyrodzie, zachodzi wsz
ę
dzie tam, gdzie wyst
ę
puj
ą
ró
ż
nice temperatury. Z punktu widzenia
fizycznych mechanizmów wyró
ż
nia si
ę
trzy sposoby przepływu ciepła:
przewodzenie, konwekcję i
promieniowanie cieplne.
Przewodzenie ciepła.
Ilo
ść
przewodzonego ciepła (w jednostce czasu i przez pole przekroju
poprzecznego normalne do kierunku rozchodzenia si
ę
ciepła) q jest proporcjonalna do spadku
temperatury T,. Mo
ż
na to zapisa
ć
nast
ę
puj
ą
co:
T
grad
q
⋅
−
=
λ
⋅
s
m
J
1
2
(10)
Równanie to nosi nazw
ę
prawa Fouriera, za
ś
współczynnik proporcjonalno
ś
ci
λ
b
ę
d
ą
cy wła
ś
ciwo
ś
ci
ą
fizyczn
ą
ciała nazywamy współczynnikiem przewodzenia ciepła, niekiedy wprost – przewodno
ś
ci
ą
ciepln
ą
– uwaga: nie myli
ć
z długo
ś
ci
ą
fali z równa
ń
1-9 , który mo
ż
e by
ć
zale
ż
ny od temperatury T
(ewentualnie tak
ż
e od ci
ś
nienia). Znak minus w równaniu (10) okre
ś
la kierunek przepływu ciepła –
przeciwny do gradientu temperatury. Wymiar współczynnika
λ
natomiast wynika z równania (10) i
wynosi: [
λ
] = [W/(m K)].
Cech
ą
szczególn
ą
przewodzenia jest przekazywanie energii (ciepła) wewn
ą
trz ciała stałego (lub płynu)
bez ruchu makroskopowego cz
ą
stek tego ciała. Przewodno
ść
cieplna ró
ż
nych ciał, czyli w istocie
zdolno
ść
przekazywania energii wewn
ę
trznej, której miar
ą
jest współczynnik
λ
, nie jest wielko
ś
ci
ą
stał
ą
. Zale
ż
y ona od rodzaju ciała, jego struktury, g
ę
sto
ś
ci, ci
ś
nienia, temperatury, niekiedy od
wilgotno
ś
ci a tak
ż
e od innych czynników.
Współczynnik przewodzenia ciepła dla gazów, przy umiarkowanych ci
ś
nieniach, le
ż
y w granicach od
0,005 do 0,6 [W/(m·K)]. Dla cieczy współczynnik -
λ
na ogół nie przekracza granic od 0,07 do 0,7
W/(m·K) (najwy
ż
sze warto
ś
ci ma woda). Stosunkowo niskie warto
ś
ci
λ
, dla płynów, z wyj
ą
tkiem
ciekłych metali, wynikaj
ą
z mechanizmu przewodzenia ciepła, który polega na zdarzeniach
chaotycznie poruszaj
ą
cych si
ę
cz
ą
stek oraz ich dyfuzji. Zgodnie z teori
ą
kinetyczn
ą
gazów
współczynnik przewodzenia ciepła jest proporcjonalny do
ś
redniej pr
ę
dko
ś
ci cz
ą
stek i do
ś
redniej
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
8
drogi swobodnej pomi
ę
dzy kolejnymi zderzeniami, z tego powodu
λ
z reguły zwi
ę
ksza si
ę
ze
wzrostem temperatury.
Ciekłe metale niskotopliwe wykazuj
ą
współczynnik
λ
od ok. 8 [W/(m·K)] (rt
ęć
dla T= 10°C) do ok. 80
[W/(m·K)] np. ciekły sód dla T= 204°C.
W ciałach stałych wyst
ę
puj
ą
dwa zasadnicze mechanizmy przewodzenia ciepła: ruch swobodnych
elektronów, które zachowuj
ą
si
ę
jak jednoatomowy gaz doskonały oraz drgania atomów w sieci
krystalicznej wokół ich stanów równowagi. W czystych metalach decyduje ruch elektronów i dlatego
najwi
ę
ksz
ą
przewodno
ść
ciepln
ą
wykazuj
ą
najlepsze przewodniki elektryczno
ś
ci: srebro -
λ
= 420
[W/(m·K)] i mied
ź
-
λ
= 395 [W/(m·K)] (dla T= 20°C). Ze wzrostem temperatury współczynnik
λ
,
czystych metali, z wyj
ą
tkiem aluminium, spada. Najwi
ę
ksze warto
ś
ci przewodno
ś
ci cieplnej
obserwuje si
ę
dla kryształów czystych metali w pobli
ż
u temperatury zera bezwzgl
ę
dnego,
współczynnik
λ
, przekracza wówczas 10 000 [W/(m·K)].
W dielektrykach, gdzie decyduj
ą
drgania atomów, współczynnik przewodzenia ciepła jest znacznie
ni
ż
szy, np. dla materiałów budowlanych zawarty jest w granicach od 0,02 [W/(m·K)] do ok. 3,0
[W/(m·K)]. Materiały o najmniejszej przewodno
ś
ci cieplnej (
λ
< 0,25 [W/(m·K)] u
ż
ywane s
ą
w
charakterze izolacji cieplnej.
Konwekcja
charakteryzuje si
ę
tym,
ż
e wyst
ę
puje równocze
ś
nie ruch makroskopowy cz
ą
stek o
ś
rodka.
Z ruchem ciepła przez konwekcj
ę
mamy do czynienia wówczas, gdy w kierunku strumienia ciepła,
tzn. w kierunku gradientu temperatury, wyst
ę
puje makroskopowe przemieszczenie si
ę
cz
ą
steczek tego
płynu, w którym ciepło jest przenoszone. Poniewa
ż
ten rodzaj ruchu ciepła jest charakterystyczny dla
cieczy i gazów, mo
ż
na wi
ę
c powiedzie
ć
,
ż
e ruch ciepła przez konwekcj
ę
jest takim przypadkiem
przenoszenia energii wewn
ą
trz płynu, w którym ruch cz
ą
steczek płynu wywiera istotny wpływ na
wielko
ść
strumienia ciepła i w rezultacie na pole temperatur.
Konwekcja
odnosi si
ę
tak
ż
e do takiego przypadku przenoszenia energii, który wyst
ę
puje pomi
ę
dzy
powierzchni
ą
przegrody i pozostaj
ą
cym z ni
ą
w kontakcie ruchomym płynem, gdy maj
ą
one
(przegroda i płyn) ró
ż
ne temperatury. Podstawowe prawo dla konwekcji zostało sformułowane jeszcze
przez Newtona, we współczesnym zapisie ma ono posta
ć
równania:
)
(
si
i
T
T
q
−
⋅
=
α
, [W/m
2
] (11)
gdzie
α
jest współczynnikiem wnikania lub przejmowania ciepła [W/m
2
]
K
⋅
, T
si
-
temperatur
ą
ś
cianki,
a T
i
- temperatur
ą
płynu (np. powietrza). Wyznaczenie tego współczynnika jest jednym z
najtrudniejszych zagadnie
ń
teorii wymiany ciepła.
Trzeci
ą
postaci
ą
przepływu ciepła jest
promieniowanie.
Prawa promieniowania opisano dokładniej
powy
ż
ej. W prawie wszystkich napotykanych praktycznych przypadkach wyst
ę
puj
ą
cy przepływ ciepła
jest z reguły sum
ą
wszystkich trzech form przepływu ciepła. Z drugiej strony analiza ka
ż
dego procesu
przepływu ciepła wymaga drobiazgowego rozdzielenia go na powy
ż
sze formy składowe, opisywane
odr
ę
bnymi prawami fizycznymi.
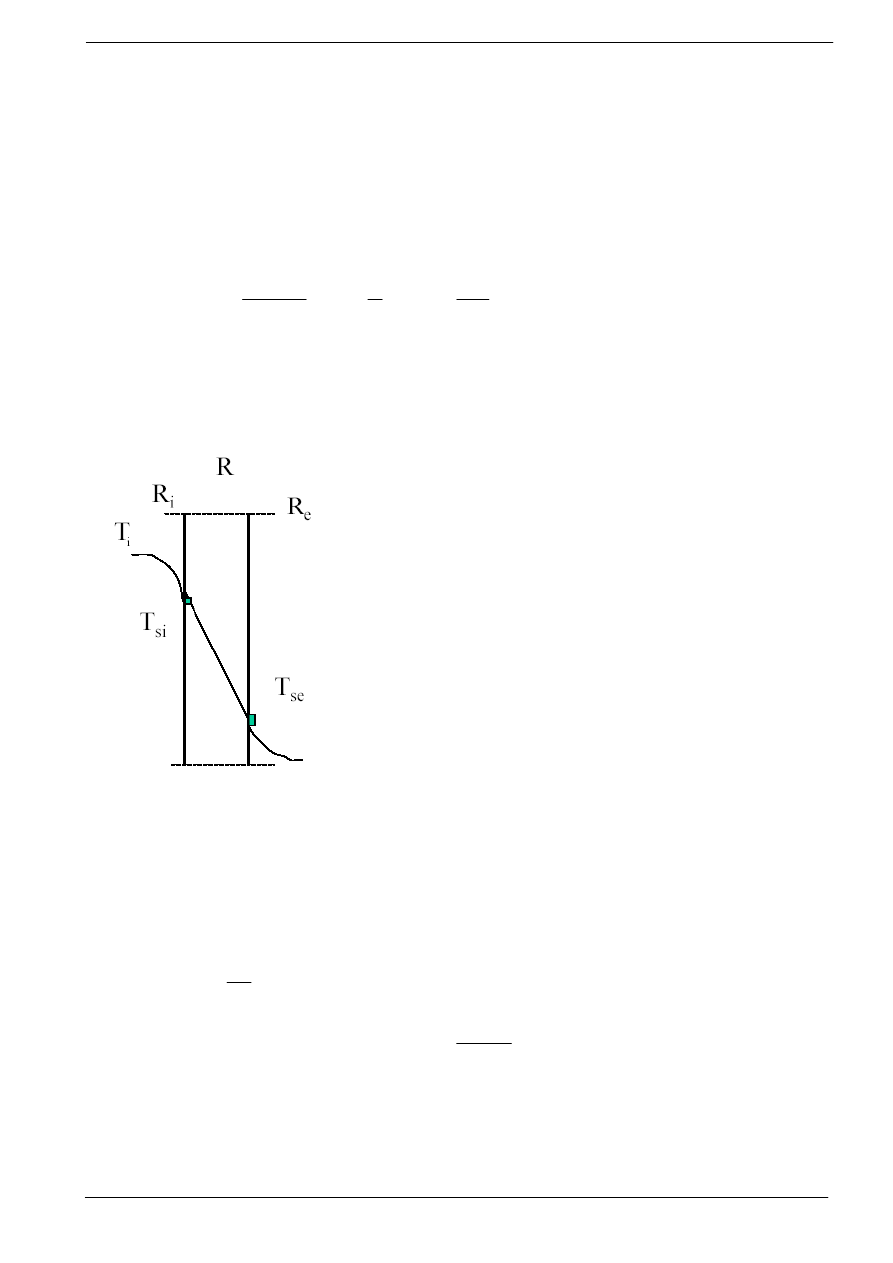
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
9
Je
ż
eli przepływ ciepła zachodzi w obiekcie całkowicie izolowanym od otoczenia i innych obiektów, to
z upływem czasu mi
ę
dzy poszczególnymi cz
ęś
ciami tego obiektu ustala si
ę
równowaga cieplna, a
przepływ ciepła ustaje. Warunkiem takiego stanu jest brak jakichkolwiek ró
ż
nic temperatur. Aby w
takim obiekcie zaistniał przepływ ciepła, musi w nim wyst
ą
pi
ć
jego
ź
ródło powoduj
ą
ce ró
ż
nice
temperatur.
Ź
ródłem ciepła w rzeczywisto
ś
ci jest miejsce lub urz
ą
dzenie, w którym inne formy energii
(elektryczna, mechaniczna lub chemiczna) zostaj
ą
zamienione w ciepło (energi
ę
jakiego
ś
zbioru
molekuł), które z tego miejsca przepływa do innych punktów obiekt.
Je
ż
eli
4
T
E
c
⋅
=
σ
ε
(
)
⋅
4
2
K
m
W
(7) to
A
Q
=ε⋅σ⋅T
4
( )
2
m
W
(12)
Ruch ciepła mi
ę
dzy dwoma o
ś
rodkami gazowymi lub ciekłymi rozdzielonymi przegrod
ą
z ciała
stałego nazywamy
przenikaniem ciepła
.
Rys. 12.4
. Przepływ ciepła przez przegrod
ę
budowlana
gdzie:
R
i,,
R
e -
opory przejmowania ciepła przez przy
ś
cienne
strugi powietrza wewn
ą
trz R
i
i na zewn
ą
trz R
e
pomieszczenia
R-
opór cieplny warstwy przegrody (
ś
ciany),
Ti, Te
- to temperatury powietrza wewn
ą
trz i na zewn
ą
trz
pomieszczenia,
Tsi, Tse
- temperatury przegrody wewn
ę
trznej i zewn
ę
trznej
Cz
ę
stym przypadkiem jest kontakt cieplny dwóch płynów o temperaturach T
i
i T
a
za po
ś
rednictwem
przegrody (
ś
cianki) o okre
ś
lonych własno
ś
ciach (kształt, rozmiary, wła
ś
ciwo
ś
ci fizyczne itp.).
Wówczas stosuje si
ę
równanie Pecleta:
)
(
e
i
T
T
U
q
−
⋅
=
,
2
m
W
(13)
w którym
współczynnik przenikania
ciepła U
(
)
⋅ K
m
W
2
.ujmuje wszystkie wymienione zjawiska.
Zale
ż
nie od charakteru urz
ą
dzenia celem mo
ż
e by
ć
zmniejszenie tego współczynnika (zapobiegnie
stratom ciepła przez stosowanie izolacji cieplnej) lub jego zwi
ę
kszenie (np. w wymiennikach ciepła).
T
e
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
10
Na rysunku 12.4. przedstawiona jest sytuacja przegrody budowlanej (
ś
ciany). W celu obliczenia
współczynnika U nale
ż
y wyznaczy
ć
opory ciepła zwi
ą
zane ze wszystkimi opisywanymi powy
ż
ej
mechanizmami przekazywania ciepła. Wyró
ż
niamy tutaj:
• opory przejmowania ciepła przez przy
ś
cienne strugi powietrza (zarówno wewn
ą
trz R
i-
jak i na
zewn
ą
trz R
e
pomieszczenia) scharakteryzowane odpowiednio przez wielko
ś
ci R
i-
i R
e
,
(
)
⋅
W
K
m
2
• opór cieplny warstwy przegrody (
ś
ciany), scharakteryzowany przez R
(
)
⋅
W
K
m
2
Zgodnie z rysunkiem 12.4. Ti, Ta- to temperatury powietrza wewn
ą
trz i na zewn
ą
trz pomieszczenia,
Tsi, Tse
- temperatury przegrody wewn
ę
trznej i zewn
ę
trznej. Współczynnik U dany jest wtedy
wzorem:
e
i
R
R
R
U
+
+
=
1
,
(
)
⋅ K
m
W
2
(14)
Bardzo du
ż
y problem (zgodnie z powiedzianym wcze
ś
niej) sprawia okre
ś
lenie współczynników R
i
i
R
e
. W ogólno
ś
ci zale
żą
one od wielu czynników: ró
ż
nicy temperatur pomi
ę
dzy płynem a
ś
ciank
ą
,
wielko
ś
ci i struktury opływanej powierzchni, pr
ę
dko
ś
ci wiatru itp. Normy budowlane rozwi
ą
zuj
ą
ten
problem narzucaj
ą
c konkretne warto
ś
ci R
i
= 0.13 [(m
2
K)/W] i R
e
=0.04 [(m
2
K)/W] jako u
ś
rednione,
najcz
ęś
ciej wyst
ę
puj
ą
ce w typowych sytuacjach (dla R
e
podawana jest tabelaryczna zale
ż
no
ść
od
pr
ę
dko
ś
ci wiatru).
Współczynniki te zwi
ą
zane s
ą
z współczynnikiem wnikania (lub przejmowania ciepła)
α
zdefiniowanym w prawie Newtona , zgodnie z nast
ę
puj
ą
cym wzorem:
⋅
α
=
⋅
α
=
W
K
m
1
R
W
K
m
;
1
R
2
e
e
2
i
i
, (15)
gdzie:
α
i
,
α
e
to odpowiednio współczynnikiem wnikania ciepła do wewn
ę
trznej
α
i
i z zewn
ę
trznej ,
α
e
warstwy przegrody ; α[W/m
2
K] (11),
Wielko
ść
R charakteryzuj
ą
ca opór cieplny materiału
ś
ciany dana jest wzorem:
λ
d
R =
,
⋅
W
K
m
2
(16)
gdzie:
λ
–
współczynnik przewodzenia ciepła (zob. równanie 10)[ W/(m K)],
d
– grubo
ść
przegrody[ m].
Materiały budowlane s
ą
przewa
ż
nie porowate, przy czym pory wypełnione powietrzem lub innym
gazem mog
ę
spełnia
ć
rol
ę
izolatora, pod warunkiem,
ż
e nie s
ą
zbyt du
ż
e i
ż
e nie wyst
ę
puje w nich
konwekcja. Z tego powodu im mniejsza g
ę
sto
ść
obj
ę
to
ś
ciowa (stosunek masy do obj
ę
to
ś
ci razem z
porami), tym przewodno
ść
cieplna materiału jest mniejsza. Efekt ten zanika przy wysokich
temperaturach (np. w piecach przemysłowych), gdy
ż
niweluje go cz
ęś
ciowo promieniowanie cieplne.
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
11
Istotnym czynnikiem wpływaj
ą
cym na przewodno
ść
ciepln
ą
materiałów porowatych jest ich
wilgotno
ść
. Przewodno
ść
cieplna materiału wilgotnego mo
ż
e by
ć
znacznie wi
ę
ksza ni
ż
materiału
suchego lub wody, na przykład dla:
• suchej cegły
λ
= 0,35 [W/(m·K)],
• wody
λ
= 0,60 [W/(m·K)],
• ale dla wilgotnej cegły
λ
≈
1,0 [W/(m·K)].
Dla materiałów włóknistych (np. drewno) lub krystalicznych charakterystyczna jest anizotropowo
ść
-
przewodno
ść
cieplna jest zale
ż
na od kierunku. To samo dotyczy niektórych materiałów budowlanych,
np. pustaków, płyt zbrojonych, cegły dziurawki itp.
W obliczeniach technicznych najcz
ęś
ciej przyjmuje si
ę
z tablic lub wykresów stał
ą
, u
ś
rednion
ą
warto
ść
współczynnika
λ
, pami
ę
taj
ą
c o tym,
ż
e dane literaturowe maj
ą
tylko orientacyjny charakter.
Podsumowuj
ą
c, wszystkie ciała mo
ż
emy podzieli
ć
ze wzgl
ę
du na zdolno
ść
przewodzenia na trzy
grupy:
1.
Dobre przewodniki ciepła (metale). Współczynniki przewodzenia ciepła dla tych ciał zmieniaj
ą
si
ę
od kilkudziesi
ę
ciu do kilkuset [W/(m·K)]. Przewodnictwo cieplne metali maleje wraz ze
wzrostem temperatury.
2.
Ciała o
ś
rednim przewodnictwie cieplnym (materiały budowlane, ogniotrwałe i ciecze).
Warto
ś
ci liczbowe współczynników
λ
dla tych ciał zmieniaj
ą
si
ę
od 0,3 do kilkudziesi
ę
ciu
[W/(m·K)].
3.
Ciała o złym
przewodnictwie
cieplnym, dla których
λ
< 0,3 [W/(m·K)]. S
ą
to tzw. materiały
izolacyjne.
Badanie przenikania ciepła
Termograficzne badania temperatury budynków s
ą
przeprowadzane w celu okre
ś
lenia wielko
ś
ci oporu
cieplnego izolacji termicznej budynku. Za pomoc
ą
pomiarów termograficznych mo
ż
liwe jest
oszacowanie
tej wielko
ś
ci, na podstawie temperatury zewn
ę
trznej badanego obiektu. Pomiar
wykonuje si
ę
przyjmuj
ą
c stacjonarne warunki jednowymiarowego przewodzenia ciepła, oznacza to,
ż
e
wahania temperatur zewn
ę
trznych musz
ą
by
ć
minimalne. Na powierzchni zewn
ę
trznej
ś
ciany zakłada
si
ę
równo
ść
g
ę
sto
ś
ci strumieni ciepła q
e
= q
i
,
gdzie
:
współczynnik wnikania
α
[W/m
2
]
K
⋅
(11),
),
(
e
se
e
e
T
T
q
−
=
α
[W/m
2
]
(17)
jest strumieniem przenikaj
ą
cym z zewn
ę
trznej powierzchni
ś
ciany do otoczenia, a natomiast:
R
T
T
q
i
se
i
i
1
1
+
−
=
α
, [W/m
2
]
(18)
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
12
jest strumieniem przenikaj
ą
cym przez wewn
ę
trzn
ą
powierzchni
ę
przegrody.
St
ą
d wynika nast
ę
puj
ą
ca równo
ść
:
)
(
1
1
e
se
e
se
i
i
T
T
T
T
R
−
−
=
+
α
α
(19)
Korzystaj
ą
c z równa
ń
13-15 współczynnik przenikania ciepła U b
ę
dzie dany wzorem:
e
i
e
se
e
T
T
T
T
R
U
−
−
⋅
=
)
(
1
,
[W/(m
2
⋅K)]
(20)
lub:
e
i
si
i
i
T
T
T
T
R
U
−
−
⋅
=
)
(
1
, [W/(m
2
⋅K)] (21)
Wzór 20 stosujemy gdy pomiar termograficzny wykonujemy z zewn
ą
trz a wzór 21 gdy pomiar
wykonujemy od wewn
ą
trz pomieszczenia.
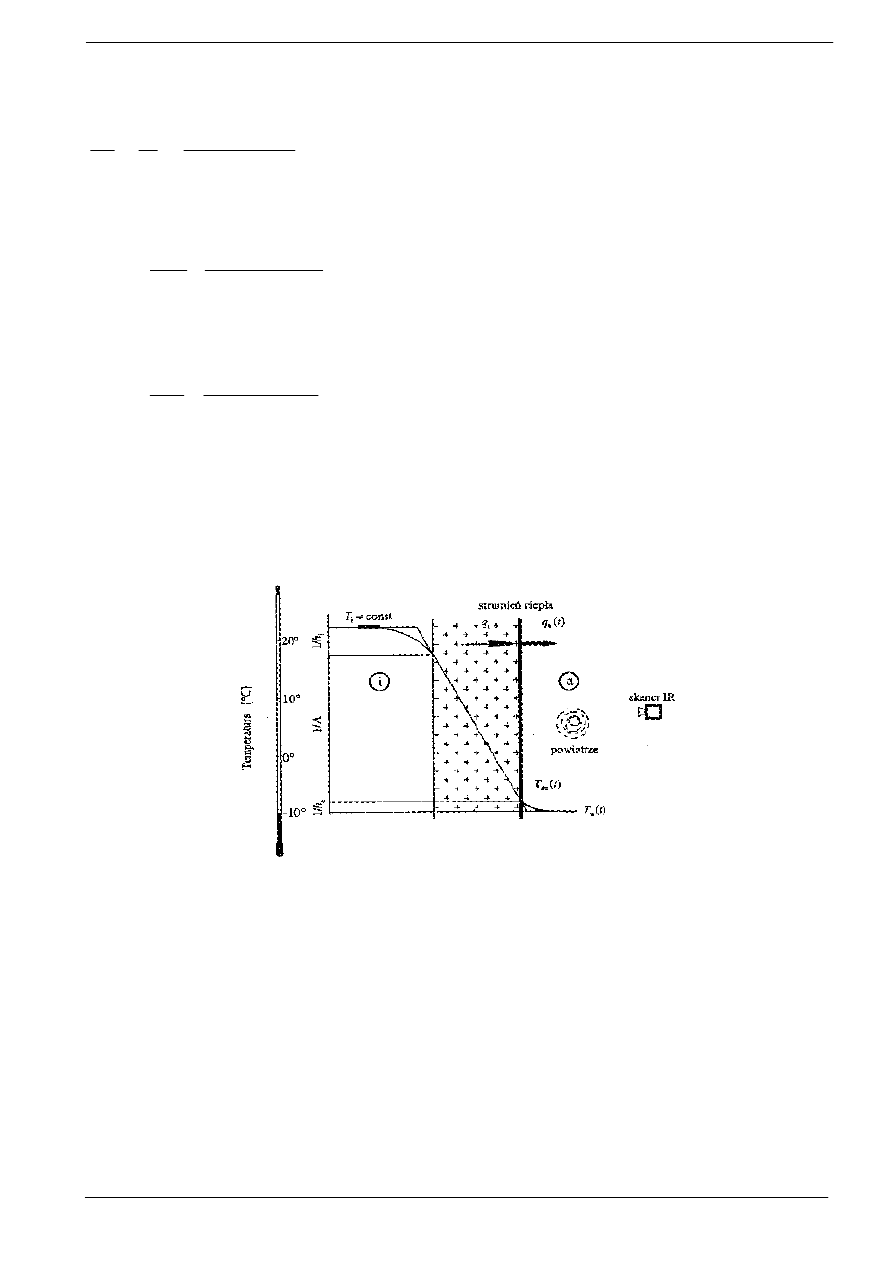
Schemat układu pomiarowego rozkładu temperatury na zewn
ę
trznej powierzchni
ś
ciany budynku jest
przedstawiony na Rys.12.5.
Rys.12.5
. Schemat pomiaru temperatury
ś
cian budynku.
Nale
ż
y zdawa
ć
sobie spraw
ę
,
ż
e ustalenie aktualnej temperatury obiektu obci
ąż
one jest bł
ę
dem
pomiarowym i bł
ę
dem okre
ś
lenia emisyjno
ś
ci. Nie da si
ę
całkowicie wyeliminowa
ć
działania
czynników takich jak promieniowanie dyfuzyjne z innych obiektów lub otoczenia oraz wpływu
warunków atmosferycznych. Mo
ż
liwo
ść
uniezale
ż
nienia wyników pomiarów od wpływu klimatu
zewn
ę
trznego, w tym opadów i wiatru, daje obrazowanie wykonywane z wn
ę
trza pomieszczenia.
Pole widzenia kamery termowizyjnej przy obrazowaniu wewn
ę
trznym obejmuje jednak niewielk
ą
powierzchni
ę
w przeciwie
ń
stwie do obrazowania zewn
ę
trznego, przy którym otrzymujemy termogram
obejmuj
ą
cy du
żą
płaszczyzn
ę
ś
cian budynku.
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
13
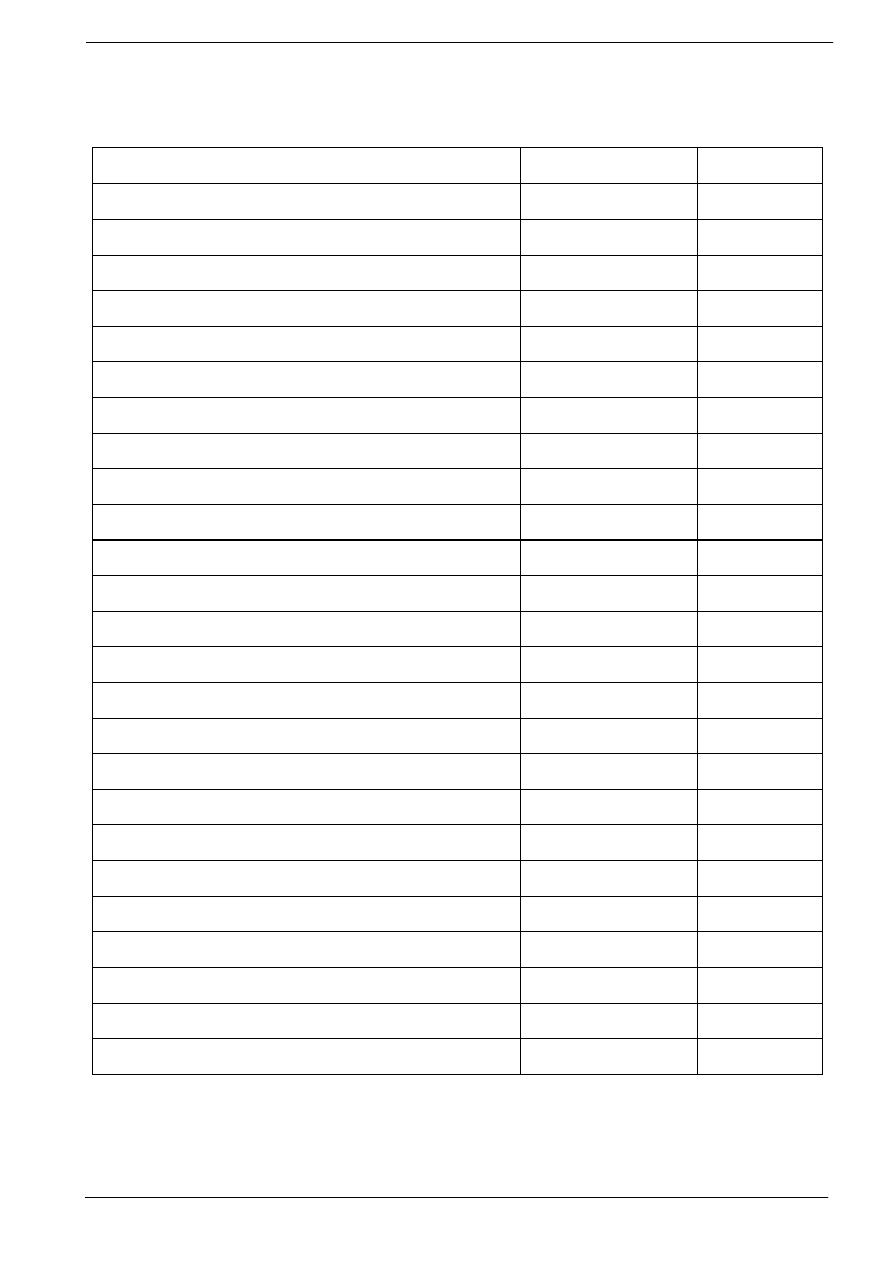
Tab.12.1
. Tabela współczynnika emisyjno
ś
ci ró
ż
nych materiałów.
Materiał
Temperatura [
0
C]
ε
ε
ε
ε
Aluminium polerowane
50 - 100
0.04 - 0.06
Aluminium z chropowat
ą
powierzchni
ą
20 - 50
0.06 - 0.07
Aluminium silnie utlenione
50 - 500
0.2 - 0.3
Azbestowa bibuła
40 - 400
0.93 - 0.95
Blacha cynkowa
50
0.20
Blacha ocynkowana błyszcz
ą
ca
30
0.23
Blacha stalowa niklowana
20
0.11
Blacha stalowa walcowana
50
0.56
Br
ą
z chropowaty
50 - 150
0.55
Br
ą
z polerowany
50
0.1
Chrom polerowany
50
0.1
Cegła czerwona porowata
20
0.88 - 0.93
Gips
20
0.8 - 0.9
Lakier emaliowany
20
0.85 - 0.95
Lód kryształ
-10
0.98
Mied
ź
polerowana
50 - 100
0.02
Mied
ź
utleniona
50
0.6 - 0.7
Papier biały
20
0.7 - 0.9
Papier czarny matowy
20
0.94
Sadza
20 - 400
0.95 - 0.97
Porcelana glazurowana
20
0.92
Srebro czyste polerowane
200
0.02
Warstwa wody na powierzchni metalowej
20
0.98
Woda (warstwa o grubo
ś
ci wi
ę
kszej ni
ż
0.1 mm)
0 - 100
0.95 - 0.98
Skóra ludzka
30
0.98 - 1.0
Ć
wiczenie MC_12. Bezstykowy pomiar temperatury, wyznaczanie współczynnika emisyjno
ś
ci.
Wydział Paliw i Energii Akademii Górniczo – Hutniczej w Krakowie
14
Tab.12.2.
Warto
ś
ci współczynników przewodzenia dla ró
ż
nych ciał stałych
Materiał
Współczynnik przewodzenia ciepła
λ
[W/(m·K)] w T=20
o
C
Współczynnik przewodzenia ciepła
λ
[W/(m·K)] w T=300
o
C
Aluminium
230
230
Beton
0,8-1,4
Wełna azbestowa
0,156
Ż
elazo
80
56
Drewno
0,14-0,21
Płyta gipsowa
0,42
Szkło
1,0-1,3
Granit
2,9
Wata szklana
0,042
0,097
Korek
0,036
Cegła
0,35-0,6
0,58
Piasek
0,33-1,13
Powietrze
0,023
Woda
0,6
0,065
Płyta
gipsowo – kartonowa
0,230
Pleksiglas
0,180
Papier
0,250
Tektura
0,140
Linoleum
0,186
Tynk lub gład
ź
cementowa
1,000
Tynk wapienny
0,700
Pianka poliuretanowa
0,035
Płyta z wełny
mineralnej
0,040
Styropian
0,040